4a. Кинетика. Теплота. Звук [Ричард Филлипс Фейнман] (fb2) читать онлайн

4a. Кинетика. Теплота. Звук

Глава 46 ХРАПОВИК И СОБАЧКА

§ 1. Как действует храповик

§ 2. Храповик как машина

§ 3. Обратимость в механике

§ 4. Необрати­мость

§ 5. Порядок и энтропия

§ 1. Как действует храповик

В этой главе мы поговорим о храповике и собачке — очень простом устройстве, позволяю­щем оси вращаться только в одном направлении. Возможность получать одностороннее вращение заслуживает глубокого и тщательного анализа, из него проистекут интересные заключения.

Вопросы, которые мы будем обсуждать, воз­никают при попытке найти с молекулярной или кинетической точки зрения простое объяснение тому, что существует предел работы, которая мо­жет быть получена от тепловой машины. Правда, мы уже знаем сущность доказательства Карно, но было бы приятно найти и элементарное его объяснение — такое, которое показало бы, что так физически на самом деле происходит. Суще­ствуют, конечно, сложные, покоящиеся на зако­нах Ньютона математические доказательства ограниченности количества работы, которое можно получить, когда тепло перетекает с од­ного места в другое; но очень непросто сделать эти доказательства элементарными. Короче говоря, мы не понимаем их, хотя можем просле­дить выкладки.

В доказательстве Карно то обстоятельство, что при переходе от одной температуры к дру­гой нельзя извлечь неограниченное количество тепла, следует из другой аксиомы: если все происходит при одной температуре, то тепло не может быть превращено в работу посредством циклического процесса. Поэтому первым делом попытаемся понять, хотя бы на одном элементар­ном примере, почему верно это более простое утверждение.

Попробуем придумать такое устройство, что­бы второй закон термодинамики нарушался, т. е. чтобы работу из теплового резервуара получали, а перепада температур не было. Пусть в сосуде находится газ при некоторой тем­пературе, а внутри имеется вертушка (фиг. 46.1), причем будем считать, что T₁=T₂=T.

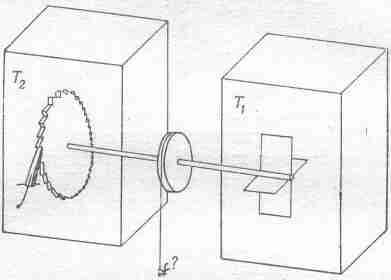Фиг. 46.1. Машина, состоящая из храповика и собачки.

От ударов молекул газа вертушка будет покачиваться. Нам остается лишь пристроить к другому концу оси колесико, которое может вертеться только в одну сторону,— храповичок с собачкой. Собачка пресечет попытки вертушки поворачиваться в одну сторону, а повороты в другую—разрешит. Колесико будет медленно поворачиваться; может быть, удастся даже подвесить на ниточку блошку, привязать нить к барабану, насаженному на ось, и поднять эту блошку!

Возможно ли это? По гипотезе Карно — нет. Но по первому впечатлению — очень даже возможно (если только мы верно рас­судили). Видно, надо посмотреть повнимательнее. И действи­тельно, если вдумаешься в работу храповика с собачкой, все оказывается не так просто.

Во-первых, хотя наш идеализированный храповик и пре­дельно прост, но есть еще собачка, а при ней положено быть пружинке. Проскочив очередной зубец, собачка должна воз­вратиться в прежнее положение, так что без пружинки не обой­тись.

Весьма существенно и другое свойство храповика и собачки (на рисунке его нельзя показать). Предположим, что части наше­го устройства идеально упруги. Когда собачка пройдет через ко­нец зубца и сработает пружинка, собачка ударится о колесико и начнет подпрыгивать. Если в это время произойдет очередная флуктуация, вертушка может повернуться и в другую сторону, так как зубец может проскользнуть под собачкой, когда та приподнята! Значит, для необратимости вертушки важно, чтобы было устройство, способное гасить прыжки собачки. Но при этом гашении энергия собачки перейдет к храповику и примет вид тепловой энергии. Выходит, что по мере вращения храповик будет все сильнее нагреваться. Для простоты пусть газ вокруг храповика уносит часть тепла. Во всяком случае, вместе с хра­повиком начнет нагреваться и сам газ. И что же, так будет про­должаться вечно? Нет! Собачка и храповик, сами обладая неко­торой температурой Т, подвержены также и броуновскому дви­жению. Это значит, что время от времени собачка случайно поднимается и проходит мимо зубца как раз в тот момент, когда броуновское движение вертушки пытается повернуть ее назад. И чем горячее предмет, тем чаще это бывает.

Вот отчего наш механизм не будет находиться в вечном дви­жении. Иногда от щелчков по крыльям вертушки собачка под­нимается и вертушка поворачивается. Но иногда, когда вертуш­ка стремится повернуть назад, собачка оказывается уже при­поднятой (из-за флуктуации движений этого конца оси) и храповик действительно поворачивает обратно. В итоге—чистый нуль. И совсем нетрудно показать, что, когда температура в обоих сосудах одинакова, в среднем вращения не будет. Будет, конечно, множество поворотов в ту или иную сторону, но чего мы хотим — одностороннего вращения,— тому не бывать.

Рассмотрим причину этого. Чтобы поднять собачку до верха зубца, надо проделать работу против натяжения пружинки. Назовем эту работу e; пусть q — угол между зубцами. Шанс, что система накопит достаточно энергии e, чтобы поднять собач­ку до края зубца, есть ехр(-e/kT). Но вероятность того, что собачка поднимется случайно, тоже есть ехр(-e/kT). Значит, сколько раз собачка случайно поднимется, давая храповику свободно повернуться назад, столько же раз окажется достаточ­но энергии, чтобы при прижатой собачке вертушка повернулась вперед. Выйдет равновесие, а не вращение.

§ 2. Храповик как машина

Пойдем дальше. Рассмотрим другой пример: температура вертушки T₁, а температура храповика Т₂; T₂меньше Т_{1. Т}ак как храповик холодный и флуктуации собачки сравнитель­но редки, ей теперь очень трудно раздобыть энергию e. Но из-за того, что вертушка горячая, она часто получает энергию e, и наше устройство начнет, как и задумано, вертеться в одну сторону.

Посмотрим-ка, удастся ли нам теперь поднимать грузы. Привяжем к барабану нить и привесим к ней грузик вроде нашей блошки. Пусть L будет момент, создаваемый грузом. Если мо­мент L не очень велик, наша машина груз поднимет, так как из-за броуновских флуктуации повороты в одну сторону веро­ятнее, чем в другую. Определим, какой вес мы сможем поднять, как быстро он будет подниматься и т. д.

Сперва рассмотрим движение вперед, для которого храповик и предназначен. Сколько энергии нужно занять у вертушки, чтобы продвинуться на шаг? Чтобы поднять собачку, нужна энер­гия e. Чтобы повернуть храповик на угол q против момента L, нужна энергия Lq. Всего нужно занять энергию e+Lq. Вероят­ность заполучить ее равна ехр[-(e+Lq)/kT₁. В действитель­ности дело не только в самой этой энергии, но и в том, сколько, раз в секунду она окажется в нашем распоряжении. Вероят­ность в секунду только пропорциональна ехр[-(e+Lq)/kT₁]; обозначим коэффициент пропорциональности 1/t (он в конце выкладок выпадет). После каждого шага вперед совершенная над грузом работа есть Lq. Энергия, взятая у вертушки, равна e+Lq. Энергией e наматывается нить, затем следует: щелк, щелк, клингенкланггеклунген..., и энергия переходит в тепло, Вся одолженная энергия идет на то, чтобы поднять блошку и собачку, которая потом падает и отдает тепло другой стороне (храповику).

Рассмотрим теперь случай обратного вращения. Что проис­ходит здесь? Чтобы храповик повернулся назад, надо лишь снабдить собачку такой энергией, чтоб ей хватило сил подняться и пропустить храповик. Эта энергия по-прежнему равна e. Вероятность (в пересчете на секунду) того, что собачка подни­мется на нужную высоту, теперь равна (1/t)ехр(-e/kT₂). (Множитель пропорциональности тот же, но в показателе стоит kT₂из-за того, что температура иная.) Когда это случается, т. е. зубчатка проскальзывает назад, работа уже высвобождается (высвободился один зубец, а вместе с ним и работа Lq). Энергия, взятая у системы храповик — собачка, есть e, а энергия, пере­данная газу на другом конце оси при температуре T₁, есть Lq+e. Это тоже легко понять. Положим, что собачка поднялась сама собой за счет флуктуации. Когда она упадет и пружинка ударит ее по зубцу, возникнет сила, стремящаяся повернуть зубчатку, ведь плоскость-то, о которую ударилась собачка, наклонная. Эта сила производит работу; то же можно сказать о весе грузика. Обе силы суммируются, и вся медленно высво­бождаемая энергия появляется в виде тепла на той стороне, где вертушка. (Конечно, так и должно быть по закону сохра­нения энергии, но мы обязаны осторожно продумать все на­сквозь!)

Мы замечаем, что все эти энергии в точности те же, что и раньше, только переставлены. Итак, смотря по тому, какое из отношений больше, грузик либо медленно поднимается, либо медленно опускается. Конечно, на самом деле он непрерывно ходит туда-сюда, покачивается, но мы говорим об усредненном поведении.

Положим, что при определенном весе вероятности окажутся равными. Тогда привесим к нити бесконечно легкий грузик. Весь груз медленно пойдет вниз, и машина будет совершать работу, энергия будет откачиваться от храповика и пересылаться вертушке. Если же убрать часть груза, неравновесность переки­нется на другую сторону. Груз поднимается, тепло отбирается от вертушки и поставляется шестерне. Мы попадаем в условия обратимого цикла Карно благодаря тому, что груз выбран как раз так, чтобы обе вероятности были равны. Это условие таково: (e+Lq)/T₁=e/T₂. Пусть машина медленно тянет груз вверх.

Таблица 46.1 · ОПЕРАТИВНАЯ СВОДКА ДЕЙСТВИЙ ХРАПОВИКА И СОБАЧКИ

Энергия Q_lотбирается от лопастей, а энергия Q₂доставляется шестерне, и эти энергии находятся в отношении (e+Lq)/e. Когда мы опускаем груз, то опять Q₁/Q₂=(e+Lq)/e. Итак (табл. 46.1), мы имеем

Q₁/Q₂=T₁/T₂. Далее, полученная работа относится к энергии, взятой у вер­тушки, как Lq к Lq+e, т. е. как (T₁-Т₂)/Т₁. Мы видим, что наше устройство, работая обратимо, ни за что не сможет высо­сать работы больше, чем позволяет это отношение. Это тот вывод, которого мы и ожидали на основе доказательства Карно, а од­новременно и главный результат этой лекции.

Однако мы можем использовать наше устройство, чтобы по­нять еще кое-какие явления, даже неравновесные, лежащие вне области применимости термодинамики.

Давайте подсчитаем теперь, как быстро наш односторонний механизм будет вращаться, если все его части одинаково нагре­ты, а к барабану подвешен грузик. Если мы потянем чересчур сильно, могут произойти любые неприятности. Собачка соскользнет вдоль храповика, пружинка лопнет или еще что-нибудь случится. Но предположим, мы тянем так осторожно, что все работает гладко. В этих условиях верен вышеприведен­ный анализ вероятностей поворота храповика вперед или назад, и нужно только учесть равенство температур. С каждым скач­ком валик поворачивается на угол 9, так что угловая скорость равна величине 9, помноженной на вероятность одного из этих скачков в секунду. Ось поворачивается вперед с вероятностью (1/t)ехр[-e+Lq)/kT], а назад она поворачивается с вероят­ностью (1/t)ехр(-e/kT). Угловая скорость равна

График зависимости w от L показан на фиг. 46.2.

Фиг. 46.2. Угловая скорость храповика как функция враща­тельного момента.

Мы видим, что, когда L положительно, результат один, когда отрицательно — совсем другой. Если L растет, будучи положительным, что бывает, когда мы хотим повернуть храповик назад, скорость вра­щения назад близка к постоянной величине. А когда L стано­вится отрицательным, w поистине «рвется вперед», так как у e показатель степени огромен! Таким образом, угловая скорость, вызываемая действием разных сил, весьма несимметрична. Пойти в одну сторону легко: мы получаем большую угловую скорость от маленькой силы. Идя в обратную сторону, мы можем прило­жить много усилий, а вал все же будет двигаться еле-еле.

Такое же положение возникает в электрическом, выпрямите­ле. Вместо силы там имеется электрическое поле, а взамен угловой скорости — сила тока. Для выпрямителя напряжение тоже не пропорционально сопротивлению, наблюдается та же несимметричность. Анализ, проделанный нами для механиче­ского выпрямителя, годится и для электрического. Вид полу­ченной выше формулы типичен для зависимости пропускной способности выпрямителя от напряжения.

Уберем теперь все грузики и обратимся к первоначальному механизму. Если бы Т₂было меньше Т₁, храповик вертелся бы вперед. Этому поверит любой. Но вот во что трудно поверить сразу, так это в обратное. Если T₂больше T₁, храповик вращает­ся назад! Динамический храповик с избытком теплоты внутри вертится назад, потому что собачка храповика отскакивает. Если собачка в какой-то момент находится на наклонной пло­скости, она толкает эту плоскость в сторону подъема. Но это происходит все время, ведь если случится, что собачка подни­мется достаточно высоко, чтобы проскочить край зубца, она окажется на новой наклонной плоскости. Словом, горячие храповик с собачкой идеально приспособлены для вращения в сторону, обратную той, в какую им первоначально предназна­чено было вертеться!

Как бы хитроумно мы ни сконструировали «однобокий» ме­ханизм, при равенстве температур он не захочет вертеться в одну сторону чаще, чем в другую. Когда мы смотрим на него, он может поворачиваться либо туда, либо сюда, но при продол­жительной работе ему никуда не уйти. Тот факт, что он не уйдет никуда, на самом деле фундаментальный, глубокий принцип; все в термодинамике покоится на нем.

§ 3. Обратимость в механике

Что же это за глубокий механический принцип, который утверждает, что при постоянстве температуры и достаточно про­должительной работе наше устройство не уйдет ни назад, ни вперед? Очевидно, мы получили фундаментальное утверждение о том, что нельзя придумать машину, которая, будучи пре­доставлена самой себе в течение долгого времени, охотней по­вернулась бы в какую-то одну определенную сторону. Попро­буем выяснить, как это вытекает из законов механики.

Законы механики действуют примерно так: сила есть масса на ускорение; сила, действующая на частицу, есть сложная функция положений всех прочих частиц. Бывает, что силы за­висят и от скорости, например в магнетизме, но не о них сейчас речь. Возьмем простой случай, скажем тяготение, когда силы определяются только расположением частиц. Положим, что мы решили нашу систему уравнений и получили для каждой части­цы определенную траекторию x(t). Для достаточно сложных систем и решения очень сложны; с течением времени возможно появление самых невероятных конфигураций. Если мы приду­маем любое, какое только нам придет в голову, расположение частиц и терпеливо подождем, то это расположение непременно наступит! Следя за решением в течение долгого времени, мы увидим, что оно как бы перепробует все, что возможно. В про­стейших устройствах это не обязательно, но в более или менее сложных системах с большим числом атомов такая вещь про­исходит.

Но решения способны и на большее. Решая уравнения дви­жения, мы можем получить некоторую функцию, скажем t+t²+t³. Мы утверждаем, что другим решением будет - t+t²-t³. Иными словами, если всюду в решение подставить -t вместо t, то мы получим еще одно решение того же уравнения. Это произойдет оттого, что при замене t на -t в первоначальном дифференциальном уравнении ничего не изменится: в нем при­сутствуют лишь вторые производные по времени. Значит, если наблюдается некоторое движение, то возможно и точно проти­воположное движение. К нашему замешательству, может ока­заться, когда мы следим за движением достаточно долго, что оно временами совершается в одну сторону, а временами — в обрат­ную. Одно направление ничем не привлекательней другого. Поэтому невозможно сконструировать машину, для которой после длительной работы одно направление окажется более вероятным, чем другое, если только машина достаточно сложна.

Можно, правда, изобрести машину, для которой это утверж­дение явным образом неверно. Взять, например, колесо, закру­тить его в пустом пространстве, и оно навсегда пойдет вертеться в одну сторону. Имеются поэтому некоторые условия, вроде сохранения момента вращения, из-за которых наши рассужде­ния нарушаются. Но это только означает, что наши доказатель­ства надо проделать поаккуратней. Надо, например, учесть, что вращательный момент забирают себе стенки или еще что-то, так что специальные законы сохранения перестают действовать. Тогда опять, если система достаточно сложна, наше доказатель­ство годится. Оно основано на обратимости законов механики.

Отдавая должное истории, мы хотели бы отметить устрой­ство, изобретенное Максвеллом, впервые разработавшим дина­мическую теорию газов. Он нарисовал такую картину: пусть имеются два сосуда с газом при одной и той же температуре. Между сосудами имеется маленькое отверстие. Возле него сидит небольшой чертик (конечно, это может быть и прибор!). В от­верстии есть дверца, чертик может ее открывать и закрывать. Он следит за молекулами, подлетающими слева. Как только он замечает быструю молекулу, он отворяет дверцу. Увидит мед­ленную — и дверцу на замок! Можно сделать его чертиком высшей квалификации, пристроив на затылок ему еще пару глаз, чтобы с молекулами в другом сосуде он поступал наобо­рот: пропускал налево медленные, а быстрые не выпускал. Вскоре левый сосуд остынет, а правый нагреется. Спраши­вается, будут ли нарушены идеи термодинамики существова­нием этакого чертика?

Оказывается, что если чертик конечного размера, то сам он вскоре так нагреется, что ничего не увидит. Простейшим чертиком явится, скажем, откидная дверца с пружинкой. Бы­строй молекуле хватает сил открыть дверцу и проскочить, а медленной не хватит, и она отлетит прочь. Но это опять-таки знакомая нам система храповик — собачка, только в другом виде; в конце концов механизм просто нагреется. Чертик не может не нагреться, если его теплоемкость не бесконечна. В нем, во всяком случае, имеется конечное число шестеренок и коле­сиков, так что он не сможет отделаться от излишка тепла, кото­рое приобретет, наблюдая молекулы. Вскоре он так начнет дрожать от броуновского движения, что не сможет сказать, что это там за молекулы, приближаются ли они, удаляются ли, словом, не сможет работать.

§ 4. Необратимость

Все ли законы физики обратимы? Конечно, нет! Попробуйте-ка, например, из яичницы слепить обратно яйцо! Или пустите фильм в обратную сторону — публика в зале тотчас же начнет смеяться. Необратимость — самая яркая черта всех событий.

Откуда же она появляется? Ведь ее нет в законах Ньютона. Если мы считаем, что любое явление может быть в конечном счете объяснено законами физики, и если также оказывается, что все уравнения обладают фантастическим свойством давать при t®-t другое решение, то ведь тогда обратимо любое явление. Но как же тогда получается, что в природе, в явлениях большого масштаба, все необратимо? Видимо, значит, есть какие-то законы, какие-то неизвестные нам, но важные уравне­ния, быть может, в электричестве, а может, в нейтринной фи­зике, для которых уже существенно, куда идет время.

Рассмотрим теперь этот вопрос. Один закон такого рода мы уже знаем — он утверждает, что энтропия только растет. Когда одно тело теплое, а другое холодное, тепло переходит от теплого к холодному. Это утверждение нам подошло бы. Но хорошо бы и этот закон понять с точки зрения механики. Нам уже удалось получить при помощи чисто механических соображений все следствия из постулата о том, что тепло не может течь в обрат­ную сторону; это помогло нам понять второй закон. Значит, не­обратимость из обратимых уравнений получать мы способны. Но использовали ли мы при этом только законы механики? Раз­беремся в этом глубже.

Так как речь зашла об энтропии, то нам придется найти ее микроскопическое описание. Когда мы говорим, что в чем-то (например, в газе) содержится определенное количество энер­гии, то мы можем обратиться к микроскопической картине этого явления и сказать, что каждый атом имеет определенную энергию. Полная энергия есть сумма энергий атомов. Равным образом, у каждого атома есть своя определенная энтропия. Суммируя, получим полную энтропию. На самом деле здесь все обстоит не так уж гладко, но все же давайте посмотрим, что получится.

В виде примера подсчитаем разницу энтропии газа при одной температуре, но в разных объемах. В гл. 44 для изменения энт­ропии мы получили

DS=∫dQ/T.

В нашем случае энергия газа до и после расширения одна и та же, потому что температура не менялась. Значит, чтобы вос­полнить работу, проделанную газом, нужно придать ему какое-то количество тепла. Для малых изменений объема

dQ=PdV. Подставив это в dQ, получим, как в гл. 44,

Например, при удвоении объема энтропия меняется на Nkln2.

Рассмотрим теперь другой интересный пример. Пусть име­ется цилиндр с перегородкой посредине. По одну ее сторону — неон («черные» молекулы), а по другую — аргон («белые» мо­лекулы). Уберем перегородку и позволим газам перемешаться. Как изменится энтропия? Можно представить себе, что вместо перегородки между газами стоит поршень с отверстиями, в ко­торые проходят белые молекулы и не проходят черные, и дру­гой поршень с обратными свойствами. Сдвигая поршень к осно­ванию цилиндра, легко понять, что для каждого газа задача сводится к только что решенной. Энтропия, таким образом, меняется на Nkln2; это значит, что энтропия на одну молекулу возрастает на kln2. Цифра 2 появилась оттого, что вдвое уве­личился объем, приходящийся на одну молекулу. Странное об­стоятельство! В нем проявилось свойство не самой молекулы, а свободного места вокруг нее. Выходит, что энтропия увели­чивается, когда температура и энергия не меняются, а измени­лось только распределение молекул!

Мы знаем, что стоит убрать перегородку, и газы через неко­торое время перемешаются из-за столкновений, колебаний, уда­ров молекул и т. д. Стоит убрать перегородку, и какая-то белая молекула начнет приближаться к черной, а черная — к белой, они проскочат мимо друг друга и т. д. Постепенно какие-то из белых молекул проникнут случайно в объем, занятый чер­ными, а черные — в область белых. Через какое-то время полу­чится смесь. В общем это необратимый процесс реального мира, он должен привести к росту энтропии.

Перед нами простой пример необратимого процесса, пол­ностью состоящего из обратимых событий. Каждый раз, когда происходит столкновение двух молекул, они разлетаются в оп­ределенных направлениях. Если запустить киноленту, на кото­рой засняты столкновения, в обратную сторону, то ничего непра­вильного на экране не появится. Ведь один вид столкновений столь же вероятен, как и другой. Поэтому перемешивание пол­ностью обратимо, и тем не менее оно необратимо. Каждому известно, что, взяв отдельно белое и отдельно черное и перемешав их, мы через несколько минут получим смесь. Подождем еще сколько-то там минут — они не отделятся, смесь останется смесью. Значит, бывает необратимость, основанная на обрати­мых ситуациях. Но теперь нам ясна и причина. Мы начали с расположения, которое в каком-то смысле упорядочено. В хаосе столкновений оно стало неупорядоченным. Переход от упоря­доченного расположения к беспорядочному является источником необратимости.

Конечно, если бы мы сняли на киноленту это движение и пустили бы потом пленку назад, то увидели бы, как постепенно устанавливается порядок. Кто-нибудь мог бы возразить: «Но это — против всех законов физики!» Тогда мы бы прокрутили фильм еще раз и просмотрели бы каждое столкновение. Все они были бы безупречны, каждое подчинялось бы законам фи­зики. Все дело, конечно, в том, что скорости каждой молекулы были бы выдержаны в точности, так что, если проследить их пути вспять, мы возвратимся к начальным условиям. Но такая ситуация крайне маловероятна. Если иметь дело не со специаль­но приготовленным газом, а просто с белыми и черными моле­кулами, их никогда не удалось бы вернуть назад.

§ 5. Порядок и энтропия

Итак, мы должны теперь потолковать о том, что понимать под беспорядком и что — под порядком. Дело не в том, что по­рядок приятен, а беспорядок неприятен. Наши смешанные и несмешанные газы отличаются следующим. Пусть мы разделили пространство на маленькие элементы объема. Сколькими спо­собами можно разместить белые и черные молекулы в элементах объема так, чтобы белые оказались на одной стороне, а черные на противоположной? И сколькими способами можно их разме­стить без этого ограничения? Ясно, во втором случае способов гораздо больше. Мы измеряем «беспорядок» в чем-то по числу способов, каким может быть переставлено его содержимое, лишь бы внешне все выглядело без изменения. Логарифм числа способов — это энтропия. В цилиндре с разделенными газами число способов меньше и энтропия меньше, т. е. меньше «бес­порядок».

Пользуясь этим техническим определением «беспорядка», можно понять наше утверждение. Во-первых, энтропия изме­ряет «беспорядок». Во-вторых, Вселенная всегда переходит от «порядка» к «беспорядку», поэтому энтропия всегда растет. Порядок не есть порядок в том смысле, что именно эта расста­новка молекул нам нравится; смысл в том, что число разных способов расставить молекулы (лишь бы со стороны расстановки выглядели одинаково) относительно ограничено. Когда мы кру­тили назад наш фильм о перемешивании газов, было не так уж много беспорядка. Каждый отдельный атом имел в точности необходимые скорость и направление, чтобы выйти куда поло­жено! Энтропия была в общем невысока, хотя это и не было за­метно.

А что можно сказать о необратимости других физических законов? Когда мы рассматривали электрическое поле ускоряе­мого заряда, было сказано, что мы должны брать запаздывающее поле. В момент t на расстоянии r от заряда надо брать поле, созданное ускорением в момент t-r/c, а не в момент t+r/c. Поэтому законы электричества на первый взгляд необратимы. Вместе с тем очень странно, что эти законы следуют из уравне­ний Максвелла, которые в действительности обратимы. Однако можно привести довод, что если бы мы пользовались только опережающим полем, полем, отвечающим положению дел в мо­мент t+r/c, и сделали это совершенно последовательно в пол­ностью замкнутом пространстве, то все происходило бы в точ­ности так же, как при употреблении запаздывающих полей! Эта кажущаяся необратимость в теории электричества, та­ким образом (по крайней мере в замкнутой полости), вовсе не является необратимостью. Вы это должны уже слегка сами чув­ствовать; вы знаете уже, что когда колеблющийся заряд создает поле, отражающееся от стен оболочки, то в конечном счете устанавливается равновесие, в котором односторонности нет места. Запаздывающие поля — только прием, удобный метод решения.

Насколько нам известно, все основные законы физики, по­добно уравнениям Ньютона, обратимы. Тогда откуда необра­тимость? Она — из-за превращения порядка в беспорядок. Но это утверждение все равно не понятно, пока мы не знаем, откуда порядок. Почему ситуации, в которых мы оказываемся ежеднев­но, никогда не бывают равновесными? Одно мыслимое объяс­нение таково. Рассмотрим снова наш цилиндр со смесью белых и черных молекул. Если следить за ним достаточно долго, может оказаться, что по чисто случайному, крайне невероятному, но все же мыслимому стечению обстоятельств белые молекулы рас­пределятся главным образом у дна, а черные — у крышки. После этого с течением времени они опять начнут перемеши­ваться.

Стало быть, одно возможное объяснение высокой степени упорядоченности нынешнего мира заключается в том, что нам просто повезло. Вероятно, как-то однажды во Вселенной слу­чилась флуктуация, все как-то разделилось, а теперь вновь воз­вращается к прежнему. Такая теория не несимметрична; на вопрос, как мог бы выглядеть разделенный газ немного раньше или немного позже, она ответит: в любом случае мы увидели бы серое пятно, потому что молекулы опять смешались бы. Как бы ни потекло время, вперед или назад, газ все равно переме­шался бы. Таким образом, по этой теории именно необратимость является одной из случайностей жизни.

Легко показать, что это не так. Предположим, что мы смот­рим не на весь цилиндр сразу, а на какую-то часть его. Пусть в какой-то момент мы открыли в этой части определенную сте­пень порядка: белое с черным в ней разделены. Что отсюда сле­дует для частей, которые мы еще не рассматривали? Если мы и впрямь считаем, что порядок возникает из беспорядка путем флуктуации, то мы обязаны рассмотреть самую вероятную флук­туацию из тех, которые способны в нашей части установить порядок. Но при такой наивероятнейшей флуктуации остальная часть сосуда вовсе не должна рассортироваться — совсем нао­борот! Значит, из гипотезы, что мир — это флуктуация, сле­дует, что, когда мы взглянем на часть мира, прежде нами не виденную, мы должны обнаружить в ней смесь, беспорядок, в отличие от известного нам прежде мира. Если весь наш поря­док есть флуктуация, выброс, мы не смеем надеяться на поря­док где-либо сверх того, где он уже обнаружен.

Теперь предположим, что разделение произошло от того, что в прошлом Вселенная была действительно упорядочена (не из-за флуктуации, а просто белое и черное были первоначально обособлены). Тогда эта теория предскажет, что в других местах тоже должен быть порядок, порядок не как случайность, а из-за того, что в прежние времена порядок был лучше. Тогда можно ожидать, что мы обнаружим в местах, которые мы еще не ви­дели, порядок.

Астрономы, например, пока наблюдали не все звезды. Каж­дую ночь они наводят свои телескопы на новые звезды, и эти звезды ведут себя так же, как и старые. Из этого мы заключаем, что Вселенная — не флуктуация и что наш порядок — это память о тех временах, когда все только начиналось. Мы не говорим, что нам понятна логика этого. По каким-то причинам Вселенная когда-то имела очень малую для своего энергосодер­жания энтропию, и с той поры энтропия выросла. Это — путь по направлению в будущее. В этом начало всех необратимостей. Именно это порождает процессы роста и распада. Именно из-за этого мы вспоминаем не будущее, а прошлое, вспоминаем собы­тия, которые ближе к тому моменту в истории мира, когда поря­док был лучше нынешнего. Именно поэтому мы не способны вспомнить события того времени, беспорядок при котором сильней теперешнего,— мы называем это время будущим.

Мы уже говорили когда-то, что в стакане вина откроется нам вся Вселенная, стоит только заглянуть в него поглубже. Ста­кан вина — штука достаточно сложная, есть там и влага, и стекло, и свет, и еще многое другое.

Прелесть физики еще и в том, что даже такие простые и иде­ализированные вещи, как храповик с собачкой, действуют лишь оттого, что и они — часть Вселенной. Храповик с собачкой работают в одну сторону только потому, что они находятся в тесном контакте с остальной Вселенной. Если бы храповик с собачкой поместить в сосуд и изолировать на некоторое время, то колесико перестанет предпочитать одно направление враще­ния другому. Но по той же причине, по какой мы, открывая шторы, впускаем свет, из-за чего мы идем остывать в тень и греть­ся на солнце, по той же причине храповик с собачкой вертятся лишь в одну сторону. Односторонность связана как-то с тем, что храповик — это часть нашей Вселенной. Часть Вселенной не только в том смысле, что подчиняется законам Вселенной, но и потому, что его одностороннее поведение связано с односторон­ним поведением всей Вселенной. Оно не может пока быть понято до конца: наука приоткрыла великую тайну ранней истории мира, которая сейчас служит лишь предметом разных гипотез.

 

 

Глава 47 ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ

§ 1. Волны

§ 2. Распростра­нение звука

§ 3. Волновое уравнение

§ 4. Решения волнового уравнения

§ 5. Скорость звука

§ 1. Волны

В этой главе мы будем обсуждать новое яв­ление — волны. О волнах часто и много гово­рится в физике, и мы наше внимание должны сконцентрировать на этом вопросе не только потому, что собираемся рассмотреть частный пример волн — звук,— но и потому, что вол­новые процессы имеют и другие многочислен­ные применения во всех областях физики.

Изучая гармонический осциллятор, мы уже отмечали, что существуют примеры как меха­нических колеблющихся систем, так и элект­рических. Волны тесно связаны с колебатель­ными системами, однако волновое движение есть не только колебание в данном месте, за­висящее от времени, но и движение в простран­стве.

Мы уже на самом деле изучали волны. Когда мы говорили о волновых свойствах света, мы обращали особое внимание на пространственную интерференцию волн одной и той же частоты от различных источников, расположенных в раз­ных местах. Существуют еще два важных явления, о которых мы не упоминали и которые свойственны как свету, т. е. электромагнитным волнам, так и любой другой форме волнового движения. Первое из них — это явление ин­терференции, но уже не в пространстве, а во времени. Когда мы слушаем звуки сразу от двух источников, причем частоты их слегка отличаются, к нам приходят то гребни обеих волн, то гребень одной волны и впадина другой (фиг. 47.1).

Фиг. 47.1. Интерференция звука во времени от двух источников с несколько отличающимися часто­тами приводит к биениям.

Звук то усиливается, то ослабевает, возникают биения, или, другими словами, происходит интерференция во времени. Второе явление — это волновое движение в замкнутом объеме, когда волны отражаются то от одной, то от другой стенки.

Все эти эффекты можно было, конечно, рассмотреть и на примере электромагнитных волн. Мы этого не сделали по той причине, что на одном примере мы не почувствовали бы общего характера явления, свойственного самым разным процессам. Чтобы подчеркнуть общность понятия волн вне рамок электро­динамики, мы рассмотрим здесь другой пример — звуковые волны.

Есть еще пример — морские волны, набегающие на берег, или мелкая водяная рябь. Кроме того, существуют два рода упругих волн в твердых телах: волны сжатия (или продольные волны), в которых частицы тела колеблются вперед и назад в направлении распространения волны (звуковые колебания в газе именно такого типа), и поперечные волны, когда частицы тела колеблются перпендикулярно направлению движения волны. При землетрясениях в результате движения участка земной коры возникают упругие волны обоих типов.

И, наконец, есть еще один тип волн, который нам дает сов­ременная физика. Это волны, определяющие амплитуду веро­ятности нахождения частицы в данном месте,— «волны мате­рии», о которых мы уже говорили. Их частота пропорциональна энергии, а волновое число пропорционально импульсу. Эти волны встречаются в квантовой механике.

В этой главе мы будем рассматривать только такие волны, скорость которых не зависит от длины волны. Пример таких волн — распространение света в вакууме. Скорость света в этом случае одна и та же для радиоволн, для синего и зеленого света и вообще для света любой длины волны. Именно поэтому, когда мы описывали волновые явления, мы сначала и не заметили са­мого факта распространения волн. Вместо этого мы говорили, что если перенести заряд в некоторую точку, то электрическое поле на расстоянии х будет пропорционально ускорению заряда, но не в момент времени t, а в более ранний момент времени t- x/c. Поэтому распределение электрического поля в про­странстве в некоторый момент времени, изображенное на фиг. 47.2, спустя время t передвинется на расстояние ct. Вы­ражаясь математически, можно сказать, что в рассматриваемом нами одномерном случае электрическое поле есть функция от x-ct. Отсюда видно, что при t=0 оно оказывается функцией только х. Если взять более поздний момент времени и несколько увеличить х, мы получим ту же самую величину поля. Напри­мер, если максимум поля возникает при x=3 и в момент времени t=0, то положение максимума в момент времени t находится из равенства

x-ct=3, или x=3+ct.

Мы видим, что такая функция отвечает распространению волны. Итак, функция f(x-ct) описывает волну. Мы можем все сказанное записать кратко так:

f(x-ct)= f[x+Dx-с(t+Dt],

если Dx=cDt. Конечно, существует еще и другая возможность, когда источник излучает волны не направо, как указано на фиг. 47.2, а налево, так что волны будут двигаться в сторону отрицательных х.

Фиг. 47.2. Примерное распределение электрического поля в некоторый момент времени (а) и электрическое поле через промежуток времени t (b).

Тогда распространение волны описывалось бы функцией g(x+ct).

Может еще случиться, что в пространстве одновременно движется несколько волн, и тогда электрическое поле есть сумма всех полей и все они распространяются независимо. Это свойство электрических полей можно выразить так: пусть f₁(x-ct) отвечает одной волне, a f₂(x-ct) — другой, тогда их сумма также описывает некоторую волну. Это утверждение на­зывается принципом суперпозиции. Он справедлив и для звуко­вых волн.

Мы хорошо знаем, что звуки воспринимаются в той после­довательности, в какой они создаются источником. А если бы высокие частоты распространялись быстрее, чем низкие, то вместо звуков музыки мы слышали бы резкий и отрывистый шум. Точно так же если бы красный свет двигался быстрее, чем синий, то вспышка белого света выглядела бы сначала красной, затем белой и наконец синей. Мы хорошо знаем, что такого на самом деле не происходит. И звук, и свет движутся в воздухе со скоростью, почти не зависящей от частоты. При­меры волнового движения, где этот принцип не выполняется, будут рассмотрены в гл. 48.

Для света (электромагнитных волн) мы получили формулу, определяющую электрическое поле в данной точке, которое воз­никает при ускорении заряда. Казалось бы, нам остается теперь подобным образом определить какую-нибудь характеристику воздуха, скажем давление на заданном расстоянии от источ­ника через движение источника, и учесть запаздывание при рас­пространении звука.

В случае света такой подход был приемлем, так как все наши знания сводились к тому, что заряд в одном месте дейст­вует с некоторой силой на заряд в другом месте. Подробности распространения взаимодействия из одной точки в другую были абсолютно несущественны. Но звук, как известно, распро­страняется по воздуху от источника к уху, и естественно спросить, чему равно давление воздуха в каждый данный мо­мент. Кроме того, хотелось бы знать, как именно движется воздух.

В случае электричества мы могли поверить в правило, поскольку законы электричества мы еще не проходили, но для звука это не так. Нам недостаточно сформулировать за­кон, определяющий распространение звукового давления в воздухе; этот процесс должен быть объяснен на основе законов механики. Короче, звук есть часть механики, и он должен быть объяснен с помощью законов Ньютона. Распространение звука из одной точки в другую есть просто следствие механики и свойств газов, если звук распространяется в газе, или свойств жидкостей и твердых тел, если звук проходит через эти среды. Позднее мы выведем также свойства света и его волновое дви­жение из законов электродинамики.

§ 2. Распространение звука

Давайте выведем теперь свойства распространения звука между источником и приемником, основываясь на законах Нью­тона, но не учитывая при этом взаимодействия звука с источ­ником и приемником. Обычно мы более подробно останавлива­лись на результате, а не на его выводе. В этой главе мы исполь­зуем противоположный подход. Главным здесь будет в некото­ром смысле само получение результата. Метод объяснения но­вых явлений с помощью старых, законы которых уже известны, представляет собой, пожалуй, величайшее искусство матема­тической физики. Математическая физика решает две проблемы: найти решение заданного уравнения и найти уравнения, опи­сывающие новое явление. То, чем мы будем заниматься, отно­сится как раз ко второй проблеме.

Рассмотрим простейший пример — распространение звука в одномерном пространстве. Для вывода нам сначала необхо­димо понять, что же в действительности происходит. В основе явления лежит следующий факт: когда тело перемещается в воздухе, возникает возмущение, которое как-то распростра­няется по воздуху. На вопрос, что это за возмущение, мы можем ответить: это такое движение тела, которое вызывает изменение давления. Конечно, если тело движется медленно, воздух лишь обтекает его, но нас интересует быстрое движение, когда воздух не успевает обойти вокруг тела. При этих условиях воздух в процессе движения сжимается и возникает избыточное давление, толкающее окружающие слои воздуха. Эти слои в свою очередь сжимаются, снова возникает избыточное давление, и вот начинает распространяться волна.

Опишем этот процесс на языке формул. Прежде всего решим, какие нам нужны переменные. В нашей задаче нам нужно знать, насколько переместился воздух, поэтому смещение воздуха в звуковой волне, несомненно, будет первой нашей переменной. Вдобавок хотелось бы знать, как меняется плотность воздуха при смещении. Давление воздуха тоже меняется, и это еще одна интересная переменная. Кроме того, воздух движется с некото­рой скоростью, и мы должны уметь определить скорость частиц воздуха. Частицы воздуха имеют еще и ускорение, но, записав все эти переменные, мы сразу же поймем, что и скорость, и ускорение будут нам известны, если известно смещение воздуха как функция времени.

Как уже говорилось, мы рассмотрим волну в одном измере­нии. Так можно поступить, если мы находимся достаточно да­леко от источника и так называемый фронт волны мало отли­чается от плоскости. На этом примере наше доказательство будет проще, поскольку можно сказать, что смещение c зависит только от х и t, а не от у и z. Поэтому поведение воздуха опи­сывается функцией c (х, t).

Насколько полно такое описание? Казалось бы, оно очень не полно, потому что нам не известны подробности движения молекул воздуха. Они движутся во всех направлениях, и этот факт не отражается функцией c(х, t). С точки зрения кинетиче­ской теории, если в одном месте наблюдается большая плот­ность молекул, а в соседнем меньшая, молекулыбудут перехо­дить из области с большей плотностью в область с меньшей плотностью, так чтобы уравнять плотности. Очевидно, что при этом никаких колебаний не происходит и звук не возникает. Для получения звуковой волны нужно, чтобы молекулы, вы­летая из области с большей плотностью и давлением, переда-пали импульс другим молекулам, находящимся в области раз­режения. Звук возникает в том случае, если размеры области изменения плотности и давления намного больше расстояния, проходимого молекулами до соударения с другими молекулами. Это расстояние есть длина свободного пробега, и оно должно быть много меньше расстояния между гребнями и впадинами давления. В противном случае молекулы перейдут из гребня во впадину, и волна моментально выровняется.

Мы, естественно, хотим описать поведение газа в масштабе, большем, чем длина свободного пробега, так что свойства газа не будут определяться поведением отдельных молекул. Напри­мер, смещение есть смещение центра инерции небольшого объема газа, а давление или плотность относятся к этому же объему. Мы обозначим давление через Р, а плотность через r, причем обе величины будут функциями от х и t. Необходимо помнить, что наше описание приближенное и справедливо лишь, когда свойства газа не слишком быстро меняются с расстоянием.

§ 3. Волновое уравнение

Итак, физические явления, происходящие в звуковой волне, обладают следующими тремя свойствами:

I. Газ движется, и плотность его меняется. II. При изменении плотности меняется и давление. III. Неравномерное распределение давления вызывает дви­жение газа.

Рассмотрим сначала свойство П. Для любого газа, жидкости или твердого тела давление является функцией плотности. До прихода звуковой волны мы имели равновесное состояние с давлением Р₀ и плотностью r. Давление Р зависит от плот­ности среды: Р=f(r), и в частности равновесное давление Р₀=f(r₀). Отклонения величины давления от равновесного в звуковой волне очень малы. Давление удобно измерять в барах (1 бар=10⁵н/м²). Давление в одну стандартную атмосферу приб­лизительно равно 1 бар (1 атм=1,0133 бар). Для звука обычно используется логарифмическая шкала интенсивности, так как восприятие уха, грубо говоря, растет логарифмически. В этой децибельной шкале уровень звукового давления I связан с амплитудой звукового давления:

I=20log₁₀(P/P_отн) дб, (47.1)

где давление отнесено к некоторому стандартному давлению Р_отн=2·10^-10 бар.

Звуковое давление Р=10³ Р_отн=2·10^-7 бар соответствует довольно сильному звуку в 60 дб. Мы видим, что давление ме­няется в звуковой волне на очень малую величину по сравнению с равновесным или средним, равным 1 атм. Смещение и перепады плотности также очень малы. При взрывах, однако, изменения уже не столь малы; избыточное звуковое давление может пре­вышать 1 атм. Такие большие перепады давления приводят к новым явлениям, которые мы рассмотрим позже. В звуковых волнах уровень силы звука выше 100 дб встречается редко; уровень силы звука в 120 дб уже вызывает боль в ушах. Поэто­му, написав для звуковой волны

Р=Р₀+Р_u, r = r₀+r_u, (47.2)

можно считать, что изменение давления P_uочень мало по сравнению с P₀, а изменение плотности r_u очень мало по сравнению с r₀. Тогда

P₀+Р_u=f(r₀+r_u)=f(r₀)+ r_uf'(r₀), (47.3)

где P₀ = f(r₀) и f'(r₀) — производная от f(r), взятая при значении r =r₀. Второе равенство здесь возможно только потому, что r_u очень мало. Таким образом, мы находим, что избыточное давление P_uпропорционально избыточной плот­ности r_u; коэффициент пропорциональности обозначается через к:

(II) Р_u=cr_u, где c=f'(r₀)=(dP/dr)₀. (47.4)

Это весьма простое соотношение и составляет точное содержа­ние свойства II.

Перейдем теперь к свойству I. Предположим, что положение элемента объема воздуха, не возмущенного звуковой волной, есть х, а звук смещает его в момент времени t на величину c(х,t), так что его новое положение есть x+c(x,t), как показано на фиг. 47.3.

Фиг. 47.3. Смещение воздуха в точке х есть c (х,t), а в точке х+Dx равно c(x+Dx,t).

Первоначальный объем, приходящийся на единицу площади в плоской звуковой волне, есть Dx, а окончательный объем равен Dx+c(x+Dx,t)-c(x,t).

Далее, положение соседнего элемента объема есть х+Dx, и его смещенное положение есть х+Dx+c(х+Dx,t). Теперь можно найти изменение плотности. Поскольку мы рас­сматриваем плоскую волну, удобно взять единичную площадку, перпендикулярную оси х, т. е. направлению распространения волны. Количество воздуха, приходящееся на единичную площадку в интервале Dx, есть r₀Dx, где r₀ — невозмущенная, или равновесная, плотность воздуха. Эта порция воздуха, сме­щенная звуковой волной, будет находиться теперь между x+c (x,t) и x+Dх+c (х+Dx,t), причем количество воздуха в этом интервале то же самое, что в интервале Dx до прихода волны. Если через r обозначить новую плотность, то

r₀Dx=r [x+Dx+c (x+Dx,t)-x-c (x,t)]. (47.5)

Поскольку Dx мало, можно написать c (x+Dx,t)-c (x,t)=(дc/дx)Dx. Здесь уже появляется частная производная, потому что c зависит и от x, и от времени. Наше уравнение принимает вид

r₀Dx =r ((дc/дx) Dx +Dx), (47.6)

или

r₀=(r₀+r_u)дc/дx+r₀+r_u. (47.7)

Но в звуковой волне все изменения малы, так что r_u мало, c мало и дc/дх тоже мало. Поэтому в уравнении, которое мы только что написали,

r_u=-r₀(дc/дx)- r_u(дc/дx), (47.8)

можно пренебречь r_u(дc/дх) по сравнению с r₀(дc/дх). Так мы приходим к соотношению, которое требовалось согласно свойству I:

(I) r_u=-r₀дc/дx. (47.9)

Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х, плотность будет изменяться. Знак тоже правильный: если сме­щение c растет с ростом х, так что воздух расширяется, плотность должна уменьшаться.

Теперь нам нужно найти третье уравнение — уравнение движения, производимого избытком давления. Зная соотноше­ние между силой и давлением, можно получить уравнение дви­жения. Возьмем объем воздуха толщиной Dx и с единичной пло­щадью грани, перпендикулярной х, тогда масса воздуха в этом объеме есть r₀Dx, а ускорение воздуха есть д²c/дt², так что масса, умноженная на ускорение для этого слоя, есть r₀Dx(д²c/дt²). (Если Dx; мало, то безразлично, где брать ускорение — на краю слоя или где-нибудь посредине.) Сила, действующая на единич­ную площадку нашего слоя, перпендикулярную оси x, должна быть равна r₀Dx(д²хc/дt²). В точке х мы имеем силу Р(х,t), дей­ствующую на единицу площади в направлении +х, а в точке x+Dx; возникает сила в обратном направлении, по величине равная Р(x;+ Dx, t) (фиг. 47.4):

Фиг. 47.4. Результирующая сила в направлении оси х, возникающая за счет давления на единичную площадку, перпендикулярную к оси х, есть — (дР/дх)Dx.

Р(х, t)-P(x+Dx, t)=-(дP/дx) Dx=(дP_u/дx) Dx. (47.10)

Мы учли, что Dx; мало и что только избыточное давление Р_и меняется в зависимости от х. Итак, согласно свойству III мы получаем

(III) r₀=д²c/дt²=-дP_u/дx. (47.11)

Теперь уже уравнений достаточно, чтобы увязать все вели­чины и привести к одной переменной, скажем х. Можно выразить Р_uв (47.11) с помощью (47.4):

r₀д²c/дt²-cдr_u/дx (47.12)

а затем исключить r_u с помощью (I). Тогда r₀ сократится и у нас останется

д2c/дt²=xд²c/дx². (47.13)

Обозначим с²_s =x, тогда можно написать

Это и есть волновое уравнение, которое описывает распростра­нение звука в среде.

§ 4. Решения волнового уравнения

Посмотрим теперь, действительно ли волновое уравнение описывает основные свойства звуковых волн в среде. Прежде всего мы хотим вывести, что звуковое колебание, или возмуще­ние, движется с постоянной скоростью. Кроме того, нам нужно доказать, что два различных колебания могут свободно прохо­дить друг через друга, т. е. принцип суперпозиции. Мы хотим еще доказать, что звук может распространяться и вправо и влево. Все эти свойства должны содержаться в нашем одном урав­нении.

Раньше мы отмечали, что любое возмущение, имеющее вид плоской волны и движущееся с постоянной скоростью, записы­вается в виде f(x-vt). Посмотрим теперь, является ли f(x-vt) решением волнового уравнения. Вычисляя дc/дх, получаем производную функции dcldx=f'(x-vt). Дифференцируя еще раз, находим

Дифференцируя эту же функцию c по t, получаем значение — V, умноженное на производную, или дc/dt=-vf (x-vt); вторая производная по времени дает

Очевидно, что f(х-vt) удовлетворяет волновому уравнению, если v равно c_s.

Таким образом, из законов механики мы получаем, что любое звуковое возмущение распространяется со скоростью c_sи, кроме того,

тем самым мы связали скорость звуковых волн со свойствами среды.

Легко увидеть, что звуковая волна может распространяться: и в направлении отрицательных х, т. е. звуковое возмущений вида c (х, t)=g(x+vt) также удовлетворяет волновому уравнению. Единственное отличие этой волны от той, которая распростра­нялась слева направо, заключается в знаке v, но знак д²c/dt²не зависит от выбора x+vt или х-vt, потому что в эту производ­ную входит только v². Отсюда следует, что решение уравнения описывает волны, бегущие в любом направлении со скоростью c_s.

Особый интерес представляет вопрос о суперпозиции решений. Допустим, мы нашли одно решение, скажем c₁ . Это значит, что вторая производная 3d по х равна второй производной c₁ по t₁, умноженной на 1/с^2s. И пусть есть второе решение c₂, обладаю­щее тем же свойством. Сложим эти два решения, тогда полу­чается

c (x, t)= c₁(x, t) + c₂(x, t). (47.17)

Теперь мы хотим удостовериться, что c (х, t) тоже представ­ляет некую волну, т. е. c тоже удовлетворяет волновому уравнению. Это очень просто доказать, так как

и вдобавок

Отсюда следует, что d²c/dx²=(l/c²_s)д²c/dt², так что справедли­вость принципа суперпозиции проверена. Само существование принципа суперпозиции связано с тем, что волновое уравнение линейно по c.

Теперь естественно было бы ожидать, что плоская световая волна, распространяющаяся вдоль оси х и поляризованная так, что электрическое поле направлено по оси y, тоже удовлет­воряет волновому уравнению

где с — скорость света. Волновое уравнение для световой волны есть одно из следствий уравнений Максвелла. Уравнения элект­родинамики приводят к волновому уравнению для света точно так же, как уравнения механики приводят к волновому урав­нению для звука.

§ 5. Скорость звука

При выводе волнового уравнения для звука мы получили формулу, которая связывает при нормальном давлении скорость движения волны и относительное изменение давления с плотностью: с²_s=(dP/dr)₀. (47.21) Чтобы оценить скорость изменения давления, очень важно знать, как при этом меняется температура. Можно ожидать, что в местах сгущения звуковой волны температура повысится, а в местах разрежения — понизится. Ньютон первым вычислил скорость изменения давления с плотностью, предположив, что температура при этом не меняется. Он считал, что тепло пере­дается из одной области звуковой волны в другую так быстро, что температура измениться не успеет. Способ Ньютона дает изотермическую скорость звука, что неправильно. Правильное вычисление было сделано позже Лапласом, считавшим вопреки Ньютону, что давление и температура в звуковой волне меня­ются адиабатически. Поток тепла из области сгущения в область разрежения пренебрежимо мал, если только длина волны ве­лика по сравнению с длиной свободного пробега. При этих условиях ничтожная утечка тепла в звуковой волне не влияет на скорость звука, хотя и приводит к небольшому поглощению звуковой энергии. Мы можем, естественно, ожидать, что погло­щение тепла усилится, когда длина волны приблизится к длине свободного пробега, но такие длины волн примерно в миллион раз меньше длины волны слышимого звука.

Итак, для звука истинная скорость изменения давления с плотностью должна вычисляться без учета отвода тепла. Это соответствует адиабатическому изменению давления, для ко­торого мы нашли, что PV^g=const, где V — объем. Поскольку плотность r обратно пропорциональна объему, связь P и r для адиабатических процессов дается соотношением

P=const·r^g, (47.22)

откуда мы получаем dP/dr=gP/r. Тогда для скорости звука возникает соотношение

c²_s =gP/r. (47.23)

Можно еще написать с²_s= gPV/rV и использовать соотноше­ние PV=NkT. Мы видим, кроме того, что rV есть масса газа, которую можно записать как Nm или m, где m — масса молекулы, а m — молекулярный вес. Таким образом, находим

откуда видно, что скорость звука зависит только от темпе­ратуры газа и не зависит от давления или плотности. Мы уже отмечали, что

kT=¹/₃m<v²>, (47.25)

где <v²> — средняя квадратичная скорость молекул. Отсюда следует, что с²_s=g/3 <v²>, или

Это равенство означает, что скорость звука есть средняя ско­рость молекул воздуха (точнее, корень квадратный из средней квадратичной скорости), умноженная на некоторое число, грубо говоря, на 1/(3)^1/2. Другими словами, она того же порядка величины, что и скорость молекул, но на самом деле несколько меньше средней скорости молекул.

В общем-то мы могли этого ожидать, потому что такое воз­мущение, как изменение плотности, передается в конечном счете движением молекул. Однако подобного рода соображения не подсказывают нам точного значения скорости; могло ведь оказаться, что звук переносится самыми быстрыми или самыми медленными молекулами. Разумно и весьма утешительно, что скорость звука оказалась равной приблизительно половине средней молекулярной скорости.

* При таком выборе P_отн Р — уже не максимальная амплитуда зву­кового давления, а «среднее квадратичное» давление, равное максималь­ному, деленному на 1/Ц2.

 

 

Глава 48 БИЕНИЯ

§ 1. Сложение двух волн

§ 2. Некоторые замечания о биениях и модуляции

§ 3. Боковые полосы

§ 4. Локализован­ный волновой пакет

§ 5. Амплитуда вероятности частиц

§ 6. Волны в простран­стве трех измерений

§ 7. Собственные колебания

§ 1. Сложение двух волн

Не так давно мы довольно подробно обсуж­дали свойства световых волн и их интерферен­цию, т. е. эффект суперпозиции двух волн от различных источников. Но при этом пред­полагалось, что частоты источников оди­наковы. В этой же главе мы остановимся на некоторых явлениях, возникающих при интер­ференции двух источников с различными ча­стотами.

Нетрудно догадаться, что при этом произой­дет. Действуя так же, как прежде, давайте предположим, что имеются два одинаковых осциллирующих источника с одной и той же частотой, причем фазы их подобраны так, что в некоторую точку Р сигналы приходят с оди­наковой фазой. Если это свет, то в этой точке он очень ярок, если это звук, то он очень громок, а если это электроны, то их очень много. С другой стороны, если приходящие волны отличаются по фазе на 180°, то в точке Р не будет никаких сигналов, ибо полная амплитуда будет иметь здесь минимум. Предположим теперь, что некто крутит ручку «регулировка фазы» одного из источников и меняет разность фаз в точке Р то туда, то сюда, скажем сначала он делает ее нулевой, затем — равной 180° и т. д. При этом, разумеется, будет меняться и сила приходящего сигнала. Ясно теперь, что если фаза одного из источников медленно, постоянно и равномерно меняется по сравнению с другим, начиная с нуля, а затем возрастает постепенно до 10, 20, 30, 40° и т. д., то в точке Р мы увидим ряд слабых и сильных «пульсаций», ибо когда разность фаз проходит через 360°, в амплитуде снова возникает максимум. Но утверждение, что один источник с постоянной скоростью меняет свою фазу по отношению к другому, равносильно утверждению, что число колебаний в 1 сек у этих двух источников несколько различно.

Итак, теперь известен ответ: если взять два источника, ча­стоты которых немного различны, то в результате сложения получаются колебания с медленно пульсирующей интенсив­ностью. Иначе говоря, все сказанное здесь действительно имеет отношение к делу!

Этот результат легко получить и математически. Предположим, например, что у нас есть две волны и забудем на минуту о всех пространственных соотношениях, а просто посмотрим, что приходит в точку Р. Пусть от одного источника приходит волна cosw₁t, а от другого — волна cosw₂t, причем обе частоты w₁ и w₂ не равны в точности друг другу. Разумеется, амплитуды их тоже могут быть различными, но сначала давайте предположим, что амплитуды равны. Общую задачу мы рассмотрим позднее. Полная амплитуда в точке Р при этом будет суммой двух косинусов. Если мы построим график зависимости амплитуды от вре­мени, как это показано на фиг.48.1,то окажется, что, когда гребни двух волн совпадают, получается большое отклонение, когда совпадают гребень и впадина — практически нуль, а когда гребни снова совпадают, вновь получается большая волна.

Фиг. 48.1. Суперпозиция двух косинусообразных волн с отношением частот 8:10. Точное повторение колебаний внутри каждого биения для общего случая не типично.

Математически нам нужно взять сумму двух косинусов и как-то ее перестроить. Для этого потребуются некоторые полез­ные соотношения между косинусами. Давайте получим их. Вы знаете, конечно, что

e^i(a+b)=e^iae^ib (48.1)

и что вещественная часть экспоненты e^iaравна cosа, а мни­мая часть равна sin а. Если мы возьмем вещественную часть ехр [-i(a+b)], то получим cos (a+b), а для произведения

e^iae^ib=(cosa+isin a)(cosb+isinb)

мы получаем cosacosb-sinasinb плюс некоторая мнимая добавка. Сейчас, однако, нам нужна только вещественная часть. Таким образом,

cos(a+b)=cosacosb-sinasinb. (48.2)

Если теперь изменить знак величины b, то, поскольку коси­нус при этом не изменяет знака, а синус изменяет знак на обратный, мы получаем аналогичное выражение для косинуса разности

cos(a-b)=cosacosb+sinasinb. (48.3)

После сложения этих двух уравнений произведение синусов сократится, и мы находим, что произведение двух косинусов равно половине косинуса суммы плюс половина косинуса разности

cosacosb=¹/₂cos (а+b)+¹/₂cos (a-b). (48.4)

Теперь можно обернуть это выражение и получить формулу для cosa+cosb, если просто положить a = а+b, a b= а-b, т. е. a =¹/₂(a+b), a b=¹/₂(a-b):

cosa+cosb=2cos¹/₂(a+b) cos¹/₂(a-b). (48.5)

Но вернемся к нашей проблеме. Сумма cosw₁t и cosw₂t равна

cosw₁t+cosw₂t=2cos¹/₂(w₁+w₂)tcos¹/₂(w₁-w₂)t. (48.6)

Пусть теперь частоты приблизительно одинаковы, так что ¹/₂(w₁+w₂) равна какой-то средней частоте, которая более или менее та же, что и каждая из них. Но разность w₁-w₂ гораздо меньше, чем w₁ и w₂, поскольку мы предположили, что w₁ и w₂ приблизительно равны друг другу. Это означает, что результат сложения можно истолковать так, как будто есть косинусообразная волна с частотой, более или менее равной пер­воначальным, но что «размах» ее медленно меняется: он пульси­рует с частотой, равной ¹l₂(w₁-w₂)- Но та ли это частота, с которой мы слышим биения? Уравнение (48.6) говорит, что амплитуда ведет себя как cos¹/₂(w₁-w₂), и это надо понимать так, что высокочастотные колебания заключены между двумя косинусоидами с противоположными знаками (пунктирная линия на фиг. 48.1). Хотя амплитуда действительно меняется с частотой ¹/₂(w₁-w₂), однако если речь идет об интенсивности волн, то мы должны представлять себе частоту в два раза боль­шую. Иначе говоря, модуляция амплитуды в смысле ее интен­сивности происходит с частотой w₁-w₂, хотя мы и умножаем на косинус половинной частоты.

Пренебрегая этими небольшими усложнениями, мы можем заключить, что если складывать две волны с частотами w₁ и w₂, то получим волну с частотой, равной средней частоте ¹/₂(w₁+w₂), «сила» которой осциллирует с частотой w₁-w₂.

Если амплитуды двух волн различны, то можно, конечно, повторить все вычисления снова, умножив предварительно косинусы на различные амплитуды А₁и А₂и произведя массу всяких математических вычислений, перестроек и т. п. с исполь­зованием уравнений, подобных (48.2) — (48.5). Однако есть и другой, более легкий путь провести этот же анализ. Известно, например, что гораздо легче работать с экспонентами, чем с синусами и косинусами, поэтому можно представить A₁созw₁t как реальную часть экспоненты А ₁ехр (iw₁t). Подобным же обра­зом вторая волна будет реальной частью A₂ехр(iw₂t). После сложения этих экспонент A₁exp(iw₁t)+A₂exp(iw₂t) и выделения в качестве множителя экспоненты со средней частотой мы получим

т. е. снова оказывается, что высокочастотная волна модули­руется малой частотой.

§ 2. Некоторые замечания о биениях и модуляции

Предположим теперь, что нас интересует интенсивность волны, описываемой уравнением (48.7). Чтобы найти ее, нужно взять квадрат абсолютной величины либо правой, либо левой части этого уравнения. Давайте возьмем левую часть. Интен­сивность при этом будет равна

I = A²₁+A²₂ + 2A₁A₂cos(w_l -w₂)t. (48.8)

Видите, интенсивность возрастает и падает с частотой w₁-w₂, изменяясь в пределах между (А₁+A₂)²и (А₁-A₂)². Если А₁№А₂, то минимальная интенсивность не равна нулю.

Те же результаты можно получить и другим путем—с по­мощью схем, подобных фиг. 48.2.

Фиг. 48.2. Результат сложения двух комплексных векторов с рав­ными частотами.

Изобразим одну из волн в виде вектора длиной A₁ в комплексной плоскости, вращающе­гося с угловой скоростью w₁. Вторую волну изобразим другим вектором, длина которого A₂, а угловая скорость вращения w₂. Если эти частоты в точности равны между собой, то мы по­лучим вращающийся вектор, длина которого все время по­стоянна. Так что интенсивность в этом случае будет все время постоянной фиксированной величиной. Если, однако, частоты хоть немного отличаются одна от другой, то эти два вектора будут крутиться с различными скоростями.

На фиг. 48.3 показано, как выглядит вся картина «с точки зрения» вектора A₁exp(iw₁t).

Фиг. 48.3. Результат сложения двух комплексных векторов с раз­личными частотами во вращаю­щейся системе отсчета первого вектора.

Показаны девять последовательных по­ложений медленно вращающегося век­тора.

Мы видим, что вектор А₂медленно «отворачивается» от вектора А₁, так что амплитуда, получаемая при сложении этих векторов, сначала велика, а затем, когда второй вектор совсем «отвернется» в другую сторону, т. е. когда угол между ними станет 180°, она будет особенно мала, и т. д. Вектор крутится, амплитуда суммы векторов становится то больше, то меньше, а интенсивность пульсирует. Идея срав­нительно простая, и ее можно реализовать множеством раз­личных способов. Этот эффект очень легко наблюдать экспери­ментально. Можно установить, например, два громкоговори­теля, каждый из которых связан со своим генератором коле­баний и может давать свой собственный тон. Таким образом, мы принимаем один сигнал от первого источника, а другой сигнал от второго. Если частоты этих сигналов в точности одинаковы, то в результате в каждой точке пространства полу­чится эффект определенной силы. Но если генераторы немного расстроить, то мы услышим некоторые изменения интенсив­ности. Чем больше мы расстраиваем генераторы, тем более быстрыми будут изменения силы звука. Однако уху становится трудно уследить за изменениями, скорость которых превышает 10 колебаний в секунду или что-то около этого.

Тот же эффект можно наблюдать и на осциллографе, кото­рый просто показывает сумму токов двух генераторов. Если частота пульсаций сравнительно мала, то мы просто видим, как на экране перед нами проходят синусоидальные волны, амплитуда которых пульсирует, но если сделать пульсации более быстрыми, то мы увидим нечто похожее на то, что пока­зано на фиг. 48.1. По мере увеличения разницы между часто­тами «вершины» сближаются все больше и больше. Если амплитуды не равны друг другу, если мы один сигнал сделаем слабее другого, то образуется волна, амплитуда которой, как это и ожидается, никогда не становится равной нулю. Все получается так, как нужно, независимо от того, электричество это или звук.

Но возможно и обратное явление! При радиопередаче ис­пользуют так называемую амплитудную модуляцию (AM). Вот как это делается. Радиопередатчик возбуждает электри­ческие колебания очень высокой частоты. Для радиовещания, например, используется частота 800 кгц. Если включен этот несущий сигнал, то передатчик будет излучать волны с часто­той 800 000 колебаний в секунду, причем амплитуда их по­стоянна. Информация же (зачастую совершенно бесполезная, вроде того, какую марку автомобиля вам следует приобрести) передается следующим образом: когда кто-то говорит в микро­фон, амплитуда несущего сигнала изменяется «в ногу» с коле­баниями звука, приходящего в микрофон.

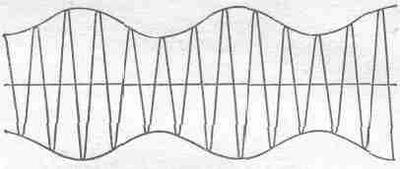Возьмем простейший с точки зрения математики случай, когда певица берет безупречную ноту с безупречным синусои­дальным колебанием голосовых связок, причем получается сигнал, сила которого меняется, как это показано на фиг. 48.4.

Фиг. 48.4. Модуляция несущей волны. На этом схематическом ри­сунке отношение w_c/w_m=5. В настоящей радиоволне w_c/w_m »100.

Изменения слышимой частоты принимаются затем приемником; мы избавляемся от несущей волны и смотрим просто на «оберт­ку», которая представляет собой колебания голосовых связок, или звук голоса певицы. Громкоговоритель же производит колебания той же частоты в воздухе, и в принципе слушатель не может обнаружить разницы между настоящим голосом пе­вицы и передачей, слышимой по радио. В действительности же из-за некоторых искажений и других тончайших эффектов можно все же определить, слышим ли мы радио или «живой» голос певицы; в других же отношениях все происходит так, как мы описали.

§ 3. Боковые полосы

Описанную выше модулированную волну математически можно записать в виде

S=(1+bcosw_mt)cosw_ct, (48.9)

где (w_с— несущая частота, а w_m— частота слышимого звука. Используя теоремы о косинусах или свойства экспоненты exp(iq) (разницы в этом никакой нет, однако легче работать с экспонентой), мы получаем

S=cosw_ct+¹/₂bcos(w_c+w_m) t+¹/₂bcos(w_с-w_m)t. (48.10)

Таким образом, с другой точки зрения можно сказать, что вы­ходящая волна состоит из суперпозиции трех волн: обычной волны с частотой w_с, т. е. несущей частоты, и затем двух новых волн с двумя другими частотами. Одна из них равна сумме несущей и модулирующей частот, а другая — разности. Если построить нечто вроде графика зависимости интенсивности излучения генератора от частоты, то сначала мы, естественно, обнаружим большую интенсивность при несущей частоте w_с,но как только певица начнет петь, мы неожиданно обнаружим интенсивность, пропорциональную силе голоса певицы b² при частотах w_с+w_mи w_с-w_m, как это показано на фиг. 48.5.

Фиг. 48.5. Спектр частот несущей волны w_с, модулированной одной косинусообразной волной w_m.

Они называются боковыми полосами. Если из передатчика вы­ходит модулированный сигнал, то возникают боковые полосы. Если в одно и то же время передаются две ноты, скажем, с частотами w_m и w_m', например играют два инструмента или какая-то другая усложненная волна, тогда из математики вид­но, что получаются две новые волны, соответствующие часто­там (w_m±w_m'.

Итак, если происходит какая-то сложная модуляция, ко­торую можно представить в виде суммы многих косинусов, то оказывается, что в действительности передатчик работает в целой области частот, именно несущей частоты плюс-минус максимальная частота, содержащаяся в модулирующем сиг­нале.

Хотя вначале мы могли поверить, что радиопередатчик ра­ботает только на номинальной несущей частоте, так как в нем находится большой сверхстабильный кристаллический осцил­лятор и все подобрано так, чтобы частота была равна в точности 800 кгц, но в тот момент, когда диктор объявляет, что станция работает на частоте 800 кгц, он тем самым модулирует эту ча­стоту и передача уже не идет точно на этой частоте. Предполо­жим, что усилители построены так, что они могут передавать широкую полосу частот в области, воспринимаемой ухом (ухо может слышать частоты вплоть до 20 000 гц, но обычно радио­приемники и радиопередатчики работают ниже частоты 10 000 гц, и по радио мы высших частот не слышим). Так что голос диктора, объявляющего что-то по радио, может содер­жать частоты вплоть до 10 000 гц, передатчик излучает ча­стоты в области от 790 до 810 кгц. Если при этом на частоте, скажем, 795 кгц работает еще одна радиостанция, то возникают большие помехи. Если мы сделаем наш приемник столь чув­ствительным, что он будет принимать только частоту 800 кгц и не будет захватывать по 10 кгц с каждой стороны, то мы не услышим, что сказал диктор, ведь информация передается именно на боковых частотах! Поэтому очень важно, чтобы стан­ции были разделены некоторой областью частот и их боковые полосы не перекрывались, а приемник не должен быть столь избирательным, чтобы не позволять принимать боковые полосы вместе с номинальной частотой. Но эта проблема не вызывает больших затруднений при радиопередачах. Мы слышим в области ±20 кгц, а радиопередача ведется обычно в области от 500 до 1500 кгц, так что места должно хватить для множества станций.

Проблема телевидения намного труднее. Когда электрон­ный луч бежит по экрану телевизионной трубки, он создает множество светлых и темных точек. Эти светлые и темные точки и есть «сигналы». Обычно, чтобы «показать» весь кадр, лучу требуется примерно в тридцатую долю секунды пробежать 500 строк. Пусть разрешение по горизонтали и по вертикали более или менее одинаково, т. е. на миллиметр каждой строки приходится ровно столько же точек, сколько строк приходится на миллиметр высоты. Нужно, чтобы мы могли различать по­следовательность светлое — темное, светлое — темное, светлое — темное на протяжении 500 линий. Чтобы это можно было сделать с помощью косинусообразной волны, требуется длина волны, т. е. расстояние от максимума до минимума, соответ­ствующая длине 1/250 части экрана. Таким образом, получается 250x500x30 «единичек информации» в секунду, поэтому выс­шая частота, которую нужно передать, оказывается равной приблизительно 4 Мгц. На самом деле, чтобы отделить телеви­зионные станции одну от другой, мы должны использовать несколько большую ширину — около 6 Мгц. Часть ее исполь­зуется для передачи звукового сопровождения и другой инфор­мации. Таким образом, телевизионный канал имеет ширину 6 Мгц. Разумеется, модулировать с частотой, превышающей частоту несущей волны, невозможно, поэтому телевизионные передачи нельзя вести на частоте, например, 800 кгц.

Во всяком случае, телевизионная полоса начинается с частоты 54 Мгц. Первый телевизионный канал в Соединенных Штатах работает в полосе от 54 до 60 Мгц, т. е. имеет ширину 6 Мгц. «Постойте,— можете сказать вы,— ведь только сейчас мы до­казали, что боковые полосы должны быть с обеих сторон, а поэтому ширина должна быть вдвое больше». Оказывается, радиоинженеры довольно хитрый народ. Если при анализе модулирующего сигнала использовать не только косинус, а косинус и синус, чтобы учесть разность фаз, то между высоко­частотной и низкочастотной боковыми полосами обнаружится наличие определенного постоянного соотношения. Этим мы хотим сказать, что вторая боковая полоса не содержит никакой новой информации по сравнению с первой, так что одну из них вполне можно выкинуть. Приемник же устроен таким образом, что потерянная информация восстанавливается из несущей ча­стоты и одной боковой полосы. Передача с помощью одной бо­ковой полосы — очень интересный метод уменьшения ширины полосы, необходимой для передачи информации.

§ 4. Локализованный волновой пакет

Следующий вопрос, который мы хотим обсудить,— это ин­терференция волн как в пространстве, так и во времени. Пред­положим, что в пространстве распространяются две волны. Вы, конечно, знаете, что распространение волны в простран­стве, например звуковой, можно описать с помощью экспонен­ты exp[i(wt-kx)]. Такая экспонента удовлетворяет волновому уравнению при условии, что w²=k²с², где с — скорость распро­странения волны. В этом случае экспоненту можно записать в виде ехр[ik(x-ct)], что является частным случаем общего решения f(x-ct). Такая экспонента должна описывать волну, распространяющуюся со скоростью w/k, равной с, и поэтому здесь все в порядке.

Давайте теперь складывать две такие волны. Пусть первая волна распространяется с одной частотой, а вторая волна — с какой-то другой. Случай неравных амплитуд рассмотрите са­мостоятельно, хотя существенного отличия здесь нет. Таким образом, мы хотим сложить exp[i(w₁t-k₁x)]+exp[i(w₂t-k₂x)]. Это можно сделать с помощью математики, аналогичной исполь­зованной нами при сложении двух сигналов. Если скорости с обеих волн одинаковы, то сделать это очень легко; за исклю­чением того, что вместо t стоит t' = t-х/с, это будет то же

самое, что мы недавно проделали:

При этом, естественно, мы получаем точно такие же модуляции, как и раньше, которые, однако, движутся вместе с волной. Другими словами, если сложить две волны, которые не просто осциллируют, но и перемещаются в пространстве, то получив­шаяся волна также будет двигаться с той же скоростью.

Хотелось бы обобщить это на случай волн, у которых отно­шение между частотой и волновым числом k не столь просто, например распространение волн в веществе с некоторым пока­зателем преломления. В гл. 31 (вып. 3) мы уже изучали по­казатель преломления n и выяснили, что он связан с волновым числом следующим образом: А=nw/с. В качестве интересного примера мы нашли показатель преломления n для рентгенов­ских лучей:

На самом деле в гл. 31 мы получали и более сложные форму­лы, однако эта ничуть не хуже, так почему бы нам не взять ее в качестве примера.

Нам известно, что даже в том случае, когда w и k не про­порциональны друг другу, отношение w/k все равно будет скоростью распространения данной частоты и данного волно­вого числа. Это отношение называется фазовой скоростью, т. е. скоростью, с которой движется фаза или узел отдельной волны:

v_фаз=w/k. (48.13)

Интересно, что, например, для случая распространения рент­геновских лучей в стекле эта фазовая скорость больше скорости света в пустоте [поскольку n, согласно (48.12), меньше единицы], а это несколько неприятно, ведь не думаем же мы, что можно посылать сигналы быстрее скорости света!

Обсудим теперь интерференцию двух волн, у которых зна­чения w и k связаны какой-то определенной зависимостью. На­пример, написанная ранее формула для показателя n говорит, что k есть определенная известная функция частоты w. Для большей определенности давайте выпишем формулу зависи­мости k и w в данной частной задаче:

k=w/c-a/wc (48.14)

где a=Nq²_e/2e₀m — постоянная. Во всяком случае, мы хотим сложить такие две волны, у которых для каждой частоты суще­ствует определенное волновое число.

Давайте сделаем это точно так же, как и при получении уравнения (48.7):

Таким образом, снова получается модулированная волна, рас­пространяющаяся со средней частотой и средним волновым числом, однако сила ее меняется в соответствии с выражением, зависящим от разности частот и разности волновых чисел.

Рассмотрим теперь случай, когда разности между двумя волнами относительно малы. Предположим, что мы складываем две волны с приблизительно равными частотами, при этом (w₁+w₂)/2 практически равно каждой из частот w. То же можно сказать и о (k₁+k₂)/2. Таким образом, скорость волны, быстрых осцилляции, узлов действительно остается равной w/k. Но смотрите, скорость распространения модуляций не та же са­мая! Как нужно изменить х, чтобы сбалансировать некоторую величину времени t? Скорость этих модулирующих волн равна

v_M=(w₁-w₂)/(k₁-k₂). (48.16)

Скорость движения модуляций иногда называют групповой скоростью. Если мы возьмем случай относительно малой раз­ности между частотами и соответственно относительно малой разности между волновыми числами, то это выражение перехо­дит в пределе в

Другими словами, чем медленнее модуляции, тем медленнее и биения, и вот что самое удивительное — существует определенная скорость их распространения, которая не равна фа­зовой скорости волны.

Групповая скорость равна производной со по k, а фазовая ско­рость равна отношению w/k.

Посмотрим, можно ли понять, почему так происходит. Рас­смотрим две волны с несколько различными длинами, как это показано на фиг. 48.1. Они то совпадают по фазе, то разли­чаются, то снова совпадают и т. д. Однако теперь эти волны в действительности представляют волны в пространстве, рас­пространяющиеся с немного различными скоростями. Но по­скольку фазовая скорость, скорость узлов этих двух волн, не в точности одинакова, то происходит нечто новое. Предпо­ложим, что мы едем рядом с одной из волн и смотрим на другую. Если бы они двигались с одинаковой скоростью, то вторая волна оставалась бы относительно нас там же, где и была с самого начала, поскольку мы едем как бы на гребне одной волны и видим гребень второй прямо около себя. Однако в действитель­ности скорости не равны. Частоты немного отличаются друг от друга, а поэтому немного отличаются и скорости. Из-за этой небольшой разницы в скоростях другая волна либо медленно обгоняет нас, либо отстает. Что же с течением времени проис­ходит с узлом? Если чуть-чуть продвинуть одну из волн, то узел при этом уйдет на значительное расстояние вперед (или назад), т. е. сумма этих двух волн имеет какую-то огибающую, кото­рая вместе с распространением волн скользит по ним с другой скоростью. Групповая скорость является той скоростью, с ко­торой передаются модулирующие сигналы.

Если мы посылаем сигнал, т. е. производим какие-то изме­нения волны, которые могут быть услышаны и расшифрованы кем-то, то это является своего рода модуляцией, но такая мо­дуляция при условии, что она относительно медленная, будет распространяться с групповой скоростью (быстрые модуляции значительно труднее анализировать).

Теперь мы можем показать (наконец-то!), что скорость рас­пространения рентгеновских лучей в куске угля, например, не больше, чем скорость света, хотя фазовая скорость больше скорости света. Чтобы сделать это, нужно найти соотношение dw/dk, которое мы вычислим дифференцированием формулы

(48.14): dk/dw=1/c+a/(w²c). А групповая скорость равна обрат­ной величине, т. е.

что меньше, чем с! Таким образом, хотя фазы могут бежать бы­стрее скорости света, модулирующие сигналы движутся мед­леннее, и в этом состоит разрешение кажущегося парадокса!

Разумеется, в простейшем случае w=kc групповая скорость dw/dk тоже равна с, т. е. когда все фазы движутся с одинако­вой скоростью, естественно, и групповая скорость будет той же самой.

§ 5. Амплитуда вероятности частиц

Рассмотрим еще один необычайно интересный пример фа­зовой скорости. Он относится к области квантовой механики. Известно, что амплитуда вероятности найти частицу в данном месте изменяется при некоторых обстоятельствах в пространстве и времени (давайте возьмем одно измерение) следующим обра­зом:

где w — частота, связанная с классической энергией, E=hw, a k — волновое число, которое связано с импульсом соотно­шением р=hk. Мы говорим, что частица имеет определенный импульс р, если волновое число в точности равно k, т. е. если бежит идеальная волна повсюду с одинаковой амплитудой. Выражение (48.19) дает амплитуду вероятности, но если мы возьмем квадрат абсолютной величины, тополучим относитель­ную вероятность обнаружения частицы как функцию поло­жения и времени. В данном случае она равна постоянной, что означает вероятность обнаружить частицу в любом месте, Рассмотрим теперь такой случай, когда известно, что обна­ружить частицу в каком-то месте более вероятно, чем в других местах. Подобную картину мы описываем волной, которая имеет максимум в данном месте и сходит на нет по мере удале­ния в стороны (фиг. 48.6).

Фиг. 48.6. Локализованный волновой пакет,

(Это не то же самое, что изображено на фиг. 48.1, где волна имеет целый ряд максимумов, но сними вполне можно расправиться, сложив несколько волн с при­близительно одинаковыми значениями w и k. Таким способом можно избавиться от всех максимумов, кроме одного.)

При этих обстоятельствах, поскольку квадрат выражения (48.19) представляет вероятность найти частицу в некотором месте, мы знаем, что в данный момент больше шансов найти ча­стицу вблизи центра «колокола», где амплитуда максимальна.

Если подождать немного, то волна передвинется, и по проше­ствии некоторого промежутка времени «колокол» перейдет в какое-то другое место. Зная, что частица вначале где-то была расположена, мы ожидали бы, согласно классической меха­нике, что она будет где-то и позднее, ведь есть же у нее ско­рость и импульс в конце концов. При этом квантовая теория дает в пределе правильные классические соотношения между энергией, импульсом и скоростью, если только групповая ско­рость, скорость модуляции, будет равна скорости классиче­ской частицы с тем же самым импульсом.

Сейчас необходимо показать, так ли это на самом деле или нет. Согласно классической теории, энергия связана со ско­ростью уравнением

Точно таким же образом импульс равен

Как следствие отсюда после исключения v получается

E²-р²c²=m²c⁴,

т. е. р_mр_m=m². Это величайший результат четырехмерья, о котором мы уже говорили много раз, устанавливающий связь между энергией и импульсом в классической теории. Теперь же, поскольку мы собираемся заменить E и p на w и k помощью подстановки Е=hwи p=hk, он означает, что в квантовой меха­нике должна существовать связь

Таким образом, возникло соотношение между частотой и вол­новым числом квантовомеханической амплитуды, описывающей частицу с массой m. Из этого уравнения можно получить

т. е. фазовая скорость w/k; снова больше скорости света!

Рассмотрим теперь групповую скорость. Она должна быть равна скорости, с которой движется модуляция, т. е. dw/dk.

Чтобы найти ее, нужно продифференцировать квадратный корень; это дело нехитрое. Производная равна

Но входящий сюда квадратный корень есть попросту w/с, так что эту формулу можно записать в виде dw/dk=е²k/w. Далее, так как k/w равно р/Е, то

Но, согласно (48.20) и (48.21), с²р/Е равно v — скорости ча­стицы в классической механике. Таким образом видно, что, принимая во внимание основные квантовомеханические соот­ношения E=hwи p=hk, определяющие w и k через классиче­ские величины Е и р и дающие только уравнение w²-k²c²= =m²с⁴/h², теперь можно понять также соотношения (48.20) и (48.21), связывающие Е и р соскоростью. Групповая скорость, разумеется, должна быть скоростью частиц, если эта интер­претация вообще имеет какой-либо смысл. Пусть в какой-то момент, как мы полагаем, частица находится в одном месте, а затем; скажем через 10 минут,— в другом. Тогда, согласно кван­товой механике, расстояние, пройденное «колоколом», разде­ленное на интервал времени, должно равняться классической скорости частицы.

§ 6. Волны в пространстве трех измерений

Мы заканчиваем наше обсуждение волн несколькими об­щими замечаниями о волновом уравнении. Эти замечания, при­званные дать нам картину того, чем нам предстоит заниматься в будущем, вовсе не претендуют на то, чтобы вы поняли их сразу; они должны скорее показать, как будут выглядеть все эти вещи, когда вы несколько больше познакомитесь с волна­ми. Мы уже записали уравнение для распространения звука в одном измерении:

здесь с — скорость того, что мы назвали волнами. Если речь идет о звуке, то это скорость звука, если о свете — то это ско­рость света. Мы показали, что для звуковой волны перемещения частиц должны распространяться с некоторой скоростью. Но из­быточное давление, как и избыточная плотность, тоже распро­страняется с некоторой скоростью. Таким образом, можно ожидать, что и давление будет удовлетворять этому же уравнению.

Так оно и есть на самом деле, однако докажите это самостоя­тельно. Указание: r_u пропорционально скорости изменения c с расстоянием х. Следовательно, продифференцировав волновое уравнение по х, мы немедленно обнаружим, что дc/дх удовлет­воряет тому же самому уравнению. Другими словами, r_u удов­летворяет тому же самому уравнению. Но Р_uпропорционально r_u, поэтому и Р_uудовлетворяет тому же самому уравнению. Та­ким образом, и давление, и перемещение — все описывается одним и тем же уравнением.

Обычно волновое уравнение для звука записывается через давление, а не через перемещение. Это проще, потому что давление — скаляр и не имеет никакого направления. Но перемещение есть вектор, и поэтому лучше иметь дело с дав­лением.

Следующий вопрос, который нам предстоит обсудить, отно­сится к волновому уравнению в трехмерном пространстве. Мы знаем, что звуковая волна в одномерном пространстве описы­вается решением ехр[i(wt-kx)], где w=kc_S. Кроме того, нам из­вестно, что в трех измерениях волна описывается выражением exp[i(wt-k_xx-k_yy-k_zz)], и в этом случае w²=k²с_S² [сокращен­ная запись (k²_x+k²_y+k²_z)c²_S]. Сейчас мы хотим просто угадать вид волнового уравнения в трехмерном пространстве. Естествен­но, что в случае звука это уравнение можно получить с помощью тех же самых динамических соображений, но уже в трехмерном пространстве. Однако мы не будем сейчас делать этого, а просто напишем ответ: уравнение для давления или перемещения (или чего-то другого) имеет вид

правильность этого уравнения может быть легко проверена подстановкой в него функции exp[i(wt-k·r)]. Ясно, что при каждом дифференцировании по х происходит умножение на -ik_x. Если мы дифференцируем дважды, то это эквивалентно умножению на -k²_x, так что для такой волны первый член получится равным -k²_xP_u. Точно таким же образом второй член окажется равным -k²_уР_u, а третий — равным -k²_zP_u. С правой же стороны мы получим -w²/c²_SР_u. Если мы вынесем 1 за скобку Р_ии изменим знаки всех членов, то увидим, что между k и w как раз получится желаемое соотношение.

Возвращаясь назад, мы должны прийти к основному урав­нению, соответствующему дисперсионному соотношению (48.22) для квантовомеханической волны. Если j — амплитуда нахождения частицы в момент t в точке с координатами х, у и z, то основное уравнение квантовой механики для свободной частицы имеет вид

Прежде всего заметим, что релятивистский характер этого уравнения гарантируется появлением координат x, y, z и вре­мени t в такой удачной комбинации, что она автоматически учитывает принцип относительности. Кроме того, это уравне­ние волновое. Если подставить в него плоскую волну, то как следствие мы получим равенство -k²+w²/c²=m²c²/h², которое должно выполняться в квантовой механике. В этом волновом уравнении содержится еще одна фундаментальная вещь: любая суперпозиция волн также будет его решением. Таким образом, это уравнение опирается на всю квантовую механику и всю теорию относительности, которая уже обсуждалась нами до сих пор, по крайней мере когда мы имели дело с единственной частицей в пустом пространстве без всяких потенциалов и воздействующих на нее сил!

§ 7. Собственные колебания

Вернемся теперь к другим очень любопытным примерам биений, которые немного отличаются от того, что мы рассмат­ривали до сих пор. Представьте себе два одинаковых маятника, которые связаны между собой слабой пружинкой. Длины их должны быть одинаковыми с возможно большей точностью. Если мы оттянем один маятник и отпустим его, то он будет качаться взад и вперед и будет тянуть то взад, то вперед связывающую пружинку, т. е. получится устройство, создающее силу с собственной частотой второго маятника. Можно заключить из знако­мой нам теории резонансов, что если к какому-то предмету при­кладывать с надлежащей частотой силу, то она будет двигать этот предмет. Таким образом, ясно, что один маятник, двигаясь взад и вперед, будет раскачивать второй. Однако при этих усло­виях происходит некое новое явление, связанное с тем, что энергия системы конечна. Первый маятник постепенно рас­трачивает свою энергию, вызывая движение другого маятника, и в конце концов полностью отдаст свою энергию и остано­вится. Вся энергия теперь будет сосредоточена во втором маятнике. Но пройдет немного времени и все будет происхо­дить наоборот: энергия из второго маятника будет перекачи­ваться назад, в первый маятник. Это очень интересное и за­нимательное явление. Мы сказали, что оно связано с теорией биений, и сейчас мы должны показать, как можно понять это явление с точки зрения этой теории.

Обратите внимание, что движение каждого из двух маятни­ков — это колебания с циклически изменяющейся амплитудой. Поэтому движение одного из маятников можно, очевидно, рас­сматривать с различных точек зрения, в частности как сумму двух одновременных колебаний с мало отличающимися часто­тами. Таким образом должно быть возможно обнаружить в этой системе два других движения и утверждать, что поскольку система наша, безусловно, линейная, то мы видим суперпози­цию этих двух решений. Действительно, легко найти два спо­соба так запустить нашу систему, что каждый из них даст в результате идеальное абсолютно периодическое колебание с одной частотой. Движение, с которого мы начали, не строго периодично, оно не продолжается все время (один маятник по­степенно передает свою энергию другому и изменяет свою ам­плитуду), но есть способы так начать движение, что не будет никаких подобных изменений. Как только вы узнаете, что это за способы, то сразу же поймете почему. Если, например, мы запустим оба маятника одновременно, то, поскольку длина их одинакова и пружинка в этом случае бездействует, оба маятника так и будут продолжать качаться все время вместе. (Разумеется, если нет трения и все достаточно хорошо подог­нано.) С другой стороны, существует еще одна возможность создать строго периодическое движение, которое также имеет определенную частоту,— когда маятники, оттянутые вначале в разные стороны на точно равные расстояния, движутся в противоположных направлениях. Нетрудно сообразить, что пружинка немного увеличивает «восстанавливающую силу», возникающую из-за действия силы тяжести, и система колеб­лется с несколько большей частотой, чем в первом случае,— вот и все. Почему с большей? Да потому что пружинка тянет, помогая силе тяжести, и это делает систему более «жесткой», так что частота такого колебания чуть-чуть больше.

Итак, создать колебания с постоянной амплитудой в нашей системе можно двумя способами: либо оба маятника качаются все время вместе с одной частотой, либо они качаются в проти­воположных направлениях с несколько большей частотой.

Действительное же движение системы, поскольку она ли­нейна, можно представить в виде суперпозиции этих двух спо­собов. (Напомним, что предметом этой главы являются эффек­ты сложения двух движений с различными частотами.) Давайте подумаем, что произошло бы, если бы мы сложили эти два ре­шения. Если в момент t=0 запустить оба эти движения (причем с равными амплитудами и одинаковой фазой), то сумма этих двух движений означает, что один маятник, на который ка­ким-то образом воздействовало первое движение и противо­положным образом воздействовало второе, должен оставаться на месте, тогда как другой маятник, двигаясь одинаково при обоих способах движения, качается с удвоенной амплитудой. С течением времени, однако, оба эти основных движения, суще­ствуя независимо одно от другого, медленно сдвигаются по фазе одно относительно другого. Это означает, что после до­статочно большого промежутка времени, такого, что в первом движении произойдет, скажем, 900,5 колебания, а во втором — только 900, относительная фаза станет как раз обратной по отношению к тому, что было вначале. Иначе говоря, маятник, имевший вначале большую амплитуду, остановится, тогда как маятник, неподвижный вначале, начнет качаться изо всех сил!

Итак, мы видим, что такое сложное движение можно рас­сматривать в рамках идеи резонансов, когда энергия от одного маятника переходит к другому, или как суперпозицию двух движений с постоянной амплитудой и различными частотами.

* В Советском Союзе изображение имеет 625 строк и ширина ка­налов несколько больше.— Прим ред.

* Следует сделать здесь небольшое примечание: в каких случаях кривая может быть представлена в виде суммы множества косинусов? Ответ: Почти всегда, за исключением небольшого числа случаев, которые могут присниться разве только математику. В каждой точке кривая, разумеется, должна иметь только одно значение и она не должна быть безумной кривой, прыгающей до бесконечности на протяжении беско­нечно малого промежутка времени или что-нибудь в этом же духе. Однако если отвлечься от этих ограничений, то любая разумная кривая (в част­ности, и та, которая получается при колебании голосовых связок певицы) всегда может быть представлена в виде суммы косинусоидальных волн

 

 

Глава 49 СОБСТВЕННЫЕ КОЛЕБАНИЯ

§ 1. Отражение волн

§ 2. Волны в огра­ниченном пространстве и собственные частоты

§ 3. Двумерные собственные колебания

§ 4. Связанные маятники

§ 5. Линейные системы

§ 1. Отражение волн

В этой главе мы рассмотрим ряд замеча­тельных явлений, возникающих в результате «заключения» волны в некоторую ограничен­ную область. Сначала нам придется устано­вить несколько частных фактов, относящихся, например, к колебанию струны, а затем, обоб­щив эти факты, мы придем, по-видимому, к наиболее далеко идущему принципу математи­ческой физики.

Первый пример волн в ограниченном про­странстве — это волны в пространстве, огра­ниченном с одной стороны. Давайте возьмем простой случай одномерной волны на струне. Можно было бы рассмотреть плоскую звуко­вую волну в пространстве, ограниченном с одной стороны стенкой, или какие-то другие примеры той же природы, но для наших тепе­решних целей вполне достаточно простой струны. Предположим, что один конец струны закреплен, ну, например, вмурован в «абсо­лютно жесткую» стенку. Математически это можно описать, указав, что перемещение струны у в точке x=0 должно быть нулем, ибо конец струны не может двигаться. Далее, если бы в этом деле не участвовала стенка, то, как мы знаем, общее решение, описывающее движение струны, можно было бы представить в виде суммы двух функций F(x-ct) и G(x+ct), причем первая описывает волну, бегущую по струне в одну сторону, а вторая — в другую, так что

y=F(x-ct)+G(x+ct) (49.1)

будет общим решением для любой струны. Но нам, помимо этого, нужно еще удовлетворить условию неподвижности одного конца. Если в уравнении (49.1) мы положим х=0 и посмотрим, какие будут у в любой момент t, то получим y=F(-ct)+G(+ct). Но эта сумма должна быть нулем в любой момент времени, а это означает, что функция G(+ct) должна быть равна -F(-ct). Другими словами, функция G от некоторой величины должна быть равна функ­ции -F от той же величины со знаком минус. Подставляя снова полученный результат в уравнение (49.1), находим ре­шение поставленной задачи:

y=F(x-ct)-F(-x-ct). (49.2)

Ясно, что это выражение всегда даст y=0, если х поло­жить равным нулю.

На фиг. 49.1 представлена волна, идущая в отрицательном x-направлении вблизи точки х=0, и гипотетическая волна, идущая в противоположном направлении с обратным знаком и с другой стороны от начала координат.

Фиг. 49.1. Отражение от стенки как суперпозиция двух бегущих волн.

Я сказал «гипотетиче­ская», потому что с другой стороны, конечно, никакой колеб­лющейся струны нет. Истинное же движение струны должно рассматриваться как сумма этих двух волн в области положи­тельных х. Достигнув начала координат, они в точке х=0 полностью уничтожат друг друга, а затем вторая (отраженная) волна, идущая, разумеется, в противоположном направлении, окажется единственной волной в области положительных х. Эти результаты эквивалентны следующему утверждению: волна, достигнув защемленного конца струны, отражается от него с изменением знака. Такое отражение всегда можно понять, если представить себе, как нечто дошедшее до конца струны вылетит затем из-за стены «вверх ногами». Короче говоря, если мы предположим, что струна бесконечна и что, где бы ни находилась волна, бегущая в одном направлении, всегда существует симметричная ей относительно точки х=0 другая волна, бегущая в противоположном направлении, то в самой точке х=0 никакого перемещения не будет, а поэтому безразлично, защемлена ли струна в этом месте или нет.

Следующий наш пример — отражение периодической вол­ны. Предположим, что волна, описываемая функцией F(x-ct), представляет собой синусоидальную волну, которая затем от­ражается. Тогда отраженная волна -F(-х-ct) тоже будет синусоидальной волной той же частоты, но пойдет она в про­тивоположном направлении. Эту ситуацию проще всего опи­сать с помощью комплексных функций

F(x-ct)=e^iw(t-x/c) и F(-х-ct)=e^iwa(t+x/c).

Нетрудно убедиться, что если подставить их в выражение (49.2) и положить х=0, то в любой момент времени t переме­щение будет равно нулю и, следовательно, необходимое условие окажется выполненным. Воспользовавшись теперь свойством экспоненты, можно записать результат в более простом виде:

y=e^iwt(e^-iwx/c-e^iwx/c)=-2ie^iwtsin(wx/c). (49.3)

Мы получили нечто новое и интересное. Из этого решения ясно, что если мы посмотрим на любую точку х нашей струны, то увидим, что она осциллирует с частотой w. Совершенно неважно, где находится эта точка, все равно частота будет той же самой! Однако на струне есть такие места (где sin (wx/c)=0), которые вообще не перемещаются. Более того, если в любой момент времени t сделать моментальный снимок колеблющейся струны, то на фотографии получится синусоидальная волна, но величина ее амплитуды будет зависеть от времени t. Из выражения (49.3) можно видеть, что длина одного цикла сину­соидальной волны равна длине какой-либо из волн;

l=2pc/w. (49.4)

Неподвижные точки удовлетворяют условию sin(wx/c)=0, которое означает, что wx/c=0, p, 2p, ..., np, ... . Эти точки на­зываются узлами. Каждая точка между двумя соседними узлами движется синусоидально вверх и вниз, но способ ее движения остается фиксированным в пространстве. Это основная харак­теристика того, что называется собственным колебанием, гармоникой или модой. Если движение обладает тем свой­ством, что каждая точка предмета движется строго синусои­дально и все точки движутся с одинаковой частотой (хотя одни, может быть, больше, а другие меньше), то мы имеем дело с собственным колебанием.

§ 2. Волны в ограниченном пространстве и собственные частоты

Перейдем к обсуждению следующей интересной задачи. Что произойдет, если струну закрепить с двух концов, скажем в точках x=0 и x=L? Давайте начнем с идеи отражения волны, с некоего горба, движущегося в одном направлении. С тече­нием времени этот горб подойдет к одному концу струны и в конце концов превратится в небольшой всплеск, поскольку здесь он складывается с перевернутым ответным горбом, идущим с другой стороны. Наконец первый горб совсем исчезнет, а в обратном направлении побежит другой, «ответный» горб, и весь процесс повторится уже на другом конце. Как видите, задача решается совсем просто, впрочем здесь возникает интересный вопрос: можно ли в этом случае получить синусоидальную вол­ну (только что описанное решение периодично, но, разумеется, не синусоидально периодично). Давайте попытаемся «вставить» в нашу струну синусоидально периодическую волну. Если один конец струны закреплен, то мы знаем, что должно полу­читься нечто похожее на наше предыдущее решение (49.3). Но то же самое должно получиться и у второго конца, ведь он тоже закреплен. Поэтому единственная возможность полу­чить периодическое синусоидальное движение—это взять волну, которая в точности укладывается на длине струны. В против­ном случае мы не получим собственной частоты, с которой струна могла бы продолжать свои колебания. Короче говоря, если по струне пустить синусоидальную волну, которая в точности укладывается на ее длине, то она сохраняет свою идеальную синусообразную форму и будет гармонически колебаться с не­которой частотой.

Математически мы можем задать форму волны в виде функ­ции sinkx, где k=w/c, как и в уравнениях (49.3) и (49.4). Эта функция обращается в нуль при х=0, однако то же условие должно выполняться и на другом конце струны. Дело в том, что k уже не будет произвольным, как в случае полуограниченной струны. Оба конца могут быть закреплены при одном-единственном условии, что sinkL=0. Но чтобы синус был равен нулю, его угол должен быть кратен целому числу p, например 0, p, 2p и т. д. Поэтому уравнение

kL=np (49.5)

в зависимости от того целого числа, которое мы подставим в него, дает полный набор различных чисел k. При этом каждому числу k соответствует частота w, которая по формуле (49.3) равна просто

w=kc=npc/L. (49.6)

Итак, мы нашли, что синусоидальные колебания струны могут происходить только с некоторыми определенными часто­тами. Это — наиболее важная характеристика волн в ограни­ченной области. Сколь бы сложна ни была система, всегда ока­зывается, что в ней могут быть чисто синусоидальные колеба­ния, но частота их определяется свойствами данной системы и природой ее границ. В случае струны возможно множество раз­личных частот, каждой из которых соответствует определенное собственное колебание — движение, синусоидально повторяющее самое себя.

На фиг. 49.2 показаны первые три собственные гармоники нашей струны.

Фиг. 49.2. Первые три гар­моники колеблющейся струны.

Длина волны l первой из них равна 2L. В этом легко убедиться, продолжив волну до точки x=2L и получив полный цикл синусоидальной волны. Угловая частота w равна в общем случае 2pc, деленному на длину волны К, а поскольку сейчас у нас l=2L, то частота будет равна pс/b, что согласуется с формулой (49.6) при n=1. Обозначим эту частоту через w₁ Следующая собственная гармоника напоми­нает бантик из двух петель с узлом посредине. Ее длина просто равна L. Соответствующая величина k, а следовательно, и ча­стота w должны быть вдвое большими, т. е частота равна 2w₁. Частота третьей собственной гармоники оказывается рав­ной Зw₁ и т. д. Таким образом, различные собственные гармо­ники кратны целому числу низшей частоты w₁ т. е. w₁, 2w₁, Зw₁ и т. д.

Вернемся теперь к общему движению струны. Оказывается, что любое возможное движение можно рассматривать как одно­временное действие некоторого числа собственных колебаний. На самом деле для описания наиболее общего движения долж­но быть одновременно возбуждено бесконечное число собствен­ных гармоник. Чтобы получить некоторое представление о том, что происходит при таком сложении, давайте посмотрим, что получится при одновременном колебании двух первых соб­ственных гармоник. Пусть первая из них колеблется так, как это показано в ряде схематических чертежей фиг. 49.3, где изображены отклонения струны через равные промежутки вре­мени на протяжении полуцикла низшей частоты.

Предположим теперь, что одновременно с первой собствен­ной гармоникой работает и вторая. Последовательные положе­ния струны при возбуждении этой собственной гармоники показаны тоже на фиг. 49.3 пунктирной линией. По отношению к первой гармонике они сдвинуты по фазе на 90°. Это означает, что в начальный момент никакого отклонения не было, но ско­рости двух половинок струны направлены в противоположные стороны. Вспомним теперь общий принцип линейных систем: если взять любые два решения, то сумма их тоже будет реше­нием. Поэтому перемещения, полученные сложением двух ре­шений, показанных на фиг. 49.3, будут третьим возможным ре­шением

Фиг. 49.3. Две гармоники, напоминающие при сложе­нии бегущую волну.

На этом же рисунке показан и результат сложения, который начинает напоминать горб, пробегающий взад и вперед по струне от одного конца до другого, хотя с помощью только двух собственных гармоник нельзя построить доста­точно хорошей картины такого движения; их нужно гораздо больше. Этот результат представляет на самом деле частный случай основного принципа линейных систем, который гла­сит:

Любое движение можно рассматривать как составленное из различных собственных гармоник, взятых с надлежащими ам­плитудами и фазами.

Значение этого принципа обусловлено тем фактом, что каж­дое собственное колебание — очень простая вещь — это просто синусоидальное движение во времени. По правде говоря, даже общее движение струны — еще не самая сложная вещь; суще­ствует движение куда более сложное, скажем такое, как виб­рация крыльев самолета. Тем не менее даже у крыльев само­лета можно обнаружить некие собственные кручения с опре­деленными частотами. А если так, то полное движение можно рассматривать как суперпозицию гармонических колебаний (за исключением тех случаев, когда вибрация настолько велика, что система уже не может рассматриваться как линейная).

§ 3. Двумерные собственные колебания

Сейчас мы перейдем к рассмотрению очень интересного поведения собственных гармоник в двумерных колебаниях. До сих пор мы говорили только об одномерных колебаниях: натянутой струне или звуковых волнах в трубе. В конце концов мы должны добраться до трех измерений, но сначала давайте остановимся на более легком этапе — этапе двумерных колеба­ний. Возьмем для большей определенности прямоугольный ре­зиновый барабан, перепонка которого закреплена по краям так, что на прямоугольном крае барабана она перемещаться не может. Пусть размеры прямоугольника будут

равны а и 6, как это показано на фиг. 49.4.

Фиг. 49.4. Колебание прямо­угольной пластинки.

Прежде всего, каковы ха­рактеристики возможного движения? Можно начать с того же, с чего мы начали, когда рассматривали пример со стру­ной. Если бы никакого закрепления не было вовсе, то можно было бы ожидать появления волн, бегущих в некото­ром направлении, например синусоидальной волны, опи­сываемой функцией ехр(iwt) ехр[-i(k_чx)+i(k_yy)], направле­ние движения которой зависит от относительной величины чисел k_xи k_y. А как теперь сделать узел на оси х, т. е. при y=0? Используя ту же идею, что и для одномерной струны, можно добавить волну, описываемую комплексной функцией

-exp(iwt)ехр[-i(k_xx)-i(k_yy)].

Суперпозиция этих волн в результате дает нулевое переме­щение при y=0 независимо от того, каковы будут значения х и t. (Хотя эти функции будут определены и для отрицательных значений у там, где никакого барабана нет и колебаться не­чему, но на это можно не обращать никакого внимания. Ведь нам хотелось устранить перемещение при у=0, и мы добились этого.) Вторую функцию в этом случае можно рассматривать как отраженную волну.

Однако нам нужно получить узел не только на линии y=0, но и на линии у=b. Как же это сделать? Решение такой задачи связано с некоторыми вещами, которыми мы занимались при изучении отражения света от кристалла. Волны, гасящие друг друга при y=0, могут сделать то же самое и при у=b, только когда 2b sin 0 равно целому числу длин волн l, (q — угол, пока­занный на фиг. 49.4):

ml=2bsinq, m=0, 1, 2, .... (49.7)

Точно таким же образом, т.е. сложением еще двух функций [-exp(iwt)]exp[i(k_xx)+ i(k_yy)] и [+exp(ict)}exp[i(k_xx)-i(k_yy)], каждая из которых представляет отражение другой от линии х=0, можно устроить узел и на оси у. Условие того, что линия х=а будет тоже узловой, получается так же, как и условие при у=b, т. е. 2acosq должно быть равно целому числу длин волн:

nl = 2acosq. (49.8)

Тогда окончательный результат таков: волны, «заключенные» в ящике, имеют вид стоячей волны, т. е. образуют какие-то определенные собственные гармоники.

Таким образом, если мы хотим иметь дело с собственными гармониками, то должны удовлетворить двум написанным выше условиям. Для начала давайте найдем длину волны. Ис­ключив из уравнений (49.7) и (49.8) угол q, можно выразить длину волны через a, b, n и т. Легче всего это сделать так: сначала разделить обе части уравнений соответственно на 2b и 2a, а затем возвести их в квадрат и сложить. В результате мы получим уравнение

sin²q+cos²q =1=(nl/2a)²+(ml/2b)²,

которое легко разрешить относительно l:

Итак, мы определили длину волны через два целых числа, а по длине волны мы немедленно получаем частоту w, ибо, как известно, частота равна 2pc, деленной на длину волны.

Этот результат настолько важен и интересен, что необхо­димо теперь получить его строго математически без использо­вания аналогий с отражением. Давайте представим колебание в виде суперпозиции четырех волн, подобранных таким обра­зом, чтобы все четыре линии x=0, х=а, y=0 и у=b были узло­выми. Потребуем еще, чтобы все эти волны имели одинаковую частоту, т. е. чтобы результирующее движение представляло собственное колебание. Из главы об отражении света мы уже знаем, что функция exp(iwt)exp[-i(k_xx)+i(k_yy)] опи­сывает волну, идущую в направлении, указанном на фиг. 49.4. По-прежнему остается справедливым уравнение (49.6), т. е. k =w/c, с той разницей, что теперь

k²=k²_x+k²_y. (49.10)

Из рисунка ясно, что k_x=kcosq, a k_y=ksinq.

Таким образом, наше выражение для перемещения прямо­угольной перепонки барабана (назовем это перемещение j запишется в виде

Хотя выглядит это довольно неприглядно, сумма таких экспо­нент, в сущности, не так уж громоздка. Их можно свернуть в синусы, так что перемещение, как оказывается, приобретает вид

Другими словами, получились знакомые синусоидальные колебания, форма которых тоже синусоидальна как в направ­лении оси х, так и в направлении оси у. Граничные условия при x= 0 и y=0 удовлетворяются автоматически. Однако мы хо­тим, кроме того, чтобы j обращалось в нуль при х=а и у=b. Для этого мы должны наложить два дополнительных условия, а именно k_xa и k_xb должны быть равны целому числу p (эти це­лые числа могут быть разными для k_xa и k_yb!). Но поскольку, как мы видели, k_x=kcosq и k_y=ksinq, то отсюда немедленно получаются уравнения (49.7) и (49.8), а из них следует оконча­тельный результат (49.9).

Возьмем теперь для примера прямоугольник, ширина ко­торого вдвое больше высоты. Если положить а=2b и восполь­зоваться уравнениями (49.4) и (49.9), то можно вычислить ча­стоты всех гармоник

В табл. 49.1 перечислено несколько простых гармоник и ка­чественно показана их форма.

Таблица 49.1 · ПРОСТЫЕ ГАРМОНИКИ И ИХ ФОРМА

Следует отметить наиболее важную особенность этого част­ного случая — частоты не кратны ни друг другу, ни какому-то другому числу. Представление о том, что собственные частоты гармонически связаны друг с другом, в общем случае неверно. Оно неверно ни для системы размерности, большей единицы, ни даже для одномерной системы, более сложной, чем однород­ная и равномерно натянутая струна. Простейшим примером может служить подвешенная цепочка, натяжение которой вверху меньше, чем внизу. Если возбудить в такой цепочке гармонические колебания, то возникнут собственные гармо­ники с различными частотами, однако частоты не будут просто кратными какому-то числу, да и сама форма гармоник больше не будет синусоидальной.

Еще причудливей оказываются гармоники более сложных систем. Человеческий рот, например, представляет собой по­лость, расположенную над голосовыми связками. Движением языка и губ можно создать либо трубу с открытым концом, либо трубу с закрытым концом, причем диаметры и формы этой трубы будут раз личными. В общем это страшно сложный резона­тор, но тем не менее все же резонатор. При разговоре мы с помощью голосовых связок создаем какой-то тон. Тон этот довольно сложен, в него входит множество звуков, но благо­даря различным резонансным частотам полость рта еще больше модифицирует его. Певец, например, может петь различные гласные: «а», «о», «у» и еще другие с той же самой высотой, но звучат они по-разному, ибо различные гармоники по-разному резонируют в этой полости. Огромную роль резонансных ча­стот полости в образовании голосовых звуков можно проде­монстрировать на очень простом опыте. Как известно, скорость звука обратно пропорциональна квадратному корню из плот­ности, поэтому для разных газов она различна. Если вместо воздуха мы используем гелий, плотность которого меньше, то скорость звука в нем окажется больше и все резонансные ча­стоты полости будут больше. Следовательно, если бы мы могли перед тем, как начать говорить, наполнить наши легкие ге­лием, то, хотя голосовые связки по-прежнему колебались бы с той же частотой, характер нашего голоса резко изменился бы.

§ 4. Связанные маятники

Напоследок необходимо подчеркнуть, что гармоники возни­кают не только в сложных непрерывных системах, но и в очень простых механических системах. Хорошим примером этого служит рассмотренная в предыдущей главе система двух свя­занных маятников. Там мы показали, что общее движение этой системы можно рассматривать как суперпозицию двух типов гармонических движений с различными частотами, так что даже такую систему можно рассматривать с точки зрения собствен­ных гармоник. В струне возбуждается бесконечное число соб­ственных гармоник, у двумерной поверхности их тоже беско­нечно много. В каком-то смысле здесь получается даже двойная бесконечность (если бы мы только знали, как работать с бесконечностями!). Но в простом механическом устройстве, обла­дающем только двумя степенями свободы и требующем для своего описания лишь двух переменных, возбуждаются всего две гар­моники.

Попробуем найти математически эти две гармоники для слу­чая, когда длины маятников одинаковы. Пусть отклонение одного маятника будет х, а другого — y, как это показано на фиг. 49.5.

Фиг. 49.5. Два связанных маят­ника.

При отсутствии пружины сила тяжести, действующая на первый маятник, пропорциональна его отклонению. Если бы здесь не было пружины, то для одного маятника появилась бы некоторая собственная частота w₀, а уравнение движения в этом случае приобрело бы вид

m(d²x/dt²)=-mw²₀x. (49.13)

Второй маятник при отсутствии пружины качался бы точно так же, как и первый. Однако при наличии пружины в допол­нение к восстанавливающей силе, возникающей в результате гравитации, появляется еще добавочная сила от пружины, ко­торая стремится «стянуть» маятники. Эта сила зависит от пре­вышения отклонения х над отклонением у и пропорциональна их разности, т. е. она равна некоторой постоянной, зависящей только от геометрии, умноженной на (х-у). Та же сила, но в обратном направлении действует на второй маятник. Поэтому уравнения движения, которые мы должны решить, будут сле­дующими:

Чтобы найти движение, при котором оба маятника колеблются с одинаковой частотой, мы должны определить, насколько отклоняется каждый из них. Другими словами, маятник А и маятник В будут колебаться с одинаковой частотой и с ка­кими-то амплитудами А и B, отношение которых фиксировано. Давайте проверим, насколько подходит такое решение:

x=Ae^iwt, у=Ве^iwt. (49.15)

Если подставить его в уравнения (49.14) и собрать подобные члены, то получим

При выводе этих уравнений мы сократили общий множитель е^iwtи разделили все на m.

Теперь мы видим, что получились два уравнения для, каза­лось бы, двух неизвестных. Однако на самом деле здесь не два неизвестных, ибо общие масштабы движения нельзя найти из этих уравнений. Они могут дать нам только отношение А к В, причем оба уравнения должны дать одинаковую величину. Тре­бование согласованности уравнений друг с другом накладывает требование на частоту: она должна быть какой-то очень спе­циальной.

Но найти частоту в этом частном случае довольно легко. Если перемножить оба уравнения, то мы получим

В обеих сторонах можно сократить произведение АВ, за исклю­чением тех случаев, когда либо А, либо В равно нулю, что означает отсутствие движения вообще. Но если движение есть, то должны быть равны между собой и другие сомножи­тели, что приводит к квадратному уравнению. В результате получаются две возможные частоты:

w²₁=w²₀ и w²₂=w²₀+2k/m. (49.18)

Более того, если подставить эти значения частот снова в уравне­ния (49.16), то для первой частоты мы получим А=В, т. е. пружина вообще не будет растягиваться и оба маятника колеб­лются с частотой w₀, как если бы пружины вообще не было. В другом решении, когда А =-В, пружина увеличивает вос­станавливающую силу и частота возрастает. Более интересен случай, когда маятники имеют различные длины. Анализ это­го случая, который очень похож на то, что мы недавно проде­лали, рекомендуем в качестве упражнения провести самим читателям.

§ 5. Линейные системы

Давайте теперь подытожим рассмотренные выше идеи, которые все являются аспектами, по-видимому, наиболее об­щего и удивительного принципа математической физики. Если у нас есть линейная система, характеристики которой не за­висят от времени, то движение ее, вообще говоря, не обязано быть каким-то особенно простым. На самом деле оно может быть чрезвычайно сложным, однако существуют такие особые дви­жения (обычно их целый ряд), при которых форма колебания синусоидально зависит от времени. Для колеблющихся систем, о которых сейчас шла речь, мы обычно получали мнимую эк­споненту, но вместо того, чтобы сказать «экспоненциально», я предпочел сказать «синусоидально». Однако если стремиться к большей общности, то нужно говорить о каких-то особых движениях, очень специальной формы, изменяющихся экспо­ненциально со временем. Наиболее общее движение систем всегда можно представить в виде суперпозиции движений, включающих каждую из различных экспонент.

Есть смысл подчеркнуть еще раз специально для случая синусоидального движения: линейная система не обязательно должна двигаться чисто синусоидально, т. е. с одной опреде­ленной частотой, но как бы она ни двигалась, это движение можно представить в виде суперпозиции чисто синусоидаль­ных колебаний. Частота каждого из этих колебаний, как и форма волны, зависит от свойств системы. Общее движение любой такой системы характеризуется заданием амплитуды и фазы каждой из гармоник при их сложении. Можно сказать это и по-другому: колебание любой линейной системы эквива­лентно набору гармонических независимых осцилляторов, ча­стоты которых соответствуют частотам собственных гармоник данной системы.

Эту главу мы закончим замечанием о связи гармоник с квантовой механикой. Колеблющимися объектами и величи­нами, которые изменяются со временем в квантовой механике, являются амплитуды вероятности, которые определяют ве­роятности обнаружения электрона или системы электронов в данном месте. Эта амплитуда может изменяться в пространстве и времени и удовлетворяет линейному уравнению. Но при пе­реходе к квантовой механике происходит переименование. То, что мы называли частотой амплитуды вероятности, переходит в энергию в ее классическом смысле. Поэтому установленный выше принцип можно перевести на язык квантовой механики, заменив слово частота словом энергия. Получится примерно так: квантовомеханическая система, например атом, не обя­зательно обладает определенной энергией, точно так же, как простая механическая система не обязательно имеет определенную частоту, но каково бы ни было поведение системы, его всегда можно представить в виде суперпозиции состояний с определенной энергией. Энергия каждого состояния, как и форма амплитуды, которая дает вероятность нахождения ча­стицы в различных местах, определяется свойствами атома. Общее движение может быть описано заданием амплитуд каж­дого из различных энергетических состояний. Именно здесь кроется причина возникновения энергетических уровней в квантовой механике. Поскольку квантовая механика все описывает в виде волн, то при некоторых обстоятельствах, когдаэлектрон не обладает достаточной энергией, чтобы бесповоротно оторваться от протона, он представляет собой просто волну в ограниченном пространстве. Поэтому, так же как и для огра­ниченной струны, при решении волнового уравнения в кванто­вой механике в подобном случае возникают определенные ди­скретные частоты. В квантовомеханической интерпретации это будут определенные энергии. Следовательно, квантовомеханическая система, вследствие того что она описывается с по­мощью волн, может иметь определенные состояния с фиксиро­ванной энергией; примером могут служить дискретные энерге­тические уровни атомов.

 

 

Глава 50 ГАРМОНИКИ

§ 1. Музыкальные звуки

§ 2. Ряд Фурье

§ 3. Качество и гармония

§ 4. Коэффициент Фурье

§ 5. Теорема об энергии

§ 6. Нелинейная реакция

§ 1. Музыкальные звуки

Говорят, что Пифагор первый обнаружил тот интересный факт, что одновременное зву­чание двух одинаковых струн различной длины приятнее для слуха, если длины этих струн относятся друг к другу как небольшие целые числа. Если длины струн относятся как 1:2, то это — музыкальная октава; если они относятся как 2:3, то это соответствует интервалу между нотами до и соль и называется квинтой. Эти интервалы считаются «приятно» звучащи­ми аккордами. На Пифагора произвело такое впечатление это открытие, что на его основе он создал школу «пифагорийцев», как их называли, которые мистически верили в вели­кую силу чисел. Они полагали, что нечто по­добное будет открыто и в отношении планет, или «сфер». Иногда можно услышать такое вы­ражение: «музыка сфер». Смысл его в том, что в природе предполагалось существование чис­ловой связи между орбитами планет или между другими вещами. Это считается чем-то вроде суеверия древних греков. Но далеко ли от этого ушел наш сегодняшний научный интерес к количественным соотношениям? Открытие Пифагора, помимо геометрии, было первым примером установления числовых связей в природе. Поистине должно быть было удиви­тельно вдруг неожиданно обнаружить, что в природе есть такие факты, которые описы­ваются простыми числовыми соотношениями. Обычное измерение длин позволяет предска­зать то, что, казалось бы, не имеет никакого отношения к геометрии,— создание «прият­ных» звуков. Это открытие привело к мысли, что арифметика и математический анализ, по-видимому, могут служить хорошим орудием в понимании при­роды. Результаты современной науки полностью подтверждают такую точку зрения.

Пифагор смог сделать свое открытие лишь с помощью экс­периментальных наблюдений. Однако все значение этого от­крытия, по-видимому, не было ему ясно. А случись это, и развитие физики началось бы гораздо раньше. (Впрочем, всегда легко рассуждать о том, что сделал кто-то когда-то и что на его месте следовало бы сделать!)

Можно отметить еще одну, третью сторону этого интерес­ного открытия: оно касается двух нот, которые звучат приятно для слуха. Но далеко ли ушли мы от Пифагора в понимании того, почему только некоторые звуки приятны для слуха? Общая теория эстетики, по-видимому, ненамного продвинулась со времен Пифагора. Итак, одно это открытие греков имеет три аспекта: эксперимент, математические соотношения и эстетику. Физики пока добились успеха только в первых двух. В этой главе мы расскажем о современном понимании открытия Пифагора.

Среди звуков, которые мы слышим, есть такой сорт, кото­рый называется шумом. Ему соответствуют какие-то нерегу­лярные колебания барабанной перепонки уха, вызванные не­регулярными колебаниями находящихся поблизости объектов. Если начертить диаграмму зависимости давления воздуха на барабанную перепонку (а следовательно, и перемещения ее) от времени, то график, соответствующий шуму, будет выглядеть так, как это изображено на фиг. 50.1,а.

Фиг. 50.1. Давление как функция времени.

а — для шума; б — для му­зыкального звука.

(Такой шум может например, вызвать топанье ногой.) А музыкальный звук имеет другой характер. Музыка характеризуется наличием более или менее длительных тонов, или музыкальных «нот». (Кстати, музыкальные инструменты тоже умеют производить шум!)

Тон может длиться сравнительно недолго, например когда мы ударяем по клавише фортепьяно, или неопределенно дол­го, когда, скажем, флейтист берет длинную ноту.

В чем состоит особенность музыкальной ноты с точки зре­ния давления воздуха? Музыкальный звук отличается от шума тем, что график его периодичен. Форма колебаний давления воздуха со временем пусть даже какая-то неправильная, но она должна повторяться снова и снова. Пример зависимости дав­ления от времени для музыкального звука показан на при­веденной выше фиг. 50.1.б.

Обычно музыканты, говоря о музыкальном тоне, опреде­ляют три его характеристики — громкость, высоту и «каче­ство». «Громкость», как известно, определяется величиной из­менения давления. «Высоте» соответствует период времени повторения основной формы давления («низкие» ноты имеют более длинный период, нежели «высокие»). А под «качеством» тона понимается разница, которую мы способны уловить между двумя нотами одинаковой громкости и высоты. Мы прекрасно различаем звучание гобоя, скрипки или сопрано, даже если высота издаваемых ими звуков кажется одинаковой. Здесь уже дело идет о структуре периодически повторяющейся формы.

Давайте кратко рассмотрим звук, производимый вибри­рующей струной.

Если оттянуть струну, а затем отпустить ее, то последую­щее движение будет определяться волнами, которые мы воз­будили. Эти волны, как вы знаете, пойдут в обоих направле­ниях по струне, а затем отразятся от ее концов. Так они будут бегать взад и вперед довольно долго. И сколь бы сложны ни были эти волны, они будут повторяться периодиче­ски снова и снова.

Период этих повторений равен просто времени T, которое требуется волне, чтобы пробежать дважды всю длину струны. Ведь это как раз то время, которое необходимо для того, чтобы любая волна, отразившись от каждого конца, вернулась в начальное положение и продолжала движение в первона­чальном направлении. Время, необходимое для того, чтобы волна достигла конца струны в любом направлении, оди­наково. Каждая точка струны после целого периода воз­вращается в свое исходное положение, затем опять отклоняется от него и снова, спустя период, возвращается, и т. д.

Возникающий при этом звук тоже должен повторять те же колебания; вот почему мы, тронув струну, получаем музыкаль­ный звук.

§ 2. Ряд Фурье

В предыдущей главе мы познакомились с другой точкой зрения на колеблющуюся систему. Мы видели, что в струне воз­никают различные собственные гармоники и что любое частное колебание, которое только возможно получить из начальных условий, можно рассматривать как составленную в надлежащей пропорции комбинацию нескольких одновременно осциллирую­щих собственных гармоник. Для струны мы нашли, что соб­ственные гармоники имеют частоты w₀, 2w₀, Зw₀, .... Поэтому наиболее общее движение струны складывается из синусои­дальных колебаний основной частоты w₀, затем второй гармо­ники 2w₀, затем третьей гармоники Зw₀ и т. д. Основная гармо­ника повторяется через каждый период T₁=2p/w₀, вторая гар­моника — через каждый период T₂=2p/2w₀; она повторяется также и через каждый период Т₁=2Т₂, т. е. после двух своих периодов. Точно таким же образом через период Т₁повторяется и третья гармоника. В этом отрезке укладываются три ее перио­да. И снова мы понимаем, почему задетая струна через период t₁полностью повторяет форму своего движения. Так получает­ся музыкальный звук.

До сих пор мы говорили о движении струны. Однако звук, который представляет собой движение воздуха, вызванное дви­жением струны, тоже должен состоять из тех же гармоник, хотя здесь мы уже не можем говорить о собственных гармониках воздуха. К тому же относительная сила различных гармоник в воздухе может быть совсем другой, чем в струне, особенно если струна «связана» с воздухом посредством «звучащей дос­ки». Разные гармоники по-разному связаны с воздухом.

Если для музыкального тона функция f(t) представляет давление воздуха в зависимости от времени (скажем, такая, как на фиг. 50.1.б), то можно ожидать, что f(t) записывается в виде суммы некоторого числа простых гармонических функ­ций от времени (подобных coswt) для каждой из различных гармонических частот. Если период колебаний равен Т, то основная угловая частота будет w=2p/Т, а следующие гармо­ники будут 2w, Зw и т. д.

Здесь появляется небольшое усложнение. Мы не вправе ожидать, что для каждой частоты начальные фазы обязательно будут равны друг другу. Поэтому нужно пользоваться функ­циями типа cos(wt+j). Вместо этого, однако, проще исполь­зовать для каждой частоты как синус, так и косинус. Напом­ним, что

coswt+j)=cosjcoswt-sinjsinwt, (50.1)

а поскольку j — постоянная, то любые синусоидальные коле­бания с частотой w могут быть записаны в виде суммы членов, в один из которых входит sinwt, а в другой — coswt.

Итак, мы приходим к заключению, что любая периодиче­ская функция f(t) с периодом Т математически может быть за­писана в виде

где w=2p/T, a a и b — числовые постоянные, указывающие, с каким весом каждая компонента колебания входит в общее колебание f(t). Для большей общности мы добавили в нашу формулу член с нулевой частотой а₀, хотя обычно для музы­кальных тонов он равен нулю. Это просто сдвиг средней вели­чины звукового давления (т. е. сдвиг «нулевого» уровня). С этим членом наша формула верна для любого случая. Уравне­ние (50.2) схематически показано на фиг. 50.2.

Фиг. 50.2. Любая периодическая функция f(t) равна сумме про­стых гармонических функций.

Амплитуды гармонических функций а_nи b_nвыбираются по специально­му правилу. На рисунке они показаны только схематически без соблюдения масштаба. [Ряд (50.2) называется рядом Фурье для функций f(t).]

Мы сказали, что любую периодическую функцию можно написать в таком виде. Следует внести небольшую поправку и подчеркнуть, что в такой ряд можно разложить вообще любую звуковую волну или любую функцию, с которой мы сталки­ваемся в физике. Математики, конечно, могут придумать такую функцию, что ее нельзя будет составить из простых гармо­нических (например, функцию, которая «заворачивает» назад, так что для некоторых величин t она имеет два значения!). Однако здесь нам не стоит беспокоиться о таких функциях.

§ 3. Качество и гармония

Теперь мы уже можем описать, чем определяется «качество» музыкального тона. Оно определяется относительным количе­ством различных гармоник, т. е. относительными величинами а и b. Тон, содержащий только первую гармонику, называется «чистым», а тон с несколькими сильными гармониками назы­вается «богатым». Скрипка дает гармоники в одной пропорции, а гобой — в другой.

Можно «изготовить» различные музыкальные тоны, если подсоединить к громкоговорителю несколько «осцилляторов». (Осциллятор обычно дает приблизительно чистые простые гар­монические колебания) В качестве частот осцилляторов мы выберем w, 2w, Зw и т. д. Приделав к каждому осциллятору ре­гулятор громкости, можно смешивать гармоники в любой же­лаемой пропорции и тем самым создавать звуки различного качества. Примерно так работает электрический орган. Кла­виши выбирают частоту основного осциллятора, а педали кон­тролируют относительную пропорцию различных гармоник. С помощью этих регуляторов можно заставить орган звучать как флейту, или как гобой, или как скрипку.

Интересно, что для получения такого «искусственного» звука нет никакой необходимости разделять осцилляторы на «синусные» и «косинусные» — для каждой частоты нам достаточно только одного осциллятора. Наше ухо не очень чувствительно к относительной фазе гармоник. Оно воспринимает «синусную» и «косинусную» части частоты в целом. Поэтому наш анализ более точен, чем это необходимо для объяснения субъективной стороны музыки. Однако реакция микрофона или другого физического инструмента все-таки зависит от фазы, и наш пол­ный анализ для таких случаев просто необходим.

«Качество» разговорной речи определяется гласными зву­ками. Форма рта определяет частоты собственных гармоник колебаний звука в нем. Некоторые из этих гармоник возбуж­даются звуковыми волнами от голосовых связок. Таким спо­собом происходит усиление одних гармоник по сравнению с другими. Когда мы меняем форму рта, мы даем преимущество гармоникам разных частот над другими. Благодаря этому эффекту, например, имеется разница между звуком «о—о—о» и звуком «а—а—а».

Всем известно, что каждый гласный звук, скажем «о—о—о», когда мы говорим или поем, всегда похож сам на себя как при высоких, так и при низких частотах. Из описанного нами ме­ханизма мы бы ожидали, что когда мы открываем рот и про­износим звук «а—а—а», то тем самым мы выделяем какие-то определенные частоты, которые не должны измениться при по­вышении голоса. Таким образом, с изменением высоты отно­шение важных гармоник к основному тону, т. е. то, что мы на­зываем «качеством», должно как будто изменяться. Очевидно, механизм, с помощью которого мы узнаем звуки речи, основан не на соотношении различных гармоник.

Что же можно теперь сказать об открытии Пифагора? Мы понимаем, что основные частоты двух струн, длины которых относятся как 2:3, тоже будут относиться как 3:2. Но почему же вместе они «приятно звучат»? Разгадку, по-видимому, нужно искать в частотах гармоник. Вторая гармоника короткой струны будет иметь ту же самую частоту, что и третья гармо­ника длинной струны. (Легко показать или просто поверить, что, задев струну, мы возбуждаем несколько сильных нижних гармоник.)

По-видимому, справедливо следующее правило: ноты звучат гармонично, когда у них есть гармоники с одинаковой часто­той. Ноты диссонируют, если их высшие гармоники имеют ча­стоты, близкие друг к другу, но достаточно отличающиеся для того, чтобы между ними возникали быстрые биения. Однако, почему биения звучат неприятно и почему унисон высших гар­моник звучит приятно, мы не умеем ни определить, ни описать. Исходя из наших знаний, мы не можем сказать, что должно приятно звучать, так же как, например, что должно приятно пахнуть. Иными словами, наше понимание этого явления не идет дальше простого утверждения, что когда ноты звучат в унисон, то это приятно. Но отсюда, кроме свойства гармонии в музыке, нам ничего не вывести.

Гармонические соотношения, которые мы только что опи­сали, легко проверить, проделав несложный опыт на форте­пьяно. Давайте обозначим три последовательные ноты до в се­редине клавиатуры через до, до' и до", а три последовательные ноты соль, расположенные непосредственно выше их, через соль, соль' и соль". Основные гармоники при этом будут иметь следующие относительные частоты:

До — 2 Соль — 3

До' —4 Соль'— 6

до" — 8 Соль"— 12

Вот как можно продемонстрировать эти гармонические соотно­шения. Давайте медленно нажмем клавишу до' так, чтобы она не зазвучала, но чтобы демпфер приподнялся. Если теперь нажать до, то вместе с основной гармоникой будет возбуждена и вторая гармоника, которая возбудит основную гармонику струны до'. Если теперь отпустить клавишу до (оставляя на­жатой клавишу до'), то демпфер заглушит струну до, и мы мо­жем услышать, как замирает тихий звук струны до'. Точно та­ким же образом третья гармоника до может вызвать звучание струны соль' или шестая гармоника до (которая звучит гораздо тише) может вызвать колебание основной гармоники струны соль".

Совершенно другой результат получится, если мы сначала потихоньку нажмем соль, а затем ударим по клавише до'. Третья гармоника до' будет соответствовать четвертой гармонике соль, так что будет возбуждена только четвертая гармоника соль. Мы можем услышать (если слушать очень внимательно) звук соль", который на две октавы выше, чем соль, которую мы нажа­ли! Можно придумать еще очень много комбинаций этой игры.

Попутно заметим, что мажорный лад можно просто опреде­лить условием, что каждый из трех мажорных аккордов (фа— ля—до), (до—ми—соль) и (соль—си-бемоль—ре) представляет последовательность тонов с отношением частот (4:5:6). Эти отношения и тот факт, что в октаве (до—до', соль—соль' и т. д.) частоты относятся как 1:2, определяют в «идеальном» случае весь строй, который называется «натуральным, или пифагорийским строем». Но обычно клавишные инструменты типа фор­тепьяно не настраиваются таким образом, а устраивается не­большая «подтасовка», так что для всех возможных начальных тонов отношение частот только приблизительно верно. При таком строе, названном «темперированным», октава (для кото­рой отношение частот по-прежнему равно 1:2) делится на 12 равных интервалов, так что отношение частот для каждого интервала равно (2)^1/12. Для квинты отношение частот будет уже не ³/₂, а (2)^7/12=1,499, но для большинства людей оно доста­точно близко к 3/2.

Итак, мы установили правила благозвучия через совпадение гармоник. Может быть, это совпадение и является причи­ной благозвучия? Кто-то утверждал, что два абсолютно чистых тона, т. е. тщательно очищенных от высших гармоник, не дают ощущения благозвучия или неблагозвучия (диссонанса), когда их частоты равны или приблизительно равны ожидаемому от­ношению. (Это очень сложный эксперимент, поскольку приго­товить чистые тоны очень трудно по причинам, которые мы увидим дальше.) Мы не можем с уверенностью сказать, срав­нивает ли ухо гармоники или занимается арифметикой, когда мы решаем, что звук нам нравится.

§ 4. Коэффициенты Фурье

Вернемся теперь к утверждению о том, что каждую ноту, т. е. любое периодическое колебание, можно представить в виде надлежащей комбинации гармоник. Хотелось бы знать, как можно найти нужную долю каждой гармоники. Конечно, если нам даны все коэффициенты а и b, то, пользуясь формулой (50.2), легко подсчитать функцию f(t). Теперь же вопрос со­стоит в том, как можно найти коэффициенты при различных гармониках, если нам задана функция f(t)? (Нетрудно испечь пирог, если есть рецепт, но как, отведав пирог, написать его рецепт?)

Фурье открыл, что на самом деле сделать это не очень труд­но. Член а₀уж наверняка нетрудно найти. Мы говорили, что он равен среднему значению f(f) на протяжении одного периода (от t=0 до t=T). Легко увидеть, что это действительно так. Среднее значение синуса или косинуса на протяжении одного периода равно нулю. На протяжении двух, или трех, или дру­гого целого числа периодов оно тоже равно нулю. Таким обра­зом, среднее значение всех членов с правой стороны (50.2), за исключением только а₀, равно нулю. (Напомним, что мы должны выбрать w=2p/T.)

Далее, поскольку среднее значение суммы равно сумме сред­них, то среднее значение функции f(t) равно просто среднему от а₀. Но ведь а₀ — просто постоянная, и ее среднее значение равно ей самой. Вспоминая определение среднего, мы полу­чаем

Найти остальные коэффициенты ненамного труднее. Чтобы сде­лать это, используем один фокус, открытый самим Фурье. Предположим, что мы умножили обе стороны уравнения (50.2) на какую-то гармоническую функцию, скажем на cos7wt. При этом получается

А теперь усредним обе стороны равенства. Среднее от члена a₀cos7wt по периоду Т пропорционально среднему от косинуса по семи его периодам. Но последнее просто равно нулю. Среднее почти всех остальных членов тоже будет равно нулю. Действи­тельно, давайте рассмотрим член с а₁. Мы знаем, что в общем случае

cosAcosВ=¹/₂cos(А+B)+¹/₂cos (А-В), (50.5)

так что член с а₁равен

a₁(cos8wt+cos6wt). (50.6)

Таким образом получаются два косинуса: один с восемью пол­ными периодами, а другой с шестью. Оба они равны нулю. Поэтому среднее значение этого члена тоже равно нулю.

Для члена с а₂ мы получаем cos9wt и cos5wt, каждый из которых при усреднении превратится в нуль. Для члена с а₉ получится соз16wt и cos(-2wt). Но cos(-2wt) — это то же са­мое, что cos2wt, так что опять оба члена дадут при усреднении нуль. Ясно, что все слагаемые с косинусами, за исключением одного, дадут при усреднении нуль. Этим единственным сла­гаемым будет член с а₇. Для него же мы получим

¹/₂a₇(cos14wt+cos0). (50.7)

Косинус нуля равен единице, а среднее от него, разумеется, тоже равно единице. Итак, мы получили, что среднее от всех членов с косинусами уравнения (50.4) равно ¹/₂а₇.

Еще легче расправиться с синусами. Когда мы умножаем их на косинус типа cos nwt, то таким же методом можно показать, что все они при усреднении обращаются в нуль.

Мы видим, что способ, придуманный Фурье, действует как своеобразное сито. Когда мы умножаем на cos7wt и усредняем, то все члены, кроме а₇, отсеиваются и в результате остается

или

Пусть читатель сам докажет, что коэффициенты b₇, например, находятся с помощью умножения (50.2) на sin 7wt и усреднения обеих частей. Результат таков:

Но то, что верно для 7, очевидно, верно и для любого дру­гого целого числа. Теперь мы запишем результат нашего дока­зательства в следующей, более элегантной математической форме. Если m и n — целые отличные от нуля числа и если w=2p/T, то

В предыдущих главах для описания простого гармониче­ского движения было удобно пользоваться экспоненциальной функцией. Вместо coswt мы использовали Re ехр(iwt) —дей­ствительную часть экспоненциальной функции. В этой главе мы использовали синус и косинус, потому что с ними, пожа­луй, немного проще проводить доказательства. Однако наш окончательный результат, уравнение (50.13), можно записать в более компактной форме:

где а_n — комплексное число а_n-ib_n(с b₀=0). Если мы всюду будем пользоваться одним и тем же обозначением, то должны также написать

Итак, теперь мы умеем раскладывать периодическую волну на ее гармонические компоненты. Эта процедура называется разложением в ряд Фурье, а отдельные члены называются фурье-компонентами. Однако до сих пор мы не показали, что, определив все фурье-компоненты и затем сложив их, мы дейст­вительно придем назад к нашей функции f(t). Математики до­казали, что для широкого класса функций (в сущности, для всех функций, интересных физикам), которые можно проин­тегрировать, мы снова получаем f(t). Но есть одно небольшое исключение. Если функция f(t) разрывна, т. е. если она неожи­данно прыгает от одного значения к другому, сумма Фурье такой функции даст в точке разрыва значение, лежащее посре­дине между верхним и нижним значениями. Таким образом, если у нас есть странная функция f(t)=0 для 0≤t<t₀и f(t)=1 для t₀≤t≤T, то ее сумма Фурье всюду даст нам правильную величину, за исключением точки t₀, где вместо единицы полу­чится ¹/₂. Во всяком случае, физически даже нельзя требовать, чтобы функция была всюду нулем вплоть до точки t₀, а в самой точке t₀вдруг стала равной единице. Может быть, стоило бы спе­циально для физиков издать такой «указ», что любая разрывная функция (которая может быть только упрощением настоящей физической функции) в точке разрыва должна принимать сред­нее значение. Тогда любая такая функция, с любым конечным числом «ступенек», как и все другие интересные для физики функции, будет правильно описываться рядом Фурье.

В качестве упражнения предлагаем читателю найти ряд Фурье для функции, показанной на фиг. 50.3.

Фиг. 50.3. Ступенчатая фун­кция. f(t)=+1 для 0<t<T/2 ,

f(t)=-1 для T/2<t<T.

Поскольку эту функцию нельзя записать в точной алгебраической форме, то брать интеграл от 0 до Т обычным способом невозможно. Однако если разделить его на две части: по интервалу от 0 до T/2 [на котором функция f(t)=1] и по интервалу от T/2 до T [на ко­тором f(t) -1], то интеграл легко берется. В результате должно получиться

где w=2p/T. Таким образом, оказывается, что для нашей сту­пенчатой волны (со специально выбранной фазой) будут только нечетные гармоники, причем их амплитуды обратно пропор­циональны частотам.

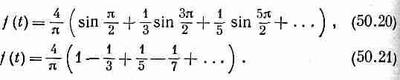Давайте проверим, что для некоторого значения t результат (50.19) действительно дает снова f(t). Возьмем f = T/4или wt=p/2. Тогда

Сумма этого ряда равна p/4, а, стало быть, f(T)=1 .

§ 5. Теорема об энергии

Энергия волны пропорциональна квадрату ее амплитуды.

Для сложной волны энергия за один период пропорциональна m

Эту энергию можно связать с коэффициентами Фурье.

Напишем

После раскрытия квадрата в правой части мы получим сумму всевозможных перекрестных членов типа a₅cos5wtb₇cos7wt. Однако выше мы уже показали [уравнения (50.11) и (50.12)], что интегралы от всех таких членов по одному периоду равны нулю, так что останутся только квадратные члены, подобные a²₅cos²5wt. Интеграл от любого квадрата косинуса или синуса по одному периоду равен Т/2, так что получаем

Это уравнение называют «теоремой об энергии», которая гово­рит, что полная энергия волны равна просто сумме энергий всех ее фурье-компонент. Применяя, например, эту теорему к ряду (50.19), мы получаем

поскольку [f(t)]²=1. Таким образом мы узнали, что сумма квад­ратов обратных нечетных чисел равна p²/8. Точно так же, выпи­сав сначала ряд Фурье для функции и используя затем теорему об энергии, можно доказать результат, понадобившийся нам в гл. 45, т. е. что 1+¹/2⁴+¹/3⁴+... равно p⁴/90.

§ 6. Нелинейная реакция

Наконец, в теории гармоник есть одно очень важное явление, которое необходимо отметить, учитывая его практическую важ­ность, но это уже относится к области нелинейных эффектов. Во всех рассмотренных нами до сих пор системах все предпола­галось линейным; реакция на действие силы, например пере­мещение или ускорение, всегда была пропорциональна силам. Токи в электрической цепи были тоже пропорциональны на­пряжениям и т. д. Теперь мы хотим рассмотреть случаи, когда строгая пропорциональность отсутствует. Представим на ми­нуту устройство, реакция которого x_выход=x_вых в момент t опре­деляется внешним воздействием x_вход = x_вх в тот же момент t.

Например, x_вх может быть силой, а х_вых— перемещением, или х_вх— ток, а x_вых— напряжение. Если бы устройство было ли­нейное, то мы бы получили

x_вых(t)=Kx_вх(t), (50.24)

где К — постоянная, не зависящая ни от t, ни от х_ек. Предполо­жим, однако, что устройство только приблизительно линейное, т. е. на самом деле нужно писать

x_вых(t)=K[x_вх(t)+ex²_вх(t)]. (50.25)

где e мало по сравнению с единицей. Такие линейная и нелиней­ная реакции показаны на фиг. 50.4.

Фиг. 50.4. Реакции, а — линейная,

x_вых=kx_вх; б—нелинейная, x_вых =k(х_вх+ex²_вх).

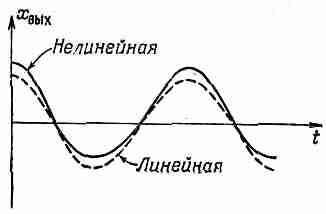Нелинейная реакция приводит к нескольким важным прак­тическим следствиям. Некоторые из них мы сейчас обсудим. Посмотрим сначала, что получается, если пропустить через по­добное устройство «чистый» тон. Пусть x_вх=coswt. Если мы по­строим график зависимости x_вых от времени, то получим сплош­ную кривую, показанную на фиг. 50.5.

Фиг. 50.5. Реакция нелинейного устройства на входящий сигнал coswt.

Для сравнения показана линейная реак­ция.

Для сравнения там же проведена пунктирная кривая, представляющая реакцию ли­нейной системы. Мы видим, что на выходе получается уже не косинусообразная функция. Она более острая в вершине и более плоская в основании. Поэтому мы говорим, что выходной сигнал искажен. Однако, как известно, такая волна не будет уже чистым тоном, а приобретает какие-то высшие гармоники Можно найти эти гармоники. Подставляя x_вх=coswt в уравнение (50.25), получаем

х_вых=К(coswt+ecos²wt). (50.26) Используя равенство cos²q = ¹/₂(l-cos2q), находим

x_вых=K(coswt+ e/2-e/2cos²wt) . (50.27)

Таким образом, в выходящей волне присутствует не только основ­ная компонента, которая была во входящей волне, но и некоторая доля второй гармоники. Кроме того, в выходящей волне появился постоянный член К(e/2), который соответствует сдви­гу среднего значения, показанному на фиг. 50.5. Эффект воз­никновения сдвига среднего значения называется выпрямлением. Нелинейное устройство будет выпрямлять и давать на выходе высшие гармоники. Хотя предположенная нами нелинейность только добавляет вторую гармонику, нелинейность высшего

порядка, например х³_вхили x⁴_вх, даст уже более высокие гармо­ники.

Другим результатом нелинейной реакции является моду­ляция. Если входящая функция содержит два (или больше) чистых тона, то на выходе получатся не только их гармоники, но и другие частотные компоненты. Пусть х_вх=Аcosw₁t+Bcosw₂t, причем w₁ и w₂ не находятся в рациональном отношении друг к другу. Тогда в дополнение к линейному члену (равному произ­ведению К на входящую волну) на выходе мы получим

x_вых=Ke(Acosw₁t+Bcosw₂t)², (50.28)

х_вых=Кe(А²cos²w₁t+В²cos²w₂t+2AB cosw₁tcosw₂t). (50.29)

Первые два члена в скобках уравнения (50.29) — старые зна­комые. Они дают нулевую и вторую гармоники, но последний член — это уже нечто новое.

На этот новый «перекрестный член» АВcosw₁tcosw₂t можно смотреть с двух сторон. Во-первых, если две частоты сильно отличаются друг от друга (например, w₁ много больше w₂), то мы можем считать, что перекрестный член представляет косинусообразные колебания с переменной амплитудой. Я имею в виду такую запись:

АВ cosw₁tcosw₂t=C(t)cosw₁t, (50.30)

где

С(t)=АВсоsw₂t. (50.31)

Мы говорим, что амплитуда колебаний cosw₁ модулируется с частотой w₂.

Во-вторых, этот же перекрестный член можно рассматри­вать с другой точки зрения:

ABcosw₁tcosw₂t= AB/2[cos (w₁-w₂) t+cos(w₁ -+w₂) t], (50.32)

т. е. можно сказать, что возникают две новые компоненты, одна из которых равна сумме частот w₁+w₂, а другая — разности

Таким образом, существуют два различных, но эквивалент­ных способа толкования одного и того же явления. В предель­ном случае w₁>>w₂ можно связать эти две различные точки зре­ния, заметив, что поскольку (w₁+w₂) и (w₁-w₂) близки друг к другу, то между ними должны наблюдаться биения. Но эти биения дают в результате модуляцию амплитуды колебаний со средней частотой w₁, половинкой разности частот 2w₂. Теперь вы видите, почему эти два описания эквивалентны.

Итак, мы обнаружили, что нелинейная реакция дает не­сколько эффектов: выпрямление, возникновение гармоник и модуляцию, т. е. возникновение компонент с суммой и разно­стью частот.

Обратите внимание, что все эти эффекты пропорциональны не только коэффициенту нелинейности e, но и произведению амплитуд: либо A², либо В², либо АВ. Поэтому мы ожидаем, что они будут более важны для сильных сигналов, чем для слабых.

Описанные нами эффекты находят множество практических приложений. Во-первых, что касается звука, то, как полагают, наше ухо — нелинейный аппарат. Такое представление воз­никло из того факта, что, даже когда звук содержит только чистые тоны, при большой громкости возникает ощущение, что мы слышим высшие гармоники, а также сумму и разность час­тот.

Аппараты, используемые обычно в звуковоспроизводящих устройствах,— усилители, громкоговорители и т. д.— всегда имеют какие-то нелинейности. Они искажают звук, порождая гармоники, которых вначале не было. Эти новые гармоники воспринимаются ухом и, несомненно, нежелательны. Именно по этой причине высокочастотная аппаратура должна быть как можно «более линейной». (Почему нелинейность нашего собст­венного уха не «неприятна» и откуда нам знать, что нелинейность «сидит» в громкоговорителе, а не в нашем ухе,— не ясно!)

Однако в некоторых случаях нелинейность совершенно необходима, и в некоторых частях радиопередающих и прини­мающих устройств она намеренно делается побольше. При ра­диопередачах с помощью амплитудной модуляции сигналы от «голоса» (частоты порядка нескольких килогерц) комбинируются с «несущим сигналом» (с частотой порядка нескольких ме­гагерц) в нелинейной цепи, которая называется модулятором. При этом получаются модулированные колебания, которые за­тем излучаются в эфир. В приемнике сигнал снова попадает в нелинейный контур, который складывает и вычитает частоты модулированного сигнала, выделяя снова звуковой сигнал.

Когда мы разбирали вопрос прохождения света через ве­щество, мы предполагали, что вынужденные колебания зарядов пропорциональны электрическому полю света, т. е. мы брали линейную реакцию. Это действительно очень хорошее прибли­жение. Только в последние несколько лет были построены источ­ники света (лазеры), которые дают интенсивность, достаточную для наблюдения нелинейных эффектов. Теперь можно создавать гармоники световых частот. Если пропускать через кусок стекла сильный красный свет, то выходит он оттуда с неболь­шим добавком второй гармоники — голубого света!

* Ее можно вычислить следующим образом. Во-первых, заметим, что

Во-вторых, разложив подынтегральное выражение

в ряд, получим l/(1+x²)=l-x²+x⁴-x⁶+... . Интегрируя затем почленно этот ряд (от нуля до х), получаем arctgx:=l-х³/3+х⁵/5-x⁷/7+..., а поло­жив x=1, мы докажем использованный результат, поскольку

arctg1=p/4.

* В основе деления октавы на 12 ступеней лежит открытие Пифагора. Он брал струну, зажимал ее посредине и получал звук на октаву выше, нем звук незажатой струны. Затем половину струны он опять зажимал посредине и получал звук еще на октаву выше и т. д. Точно так же, за­жимая последовательно струну на ¹/₃ длины, он каждый раз получал звук выше на квинту. И вот оказалось, что 12 квинт почти точно уклады­ваются на интервале в 7 октав [т. е. 2⁷~=(³/₂)¹²]. Если же теперь от каждой квинты отложить целое число октав вверх и вниз, то каждая первона­чальная октава разделится на 12 частей. Так возник нифагорийский строй. Однако беда в том, что 12 квинт только приблизительно равны 7 октавам, поэтому в разных местах диапазона «лесенки» получались неровные. При развитии мелодии эти неточности накапливались и возникали про­тивные уху интервалы, так называемые «волки», которые страшно досаж­дали музыкантам. Иногда дело доходило до курьезов. Рассказывают, что известный композитор Жак Рамо сумел так ловко извлекать из органа «волчьи» звуки, что однажды, желая отказаться от должности церковного органиста, привел своей «игрой» в ужас святых отцов и убедил их в своей «бесталанности». Много сил было потрачено на изгнание «волков». Этим, в частности, безуспешно занимались такие умы, как Кеплер и Эйлер. Однако сделать это удалось не физику и не математику, а органисту Анд­рею Веркмейстеру. Решение его гениально просто: он отказался от чистых квинт, укоротив их как раз настолько, чтобы дюжина вместилась в 7 октав, и несовместимое совместилось, а «волки» исчезли. Так возник современный темперированный строй.— Прим. ред.

 

 

Глава 51 ВОЛНЫ

§ 1. Волна от движущегося предмета

§ 2. Ударные волны

§ 3. Волны в твердом теле

§ 4. Поверхностные волны

§ 1. Волна от движущегося предмета

Мы закончили количественный анализ волн, но посвятим еще одну дополнительную главу некоторым качественным оценкам различных явлений, связанных с волнами; для подробного анализа они слишком сложны. Волнами мы занимаемся уже на протяжении нескольких глав, поэтому предмет настоящей главы было бы вер­нее назвать «некоторые из более сложных яв­лений, связанных с волнами».

Первым объектом нашего обсуждения будет эффект, производимый источником волн, дви­жущимся со скоростью, превышающей ско­рость распространения волн, т. е. быстрее их фазовой скорости. Рассмотрим сначала волны, которые, подобно звуку или свету, имеют опре­деленную постоянную скорость. Если источник звука движется со сверхзвуковой скоростью, то произойдет нечто вроде следующего. Пусть в данный момент источник, находящийся в точ­ке x₁, порождает звуковую волну (фиг. 51.1), тогда в следующий момент источник переме­стится в точку х₂, а волна из точки х₁распро­странится в радиусе r₁, который меньше расстоя­ния, пройденного источником, а из точки х₂, разумеется, пойдет другая волна.

Фиг. 51.1. Фронт ударной волны, образующий конус с вершиной в источнике и углом полураствора q=arcsin(c_w/v).

Когда источ­ник переместится еще дальше, в точку х₃, и отсюда тоже пойдет волна, то волна из точки х₂ распространится в радиусе r₂, а волна из точ­ки х₁— в радиусе r₃. Конечно, все это происхо­дит непрерывно, а не какими-то этапами, и по­этому получается целый ряд таких волновых колец с общей касательной линией, проходя­щей через центр источника. Мы видим, что источник, вместо того чтобы порождать сфери­ческие волны, как это произошло бы, будь он неподвижен, порождает фронт, образующий в трехмерном про­странстве конус или в двухмерном пару пересекающихся пря­мых линий. Из рисунка нетрудно найти угол между этими дву­мя линиями. За данный отрезок времени источник проходит расстояние, пропорциональное его скорости v, скажем х₃-х₁ . Тем временем фронт волны распространится на расстояние r₃, пропорциональное c_w— скорости волны. Ясно поэтому, что си­нус угла полураствора равен отношению скорости волны к ско­рости источника, а это может быть только тогда, когда c_wмень­ше v, или скорость объекта больше скорости волны:

sinq=c_w/v. (51.1)

Интересно, что движущийся предмет вовсе не обязан быть источником звука, оказывается, что когда предмет движется быстрее скорости звука, то он сам производит звук. Ему для этого вовсе не обязательно вибрировать. Любой предмет, дви­жущийся через среду быстрее, чем эта среда переносит волны, будет автоматически порождать волны просто благодаря свое­му движению. Это проще понять для случая звука, но тоже самое происходит и со светом. Сначала может показаться, что ничто не может двигаться быстрее скорости света. Однако фа­зовая скорость света в стекле, например, меньше, чем в пустоте, а через кусок стекла можно пропустить такую частицу, ско­рость которой будет очень близка к скорости света в пустоте, тогда как фазовая скорость света в стекле может быть равна только ²/₃ этой скорости. Частица, летящая быстрее света в среде, порождает коническую световую волну с вершиной в источнике, подобно волнам, вызванным лодкой (эти волны одной и той же природы). Измеряя угол при вершине конуса, мы можем определить скорость частицы. В физике это исполь­зуется для измерения скорости частиц как один из методов оп­ределения их энергии при высокоэнергетических исследованиях. Единственное, что приходится измерять,— это направление излучения света.

Такое излучение называют излучением Черенкова, который первый наблюдал его. Тамм и Франк теоретически выяснили, насколько оно должно быть интенсивным. За эту работу этим ученым в 1958 г. совместно была присуждена Нобелевская премия.

Подобное же явление для случая звука показано здесь на фиг. 51.2; это фотография объекта, движущегося через газ со ско­ростью, превышающей скорость звука.

Фиг. 51.2. Ударная волна в газе, вызванная сна­рядом, движущимся бы­стрее звука.

Изменение в давлении приводит к изменению показателя преломления, поэтому гра­ницу волн с помощью специальной оптической системы можно сделать видимой. Итак, предмет, движущийся быстрее скорости звука, действительно дает коническую волну. Однако при бо­лее внимательном рассмотрении оказывается, что граница на самом деле искривлена. В асимптотике это действительно пря­мая линия, но вблизи вершины она искривлена, и сейчас мы обсудим, отчего так может получаться. Это непосредственно приводит нас ко второй теме данной главы.

§ 2. Ударные волны

Зачастую скорость волны зависит от ее амплитуды, и в слу­чае звука эта зависимость возникает следующим образом. Движущийся в воздухе предмет должен сдвигать его со своего пути, вызывая при этом возмущение в виде какой-то ступенча­той функции давления, причем давление за волновым фронтом оказывается выше, чем в невозмущенной области, т. е. в обла­сти, куда волна (которая распространяется с нормальной ско­ростью) еще не добралась. Воздух за волновым фронтом оказы­вается адиабатическисжатым, поэтому температура его будет выше, чем перед фронтом. Но скорость звука с температурой увеличивается, поэтому в области позади скачка она оказы­вается больше скорости звука впереди него.

Это означает, что любое другое возмущение за скачком, вызванное, например, постоянным напором тела или чем-то другим, будет бежать быстрее, чем сам фронт: с увеличением давления скорость увеличивается. Эта картина показана на фиг. 51.3, причем для большей наглядности дополнительные возмущения взяты в виде небольших горбиков.

Фиг. 51.3. «Мгновенные снимки» ударного фронта в последовательные моменты времени.

Мы видим, что области высокого давления с течением времени «подгоняют» фронт волны, пока волна давления в конце концов не пре­вратится в волну с резким фронтом. Если сила волны очень велика, то «в конце концов» означает — сразу же; если же волна довольно слабая, то это займет сравнительно много времени; обычно звук скорее рассеивается и замирает прежде, чем это превращение успеет произойти.

Давление, вызываемое звуком нашей речи, очень мало по сравнению с атмосферным — только одна миллионная часть или что-то в этом роде. Но при изменении давления на величину порядка 1 атм скорость волны увеличивается примерно на 20% и «заострение» фронта волны происходит соответственно быстрее. В природе, по-видимому, ничего не протекает бесконечно быстро и то, что мы называем «резким» фронтом, на самом деле имеет все же небольшую толщину; он не бесконечно крут. Рас­стояние, на котором все это происходит,— порядка средней дли­ны свободного пробега молекулы, но на таких расстояниях вол­новое уравнение становится несправедливым, ведь при выводе его мы не учитываем молекулярной структуры газа.

Вернемся снова к фиг. 51.2. Мы видим, что кривизну легко объяснить, если понять, что давление вблизи вершины выше, чем вдали от нее, поэтому угол 0 здесь больше. Таким образом, кривизна возникла вследствие зависимости скорости от силы волны. Например, волна от взрыва атомной бомбы в течение некоторого времени движется гораздо быстрее звука, пока не отойдет достаточно далеко и в результате расплывания не бу­дет ослаблена в такой степени, что перепад давления станет ма­лым по сравнению с атмосферным. При этом скорость фронта приближается к скорости звука в газе, в котором он распро­страняется. (Скорость ударной волны всегда оказывается выше скорости звука в газе перед ней и ниже скорости звука в газе за ней. Таким образом, импульсы, идущие сзади, будут догонять фронт, но сам он движется в среде быстрее, чем нормальная скорость звукового сигнала. Поэтому только по звуку никто не в силах предсказать появление ударной волны, пока не ста­новится слишком поздно. Конечно, свет от взрыва бомбы виден раньше, но предугадать приход ударной волны невозможно, никакого звукового сигнала впереди нее нет.)

Накапливание волн — очень интересное явление, и в основ­ном причина его состоит в том, что после прохода одной волны скорость следующей за ней волны должна возрасти.

Рассмотрим еще один пример того же явления. Представьте себе длинный канал конечной ширины и глубины, заполнен­ный водой. Если с достаточной быстротой двигать вдоль канала поршень, то вода будет собираться перед ним, как снег перед снегоочистителем. Теперь вообразите ситуацию, подобную изображенной на фиг. 51.4, когда где-то в канале вдруг возни­кает скачок высоты уровня воды

Фиг. 51.4. Падение воды и водовороты.

Можно показать, что длинные волны в канале идут быстрее по глубокой воде, чем по мелкой. Поэтому любой новый толчок или какие-то иные нерегулярно­сти в энергии, поступающей от поршня, побегут вперед и собе­рутся на фронте волны. Теоретически мы снова в конце концов должны получить резкий фронт. Однако (см. фиг. 51.4) здесь возникают некоторые усложнения. Вы видите волну, идущую вверх по каналу, причем поршень находится где-то далеко с правой стороны канала. Сначала может показаться, что это хорошая волна, такая, какую и следует ожидать, но дальше она становится острее и острее, пока не произойдет то, что изображено на рисунке. Вода на поверхности начинает сильно бурлить и переливаться вниз, но, что самое существен­ное, край по-прежнему остается резким, и впереди него нет никакого возмущения.

В действительности волна на воде — вещь куда более слож­ная, чем звук. Однако для иллюстрации мы попытаемся проа­нализировать скорость так называемого высокого прилива в ка­нале. Дело не в том, что это очень важно для наших целей (ни­какого обобщения здесь не будет), это только иллюстрация того, как законы механики, которые мы хорошо знаем, способны объяснить подобное явление.

Вообразите на минуту, что поверхность воды имеет такой вид, как изображено на фиг. 51.5,а, и что на верхнем уровне h₂ она движется со скоростью v, а фронт со скоростью u надви­гается на невозмущенную поверхность, высота которой h₁. Мы хотим определить скорость, с которой движется фронт. За промежуток времени Dt вертикальная плоскость, проходив­шая вначале через точку x₁передвинется на расстояние vDt, т. е. от х₁до х₂, а фронт волны пройдет расстояние uDt.

Применим теперь законы сохранения вещества и импульса. Возьмем сначала первый из них: мы видим, что на единицу ши­рины канала количество вещества h₂vDt, прошедшее мимо точки x₁ (область, заштрихованная на фиг. 51.5,6), компенсируется другой заштрихованной областью, представляющей количество вещества (h₂-h₁)uDt. Разделив на Dt, получим vh₂=u(h₂-h₁). Но этого еще недостаточно, так как, хотя нам известны h₁ и h₂, мы еще не знаем ни u, ни v, а хотим найти обе величины.

Следующим шагом будет использование закона сохранения импульса. Мы еще не касались вопросов давления в воде и про­чей гидродинамики, но и так ясно, что давление в воде на какой-то глубине должно быть как раз достаточным, чтобы поддержи­вать столбик воды над этой глубиной. Следовательно, давление воды равно произведению плотности r на g и на глубину. Так как давление воды возрастает линейно с глубиной, то среднее давление на плоскость, проходящую, например, через точку х₁, равно ^l/₂rgh₂, что также представляет среднюю силу на еди­ничную ширину и на единичную длину, толкающую плоскость к точке х₂. Чтобы получить полную силу, давящую на воду сле­ва, мы должны еще раз умножить на h₂. С другой стороны, дав­ление на рассматриваемую область справа дает противоположно направленную силу, которая по тем же причинам равна ^ll₂rgh²₁. Теперь мы должны приравнять эти силы к скорости изменения импульса. Таким образом, нам нужно выяснить, насколько в случае, изображенном на фиг. 51.5,6, импульс больше, чем в случае, показанном на фиг. 51.5,а.

Мы видим, что дополнительная масса, которая приобрела скорость v, равна просто rh₂uDt—rh₂vDt (на единицу ширины), а умножение ее на v дает дополнительный импульс, который должен быть приравнен к импульсу силы FDt:

(rh₂uDt-rh₂vDt)v=(¹/₂rgh²₂-¹/₂rgh²₁}Dt.

Исключая из этого уравнения v подстановкой vh₂=и(h₂-h₁) и упрощая его, получаем окончательно u²=gh₂(h₁+h₂)/2h₁.

Если разность высот очень мала, так что h₁и h₂приблизи­тельно одинаковы, то скорость будет равна Цgh. Как мы увидим позднее, это справедливо только при условии, что длина волны много больше глубины канала.

Аналогичную вещь можно сделать и для ударных волн, только теперь нужно добавить уравнение сохранения внутрен­ней энергии, потому что ударная волна — явление необра­тимое. Действительно, если в задаче о высокой приливной волне проверить закон сохранения энергии, то мы увидим, что он не выполняется. Когда разность высот мала, то энергия почти сохраняется, но как только разность высот становится более заметной, возникают большие потери. Это проявляется в падении воды и водоворотах, показанных на фиг. 51.4.

С точки зрения адиабатического процесса в ударной волне тоже происходит аналогичная потеря энергии. Энергия в зву­ковой волне за ударным фронтом уходит на нагревание газа, что соответствует бурлению воды при высоком приливе. Оказы­вается, что необходимо решить три уравнения, чтобы описать все это для случая звука, причем нужно учесть, что температура за ударной волной и перед ней, как мы видели, не одинакова.

Если мы попытаемся пустить высокий прилив в обратную сторону (h₂<h₁), то окажется, что потеря энергии отрицательна.

Но поскольку энергию взять неоткуда, высокий прилив не может поддерживать сам себя — он не стабилен. Если попытаться создать волну такого вида, то дальше она становится все более и более плоской, ведь зависимость скорости от высоты, которая раньше давала резкий фронт, в нашем случае будет работать в обратную сторону.

§ 3. Волны в твердом теле

Следующий тип волн, о которых нам следует поговорить,— это волны в твердом теле. Мы уже рассмотрели звуковые волны в жидкости и газе, а между ними и звуковыми волнами в твер­дом теле имеется непосредственная аналогия. Если резко толк­нуть твердое тело, то оно сожмется. Оно сопротивляется сжа­тию и в нем возникнут волны, аналогичные звуковым. Однако в твердом теле могут быть волны и другого рода, которых не бывает в жидкости. Если мы возбудим колебания твердого тела с помощью бокового давления (это называется сдвигом), то тело стремится вернуться в начальное положение. Именно этим, по определению, твердое тело отличается от жидкого. Если искривить жидкость и подержать ее так немного, чтобы она успокоилась, а затем отпустить, то она останется в том же со­стоянии, но если мы возьмем твердое тело, похожее на дрожа­щий кусок желе, надавим на него и отпустим, то оно вернется на­зад, а в теле возникает волна сдвига, которая распространяется так же, как и волна сжатия. Во всех случаях скорость этих волн меньше скорости продольных волн. В каком-то отноше­нии волны сдвига больше напоминают световые волны, ибо здесь мы тоже имеем дело с поляризацией. У звука нет ника­кой поляризации, это просто волна сжатия, а световые колеба­ния имеют характерную ориентацию, перпендикулярную к направлению их распространения.

Итак, в твердом теле могут быть волны обоих сортов. Во-пер­вых, там распространяются волны сжатия, аналогичные звуку в воздухе, и, во-вторых, волны сдвига. Если наше твердое тело не кристалл, то волна сдвига может быть поляризована в лю­бом направлении. (Конечно, все твердые тела — кристаллы, но если мы возьмем кусок, состоящий из микрокристаллов всех ориентации, то кристаллическая анизотропия усредняется.)

Есть еще один интересный вопрос, касающийся звуковых волн. Что получится, если длина волны в твердом теле стано­вится все меньше и меньше? До каких пор может это продол­жаться? Ясно, что она не может стать меньше расстояния между атомами, ибо если под волной мы понимаем такое явление, когда одна точка идет вниз, а следующая — вверх и т. д., то кратчайшая возможная длина волны при этом, очевидно, равна межатомному расстоянию. Вам известно, что колебания могут быть как про­дольные, так и поперечные, длинноволновые и коротковолновые.

Если мы рассматриваем длины волн, сравнимые с межатомным расстоянием, то скорость уже не будет постоянной; возникает дисперсионный эффект, когда скорость становится зависимой от волнового числа. А высшая гармоника поперечных волн все же должна характеризоваться именно тем, что каждые два со­седних атома делают нечто противоположное друг другу.

С атомистической точки зрения ситуация здесь напоминает два связанных маятника, о которых мы уже говорили. У них могут быть два вида собственных колебаний: один — когда они качаются вместе, и другой — когда в противоположные стороны. Так что волны в твердом теле можно рассматривать и с иной точки зрения — как колебания связанных гармонических ос­цилляторов, подобных огромному числу связанных маятничков, причем высшая гармоника получается, когда маятнички колеблются в противоположные стороны, и низшие — при дру­гих соотношениях фаз.

Эти кратчайшие волны настолько малы, что обычно их не­возможно получить технически. Однако они очень интересны, поскольку свойства этих коротких звуковых волн помогают нам объяснить в термодинамической теории твердого тела его тепловые свойства, в частности удельную теплоемкость. Переход к предельно коротким звуковым волнам означает переход к ин­дивидуальному движению атомов; это в конечном счете одно и то же.

Очень интересным примером звуковых волн в твердом теле являются волны, идущие по земному шару, как продольные, так и поперечные. Хотя нам и не известно почему, но внутри Земли время от времени происходят землетрясения. Одни породы сдви­гаются относительно других, и это движение сходно с очень низким звуком. Из такого источника выходят и путешествуют по всей Земле волны, подобные звуковым, и хотя их длина зна­чительно больше длины обычных звуковых волн, но все же это звуковые волны. Наша Земля не однородна: давление, плотность, сжимаемость и т. д. изменяются с изменением глубины, а поэ­тому изменяется и скорость. Возникает нечто похожее на пока­затель преломления, и волны идут не по прямому пути, а по некоторой кривой. Кроме того, картина осложняется тем, что продольные и поперечные волны распространяются с разной скоростью, а поэтому и решения для них будут разными. Если мы в каком-то месте поставим сейсмограф и будем наблюдать, как скачет его самописец после того, как где-то произошло землетрясение, то мы увидим не просто какие-то неправильные прыжки. Мы увидим, как самописец сначала запрыгает, затем успокоится, затем опять запрыгает. Более конкретные детали происходящего зависят от положения сейсмографа. Если он расположен достаточно близко к месту землетрясения, то сна­чала мы примем продольные волны от возмущения, а уж потом, несколько секунд спустя,— поперечные, ибо они идут медленней. Измеряя разницу времени между их приходами, можно ска­зать, насколько далеко произошло землетрясение, разумеется, если мы достаточно хорошо знаем скорости и состав внутрен­них областей.

На фиг. 51.6 показан пример поведения различных видов волн в Земле.

Фиг. 51.6. Схема земного шара.

Показаны пути продольных и поперечных звуковых волн.

Два сорта волн обозначены различными знач­ками. Если в каком-то месте (назовем его «источник») произошло землетрясение, то поперечные и продольные волны, идущие по прямому пути, придут на станцию в разные моменты времени. Кроме того, возникнут отражения от границ неоднородности, дающие в результате другие пути и времена. Подобные иссле­дования показали, что у Земли есть некое ядро, не проводящее поперечных волн. Однако даже если станция расположена диа­метрально противоположно источнику, то поперечные волны все же приходят, но с неправильной фазой. Это получается от­того, что поперечные волны, падающие наклонно на поверх­ность, разделяющую два вещества, всегда рождают две новые волны: поперечную и продольную. Но внутри ядра Земли по­перечные волны не распространяются (по крайней мере в отли­чие от продольных волн для них этого не обнаружено). Затем на границе ядра оба вида волн возникают вновь и попадают на станцию.

Именно по поведению волн, вызванных землетрясениями, было обнаружено, что поперечные волны не могут распростра­няться в некоторой сфере внутри Земли. Это означает, что центр Земли жидкий в том смысле, что он не проводит поперечных волн. Изучение землетрясений — это единственный источник наших сведений о внутреннем строении Земли. Таким образом, в результате большого числа наблюдений на различных стан­циях в период многих землетрясений были выяснены все детали; известно все: скорости, кривые и т. д. Мы знаем скорости раз­личных сортов волн на любой глубине. А зная это, мы, следо­вательно, можем выяснить, каковы собственные гармоники Земли, ибо нам известна скорость распространения звуковых волн: другими словами, известны упругие свойства на любой глубине. Предположим, что мы приплюснули земной эллипсоид и затем отпустили его. Задача определения периода и формы сво­бодных колебаний сводится просто к вопросу о суперпозиции волн, идущих по эллипсоиду. Мы уже выяснили, что при по­добном возмущении возникает множество гармоник, начиная от низшей, которая для Земли эллипсоидальна, и вплоть до более высоких и более сложных.

Чилийское землетрясение в мае 1960 г. произвело такой «шум», что его эхо много раз обошло вокруг Земли. Как раз к этому времени были изготовлены новые высокочувствитель­ные сейсмографы, с помощью которых определялись основные гармоники Земли и сравнивались с величинами, вычисленными из теории звука по известным скоростям, найденным из других независимых землетрясений. Результат этого эксперимента по­казан на фиг. 51.7, где отложена сила сигнала в зависимости от его частоты (фурье-анализ).

Фиг. 51.7. Зависимость силы от частоты, зарегистрированная сейсмографом в городах Нака (Перу) и Изабелла (Калифорния).

Согласованность (или когерентность) обозначает степень связанности сигналов, регистрируемых этими станциями.

Заметьте, что одни из прини­маемых частот оказывались более сильными, чем другие; на­блюдались очень четкие максимумы. Это и есть собственные ча­стоты Земли, поскольку они являются главными частотами ее колебаний.

Иными словами, если все движение Земли сводится к су­перпозиции множества различных гармоник, то можно на­деяться, что запись нерегулярных толчков на любой станции даст одну и ту же суперпозицию многих частот. Если проанали­зировать это в терминах частот, то мы сможем определить ха­рактеристические частоты Земли. Тонкие вертикальные линии на рисунке изображают рассчитанные частоты, и мы видим за­мечательное согласие, убеждающее нас, что теория звука вполне работает и внутри Земли.

Очень интересный факт обнаруживается на фиг. 51.8, где представлены очень точные измерения (с еще большим разреше­нием) низшей эллипсоидальной гармоники.

Фиг. 51.8.Фурье-ана­лиз записи высокочувст­вительного сейсмографа на станции Изабелла. Хорошо виден спектральный дублет.

Заметьте, что здесь не один, а два немного отличающихся максимума: первый — с периодом 54,7 мин и второй — 53,1 мин. Природа этих двух максимумов не была известна, когда они были обнаружены, хотя с тех пор ее могли найти. Существуют по крайней мере два правдоподобных объяснения. Одно из них — это возможная асимметрия в распределении вещества Земли, которая может дать два подобных максимума. Другое, еще более интересное объяснение состоит в следующем. Вообразите волны, идущие от источника вокруг Земли в двух направлениях. Если мы в уравнениях движения учтем эффект вращения Земли, кото­рым обычно пренебрегали при анализе, то скорости этих волн окажутся разными. Движение во вращающейся системе из-за действия кориолисовой силы изменяется, и это может вызвать наблюдаемое расщепление.

Коротко о методе получения этих кривых. На сейсмографе мы записываем не зависимость амплитуды от частоты, а пере­мещение как функцию времени, причем всегда какой-то очень неправильной и причудливой формы.

Чтобы найти из нее долю различных синусообразных волн для всех частот, мы уже знаем, что нужно делать. Фокус состоит в умножении полученных данных на синусообразную волну данной частоты и интегрировании, т. е. усреднении; при этом усреднении все другие частоты исчезают.

Таким образом, на рисунках фактически показаны гра­фики интегралов от произведения полученных данных на синусообразные волны с различным числом периодов в ми­нуту.

§ 4. Поверхностные волны

Следующий интересный тип волн, которые, несомненно, видел каждый и которые обычно в элементарных курсах служат примером волн,— это волны на поверхности воды. Вы скоро убедитесь, что более неудачного примера придумать трудно, ибо они нисколько не похожи ни на звук, ни на свет; здесь соб­рались все трудности, которые только могут быть в волнах. Давайте начнем с длинных волн на глубокой воде. Если считать океан бесконечно глубоким и на его поверхности происходят какие-то возмущения, то возникнут волны. Вообще говоря, возможны любые возмущения, но синусоидальное движение с очень небольшим возмущением дает волны, напоминающие обычные гладкие океанские волны, идущие к берегу. Вода, разумеется, в среднем остается на месте, а движутся сами волны. Что ж это за движение — поперечное или продольное? Оно не может быть ни тем, ни другим: ни поперечным, ни продольным. Хотя в каждом данном месте горбы чередуются со впадинами, оно не может быть движением вверх и вниз просто из-за закона сохранения количества воды. Куда должна деваться вода из впадины? Ведь она же практически несжимаема. Скорость волн сжатия, т. е. звука в воде, во много раз больше: мы сейчас их не рассматриваем. Итак, для нас сейчас вода несжимаема, поэ­тому при образовании впадины вода из этого места может дви­гаться только в стороны. Так оно и получается на самом деле: частички воды вблизи поверхности будут двигаться прибли­зительно по окружности. Как-нибудь, когда вы будете нежиться на воде, лежа на круге, и придет такой гладкий вал, посмот­рите на соседние предметы и вы увидите, что они движутся по окружностям. Так что картина получается неожиданная: здесь мы имеем дело со смесью продольных и поперечных волн. С увеличением глубины круги уменьшаются, пока на достаточ­ной глубине от них ничего не останется (фиг. 51.9).

Фиг. 51.9. Волны, на глубокой воде образуются частицами, движущимися по окружности.

Обратите внимание на систематический сдвиг фазы от одной окружности к другой. Кок может при этом двигаться плавающий предмет?

Очень интересно определить скорость таких волн. Это дол­жно быть какой-то комбинацией плотности воды, ускорения силы тяжести, которая в данном случае является восстанавли­вающей силой, и, возможно, длины волны и глубины. Если мы рассмотрим случай бесконечной глубины, то скорость больше не будет зависеть от нее. Но какую бы формулу для фазовой скорости волн мы ни взяли, она должна содержать эти величины в такой комбинации, чтобы давать правильную размерность. Испробовав множество различных способов, мы найдем, что только одна комбинация g и l может дать нам размерность ско­рости, именно Цgl, которая совсем не включает плотности. На самом деле эта формула для фазовой скорости не вполне точна, и полный анализ динамики, в который мы не будем входить, показывает, что все действительно получится так, как у нас, за исключением Ц2p, т. е.

v_фаз=Цgl/2p (для волн «тяжести»).

Интересно, что длинные волны бегут быстрее коротких. Так что когда проходящая вдали моторная лодка создает волны, то после некоторого промежутка времени они достигнут берега, но сначала это будут редкие всплески, поскольку первыми приходят длинные волны. Затем приходящие волны становятся все короче и короче, ибо скорость падает как квадратный ко­рень из длины волны.

«Это же неверно,— может возразить кто-нибудь,— ведь чтобы делать такое утверждение, мы должны смотреть на групповую скорость». Правильно, конечно. Формула для фазо­вой скорости не говорит нам о том, что приходит первым; об этом может нам сказать только групповая скорость. Так что мы должны получить групповую скорость и мы сможем показать, что она равна половине фазовой скорости. Для этого нужно только вспомнить, что фазовая скорость ведет себя как квадрат­ный корень из длины волны. Так же, т. е. как квадратный ко­рень из длины волны, ведет себя и групповая скорость. Но как может групповая скорость быть вдвое меньше фазовой? Посмот­рите на группу волн, вызванных проходящей мимо лодкой, и проследите за каким-то определенным гребнем. Вы обнаружите, что он бежит вместе с группой, но постепенно становится все меньше и меньше, а дойдя до переднего фронта, совсем умирает. Но таинственным и непостижимым образом на смену ему с заднего фронта поднимается слабенькая волна и становится она все сильнее и сильнее. Короче говоря, по группе движутся вол­ны, тогда как сама группа движется вдвое медленнее этих волн.

Поскольку групповая и фазовая скорости не равны друг другу, то волны, вызванные движущимся объектом, будут уже не просто коническими, а гораздо более сложными и интерес­ными. Вы можете видеть это на фиг. 51.10, где показаны волны, вызванные движущейся по воде лодкой.

Фиг. 51.10. След про­шедшей моторной лодки.

Заметьте, что они сов­сем не похожи на то, что мы получали для звука (когда скорость не зависит от длины волны), где фронт волны был просто рас­пространяющимся в стороны конусом. Вместо него мы получили волны позади движущегося объекта, фронт которых перпенди­кулярен его движению, да еще движущиеся под другими угла­ми небольшие волны с боков. Всю эту картину движения волн в целом можно очень красиво воссоздать, зная только, что фа­зовая скорость пропорциональна квадратному корню из длины волны. Весь фокус заключается в том, что картина волн стацио­нарна относительно лодки (движущейся с постоянной скоро­стью); все другие виды волн отстанут от нее.

До сих пор мы рассматривали длинные волны, для которых восстанавливающей силой была сила тяжести. Но когда волны становятся очень короткими, то основной восстанавливающей силой оказывается капиллярное притяжение, т. е. энергия по­верхностного натяжения. Для волн поверхностного натяжения фазовая скорость равна

v_фаз=Ц2pT/lr(для ряби),

где Т — поверхностное натяжение, а r — плотность. Здесь все наоборот: чем короче длина волн, тем большей оказывается фа­зовая скорость. Если же действуют и сила тяжести и капилляр­ная сила, как это обычно бывает, то мы получаем комби­нацию

где k=2p/l — волновое число. Как видите, скорость волн на воде — вещь действительно довольно сложная. На фиг. 51.11 показана фазовая скорость как функция длины волны.

Фиг. 51.11. График за­висимости фазовой ско­рости от длины волны для воды.

Она ве­лика для очень коротких волн, велика для очень длинных волн, но между ними существует некоторая минимальная скорость распространения. Исходя из этой формулы, можно вычислить и групповую скорость: она оказывается равной ³/₂ фазовой ско­рости для ряби и ¹/₂ фазовой скорости для волн «тяжести». Сле­ва от минимума групповая скорость больше фазовой, а справа групповая скорость меньше. С этим фактом связано несколько интересных явлений. Поскольку групповая скорость с умень­шением длины волны быстро увеличивается, то, если мы созда­дим какие-то возмущения, возникнут волны соответствующей длины, которые идут с минимальной скоростью, а впереди них с большей скоростью побегут короткие и очень длинные волны. В любом водоеме можно легко увидеть очень короткие волны, а вот длинные волны наблюдать труднее.

Таким образом, мы убедились, что рябь, которая столь ча­сто используется для иллюстрации простых волн, на самом деле гораздо сложнее и интереснее: у нее нет резкого волнового фронта, как в случае простых волн, подобных звуку или свету. Основная волна, которая вырывается вперед, состоит из мелкой ряби. Благодаря дисперсии резкое возмущение поверхности воды не приводит к резкой волне. Первыми все равно идут очень мелкие волны. Во всяком случае, когда по воде с некоторой скоростью движется объект, то возникает очень сложная кар­тина, поскольку разные волны идут с разной скоростью. Взяв корыто с водой, можно легко продемонстрировать, что самыми быстрыми будут мелкие капиллярные волны, а уже за ними идут более крупные. Кроме того, наклонив корыто, можно увидеть, что там, где меньше глубина, меньше и скорость. Если волна идет под каким-то углом к линии максимального наклона, то она заворачивает в сторону этой линии. Таким способом можно продемонстрировать множество различных вещей и прийти к заключению, что волны на воде — куда более сложная вещь, чем волны в воздухе.

Скорость длинных волн с круговым движением воды умень­шается на мелком месте и увеличивается на глубоком. Таким образом, когда волна идет к берегу, где глубина меньше, она замедляется. Но там, где вода глубже, волна движется быстрее, так что мы снова сталкиваемся с механизмом ударной волны. Однако на этот раз, поскольку волна не столь проста, ударный фронт ее гораздо больше искажен: волна «перегибается через себя» самым привычным для нас образом (фиг. 51.12).

Фиг. 51.12. Морская волна.

Именно это мы видим, когда волна набегает на берег: в ней выявляются все присущие природе трудности. Никому до сих пор не удалось вычислить форму волны в тот момент, когда она разбивается. Это очень легко сделать, когда волны малы, но когда они ста­новятся большими, все слишком усложняется.

Интересное свойство капиллярных волн можно наблюдать при возмущении поверхности движущимся объектом. С точки зрения самого объекта вода течет мимо него, и волны, которые в конечном итоге останутся вместе с ним, всегда будут волнами, которые как раз имеют нужную скорость, чтобы оставаться на воде вместе с объектом. Точно так же если поместить объект в поток, который будет омывать его, то картина волн окажется стационарной и как раз нужной длины волны для того, чтобы двигаться с той же скоростью, что и вода. Но если групповая скорость меньше фазовой, то возмущение идет по потоку назад, поскольку групповая скорость недостаточна для того, чтобы дог­нать поток. Если же групповая скорость больше фазовой, то волновая картина появится перед объектом. Если пристально следить за плывущим в потоке объектом, то можно заметить впереди него небольшую рябь, а позади него — длинные волны.

Другие интересные явления подобного рода можно наблю­дать в льющейся жидкости. Если, например, быстро выливать молоко из бутылки, то можно заметить, как струя молока пере­секается множеством перекрещивающихся линий. Это волны, вызванные возмущением на краях бутылки; они очень похожи на волны, вызванные объектом, плывущим по потоку. Но теперь такой эффект возникает с обеих сторон, поэтому получается картина пересекающихся линий.

Итак, мы познакомились с некоторыми интересными свойст­вами волн, с различными усложнениями, зависящими от фазо­вой скорости и длины волны, а также с зависимостью скорости волны от глубины и т. д.; все это приводит к весьма сложным, а потому и интересным явлениям природы.

 

 

Глава 52 СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ

§ 1. Симметричные операции

§ 2. Симметрия в пространстве и времени

§ 3. Симметрия и законы сохранения

§ 4. Зеркальное отражение

§ 5. Полярный и аксиальный векторы

§ 6. Какая же рука правая?

§ 7. Четность не сохраняется!

§ 8. Антивещество

§ 9. Нарушенная симметрия

§ 1. Симметричные операции

В этой главе мы будем говорить о том, что мы называем симметрией физических законов. Подобные симметрии уже обсуждались нами в ряде мест нашего курса, когда говорилось о векторном анализе (вып. 1, гл. 11), теории от­носительности (вып. 2, гл. 16) и вращениях (вып. 2, гл. 20).

Почему же симметрии так интересуют нас? Прежде всего потому, что симметрия импони­рует нашему складу ума, каждому доставляет удовольствие любоваться предметом, который в каком-то смысле симметричен. Любопытно, что окружающий нас мир буквально заполнен симметричными объектами, созданными самой природой. Пожалуй, самый симметричный объект, который только можно себе предста­вить,— это сфера, а природа дает нам массу примеров сферических тел: звезды, планеты, капельки воды в облаках и т. д. А сколько раз­личных, порой причудливых примеров симмет­рии находим мы в кристаллах горных пород! Изучение их позволяет нам заглянуть внутрь вещества и получить важные сведения о струк­туре твердого тела. Столь же полон симметриями окружающий нас животный и растительный мир, хотя симметрия цветка или бабочки уже не столь совершенна и не столь фундаментальна, как симметрия кристалла.

Но тема этой главы все же не симметрия предметов, а куда более удивительная симмет­рия Вселенной — симметрия тех фундаменталь­ных законов, которые управляют всеми процес­сами физического мира.

Однако что же такое симметрия? Каким образом физический закон может быть «симметричным»? Проблема определения симметрии — одна из основ­ных. Мы уже говорили об очень хорошем определении, которое было дано Вейлем. Суть его состоит в том, что объект считается симметричным, если с ним можно сделать нечто такое, после чего он будет выглядеть точно так же, как и прежде. Например, симметрична ваза, которая, отразившись в зеркале или будучи повернута вокруг своей оси, выглядит точно так же, как и до поворота или отражения. Вопрос, который мы хотим разобрать здесь,— это, что можно сделать с физическим явлением или ситуацией, возникшей при эксперименте, чтобы получился тот же самый результат. Список операций симметрии, в результате которых различные физические явления остаются неизмен­ными, приведен в табл. 52.1.

Таблица 52.1 · операции симметрии

§ 2. Симметрия в пространстве и времени

Самое простое, что можно попытаться сделать — это перено­сить (транслировать) различные явления в пространстве. Если мы в некотором месте сделаем какой-то опыт, а потом построим такую же установку (или просто перенесем старую) в другом месте и повторим наш опыт, то все должно повториться, причем в той же самой последовательности. При этом, конечно, все де­тали окружения и условия работы, существенные для нашего опыта, на новом месте должны быть теми же, что и прежде, т. е. должны быть тоже перенесены вместе с нашей аппаратурой. О том, что существенно и что не существенно, мы уже говорили и больше не будем останавливаться на этом.

Насколько нам сегодня известно, перемещение во времени тоже не должно изменять физических законов. (Впрочем, обо всем, содержащемся в этой главе, можно сказать: насколько нам известно сегодня!) Это означает, что если мы построим какую-то установку и запустим ее в некоторый момент времени, скажем в 10 часов утра во вторник, а затем построим вторую, точно та­кую же установку и запустим ее при тех же самых условиях, но ровно на три дня позднее, то эта вторая установка будет рабо­тать точно так же, как и первая, т. е. она будет повторять те же действия, в той же последовательности и с теми же интерва­лами длительности. При этом, конечно, снова подразумевается, что существенные свойства окружения изменяются со временем точно таким же образом, как и прежде.

Необходимо обращать внимание и на разницу, вносимую географией, ибо с изменением положения на Земле некоторые характеристики могут тоже меняться. Если мы в каком-то ме­сте измеряем магнитное поле, а затем вместе со всей аппарату­рой переедем куда-то в другое место, то приборы могут и не ра­ботать точно таким же образом, как раньше, поскольку магнит­ное поле в этих различных районах может быть разным. Однако всю ответственность за разницу в этом случае мы можем свалить на магнитное поле Земли. Но если вообразить, что мы передви­гаем аппаратуру вместе со всем земным шаром, то, разумеется, никакой разницы быть не должно.

Другое свойство, которое мы тоже подробно обсуждали,— это вращение в пространстве. Если мы повернем нашу аппаратуру на некоторый угол, то она будет работать точно так же, как и прежде, но, разумеется, при непременном условии, что вместе с ней мы повернем все существенное для работы аппаратуры окружение. Проблеме симметрии при вращении в пространстве была посвящена глава 11. Там вы познакомились и с векторным анализом — математическим аппаратом, который наиболее пол­но и изящно учитывает вращательную симметрию.

Поднявшись в изучении природы на ступеньку выше, мы познакомились с более сложной симметрией — симметрией при равномерном и прямолинейном движении. Это поистине замечательная вещь. Если мы погрузим нашу работающую уста­новку на автомашину (со всем, конечно, существенным окруже­нием) и поедем с постоянной скоростью по прямой дороге, то явления, происходящие в движущейся машине, будут протекать точно так же, как если бы она стояла на месте, т. е. все законы физики остаются теми же самыми.

Нам даже известно, как математически выражается эта сим­метрия: все математические уравнения должны оставаться неиз­менными при преобразованиях Лоренца. Кстати, именно изучение проблем теории относительности заострило внимание физи­ков на симметриях физических законов.

Однако все упомянутые виды симметрии имеют геометриче­скую природу, причем в некотором смысле утверждается экви­валентность пространства и времени. Но существуют симмет­рии совершенно другого рода. Например, можно заменить один атом другим атомом того же сорта, или (в несколько другой постановке) существуют атомы одного и того же сорта, т. е. существуют такие группы атомов, что если мы переставим любые два из них, то ничто не изменится. То, что может сделать один атом кислорода определенного сорта, способен сделать и второй.

«Ерунда какая-то,— может возразить какой-нибудь скеп­тик,— ведь это же просто определение того, что означают атомы одного и того же сорта!» Согласен, это может быть просто определением, но все дело в том, что до опыта нам не известно, существуют ли в природе атомы «одного и того же сорта», а экспериментальный факт состоит в том, что таких атомов много, очень много, так что наше утверждение все-таки что-то означает. В указанном смысле одинаковы и так называемые элементарные частицы, из которых сделаны атомы; одинаковы все протоны, одинаковы все положительные p-мезоны и т. д.

После столь длинного списка того, что можно делать, не из­меняя при этом явлений, может создаться впечатление, что прак­тически позволено делать все что угодно. Совсем нет. Вот вам пример — просто для того, чтобы продемонстрировать разницу. Допустим, что нас интересует вопрос: «А не остаются ли законы физики теми же самыми при изменении масштаба?» Пусть вы построили какую-то машину, а затем построили точ­ную ее копию, но увеличенную, скажем, в пять раз. Будет ли копия работать точно так же? Нет, не будет! Длина волны света, испускаемого, например, атомами кальция, находящимися внутри ящика, и длина волны, излученная газом атомов каль­ция, которых в пять раз больше, будет не в пять раз больше, а в точности той же самой. Так что изменится отношение длины волны к размеру излучателя.

Возьмем другой пример. Время от времени в газетах вы видите фотографии моделей знаменитых соборов, сделанные из спичек, — удивительное произведение искусства, более уди­вительное и потрясающее, чем настоящий собор. А представьте себе, что такой деревянный собор в самом деле построен в на­туральную величину. Вы уже чувствуете, что из этого получится! Он не будет стоять, он рухнет, ибо такие увеличенные модели из «спичек» недостаточно прочны. «Правильно,— может ска­зать кто-нибудь из вас, —но ведь существует внешнее влияние, которое тоже необходимо изменить в соответствующей пропор­ции!» Вы имеете в виду способность предметов противостоять силе тяжести? Хорошо. Сначала, когда мы взяли модель собора, сделанного из настоящих спичек, и настоящую Землю, то все было отлично и устойчиво. Но потом, когда мы увеличили собор, то должны увеличить и Землю, а это для собора будет еще хуже: ведь сила тяжести станет еще больше!

Сейчас вы, конечно, понимаете, что в основе зависимости явлений от размеров лежит атомная природа строения вещества. Если бы нам удалось построить аппаратуру, которая была бы так мала, что содержала бы всего пять атомов, то такую штуку нельзя было бы произвольно уменьшить или увеличить. Ведь размер отдельного атома не произвольный, он совершенно опре­деленный.

Тот факт, что законы физики не остаются теми же при из­менении масштаба, открыл еще Галилей. Он понял, что проч­ность материалов изменяется не в прямой пропорции с их раз­мерами, и иллюстрировал это свойство на примере, очень похо­жем на наш собор из спичек. Он рисовал два скелета собаки, один из них обычный, в той пропорции, которая необходима для поддержания ее веса, а второй — необходимый для некой вооб­ражаемой «суперсобаки», которая в десять или, может быть, в тысячу раз больше обычной. Получилось нечто громадное и внушительное с совершенно другими пропорциями. Не извест­но, привели ли Галилея эти соображения к заключению о том, что законы природы должны иметь определенный масштаб; ясно лишь одно, что он был настолько потрясен своим открытием, что счел его столь же важным, как и открытие законов дви­жения. Именно поэтому Галилей опубликовал оба эти зако­на в одном и том же томе под заглавием «О двух Новых Науках».

Другой хорошо известный пример несимметрии законов — это вращение. В системе, вращающейся с постоянной угловой скоростью, законы физики будут выглядеть совсем иначе, чем в покоящейся. Если мы произведем какой-то опыт, а затем по­грузим всю аппаратуру в космический корабль и заставим его вращаться в межпланетном пространстве с постоянной угловой скоростью, то аппаратура из-за наличия центробежных и кориолисовых сил уже не будет работать так, как раньше. В сущ­ности, ведь о вращении Земли мы узнаем, наблюдая лишь за поведением маятника (так называемого «маятника Фуко»). Нам вовсе не нужно для этого «выглядывать наружу», т. е. смотреть на звезды, например.

Следующей в нашем списке стоит очень интересная симмет­рия. Это обращение времени. На первый взгляд кажется, что оно неверно, что физические законы не могут быть обращены. Ведь всем ясно, что в нашем обычном масштабе явления необра­тимы.

«Скользит по бумаге перо,

За строчкой написанной — новая строчка...»

Насколько нам сейчас известно, причиной этой необрати­мости является огромное число частиц, принимающих участие в обычных процессах. Ноесли бы мы видели отдельные мо­лекулы, то не могли бы сказать, работает ли вся машина впе­ред или назад. Поясним, что мы имеем в виду: построим такой прибор, в котором нам известно, что делает каждый из атомов (мы можем наблюдать за всеми их проделками). Построим теперь второй, точно такой же прибор, но запустим его в обратную сторону, т. е. установим его в конечном положении, а все ско­рости изменим на противоположные. После этого мы увидим в точности то же самое движение, но только все будет происхо­дить в обратной последовательности. Возьмем другой пример. Предположим, что мы засняли на киноленту какой-то процесс, происходящий с веществом, и запустили пленку задом наперед. Тогда ни один из физиков не мог бы сказать: «Это противоречит физическим законам, происходит что-то не то». Если деталей не видно, то все становится совершенно ясно. Например, когда на тротуар падает яйцо и разбивается вдребезги, то вы сразу скажете: «Этот процесс необратим; если мы заснимем его на ки­нопленку и прокрутим ее наоборот, то яйцо само соберется в скорлупу, которая тут же склеится обратно, а это бессмыслица!» Но если мы видим отдельные атомы, то все кажется нам полно­стью обратимым. Открыть эту симметрию было, конечно, го­раздо труднее, чем другие, но все-таки то, что фундаментальные законы физики, управляющие атомами и молекулами, обратимы во времени, по-видимому, верно.

§ 3. Симметрия и законы сохранения

Даже на этом уровне симметрии физических законов очень увлекательны, но оказывается, что они куда более интересны и удивительны при переходе к квантовой механике. Факт, причи­ну которого я не могу вам объяснить с вашим запасом знаний, но который до сих пор потрясает большинство физиков своей глу­биной и красотой, состоит в следующем: в квантовой механике каждой из симметрии соответствует закон сохранения — су­ществует вполне определенная связь между законами сохране­ния и симметриями физических законов. Сейчас мы можем толь­ко это констатировать, не пытаясь вдаваться в объяснения.

Оказывается, например, что симметрия законов физики по отношению к переносу в пространстве вместе с принципами квантовой механики означает сохранение импульса.

То, что законы симметричны при перемещении во времени, означает в квантовой механике сохранение энергии.

Неизменность (инвариантность) при повороте на фиксиро­ванный угол в пространстве соответствует сохранению момента количества движения. Среди наиболее мудрейших и удивитель­нейших вещей в физике эти связи — одни из самых интересных и красивых.

В квантовой механике, кроме того, возникают некоторые сим­метрии, которые, к несчастью, не имеют классического аналога; их нельзя описать методами классической физики. Вот одна из них. Если y— это амплитуда некоторого процесса или чего-то другого, то, как мы знаем, квадрат ее абсолютной величины будет вероятностью этого процесса. Пусть теперь некто сделал свои вычисления, используя не y, а y', которая отличается от y только по фазе [т. е. прежняя y) умножается на ехр(iD), где D — какая-то постоянная], тогда квадрат абсолютной вели­чины y', который тоже будет вероятностью события, равен

квадрату абсолютной величины y:

Следовательно, физические законы не изменяются от того, что мы сдвигаем фазу волновой функции на некоторую произволь­ную постоянную. Это еще одна симметрия. Природа физических законов такова, что сдвиг квантовомеханической фазы не из­меняет их. В начале этого параграфа мы говорили, что в кван­товой механике каждой симметрии соответствует закон сохра­нения. И вот оказывается, что закон сохранения, связанный с квантовомеханической фазой, не что иное, как закон сохране­ния электрического заряда. Словом, это удивительнейшая вещь!

§ 4. Зеркальное отражение

Перейдем к следующему вопросу, который будет занимать нас до конца главы,— это симметрия при отражении в про­странстве. Проблема заключается в следующем: симметричны ли физические законы при отражении? Можно ее сформулировать и по-другому. Предположим, что мы построили некое устрой­ство, например часы с множеством колесиков, стрелок и пр. Они идут, внутри у них есть устройство для заводки. Посмот­рим теперь на часы в зеркало. Дело не в том, как они выглядят в зеркале. Нет, давайте построим другие часы, в точности такие же, как те первые, отраженные в зеркале. Там, где у первых часов находится винт с правой резьбой, мы поставим винт с левой резьбой, там, где на циферблате стоит цифра «XII», мы на циферблате вторых часов нарисуем «IIX», каждая спиральная пружина закручена в одну сторону у первых часов и в проти­воположную у зеркально отраженных. Когда все будет за­кончено, получатся двое часов, каждые из которых будут точ­ным зеркальным отражением других, хотя заметьте, что и те и другие настоящие физические материальные объекты. Возникает вопрос: а что, если и те и другие часы запущены при одинаковых условиях, если пружины их закручены одинаково туго, будут ли они идти и тикать, как точное зеркальное от­ражение? (Это чисто физический, а вовсе не философский во­прос.) Наша интуиция и наше знание физических законов под­сказывают, что будут.

Мы подозреваем, что по крайней мере в этом случае отраже­ние будет одной из симметрии физических законов, т. е. если заменить «право» на «лево», а все остальное оставить тем же самым, то никакой разницы при этом мы обнаружить не смо­жем. Предположим на минуту, что все это верно. Тогда ника­кими физическими явлениями невозможно различить, где «право», а где «лево», точно так же, как, скажем, никаким фи­зическим опытом невозможно найти абсолютной скорости дви­жения. Таким образом, с помощью каких-то опытов невоз­можно абсолютно определить, что мы понимаем под «правым», как противоположностью «левого», поскольку все физические законы должны быть симметричны.

Разумеется, мир наш не должен быть симметричным. Если, например, взять то, что мы называем «географией», то здесь вполне можно определить, где правая сторона. Пусть мы на­ходимся в Нью-Орлеане и смотрим в сторону Чикаго. Тогда Флорида будет от нас справа (конечно, если мы стоим ногами на Земле!). Так что в географии можно определить, где «право» и где «лево». В любой системе реальное положение не должно иметь ту симметрию, о которой идет речь, вопрос в том — сим­метричны ли законы? Другими словами, противоречит ли фи­зическим законам наличие подобного Земле шара с «левосто­ронней поверхностью» и человеком, подобным нам, смотрящим в сторону города, подобного Чикаго, с места, подобного Нью-Орлеану, но со всем остальным, перевернутым наоборот, так что Флорида у него будет уже с другой стороны? Ясно, что та­кая ситуация не кажется невозможной, физическим законам не противоречит такая замена всего левого на правое.

Еще одно обстоятельство: наше определение «правой» сто­роны не должно зависеть от истории. Иначе было бы очень просто отличить «левое» от «правого» — пойти в магазин зап­частей и наугад взять какой-нибудь болт. Вообще говоря, у нас в руках не обязательно окажется «правый болт», но все же более вероятно, что он будет именно правым, а не левым. Но это вопрос истории, или условностей, или общего положения вещей, а не фундаментальных законов. Ведь кто-то может начать выпускать болты с левой резьбой.

Таким образом, нам нужно поискать какие-то другие явле­ния, где бы «правое» входило более фундаментальным образом. Рассмотрим следующую возможность. Известно, что поляри­зованный свет, пропущенный через сахарный раствор, повора­чивает свою плоскость поляризации. Как мы видели в гл. 33 (вып. 3), плоскость поляризации при определенной концентра­ции сахара поворачивается направо. Казалось бы, мы нашли способ определения «правой стороны», потому что, растворив в воде некоторое количество сахара, мы можем повернуть пло­скость поляризации вправо. Но сахар получается из живых организмов, а если мы сделаем его искусственно, то обнаружим, что он не поворачивает плоскости поляризации. Если в этот искусственный сахар, который не поворачивает плоскости по­ляризации, напустить бактерий (они съедают некоторое коли­чество сахара) и затем отфильтровать их, то обнаружится, что, хотя сахар остался (почти половина первоначального ко­личества), и он поворачивает плоскость поляризации, но теперь уже в другую сторону! Этот факт кажется очень обескураживаю­щим, однако его можно легко объяснить.

Приведем другой пример. Одно из веществ, общее для всех живых существ, основа жизни — это белки (протеин). Белок состоит из цепочек аминокислот. На фиг. 52.1 показана модель аминокислоты, выделенной из белка.

Фиг. 52.1. Модели моле­кул аланина.

Слева — L-аланин; справа — D-аланин.

Эта кислота названа аланином, и на фиг. 52.1 (слева) показано расположение атомов в молекуле аланина, выделенного из белка живых существ. Если же мы попытаемся создать аланин из двуокиси углерода, этана и аммиака (что в самом деле можно сделать — это не столь уже сложная молекула), то обнаружим, что получились не толь­ко такие молекулы, но и другие, подобные показанной на фиг. 52.1 (справа), причем в равных количествах! Первые молеку­лы, те, которые произошли от живых существ, называются L-ала-нином. Другие же, одинаковые с ним химически в том смысле, что состоят из тех же атомов с теми же связями между ними, образуют «правосторонние» молекулы, которые в отличие от «левосторонних» молекул L-аланина называются D-аланином. Интересно, что если мы будем приготовлять аланин в лабора­тории из простых газов, то получится смесь обоих сортов в рав­ных количествах. Жизнь, однако, использует только L-аланин. (Но не без исключения, конечно: то там, то здесь в живых су­ществах встречается и .D-аланин, однако эти случаи очень редки. Во все белки входит исключительно L-аланин.) Если мы приготовим оба сорта и будем этой смесью кормить животных, которые любят «есть» его (т. е. усваивают аланин), то окажется, что они не смогут использовать D-аланин, а «съедят» только L-аланин. В результате получится то же, что и с нашим саха­ром; после того как бактерии «съедят» тот сахар, который им нравится, остается только «ненастоящий» сорт! (Левосторонний сахар тоже сладкий, а все же не такой, как настоящий, право­сторонний!)

Итак, похоже, что явления жизни позволяют отличить «правую» сторону от «левой», поскольку две молекулы хими­чески отличны одна от другой. И все-таки — нет, не могут! Пока мы занимались физическими измерениями, подобными определению энергий или скоростей химических реакций и т. д., эти два сорта вели себя совершенно одинаковым образом, если, разумеется, все остальное тоже было зеркально отражено. Одни молекулы поворачивают свет направо, а другие, проходя то же количество раствора,— налево на точно ту же величину. Таким образом, с точки зрения физики можно использовать лю­бую из этих двух аминокислот. Насколько мы понимаем основу вещей сегодня, уже в уравнение Шредингера заложено, что две молекулы должны вести себя в точности одинаковым образом, хотя там, где у одной правая сторона, у другой — левая. Но в природе тем не менее все устроено только одним способом!

Как полагают, причина этого состоит в следующем. Пред­ставьте себе, например, что в один прекрасный момент возникли такие условия, что все белки у каких-то существ содержали только левосторонние аминокислоты. Это привело к тому, что все на свете «перекосилось», «перекосились» все вещества в живых клетках, «перекосились» все ферменты— все стало не­симметричным. Когда пищеварительные ферменты пытались сменять химию своей пищи с одного сорта на другой, то один сорт пищи «подходил» им, а другой — нет (совсем как золушкин башмачок, с тем исключением, что мы меряем его на «левую но­гу»). Насколько нам известно сейчас, в принципе возможно создать такую лягушку, у которой, например, каждая молекула окажется «перевернутой», т. е. создать точное зеркальное отра­жение настоящей лягушки, так сказать, «левостороннюю» ля­гушку. Некоторое время эта «левосторонняя лягушка» чувство­вала бы себя вполне нормально, но не смогла бы найти себе пищи: если бы она проглотила муху, то ее ферменты не способны были бы переварить ее. Ведь муха-то настоящая, с правосторон­ней аминокислотой (разумеется, если мы не разведем специаль­но для нашей лягушки «левосторонних мух»). Итак, насколько нам сегодня известно, химические и жизненные процессы, если бы мы все «перевернули», протекали бы точно так же, как и сейчас.

Если жизнь — полностью физико-химическое явление, то факт «закрученности» всех белков только в одном направлении можно понять лишь с той точки зрения, что с самого начала со­вершенно случайно победил какой-то один сорт молекул. Где-то однажды органическая молекула как-то «перекосилась», и пра­вая сторона оказалась выделенной; какой-то случай в истории создал одностороннюю ситуацию, и с тех пор «перекос» разра­стался все шире и шире. Но, возникнув однажды, ситуация, которую мы наблюдаем сейчас, будет продолжаться вечно: все ферменты переваривают и приготовляют только «правосто­ронние» вещества. Когда в листья растений входит углекислый газ, водяной пар и другие вещества, то ферменты, приготовляю­щие из них сахар, делают его правосторонним, ибо они сами правосторонние. Если бы в более позднее время возник какой-то новый сорт вирусов или каких-то других живых существ, то они смогли бы выжить только, если оказались бы способны питаться уже существующими органическими веществами. А, стало быть, и сами они должны быть того же сорта.

Для правосторонних молекул не существует закона сохра­нения их числа. Жизнь может только увеличивать его. Пред­положение, таким образом, состоит в том, что жизненные явле­ния говорят нам не об отсутствии симметрии физических за­конов, а, наоборот, об универсальности природы и общности начала всех живых созданий на Земле в описанном выше смысле.

§ 5. Полярный и аксиальный векторы

Пойдем дальше. Вы видели, что в физике имеется масса при­меров применимости правила правой и левой руки. В самом деле, когда мы изучали векторный анализ, то узнали о правиле пра­вой руки, которым необходимо пользоваться, чтобы получить правильный момент количества движения и момент силы, маг­нитное поле и т. п. Например, сила, действующая на заряд в магнитном поле, равна F=qvXB. Но представьте себе та­кое положение: пусть мы знаем F, v и В. Как ив этого узнать, где у нас правая сторона? Если вернуться назад и посмотреть, откуда произошли векторы, то увидим, что правило правой руки — просто соглашение, своего рода трюк. В самом начале такие величины, как угловая скорость и момент количества движения и другие, подобные им, в действительности вообще не были настоящими векторами! Все они каким-то образом связа­ны с определенными плоскостями, и только благодаря тому, что наше пространство трехмерно, эти величины можно связать с направлением, перпендикулярным данной плоскости. Мы же из двух возможных направлений выбрали правое.

Представьте себе, что какой-то озорной чертик, решив под­шутить над физиками, пробрался во все лаборатории и всюду заменил слово «правое» на «левое». И в результате, где было написано правило правой руки, мы вынуждены были бы поль­зоваться правилом левой руки. Ну что ж, физики бы просто не заметили этого, ибо ни к какому изменению в физических за­конах это бы не привело, разумеется, если физические законы симметричны.

Покажем это на примере. Вы знаете, что существуют два сорта векторов. Имеются обыкновенные, «настоящие» векторы, подобные, например, отрезку расстояния Dr в пространстве. Пусть в нашей аппаратуре что-то находится «здесь», а нечто другое — «там», тогда те же самые «что-то» будут присутство­вать и в зеркально отраженной аппаратуре. Если мы в обоих случаях проведем векторы от «сюда» до «туда», то один вектор будет отражением другого (фиг. 52.2), причем направление стрелки вектора точно, как и все пространство, «выворачивает­ся наизнанку».

Фиг. 52.2. Отрезок в простран­стве и его зеркальное отраже­ние.

Такие векторы мы называем полярными.

Но второй сорт векторов, связанных с вращением, имеет совсем другую природу. Представьте себе нечто вращающееся в трехмерном пространстве (фиг. 52.3).

Фиг. 52.3. Вращающееся колесо и его зеркальное от­ражение.

Заметьте, что направление «вектора» угловой скорости т изменяется.

Если посмотреть на это в зеркало, то вращение будет происходить так, как показано на рисунке, т. е. как зеркальное изображение первоначального вращения. Условимся теперь представлять зеркальное враще­ние с помощью того же самого правила. В результате мы полу­чим «вектор», который в отличие от полярного вектора не изме­няется при отражении и оказывается перевернутым по отно­шению к полярному вектору и геометрии всего пространства. Такой вектор мы называем аксиальным.

Если физический закон симметрии относительно отражения правилен, то уравнения должны быть устроены так, чтобы при изменении знака каждого аксиального вектора и каждого век­торного произведения (что соответствует отражению) ничего не произошло. Например, когда мы пишем формулу для момента количества движения L=rXp, то здесь все в порядке, потому что при переходе в левую систему координат мы изменяем знак L, а знак р и r не изменяется. Кроме того, изменится и векторное произведение, поскольку мы должны правило правой руки за­менить правилом левой руки. Возьмем другой пример.

Известно, что сила, действующая на заряд в магнитном поле, равна F=qvXВ, но если мы от правой системы перей­дем к левой, то, поскольку, как известно, F и v — поляр­ные векторы, изменение знака из-за наличия векторного произведения должно компенсироваться изменением знака В, а это означает, что В должен быть аксиальным вектором. Дру­гими словами, при таком отражении В должен переходить в —В. Таким образом, если мы изменяем левые координаты на правые, то одновременно нужно северный полюс магнита изменить на южный.

Давайте посмотрим на примере, как это все получается. Пусть у нас имеются два магнита, похожих на изображенные на фиг. 52.4.

Фиг. 52.4. Электромагнит и его зеркальное отражение.

Один из магнитов выглядит в точности так, как зеркальное отражение другого, т. е. витки его накручены в дру­гую сторону, и все, что происходит внутри катушки, должно быть в точности обращено в другую сторону; ток течет, как это показано на рисунке. Теперь из законов магнетизма (которые вы хотя еще и не знаете официально, но, по-видимому, помните из школьного курса) получается, что магнитное поле направлено так, как это показано на рисунке. Там, где у первого магнита южный полюс, у другого магнита будет северный, ибо у него ток течет в другую сторону, а магнитное поле перевернуто. Таким образом, выходит, что при переходе от правой системы к левой мы действительно должны заменить северный полюс на южный!

Но северный и южный полюсы — это просто договоренность, и замена их еще ничего не означает. Давайте посмотрим на само явление. Предположим, что электрон движется от нас через маг­нитное поле перпендикулярно к плоскости страницы. Тогда, если воспользоваться формулой для силы vXВ (не забудьте, что электрон отрицательный!), мы получим, что в соответствии с этим физическим законом электрон должен отклоняться в указанном направлении. Таким образом, явление заключается вот в чем. Если в катушке в определенном направлении течет ток, то электрон как-то отклоняется. Это и есть физика, и не­важно, как мы будем называть все по дороге.

А теперь проделаем тот же опыт с зеркально отраженным маг­нитом: пошлем электрон в соответствующем направлении. Теперь на него будет действовать обратная сила. Вычислив ее по тем же правилам, мы получим правильный результат: соот­ветствующее движение будет зеркальным отражением преды­дущего!

§ 6. Какая же рука правая?

Дело в том, что существует один интересный факт: в любом явлении правило правой руки всегда встречается два или вооб­ще четное число раз, и в результате любое явление всегда выглядит симметричным. Короче говоря, раз мы не можем от­личить северный полюс от южного, то не можем отличить и правую сторону от левой. Может показаться, что определить, где находится северный полюс магнита, очень просто. Северным концом магнитной стрелки компаса будет тот, который указывает на север. Но это опять локальное свойство, связанное с геогра­фией Земли, все равно, что указание, в какой стороне находится Чикаго, и поэтому не идет в счет. Если вы видели стрелку ком­паса, то, вероятно, заметили, что ее северный конец окрашен в какое-то подобие синего цвета. Но это уже дело рук чело­века, который окрасил стрелку. Так что все это — условные критерии.

Вот если бы магнит обладал тем свойством, что, посмотрев на него внимательно, мы бы обнаружили на его северном полюсе растущую бороду, которой нет на южном, и это было бы общим правилом, т. е. если бы существовал какой-то единый способ, позволяющий отличить северный полюс магнита от южного, то это было бы концом симметрии при отражении.

Чтобы яснее представить себе всю проблему в целом, во­образите, что вы разговариваете по радио с каким-то существом, находящимся очень далеко от вас. Мы не можем послать ему какого-нибудь образца, чтобы он его увидел; вот если бы мы, к примеру, могли послать пучок света, то мы послали бы свет, поляризованный по кругу в правую сторону, и сказали бы: «Обрати внимание на направление вращения поляризации это­го света, мы называем его правым». Но мы не можем послать ему ничего подобного, а можем только говорить с ним. Наш собеседник находится очень, очень далеко, в каком-нибудь неизвестном мире, и не может видеть того, что видим мы. Мы не можем сказать: «Взгляни на Большую Медведицу. Смотри, как расположены ее звезды. Под правой стороной мы понимаем...» Мы можем только говорить с ним по радио.

Предположим, нам захотелось рассказать ему о себе. Ну, лучше всего начать с чисел: «Тик, тик — два, тик, тик, тик — три...», так что постепенно он выучит эти два слова, а потом больше. Спустя некоторое время вы настолько познакомитесь с ним, что он вас спросит: «Послушай, приятель, а как ты выглядишь?» Вы начнете описывать себя и первым делом ска­жете: «Мой рост один метр 75». «Подожди,— скажет он,— что такое метр?» Можно ли объяснить ему, что такое метр? Конечно, можно! Вы скажете: «Тебе известен диаметр атома водорода, так вот, мой рост составляет 17 000 000 000 диаметров атома водорода!» Это возможно, ибо физические законы не инвариант­ны относительно изменения масштаба, а поэтому мы можем определить абсолютную длину. Итак, мы определили размер нашего тела; можно описать и общую форму тела: рассказать, что у нас есть конечности с пятью отростками на концах и т. д., и так без особых трудностей он из нашего описания поймет, как мы выглядим. Он даже может вылепить нашу модель и, поглядев на нее, сказать: «Э-э, да ты, приятель, совсем, недурен. Но вот что у тебя внутри?» И мы начнем описывать ему наши внутренние органы, дойдем до сердца, тщательно опишем его форму и скажем: «Помести его в левую сторону груди». «Куда, куда? В левую сторону? А что это такое?» — удивится он. И вот как же описать ему, в какой стороне находится сердце, если он не может видеть то, что видим мы, и никогда не получал от нас ничего, что позволило бы ему понять, где же собственно левая сторона. Можно ли это сделать?

§ 7. Четность не сохраняется!

Оказывается, что законы тяготения, законы электричества и магнетизма, законы ядерных сил — все подчиняется прин­ципу симметрии при отражении, так что ни эти законы, ни все, что получено из них, не может помочь нам. Однако в природе было обнаружено явление, которое может происходить со мно­гими частицами, и называется оно бета-распадом, или слабым распадом. Один из видов слабого распада, связанный с частицей, открытой в 1954 г., задал физикам трудную головоломку. Есть такая заряженная частица, которая распадается на три p-мезона, как это схематически показано на фиг. 52.5.

Фиг. 52.5. Схематические диаграммы распадов t- и q-мезонов.

Частицу эту временно назвали t-мезоном. На том же рисунке показана и другая частица, которая распадается на два p-мезона. По за­кону сохранения заряда один должен быть нейтральным. Эта частица была названа q-мезоном,. Итак, у нас есть t-мезон, рас­падающийся на три p-мезона, и есть q-мезон, распадающийся на два p-мезона. Вскоре, однако, обнаружилось, что массы t и q почти равны друг другу, точнее, в пределах эксперимен­тальных ошибок они просто равны. Кроме того, где бы они ни появлялись, они всегда рождаются в одной и той же пропор­ции, скажем 14% t-частиц и 86% q-частиц.

Кто подогадливей, тот сразу поймет, что здесь мы имеем дело с одной и той же частицей, т. е. что рождаются не две частицы, а всего лишь одна, которая может распадаться двумя различными способами. Поэтому мы получали один и тот же про­цент рождения (ведь это же просто процент, отражающий способы, которыми она распадается).

Однако квантовая механика из принципа симметрии при отражении позволяет доказать (сейчас я, к сожалению, не могу объяснить вам, как это делается), что совершенно невозможно, чтобы оба эти способа распада принадлежали одной частице: одна частица никак не может распадаться двумя различными способами. Закон сохранения, соответствующий принципу сим­метрии при отражении, не имеет аналога в классической физике, и этот специфический закон сохранения в квантовой ме­ханике был назван законом сохранения четности. Таким обра­зом, вследствие закона сохранения четности, или, точнее, из симметрии квантовомеханических уравнений слабого распада относительно отражения, получалось, что одна и та же частица не может распасться обоими способами, так что здесь мы встре­чаемся с каким-то удивительным совпадением в массах, вре­менах жизни и т. д. Но чем больше изучалось это явление, тем более удивительным становились совпадения и постепенно росло подозрение в несправедливости фундаментального закона сим­метрии природы относительно отражения.

Это кажущееся нарушение побудило физиков Ли и Янга предложить поставить другие эксперименты и проверить, будет ли закон сохранения четности выполняться в других родствен­ных распадах. Первый такой эксперимент выполнила By в Ко­лумбийском университете. Заключался он в следующем. Оказы­вается, что у кобальта, который является хорошим магнетиком, существует изотоп, распадающийся с испусканием электронов. Поместим его в очень сильное магнитное поле при очень низкой температуре, так чтобы тепловые колебания не слишком силь­но сбивали атомные «магнитики», тогда все они «выстроятся» вдоль магнитного поля. Таким образом, все атомы кобальта «выстраиваются» в этом сильном поле одинаковым образом. Потом они распадаются, испускают электроны, и вот оказалось, что когда атомы «выстраиваются» в магнитном поле с направлен­ным вверх вектором В, то большинство электронов летит вниз.

Тому, кто не очень «на ты» с миром физики, это замечание мало что говорит, однако тот, кого волнуют тайны природы, уви­дит, что это наиболее удивительное открытие нашего времени. Если поместить атомы кобальта в очень сильное магнитное поле, то вылетевшие электроны более охотно летят вниз, чем вверх. Поэтому если бы мы отразили этот опыт в зеркале так, чтобы атомы кобальта были «выстроены» наоборот, т. е. вверх, то они бы испускали свои электроны вверх, а не вниз, и симметрия ис­чезла бы. Вот у магнита и выросла борода!

Теперь мы знаем, что южный полюс магнита это тот, от ко­торого летят b-распадные электроны; таким образом, физически возможно отличить северный полюс от южного.

После этого было сделано множество других эксперимен­тов: распад p-мезона на m и v, распад m-мезона на электрон и два нейтрино, распад Л-частицы на протон и p-мезон, распад 2S-частицы и много других распадов. И почти во всех тех слу­чаях, где этого можно было ожидать, обнаружено отсутствие принципа зеркальной симметрии! Фундаментальный закон фи­зики — закон симметрии при отражении — оказался на этом уровне несправедливым.

Короче говоря, теперь мы уже могли бы объяснить нашему приятелю из космоса, где у нас расположено сердце.«Послушай,— сказали бы мы ему,— сделай себе магнит, намотай на него про­волоку и пусти по ней ток. Затем возьми кусок кобальта, охлади его до низкой температуры. Расположи все устройство так, чтобы испущенные электроны летели от ног к голове, тогда направле­ние тока в катушке скажет тебе, какую сторону мы называем правой, а какую — левой: ток входит с правой стороны и выхо­дит с левой». Итак, с помощью эксперимента такого рода можно определить, где правая, а где левая сторона.

Было предсказано множество других свойств. Оказалось, например, что спин, т. е. угловой момент, или момент количества движения ядра кобальта, до распада равен пяти единицам h, а после распада — четырем. Половину этого момента количества движения уносит электрон, а половину — нейтрино. Нетрудно теперь сообразить, что момент количества движения, уносимый электроном, должен быть направлен по линии его движения, как и момент количества движения нейтрино. Казалось, что электрон вертится справа налево; это тоже было проверено. Сделано это было прямо здесь в КАЛТЕХ'е. Бем и Вапстра, поставившие эксперимент, обнаружили, что электрон действи­тельно крутится налево. (Были и другие эксперименты, давав­шие противоположный ответ, но они оказались неверными!)

Следующей задачей было нахождение правила нарушения закона сохранения четности. Есть ли какое-нибудь правило, говорящее нам, насколько велико должно быть это нарушение? Оно оказалось следующим: нарушение происходит только в очень медленных реакциях, названных слабыми распадами, и если уж оно произошло, то частицы, уносящие спин, такие, как электрон или нейтрино, вылетают, преимущественно враща­ясь налево. Это как бы «правило перекоса», оно связывает поляр­ный вектор скорости и аксиальный вектор момента количества движения и говорит, что моменту количества движения более присуще направление против вектора скорости, нежели по нему. Таково правило, но мы еще не очень понимаем всех его «по­чему» и «поэтому». Почему справедливо именно это правило, в чем его фундаментальная причина и как оно связано с дру­гими явлениями? Сейчас мы настолько потрясены самим фак­том несимметрии мира, что до сих пор еще не можем оправиться и понять, как же оно отразится на всех остальных правилах. Тем не менее проблема эта интересная, животрепещущая и, увы, до сих пор не решенная. Поэтому сейчас самое время об­судить некоторые вопросы, связанные с этим правилом.

§ 8. Антивещество

Когда исчезает одна из симметрии, то первым делом нуж­но немедленно обратиться к списку известных или предположен­ных симметрии и посмотреть, не может ли еще нарушиться ка­кая-то из них. Мы не упомянули одну операцию из нашего списка, а к ней наш вопрос относится в первую очередь — это от­ношение между веществом и антивеществом. Дирак предсказал, что в дополнение к электронам в мире должны существовать другие частицы, называемые позитронами (открытые Андерсоном в КАЛТЕХ'е), и они тесно связаны с электронами. Все свойства этих двух частиц подчиняются определенным правилам соот­ветствия: энергии их равны, массы равны, заряды противопо­ложны, но самое важное, столкнувшись, они могут уничтожить друг друга (аннигилировать), превратив всю свою массу в энер­гию, например g- излучение. Позитрон называется античасти­цей электрона, и эти свойства являются основными свойствами частицы и ее античастицы. Из рассуждений Дирака было ясно, что у всех остальных частиц тоже должны быть соответствую­щие античастицы. Например, наряду с протоном должен существовать и антипротон, который сейчас обозначается симво­лом р. У него должен быть отрицательный электрический заряд, та же, что и у протона, масса и т. д. Однако наиболее важным свойством является то, что протон и антипротон, столкнувшись, могут уничтожить друг друга. Я особенно подчеркиваю это по­тому, что люди обычно удивляются, когда говоришь, что наряду с нейтроном существует и антинейтрон; они говорят: «Как ан­тинейтрон может иметь противоположный заряд, ведь он нейтральный?» Приставка «анти» означает не просто противополож­ный заряд, частица характеризуется целым набором свойств, многие из которых становятся противоположными. Антинейт­рон можно отличить от нейтрона следующим способом: если поместить рядом два нейтрона, они так и останутся двумя нейт­ронами, но если мы поместим рядом нейтрон и антинейтрон, то они уничтожат друг друга, причем выделят большое коли­чество энергии в виде разных p-мезонов, g-квантов и т. п.

Далее, если у нас есть антипротоны, антинейтроны и по­зитроны, то из них в принципе можно составить антиатомы. Это еще не сделано, но в принципе вполне возможно. В атоме водорода, например, в центре расположен протон, вокруг ко­торого крутится электрон. Вообразите теперь, что мы сделали антипротон и запустили вокруг него позитрон. Будет ли он кру­титься? Ну прежде всего антипротон заряжен отрицательно, а позитрон — положительно, так что они будут притягиваться друг к другу с соответствующей силой, а поскольку массы у них одинаковы с протоном и электроном, то одинаково будет и все остальное. В этом состоит один из принципов симметрии в фи­зике: уравнения, по-видимому, говорят нам, что если сделать одни часы из вещества, а другие, точно такие же, из антиве­щества, то они будут идти совершенно одинаково. (Разумеется, если мы поместим эти часы рядом, то они уничтожат друг друга, но это уже совсем другое дело.)

Тогда немедленно возникает вопрос. Можно сделать двое часов из вещества, причем одни «правосторонние», а другие «левосторонние». Можно, скажем, сделать не простые часы, а часы с кобальтом, магнитами и детекторами, регистрирую­щими b-распадные электроны и считающими их. Всякий раз, ког­да регистрируется электрон, секундная стрелка слегка подви­гается. Но тогда зеркально отраженные часы, в которые при­ходит меньше электронов, не будут идти с той же скоростью. Итак, теперь нам ясно, что возможно построить такую пару ча­сов, что правосторонние не будут согласовываться с левосто­ронними. Давайте сделаем часы из вещества и назовем их стан­дартными, или правосторонними, и сделаем еще часы тоже из вещества и назовем их левосторонними. Мы только что устано­вили, что эти двое часов, вообще говоря, не будут идти одина­ковым образом, а до этого выдающегося открытия в физике считалось, что будут. Далее мы, кроме того, полагали, что ве­щество и антивещество эквивалентны, т. е. если бы мы сделали часы из антивещества, такие же правосторонние, той же самой формы, то они шли бы точно так же, как и правосторонние часы из вещества, а если бы мы сделали такие же левосторонние часы, то и они тоже ходили бы точно таким же образом. Другими сло­вами, первоначально мы полагали, что все четверо таких часов должны работать совершенно одинаково. Но теперь мы знаем, что правосторонние и левосторонние часы из вещества не оди­наковы. А следовательно, право- или левосторонние часы из антивещества тоже, по-видимому, не одинаковы.

Теперь возникает очевидный вопрос: есть ли пара часов, которые идут одинаково? Иначе говоря, ведет ли себя правосто­роннее вещество так же, как правостороннее антивещество? Или же правостороннее вещество ведет себя так же, как лево­стороннее антивещество? Эксперименты с b-распадом, но не с электронным, а с позитронным b-распадом, указывают, что эта связь такова: «правое» вещество ведет себя точно так же, как «левое» антивещество.

Итак, в конечном счете право-левая симметрия все же реа­билитирована! Если мы изготовим левосторонние часы, но изготовим их из материала совершенно другого рода — из анти­вещества, а не из вещества, то они будут идти точно таким же образом. В итоге произошло вот что: вместо двух независимых правил в нашем списке симметрии мы получили одно новое комбинированное правило, гласящее, что правостороннее вещество симметрично с левосторонним антивеществом.

Таким образом, если наш приятель из космоса сделан из антивещества и мы даем ему указания, как сделать нашу «пра­востороннюю» модель, то он, разумеется, сделает все наоборот. Что произошло бы, если бы после долгих переговоров мы научи­лись другу друга строить космические корабли и договорились бы о встрече где-то в космическом пространстве, на полпути между ним и нами? Разумеется, мы бы предварительно рас­сказали друг другу о своих обычаях и прочем, и вот наконец вы спешите навстречу, чтобы пожать ему руку. Но будьте внимательны. Если он протянет вам левую руку — берегитесь!

§ 9. Нарушенная симметрия

А что нам делать с законами, которые только приблизительно симметричны? Самое удивительное здесь то, что в широкой об­ласти важнейших явлений—ядерные силы, электромагнитные явления и даже некоторые слабые взаимодействия типа грави­тации, словом, все законы в широчайшей области физики ока­зываются симметричными. Но, с другой стороны, вдруг всплы­вает какое-то слабенькое явление и говорит: «Нет, не все на свете симметрично!» Но как могло случиться, что природа почти симметрична, а не абсолютно симметрична? Что нам с ней делать? Прежде всего давайте все-таки посмотрим, нет ли каких-то дру­гих примеров подобного рода? Да, такие примеры есть и даже не один. Например, ядерные части сил между протоном и про­тоном, между протоном и нейтроном или нейтроном и нейтро­ном в точности равны друг другу. Это некая новая симметрия — симметрия ядерных сил: в ядерных взаимодействиях протон и нейтрон вполне могут заменять друг друга. Но она, очевидно, не всеобщая симметрия, ибо между двумя нейтронами не су­ществует электрического отталкивания, как между двумя про­тонами. Поэтому мы не можем всегда заменять протона нейтро­ном, это, вообще говоря, неверно, хотя и является хорошим приближением. Почему хорошим,? Да потому, что ядерные силы гораздо больше электрических. Так что это тоже «почти сим­метрия». Итак, подобные примеры все же есть и в других об­ластях.

Нас всегда тянет рассматривать симметрию как некоего рода совершенство. Это напоминает старую идею греков о совершен­стве кругов. Им было даже страшно представить, что планетные орбиты не круги, а только почти круги. Но между кругом и почти кругом разница немалая, а если говорить об образе мыс­лей, то это изменение просто огромно. Совершенство и симмет­рия круга исчезают как только чуть-чуть исказить его. Дефор­мируйте немного круг, и это будет концом его симметрии и со­вершенства. Спрашивается, почему же орбиты только почти круги? Это куда более трудный вопрос. Истинное движение планет, вообще говоря, должно происходить по эллипсам, но в течение веков благодаря приливным силам они превратились в почти окружности. Но везде ли есть подобная проблема? Если бы пути планет были действительно кругами, то проблема не требовала бы пространных объяснений — они просты. Но поскольку эти пути только почти круговые, то объяснить нуж­но очень многое. Результат же превращается в большую дина­мическую проблему, и теперь нам нужно объяснить, привлекая приливные силы или что-то еще, почему они приблизительно симметричны.

Итак, наша цель понять, откуда взялась симметрия. Почему природа столь близка к симметрии? По этому вопросу ни у кого нет никакой разумной мысли. Единственное, что я могу пред­ложить вам,— это старое японское предание. В японском городе Никко есть ворота, которые японцы называют самыми краси­выми воротами страны. Они были построены в период большого влияния китайского искусства. Это необычайно сложные ворота, со множеством фронтонов, изумительной резьбой и большим количеством колонн, на основании которых вырезаны драконьи головы, божества и т. п. Но, приглядевшись, можно заметить, что в сложном и искусном рисунке на одной из колонн неко­торые из его мелких деталей вырезаны вверх ногами. В остальном рисунок полностью симметричен. Спрашивается, для чего это было нужно? Как говорит предание, это было сделано для того, чтобы боги не заподозрили человека в совершенстве. Ошибка была сделана намеренно, дабы не вызвать зависти и гнева богов.

Мы можем, вообще говоря, подхватить эту мысль и сказать, что истинное объяснение приблизительной симметрии мира состоит в следующем: боги сотворили свои законы только приближенно симметричными, чтобы мы не завидовали их со­вершенству!

КОНЕЦ ПЕРВОГО ТОМА

* Их построил архитектор и резчик Цингору в середине XVII ве­ка. —Прим. ред.

* Автор не зря предупреждал, что обо всем содержании этой гла­вы можно сказать: «насколько нам известно сегодня». Ведь это уже «передний край» физики, где возможны любые изменения. Так и выш­ло. Совсем недавно было установлено, что симметрия между правым веществом и левым антивеществом не всегда существует. Комбиниро­ванная симметрия тоже оказалась приближенной. Мы пока не знаем, как и почему это происходит, пока строим только гипотезы, но вполне возможно, что, когда дело дойдет до встречи с нашим приятелем из другого мира, мы предварительно сможем выяснить, сделан ли он из вещества, как и мы, или из антивещества. — Прим. ред.

* Сейчас уже научились делать еще два антиизотопа водорода: антидейтрон и антитритий. — Прим. ред.

 

Оглавление

Глава 46 ХРАПОВИК И СОБАЧКА

Глава 47 ЗВУК. ВОЛНОВОЕ УРАВНЕНИЕ

Глава 48 БИЕНИЯ

Глава 49 СОБСТВЕННЫЕ КОЛЕБАНИЯ

Глава 50 ГАРМОНИКИ

Глава 51 ВОЛНЫ

Глава 52 СИММЕТРИЯ ЗАКОНОВ ФИЗИКИ