Математика и искусство [Александр Викторович Волошинов] (fb2) читать онлайн
[Настройки текста] [Cбросить фильтры]
[Оглавление]
Волошинов Александр Викторович Математика и искусство
Книга для тех, кто не только любит математику или искусство, но и желает задуматься о природе прекрасного и красоте науки
Вступление
В природе существует много такого, что не может быть ни достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело и надежно использовано на практике без помощи вмешательства математики. Это можно сказать о перспективе, музыке, ...архитектуре...На фронтисписе предлагаемой книги изображен древнекитайский символ гармонии Ин-Ян[1]. Этим символом выражалась сущность материи, сущность всего живого, которая, по древнекитайским воззрениям, заключалась в единстве противоположностей, в симметрии взаимодополняющих начал. Столкновение и борьба этих двух мировых начал — источник жизни. Ян для древних китайцев обозначал одновременно Солнце, свет, добро, красоту, правду, действие, мужское начало; Ин — Землю, тьму, зло, безобразие, ложь, бездействие, женское начало. (Можно с удовлетворением отметить, что взгляды современного человечества в отношении "женского начала" претерпели существенные изменения по сравнению с древнекитайскими.) Маленькие круги противоположного цвета в символе Ин-Ян напоминали о том, что даже в самом центре одного начала имеется элемент начала противоположного: даже добро содержит крупицу зла, а во всяком начале есть частица добра; даже безобразное может быть в чем-то привлекательным, а всякая красота может иметь что-то отталкивающее; даже в истине содержится кое-что от заблуждения, а во всяком заблуждении имеется элемент истины. Нам представляется, что мудрый и красивый символ Ин-Ян, составленный из самых совершенных, как считали древние, линий — окружностей, может стать и символом нашей книги, в которой речь идет о науке (математике) и искусстве. Наука и искусство — два основных начала в человеческой культуре, две дополняющие друг Друга формы высшей творческой деятельности человека. В истории человечества были периоды, когда эти начала дружно уживались, а были и времена, когда они противоборствовали. Но видимо, высшая их цель — быть взаимодополняющими гранями человеческой культуры, как принципы Ин-Ян в древнекитайском знаке. Более того, как и в этом мудром знаке, даже в самой сердцевине науки есть элемент искусства, а всякое искусство несет в себе частицу научной мудрости. Но почему из всей науки выбрана именно математика? Потому что первоначальное значение слова "математика" (от греч. mathema — знание, наука) не утрачено и сегодня. Математика остается олицетворением науки, символом мудрости, царицей всех наук. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. За долгую историю человеческой культуры накоплена необъятная литература об искусстве и огромная — о математике. Достаточно указать на блестящие книги "Что такое искусство?" Льва Толстого и "Что такое математика?" Р. Куранта и Г. Роббинса. Однако в то время как библиотечные полки прогибаются "под мудрой тяжестью подробнейших сочинений о науке и об искусстве, отдельно — о науке, и отдельно — об искусстве, ...о механизме и об истории теснейшего взаимодействия этих органов жизни человечества не написано почти ничего". Эта мысль писателя Д. Данина и служила автору оправданием при работе над книгой. Из многих искусств, с которыми взаимодействует математика, в книге выбраны три: музыка, архитектура и живопись. Автор надеется, что "математические начала" литературы (в особенности поэзии), а также интереснейшая тема "Искусство и ЭВМ" составят предмет будущей книги. Но и при таком ограничении автор понимает, что тема, собранная в названии книги, настолько сложна и многообразна, что сил и возможностей одного человека хватит только на объяснение союза "и" в этом заголовке. Собственно, такое объяснение и рассматривалось как главная задача книги: показать, что между словами "математика" и "искусство" действительно должен стоять соединительный союз "и", а не разделительный "или". Если автору удалось это сделать, то цель можно считать достигнутой. В заключение считаю своим приятным долгом выразить искреннюю благодарность академику Ю. В. Гуляеву и профессору В. А. Крысько, поддержавшим на самой трудной для автора ранней стадии идею написания этой книги. Мне хочется также сказать теплые слова признательности моей жене Е. В. Волошиновой, первому читателю и суровому рецензенту этой книги. Автор с благодарностью примет отзывы и замечания, которые можно направлять по адресу: 129846, Москва, 3-й проезд Марьиной рощи, 41, издательство "Просвещение", редакция математики.Ф. Бэкон
I. Искусство, наука, красота
Потребность красоты и творчества, воплощающего ее,- неразлучна с человеком, и без нее человек, быть может, не захотел бы жить на свете.Ф. Достоевский
Едва ли кто-нибудь из не математиков в состоянии освоиться с мыслью, что цифры могут представлять собой культурную или эстетическую ценность или иметь какое-нибудь отношение к таким понятиям, как красота, сила, вдохновение. Я решительно протестую против этого костного представления о математике.Н. Винер
 Искусство, наука, красота... Как часто мы произносим и слышим эти слова и как редко утруждаем себя задуматься над их смыслом и содержанием! Как любим мы поговорить о произведениях искусства или достижениях науки и как редко замечаем, что обе эти великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! Как мало мы знаем о том, насколько давно образовались эти узы, сколь они крепки и необходимы и науке, и искусству, так что разорвать их нельзя, не повредив и тому и другому, и что красота является самым крепким связующим звеном между наукой и искусством!
Добро, Истина, Красота... Еще древние учили о триединстве этих трех ликов культуры. Со временем, увы, это триединство распалось: Истина отошла к науке, Красота — к искусству, Добро вообще повисло в воздухе. Сегодня, как никогда, важно возродить это утраченное триединство. Наука, не освященная гуманистическими идеалами Добра, ведет мир к катастрофе. Искусство, потерявшее луч Истины, погружается в сумерки декаданса. Красота в равной мере должна питать искусство и науку.
Искусство, наука, красота... Как часто мы произносим и слышим эти слова и как редко утруждаем себя задуматься над их смыслом и содержанием! Как любим мы поговорить о произведениях искусства или достижениях науки и как редко замечаем, что обе эти великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! Как мало мы знаем о том, насколько давно образовались эти узы, сколь они крепки и необходимы и науке, и искусству, так что разорвать их нельзя, не повредив и тому и другому, и что красота является самым крепким связующим звеном между наукой и искусством!
Добро, Истина, Красота... Еще древние учили о триединстве этих трех ликов культуры. Со временем, увы, это триединство распалось: Истина отошла к науке, Красота — к искусству, Добро вообще повисло в воздухе. Сегодня, как никогда, важно возродить это утраченное триединство. Наука, не освященная гуманистическими идеалами Добра, ведет мир к катастрофе. Искусство, потерявшее луч Истины, погружается в сумерки декаданса. Красота в равной мере должна питать искусство и науку.
 П. Филонов. Беспредметная композиция. 1920. Характерное произведение одного из лидеров русского авангарда — человека яркого дарования и трагической судьбы
Красота... Сколько волнений, тревог и радостей доставляла она каждому! Но знаем ли мы, что это такое, может ли хоть кто-нибудь ответить на простой вопрос: "Что есть красота?"
П. Филонов. Беспредметная композиция. 1920. Характерное произведение одного из лидеров русского авангарда — человека яркого дарования и трагической судьбы
Красота... Сколько волнений, тревог и радостей доставляла она каждому! Но знаем ли мы, что это такое, может ли хоть кто-нибудь ответить на простой вопрос: "Что есть красота?"
 Дипилонская амфора. VIII в. до н. э. Типичный образец 'геометрического стиля' периода гомеровской Греции
Дипилонская амфора. VIII в. до н. э. Типичный образец 'геометрического стиля' периода гомеровской Греции
 Почти три тысячелетия разделяет эти два произведения искусства. Сколь различны и сколь похожи они! Не оттого ли, что геометрия пронизывает и соединяет эти два антипода в истории искусства?
Искусство... Мы много спорим об искусстве, хотя и говорим, что о вкусах не спорят. Но раз мы все-таки спорим, значит, возможны какие-то общепринятые точки зрения во вкусах, в оценках произведений искусства, во взглядах на прекрасное. Но есть ли законы красоты и каковы они?
Наука... Мы преклоняемся перед ее мудростью, ее успехи окружают нас со всех сторон и кружат нам голову. Но многие ли ощущают, что наука прекрасна, как и искусство? В чем же красота науки?
В предлагаемой книге вы не найдете ответов на эти вопросы. Не найдете потому, что их до сих пор нет. Это ?вечные" проблемы, существующие ровно столько, сколько существуют сами понятия. Но нам кажется, что, прежде чем начать разговор о "математических началах" искусства, разумно было бы, по крайней мере, поставить эти вопросы, обратить на них внимание и по возможности кое-что разъяснить. Впрочем, и цель на стоящей книги мы видим прежде всего в том, чтобы читатель задумался над вопросами, которые, возможно, Казались ему слишком очевидными.
Почти три тысячелетия разделяет эти два произведения искусства. Сколь различны и сколь похожи они! Не оттого ли, что геометрия пронизывает и соединяет эти два антипода в истории искусства?
Искусство... Мы много спорим об искусстве, хотя и говорим, что о вкусах не спорят. Но раз мы все-таки спорим, значит, возможны какие-то общепринятые точки зрения во вкусах, в оценках произведений искусства, во взглядах на прекрасное. Но есть ли законы красоты и каковы они?
Наука... Мы преклоняемся перед ее мудростью, ее успехи окружают нас со всех сторон и кружат нам голову. Но многие ли ощущают, что наука прекрасна, как и искусство? В чем же красота науки?
В предлагаемой книге вы не найдете ответов на эти вопросы. Не найдете потому, что их до сих пор нет. Это ?вечные" проблемы, существующие ровно столько, сколько существуют сами понятия. Но нам кажется, что, прежде чем начать разговор о "математических началах" искусства, разумно было бы, по крайней мере, поставить эти вопросы, обратить на них внимание и по возможности кое-что разъяснить. Впрочем, и цель на стоящей книги мы видим прежде всего в том, чтобы читатель задумался над вопросами, которые, возможно, Казались ему слишком очевидными.
1. Эстетика: наука о прекрасном
Скажи, откуда ты приходишь, Красота? Твой взор — лазурь небес иль порожденье ада? Ты, как вино, пьянишь прильнувшие уста, Равно ты радости и козни сеять рада.Ш. Бодлер
А если это так, то что есть красота И почему ее обожествляют люди? Сосуд она, в котором пустота, Или огонь, мерцающий в сосуде?Что такое искусство? Как объяснить пронзительное воздействие искусства на человека? Какая потребность побуждает людей создавать произведения искусства? Сколь долго существует искусство?.. Непростые это вопросы, и однозначно ответить можно, пожалуй, лишь на последний из них: искусство существует столько, сколько существует человек! Доказательством тому служит не только искусство Шумера и Древнего Египта, зародившееся в IV-III тысячелетиях до н. э., но и первобытное искусство верхнего палеолита, уходящее корнями в XL тысячелетие (400 веков!) до н. э. "Что такое искусство?" — этим вопросом Лев Толстой озаглавил свою крупнейшую работу об искусстве, которая стоила ему пятнадцати лет напряженного труда. Величайший мыслитель пытается разобраться в удивительном феномене искусства, изучает все доступные ему работы предшественников, разбирает около семидесяти определений искусства, но... вопросы, вопросы растут, как снежный ком, а истина все ускользает. Почему? "В каждом большом городе строятся огромные здания для музеев, академий, консерваторий, драматических школ, для представлений и концертов. Сотни тысяч рабочих — плотники, каменщики, красильщики, столяры, обойщики, портные, парикмахеры, ювелиры, бронзовщики, наборщики — целые жизни проводят в тяжелом труде для удовлетворения требований искусства, так что едва ли есть какая-нибудь другая деятельность человеческая, кроме военной, которая поглощала бы столько сил, сколько эта" (Лев Толстой).Н. Заболоцкий
 Изображение бизона. Фрагмент наскальной живописи из 'Большого зала' или 'Зала быков' пещеры Ласко, Франция. Верхний палеолит, мадленский период, XII тыс. до н. э.- период расцвета пещерного искусства. Высокое качество живописи и ее прекрасная сохранность позволяют отнести пещерный комплекс Ласко к разряду первоклассных образцов пещерного искусства
Почему? "Во все времена молодые люди шли в искусство, обрекая себя на нищету, непризнание, неимоверно тяжелый труд, который в девяноста девяти случаях из ста не приносил ни славы, ни благополучия, ни даже внутреннего сознания успеха. Образ нищего художника — один из самых привычных в литературе всех времен. Но снова и снова люди несли свои жизни в жертву тому же искусству. Они шли непреклонно, как идет рыба — через пороги, через препятствия в извечные места нереста, погибая в пути, лишь бы выполнить заложенную природой высокую обязанность". А это наш современник, физик-теоретик, член-корреспондент АН СССР Е. Л. Фейнберг в работе "Кибернетика, логика, искусство" через 100 лет после Льва Толстого пытается распутать все тот же клубок вопросов. Возможно, многих удивит, что представитель точных наук занялся вопросами искусства. Ничего удивительного! Тайна искусства, загадка прекрасного всегда волновали ученых, и в этом мы еще не раз убедимся.
Изображение бизона. Фрагмент наскальной живописи из 'Большого зала' или 'Зала быков' пещеры Ласко, Франция. Верхний палеолит, мадленский период, XII тыс. до н. э.- период расцвета пещерного искусства. Высокое качество живописи и ее прекрасная сохранность позволяют отнести пещерный комплекс Ласко к разряду первоклассных образцов пещерного искусства
Почему? "Во все времена молодые люди шли в искусство, обрекая себя на нищету, непризнание, неимоверно тяжелый труд, который в девяноста девяти случаях из ста не приносил ни славы, ни благополучия, ни даже внутреннего сознания успеха. Образ нищего художника — один из самых привычных в литературе всех времен. Но снова и снова люди несли свои жизни в жертву тому же искусству. Они шли непреклонно, как идет рыба — через пороги, через препятствия в извечные места нереста, погибая в пути, лишь бы выполнить заложенную природой высокую обязанность". А это наш современник, физик-теоретик, член-корреспондент АН СССР Е. Л. Фейнберг в работе "Кибернетика, логика, искусство" через 100 лет после Льва Толстого пытается распутать все тот же клубок вопросов. Возможно, многих удивит, что представитель точных наук занялся вопросами искусства. Ничего удивительного! Тайна искусства, загадка прекрасного всегда волновали ученых, и в этом мы еще не раз убедимся.
 Венера Таврическая, III в. до н. э. Одно из первых в России произведений античного искусства
Так что же такое искусство? Каких только ответов на этот вопрос не было! Искусство объявлялось "подражанием природе" и "учебником жизни", "воспроизведением действительности" и "свободным формотворчеством", "недостижимым идеалом" и "высшей молитвой". Теоретики, критики, деятели и любители искусства наперебой утверждали, что искусство должно Услаждать и развлекать и что оно призвано воспитывать, что оно служит познанию жизни и что оно должно возносить душу человека к Богу, что оно призвано быть высшей формой общения между людьми и что оно есть недоступная для понимания "толпы" форма самовыражения художника...
Венера Таврическая, III в. до н. э. Одно из первых в России произведений античного искусства
Так что же такое искусство? Каких только ответов на этот вопрос не было! Искусство объявлялось "подражанием природе" и "учебником жизни", "воспроизведением действительности" и "свободным формотворчеством", "недостижимым идеалом" и "высшей молитвой". Теоретики, критики, деятели и любители искусства наперебой утверждали, что искусство должно Услаждать и развлекать и что оно призвано воспитывать, что оно служит познанию жизни и что оно должно возносить душу человека к Богу, что оно призвано быть высшей формой общения между людьми и что оно есть недоступная для понимания "толпы" форма самовыражения художника...
 Шарден. Прачка. Ок. 1737
Шарден. Прачка. Ок. 1737
 Император Октавиан Август в образе Юпитера. I в. Волшебство искусства превратило тщедушного Октавиана в величавого Юпитера
Император Октавиан Август в образе Юпитера. I в. Волшебство искусства превратило тщедушного Октавиана в величавого Юпитера
 Микеланджело. Скорчившийся мальчик. Между 1520-1534
Микеланджело. Скорчившийся мальчик. Между 1520-1534
 Камея Гонзаго. III в. до н. э
Камея Гонзаго. III в. до н. э
 Эрмитаж. В центре зала ваза Колыванской гранильной фабрики. XIX в.
Никакая другая область человеческой деятельности — ни наука, ни политика, ни религия — не истолковывалась столь разноречиво и противоречиво, как искусство. В самом деле, чтобы объяснить, что такое искусство, в нем надо найти такие свойства, которые одинаково подходили бы к музыке и литературе, архитектуре и живописи, скульптуре и танцу. Но как найти внутреннюю связь между торжественным великолепием здания Зимнего дворца и собранными в нем сокровищами Эрмитажа? Какая незримая нить связывает между собой Венеру Таврическую и прачку Шардена, грозного Юпитера и скорчившегося мальчика Микеланджело, миниатюрную античную камею и огромную колыванскую вазу? Споры об определении и назначении искусства велись на протяжении всей его истории и не затихли по сей день. И в том, что человечество, давно и однозначно определившее назначение других форм своей духовной и практической деятельности, никак не может "договориться" в определении искусства, и кроется, по-видимому, разгадка самого феномена искусства.
Эрмитаж. В центре зала ваза Колыванской гранильной фабрики. XIX в.
Никакая другая область человеческой деятельности — ни наука, ни политика, ни религия — не истолковывалась столь разноречиво и противоречиво, как искусство. В самом деле, чтобы объяснить, что такое искусство, в нем надо найти такие свойства, которые одинаково подходили бы к музыке и литературе, архитектуре и живописи, скульптуре и танцу. Но как найти внутреннюю связь между торжественным великолепием здания Зимнего дворца и собранными в нем сокровищами Эрмитажа? Какая незримая нить связывает между собой Венеру Таврическую и прачку Шардена, грозного Юпитера и скорчившегося мальчика Микеланджело, миниатюрную античную камею и огромную колыванскую вазу? Споры об определении и назначении искусства велись на протяжении всей его истории и не затихли по сей день. И в том, что человечество, давно и однозначно определившее назначение других форм своей духовной и практической деятельности, никак не может "договориться" в определении искусства, и кроется, по-видимому, разгадка самого феномена искусства.
Кто осмелится сказать, что определил Искусство? перечислил все его стороны? А может быть, уже и понимал, и называл нам в прошлые века, но мы недолго могли на том застояться: мы послушали, и пренебрегли, и откинули тут же, как всегда спеша сменить хоть и самое лучшее — а только бы на новое!Искусство многофункционально: оно способно решать самые различные социальные задачи, которые сплетены в нем в единый неразрывный узел. Среди других строго разграниченных форм человеческой деятельности искусство сохраняет поразительное свойство: быть всем и ничем особенным одновременно. Подобно науке искусство служит познанию окружающей действительности; подобно языку оно является средством общения людей, разрабатывая для этого специальные художественные "языки" музыки, живописи, поэзии и т. д.; вместе с идеологией оно участвует в определении системы ценностей; вместе с педагогикой оно служит исключительно сильным средством воспитания. Человеку свойственно в многообразных по форме явлениях искать общую первопричину. Замечательных результатов на этом пути достигла наука физика. Достаточно напомнить закон всемирного тяготения Ньютона, связавший воедино и падение яблока, и движение планет. Поэтому символично, что именно физик Фейнберг в упоминавшейся работе пытается найти некоторую общую подоснову, которая могла бы объединить множество столь несходных функций искусства. Перечислим кратко лишь основные из них. Прежде всего искусство является средством передачи чувств художника, оно позволяет сохранить для грядущих поколений духовный опыт, накапливаемый человечеством. Благодаря искусству происходит тот животворный обмен мыслями, чувствами, устремлениями, без которого немыслимо существование человека. Искусство делает духовный мир художника, способного постигать действительность с особой чуткостью и проникновенностью, достоянием каждого. Таким образом, благодаря гению Гомера, Рафаэля, Шостаковича мы становимся умнее, зорче, душевно богаче. В этом заключается так называемая коммуникативная (от лат. communicatio — сообщение) функция искусства. Огромную роль играет просветительская функция искусства. Любой из нас может признаться в том, что многие яркие и незабываемые сведения он с наслаждением извлек не из учебников истории или географии, а из художественных произведений А. Дюма, Ж. Верна, М. Шолохова. Еще древние греки заметили удивительное свойство искусства: поучать развлекая. Эту же особенность искусства имел в виду и Н. Г. Чернышевский, когда говорил, что искусство — такой учебник жизни, который с удовольствием читают даже те, кто не любит других учебников. Ф. Энгельс отмечал, что из романов Бальзака он узнал об истории французского общества гораздо больше, чем из работ специалистов. Но еще важнее — способность искусства раскрывать тайники духовного мира человека, благодаря чему оно становится не только средством познания, но и инструментом самопознания. Раскрывая перед нами духовный мир своих героев, художник дает нам возможность познать и самих себя, понять в себе то, что без помощи искусства мы никогда бы не заметили и не осмыслили. Каждый испытал на себе и воспитательную функцию искусства. Воспитывая, искусство обращается не только к нашей мысли, но и к нашему чувству; оно требует от нас не только понимания, но и сопереживания, и это последнее западает в глубины нашего сознания. Искусство позволяет нам прочувствовать и пережить то, чего никогда не было с нами в действительной жизни, и тем самым воспитывает нас, заставляя сделать выбор и встать на те или иные позиции. Таким образом, искусство становится средством не только эмоционального, но и идеологического воспитания. Искусство должно нести людям радость наслаждения красотой, в противном случае оно перестает быть искусством. Так мы приходим к гедонистической (от греч. hedone — наслаждение) функции искусства. Без этой функции человек отвернется и от познавательных, и от идейно-воспитательных достоинств произведения искусства. Не случайно поэтому искусство часто смешивают с красотой. Но не только красота искусства доставляет нам наслаждение. Мы испытываем радость от соприкосновения с произведением искусства, от способности проникнуть в мысли и чувства гения, создавшего это произведение, от возможности приобщиться к великому таинству творчества. Прекрасно сказал В. И. Ленин, любивший "Аппассионату" Бетховена: "Изумительная, нечеловеческая музыка. Я всегда с гордостью, может быть наивной, думаю: вот какие чудеса могут делать люди!"А. Солженицын. Нобелевская лекция
 Шарден. Атрибуты искусств. 1760-е
Шарден. Атрибуты искусств. 1760-е
Для среднего человека кажется ясным и понятным то, что искусство есть проявление красоты; и красотою объясняются для него все вопросы искусства.Л. Толстой
Что красота есть необходимое условие искусства, что без красоты нет и не может быть искусства — это аксиома.Таковы основные функции искусства. Понятно, что каждый из исследователей искусства волей или неволей выделял ту функцию искусства, которая была ему более близка. Так, гуманист Лев Толстой считал важнейшей коммуникативную функцию: "Искусство есть деятельность человеческая, состоящая в том, что один человек сознательно известными внешними знаками передает другим испытываемые им чувства, а другие люди заражаются этими чувствами и переживают их". Философ Гегель — познавательную, пытаясь в чувственной форме познать "абсолютную истину". Физик Фейнберг считает, что "искусство... есть постижение интуитивных истин". Нас же будет интересовать гедонистическая функция искусства, ибо наша задача — заглянуть в тайны прекрасного и попытаться хоть краем глаза увидеть в них математические начала. Что же такое прекрасное? Обратимся вновь ко Льву Толстому, гениальному мыслителю и мастеру слова. "Для среднего человека кажется ясным и понятным то, что искусство есть проявление красоты; и красотою объясняются для него все вопросы искусства. Но что же такое красота, которая составляет, по его мнению, содержание искусства? Как она определяется и что это такое? Как это бывает во всяком деле, чем не яснее, запутаннее понятие, которое передается словом, тем с большим апломбом и самоуверенностью употребляют люди это слово, делая вид, будто то, что подразумевается под этим словом, так просто и ясно, что не стоит и говорить о том, что собственно оно значит... Предполагается, что то, что разумеется под словом "красота", всем известно и понятно. А между тем это не только неизвестно, но... вопрос о том, что такое красота, до сих пор остается совершенно открытым и с каждым новым сочинением по эстетике решается новым способом." Сказано по-толстовски сильно и ясно! Нам остается лишь добавить, что и задолго до нашей эры, и через много лет после смерти Льва Толстого философы, искусствоведы, сами художники и представители точных наук пытались и пытаются найти пути к решению вопроса о сущности прекрасного[2]. Еще на заре цивилизации основатель античной математики Пифагор (VI в. до н. э.) учил: "Все прекрасно благодаря числу". Древнегреческий философ Гераклит (кон. VI в.- нач. V в. до н. э.), названный В. И. Лениным одним из основоположников диалектики, указывал на относительность понятия прекрасного: "Самая прекрасная обезьяна безобразна по сравнению с родом людей". Величайший из философов Платон (428-348 гг. до н. э.) писал: "Умеренность и соразмерность всюду становится красотой". Платону вторил его любимый ученик Аристотель (384-322 гг. до н. э.): "Красота состоит в соразмерности и правильном расположении". Средневековые мыслители Аврелий Августин (354-430) и Фома Аквинский (1226-1274) источник прекрасного усматривали в боге. Выдающийся итальянский ученый-гуманист и архитектор Леон Баттиста Альберти (1404-1472) как. истинный представитель эпохи Возрождения свои идеалы и убеждения черпал из греческой классики: "Что такое красота и украшение и чем они между собой разнятся, мы, пожалуй, отчетливее поймем чувством, чем я могу изъяснить это словами. Тем не менее совсем кратко мы скажем так: красота есть строгая соразмерная гармония всех частей, объединяемых тем, чему они принадлежат,- такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже" (легко Заметить, что определение Альберти перекликается с высказываниями Платона и Аристотеля). В эпоху Просвещения прекрасное рассматривалось как связующее звено между разумом и чувствами, между долгом (разум) и увлечениями (чувства). Широко известна формула Н. Г. Чернышевского (1828-1889): "Прекрасное есть жизнь". Но пожалуй, наибольшую мудрость в определении формулы прекрасного проявил человек, всю свою жизнь посвятивший служению красоте,- выдающийся немецкий художник эпохи Возрождения Альбрехт Дюрер (1471 -1528): "Что такое красота — этого я не знаю. Но для себя здесь понимаю красоту таким образом: что разные человеческие времена большинством почитать прекрасным, то мы и должны усердно стремиться создавать". Да, Дюрер оказался удивительно прозорливым: и спустя полтысячелетия абсолютно строгого, "математического" определения прекрасного нет. Дискуссии о сущности красоты сегодня ведутся не только представителями противоположных мировоззренческих позиций, материалистами и идеалистами, но и внутри однородных научных школ. В нашей стране проблема прекрасного на протяжении последних трех десятилетий является предметом дискуссии между сторонниками "природнической" и "общественной" концепций.В. Белинский
 Агесандр. Афродита Милосская. III-II вв. до н. э. С тех пор, как в 1820 г. статуя Венеры была извлечена из земли острова Милос, она олицетворяет вечный идеал красоты
Агесандр. Афродита Милосская. III-II вв. до н. э. С тех пор, как в 1820 г. статуя Венеры была извлечена из земли острова Милос, она олицетворяет вечный идеал красоты
Кажется мне, я узнал, что значит пословица "прекрасное — трудно".Платон
Что такое красота — этого я не знаю. Но для себя здесь понимаю красоту таким образом: что в разные человеческие времена большинством почиталось прекрасным, то мы и должны усердно стремиться создавать."Природники" считают красоту объективной закономерностью, которая рождается в недрах самой природы. "Общественники" видят прекрасное как продукт общественно-исторической практики, творческой деятельности человека. Однако "природники" встают в тупик, пытаясь ответить на вопрос, поставленный еще Чернышевским: почему "полувоздушная" светская красавица не нравится крестьянину, который считает ее просто "заморышем", а пышущая здоровьем "русская Венера" не угождает вкусам света? Ведь обе они являются "продуктом природы"! "Общественники" же не могут объяснить наш восторг перед сверкающим горным пейзажем, который никак не назовешь "продуктом творческой деятельности человека". Односторонность обоих подходов к проблеме прекрасного представляется очевидной. Обе стороны недооценивают диалектику объективного и субъективного в прекрасном. Обе стороны в полемическом задоре забывают, что у красоты не один, а по крайней мере два истока: это творческая, преобразующая мир деятельность человека — создателя красоты, и это природа, ибо, как писал Энгельс, "мы отнюдь не властвуем над природой так, как завоеватель властвует над чужим народом", а, "наоборот, нашей плотью, кровью и мозгом принадлежим ей и находимся внутри ее" (т. 20, с. 496). В спорах, как известно, рождается истина. И подтверждением этому служит тот факт, что зачинатель спора "природников" и "общественников" (в прошлом ярый "общественник") А. И. Буров в конце концов пришел к "золотой середине" — признанию как природной, так и общественной основ прекрасного. Итак, вопросы о том, что такое искусство и что такое красота, отнюдь не элементарны. Они порождают лавину вопросов-следствий, распутать которые может только особая наука о прекрасном. Такая наука есть, и имя ей — эстетика. 1735 год, год, когда немецким философом Александром Баумгартеном (1714-1762) был изобретен термин "эстетика" (от греч. aisthА. Дюрер
 tikos — относящийся к области чувств), считается официальным годом рождения эстетики как самостоятельной науки. Но фактически эстетика родилась в глубокой древности, в суждениях философов, ученых и мудрецов, в их отдельных высказываниях, а затем и в специальных трактатах. И хотя различные "эстетические фрагменты" дошли до нас из Древнего Египта, и из Вавилона, и из Древней Индии, история эстетики как науки, безусловно, начинается в Древней Греции. Нам еще не раз предстоит обращаться к духовной сокровищнице древних греков, "к достижениям того маленького народа, универсальная одаренность и деятельность которого обеспечили ему в истории человечества место, на какое не может претендовать ни один другой народ" (Ф. Энгельс, т. 20, с. 369).
В древнегреческой философии — науке наук — берут начало все будущие философские течения, многие теории и науки. Древними было замечено, что люди познают мир с помощью органов чувств и осмысливают познанное разумом. Чувство и мышление не только два уровня, но и два звена в цепи познания. И как нужна наука о законах мышления — логика, столь же необходима и наука о чувственном восприятии — эстетика. Обе эти науки зарождаются одновременно в Древней Греции.
Греки обратили внимание и на то, что самые сильные чувственные восприятия связаны у человека с прекрасным, с искусством, которое несет людям красоту. Это особого рода чувства, лишенные корыстных побуждений, очищенные от жизненных забот и неурядиц, переносящие человека в иной удивительный мир — мир прекрасного. В попытках осмыслить эти чувства, понять их первопричину, проникнуть в тайну красоты и постигнуть ее законы и родилась наука эстетика. К сожалению, у нас нет возможности сделать хотя бы краткий обзор развития эстетического учения. Но к какому бы периоду истории эстетики мы ни обратились, во все времена и на всех направлениях ее главным содержанием оставалось прекрасное и искусство. Так понимали предмет эстетики и идеалист Гегель, и материалист Чернышевский, хотя само прекрасное они трактовали по-разному, в соответствии со своими философскими воззрениями.
tikos — относящийся к области чувств), считается официальным годом рождения эстетики как самостоятельной науки. Но фактически эстетика родилась в глубокой древности, в суждениях философов, ученых и мудрецов, в их отдельных высказываниях, а затем и в специальных трактатах. И хотя различные "эстетические фрагменты" дошли до нас из Древнего Египта, и из Вавилона, и из Древней Индии, история эстетики как науки, безусловно, начинается в Древней Греции. Нам еще не раз предстоит обращаться к духовной сокровищнице древних греков, "к достижениям того маленького народа, универсальная одаренность и деятельность которого обеспечили ему в истории человечества место, на какое не может претендовать ни один другой народ" (Ф. Энгельс, т. 20, с. 369).
В древнегреческой философии — науке наук — берут начало все будущие философские течения, многие теории и науки. Древними было замечено, что люди познают мир с помощью органов чувств и осмысливают познанное разумом. Чувство и мышление не только два уровня, но и два звена в цепи познания. И как нужна наука о законах мышления — логика, столь же необходима и наука о чувственном восприятии — эстетика. Обе эти науки зарождаются одновременно в Древней Греции.
Греки обратили внимание и на то, что самые сильные чувственные восприятия связаны у человека с прекрасным, с искусством, которое несет людям красоту. Это особого рода чувства, лишенные корыстных побуждений, очищенные от жизненных забот и неурядиц, переносящие человека в иной удивительный мир — мир прекрасного. В попытках осмыслить эти чувства, понять их первопричину, проникнуть в тайну красоты и постигнуть ее законы и родилась наука эстетика. К сожалению, у нас нет возможности сделать хотя бы краткий обзор развития эстетического учения. Но к какому бы периоду истории эстетики мы ни обратились, во все времена и на всех направлениях ее главным содержанием оставалось прекрасное и искусство. Так понимали предмет эстетики и идеалист Гегель, и материалист Чернышевский, хотя само прекрасное они трактовали по-разному, в соответствии со своими философскими воззрениями.
 Эстетика: наука о прекрасном
Итак, в главном эстетика — это наука о прекрасном. Однако многие современные авторы такое традиционное определение эстетики считают слишком узким и неточным. и вот учебники и справочники начинают определять эстетику как науку об... эстетическом воении действительности. Но ведь это же замкнутый РУг, логическое кольцо!
Что же думают об этом сами эстетики? "Наша наука крайне далека еще от того, чтобы построить своего рода "таблицу Менделеева" для эстетических "элементов",- читаем мы в "Лекциях по марксистско-ленинской эстетике" М. С. Кагана. "Давно известно, что гораздо легче отбросить старые понятия, чем создать новые,- пишет Е. С. Громов в книге "Начала эстетических знаний".- Традиционное определение, при всей своей краткости, а отчасти именно благодаря ей, ясно и понятно указывает на главную задачу всех эстетических исследований: постижение прекрасного в разных его видах и проявлениях". А вот строки из статьи Б. И. Благодыря "К проблеме "законов красоты": "...наука о прекрасном до сих пор не имеет в своем понятийном арсенале фундаментального определения прекрасного вообще, в котором нашло бы теоретическое выражение существенно общее, дающее нам право говорить о прекрасном во всех вферах действительности: природе, обществе, истории, науке, искусстве, человеке, начиная от бытия и кончая утонченным миром его чувств".
Эстетика: наука о прекрасном
Итак, в главном эстетика — это наука о прекрасном. Однако многие современные авторы такое традиционное определение эстетики считают слишком узким и неточным. и вот учебники и справочники начинают определять эстетику как науку об... эстетическом воении действительности. Но ведь это же замкнутый РУг, логическое кольцо!
Что же думают об этом сами эстетики? "Наша наука крайне далека еще от того, чтобы построить своего рода "таблицу Менделеева" для эстетических "элементов",- читаем мы в "Лекциях по марксистско-ленинской эстетике" М. С. Кагана. "Давно известно, что гораздо легче отбросить старые понятия, чем создать новые,- пишет Е. С. Громов в книге "Начала эстетических знаний".- Традиционное определение, при всей своей краткости, а отчасти именно благодаря ей, ясно и понятно указывает на главную задачу всех эстетических исследований: постижение прекрасного в разных его видах и проявлениях". А вот строки из статьи Б. И. Благодыря "К проблеме "законов красоты": "...наука о прекрасном до сих пор не имеет в своем понятийном арсенале фундаментального определения прекрасного вообще, в котором нашло бы теоретическое выражение существенно общее, дающее нам право говорить о прекрасном во всех вферах действительности: природе, обществе, истории, науке, искусстве, человеке, начиная от бытия и кончая утонченным миром его чувств".
 М. Эшер. Ящерицы. В основе орнамента лежит поворотная симметрия второго порядка и переносная симметрия, определяемая гексагональной решеткой. Творчество современного голландского художника и графика Маурица Эшера отличается необычайной фантазией, обостренным видением глубоких законов симметрии окружающего нас мира, органической связью художественного и научного мышления
Как видим, самим эстетикам не нравится определение своей науки. Что уж говорить, например, о физиках! Так, А. И. Китайгородский, анализируя в своей книге "Невероятно — не факт" определения из "Краткого эстетического словаря", называет их "пустословием". Врят ли стоит впадать в такую крайность. Следует помнить, что предмет эстетики чрезвычайно сложен и тонок, что эстетики только начинает касаться процесс математизации, который привел физику к своему триумфальному шествию в науке. В этой связи определение прекрасного, данное Альбрехтом Дюрером 500 лет назад, представляется наиболее точным и откровенным.
Так что же такое эстетика и что такое прекрасное? Обратимся к книге доктора философских наук А. В. Гулыги "Принципы эстетики", вышедшей в серии "Над чем работают, о чем спорят философы". Само название серии говорит о том, что книга не претендует на истину в последней инстанции (об этом же говорит и сам автор). Тем не менее, на наш взгляд, это наиболее глубокая и наиболее откровенная работа по проблемам эстетики.
Прежде всего заметим, что А. Гулыга возвращается к классическому определению эстетики как науки о прекрасном: "...все, чем занимается эстетика, представляет собой модификацию прекрасного... В широком смысле слова красота — синоним эстетического".
В вопросе об истоках красоты автор примиряет "природников" и "общественников", мудро выбирая "золотую середину": "Отец красоты — труд, мать — природа, дитя рождается от соединения этих двух начал жить может только в их присутствии, взаимодействии, взаимном согласии и понимании". Таким образом подтверждается тезис о двуединой объективно-субъективной природе красоты. Эту мысль высказывал еще Шиллер: "Красота есть одновременно предмет для нас состояние нашего субъекта". Заметим, что "состоянием субъекта" при оценке красоты и объясняется изменчивость взглядов на прекрасное как отдельных людей, так и представителей различных эпох и народов. Но истинное произведение искусства прекрасно во все времена, и нет оснований его отвергать только потому, что оно не соответствует нашим сиюминутным определениям красоты. К сожалению, история знает немало примеров, когда непонимание принятых в другую эпоху "законов красоты" приводило к уничтожению бесценных памятников прошлого, что попросту граничит с варварством.
Теперь остается самое трудное — ответить на вопрос, стоящий эпиграфом к этому параграфу: "Что есть красота?" В определении прекрасного А. Гулыга опирается на методологический принцип выдающегося немецкого философа Георга Гегеля (1770-1831) — принцип восхождения от абстрактного к конкретному. Этот принцип был успешно применен Гегелем в его логике, где в качестве изначальной категории было взято предельно абстрактное понятие "бытие", которое затем наполнялось содержанием через другие более конкретные категории. Однако в эстетике этот принцип оставался в забвении.
В качестве изначального понятия системы эстетических категорий Гулыга предлагает рассматривать прекрасное в его узком смысле, понимаемом как ценностно-значимая форма. Постепенно эта форма наполняется содержанием через другие более конкретные понятия, такие, как "возвышенное", "трагическое", "комическое", "эстетический идеал". Идеал — наиболее содержательная эстетическая категория, это всеполнота прекрасного. Таким образом, восхождение от ценностно-значимой, т. е. радующей наш глаз и слух формы, к тому Держанию, которое несет эта форма, и, наконец, к тому идеалу, который покоряет наше сердце и разум, и есть путь постижения загадочного феномена, именуемого прекрасным.
М. Эшер. Ящерицы. В основе орнамента лежит поворотная симметрия второго порядка и переносная симметрия, определяемая гексагональной решеткой. Творчество современного голландского художника и графика Маурица Эшера отличается необычайной фантазией, обостренным видением глубоких законов симметрии окружающего нас мира, органической связью художественного и научного мышления
Как видим, самим эстетикам не нравится определение своей науки. Что уж говорить, например, о физиках! Так, А. И. Китайгородский, анализируя в своей книге "Невероятно — не факт" определения из "Краткого эстетического словаря", называет их "пустословием". Врят ли стоит впадать в такую крайность. Следует помнить, что предмет эстетики чрезвычайно сложен и тонок, что эстетики только начинает касаться процесс математизации, который привел физику к своему триумфальному шествию в науке. В этой связи определение прекрасного, данное Альбрехтом Дюрером 500 лет назад, представляется наиболее точным и откровенным.
Так что же такое эстетика и что такое прекрасное? Обратимся к книге доктора философских наук А. В. Гулыги "Принципы эстетики", вышедшей в серии "Над чем работают, о чем спорят философы". Само название серии говорит о том, что книга не претендует на истину в последней инстанции (об этом же говорит и сам автор). Тем не менее, на наш взгляд, это наиболее глубокая и наиболее откровенная работа по проблемам эстетики.
Прежде всего заметим, что А. Гулыга возвращается к классическому определению эстетики как науки о прекрасном: "...все, чем занимается эстетика, представляет собой модификацию прекрасного... В широком смысле слова красота — синоним эстетического".
В вопросе об истоках красоты автор примиряет "природников" и "общественников", мудро выбирая "золотую середину": "Отец красоты — труд, мать — природа, дитя рождается от соединения этих двух начал жить может только в их присутствии, взаимодействии, взаимном согласии и понимании". Таким образом подтверждается тезис о двуединой объективно-субъективной природе красоты. Эту мысль высказывал еще Шиллер: "Красота есть одновременно предмет для нас состояние нашего субъекта". Заметим, что "состоянием субъекта" при оценке красоты и объясняется изменчивость взглядов на прекрасное как отдельных людей, так и представителей различных эпох и народов. Но истинное произведение искусства прекрасно во все времена, и нет оснований его отвергать только потому, что оно не соответствует нашим сиюминутным определениям красоты. К сожалению, история знает немало примеров, когда непонимание принятых в другую эпоху "законов красоты" приводило к уничтожению бесценных памятников прошлого, что попросту граничит с варварством.
Теперь остается самое трудное — ответить на вопрос, стоящий эпиграфом к этому параграфу: "Что есть красота?" В определении прекрасного А. Гулыга опирается на методологический принцип выдающегося немецкого философа Георга Гегеля (1770-1831) — принцип восхождения от абстрактного к конкретному. Этот принцип был успешно применен Гегелем в его логике, где в качестве изначальной категории было взято предельно абстрактное понятие "бытие", которое затем наполнялось содержанием через другие более конкретные категории. Однако в эстетике этот принцип оставался в забвении.
В качестве изначального понятия системы эстетических категорий Гулыга предлагает рассматривать прекрасное в его узком смысле, понимаемом как ценностно-значимая форма. Постепенно эта форма наполняется содержанием через другие более конкретные понятия, такие, как "возвышенное", "трагическое", "комическое", "эстетический идеал". Идеал — наиболее содержательная эстетическая категория, это всеполнота прекрасного. Таким образом, восхождение от ценностно-значимой, т. е. радующей наш глаз и слух формы, к тому Держанию, которое несет эта форма, и, наконец, к тому идеалу, который покоряет наше сердце и разум, и есть путь постижения загадочного феномена, именуемого прекрасным.
 Эстетика: наука о прекрасном
Знаменитое триединство истины, добра и красоты, воплащающее, начиная с античности, представление человека о высших духовных ценностях,- это три ипостаси идеала. Красота является связующим звеном между истиной и добром. Во все времена красота являлась путеводной звездой в поисках истины, могучим стимулом к научному творчеству и озарению в науке (об этом мы подробно поговорим в следующей главе). С другой стороны, во все времена красота, словно магнитное поле стрелку компаса, обращала человека к доброте. Именно это свойство красоты отразил Достоевский в своей знаменитой формуле: "Красота спасет мир".
Эстетика: наука о прекрасном
Знаменитое триединство истины, добра и красоты, воплащающее, начиная с античности, представление человека о высших духовных ценностях,- это три ипостаси идеала. Красота является связующим звеном между истиной и добром. Во все времена красота являлась путеводной звездой в поисках истины, могучим стимулом к научному творчеству и озарению в науке (об этом мы подробно поговорим в следующей главе). С другой стороны, во все времена красота, словно магнитное поле стрелку компаса, обращала человека к доброте. Именно это свойство красоты отразил Достоевский в своей знаменитой формуле: "Красота спасет мир".
 Рафаэль. Мадонна со щегленком. 1507. Деталь
Свое воплощение эстетический идеал находит в искусстве. Ни природа, ни общество часто не дают человеку его эстетического идеала. Вспомним слова Рафаэля: "Я скажу вам, что для того, чтобы написать красавицу, мне надо видеть многих красавиц... Но ввиду недостатка как в хороших судьях, так и в красивых женщинах я пользуюсь некоторой идеей, которая приходит мне на ум". Ясно, что "идея", о которой говорит Рафаэль, и есть эстетический идеал художника. Так красота через эстетический идеал приводит нас к искусству. Именно это и имел в виду Лев Толстой, когда говорил, что "для среднего человека кажется ясным и понятным, что искусство есть проявление красоты".
Да, вне красоты нет искусства. Но искусство — особая и своеобразная область прекрасного. В жизни прекрасное нередко уживается с безобразным, и истинное искусство — "учебник жизни" — не может ограничить себя одною лишь красотой. Художник не имеет права ни брезгливо отворачиваться, ни трусливо сдаваться перед безобразным. Победа над безобразным — одно из средств утверждения красоты. Мастерство и эстетическое осуждение безобразного ведут художника к торжеству его эстетического идеала — красоте. Вот почему образы искусства прекрасны всегда, даже если они рисуют истерзанные жизненными невзгодами, изможденные лица стариков на полотнах Рембрандта. Хорошо сказал об этом французский скульптор Огюст Роден (1840-1917): "Но стоит великому артисту или великому писателю прикоснуться к какому-нибудь безобразию, чтобы оно мгновенно преобразилось: ударом волшебного жезла безобразие превращается в красоту: это алхимия, это колдовство! "
Рафаэль. Мадонна со щегленком. 1507. Деталь
Свое воплощение эстетический идеал находит в искусстве. Ни природа, ни общество часто не дают человеку его эстетического идеала. Вспомним слова Рафаэля: "Я скажу вам, что для того, чтобы написать красавицу, мне надо видеть многих красавиц... Но ввиду недостатка как в хороших судьях, так и в красивых женщинах я пользуюсь некоторой идеей, которая приходит мне на ум". Ясно, что "идея", о которой говорит Рафаэль, и есть эстетический идеал художника. Так красота через эстетический идеал приводит нас к искусству. Именно это и имел в виду Лев Толстой, когда говорил, что "для среднего человека кажется ясным и понятным, что искусство есть проявление красоты".
Да, вне красоты нет искусства. Но искусство — особая и своеобразная область прекрасного. В жизни прекрасное нередко уживается с безобразным, и истинное искусство — "учебник жизни" — не может ограничить себя одною лишь красотой. Художник не имеет права ни брезгливо отворачиваться, ни трусливо сдаваться перед безобразным. Победа над безобразным — одно из средств утверждения красоты. Мастерство и эстетическое осуждение безобразного ведут художника к торжеству его эстетического идеала — красоте. Вот почему образы искусства прекрасны всегда, даже если они рисуют истерзанные жизненными невзгодами, изможденные лица стариков на полотнах Рембрандта. Хорошо сказал об этом французский скульптор Огюст Роден (1840-1917): "Но стоит великому артисту или великому писателю прикоснуться к какому-нибудь безобразию, чтобы оно мгновенно преобразилось: ударом волшебного жезла безобразие превращается в красоту: это алхимия, это колдовство! "
 Рембрандт. Портрет старика в красном. 1652-1654. В изможденном лице и натруженных руках старца — красота и мудрость прожитой им жизни
Рембрандт. Портрет старика в красном. 1652-1654. В изможденном лице и натруженных руках старца — красота и мудрость прожитой им жизни
Мы должны определить красоту как преображение материи через воплощение в ней другого, сверхматериального начала.Вл. Соловьев
Кеплер говорит: "Geometria est archetypus pulchritudinis mundi",- то есть, если перевести его слова более обобщенными терминами: "Математика есть прообраз красоты мира".Итак, красота начинается с формы, но не сводится к ней. Красота — это форма, взятая в единстве с содержанием, от которого она не может быть оторвана. Попытки рассмотреть красоту только с формальной точки зрения никогда не оканчивались успехом. Еще немецкий философ Иммануил Кант (1724-1804), указав четыре формальных признака "чистой красоты", был вынужден обратиться и к содержательной стороне прекрасного, когда "нравится не только форма продукта природы, но также само существо его...". Красивая форма стремится сделать прекрасным и содержание, которое, по выражению Белинского, становится "опоэтизированным". Мысль о диалектическом единстве формы и содержания в прекрасном, кажущаяся сегодня аксиомой, была впервые разработана Гегелем. Но эта мысль "витала в воздухе" и до Гегеля. Ее мы находим, например, у Шекспира:В. Гейзенберг
 Эстетика: наука о прекрасном
А вот мнение по тому же вопросу философа А. Гулыги: "Феномен красоты содержит в себе некоторую тайну, постигаемую лишь интуитивно и недоступную дискурсивному мышлению". Просто замечательно, сколь единодушными делают чары искусства и тайна прекрасного и "физиков", и "лириков". (Такое бывает далеко не всегда, в чем легко убедиться, прочитав главу 3.)
И в заключение отметим одну важную мысль, впервые высказанную К. Марксом: первые шаги человечества к красоте сделаны благодаря труду. Именно в результате трудовой деятельности человек начинает находить и в природе, и в общественной жизни разнообразные эстетические ценности.
Приведем знаменитые слова К. Маркса, указывающие на отличительные особенности человеческого труда: "Животное, правда, тоже производит. Оно строит себе гнездо или жилище, как это делают пчела, бобр, муравей и т. д. Но животное производит лишь то, в чем непосредственно нуждается Оно само или его детеныш; оно производит односторонне, тогда как человек производит универсально... Животное строит только сообразно мерке и потребности того вида, к которому оно принадлежит, тогда как человек умеет производить по меркам любого вида и всюду он умеет прилагать к предмету присущую мерку; в силу этого человек строит также и по законам красоты".
"И по законам красоты"... Эти слова Маркса являются девизом творческой деятельности человека на любом поприще. Они означают, что сфера эстетических закономерностей, сфера прекрасного, выходит далеко за пределы искусства и распространяется на все без исключения области человеческой деятельности. Но если это так, то существует еще одна не менее удивительная область проявления прекрасного. Это — наука. Есть ликрасота в науке? Можно ли говорить об эстетике науки? На эти вопросы мы попытаемся ответить в следующей главе.
Эстетика: наука о прекрасном
А вот мнение по тому же вопросу философа А. Гулыги: "Феномен красоты содержит в себе некоторую тайну, постигаемую лишь интуитивно и недоступную дискурсивному мышлению". Просто замечательно, сколь единодушными делают чары искусства и тайна прекрасного и "физиков", и "лириков". (Такое бывает далеко не всегда, в чем легко убедиться, прочитав главу 3.)
И в заключение отметим одну важную мысль, впервые высказанную К. Марксом: первые шаги человечества к красоте сделаны благодаря труду. Именно в результате трудовой деятельности человек начинает находить и в природе, и в общественной жизни разнообразные эстетические ценности.
Приведем знаменитые слова К. Маркса, указывающие на отличительные особенности человеческого труда: "Животное, правда, тоже производит. Оно строит себе гнездо или жилище, как это делают пчела, бобр, муравей и т. д. Но животное производит лишь то, в чем непосредственно нуждается Оно само или его детеныш; оно производит односторонне, тогда как человек производит универсально... Животное строит только сообразно мерке и потребности того вида, к которому оно принадлежит, тогда как человек умеет производить по меркам любого вида и всюду он умеет прилагать к предмету присущую мерку; в силу этого человек строит также и по законам красоты".
"И по законам красоты"... Эти слова Маркса являются девизом творческой деятельности человека на любом поприще. Они означают, что сфера эстетических закономерностей, сфера прекрасного, выходит далеко за пределы искусства и распространяется на все без исключения области человеческой деятельности. Но если это так, то существует еще одна не менее удивительная область проявления прекрасного. Это — наука. Есть ликрасота в науке? Можно ли говорить об эстетике науки? На эти вопросы мы попытаемся ответить в следующей главе.
 Эстетика: наука о прекрасном
Эстетика: наука о прекрасном
2. Математика: прекрасное в науке
Математика владеет не только истиной, но и высшей красотой — красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.Французский энциклопедический словарь Ларусс определяет прекрасное как то, что "радует глаз или разум". Просто и ясно. Не будем обсуждать достоинства еще одного определения красоты, а обратим внимание на вторую часть данного определения, на то, что красота радует разум. Да, кроме красоты, постигаемой чувствами, есть и другая красота, постигаемая разумом. Это особый вид красоты — красота науки. Как ни удивительно, но и эту необыкновенную красоту, красоту разума, успели прочувствовать древние греки. В диалоге Платона "Пир" мы читаем о том, как "беременный духовно" (говоря современными штампами — "ученый-теоретик, разрабатывающий сложнейшую проблему") "ищет везде прекрасное, в котором он мог бы разрешиться от бремени". Платон взволнованно говорит о том, как происходит восхождение к высшей красоте — красоте разума, красоте познания. "Начав с отдельных проявлений прекрасного, надо все время, словно бы по ступенькам, подниматься ради самого прекрасного вверх — от одного прекрасного тела к двум, от двух — ко всем, а затем от прекрасных тел к прекрасным нравам, а от прекрасных нравов к прекрасным учениям, пока не поднимешься от этих учений к тому, которое и есть учение о самом прекрасном, и не познаешь наконец, что же это — прекрасное. И в созерцании прекрасного самого по себе.. . только и может жить человек..." Слова Платона — вдохновенный гимн торжеству Разума, стремлению к прекрасному, которое неотделимо от научного творчества. Раздумья о красоте научного поиска, о величии человеческого духа никогда не переставали волновать мыслящих людей. И через два тысячелетия в унисон Платону звучат слова великого представителя нашего столетия М. Горького: "Наука — высший разум человечества, это солнце, которое человек создал из плоти и крови своей, создал и зажег перед Оою для того, чтобы осветить тьму своей тяжелой Пзни, чтобы найти из нее выход к свободе, справедливей, красоте".Б. Рассел
Кто, наставляемый на пути любви, будет в правильном порядке созерцать прекрасное, тот, достигнув конца этого пути, вдруг увидит нечто удивительно прекрасное по природе... Он увидит прежде всего, что прекрасное существует вечно, что оно не возникает, не уничтожается, не увеличивается, не убывает...Платон
 Математика: прекрасное в науке
В чем же заключается красота науки? И если таковая существует, то есть ли эстетика науки, изучающая законы этой необычной красоты? Как самостоятельной дисциплины науки эстетики нет. И сегодня категории эстетики применяются главным образом к искусству, реже — к технике (техническая эстетика) и как исключение — к науке. Мысли о красоте науки, как говорят, только витают в воздухе, иногда они оседают на бумаге в виде отдельных высказываний некоторых ученых, но философскому анализу эти мысли практически не подвергались. Почему? Видимо, и потому, что великие ученые, которым прежде всего и "дано" увидеть истинную красоту науки, лишь останавливаются на мгновение, завороженные ее красотой. Нечасто позволяют они себе такие остановки, еще реже — философские или поэтические размышления об их причинах. Ведь научный поиск — это беспрерывное восхождение к истине, постоянная работа разума на пределе сил и возможностей, работа, не терпящая расслабления и отдыха. Так альпинисты на восхождении к вершине лишь на мгновение останавливаются, пораженные красотой и величием гор. Останавливаются, молча вытирая со лба струи соленого пота, и вновь устремляются к вершине, не имея возможности на неспешное наслаждение красотой.
И тем не менее в богатой истории человеческой цивилизации находились люди, бравшие на себя смелость заняться анализом красоты науки. В их числе следует назвать Френсиса Хатчесона (1694-1747), шотландского философа эпохи Просвещения, автора "Исследования о происхождении наших идей красоты и добродетели в двух трактатах". Для нас особый интерес представляет раздел "О красоте теорем" первого трактата Хатчесона "О красоте, порядке, гармонии, целесообразности", начинающийся словами: "Красота теорем, или доказательств правильности всеобщих истин, заслуживает отдельного рассмотрения, поскольку по природе своей она значительно отличается от ранее рассмотренных видов красоты; и, однако, нет такой другой, в которой мы могли бы увидеть такое поразительное разнообразие при единообразии..."
Внимательно читая раздел "О красоте теорем", можно выделить три признака красоты науки, установленых Хатчесоном: 1) красота есть единство в многообразии; 2) красота заключена во всеобщности научных истин; 3) научная красота — это обретение неочевидной истины.
Принцип единства в многообразии Хатчесон считает универсальным эстетическим принципом, равно применимым и к неживой, и к живой природе, и к эстетической оценке науки. Действительно, любая математическая теорема содержит в себе бесчисленное множество истин, справедливых для каждого конкретного объекта, н0 в то же время эти конкретные истины собраны в единой общей для всех истине, устанавливаемой теоремой. Например, теорема Пифагора справедлива для бесчисленного множества конкретных прямоугольных треугольников, но все это многообразие треугольников обладает единственным общим свойством, описываемым теоремой. Вероятно, каждый школьник испытывал чувство радости, чувство научной красоты, когда впервые обнаружил, что, например, переместительное свойство сложения, замеченное им на множестве конкретных арифметических примеров, есть не что иное, как единый универсальный закон алгебры: a+b = b+a, справедливый для любых чисел.
Перейдем ко второму признаку красоты — всеобщности научных истин. "У теорем,- читаем мы у Хатчесона,- есть еще одна красота, которую нельзя обойти и которая состоит в том, что одна теорема может содержать огромное множество следствий, которые легко из нее выводятся. .. Когда исследуют природу, подобной красотой обладает познание определенных великих принципов или всеобщих сил, из которых вытекают бесчисленные следствия. Таково тяготение в схеме сэра Исаака Ньютона... И мы наслаждаемся этим удовольствием, даже если у нас нет никаких перспектив на получение какой-либо иной выгоды от такого способа Дедукции, кроме непосредственного удовольствия от созерцания красоты". Как точно сказано! И как чутко предвидит Хатчесон в 1725 г. могущество закона тяготения Ньютона, который пока еще называется "схемой Ньютона": ведь прощло только 38 лет со дня его опубликования (1687) — срок не столь уж большой для осознания столь грандиозного открытия!
Математика: прекрасное в науке
В чем же заключается красота науки? И если таковая существует, то есть ли эстетика науки, изучающая законы этой необычной красоты? Как самостоятельной дисциплины науки эстетики нет. И сегодня категории эстетики применяются главным образом к искусству, реже — к технике (техническая эстетика) и как исключение — к науке. Мысли о красоте науки, как говорят, только витают в воздухе, иногда они оседают на бумаге в виде отдельных высказываний некоторых ученых, но философскому анализу эти мысли практически не подвергались. Почему? Видимо, и потому, что великие ученые, которым прежде всего и "дано" увидеть истинную красоту науки, лишь останавливаются на мгновение, завороженные ее красотой. Нечасто позволяют они себе такие остановки, еще реже — философские или поэтические размышления об их причинах. Ведь научный поиск — это беспрерывное восхождение к истине, постоянная работа разума на пределе сил и возможностей, работа, не терпящая расслабления и отдыха. Так альпинисты на восхождении к вершине лишь на мгновение останавливаются, пораженные красотой и величием гор. Останавливаются, молча вытирая со лба струи соленого пота, и вновь устремляются к вершине, не имея возможности на неспешное наслаждение красотой.
И тем не менее в богатой истории человеческой цивилизации находились люди, бравшие на себя смелость заняться анализом красоты науки. В их числе следует назвать Френсиса Хатчесона (1694-1747), шотландского философа эпохи Просвещения, автора "Исследования о происхождении наших идей красоты и добродетели в двух трактатах". Для нас особый интерес представляет раздел "О красоте теорем" первого трактата Хатчесона "О красоте, порядке, гармонии, целесообразности", начинающийся словами: "Красота теорем, или доказательств правильности всеобщих истин, заслуживает отдельного рассмотрения, поскольку по природе своей она значительно отличается от ранее рассмотренных видов красоты; и, однако, нет такой другой, в которой мы могли бы увидеть такое поразительное разнообразие при единообразии..."
Внимательно читая раздел "О красоте теорем", можно выделить три признака красоты науки, установленых Хатчесоном: 1) красота есть единство в многообразии; 2) красота заключена во всеобщности научных истин; 3) научная красота — это обретение неочевидной истины.
Принцип единства в многообразии Хатчесон считает универсальным эстетическим принципом, равно применимым и к неживой, и к живой природе, и к эстетической оценке науки. Действительно, любая математическая теорема содержит в себе бесчисленное множество истин, справедливых для каждого конкретного объекта, н0 в то же время эти конкретные истины собраны в единой общей для всех истине, устанавливаемой теоремой. Например, теорема Пифагора справедлива для бесчисленного множества конкретных прямоугольных треугольников, но все это многообразие треугольников обладает единственным общим свойством, описываемым теоремой. Вероятно, каждый школьник испытывал чувство радости, чувство научной красоты, когда впервые обнаружил, что, например, переместительное свойство сложения, замеченное им на множестве конкретных арифметических примеров, есть не что иное, как единый универсальный закон алгебры: a+b = b+a, справедливый для любых чисел.
Перейдем ко второму признаку красоты — всеобщности научных истин. "У теорем,- читаем мы у Хатчесона,- есть еще одна красота, которую нельзя обойти и которая состоит в том, что одна теорема может содержать огромное множество следствий, которые легко из нее выводятся. .. Когда исследуют природу, подобной красотой обладает познание определенных великих принципов или всеобщих сил, из которых вытекают бесчисленные следствия. Таково тяготение в схеме сэра Исаака Ньютона... И мы наслаждаемся этим удовольствием, даже если у нас нет никаких перспектив на получение какой-либо иной выгоды от такого способа Дедукции, кроме непосредственного удовольствия от созерцания красоты". Как точно сказано! И как чутко предвидит Хатчесон в 1725 г. могущество закона тяготения Ньютона, который пока еще называется "схемой Ньютона": ведь прощло только 38 лет со дня его опубликования (1687) — срок не столь уж большой для осознания столь грандиозного открытия!
 Математика: прекрасное в науке
Каждый может проиллюстрировать эту мысль Хатчесона своими примерами: в математике — это любая из теорем, например теорема Пифагора, в физике — закон тяготения или законы электромагнетизма, в химии — периодический закон Менделеева, в биологии — законы генетики, всеобщность которых мы постигаем на самих себе. Возвращаясь к теореме Пифагора, заметим, что существование около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т. д.) свидетельствует об огромном числе конкретных реализаций этой теоремы и ее следствий.
Наконец, третий признак — обретение неочевидной истины. Любой из нас согласится с тем, что постижение очевидной истины (ее символом стало утверждение, что дважды два — четыре) не доставляет ему эстетического наслаждения. В аксиомах мало красоты, утверждает Хатчесон, ибо их справедливость очевидна. Немного удовольствия доставляют нам и легкие теоремы, истинность которых видна "невооруженным глазом". Только открытие истин, спрятанных от нас наукой или природой, открытие, требующее поиска и серьезных усилий, доставляет нам в конце пути истинное наслаждение — познание неведомой истины. В этом и состоит радость и красота познания. Свою мысль Хатчесон подтверждает интересным примером. Ясно, что объем цилиндра больше объема вписанного в него шара, объем которого больше объема конуса, вписанного в цилиндр. Это очевидная истина, не приносящая нам никакого удовлетворения. Но когда мы установим, что объемы этих тел относятся как 3:2:1, т. е. когда мы обретем неочевидную истину, мы почувствуем, как прекрасна эта теорема и какое мы получаем удовольствие от ее первого открытия. Напомним, что первая часть этой теоремы, связывающая объемы цилиндра и вписанной в него сферы, была доказана Архимедом и почиталась им как лучшее из всех своих замечательных открытий.
Математика: прекрасное в науке
Каждый может проиллюстрировать эту мысль Хатчесона своими примерами: в математике — это любая из теорем, например теорема Пифагора, в физике — закон тяготения или законы электромагнетизма, в химии — периодический закон Менделеева, в биологии — законы генетики, всеобщность которых мы постигаем на самих себе. Возвращаясь к теореме Пифагора, заметим, что существование около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т. д.) свидетельствует об огромном числе конкретных реализаций этой теоремы и ее следствий.
Наконец, третий признак — обретение неочевидной истины. Любой из нас согласится с тем, что постижение очевидной истины (ее символом стало утверждение, что дважды два — четыре) не доставляет ему эстетического наслаждения. В аксиомах мало красоты, утверждает Хатчесон, ибо их справедливость очевидна. Немного удовольствия доставляют нам и легкие теоремы, истинность которых видна "невооруженным глазом". Только открытие истин, спрятанных от нас наукой или природой, открытие, требующее поиска и серьезных усилий, доставляет нам в конце пути истинное наслаждение — познание неведомой истины. В этом и состоит радость и красота познания. Свою мысль Хатчесон подтверждает интересным примером. Ясно, что объем цилиндра больше объема вписанного в него шара, объем которого больше объема конуса, вписанного в цилиндр. Это очевидная истина, не приносящая нам никакого удовлетворения. Но когда мы установим, что объемы этих тел относятся как 3:2:1, т. е. когда мы обретем неочевидную истину, мы почувствуем, как прекрасна эта теорема и какое мы получаем удовольствие от ее первого открытия. Напомним, что первая часть этой теоремы, связывающая объемы цилиндра и вписанной в него сферы, была доказана Архимедом и почиталась им как лучшее из всех своих замечательных открытий.


 В заключение Хатчесон делает важный вывод: красота науки неравнозначна научному знанию. Красота науки заключается не в собрании застывших законов, а в обретении новых знаний, в открытии новых истин, в обнаружении стройности и порядка там, где еще недавно царил хаос. Только беспрерывное движение вперед, а точнее вверх, к новым вершинам истины,- такова формула прекрасного в науке.
Отметим еще одно существенное обстоятельство. Ясно, что все три выведенных Хатчесоном эстетических принципа справедливы для любой науки, но получены они Хатчесоном для математики. И дело здесь не в том, что остальные науки во времена Хатчесона были еще недостаточно развиты по сравнению с математикой. Дело в том, что математика во все времена была и остается "первой красавицей" среди наук и, следовательно, эстетические принципы науки наиболее ярко проявляются в математике. Чуть позже мы попытаемся обосновать эту мысль.
Хатчесон оказал заметное влияние на формирование эстетических взглядов последующих философов: Давида Юма (1711 — 1776), Адама Смита (1723-1790). Мысль Хатчесона о красоте единства в многообразии мы находим и в трудах родоначальника немецкой классической философии, "кенигсбергского затворника"[4] Иммануила Канта. В книге "Естественная история и теория неба" Кант признается в том, что космогонические проблемы для него являются не только предметом научных исследований, но и источником светлой радости. Многие строки этой книги представляют собой непревзойденные образцы вдохновенных научных стихотворений в прозе, вечный и немеркнущий сплав логики науки и поэзии искусства.
Но перенесемся из XVIII века в век XX. В 1931 г. в Москве вышла в свет небольшая книга драматурга и искусствоведа В. М. Волькенштейна "Опыт современной эстетики". Авторское введение прекрасно рисует дух того времени: "...автор ищет прежде всего определение той новой красоты, которая характеризует нашу бурную эпоху... Эта новая красота перед нами в еще невиданных произведениях искусств, в удивительных изобретениях техники, в новых методах мышления..." Последнее для нас является самым главным. Впрочем, это было отмечено и в предисловии первого наркома просвещения, писателя, искусствоведа, академика А. В. Луначарского (1875-1933), которым открывалась книга: "Само оглавление книги показывает, что Волькенштейн стремится распространить понятия эстетического на область мышления, считая возможным оценивать с эстетической точки зрения понятия: математические, физические, шахматную игру, всякое научное построение или формулу. Не подлежит сомнению, что это так. Беспрестанно у самих ученых... с уст срываются замечания: красивая теория, изящное разрешение затруднений и т. д. и т. д. Восхищение перед силой человеческого ума есть, конечно, глубоко эстетическое явление, своеобразное, но ничем радикально не различающееся от восхищения перед физической ловкостью человека, перед красотою здания и т. д.".
В заключение Хатчесон делает важный вывод: красота науки неравнозначна научному знанию. Красота науки заключается не в собрании застывших законов, а в обретении новых знаний, в открытии новых истин, в обнаружении стройности и порядка там, где еще недавно царил хаос. Только беспрерывное движение вперед, а точнее вверх, к новым вершинам истины,- такова формула прекрасного в науке.
Отметим еще одно существенное обстоятельство. Ясно, что все три выведенных Хатчесоном эстетических принципа справедливы для любой науки, но получены они Хатчесоном для математики. И дело здесь не в том, что остальные науки во времена Хатчесона были еще недостаточно развиты по сравнению с математикой. Дело в том, что математика во все времена была и остается "первой красавицей" среди наук и, следовательно, эстетические принципы науки наиболее ярко проявляются в математике. Чуть позже мы попытаемся обосновать эту мысль.
Хатчесон оказал заметное влияние на формирование эстетических взглядов последующих философов: Давида Юма (1711 — 1776), Адама Смита (1723-1790). Мысль Хатчесона о красоте единства в многообразии мы находим и в трудах родоначальника немецкой классической философии, "кенигсбергского затворника"[4] Иммануила Канта. В книге "Естественная история и теория неба" Кант признается в том, что космогонические проблемы для него являются не только предметом научных исследований, но и источником светлой радости. Многие строки этой книги представляют собой непревзойденные образцы вдохновенных научных стихотворений в прозе, вечный и немеркнущий сплав логики науки и поэзии искусства.
Но перенесемся из XVIII века в век XX. В 1931 г. в Москве вышла в свет небольшая книга драматурга и искусствоведа В. М. Волькенштейна "Опыт современной эстетики". Авторское введение прекрасно рисует дух того времени: "...автор ищет прежде всего определение той новой красоты, которая характеризует нашу бурную эпоху... Эта новая красота перед нами в еще невиданных произведениях искусств, в удивительных изобретениях техники, в новых методах мышления..." Последнее для нас является самым главным. Впрочем, это было отмечено и в предисловии первого наркома просвещения, писателя, искусствоведа, академика А. В. Луначарского (1875-1933), которым открывалась книга: "Само оглавление книги показывает, что Волькенштейн стремится распространить понятия эстетического на область мышления, считая возможным оценивать с эстетической точки зрения понятия: математические, физические, шахматную игру, всякое научное построение или формулу. Не подлежит сомнению, что это так. Беспрестанно у самих ученых... с уст срываются замечания: красивая теория, изящное разрешение затруднений и т. д. и т. д. Восхищение перед силой человеческого ума есть, конечно, глубоко эстетическое явление, своеобразное, но ничем радикально не различающееся от восхищения перед физической ловкостью человека, перед красотою здания и т. д.".
Вселенная своей неизмеримой громадностью, безграничным разнообразием и красотой, которые сияют в ней со всех сторон, повергает дух в немое удивление.И. Кант
Две вещи наполняют душу всегда новым и все более сильным удивлением и благоговением...- это звездное небо надо мной и моральный закон во мне.И. Кант
 Математика: прекрасное в науке
Математика: прекрасное в науке
 Математика: прекрасное в науке
Итак, стремясь дать новое определение прекрасного, Волькенштейн пытается найти признаки красоты в науке: математике, физике, химии. Эти признаки, по Волькенштейну, таковы: 1) эстетическое впечатление "возникает только в связи с целесообразным, сложным (трудным) преодолением"; 2) "красиво сведение сложности к простоте"; 3) "всякое математическое оформление научных достижений, если оно наглядно и гармонично, вызывает эстетическое впечатление".
Легко видеть, что формула "красота есть целесообразное, трудное преодоление" перекликается с формулой Хатчесона "красота есть обретение неочевидной истины". Да, Природа прячет свои законы в сокровенных тайниках и открываются они только тому, у когс хватает сил на трудное преодоление. И как вознаграждение в конце пути ожидает ученого красота открывающейся истины. Альберт Эйнштейн (1879-1955) любил повторять, что Бог (т. е. Природа) изощрен но не злонамерен (эта надпись была сделана у Эйнштейна на камине). Изощренность Природы состоит в том что она ловко скрывает от человека свои законы, а ю внешнее проявление выглядит поначалу как полный хаос. Не злонамеренность же Природы означает существование у нее законов и принципиальную возможность их обнаружения в конце целесообразного и трудное преодоления. Познание гармонии Природы, когда лиш нее и кажущееся отпадает, когда истина обретает вели чавую простоту и ясность, и есть высшая красота научного поиска.
Математика: прекрасное в науке
Итак, стремясь дать новое определение прекрасного, Волькенштейн пытается найти признаки красоты в науке: математике, физике, химии. Эти признаки, по Волькенштейну, таковы: 1) эстетическое впечатление "возникает только в связи с целесообразным, сложным (трудным) преодолением"; 2) "красиво сведение сложности к простоте"; 3) "всякое математическое оформление научных достижений, если оно наглядно и гармонично, вызывает эстетическое впечатление".
Легко видеть, что формула "красота есть целесообразное, трудное преодоление" перекликается с формулой Хатчесона "красота есть обретение неочевидной истины". Да, Природа прячет свои законы в сокровенных тайниках и открываются они только тому, у когс хватает сил на трудное преодоление. И как вознаграждение в конце пути ожидает ученого красота открывающейся истины. Альберт Эйнштейн (1879-1955) любил повторять, что Бог (т. е. Природа) изощрен но не злонамерен (эта надпись была сделана у Эйнштейна на камине). Изощренность Природы состоит в том что она ловко скрывает от человека свои законы, а ю внешнее проявление выглядит поначалу как полный хаос. Не злонамеренность же Природы означает существование у нее законов и принципиальную возможность их обнаружения в конце целесообразного и трудное преодоления. Познание гармонии Природы, когда лиш нее и кажущееся отпадает, когда истина обретает вели чавую простоту и ясность, и есть высшая красота научного поиска.
Знай же, художник, что нужны во всем простота и единство."Красиво сведение сложности к простоте". Это принцип, видимо, является главным эстетическим принципом науки. Впрочем, вот мнение Эйнштейна: "Наш опыт убеждает нас, что Природа — это сочетание самых простых математических идей", "Бог ни за что не упустил бы возможности сделать Природу такой простой", другой выдающийся соотечественник Эйнштейна Гей-зенберг в одной из своих работ писал: "Все еще может считаться лучшим критерием корректности новых концепций старая латинская пословица "Simplex sigillum veri" ("Простота — признак истинности"), которая была выведена большими буквами в физической аудитории Геттингенского университета ".Гораций
(Б. Пастернак)
 Система мира по Птолемею. Иллюстрация из 'Небесного атласа' Целлариуса. Амстердам. 1708
Система мира по Птолемею. Иллюстрация из 'Небесного атласа' Целлариуса. Амстердам. 1708
 Математика: прекрасное в науке
Согласно третьему признаку Волькенштейна, математика несет красоту в любую науку. Строго говоря, этот тезис является следствием предыдущего: красиво сведение сложности к простоте, ибо математика и есть тот инструмент науки, который позволяет, говоря словами основоположника кибернетики Норберта Винера (1894-1964), "находить порядок в хаосе, который нас окружает". Волькенштейн отмечает эту особую роль математики в науке и, следовательно, ее особую эстетическую ценность: "Математика есть область утонченной красоты. Ее формулы выражают сложные соотношение чисел в определенной форме. Поэтому они могут быть красивы, или, как говорят математики, "изящны".
Широко известно, какой эстетический восторг испытывал выдающийся немецкий физик Людвиг Больцман (1844-1906) при виде уравнений Максвелла: "Не Бог ли начертал эти письмена? " Мы позволим себе привести здесь эти уравнения без необходимых пояснений, а просто как "письмена" — красивые, но непонятные иероглифы:
Математика: прекрасное в науке
Согласно третьему признаку Волькенштейна, математика несет красоту в любую науку. Строго говоря, этот тезис является следствием предыдущего: красиво сведение сложности к простоте, ибо математика и есть тот инструмент науки, который позволяет, говоря словами основоположника кибернетики Норберта Винера (1894-1964), "находить порядок в хаосе, который нас окружает". Волькенштейн отмечает эту особую роль математики в науке и, следовательно, ее особую эстетическую ценность: "Математика есть область утонченной красоты. Ее формулы выражают сложные соотношение чисел в определенной форме. Поэтому они могут быть красивы, или, как говорят математики, "изящны".
Широко известно, какой эстетический восторг испытывал выдающийся немецкий физик Людвиг Больцман (1844-1906) при виде уравнений Максвелла: "Не Бог ли начертал эти письмена? " Мы позволим себе привести здесь эти уравнения без необходимых пояснений, а просто как "письмена" — красивые, но непонятные иероглифы:

 Система мира по Копернику. Иллюстрация из 'Небесного атласа' Целлариуса. По сравнению с гелиоцентрической моделью Птолемея это была более простая и более красивая научная теория.
Система мира по Копернику. Иллюстрация из 'Небесного атласа' Целлариуса. По сравнению с гелиоцентрической моделью Птолемея это была более простая и более красивая научная теория.
 Математика: прекрасное в науке
Что же восхищало Больцмана в этих уравнениях? Конечно, и красота формы, которую можно оценить, не понимая сути уравнений. Действительно, сами уравнения просты по форме. Части уравнений, содержащие пары
Математика: прекрасное в науке
Что же восхищало Больцмана в этих уравнениях? Конечно, и красота формы, которую можно оценить, не понимая сути уравнений. Действительно, сами уравнения просты по форме. Части уравнений, содержащие пары  , почти полностью равноправны, а сами уравнения почти полностью симметричны. Но главное, конечно, в красоте содержания уравнений, которая раскрывается далеко не каждому. Эта красота содержания заключается в том, что сами уравнения подсказали английскому физику, основателю классической электродинамики Джеймсу Клерку Максвеллу (1831 — 1879) идею электромагнитных волн и позволили связать воедино электричество, магнетизм и свет.
Более доступным примером красоты формы и содержания в науке, а также красоты математического оформления являются структурные формулы в химии, в особенности структурная формула бензола С6Н6 как основа многих формул органической химии:
, почти полностью равноправны, а сами уравнения почти полностью симметричны. Но главное, конечно, в красоте содержания уравнений, которая раскрывается далеко не каждому. Эта красота содержания заключается в том, что сами уравнения подсказали английскому физику, основателю классической электродинамики Джеймсу Клерку Максвеллу (1831 — 1879) идею электромагнитных волн и позволили связать воедино электричество, магнетизм и свет.
Более доступным примером красоты формы и содержания в науке, а также красоты математического оформления являются структурные формулы в химии, в особенности структурная формула бензола С6Н6 как основа многих формул органической химии:
 Внешняя красота этой формулы видна с первого взгляда. Объясняется она прежде всего ее математическим оформлением: в основе формулы лежит правильный шестиугольник — геометрическая фигура, обладающая многими видами симметрии. Но помимо внешней красоты эта формула излучает и красоту внутреннюю. В чем она? В том, что структурная формула отражает взаимное расположение атомов в молекуле и порядок связи между ними. Таким образом, структурная формула определяет свойства вещества, объясняет внутреннее строение вещества, и в этом ее внутренняя красота, красота содержания.
А кто сегодня занимается вопросами эстетики науки? Пожалуй, пальму первенства здесь следует отдать академику А. Б. Мигдалу — физику-теоретику, основоположнику многих научных направлений в ядерной физике. Будучи человеком широких интересов, Мигдал ходит Время и на интенсивную научную и организаторскую деятельность, и на занятия альпинизмом и горными лыжами, и на поиски красоты в науке. В статье Мигдала "О красоте науки" мы читаем: "Что можно сказать о красоте науки, красоте мысленных построений, которых не нарисовать на бумаге, не высечь на камне, не переложить на музыку? Красота науки, как и искусства, определяется ощущением соразмерности и взаимосвязанности частей, образующих целое, и отражает гармонию мира".
В книге "Поиски истины", адресованной юношеству, Мигдал высказывает интереснейшую мысль о том, что "понятие красоты играет важную роль для проверки правильности результатов и для отыскания новых законов и является отражением гармонии, существующей в природе". Это, вообще, любимая мысль всех современных физиков, начиная от Альберта Эйнштейна и английского физика Поля Дирака, которому принадлежит афоризм о том, что красота является критерием истинности физической теории. Более того, красота являлась путеводной звездой в поисках истины и для Платона, и для Кеплера, к чему мы еще вернемся на страницах этой книги.
Отдавая должное признакам внешней красоты математических формул, Мигдал считает, что "гораздо важнее не внешние, а более глубокие признаки красоты результатов. Красиво, если выражение связывает в простой форме разнородные явления, если устанавливаются неожиданные связи. Одна из красивейших формул теоретической физики — это формула теории тяготения Эйнштейна, связывающая радиус кривизны пространства с плотностью материи... Требование красоты" не являясь абсолютным, играет важнейшую роль как для отыскания новых законов природы, так и для проверки полученных результатов".
Наконец, Мигдал анализирует понятие симметрии как источник красоты в физике. Следует сказать, что истинная роль симметрии в науке стала проясняться только в XX веке. В 1918 г. немецкий математик Эмми Иетер (1882-1935) доказала замечательную теорему, согласно которой каждому виду симметрии соответствует свой закон сохранения. Например, знаменитый закон сохранения энергии является следствием однородности времени, т. е. симметрии относительно сдвигов по времени. В 1963 г. американский физик-теоретик Юджин Пол Вигнер получил Нобелевскую премию по физике за исследования принципов симметрии, лежащих в основе взаимодействия элементарных частиц. Выдающаяся роль симметрии в искусстве известна давно: симметрия сопровождает искусство едва ли не с момента его зарождения. И вот в XX веке человечество убеждается в огромной роли симметрии в формировании законов природы. Таким образом, симметрия является едва ли не единственным общепризнанным критерием красоты как в науке, так и в искусстве. (Этот важный вопрос мы рассмотрим подробнее в главе 4.)
Внешняя красота этой формулы видна с первого взгляда. Объясняется она прежде всего ее математическим оформлением: в основе формулы лежит правильный шестиугольник — геометрическая фигура, обладающая многими видами симметрии. Но помимо внешней красоты эта формула излучает и красоту внутреннюю. В чем она? В том, что структурная формула отражает взаимное расположение атомов в молекуле и порядок связи между ними. Таким образом, структурная формула определяет свойства вещества, объясняет внутреннее строение вещества, и в этом ее внутренняя красота, красота содержания.
А кто сегодня занимается вопросами эстетики науки? Пожалуй, пальму первенства здесь следует отдать академику А. Б. Мигдалу — физику-теоретику, основоположнику многих научных направлений в ядерной физике. Будучи человеком широких интересов, Мигдал ходит Время и на интенсивную научную и организаторскую деятельность, и на занятия альпинизмом и горными лыжами, и на поиски красоты в науке. В статье Мигдала "О красоте науки" мы читаем: "Что можно сказать о красоте науки, красоте мысленных построений, которых не нарисовать на бумаге, не высечь на камне, не переложить на музыку? Красота науки, как и искусства, определяется ощущением соразмерности и взаимосвязанности частей, образующих целое, и отражает гармонию мира".
В книге "Поиски истины", адресованной юношеству, Мигдал высказывает интереснейшую мысль о том, что "понятие красоты играет важную роль для проверки правильности результатов и для отыскания новых законов и является отражением гармонии, существующей в природе". Это, вообще, любимая мысль всех современных физиков, начиная от Альберта Эйнштейна и английского физика Поля Дирака, которому принадлежит афоризм о том, что красота является критерием истинности физической теории. Более того, красота являлась путеводной звездой в поисках истины и для Платона, и для Кеплера, к чему мы еще вернемся на страницах этой книги.
Отдавая должное признакам внешней красоты математических формул, Мигдал считает, что "гораздо важнее не внешние, а более глубокие признаки красоты результатов. Красиво, если выражение связывает в простой форме разнородные явления, если устанавливаются неожиданные связи. Одна из красивейших формул теоретической физики — это формула теории тяготения Эйнштейна, связывающая радиус кривизны пространства с плотностью материи... Требование красоты" не являясь абсолютным, играет важнейшую роль как для отыскания новых законов природы, так и для проверки полученных результатов".
Наконец, Мигдал анализирует понятие симметрии как источник красоты в физике. Следует сказать, что истинная роль симметрии в науке стала проясняться только в XX веке. В 1918 г. немецкий математик Эмми Иетер (1882-1935) доказала замечательную теорему, согласно которой каждому виду симметрии соответствует свой закон сохранения. Например, знаменитый закон сохранения энергии является следствием однородности времени, т. е. симметрии относительно сдвигов по времени. В 1963 г. американский физик-теоретик Юджин Пол Вигнер получил Нобелевскую премию по физике за исследования принципов симметрии, лежащих в основе взаимодействия элементарных частиц. Выдающаяся роль симметрии в искусстве известна давно: симметрия сопровождает искусство едва ли не с момента его зарождения. И вот в XX веке человечество убеждается в огромной роли симметрии в формировании законов природы. Таким образом, симметрия является едва ли не единственным общепризнанным критерием красоты как в науке, так и в искусстве. (Этот важный вопрос мы рассмотрим подробнее в главе 4.)
Геометрия есть познание всего сущего.Нам остается ответить еще на один вопрос, который следует из заголовка этого параграфа: почему именно математика претендует на роль "первой красавицы" среди остальных наук?Платон
 Математика: прекрасное в науке
Конечно, проще всего было бы ответить на данный вопрос известным афоризмом "короля математиков" Карла Гаусса (1777-1855): "Математика — царица всех наук... Она часто снисходит до оказания услуг астрономии и другим естественным наукам, но при всех обстоятельствах первое место, несомненно, останется за ней". Однако ясно, что это не объяснение, а декларация, и, чтобы разобраться в существе дела, мы должны вновь спросить себя: что такое математика? Гораздо легче ответить на аналогичный вопрос биологу или геологу. Первый скажет, что биология — это наука о живой природе, а второй — что геология — это наука о недрах Земли. А вот у математики нет своего материального предмета исследования, его нельзя потрогать руками или увидеть глазами. Тем не менее значительная часть математических понятий и теорий родилась при изучении реальных явлений (всем известна история возникновения и развития арифметики и геометрии). Как это ни парадоксально, но именно математика в процессе своего развития лишилась материального предмета изучения, и это сделало ее всемогущественной наукой. Сегодня любой человек, даже совершенно далекий от математики, знает, что математика представляет собой могучую силу, сфера влияния которой практически не ограничена.
"Что такое математика?" — так называется книга американских математиков Р. Куранта и Г. Роббинса, которую мы рекомендуем всем, кто захочет увидеть математику во всем блеске ее красоты и могуществе ее приложений, ибо, как сказано в авторском введении, "и для специалистов, и для любителей не философия, а именно активные занятия математикой смогут дать ответ на вопрос: что такое математика?"
Тем не менее попробуем немного пофилософствовать. Известно классическое определение математики, данное Ф. Энгельсом: "Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира". Это определение указывает не только на предмет математики, но и на его происхождение — реальный мир. Однако за сто лет своего интенсивного развития математика ушла далеко вперед, у нее появились новые нетрадиционные разделы, и стало ясно, что данное определение нуждается в уточнении.
Математика: прекрасное в науке
Конечно, проще всего было бы ответить на данный вопрос известным афоризмом "короля математиков" Карла Гаусса (1777-1855): "Математика — царица всех наук... Она часто снисходит до оказания услуг астрономии и другим естественным наукам, но при всех обстоятельствах первое место, несомненно, останется за ней". Однако ясно, что это не объяснение, а декларация, и, чтобы разобраться в существе дела, мы должны вновь спросить себя: что такое математика? Гораздо легче ответить на аналогичный вопрос биологу или геологу. Первый скажет, что биология — это наука о живой природе, а второй — что геология — это наука о недрах Земли. А вот у математики нет своего материального предмета исследования, его нельзя потрогать руками или увидеть глазами. Тем не менее значительная часть математических понятий и теорий родилась при изучении реальных явлений (всем известна история возникновения и развития арифметики и геометрии). Как это ни парадоксально, но именно математика в процессе своего развития лишилась материального предмета изучения, и это сделало ее всемогущественной наукой. Сегодня любой человек, даже совершенно далекий от математики, знает, что математика представляет собой могучую силу, сфера влияния которой практически не ограничена.
"Что такое математика?" — так называется книга американских математиков Р. Куранта и Г. Роббинса, которую мы рекомендуем всем, кто захочет увидеть математику во всем блеске ее красоты и могуществе ее приложений, ибо, как сказано в авторском введении, "и для специалистов, и для любителей не философия, а именно активные занятия математикой смогут дать ответ на вопрос: что такое математика?"
Тем не менее попробуем немного пофилософствовать. Известно классическое определение математики, данное Ф. Энгельсом: "Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира". Это определение указывает не только на предмет математики, но и на его происхождение — реальный мир. Однако за сто лет своего интенсивного развития математика ушла далеко вперед, у нее появились новые нетрадиционные разделы, и стало ясно, что данное определение нуждается в уточнении.
 Математика: прекрасное в науке
Новое определение математики предложила группа французских математиков, объединившаяся под псевдонимом Никола Бурбаки, которая определяет математику как науку о математических структурах. К великому удовольствию любителей искусства, мы должны констатировать, что история повторяется: эстетику по-новому определяют как науку об эстетическом, а математику — как науку о математических структурах! Но не надо спешить иронизировать по этому поводу. Вспомним предостережение выдающегося американского математика Рихарда Куранта (1888-1972), данное им в статье "Математика в современном мире": "На вопрос "Что такое математика?" невозможно дать обстоятельный ответ на основе одних лишь только философских обобщений семантических предложений или с помощью обтекаемого газетно-журнального многословия. Так же как нельзя дать общее определение музыке или живописи: никто не может оценить эти виды искусства, не понимая, что такое ритм, гармония и строй в музыке или форма, цвет и композиция в живописи. Для понимания же сути математики еще в большей степени необходимо подлинное проникновение в составляющие ее элементы".
Определение математики, предлагаемое Бурбаки страдает еще одним важным дефектом: оно не отражает отношения математики к окружающему нас миру, еэкду тем если исходить из определения Ф. Энгельса, т. е. в вопросе об отношении математики к действительности занимать материалистические позиции, то ановится понятным, почему "книга природы написана языке математики" (Галилей). "Но совершенно неверно,- указывал Ф. Энгельс,- будто в чистой математике разум имеет дело только с продуктами своего собственного творчества и воображения. Понятия числа и фигуры взяты не откуда-нибудь, а только из действительного мира" (т. 20, с. 37). Зародившись в реальном мире и пройдя путь абстракции и развития в самой математике, математические понятия вновь "спускаются на землю" и идут по ней в своем триумфальном шествии. Именно "земным происхождением" и объясняется поразительная эффективность математики в естествознании.
Математика: прекрасное в науке
Новое определение математики предложила группа французских математиков, объединившаяся под псевдонимом Никола Бурбаки, которая определяет математику как науку о математических структурах. К великому удовольствию любителей искусства, мы должны констатировать, что история повторяется: эстетику по-новому определяют как науку об эстетическом, а математику — как науку о математических структурах! Но не надо спешить иронизировать по этому поводу. Вспомним предостережение выдающегося американского математика Рихарда Куранта (1888-1972), данное им в статье "Математика в современном мире": "На вопрос "Что такое математика?" невозможно дать обстоятельный ответ на основе одних лишь только философских обобщений семантических предложений или с помощью обтекаемого газетно-журнального многословия. Так же как нельзя дать общее определение музыке или живописи: никто не может оценить эти виды искусства, не понимая, что такое ритм, гармония и строй в музыке или форма, цвет и композиция в живописи. Для понимания же сути математики еще в большей степени необходимо подлинное проникновение в составляющие ее элементы".
Определение математики, предлагаемое Бурбаки страдает еще одним важным дефектом: оно не отражает отношения математики к окружающему нас миру, еэкду тем если исходить из определения Ф. Энгельса, т. е. в вопросе об отношении математики к действительности занимать материалистические позиции, то ановится понятным, почему "книга природы написана языке математики" (Галилей). "Но совершенно неверно,- указывал Ф. Энгельс,- будто в чистой математике разум имеет дело только с продуктами своего собственного творчества и воображения. Понятия числа и фигуры взяты не откуда-нибудь, а только из действительного мира" (т. 20, с. 37). Зародившись в реальном мире и пройдя путь абстракции и развития в самой математике, математические понятия вновь "спускаются на землю" и идут по ней в своем триумфальном шествии. Именно "земным происхождением" и объясняется поразительная эффективность математики в естествознании.
Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства.Леонардо да Винчи
Среди всех наук Математика пользуется особенным уважением; основанием этому служит то единственное обстоятельство, что ее положения абсолютно верны и неоспоримы, в то время как положения других наук до известной степени спорны, и всегда существует опасность их опровержения новыми открытиями.А. Эйнштейн
 Математика: прекрасное в науке
Вот как важно даже в такой абстрактной науке, как математика, стоять на правильных философских позициях. Несмотря на непререкаемый авторитет группы Н. Бурбаки в современном математическом мире и беспрецедентную задачу, решаемую этой группой,- попытку изложить главнейшие разделы математики на основе единого формального аксиоматического метода, некоторые философские воззрения Н. Бурбаки нельзя назвать бесспорными. Но бесспорно в этом определении математики следующее: "математическая структура" в математике, так же как и "бытие" в логике Гегеля или "прекрасное" в эстетике, является той изначальной категорией, с которой начинается восхождение от абстрактного к конкретному в математике, начинается "проникновение в составляющие элементы", о котором говорил Р. Курант.
Так что же такое математика и в чем ее особая красота? "Математика — это больше, чем наука, это язык" — так определил место математики в системе наук знаменитый датский физик Нильс Бор (1885-1962). Математика может быть языком любой науки, умеющей на нем разговаривать. В этом универсальность и могущество математики, но в этом и особая красота математики, выделяющая ее среди других наук. Ибо всякий язык красив уже сам по себе как средство общения.
В самом деле, как только любая из наук переведет свои проблемы на язык математики, так тут же к ее услугам откроется весь богатейший арсенал математики, обладающий массой универсальных методов и способный решать многие конкретные задачи. Например, сформулировав задачу на языке дифференциальных уравнений, представитель любой науки получит в руки полный набор математических методов от качественных методов исследования дифференциальных уравнений до современных численных методов решения этих уравнений на ЭВМ.
Математика: прекрасное в науке
Вот как важно даже в такой абстрактной науке, как математика, стоять на правильных философских позициях. Несмотря на непререкаемый авторитет группы Н. Бурбаки в современном математическом мире и беспрецедентную задачу, решаемую этой группой,- попытку изложить главнейшие разделы математики на основе единого формального аксиоматического метода, некоторые философские воззрения Н. Бурбаки нельзя назвать бесспорными. Но бесспорно в этом определении математики следующее: "математическая структура" в математике, так же как и "бытие" в логике Гегеля или "прекрасное" в эстетике, является той изначальной категорией, с которой начинается восхождение от абстрактного к конкретному в математике, начинается "проникновение в составляющие элементы", о котором говорил Р. Курант.
Так что же такое математика и в чем ее особая красота? "Математика — это больше, чем наука, это язык" — так определил место математики в системе наук знаменитый датский физик Нильс Бор (1885-1962). Математика может быть языком любой науки, умеющей на нем разговаривать. В этом универсальность и могущество математики, но в этом и особая красота математики, выделяющая ее среди других наук. Ибо всякий язык красив уже сам по себе как средство общения.
В самом деле, как только любая из наук переведет свои проблемы на язык математики, так тут же к ее услугам откроется весь богатейший арсенал математики, обладающий массой универсальных методов и способный решать многие конкретные задачи. Например, сформулировав задачу на языке дифференциальных уравнений, представитель любой науки получит в руки полный набор математических методов от качественных методов исследования дифференциальных уравнений до современных численных методов решения этих уравнений на ЭВМ.
 Математика: прекрасное в науке
Но математика — это особое средство общения: она помогает найти общий язык служителям разных наук и, что еще важнее, она помогает ученому "разговаривать" с природой. Так, волны на воде, звуковые волны и радиоволны описываются на языке математики одним и тем же дифференциальным уравнением, известным под названием волнового уравнения (см. (10.1)). Радиофизикам уже нет нужды решать волновое уравнение, которое за них решили акустики. Более того, с помощью математики здесь выявляется родство в столь разнородных на первый взгляд физических явлениях, как распространение радиоволн и волн на воде и в воздухе.
Таким образом, в математике как ни в какой другой науке находит выражение важнейший критерий научной красоты — единство в многообразии. Математика раскрывает перед человеком красоту внутренних связей, существующих в природе, и указывает на внутреннее единство мира. То, что именно в математике достигается в наивысшей форме единство в многообразии, а следовательно, и наибольшая красота в науке, отмечал в статье "Смысл и значение красоты в точных науках" В. Гейзенберг: "Понимание всего богато окрашенного многообразия явлений достигается путем осознания присущего всем явлениям объединяющего принципа форм, выражаемого на языке математики. Таким же образом устанавливается тесная взаимосвязь между тем, что воспринимается как прекрасное, и тем, что доступно пониманию лишь с помощью интеллекта ".
Язык математики — это особый язык науки. В отличие от естественного языка (русского или английского), который в основном классифицирует предметы и потому является языком качественным, язык математики прежде всего количественный. Количественный язык представляет собой дальнейшее развитие и уточнение обычного качественного языка, но он не исключает а скорее дополняет последний.
Математика: прекрасное в науке
Но математика — это особое средство общения: она помогает найти общий язык служителям разных наук и, что еще важнее, она помогает ученому "разговаривать" с природой. Так, волны на воде, звуковые волны и радиоволны описываются на языке математики одним и тем же дифференциальным уравнением, известным под названием волнового уравнения (см. (10.1)). Радиофизикам уже нет нужды решать волновое уравнение, которое за них решили акустики. Более того, с помощью математики здесь выявляется родство в столь разнородных на первый взгляд физических явлениях, как распространение радиоволн и волн на воде и в воздухе.
Таким образом, в математике как ни в какой другой науке находит выражение важнейший критерий научной красоты — единство в многообразии. Математика раскрывает перед человеком красоту внутренних связей, существующих в природе, и указывает на внутреннее единство мира. То, что именно в математике достигается в наивысшей форме единство в многообразии, а следовательно, и наибольшая красота в науке, отмечал в статье "Смысл и значение красоты в точных науках" В. Гейзенберг: "Понимание всего богато окрашенного многообразия явлений достигается путем осознания присущего всем явлениям объединяющего принципа форм, выражаемого на языке математики. Таким же образом устанавливается тесная взаимосвязь между тем, что воспринимается как прекрасное, и тем, что доступно пониманию лишь с помощью интеллекта ".
Язык математики — это особый язык науки. В отличие от естественного языка (русского или английского), который в основном классифицирует предметы и потому является языком качественным, язык математики прежде всего количественный. Количественный язык представляет собой дальнейшее развитие и уточнение обычного качественного языка, но он не исключает а скорее дополняет последний.
 Дюрер. Меланхолия. Гравюра на меди. 1514. Во времена Возрождения меланхолический темперамент отождествляли с творческим началом. На гравюре Дюрера Меланхолия окружена атрибутами зодчества и геометрии, отчего математики любят считать этот шедевр графического искусства олицетворением творческого духа математика, а саму Меланхолию — представительницей математики в мире прекрасного
Важнейшим преимуществом количественного языка математики является краткость и точность. В этом его огромное преимущество и в этом его красота, ибо именно в математическом языке претворяется один из основных признаков красоты в науке: сведение сложности к простоте. Всем известно, что с помощью математического языка — функций, уравнений, формул — точно и кратко описываются самые разнообразные свойства и явления, происходящие в природе и обществе. Древнегреческому математику Апполонию из Перги (ок. 260 — ок. 170 гг. до н. э.) потребовалось восемь книг, чтобы описать свойства конических сечений. Между тем на языке аналитической геометрии, т. е. с помощью алгебраических формул, эти свойства доказываются на нескольких страницах. Эталоном простоты и красоты, символом современной физики стала знаменитая формула Эйнштейна
Дюрер. Меланхолия. Гравюра на меди. 1514. Во времена Возрождения меланхолический темперамент отождествляли с творческим началом. На гравюре Дюрера Меланхолия окружена атрибутами зодчества и геометрии, отчего математики любят считать этот шедевр графического искусства олицетворением творческого духа математика, а саму Меланхолию — представительницей математики в мире прекрасного
Важнейшим преимуществом количественного языка математики является краткость и точность. В этом его огромное преимущество и в этом его красота, ибо именно в математическом языке претворяется один из основных признаков красоты в науке: сведение сложности к простоте. Всем известно, что с помощью математического языка — функций, уравнений, формул — точно и кратко описываются самые разнообразные свойства и явления, происходящие в природе и обществе. Древнегреческому математику Апполонию из Перги (ок. 260 — ок. 170 гг. до н. э.) потребовалось восемь книг, чтобы описать свойства конических сечений. Между тем на языке аналитической геометрии, т. е. с помощью алгебраических формул, эти свойства доказываются на нескольких страницах. Эталоном простоты и красоты, символом современной физики стала знаменитая формула Эйнштейна
 выражающая в простой и изящной математической форме глубокие физические идеи.
выражающая в простой и изящной математической форме глубокие физические идеи.
 Математика: прекрасное в науке
Итак, математика — это не только самостоятельная наука о "математических структурах", но и язык других наук, язык единый, универсальный, точный, простой и, следовательно, "красивый. Хорошо сказал об этих качествах математики наш современник, замечательный советский математик С. Л. Соболев, в 31 год ставший академиком: "Есть одна наука, без которой невозможна никакая другая. Это математика. Ее понятия, представления и символы служат языком, на котором говорят, пишут и думают другие науки. Она объясняет закономерности сложных явлений, сводя их к простым, элементарным явлениям природы. Она предсказывает и предвычисляет далеко вперед с огромной точностью ход вещей".
Последнее свойство математики, о котором говорит Соболев, дающее возможность "выспрашивать" у природы ее тайны и позволяющее делать потрясающие воображение открытия "на кончике пера", ставит математику в исключительное положение среди наук. Классическим примером триумфа математики в естествознании стало открытие планеты Нептун. Его история такова. Еще в XVIII веке (вскоре после открытия планеты Уран) в ее движении астрономы обнаружили некоторые "неправильности". Тогда же было высказано предположение о том, что эти отклонения орбиты вызваны притяжением неизвестной еще планеты. Однако только к середине XIX века параметры орбиты Неизвестной планеты были вычислены независимо друг от Друга англичанином Джоном Адамсом (1819-1892) и Французом Урбеном Леверье (1811 — 1877). Результаты вычислений Адаме в сентябре 1845 г. передал в Гриничскую обсерваторию (Великобритания), а Леверье 18 сентября 1846 г. послал в Берлинскую обсерваторию.
Но если расчеты Адамса продолжали пылиться в архивах Гринвичской обсерватории, то по расчетам Леверье 23 сентября 1846 г., в первый же вечер после получения письма от Леверье, немецкий астроном Иоганн Галле (1812-1910) обнаружил неизвестную планету точно в указанном месте небосвода! Как видим, история научных открытий полна драматизма. Открытие Нептуна было величайшим триумфом математики: далекая неизвестная планета была найдена в кабинете ученого только с помощью карандаша и бумаги, т. е. с помощью математики!
Математика: прекрасное в науке
Итак, математика — это не только самостоятельная наука о "математических структурах", но и язык других наук, язык единый, универсальный, точный, простой и, следовательно, "красивый. Хорошо сказал об этих качествах математики наш современник, замечательный советский математик С. Л. Соболев, в 31 год ставший академиком: "Есть одна наука, без которой невозможна никакая другая. Это математика. Ее понятия, представления и символы служат языком, на котором говорят, пишут и думают другие науки. Она объясняет закономерности сложных явлений, сводя их к простым, элементарным явлениям природы. Она предсказывает и предвычисляет далеко вперед с огромной точностью ход вещей".
Последнее свойство математики, о котором говорит Соболев, дающее возможность "выспрашивать" у природы ее тайны и позволяющее делать потрясающие воображение открытия "на кончике пера", ставит математику в исключительное положение среди наук. Классическим примером триумфа математики в естествознании стало открытие планеты Нептун. Его история такова. Еще в XVIII веке (вскоре после открытия планеты Уран) в ее движении астрономы обнаружили некоторые "неправильности". Тогда же было высказано предположение о том, что эти отклонения орбиты вызваны притяжением неизвестной еще планеты. Однако только к середине XIX века параметры орбиты Неизвестной планеты были вычислены независимо друг от Друга англичанином Джоном Адамсом (1819-1892) и Французом Урбеном Леверье (1811 — 1877). Результаты вычислений Адаме в сентябре 1845 г. передал в Гриничскую обсерваторию (Великобритания), а Леверье 18 сентября 1846 г. послал в Берлинскую обсерваторию.
Но если расчеты Адамса продолжали пылиться в архивах Гринвичской обсерватории, то по расчетам Леверье 23 сентября 1846 г., в первый же вечер после получения письма от Леверье, немецкий астроном Иоганн Галле (1812-1910) обнаружил неизвестную планету точно в указанном месте небосвода! Как видим, история научных открытий полна драматизма. Открытие Нептуна было величайшим триумфом математики: далекая неизвестная планета была найдена в кабинете ученого только с помощью карандаша и бумаги, т. е. с помощью математики!
Наука чистой математики в ее современных вариантах может быть представлена в качестве самого оригинального продукта человеческого духа. Другим претендентом на это звание является музыка.А. Уайтхед
 Математика: прекрасное в науке
Последующие сто лет истории науки были цепью блестящих побед и предсказаний математики и в других науках. И ядерная физика, и освоение космоса немыслимы без математики! Одним из последних открытий "на кончике пера" является открытие физического эффекта Т-слоя в плазме, сделанное группой советских ученых под руководством академиков А. Н. Тихонова и А. А. Самарского. Правда, вместо карандаша и бумаги современные математики располагают мощными ЭВМ, но суть остается той же: математические уравнения предсказывают физические явления.
В этом удивительном свойстве математики, называемом эвристическим (от архимедовой "эврики"), заключено высшее выражение еще одного признака красоты в науке — обретение неочевидной истины. Роль математики в постижении неочевидных истин, а значит, и красота математики непревзойдены.
"Непостижимая эффективность математики в естественных науках" — так называется знаменитая статья Вигнера и так с его легкой руки называют теперь это свойство математики. "Чудесная загадка соответствия математического языка законам физики является удивительным даром, который мы не в состоянии понять и которого мы, возможно, недостойны. Мы должны испытывать чувство благодарности за этот дар. Следует надеяться, что он не покинет нас в будущих исследованиях и что он будет — хорошо это или плохо — развиваться к нашему большому удовлетворению, а быть может, и к нарастающему беспокойству, расширяя область познания окружающего нас мира". Эти слова Ю. Вигнера — взволнованный гимн математике. Правда, в них звучит и растерянность перед необъяснимой загадкой, которая, как и в случае с Н. Бурбаки, вызвана философскими заблуждениями автора.
Математика: прекрасное в науке
Последующие сто лет истории науки были цепью блестящих побед и предсказаний математики и в других науках. И ядерная физика, и освоение космоса немыслимы без математики! Одним из последних открытий "на кончике пера" является открытие физического эффекта Т-слоя в плазме, сделанное группой советских ученых под руководством академиков А. Н. Тихонова и А. А. Самарского. Правда, вместо карандаша и бумаги современные математики располагают мощными ЭВМ, но суть остается той же: математические уравнения предсказывают физические явления.
В этом удивительном свойстве математики, называемом эвристическим (от архимедовой "эврики"), заключено высшее выражение еще одного признака красоты в науке — обретение неочевидной истины. Роль математики в постижении неочевидных истин, а значит, и красота математики непревзойдены.
"Непостижимая эффективность математики в естественных науках" — так называется знаменитая статья Вигнера и так с его легкой руки называют теперь это свойство математики. "Чудесная загадка соответствия математического языка законам физики является удивительным даром, который мы не в состоянии понять и которого мы, возможно, недостойны. Мы должны испытывать чувство благодарности за этот дар. Следует надеяться, что он не покинет нас в будущих исследованиях и что он будет — хорошо это или плохо — развиваться к нашему большому удовлетворению, а быть может, и к нарастающему беспокойству, расширяя область познания окружающего нас мира". Эти слова Ю. Вигнера — взволнованный гимн математике. Правда, в них звучит и растерянность перед необъяснимой загадкой, которая, как и в случае с Н. Бурбаки, вызвана философскими заблуждениями автора.
 Математика: прекрасное в науке
Большинство математиков склонны видеть "непостижимую эффективность" воей науки в глубинных связях с реальным миром. Так считает и выдающийся мериканский математик, один из создатели ЭВМ, Дж. фон Нейман (1903-1957). развитые математические идеи, отмечает Нейман, начинают жить собственной лсизнью, благодаря чему математика становится похожей на искусство. Но слова Неймана служат и предостережением некоторым "эстетам от математики", ибо отрыв от реальности делает "математику для математики", как и "искусство для искусства", чахлым декадентским течением.
Но в одном вопросе сходятся все ученые: математика является символом мудрости науки, образцом научной строгости и простоты, эталоном совершенства и красоты в науке. Вот только несколько высказываний по этому поводу.
Математика: прекрасное в науке
Большинство математиков склонны видеть "непостижимую эффективность" воей науки в глубинных связях с реальным миром. Так считает и выдающийся мериканский математик, один из создатели ЭВМ, Дж. фон Нейман (1903-1957). развитые математические идеи, отмечает Нейман, начинают жить собственной лсизнью, благодаря чему математика становится похожей на искусство. Но слова Неймана служат и предостережением некоторым "эстетам от математики", ибо отрыв от реальности делает "математику для математики", как и "искусство для искусства", чахлым декадентским течением.
Но в одном вопросе сходятся все ученые: математика является символом мудрости науки, образцом научной строгости и простоты, эталоном совершенства и красоты в науке. Вот только несколько высказываний по этому поводу.
"Математические доказательства, как алмазы, тверды и прозрачны и поддаются лишь самой строгой логике".Джон Локк (1632-1704), английский философ.
"Творчество математика в такой же степени есть создание прекрасного, как творчество живописца или поэта,- совокупность идей, подобно совокупности красок или слов, должна обладать внутренней гармонией. Красота есть первый пробный камень для математической идеи; в мире нет места уродливой математике".Годфри Харди (1877-1947), английский математик.
"Но ведь мы определенно носим в себе ощущение математической красоты, гармонии чисел и формы, геометрического изящества. Все эти чувства — настоящие эстетические чувства, и они хорошо знакомы всем настоящим математикам".Анри Пуанкаре, французский математик.
"В математике есть тоже своя красота, как в живописи и поэзии. Эта красота проявляется иногда в отчетливых, ярко очертанных идеях, где на виду всякая деталь умозаключений, а иногда поражает она нас в широких замыслах, скрывающих в себе кое-что недосказанное, но многообещающее".Н. Е. Жуковский (1847-1921), русский математик, механик, основоположник современой гидроаэродинамики, "отец русской авиации".
"Холодные числа, внешне сухие формулы математи-и полны внутренней красоты и жара сконцентрированной в них мысли".А. Д. Александров, советский математик, академик.
Математические доказательства, как алмазы, тверды и прозрачны...Дж. Локк
"Для нас, чьи плечи ноют под тяжестью наследия греческой мысли, кто идет по стопам героев эпохи Возрождения, цивилизация немыслима без математики".Андре Вей ль, французский математик.
"Музыка может возвышать или умиротворять душу, живопись — радовать глаз, поэзия — пробуждать чувства, философия — удовлетворять потребности разума, инженерное дело — совершенствовать материальную сторону жизни людей. Но математика способна достичь всех этих целей".Лучше не скажешь! Однако возникает новый вопрос. Если наука, а тем более математика так богаты собственной немеркнущей красотой, то почему многие крупнейшие ученые, как никто знающие толк в эстетике науки, едва только речь заходит о прекрасном, непременно обращаются именно к искусству, словно к пещере Алладина, где собраны все сокровища культуры, где хранятся вечные и недосягаемые образцы эстетических ценностей человечества? Таким образом, мы подходим к интереснейшей и захватывающей проблеме, проблеме взаимодействия науки и искусства, которую мы и рассмотрим далее.Морис Клайн, американский математик.
3. Наука и искусство — грани творчества
Наука и искусство так же тесно связаны между собой, как сердце и легкие...Л. Толстой
...Я подумал, что чутье художника стоит иногда мозгов ученого, что то и другое имеют одни цели, одну природу и что, быть может, со временем при совершенстве методов им суждено слиться вместе в гигантскую, чудовищную силу, которую теперь трудно и представить себе..."Поэзия — просто ерунда" — так ответил однажды Ньютон на вопрос, что он думает о поэзии. Другой великий творец дифференциального и интегрального исчисления, философ, физик, изобретатель, юрист, историк, языковед, дипломат и тайный советник Петра I Готфрид Лейбниц (1646 -1716) более сдержанно определял ценность поэзии по отношению к науке примерно как 1:7. Вспомним, что тургеневский Базаров был более категоричен в количественных оценках: "Порядочный химик,- заявлял он,- в двадцать раз полезнее всякого поэта". Впрочем, поэты часто также не стесняли себя в выражениях в адрес ученых. Так, английский поэт и художник Уильям Блейк (1757-1827) писал:А. Чехов
 У. Блейк. Ньютон. 1795. Несмотря на отсутствие пиетета к Ньютону в стихах поэта Блейка, художник Блейк воплотил в образе гениального естествоиспытателя величиечеловеческого разума
У. Блейк. Ньютон. 1795. Несмотря на отсутствие пиетета к Ньютону в стихах поэта Блейка, художник Блейк воплотил в образе гениального естествоиспытателя величиечеловеческого разума
 Наука и искусство — грани творчества
И мы вновь возвращаемся в Древнюю Грецию... Из всех народов античности греки оказали самое сильное влияние на развитие европейской цивилизации. Вероятно, источник греческого гения и в том, что, входя в контакты с великими и более древними восточными цивилизациями, греки сумели не отвергать, а усваивать их уроки, дабы извлечь из них оригинальную культуру, ставшую основой и непревзойденным образцом для дальнейшего развития человечества. Примечательно, что именно восточные греки заложили фундамент философии (Фалес из Милета), математики (Пифагор с острова Самос) и лирической поэзии (Сапфо с острова Лесбос). Своего апогея греческая цивилизация достигает в V веке до н. э. В это время стратег Перикл возводит грандиозные монументы Акрополя, скульпторы Фидий и Поликлет высекают свои бессмертные шедевры, Эсхил, Софокл и Еврипид пишут трагедии, Геродот и Фукидид составляют бесценную хронику древней истории, философы и ученые Зенон, Демокрит, Сократ прославляют торжество человеческого разума. Затем Греция дарит миру РЛЙКИХ философов Платона и Аристотеля, чьи бессмертные идеи третье тысячелетие питают философов его мира, основоположника геометрии, автора знаменитых "Начал" Евклида, величайшего математика древнего мира Архимеда.
Наука и искусство — грани творчества
И мы вновь возвращаемся в Древнюю Грецию... Из всех народов античности греки оказали самое сильное влияние на развитие европейской цивилизации. Вероятно, источник греческого гения и в том, что, входя в контакты с великими и более древними восточными цивилизациями, греки сумели не отвергать, а усваивать их уроки, дабы извлечь из них оригинальную культуру, ставшую основой и непревзойденным образцом для дальнейшего развития человечества. Примечательно, что именно восточные греки заложили фундамент философии (Фалес из Милета), математики (Пифагор с острова Самос) и лирической поэзии (Сапфо с острова Лесбос). Своего апогея греческая цивилизация достигает в V веке до н. э. В это время стратег Перикл возводит грандиозные монументы Акрополя, скульпторы Фидий и Поликлет высекают свои бессмертные шедевры, Эсхил, Софокл и Еврипид пишут трагедии, Геродот и Фукидид составляют бесценную хронику древней истории, философы и ученые Зенон, Демокрит, Сократ прославляют торжество человеческого разума. Затем Греция дарит миру РЛЙКИХ философов Платона и Аристотеля, чьи бессмертные идеи третье тысячелетие питают философов его мира, основоположника геометрии, автора знаменитых "Начал" Евклида, величайшего математика древнего мира Архимеда.
 Наука и искусство — грани творчества
Характерно, что наука, искусство и ремесло в то счастливое для человеческой культуры время не отгородились еще друг от друга высокими стенами. Ученый писал философские трактаты страстно и образно, как поэт, поэт непременно был философом, а ремесленник — истинным художником. Математика и астрономия входили в число "семи свободных искусств" наряду с музыкой и поэзией. Аристотель считал, что наука и искусство должны объединяться во всеобщей мудрости, но вопрос о том, на чьей стороне лежит обладание этой мудростью — на стороне поэтов или ученых,- уже назрел.
Была и другая эпоха единого взлета науки и искусства — эпоха Возрождения. Человечество вновь, через тысячу лет, открывало для себя забытые сокровища античной культуры, утверждало идеалы гуманизма, возрождало великую любовь к красоте мира и непреклонную волю познать этот мир. "Это был величайший прогрессивный переворот из всех пережитых до того времени человечеством, эпоха, которая нуждалась в титанах и которая породила титанов по силе мысли, страсти и характеру, по многосторонности и учености" (Ф. Энгельс, т. 20, с. 346).
Олицетворением многосторонних интересов человека эпохи Возрождения, символом слияния науки и искусства является гениальная фигура Леонардо да Винчи (1452-1519), итальянского живописца, скульптора, архитектора, теоретика искусств, математика, механика, гидротехника, инженера, изобретателя, анатома, биолога. Леонардо да Винчи — одна из загадок в истории человечества. Его разносторонний гений непревзойденного художника, великого ученого и неутомимого исследователя во все века повергал человеческий разум в смятение. Для самого Леонардо да Винчи наука и искусство были слиты воедино. Отдавая в "споре искусств" пальму первенства живописи, Леонардо да Винчи считал ее универсальным языком, наукой, которая подобно математике в формулах отображает в пропорциях и перспективе все многообразие и разумное начало природы. Оставленные Леонардо да Винчи около 7000 листов научных записок и поясняющих рисунков являются недосягаемым образцом синтеза науки и искусства. Листы эти долгое время кочевали из рук в руки, оставаясь неизданными, а за право обладать хоть несколькими из них на протяжении веков велись ожесточенные споры. Вот почему рукописи Леонардо рассеяны по библиотекам и музеям всего мира. Вместе с Леонардо да Винчи и другие титаны Возрождения, возможно, не столь универсальные, но не менее гениальные, воздвигали бессмертные памятники искусства и науки: Микеланджело, Рафаэль, Дюрер, Шекспир, Бэкон, Монтень, Коперник, Галилей...
Наука и искусство — грани творчества
Характерно, что наука, искусство и ремесло в то счастливое для человеческой культуры время не отгородились еще друг от друга высокими стенами. Ученый писал философские трактаты страстно и образно, как поэт, поэт непременно был философом, а ремесленник — истинным художником. Математика и астрономия входили в число "семи свободных искусств" наряду с музыкой и поэзией. Аристотель считал, что наука и искусство должны объединяться во всеобщей мудрости, но вопрос о том, на чьей стороне лежит обладание этой мудростью — на стороне поэтов или ученых,- уже назрел.
Была и другая эпоха единого взлета науки и искусства — эпоха Возрождения. Человечество вновь, через тысячу лет, открывало для себя забытые сокровища античной культуры, утверждало идеалы гуманизма, возрождало великую любовь к красоте мира и непреклонную волю познать этот мир. "Это был величайший прогрессивный переворот из всех пережитых до того времени человечеством, эпоха, которая нуждалась в титанах и которая породила титанов по силе мысли, страсти и характеру, по многосторонности и учености" (Ф. Энгельс, т. 20, с. 346).
Олицетворением многосторонних интересов человека эпохи Возрождения, символом слияния науки и искусства является гениальная фигура Леонардо да Винчи (1452-1519), итальянского живописца, скульптора, архитектора, теоретика искусств, математика, механика, гидротехника, инженера, изобретателя, анатома, биолога. Леонардо да Винчи — одна из загадок в истории человечества. Его разносторонний гений непревзойденного художника, великого ученого и неутомимого исследователя во все века повергал человеческий разум в смятение. Для самого Леонардо да Винчи наука и искусство были слиты воедино. Отдавая в "споре искусств" пальму первенства живописи, Леонардо да Винчи считал ее универсальным языком, наукой, которая подобно математике в формулах отображает в пропорциях и перспективе все многообразие и разумное начало природы. Оставленные Леонардо да Винчи около 7000 листов научных записок и поясняющих рисунков являются недосягаемым образцом синтеза науки и искусства. Листы эти долгое время кочевали из рук в руки, оставаясь неизданными, а за право обладать хоть несколькими из них на протяжении веков велись ожесточенные споры. Вот почему рукописи Леонардо рассеяны по библиотекам и музеям всего мира. Вместе с Леонардо да Винчи и другие титаны Возрождения, возможно, не столь универсальные, но не менее гениальные, воздвигали бессмертные памятники искусства и науки: Микеланджело, Рафаэль, Дюрер, Шекспир, Бэкон, Монтень, Коперник, Галилей...
 Леонардо да Винчи. Чертеж механизма для прокатки железных полос. Около 1490-1495. Рисунок пером из 'Атлантического кодекса'
И все-таки, несмотря на творческий союз науки и искусства и стремление ко "всеобщей мудрости", часто сочетавшиеся в лице одного гения, искусство античности и Возрождения шло впереди науки. В первую эпоху наука только зарождалась, а во вторую — "возрождаюсь", сбрасывала с себя путы долгого религиозного плена. Наука значительно дольше и мучительнее, чем искусство, проходит путь от рождения до зрелости. Потребовалось еще одно столетие — XVII век, принесший науке гениальные открытия Ньютона, Лейбница, Декарта, чтобы наука смогла заявить о себе в полный голос.
Следующий, XVIII век, был веком стремительного развития и торжества науки, "веком разума", эпохой безграничной веры в человеческий разум — эпохой Просвещения. Во многом просветители XVIII "века — Вольтер, Дидро, Руссо, Д'Аламбер, Шиллер, Лессинг, Кант, Локк, Свифт, Татищев, Ломоносов, Новиков — похожи на титанов Возрождения: универсальность таланта, могучая сила жизни. Но что отличало просветителей — это вера в торжество разума, культ разума как лекарства от всех бед и разочарование в силе нравственных идеалов. Пути науки и искусства расходятся, а в XIX веке между ними вырастает стена непонимания и отчужденности:
Леонардо да Винчи. Чертеж механизма для прокатки железных полос. Около 1490-1495. Рисунок пером из 'Атлантического кодекса'
И все-таки, несмотря на творческий союз науки и искусства и стремление ко "всеобщей мудрости", часто сочетавшиеся в лице одного гения, искусство античности и Возрождения шло впереди науки. В первую эпоху наука только зарождалась, а во вторую — "возрождаюсь", сбрасывала с себя путы долгого религиозного плена. Наука значительно дольше и мучительнее, чем искусство, проходит путь от рождения до зрелости. Потребовалось еще одно столетие — XVII век, принесший науке гениальные открытия Ньютона, Лейбница, Декарта, чтобы наука смогла заявить о себе в полный голос.
Следующий, XVIII век, был веком стремительного развития и торжества науки, "веком разума", эпохой безграничной веры в человеческий разум — эпохой Просвещения. Во многом просветители XVIII "века — Вольтер, Дидро, Руссо, Д'Аламбер, Шиллер, Лессинг, Кант, Локк, Свифт, Татищев, Ломоносов, Новиков — похожи на титанов Возрождения: универсальность таланта, могучая сила жизни. Но что отличало просветителей — это вера в торжество разума, культ разума как лекарства от всех бед и разочарование в силе нравственных идеалов. Пути науки и искусства расходятся, а в XIX веке между ними вырастает стена непонимания и отчужденности:
(Е. Баратынский)
 Дюрер. Построение эллипса как конического сечения. Рисунок из 'Руководства к измерению'. 1525. Нетрудно заметить, что эллипс у Дюрера имеет яйцевидную форму. Эта ошибка великого художника обусловлена, видимо, тем интуитивным соображением, что эллипс должен расширяться по мере расширения конуса
Дюрер. Построение эллипса как конического сечения. Рисунок из 'Руководства к измерению'. 1525. Нетрудно заметить, что эллипс у Дюрера имеет яйцевидную форму. Эта ошибка великого художника обусловлена, видимо, тем интуитивным соображением, что эллипс должен расширяться по мере расширения конуса
И. В. Гёте
 Наука и искусство — грани творчества
Искусству же отводилась роль падчерицы, и то, что эта падчерица вопреки прогнозам столетней давности всегда мешалась под ногами, только раззадоривало технократов.
Итак, атмосфера была накалена и оставалось только высечь искру, чтобы грянул взрыв. Это сделал английский писатель, физик по образованию Чарльз Сноу, выступив в мае 1959 г. в Кембридже (США) с лекцией "Две культуры и научная революция". Лекция Сноу взбудоражила научную и художественную общественность Запада: одни стали его убежденными сторонниками, другие — ярыми противниками, третьи пытались найти золотую середину. Основной мотив лекции — взаимное обособление науки и искусства, которое ведет к образованию двух самостоятельных культур — "научной" и "художественной". Между этими полюсами интеллектуальной жизни общества, по мнению Сноу, разверзлась пропасть взаимного непонимания, а иногда и враждебности и неприязни. Традиционная культура, не способная воспринять новейшие достижения науки, якобы неизбежно скатывается на путь антинаучности. С другой стороны, научно-технической среде, которая игнорирует художественные ценности, грозит эмоциональный голод и антигуманность. Сноу полагал, что причина разобщенности двух культур кроется в чрезмерной специализации образования на Западе, указывая при этом на Советский Союз, где система образования более универсальна, а значит, и нет проблемы взаимоотношения науки и искусства.
Здесь Сноу заблуждался. Практически одновременно, в сентябре 1959 г., на страницах наших газет вспыхнул знаменитый спор "физиков" и "лириков", как Условно обозначили представителей науки и искусства.
Дискуссия началась статьей писателя И. Эренбурга. Это был ответ на письмо некой студентки, рассказывавшей о своем конфликте с неким инженером, который, кроме физики, ничего другого в жизни не признает (и прежде всего искусства). Увидев в частном письме назревшую проблему, Эренбург поместил в "Комсомольской правде" обширный ответ. Писатель подчеркивал" что в условиях небывалого прогресса науки очень ясно, чтобы искусство не отставало от науки, чтобы место в обществе было "местом пророка, который жжет глаголом сердца людей, как говорил Пушкин, а не местом исправного писца или равнодушного декоратора". "Все понимают,- писал Эренбург,- что наука помогает понять мир; куда менее известно то познание, которое несет искусство. Ни социологи, ни психологи не могут дать того объяснения душевного мира человека, которое дает художник. Наука помогает узнать известные законы, но искусство заглядывает в душевные глубины, куда не проникают никакие рентгеновские лучи..."
Статья Эренбурга вызвала цепную реакцию мнений. Одна статья породила несколько других, и все вместе они грохотали, как лавина. У Эренбурга были союзники, но были и противники. Среди последних "прославился" инженер. Полетаев, который писал: "Мы живем творчеством разума, а не чувства, поэзией идей, теорией экспериментов, строительства. Это наша эпоха. Она требует всего человека без остатка, и некогда нам восклицать: ах, Бах! ах, Блок! Конечно же, они устарели и стали не в рост с нашей жизнью. Хотим мы этого или нет, они стали досугом, развлечением, а не жизнью... Хотим мы этого или нет, но поэты все меньше владеют нашими душами и все меньше учат нас. Самые увлекательные сказки преподносят сегодня наука и техника, смелый и беспощадный разум. Не признавать этого — значит не видеть, что делается вокруг. Искусство отходит на второй план — в отдых, в досуг, и я жалею об этом вместе с Эренбургом".
Наука и искусство — грани творчества
Искусству же отводилась роль падчерицы, и то, что эта падчерица вопреки прогнозам столетней давности всегда мешалась под ногами, только раззадоривало технократов.
Итак, атмосфера была накалена и оставалось только высечь искру, чтобы грянул взрыв. Это сделал английский писатель, физик по образованию Чарльз Сноу, выступив в мае 1959 г. в Кембридже (США) с лекцией "Две культуры и научная революция". Лекция Сноу взбудоражила научную и художественную общественность Запада: одни стали его убежденными сторонниками, другие — ярыми противниками, третьи пытались найти золотую середину. Основной мотив лекции — взаимное обособление науки и искусства, которое ведет к образованию двух самостоятельных культур — "научной" и "художественной". Между этими полюсами интеллектуальной жизни общества, по мнению Сноу, разверзлась пропасть взаимного непонимания, а иногда и враждебности и неприязни. Традиционная культура, не способная воспринять новейшие достижения науки, якобы неизбежно скатывается на путь антинаучности. С другой стороны, научно-технической среде, которая игнорирует художественные ценности, грозит эмоциональный голод и антигуманность. Сноу полагал, что причина разобщенности двух культур кроется в чрезмерной специализации образования на Западе, указывая при этом на Советский Союз, где система образования более универсальна, а значит, и нет проблемы взаимоотношения науки и искусства.
Здесь Сноу заблуждался. Практически одновременно, в сентябре 1959 г., на страницах наших газет вспыхнул знаменитый спор "физиков" и "лириков", как Условно обозначили представителей науки и искусства.
Дискуссия началась статьей писателя И. Эренбурга. Это был ответ на письмо некой студентки, рассказывавшей о своем конфликте с неким инженером, который, кроме физики, ничего другого в жизни не признает (и прежде всего искусства). Увидев в частном письме назревшую проблему, Эренбург поместил в "Комсомольской правде" обширный ответ. Писатель подчеркивал" что в условиях небывалого прогресса науки очень ясно, чтобы искусство не отставало от науки, чтобы место в обществе было "местом пророка, который жжет глаголом сердца людей, как говорил Пушкин, а не местом исправного писца или равнодушного декоратора". "Все понимают,- писал Эренбург,- что наука помогает понять мир; куда менее известно то познание, которое несет искусство. Ни социологи, ни психологи не могут дать того объяснения душевного мира человека, которое дает художник. Наука помогает узнать известные законы, но искусство заглядывает в душевные глубины, куда не проникают никакие рентгеновские лучи..."
Статья Эренбурга вызвала цепную реакцию мнений. Одна статья породила несколько других, и все вместе они грохотали, как лавина. У Эренбурга были союзники, но были и противники. Среди последних "прославился" инженер. Полетаев, который писал: "Мы живем творчеством разума, а не чувства, поэзией идей, теорией экспериментов, строительства. Это наша эпоха. Она требует всего человека без остатка, и некогда нам восклицать: ах, Бах! ах, Блок! Конечно же, они устарели и стали не в рост с нашей жизнью. Хотим мы этого или нет, они стали досугом, развлечением, а не жизнью... Хотим мы этого или нет, но поэты все меньше владеют нашими душами и все меньше учат нас. Самые увлекательные сказки преподносят сегодня наука и техника, смелый и беспощадный разум. Не признавать этого — значит не видеть, что делается вокруг. Искусство отходит на второй план — в отдых, в досуг, и я жалею об этом вместе с Эренбургом".
 Наука и искусство — грани творчества
Возмущенные "лирики" и рассудительные "физики" на все лады склоняли Полетаева[7]. Появились и статьи-крики: "Я с тобой, инженер Полетаев!", появились и самобичующие стихи:
Наука и искусство — грани творчества
Возмущенные "лирики" и рассудительные "физики" на все лады склоняли Полетаева[7]. Появились и статьи-крики: "Я с тобой, инженер Полетаев!", появились и самобичующие стихи:
(Б. Слуцкий)
 Наука и искусство — грани творчества
Что же сближает и что разъединяет науку и искусство? Прежде всего, наука и искусство — две грани одного и того же процесса — творчества. Наука и искусство — это дороги, а часто и крутые нехоженые тропы к вершинам человеческой культуры. Таким образом, цель и у науки, и у искусства одна — торжество человеческой культуры, хотя достигается она разными путями. "И в науке, и в литературе творчество не просто радость, сданная с риском,- это жестокая необходимость,- говорит американский писатель, физик по образованию Митчел Уилсон (1913-1973).- И ученый, и писатель в какой бы обстановке они ни росли, в конце концов находят свое призвание, словно под влиянием той жe силы, которая заставляет подсолнечник поворачиваться к солнцу".
Наука и искусство — грани творчества
Что же сближает и что разъединяет науку и искусство? Прежде всего, наука и искусство — две грани одного и того же процесса — творчества. Наука и искусство — это дороги, а часто и крутые нехоженые тропы к вершинам человеческой культуры. Таким образом, цель и у науки, и у искусства одна — торжество человеческой культуры, хотя достигается она разными путями. "И в науке, и в литературе творчество не просто радость, сданная с риском,- это жестокая необходимость,- говорит американский писатель, физик по образованию Митчел Уилсон (1913-1973).- И ученый, и писатель в какой бы обстановке они ни росли, в конце концов находят свое призвание, словно под влиянием той жe силы, которая заставляет подсолнечник поворачиваться к солнцу".
 Рафаэль. Афинская школа. 1510-1511. Фреска Ватиканского дворца в Риме. Это величайшее творение Рафаэля является торжественным гимном науке. В центре фрески изображены Платон и Аристотель, внизу слева — Пифагор, справа — Евклид (или Архимед)
Задача научного творчества состоит в нахождении объективных законов природы, которые, разумеется, не зависят от индивидуальности ученого. Поэтому творец науки стремится не к самовыражению, а к установлению независимых от него истин, ученый обращается к разуму, а не к эмоциям. Более того, ученый понимает, что его произведения носят преходящий характер и через некоторое время будут вытеснены новыми теориями. Хорошо об этом сказал Эйнштейн: "Лучший жребий физической теории — послужить основой для более общей теории, оставаясь в ней предельным случаем".
Никто, кроме людей, занимающихся историей науки, не читает труды ученых в подлинниках. Да и очень трудно сегодня разобраться, скажем, в "Математических началах натуральной философии" Ньютона, хотя законы Ньютона и известны каждому. Дело в том, что язык науки очень быстро меняется и для новых поколений становится непонятным. Таким образом, в науке остаются жить лишь объективные законы, открытые ученым, но не субъективные средства их выражения.
В искусстве все наоборот. Задача художественного творчества — это постижение мира на основе субъективных мыслей и переживаний создателя. Произведение искусства всегда индивидуально, поэтому оно более понятно, чем научный труд. Истинные шедевры искусства живут вечно — и Гомер, и Бетховен, и Пушкин будут звучать, пока существует человечество, они не устаревают и не вытесняются новыми художественными произведениями.
Правда, ученые имеют свое преимущество. Ученый может проверить истинность своих теорий на практике, он спокоен и уверен в том, что его творения ложатся кирпичиками в огромном здании науки. Иное дело — художник, который не имеет объективных критериев для проверки истинности своих произведений, кроме внутреннего интуитивного убеждения. Даже когда художник уверен в своей правоте, его гложет червь сомнения относительно избранной формы и ее вопл щения. Поэтому, даже когда произведение создано" художник вынужден бороться за свое признание, постоянно заявлять о себе. Не случайно и Гораций, и Державин, и Пушкин не скупятся на слова в оценке своего творчества:
Рафаэль. Афинская школа. 1510-1511. Фреска Ватиканского дворца в Риме. Это величайшее творение Рафаэля является торжественным гимном науке. В центре фрески изображены Платон и Аристотель, внизу слева — Пифагор, справа — Евклид (или Архимед)
Задача научного творчества состоит в нахождении объективных законов природы, которые, разумеется, не зависят от индивидуальности ученого. Поэтому творец науки стремится не к самовыражению, а к установлению независимых от него истин, ученый обращается к разуму, а не к эмоциям. Более того, ученый понимает, что его произведения носят преходящий характер и через некоторое время будут вытеснены новыми теориями. Хорошо об этом сказал Эйнштейн: "Лучший жребий физической теории — послужить основой для более общей теории, оставаясь в ней предельным случаем".
Никто, кроме людей, занимающихся историей науки, не читает труды ученых в подлинниках. Да и очень трудно сегодня разобраться, скажем, в "Математических началах натуральной философии" Ньютона, хотя законы Ньютона и известны каждому. Дело в том, что язык науки очень быстро меняется и для новых поколений становится непонятным. Таким образом, в науке остаются жить лишь объективные законы, открытые ученым, но не субъективные средства их выражения.
В искусстве все наоборот. Задача художественного творчества — это постижение мира на основе субъективных мыслей и переживаний создателя. Произведение искусства всегда индивидуально, поэтому оно более понятно, чем научный труд. Истинные шедевры искусства живут вечно — и Гомер, и Бетховен, и Пушкин будут звучать, пока существует человечество, они не устаревают и не вытесняются новыми художественными произведениями.
Правда, ученые имеют свое преимущество. Ученый может проверить истинность своих теорий на практике, он спокоен и уверен в том, что его творения ложатся кирпичиками в огромном здании науки. Иное дело — художник, который не имеет объективных критериев для проверки истинности своих произведений, кроме внутреннего интуитивного убеждения. Даже когда художник уверен в своей правоте, его гложет червь сомнения относительно избранной формы и ее вопл щения. Поэтому, даже когда произведение создано" художник вынужден бороться за свое признание, постоянно заявлять о себе. Не случайно и Гораций, и Державин, и Пушкин не скупятся на слова в оценке своего творчества:
 Наука и искусство — грани творчества
Наука и искусство — грани творчества
Наука и искусство — это два крыла, которые поднимают вас к Богу.Мы уже отмечали в главе 1 познавательную функцию искусства. Но важно подчеркнуть, что научное и художественное познание мира как бы дополняют друг друга, но не могут быть сведены одно к другому или выведены одно из другого. Видимо, этим и объясняется тот факт, что не сбылся мрачный прогноз Гегеля о судьбе искусства в эпоху торжества разума. В век научно-технической революции искусство не только сохраняет свои высокие позиции в человеческой культуре, но и в чем-то приобретает даже более высокий авторитет. Ведь наука со своими однозначными ответами не может заполнить человеческую душу до конца, оставляя место для свободных фантазий искусства. "Причина, почему искусство может нас обогатить,- писал Ни лье Бор,- заключается в его способности напоминать нам о гармониях, недоступных для систематического анализа..." "- Мне лично,- заявил Эйнштейн,- ощущение высшего счастья дают произведения искусства, в них я черпаю такое духовное блаженство, как ни в какой другой области.М. X. А. Бехаулла
 Г. Эрни. Эйнштейн. 1954. Фрагмент фрески Музея этнографии в Невшателе. Швейцария
Г. Эрни. Эйнштейн. 1954. Фрагмент фрески Музея этнографии в Невшателе. Швейцария
Единственная вещь, которая доставляет мне удовольствие, кроме моей работы, моей скрипки и моей яхты,- это одобрение моих товарищей.— Профессор! — воскликнул я.- Ваши слова изумит меня как настоящее откровение! Не то чтобы я да,нибудь сомневался в Вашей восприимчивости искусству: я слишком часто видел, как на Вас действуют звуки хорошей музыки и с каким увлечением Вы сами играете на скрипке. Но даже в эти минуты, когда Вы, словно отрешившись от мира, целиком отдавались художественному впечатлению, я говорил себе: в жизни Энштейна это лишь чудесная арабеска, и я никогда бы не подумал, что это украшение жизни является для Вас источником высшего счастья. — В настоящий момент я думал главным образом о поэзии. — О поэзии вообще? Или о каком-нибудь определенном поэте? — Я имел в виду поэзию вообще. Но если Вы спросите, кто вызывает сейчас во мне наибольший интерес, то я отвечу: Достоевский! Он повторил это имя несколько раз с особенным ударением, и, чтобы пресечь в корне всякие возражения, он добавил:- Достоевский дает мне больше, чем любой научный мыслитель, больше, чем Гаусс!" Эти слова Эйнштейна, сказанные им в беседе с немецким публицистом начала XX века А. Мошковским, вот уже более полувека будоражат умы и ученых, и художников. Сотни статей комментируют несколько слов великого физика, выдвигаются различные гипотезы и толкования, проводятся параллели между мечтой Достоевского о социальной и моральной гармонии и поисками универсальной гармонии мироздания, которой Эйнштейн посвятил свою жизнь, но в одном сходятся все: современная наука не может развиваться без способности ученых к образному мышлению. Воспитывается же образное мышление искусством. Тема "Эйнштейн и Достоевский" стала олицетворением проблемы взаимодействия науки и искусства, и те, кто заинтересуется ею, могут прочитать прекрасную статью профессора Б. Г. Кузнецова под тем же названием (Наука и жизнь, 1965, № 6).А. Эйнштейн
Без веры в то, что возможно охватить реальность нашими теоретическими построениями, без веры во внутреннюю гармонию нашего мира, не могло бы быть никакой науки. Эта вера есть и всегда останется основным мотивом всякого научного творчества.А. Эйнштейн
Красота и истина суть одно и то же, ибо прекрасное должно быть истинным в самом себе. Но столь же верно, что истинное отличается от прекрасного.Есть и еще одна причина, объясняющая обострение интереса ученых XX века к искусству. Дело в том, что современная наука перешагнула рубеж собственной прикосновенности. До Эйнштейна механика Ньютона казалась всесильной и незыблемой. Жозеф Лагранж (1736-1813) — "величественная пирамида математических наук", как сказал о нем Наполеон,- завидовал Ньютону: "Ньютон был счастливейшим из смертных, существует только одна Вселенная и Ньютон открыл ее законы". Но вот пришел Эйнштейн и построил новую механику, в которой механика Ньютона оказалась пре, дельным случаем. Последним бастионом "непогрешимых и вечных" истин в науке оставалась математика. "Среди все наук,- писал Эйнштейн,- математика пользуется особенным уважением; основанием этому служит то единственное обстоятельство, что ее положения абсолютно верны и неоспоримы, в то время как положения других наук до известной степени спорны, и всегда существует опасность их опровержения новыми открытиями". Однако открытия XX века вынудили математиков осознать, что и сама математика, и математические законы в других науках не есть абсолютные истины. В 1931 г. математику постиг удар ужасающей силы: 25-летним австрийским логиком Куртом Геделем была доказана знаменитая теорема, согласно которой в рамках любой системы аксиом существуют неразрешимые утверждения, ни доказать, ни опровергнуть которые невозможно. Теорема Геделя вызвала смятение. Вопрос об основаниях математики привел к таким трудностям, что ее крупнейший представитель Герман Вейль (1885-1955) безрадостно констатировал: "...мы не знаем, в каком направлении будет найдено его последнее решение, и даже не знаем, можно ли вообще ожидать объективного ответа на него". Разумеется, катастрофы не произошло и наука не остановилась. Наоборот, ученые еще раз убедились в том, что наука находится в постоянном движении, что конечная цель познания — "абсолютная истина" — недостижима. А как хотелось бы ученому, чтобы его любимое детище жило вечно! И вот ученые обращаются к искусству как сокровищнице вечных и неподвластных времени ценностей. В искусстве не так, как в науке: истинное произведение искусства есть законченный и неприкосновенный продукт творчества художника. Научный закон существует вне теории и вне ученого, тогда как закон художественного произведения рождается вместе с самим произведением. Сначала художник свободно диктует произведению свою волю, но по мере завершения работы "детище" обретает власть над создателем. Произведение начинает терзать создателя, и он мучительно ищет тот единственный последний штрих, найти который дано лишь большому мастеру. С этим штрихом обрывается власть художника над своим созданием, он уже бессилен изменить в нем что-либо, и оно отправляется в самостоятельный путь во времени. Вот этот несбыточный идеал вечного совершенства, досягаемый для научного знания, и является тем магнитом, который постоянно притягивает ученого к искусству. Но и наука притягивает искусство. Это выражается только в том, что появляются новые "технические" виды искусств, такие, как кино и телевидение, не только в том, что ученый все чаще становится объектом внимания художника, но и в изменении самого мировоззрения художника. Замечательного русского поэта ученого Валерия Брюсова (1873-1924) можно назвать родоначальником "научной поэзии". В предисловии к своему сборнику стихов "Дали" Брюсов писал: "...поэт должен по возможности стоять на уровне современного научного знания и вправе мечтать о читателе с таким же миросозерцанием. Было бы неправильно, если бы поэзия навеки должна была ограничиться, с одной стороны, мотивами о любви и природе, с другой — гражданскими темами. Все, что интересует и волнует современного человека, имеет право на отражение в поэзии". Стихотворение Брюсова "Мир N измерений" нам хочется привести здесь полностью :Г. В. Ф. Гегель
 А. Леонов. Солнечная корона. 1965. Картины летчика-космонавта СССР Алексея Леонова являются современным символом единения науки, техники и искусства
Итак, взаимоотношение науки и искусства — сложный и трудный процесс. В науке, где требуется ум, нужна и фантазия, иначе наука становится сухой и вырождается в схоластику. В искусстве, где требуется фантазия, нужен и ум, ибо без систематического познания профессионального мастерства настоящее искусство невозможно. Наука и искусство проходят путь от нерасчлененного единства (античность и Возрождение) через противопоставление противоположностей (эпоха Просвещения) к высшему синтезу, контуры которого только проглядывают сегодня.
Сегодня сбываются слова писателя Горького: "Наука, становясь все более чудесной и мощной силой, сама, во всем ее объеме, становится все более величественной и победоносной поэзией познания".
И хочется верить, что сбудутся слова ученого М. Волькенштейна: "Единство науки и искусства — важнейший залог последующего развития культуры. Нужно искать и культивировать то, что объединяет науку и искусство, а не разъединяет их. За научно-технической революцией должна последовать новая эпоха Возрождения".
А. Леонов. Солнечная корона. 1965. Картины летчика-космонавта СССР Алексея Леонова являются современным символом единения науки, техники и искусства
Итак, взаимоотношение науки и искусства — сложный и трудный процесс. В науке, где требуется ум, нужна и фантазия, иначе наука становится сухой и вырождается в схоластику. В искусстве, где требуется фантазия, нужен и ум, ибо без систематического познания профессионального мастерства настоящее искусство невозможно. Наука и искусство проходят путь от нерасчлененного единства (античность и Возрождение) через противопоставление противоположностей (эпоха Просвещения) к высшему синтезу, контуры которого только проглядывают сегодня.
Сегодня сбываются слова писателя Горького: "Наука, становясь все более чудесной и мощной силой, сама, во всем ее объеме, становится все более величественной и победоносной поэзией познания".
И хочется верить, что сбудутся слова ученого М. Волькенштейна: "Единство науки и искусства — важнейший залог последующего развития культуры. Нужно искать и культивировать то, что объединяет науку и искусство, а не разъединяет их. За научно-технической революцией должна последовать новая эпоха Возрождения".
4. Симметрия, пропорция, гармония — слагаемые прекрасного
Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.Г. Вейль
Ничто не нравится, кроме красоты, в красоте — ничто, кроме форм, в формах — ничто, кроме пропорций, в пропорциях — ничто, кроме числа.А. Августин
Гармония — магическое слово, сулящее всевозможные блага, это синтетическое понятие, слово завтрашнего дня."Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?" (Л. Толстой. "Отрочество"). Вместе с Николенькой Иртеньевым из трилогии Льва Толстого задумаемся и мы над тем, почему в природе царит симметрия. Почему симметрично все Живое от микроорганизмов до человека? Наконец, почему симметричное часто ассоциируется с прекрасным?Ле Корбюзье
 Бабочка парусник махаон — прекрасный пример билатеральной симметрии в природе
На первые два вопроса ответ существует: господство симметрии в природе прежде всего объясняется силой Тяготения, действующей во всей Вселенной. Действием Тяготения или отсутствием такового объясняется то, что и Космические тела, плывущие во Вселенной, и Микроорганизмы, взвешенные в воде, обладают высшей Формой симметрии — сферической (при любом повороте относительно центра фигура совпадает сама с собой). Все организмы, растущие в прикрепленном состоянии (деревья) или живущие на дне океана (морские звезды), т. е. организмы, для которых направление силы тяжести является решающим, имеют ось симметрии (множество всевозможных поворотов вокруг центра сужается д0 множества всех поворотов вокруг вертикальной оси). Наконец, для животных, способных передвигаться в воде, воздухе или по земле, кроме направления силы тяжести, важным оказывается и направление движения животного. Такие животные могут обладать только плоскостью симметрии, которая определяется векторами силы тяжести и направления движения. Биологи эту плоскость симметрии называют билатеральной, а тип симметрии — зеркальным. Ясно, что в случае асимметричного развития животного поворот в одну из сторон был бы для него затруднен и естественным для животного стало бы не прямолинейное, а круговое движение. Хождение же по кругу рано или поздно закончится трагически для животного. Билатеральной симметрией обладает, например, автомобиль, одинаково хорошо поворачивающий и вправо, и влево, чего нельзя сказать о мотоцикле с коляской, который такой симметрией не обладает и постепенно вытесняется автомобилем и своим двухколесным (зеркально-симметричным) собратом.
Любопытно, что переход от сферической симметрии у низших животных к зеркальной у высших (в частности, у человека) пытались объяснить еще древние греки. Так, в диалоге Платона "Пир" Аристофан рассказывает о том, что первоначально люди были круглыми, "спина не отличалась от груди, рук было четыре, ног столько же, сколько и рук, и у каждого на круглой шее два лица, совершенно одинаковых... Страшные своей силой и мощью, они питали великие замыслы и посягали даже на власть богов...
И вот Зевс и прочие боги стали совещаться, как поступить с ними... Наконец, Зевс, насилу кое-что придумав, говорит:
— Кажется, я нашел способ и сохранить людей, и положить конец их буйству, уменьшив их силу. Я разрежу каждого из них пополам, и тогда они, во-первых, станут слабее, а во-вторых, полезней для нас, потому что число их увеличится. И ходить они будут прямо, на двух ногах. А если они и после этого не угомонятся и начнут буйствовать, я, сказал он, рассеку их пополам снова, и они запрыгают у меня на одной ножке".
Симметрия господствует на Земле благодаря силе тяготения. Более того, поскольку эта сила действует повсюду во Вселенной, то и предполагаемые космические пришельцы не могут быть безудержно чудовищами, как их порой изображают, а обязательно должны быть симметричными.
Таким образом, мы подошли к самому трудному вопросу: "почему симметрия приятна для глаз?" Этот вопрос является составной частью более широкой проблемы: существуют ли объективные законы прекрасного? В чем тайна прекрасного, которая делает красоту предметом поклонения?
Бабочка парусник махаон — прекрасный пример билатеральной симметрии в природе
На первые два вопроса ответ существует: господство симметрии в природе прежде всего объясняется силой Тяготения, действующей во всей Вселенной. Действием Тяготения или отсутствием такового объясняется то, что и Космические тела, плывущие во Вселенной, и Микроорганизмы, взвешенные в воде, обладают высшей Формой симметрии — сферической (при любом повороте относительно центра фигура совпадает сама с собой). Все организмы, растущие в прикрепленном состоянии (деревья) или живущие на дне океана (морские звезды), т. е. организмы, для которых направление силы тяжести является решающим, имеют ось симметрии (множество всевозможных поворотов вокруг центра сужается д0 множества всех поворотов вокруг вертикальной оси). Наконец, для животных, способных передвигаться в воде, воздухе или по земле, кроме направления силы тяжести, важным оказывается и направление движения животного. Такие животные могут обладать только плоскостью симметрии, которая определяется векторами силы тяжести и направления движения. Биологи эту плоскость симметрии называют билатеральной, а тип симметрии — зеркальным. Ясно, что в случае асимметричного развития животного поворот в одну из сторон был бы для него затруднен и естественным для животного стало бы не прямолинейное, а круговое движение. Хождение же по кругу рано или поздно закончится трагически для животного. Билатеральной симметрией обладает, например, автомобиль, одинаково хорошо поворачивающий и вправо, и влево, чего нельзя сказать о мотоцикле с коляской, который такой симметрией не обладает и постепенно вытесняется автомобилем и своим двухколесным (зеркально-симметричным) собратом.
Любопытно, что переход от сферической симметрии у низших животных к зеркальной у высших (в частности, у человека) пытались объяснить еще древние греки. Так, в диалоге Платона "Пир" Аристофан рассказывает о том, что первоначально люди были круглыми, "спина не отличалась от груди, рук было четыре, ног столько же, сколько и рук, и у каждого на круглой шее два лица, совершенно одинаковых... Страшные своей силой и мощью, они питали великие замыслы и посягали даже на власть богов...
И вот Зевс и прочие боги стали совещаться, как поступить с ними... Наконец, Зевс, насилу кое-что придумав, говорит:
— Кажется, я нашел способ и сохранить людей, и положить конец их буйству, уменьшив их силу. Я разрежу каждого из них пополам, и тогда они, во-первых, станут слабее, а во-вторых, полезней для нас, потому что число их увеличится. И ходить они будут прямо, на двух ногах. А если они и после этого не угомонятся и начнут буйствовать, я, сказал он, рассеку их пополам снова, и они запрыгают у меня на одной ножке".
Симметрия господствует на Земле благодаря силе тяготения. Более того, поскольку эта сила действует повсюду во Вселенной, то и предполагаемые космические пришельцы не могут быть безудержно чудовищами, как их порой изображают, а обязательно должны быть симметричными.
Таким образом, мы подошли к самому трудному вопросу: "почему симметрия приятна для глаз?" Этот вопрос является составной частью более широкой проблемы: существуют ли объективные законы прекрасного? В чем тайна прекрасного, которая делает красоту предметом поклонения?
 Симметрия, пропорция, гармония — слагаемые прекрасного
"Человек останавливается, пораженный, перед такими вещами, какие не могут играть никакой роли в его жизни: перед отражениями воды, которые нельзя схватить, перед отвесными скалами, которые нельзя засеять, перед удивительным цветом неба",- писал английский теоретик искусства Джон Рескин (1819-1900). Сколько усилий ума и сердца потрачено на постижение этой тайны! Вместе с истиной (наукой) красота (искусство) влекла за собой лучших представителей всех времен и народов. Но в отличие от истины красота понятна человеку даже тогда, когда ее внутренние закономерности остаются непознанными. Так, каждый достаточно ясно видит разницу между правильными и неправильными чертами человеческого лица, но до сих пор никто не может сформулировать точно закон, которому подчинена форма красивого лица, хотя такие попытки делались еще в глубокой древности. Или, скажем, струи наклонно бьющих фонтанов привлекают правильностью и красотою своих линий, хотя отнюдь не каждый знает, что это параболы, и тем более не в состоянии написать их уравнения. Пользуясь тем, что красота часто понятна интуитивно, без предварительной подготовки, люди искусства порой не хотят говорить о законах красоты, считая, что наука и искусство несовместимы. Суть этой неприязни искусства к науке заключена в убеждении, что математически точный закон обедняет искусство, лишает его некоей таинственности, вносит будни в праздник поэзии.
Разумеется, это не так. И лучшие представители искусства это ясно понимали. "Красота... следует своим собственным законам",- считал Шиллер. Гёте подчеркивал: "Для прекрасного требуется закон, который входит в явление". О людях науки говорить не приходится. "Если ты хочешь наслаждаться искусством, писал К. Маркс,- то ты должен быть художество образованным человеком"*.
* (Маркс К., Энгельс Ф. Из ранних произведений.- М., 1956.- с. 620. )
Симметрия, пропорция, гармония — слагаемые прекрасного
"Человек останавливается, пораженный, перед такими вещами, какие не могут играть никакой роли в его жизни: перед отражениями воды, которые нельзя схватить, перед отвесными скалами, которые нельзя засеять, перед удивительным цветом неба",- писал английский теоретик искусства Джон Рескин (1819-1900). Сколько усилий ума и сердца потрачено на постижение этой тайны! Вместе с истиной (наукой) красота (искусство) влекла за собой лучших представителей всех времен и народов. Но в отличие от истины красота понятна человеку даже тогда, когда ее внутренние закономерности остаются непознанными. Так, каждый достаточно ясно видит разницу между правильными и неправильными чертами человеческого лица, но до сих пор никто не может сформулировать точно закон, которому подчинена форма красивого лица, хотя такие попытки делались еще в глубокой древности. Или, скажем, струи наклонно бьющих фонтанов привлекают правильностью и красотою своих линий, хотя отнюдь не каждый знает, что это параболы, и тем более не в состоянии написать их уравнения. Пользуясь тем, что красота часто понятна интуитивно, без предварительной подготовки, люди искусства порой не хотят говорить о законах красоты, считая, что наука и искусство несовместимы. Суть этой неприязни искусства к науке заключена в убеждении, что математически точный закон обедняет искусство, лишает его некоей таинственности, вносит будни в праздник поэзии.
Разумеется, это не так. И лучшие представители искусства это ясно понимали. "Красота... следует своим собственным законам",- считал Шиллер. Гёте подчеркивал: "Для прекрасного требуется закон, который входит в явление". О людях науки говорить не приходится. "Если ты хочешь наслаждаться искусством, писал К. Маркс,- то ты должен быть художество образованным человеком"*.
* (Маркс К., Энгельс Ф. Из ранних произведений.- М., 1956.- с. 620. )
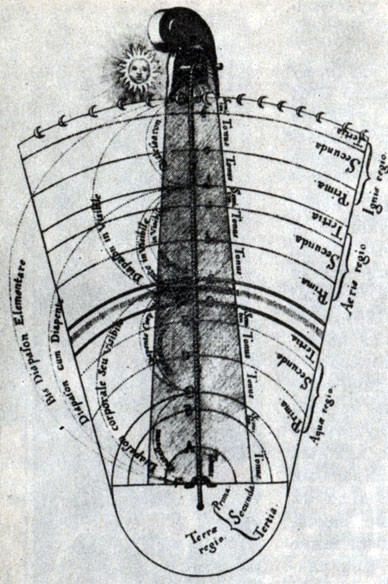 Монохорд, или Гармония мира. Иллюстрация к трактату Р. Флудда 'О космическом двуединстве'. Франкфурт. 1617. Со времен Пифагора музыка была для греков синонимом математической гармонии мироздания
Поиски объективных законов прекрасного велись с незапамятных времен, и первые находки здесь закономерно выпали на долю древних греков. Античная эстетика не только выработала систем взглядов, которые характеризуют эстетическое сознание древних греков, но и оказала решающее влияние на все последующее развитие эстетической культуры человечества.
Греки верили, что все мироздание по своей глубокой сущности прекрасно. Поэтому Вселенную они называли словом "космос", что значит "прекрасно устроенный". А коль скоро красота лежит в основе космоса, то искусству остается только открыть эти объективные законы красоты и руководствоваться ими.
Какие же объективные критерии прекрасного были выработаны в античную эпоху? Прежде всего, это категория меры, включающая в себя как составные элементы понятия симметрии, пропорциональности и ритма, и категория гармонии. Мера характеризует общие принципы строения, целостность предмета, тогда как понятия симметрии, пропорциональности и ритма добавляют к характеристике целого тот или иной специфической оттенок. Исходя из меры, определяет красоту Аристотель: "Красота заключается в величине и порядке, вследствие чего ни чрезмерно малое существо не могло бы стать прекрасным, так как обозрение его, сделанное в почти незаметное время, сливается, ни чрезмерно большое, так как обозрение его совершается не сразу, но единство и целостность его теряются для обозревающих.. ."
Принцип меры носил у древних греков не только формальный структурно-математический характер. Мера для греков — это прежде всего человек, это норма поведения, закон мироздания, структура художественного произведения. Греческое искусство возвеличивало человека даже тогда, когда говорило о богах.
Понятия симметрии, пропорции и ритма играли важную роль в познании греками пространственно-временной структуры окружающего мира. Закономерность и красота мироздания раскрывались перед ними и в симметрии живых организмов, и в пропорциональности человеческого тела, и в ритмах чередования дня и ночи, смены времен года и т. д. Вся античная архитектура и скульптура воплощали в себя эти принципы красоты. Блестящими примерами тому служат и величественные пропорции Парфенона, и знаменитый "Канон" Поликлета — скульптура и теоретический трактат, в которых автор попытался воплотить идеальные" по его мнению, пропорции мужского тела.
Монохорд, или Гармония мира. Иллюстрация к трактату Р. Флудда 'О космическом двуединстве'. Франкфурт. 1617. Со времен Пифагора музыка была для греков синонимом математической гармонии мироздания
Поиски объективных законов прекрасного велись с незапамятных времен, и первые находки здесь закономерно выпали на долю древних греков. Античная эстетика не только выработала систем взглядов, которые характеризуют эстетическое сознание древних греков, но и оказала решающее влияние на все последующее развитие эстетической культуры человечества.
Греки верили, что все мироздание по своей глубокой сущности прекрасно. Поэтому Вселенную они называли словом "космос", что значит "прекрасно устроенный". А коль скоро красота лежит в основе космоса, то искусству остается только открыть эти объективные законы красоты и руководствоваться ими.
Какие же объективные критерии прекрасного были выработаны в античную эпоху? Прежде всего, это категория меры, включающая в себя как составные элементы понятия симметрии, пропорциональности и ритма, и категория гармонии. Мера характеризует общие принципы строения, целостность предмета, тогда как понятия симметрии, пропорциональности и ритма добавляют к характеристике целого тот или иной специфической оттенок. Исходя из меры, определяет красоту Аристотель: "Красота заключается в величине и порядке, вследствие чего ни чрезмерно малое существо не могло бы стать прекрасным, так как обозрение его, сделанное в почти незаметное время, сливается, ни чрезмерно большое, так как обозрение его совершается не сразу, но единство и целостность его теряются для обозревающих.. ."
Принцип меры носил у древних греков не только формальный структурно-математический характер. Мера для греков — это прежде всего человек, это норма поведения, закон мироздания, структура художественного произведения. Греческое искусство возвеличивало человека даже тогда, когда говорило о богах.
Понятия симметрии, пропорции и ритма играли важную роль в познании греками пространственно-временной структуры окружающего мира. Закономерность и красота мироздания раскрывались перед ними и в симметрии живых организмов, и в пропорциональности человеческого тела, и в ритмах чередования дня и ночи, смены времен года и т. д. Вся античная архитектура и скульптура воплощали в себя эти принципы красоты. Блестящими примерами тому служат и величественные пропорции Парфенона, и знаменитый "Канон" Поликлета — скульптура и теоретический трактат, в которых автор попытался воплотить идеальные" по его мнению, пропорции мужского тела.
 Поликлет. Дорифор (копьеносец), или Канон. Ок. 440 до н. э. Римская копия с утраченного оригинала. В пропорциях статуи воплощен закон золотого сечения
Поликлет. Дорифор (копьеносец), или Канон. Ок. 440 до н. э. Римская копия с утраченного оригинала. В пропорциях статуи воплощен закон золотого сечения
 Приведен математический анализ пропорций Канона
Приведен математический анализ пропорций Канона
Ведь назначение и цель гармонии — упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту.Не менее содержательным было и античное понятие гармонии. В древнегреческой философии гармония в противоположность хаосу означала организованность Вселенной. Гармония трактовалась не как внешнее объединение разрозненных частей, а как внутреннее их единство, как единство противоположностей предела и беспредельного, частей и целого. Пифагор, не только великий математик, но и основоположник античной эстетики, считал, что гармония "внутренне присуща вещам, из которых составлен мир". Ее только нужно извлечь из вещей, что и делает художник благодаря своему мастерству, уму и таланту. В главе 7 мы познакомимся с пифагорейским учением о гармонии сфер, согласно которому расстояния между планетами соответствуют числовым отношениям музыкальной гаммы и весь космос звучит единым благозвучным аккордом. Вообще, пифагорейцы благоговели перед количественной картиной мира, выраженной в числе. Это была своеобразная философия числа, о которой мы расскажем в главе 5. Понятию гармонии древнегреческий философ Платон придал социальное значение, рассматривая гармонию как совокупность физических достоинств и высоких нравственных принципов человека-гражданина. Отсюда пошло выражение "гармонически развитая личность". Разумеется, античная эстетика не решила всех проблем. Так, оставалось непонятным, откуда возникает субъективизм и релятивизм в эстетических оценках (типа "На вкус и цвет товарищей нет"), если прекрасное едино. Однако античное учение о мере и гармонии как объективных признаках прекрасного прошло через эпохи средневековья, Возрождения, Просвещения вплоть до наших дней, хотя происхождение красоты в каждую эпоху трактовалось по-своему. Во времена средневековья для философа Фомы Аквинского красота заключалась в боге, который "именуется прекрасным как причина гармонии и ясности". Как отголоски этой веры в божественное происхождение прекрасного сохранились выражения "ангельское лицо", "божественный голос", "чудесная погода". Для ренессансного гуманиста Альберти гармония есть "абсолютное и первичное начало природы". Французские просветители-материалисты также подчеркивали природную основу красоты. С тех пор как в 1844 г. К. Маркс впервые высказался о "законах красоты" (см. с. 26), о них заговорили как о чем-то давно известном, не утруждая себя необходимостью раскрыть содержание этих законов. Между тем дальше того, что в данном вопросе эстетики разделились на два противоборствующих лагеря "природников" и "общественников", дело не пошло. Проблема законов красоты в эстетике скорее только поставлена, но не решена. Однако то, что законы меры и гармонии являются объективными законами прекрасного, по которым природа стихийно, а человек сознательно формируют материю, создавая совершенные формы, является бесспорным. Остановимся несколько подробнее на эстетическом удержании законов симметрии, пропорциональности и гармонии как слагаемых прекрасного. Что касается закона ритма, который проявляется и в музыке, и в архитектуре, и в изобразительном искусстве, и в стихосложении, то он заслуживает отдельного разговора и в данной книге рассматриваться не будет. 4.1. Симметрия. Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863-1945), "слагалось в течение десятков, сотен, тысяч поколений". "Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм". Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою долгую жизнь, академика А. В. Шубникова (1887-1970). Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о "соразмерности", что и означает в переводе с греческого слово "симметрия", с течением времени приобрелоуниверсальный характер и было осознано как всеобщая идея инвариантности (т. е. неизменности) относительно некоторых преобразований. Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными. Например, пятиконечная звезда, будучи повернута на 72° (360°: 5), займет первоначальное положение, а ваш будильник одинаково звенит в любом углу комнаты. Первый пример дает понятие об одном из видов геометрической симметрии — поворотной, а второй иллюстрирует важную физическую симметрию — однородность и изотропность (равнозначность всех направлений) пространства. Благодаря последней симметрии все физические приборы (в том числе будильник) одинаково работают в разных точках пространства, если, конечно, не изменяются окружающие физические условия. Легко вообразить, бы царила на Земле неразбериха, если бы эта симметрия была нарушена!Л. Б. Альберти
 Морская звезда — пример живого организма с поворотной симметрией 5-го порядка. Этот тип симметрии наиболее распространен в живой природе (цветы незабудки, гвоздики, колокольчика, вишни, яблони и т. д.) и принципиально невозможен в кристаллических решетках неживой природы. Симметрию 5-го порядка называют симметрией жизни. Это своеобразный защитный механизм живой природы против кристаллизации, против окаменения, за сохранение живой индивидуальности
Морская звезда — пример живого организма с поворотной симметрией 5-го порядка. Этот тип симметрии наиболее распространен в живой природе (цветы незабудки, гвоздики, колокольчика, вишни, яблони и т. д.) и принципиально невозможен в кристаллических решетках неживой природы. Симметрию 5-го порядка называют симметрией жизни. Это своеобразный защитный механизм живой природы против кристаллизации, против окаменения, за сохранение живой индивидуальности
Почти все утверждают, что красоту, воспринимаемую зрением, порождает соразмерность частей друг с другом и целым и с прелестью красок. И для тех, кто это утверждает, и вообще для всех остальных, быть прекрасным — значит быть симметричным и соразмерным.Таким образом, не только симметричные формы окружают нас повсюду, но и сами многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности пронизаны общим для всех них принципом симметрии. "Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности",- писал Вернадский. Действительно, еще Платон мыслил атомы четырех стихий — земли, воды, огня и воздуха — геометрически симметричными в виде правильных многогранников (см. гл. 7). И хотя сегодня "атомная физика" Платона кажется наивной, принцип симметрии и через два тысячелетия остается основополагающим принципом современной физики атома. За это время наука прошла путь от осознания симметрии геометрических тел к пониманию симметрии физических явлений. Итак, в современном понимании симметрия — это общенаучная философская категория, характеризующая структуру организации систем. Важнейшим свойством симметрии является сохранение (инвариантность) тех или иных признаков (геометрических, физических, биологических и т. д.) по отношению к вполне определенным преобразованиям. Математическим аппаратом изучения симметрии сегодня является теория групп и теория инвариантов. "Принцип симметрии в XX веке охватывает все новые области. Из области кристаллографии, физики твердого тела он вошел в область химии, в область молекулярных процессов и в физику атома. Нет сомнения, что его проявления мы найдем в еще более далеком от окружающих нас комплексов мире электрона и ему подчинены будут явления квантов". Этими словами академика В. И. Вернадского и хочется закончить короткий разговор (который и так перерос рамки нашей темы) о всеобщности принципа симметрии. О симметрии написано огромное количество замечательных книг. Некоторые из них приведены в конце книги, в списке рекомендуемой литературы.Платон
 Ёмеймон (Ворота сияния солнца) — вход в комплекс погребального ансамбля Тосёгу в г. Никко. Япония. 1634-1636. Японская пословица гласит: 'Не говори кекко (чудесно), если ты не видел Никко!'
Ёмеймон (Ворота сияния солнца) — вход в комплекс погребального ансамбля Тосёгу в г. Никко. Япония. 1634-1636. Японская пословица гласит: 'Не говори кекко (чудесно), если ты не видел Никко!'
 Отражение в воде — единственный пример горизонтальной симметрии в природе. Быть может, в этом и состоит тайна его очарования? Алтай. Озеро горных духов. Фото автора
Прежде чем перейти к еще одной грани симметрии — эстетической, следует сказать несколько слов о нарушении симметрии. Мы уже отмечали, что все физические законы являются симметричными. Но при ближайшем рассмотрении в каждой такой симметрии обнаруживается маленький изъян. Оказывается, природа не терпит точных симметрии! Природа почти симметрична, но не абсолютно симметрична! Так, планетные орбиты, которые еще Пифагором мыслились в виде совершенных окружностей, на самом деле оказались почти окружностями, но все-таки не окружностями, а эллипсами. Нарушение симметрии обнаружено во многих явлениях ядерной физики. Приблизительная симметрия является сегодня одной из научных загадок. Вот что по этому поводу пишет современный американский физик, лауреат Нобелевской премии Ричард Фейнман: "Почему природа столь близка к симметрии? По этому вопросу ни у кого нет никакой разумной мысли. Единственное, что я могу предложить вам,- это старое японское предание. В японском городе Никко есть ворота, которые японцы называют самыми красивыми воротами страны. Они были построены в период большого влияния китайского искусства. Это необычайно сложные ворота, со множеством фронтонов, изумительной резьбой и большим количеством колонн, на основании которых вырезаны драконьи головы, божества и т. п. Но, приглядевшись, можно заметить, что в сложном и искусном рисунке на одной из колонн некоторые из его мелких деталей вырезаны вверх ногами. В остальном рисунок полностью симметричен. Спрашивается: для чего это было нужно? Как говорит предание, это было сделано для того, чтобы боги не заподозрили человека в совершенстве. Ошибка была сделана намеренно, дабы не вызвать зависти и гнева богов.
Мы можем, вообще говоря, подхватить эту мысль и сказать, что истинное объяснение приблизительной симметрии мира состоит в следующем: боги сотворили свои законы только приближенно симметричными, чтобы мы не завидовали их совершенству!" Более серьезной "разгадки" тайны приближенной симметрии наука пока предложить не может.
Перейдем, наконец, к эстетическому содержанию симметрии, к ответу на толстовский вопрос: "почему симметрия приятна для глаз?" Видимо, господством симметрии в природе, о котором мы не случайно так много говорили, и объясняется прежде всего эстетическая ценность симметрии для человека. С детства человек привыкает к билатерально симметричным родителям, затем у него появляются билатерально симметричные друзья; он видит зеркальную симметрию в бабочках, птицах, рыбах, животных, поворотную — в стройных елях и волшебных узорах снежинок, переносную — в оградах парков, решетках мостов, лестничных маршах, бордюрах, которые издревле были любимым декоративным элементом. Человек привыкает видеть в природе вертикальные оси и плоскости симметрии, и вертикальная симметрия воспринимается нами гораздо охотнее. Мы нигде не увидим обои с горизонтальными осями симметрии, ибо это вызвало бы неприятный контраст с вертикальной симметрией растущих за окном деревьев. Единственная горизонтальная симметрия, которую мы встречаем в природе,- это отражения в зеркале воды. Возможно, в необычности такой симметрии и заключается ее завораживающая сила.
Таким образом, симметрия воспринимается человеком как проявление закономерности, порядка, царящего в природе. Восприятие же закономерного всегда доставляет нам удовольствие, сообщает некоторую уверенность и даже бодрость. "Порядок освобождает мысль",- любил повторять великий французский математик, философ и храбрый воин Рене Декарт (1596-- 1650). Его соотечественник, выдающийся зодчий XX века, авторитет, равного которому в архитектуре не было со времен Микеланджело, Ле Корбюзье (1887-1965) писал: "Человеку необходим порядок; без него все его действия теряют согласованность, логическую взаимосвязь. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядке, который продиктован ему потребностями его психики,- это творческий процесс. Творчество есть акт упорядочения".
Итак, симметрия, воспринимаемая человеком как закономерность структуры, как внешнее проявление внутреннего порядка, начинает обладать эстетической ценностью, т. е. воспринимается как красота. Простой пример убеждает в этом. Чернильная клякса сама по себе некрасива. Но стоит перегнуть лист бумаги с невысохшей кляксой пополам, и мы получим кляксу, которая уже производит приятное впечатление. Зеркальная симметрия новой кляксы, т. е. закономерное расположение ее частей, и определяет красоту нашей "рукотворной" кляксы. Знание законов геометрической симметрии сделает такие поиски быстрыми и плодотворными.
Отражение в воде — единственный пример горизонтальной симметрии в природе. Быть может, в этом и состоит тайна его очарования? Алтай. Озеро горных духов. Фото автора
Прежде чем перейти к еще одной грани симметрии — эстетической, следует сказать несколько слов о нарушении симметрии. Мы уже отмечали, что все физические законы являются симметричными. Но при ближайшем рассмотрении в каждой такой симметрии обнаруживается маленький изъян. Оказывается, природа не терпит точных симметрии! Природа почти симметрична, но не абсолютно симметрична! Так, планетные орбиты, которые еще Пифагором мыслились в виде совершенных окружностей, на самом деле оказались почти окружностями, но все-таки не окружностями, а эллипсами. Нарушение симметрии обнаружено во многих явлениях ядерной физики. Приблизительная симметрия является сегодня одной из научных загадок. Вот что по этому поводу пишет современный американский физик, лауреат Нобелевской премии Ричард Фейнман: "Почему природа столь близка к симметрии? По этому вопросу ни у кого нет никакой разумной мысли. Единственное, что я могу предложить вам,- это старое японское предание. В японском городе Никко есть ворота, которые японцы называют самыми красивыми воротами страны. Они были построены в период большого влияния китайского искусства. Это необычайно сложные ворота, со множеством фронтонов, изумительной резьбой и большим количеством колонн, на основании которых вырезаны драконьи головы, божества и т. п. Но, приглядевшись, можно заметить, что в сложном и искусном рисунке на одной из колонн некоторые из его мелких деталей вырезаны вверх ногами. В остальном рисунок полностью симметричен. Спрашивается: для чего это было нужно? Как говорит предание, это было сделано для того, чтобы боги не заподозрили человека в совершенстве. Ошибка была сделана намеренно, дабы не вызвать зависти и гнева богов.
Мы можем, вообще говоря, подхватить эту мысль и сказать, что истинное объяснение приблизительной симметрии мира состоит в следующем: боги сотворили свои законы только приближенно симметричными, чтобы мы не завидовали их совершенству!" Более серьезной "разгадки" тайны приближенной симметрии наука пока предложить не может.
Перейдем, наконец, к эстетическому содержанию симметрии, к ответу на толстовский вопрос: "почему симметрия приятна для глаз?" Видимо, господством симметрии в природе, о котором мы не случайно так много говорили, и объясняется прежде всего эстетическая ценность симметрии для человека. С детства человек привыкает к билатерально симметричным родителям, затем у него появляются билатерально симметричные друзья; он видит зеркальную симметрию в бабочках, птицах, рыбах, животных, поворотную — в стройных елях и волшебных узорах снежинок, переносную — в оградах парков, решетках мостов, лестничных маршах, бордюрах, которые издревле были любимым декоративным элементом. Человек привыкает видеть в природе вертикальные оси и плоскости симметрии, и вертикальная симметрия воспринимается нами гораздо охотнее. Мы нигде не увидим обои с горизонтальными осями симметрии, ибо это вызвало бы неприятный контраст с вертикальной симметрией растущих за окном деревьев. Единственная горизонтальная симметрия, которую мы встречаем в природе,- это отражения в зеркале воды. Возможно, в необычности такой симметрии и заключается ее завораживающая сила.
Таким образом, симметрия воспринимается человеком как проявление закономерности, порядка, царящего в природе. Восприятие же закономерного всегда доставляет нам удовольствие, сообщает некоторую уверенность и даже бодрость. "Порядок освобождает мысль",- любил повторять великий французский математик, философ и храбрый воин Рене Декарт (1596-- 1650). Его соотечественник, выдающийся зодчий XX века, авторитет, равного которому в архитектуре не было со времен Микеланджело, Ле Корбюзье (1887-1965) писал: "Человеку необходим порядок; без него все его действия теряют согласованность, логическую взаимосвязь. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядке, который продиктован ему потребностями его психики,- это творческий процесс. Творчество есть акт упорядочения".
Итак, симметрия, воспринимаемая человеком как закономерность структуры, как внешнее проявление внутреннего порядка, начинает обладать эстетической ценностью, т. е. воспринимается как красота. Простой пример убеждает в этом. Чернильная клякса сама по себе некрасива. Но стоит перегнуть лист бумаги с невысохшей кляксой пополам, и мы получим кляксу, которая уже производит приятное впечатление. Зеркальная симметрия новой кляксы, т. е. закономерное расположение ее частей, и определяет красоту нашей "рукотворной" кляксы. Знание законов геометрической симметрии сделает такие поиски быстрыми и плодотворными.
Чувство глубочайшего уважения к мощи законов симметрии никогда не ослабевает у того, кто обдумывал изящество и красоту безупречных математических доказательств и сопоставлял это со сложными и далеко идущими физическими и философскими следствиями.На рисунке изображены узоры, полученные с использованием различных типов геометрической симметрии из простой, достаточно бесформенной кляксы. Узор на рисунке б получен с помощью зеркальной симметрии. Однако закон его построения слишком прост и очевиден, потому и эстетическая ценность такого узора невелика.Чжень-нин Янг Нобелевская лекция
 'Кляксография' — узоры, полученные из обыкновенной кляксы (а) с помощью зеркальной симметрии (б), переносной симметрии (в)у поворотной симметрии (г) и орнаментальной симметрии(d)
Узоры, приведенные на рисунке в, называются бордюрами и представляют собой тип переносной симметрии, когда каждая предыдущая фигура совпадает с последующей при поступательном перемещении вдоль бордюра на постоянный интервал (шаг симметрии). Нижний бордюр имеет более сложный закон построения, чем простая переносная симметрия. Всего же существует семь типов бордюров.
На рисунке г показаны так называемые "розетки". Розетки получаются поворотом фигуры вокруг вертикальной оси на угол 360°/n (n = 2, 3, 4, ...), т. е. обладают поворотной симметрией n-го порядка. (Верхняя розетка имеет поворотную симметрию 6-го порядка, средняя — 8-го, нижняя же сочетает зеркальную и поворотную симметрии, но в то же время она имеет чисто поворотную симметрию 3-го порядка.)
Наконец, на рисунке д показаны два орнамента из семнадцати возможных. Орнаментальная симметрия строится на одной из пяти возможных плоских решеток. Верхний орнамент имеет квадратную решетку, а нижний — гексагональную (правильный шестиугольник). Заполнив одну ячейку решетки, мы получим с помощью переносной симметрии весь орнамент.
Вот так с помощью симметрии простая клякса превращается в затейливые узоры, которые уже никак не назовешь некрасивыми. Нам нравится вглядываться в узоры симметрии, постигать их законы, и они воспринимаются нами как красивые. "Смысл эстетического воздействия симметрии (и всякой иной закономерности), по нашему мнению,- писал Шубников,- заключается в том психическом процессе, который связан с открытием ее законов".
Другим важным фактором, составляющим эстетическое содержание симметрии, является ее целесообразность, которая также есть проявление закономерного. Уже первобытные люди понимали, что симметричные орудия более целесообразны, чем несимметричные. Таким образом, уже в эпоху неолита симметрия была выделена как наиболее совершенная форма, о чем свидетельствуют многочисленные украшения с симметричными рисунками.
Современный человек просто не в состоянии представить себе несимметричный (а значит, и нефункциональный) самолет или автомобиль. В этой связи показательны наблюдения известного летчика-испытателя, Героя Советского Союза Марка Галлая: "Я заметил, что красивая, ласкающая своими пропорциями взор машина обычно к тому же и хорошо летает. Эта, на первый взгляд, почти мистическая закономерность имеет, я думаю, свое вполне рациональное объяснение: дело, по-видимому, обстоит как раз наоборот — хорошо летающая машина начинает представляться "красивой". Эстетическое формируется под влиянием рационального".
'Кляксография' — узоры, полученные из обыкновенной кляксы (а) с помощью зеркальной симметрии (б), переносной симметрии (в)у поворотной симметрии (г) и орнаментальной симметрии(d)
Узоры, приведенные на рисунке в, называются бордюрами и представляют собой тип переносной симметрии, когда каждая предыдущая фигура совпадает с последующей при поступательном перемещении вдоль бордюра на постоянный интервал (шаг симметрии). Нижний бордюр имеет более сложный закон построения, чем простая переносная симметрия. Всего же существует семь типов бордюров.
На рисунке г показаны так называемые "розетки". Розетки получаются поворотом фигуры вокруг вертикальной оси на угол 360°/n (n = 2, 3, 4, ...), т. е. обладают поворотной симметрией n-го порядка. (Верхняя розетка имеет поворотную симметрию 6-го порядка, средняя — 8-го, нижняя же сочетает зеркальную и поворотную симметрии, но в то же время она имеет чисто поворотную симметрию 3-го порядка.)
Наконец, на рисунке д показаны два орнамента из семнадцати возможных. Орнаментальная симметрия строится на одной из пяти возможных плоских решеток. Верхний орнамент имеет квадратную решетку, а нижний — гексагональную (правильный шестиугольник). Заполнив одну ячейку решетки, мы получим с помощью переносной симметрии весь орнамент.
Вот так с помощью симметрии простая клякса превращается в затейливые узоры, которые уже никак не назовешь некрасивыми. Нам нравится вглядываться в узоры симметрии, постигать их законы, и они воспринимаются нами как красивые. "Смысл эстетического воздействия симметрии (и всякой иной закономерности), по нашему мнению,- писал Шубников,- заключается в том психическом процессе, который связан с открытием ее законов".
Другим важным фактором, составляющим эстетическое содержание симметрии, является ее целесообразность, которая также есть проявление закономерного. Уже первобытные люди понимали, что симметричные орудия более целесообразны, чем несимметричные. Таким образом, уже в эпоху неолита симметрия была выделена как наиболее совершенная форма, о чем свидетельствуют многочисленные украшения с симметричными рисунками.
Современный человек просто не в состоянии представить себе несимметричный (а значит, и нефункциональный) самолет или автомобиль. В этой связи показательны наблюдения известного летчика-испытателя, Героя Советского Союза Марка Галлая: "Я заметил, что красивая, ласкающая своими пропорциями взор машина обычно к тому же и хорошо летает. Эта, на первый взгляд, почти мистическая закономерность имеет, я думаю, свое вполне рациональное объяснение: дело, по-видимому, обстоит как раз наоборот — хорошо летающая машина начинает представляться "красивой". Эстетическое формируется под влиянием рационального".
 Симметрия, пропорция, гармония — слагаемые прекрасного
Итак, целесообразность симметричных форм была осознана человечеством в доисторические времена, а в сознании древних греков симметрия стала олицетворением закономерности, целесообразности, а следовательно, и красоты. Идея связи прекрасного с симметрией пронизывала всю греческую философию, все греческое искусство. Достаточно вспомнить строго симметричные формы античных архитектурных памятников, изумительную стройность греческих ваз, математическую строгость их орнамента. С тех пор симметрия и красота в сознании человека слиты воедино. В "Фаусте" Гёте противопоставляет в образах Прекрасной Елены и одноглазой, однозубой старухи Форкиады красоту симметрии и уродство асимметрии. В "Сказке о царе Салтане" Пушкин рисует величавую Царевну-Лебедь со звездой во лбу (красота-симметрия) и окривевших злодеек ткачиху с поварихой (уродство-асимметрия). В "Войне и мире" Льва Толстого мы читаем: "Это был огромный, в два обхвата, дуб, с обломанными, давно видно, суками и с обломанной корой, заросшей старыми болячками. С огромными своими неуклюже, несимметрично растопыренными корявыми руками и пальцами, он старым, сердитым и презрительным уродом стоял между улыбающимися березами".
Симметрия как объективный признак красоты проходит через всю историю искусств. "Равенство, неравенство, повторение и симметрия, определенные структуры играют в искусстве, как и в математике, фундаментальную роль",- считает физик Гейзенберг. Не говоря уже об архитектуре и скульптуре, симметрия господствует в изобразительном искусстве Древнего Египта, Древней Греции и Рима, средневековья и Возрождения. Зеркальная симметрия была особенно излюблена шумерами.
Симметрия, пропорция, гармония — слагаемые прекрасного
Итак, целесообразность симметричных форм была осознана человечеством в доисторические времена, а в сознании древних греков симметрия стала олицетворением закономерности, целесообразности, а следовательно, и красоты. Идея связи прекрасного с симметрией пронизывала всю греческую философию, все греческое искусство. Достаточно вспомнить строго симметричные формы античных архитектурных памятников, изумительную стройность греческих ваз, математическую строгость их орнамента. С тех пор симметрия и красота в сознании человека слиты воедино. В "Фаусте" Гёте противопоставляет в образах Прекрасной Елены и одноглазой, однозубой старухи Форкиады красоту симметрии и уродство асимметрии. В "Сказке о царе Салтане" Пушкин рисует величавую Царевну-Лебедь со звездой во лбу (красота-симметрия) и окривевших злодеек ткачиху с поварихой (уродство-асимметрия). В "Войне и мире" Льва Толстого мы читаем: "Это был огромный, в два обхвата, дуб, с обломанными, давно видно, суками и с обломанной корой, заросшей старыми болячками. С огромными своими неуклюже, несимметрично растопыренными корявыми руками и пальцами, он старым, сердитым и презрительным уродом стоял между улыбающимися березами".
Симметрия как объективный признак красоты проходит через всю историю искусств. "Равенство, неравенство, повторение и симметрия, определенные структуры играют в искусстве, как и в математике, фундаментальную роль",- считает физик Гейзенберг. Не говоря уже об архитектуре и скульптуре, симметрия господствует в изобразительном искусстве Древнего Египта, Древней Греции и Рима, средневековья и Возрождения. Зеркальная симметрия была особенно излюблена шумерами.
 Симметрия в искусстве. Зеркальная симметрия: нагрудное украшение с именем фараона. XX в. до н. э. (а)
Симметрия в искусстве. Зеркальная симметрия: нагрудное украшение с именем фараона. XX в. до н. э. (а)
 Симметрия в искусстве. Зеркальная симметрия: капитель колонны из дворца Артаксеркса II в Сузах. V-IV вв. до н. э. (б)
Симметрия в искусстве. Зеркальная симметрия: капитель колонны из дворца Артаксеркса II в Сузах. V-IV вв. до н. э. (б)
 Поворотная симметрия 12-го порядка: мозаика купола баптистерия в Равенне. V в. (в)
Поворотная симметрия 12-го порядка: мозаика купола баптистерия в Равенне. V в. (в)
 Переносная симметрия: рельефы ападаны в Персеполе. VI-V вв. до н. э. (г)
Симметрия в искусстве — это волнующая тема, которая заслуживает особого разговора. Поэтому мы ограничимся только замечанием о том, что следование принципу зеркальной симметрии в искусстве иногда приводило к парадоксальным результатам. Так, на мозаике Киевского собора св. Софии под знаменитой Орантой изображены два зеркально-симметричных Христа, обращенных лицом к ученикам. Правда, при ближайшем рассмотрении мы увидим, что симметрия здесь лишь приблизительная, так как один Христос преломляет хлеб, а другой разливает вино. Этот прием, позволяющий одновременно изобразить два важнейших момента тайного причастия, безусловно, является слишком "математичным" и со временем был вытеснен более реалистическим изображением тайной вечери.
Как и в любом деле, абсолютизация одной идеи не могла привести ни к чему хорошему. Симметрия в искусстве не составила исключения. "Красота неправильная", асимметрия, стала пробивать себе дорогу в искусстве, ибо сведение красоты только к симметрии ограничивало богатство ее внутреннего содержания, лишало красоту жизни. Истинную красоту можно постичь только в единстве противоположностей. Вот почему именно единство симметрии и асимметрии определяет сегодня внутреннее содержание прекрасного в искусстве. Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.
Переносная симметрия: рельефы ападаны в Персеполе. VI-V вв. до н. э. (г)
Симметрия в искусстве — это волнующая тема, которая заслуживает особого разговора. Поэтому мы ограничимся только замечанием о том, что следование принципу зеркальной симметрии в искусстве иногда приводило к парадоксальным результатам. Так, на мозаике Киевского собора св. Софии под знаменитой Орантой изображены два зеркально-симметричных Христа, обращенных лицом к ученикам. Правда, при ближайшем рассмотрении мы увидим, что симметрия здесь лишь приблизительная, так как один Христос преломляет хлеб, а другой разливает вино. Этот прием, позволяющий одновременно изобразить два важнейших момента тайного причастия, безусловно, является слишком "математичным" и со временем был вытеснен более реалистическим изображением тайной вечери.
Как и в любом деле, абсолютизация одной идеи не могла привести ни к чему хорошему. Симметрия в искусстве не составила исключения. "Красота неправильная", асимметрия, стала пробивать себе дорогу в искусстве, ибо сведение красоты только к симметрии ограничивало богатство ее внутреннего содержания, лишало красоту жизни. Истинную красоту можно постичь только в единстве противоположностей. Вот почему именно единство симметрии и асимметрии определяет сегодня внутреннее содержание прекрасного в искусстве. Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.
 Евхаристия. Мозаика апсиды собора Св. Софии в Киеве. 1043-1046. Зеркально-симметрическое раздвоение фигуры Христа позволяло одновременно изображать два важнейших момента евхаристии: причащение хлебом, символизировавшим тело Христово, и причащение вином, обозначавшим кровь Христа. Зеркальное раздвоение Христа было одним из излюбленных приемов в иконографии тайной вечери
Евхаристия. Мозаика апсиды собора Св. Софии в Киеве. 1043-1046. Зеркально-симметрическое раздвоение фигуры Христа позволяло одновременно изображать два важнейших момента евхаристии: причащение хлебом, символизировавшим тело Христово, и причащение вином, обозначавшим кровь Христа. Зеркальное раздвоение Христа было одним из излюбленных приемов в иконографии тайной вечери
 Покровский собор на Рву — храм Василия Блаженного. Москва. 1555-1560. Зодчие Барма и Постник. Гармоническое сочетание симметрии частей и асимметрии целого
Примером удивительного сочетания симметрии и Симметрии является Покровский собор (храм Василия блаженного) на Красной площади в Москве. Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом Не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!
Итак, "сфера влияния" симметрии (а значит, и ее антипода — асимметрии) поистине безгранична. Природа — наука — искусство. Всюду мы видим противоборство, а часто и единство двух великих начал — симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.
4.2. Пропорция. Слово "пропорция" ввел в употребление Цицерон в I веке до н. э., переведя им на латынь платоновский термин "аналогия", который буквально означал "вновь-отношение", или, как мы говорим, "соотношение". С тех пор вот уже 2000 лет пропорцией в математике называют равенство между отношениями четырех величин а, b, с, d:
Покровский собор на Рву — храм Василия Блаженного. Москва. 1555-1560. Зодчие Барма и Постник. Гармоническое сочетание симметрии частей и асимметрии целого
Примером удивительного сочетания симметрии и Симметрии является Покровский собор (храм Василия блаженного) на Красной площади в Москве. Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом Не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!
Итак, "сфера влияния" симметрии (а значит, и ее антипода — асимметрии) поистине безгранична. Природа — наука — искусство. Всюду мы видим противоборство, а часто и единство двух великих начал — симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.
4.2. Пропорция. Слово "пропорция" ввел в употребление Цицерон в I веке до н. э., переведя им на латынь платоновский термин "аналогия", который буквально означал "вновь-отношение", или, как мы говорим, "соотношение". С тех пор вот уже 2000 лет пропорцией в математике называют равенство между отношениями четырех величин а, b, с, d:
 (4.1)
Пропорция в искусстве также определяет соотношение величин элементов художественного произведения либо соотношение отдельных элементов и всего произведения в целом. В эстетике пропорция, как и симметрия, является составным элементом категории меры и выражает закономерность структуры эстетического образа.
Издревле в пропорции художники видели объективную основу красоты, по крайней мере формы прекрасного. Не все художники желали рассматривать искусство лишь как плод безудержной фантазии и чистой интуиции. И те из них, кто пытался постигнуть объективные законы прекрасного, находили их прежде всего в пропорции.
Мы уже отмечали, что симметрия воспринимается слишком статично, скованно и только единство симметрии и асимметрии создает подлинную гармонию красоты. Так вот, в качестве меры соотношения симметричного и асимметричного часто и выступает пропорция. Возьмем простой пример: деление отрезка прямой. Если отрезок разделить пополам, зеркально-симметрично, то такое деление выглядит уравновешенным, мертвым. Если же точку деления взять слишком близко к одному из концов отрезка, то новая конфигурация будет чересчур неуравновешенной и беспокойной. Только некоторая "золотая середина", которая в данном случае отнюдь не является геометрической серединой, обеспечит йам желаемое единство симметрии и асимметрии.
(4.1)
Пропорция в искусстве также определяет соотношение величин элементов художественного произведения либо соотношение отдельных элементов и всего произведения в целом. В эстетике пропорция, как и симметрия, является составным элементом категории меры и выражает закономерность структуры эстетического образа.
Издревле в пропорции художники видели объективную основу красоты, по крайней мере формы прекрасного. Не все художники желали рассматривать искусство лишь как плод безудержной фантазии и чистой интуиции. И те из них, кто пытался постигнуть объективные законы прекрасного, находили их прежде всего в пропорции.
Мы уже отмечали, что симметрия воспринимается слишком статично, скованно и только единство симметрии и асимметрии создает подлинную гармонию красоты. Так вот, в качестве меры соотношения симметричного и асимметричного часто и выступает пропорция. Возьмем простой пример: деление отрезка прямой. Если отрезок разделить пополам, зеркально-симметрично, то такое деление выглядит уравновешенным, мертвым. Если же точку деления взять слишком близко к одному из концов отрезка, то новая конфигурация будет чересчур неуравновешенной и беспокойной. Только некоторая "золотая середина", которая в данном случае отнюдь не является геометрической серединой, обеспечит йам желаемое единство симметрии и асимметрии.
 Симметрия, пропорция, гармония — слагаемые прекрасного
Такое "радующее глаз" деление отрезка, по преданию, было известно еще Пифагору и называлось им золотой пропорцией. Впрочем, скорее всего золотая пропорция была заимствована Пифагором у древних египтян, которые знали ее задолго до Пифагора и которых он посетил в своих странствиях по свету. Золотая пропорция определяется как деление отрезка на две неравные части, при котором меньшая из них так относится к большей, как последняя ко всей длине отрезка. С тех пор золотая пропорция становится общепризнанным каноном искусства. Художник и инженер Леонардо да Винчи, изучавший и восхвалявший золотую пропорцию на протяжении всей своей жизни, называет ее "Sectio aurea" (золотое сечение), а математик и астроном Иоганн Кеплер, обнаруживший золотую пропорцию в ботанике, говорит о ней как о бесценном сокровище, как об одном из двух сокровищ геометрии* и именует ее "Sectio divina" (божественное сечение). Название Леонардо да Винчи сохранилось и сегодня.
*(К другому "геометрическому сокровищу", по мнению еплера, относилась теорема Пифагора.)
Последующие научные открытия показали, что золотое сечение составляет основу многих природных явлений, что оно связано с глубокими естественнонаучными закономерностями. Таким образом, будучи мерой, законом природы, золотое сечение становится и мерой человеческого творчества, "законом красоты": совершенная природа дает человеку образец совершенства. Так раскрывается еще одна эстетическая грань золотого сечения — целесообразность, ибо в целесообразности природы сомнений у человечества никогда не было.
Симметрия, пропорция, гармония — слагаемые прекрасного
Такое "радующее глаз" деление отрезка, по преданию, было известно еще Пифагору и называлось им золотой пропорцией. Впрочем, скорее всего золотая пропорция была заимствована Пифагором у древних египтян, которые знали ее задолго до Пифагора и которых он посетил в своих странствиях по свету. Золотая пропорция определяется как деление отрезка на две неравные части, при котором меньшая из них так относится к большей, как последняя ко всей длине отрезка. С тех пор золотая пропорция становится общепризнанным каноном искусства. Художник и инженер Леонардо да Винчи, изучавший и восхвалявший золотую пропорцию на протяжении всей своей жизни, называет ее "Sectio aurea" (золотое сечение), а математик и астроном Иоганн Кеплер, обнаруживший золотую пропорцию в ботанике, говорит о ней как о бесценном сокровище, как об одном из двух сокровищ геометрии* и именует ее "Sectio divina" (божественное сечение). Название Леонардо да Винчи сохранилось и сегодня.
*(К другому "геометрическому сокровищу", по мнению еплера, относилась теорема Пифагора.)
Последующие научные открытия показали, что золотое сечение составляет основу многих природных явлений, что оно связано с глубокими естественнонаучными закономерностями. Таким образом, будучи мерой, законом природы, золотое сечение становится и мерой человеческого творчества, "законом красоты": совершенная природа дает человеку образец совершенства. Так раскрывается еще одна эстетическая грань золотого сечения — целесообразность, ибо в целесообразности природы сомнений у человечества никогда не было.
 Гармония мира. Иллюстрация из книги итальянского теоретика музыки . Ф. Гафурио 'Практика музыки'. Милан. 1498
Золотое сечение мы находим всюду: в изобразительном и прикладном искусстве, в архитектуре и музыке, в литературе, в предметах быта и машинах. Многочисленные исследования показали, что на точке золотого сечения обычно бывает кульминация в поэтических, драматургических и музыкальных произведениях (см. с. 164). Золотое сечение мы находим в общей композиции произведения и в соотношении его частей. Не менее удивительно и то, что золотое сечение мы находим всегда, в совершенно различных цивилизациях, отделенных друг от друга тысячелетиями: в усыпальнице Хеопса в Древнем Египте и в храме Парфенон в Древней Греции, в Баптистерии эпохи Возрождения в Пизе и в храме Покрова на Нерли, в ленинградском Адмиралтействе и в ультрасовременных сооружениях Ле Корбюзье. Золотое сечение мы обнаруживаем и в музыкальных шедеврах Баха, Моцарта, Вагнера, Шопена, Глинки, и в поэтических произведениях от Лермонтова до Вознесенского.
Загадка притягательной силы золотого сечения давно волнует человечество. Были и чисто математические "доказательства" эстетического предпочтения человеком золотого сечения, были и физиологические, связанные, например, со спецификой сокращения глазных мышц. Нам представляется наиболее правдоподобным наиболее простое объяснение: эстетическое превосходство золотого сечения является не врожденным, а "благоприобретенным" в процессе исторического развития человечества. Поскольку золотое сечение дано человеку самой природой в пропорциях его же тела, оно постепенно и стало для него идеалом красоты. Эту мысль подтверждает и эстетическое "равнодушие" детей к золотому сечению, проверенное экспериментально.
Эстетике и математике золотого сечения мы посвятили отдельную главу (гл. 15). Здесь же мы отметим, что золотое сечение было не единственным каноном пропорциональности в искусстве. Например, готическая архитектура основана на совершенно иной системе пропорций, а английский художник и эстетик XVIII века Уильям Хогарт (1697-1764) в своем трактате "Анализ красоты" призывал к использованию асимметричных "змеевидных" линий, позволяющих воспроизвести жизнь во всем ее многообразии. Хогарт нашел даже особую "линию красоты" — плавную синусоидальную кривую, которая, согласно его взглядам, выражала сущность прекрасного. Впрочем, различным системам пропорциональности посвящена фактически вся третья часть нашей книги, ибо архитектура как искусство во многом определяется принятой системой пропорциониро-вания. Поэтому мы не будем более останавливаться на пропорции и перейдем к следующему слагаемому прекрасного — гармонии.
4.3. Гармония. Идея Гармонии, как антитеза идеи Хаоса, имеет тысячелетнюю традицию: Хепри и Нун в космологических мифах Древнего Египта, Сат и Асат в гимнах Ригведы, Ин-Ян и Дао в книгах даосских мудрецов, Свет и Тьма в Библии, Космос и Хаос в поэмах Гесиода и Гомера. Несмотря на множество вариантов и оттенков, а порой и отличий между этими двумя величайшими смыслообразами двух великих культур — Востока и Запада, их объединяла единая йдеЯ — идея безмерной пучины первобытия, рождающей в своих клокочущих недрах светлый луч гармония жизни. Эту древнейшую в истории мировой культуры идею не поглотили тысячелетия, и сегодня она ясно видна — будь то в последней мандале Ригведы:
Гармония мира. Иллюстрация из книги итальянского теоретика музыки . Ф. Гафурио 'Практика музыки'. Милан. 1498
Золотое сечение мы находим всюду: в изобразительном и прикладном искусстве, в архитектуре и музыке, в литературе, в предметах быта и машинах. Многочисленные исследования показали, что на точке золотого сечения обычно бывает кульминация в поэтических, драматургических и музыкальных произведениях (см. с. 164). Золотое сечение мы находим в общей композиции произведения и в соотношении его частей. Не менее удивительно и то, что золотое сечение мы находим всегда, в совершенно различных цивилизациях, отделенных друг от друга тысячелетиями: в усыпальнице Хеопса в Древнем Египте и в храме Парфенон в Древней Греции, в Баптистерии эпохи Возрождения в Пизе и в храме Покрова на Нерли, в ленинградском Адмиралтействе и в ультрасовременных сооружениях Ле Корбюзье. Золотое сечение мы обнаруживаем и в музыкальных шедеврах Баха, Моцарта, Вагнера, Шопена, Глинки, и в поэтических произведениях от Лермонтова до Вознесенского.
Загадка притягательной силы золотого сечения давно волнует человечество. Были и чисто математические "доказательства" эстетического предпочтения человеком золотого сечения, были и физиологические, связанные, например, со спецификой сокращения глазных мышц. Нам представляется наиболее правдоподобным наиболее простое объяснение: эстетическое превосходство золотого сечения является не врожденным, а "благоприобретенным" в процессе исторического развития человечества. Поскольку золотое сечение дано человеку самой природой в пропорциях его же тела, оно постепенно и стало для него идеалом красоты. Эту мысль подтверждает и эстетическое "равнодушие" детей к золотому сечению, проверенное экспериментально.
Эстетике и математике золотого сечения мы посвятили отдельную главу (гл. 15). Здесь же мы отметим, что золотое сечение было не единственным каноном пропорциональности в искусстве. Например, готическая архитектура основана на совершенно иной системе пропорций, а английский художник и эстетик XVIII века Уильям Хогарт (1697-1764) в своем трактате "Анализ красоты" призывал к использованию асимметричных "змеевидных" линий, позволяющих воспроизвести жизнь во всем ее многообразии. Хогарт нашел даже особую "линию красоты" — плавную синусоидальную кривую, которая, согласно его взглядам, выражала сущность прекрасного. Впрочем, различным системам пропорциональности посвящена фактически вся третья часть нашей книги, ибо архитектура как искусство во многом определяется принятой системой пропорциониро-вания. Поэтому мы не будем более останавливаться на пропорции и перейдем к следующему слагаемому прекрасного — гармонии.
4.3. Гармония. Идея Гармонии, как антитеза идеи Хаоса, имеет тысячелетнюю традицию: Хепри и Нун в космологических мифах Древнего Египта, Сат и Асат в гимнах Ригведы, Ин-Ян и Дао в книгах даосских мудрецов, Свет и Тьма в Библии, Космос и Хаос в поэмах Гесиода и Гомера. Несмотря на множество вариантов и оттенков, а порой и отличий между этими двумя величайшими смыслообразами двух великих культур — Востока и Запада, их объединяла единая йдеЯ — идея безмерной пучины первобытия, рождающей в своих клокочущих недрах светлый луч гармония жизни. Эту древнейшую в истории мировой культуры идею не поглотили тысячелетия, и сегодня она ясно видна — будь то в последней мандале Ригведы:
 Симметрия, пропорция, гармония — слагаемые прекрасного
Таким образом, в конце XX века обретает свое второе рождение древняя библейская идея о возникновении Гармонии из Хаоса. В строгой естественно-ручной теории вновь оживают древние ведические Истины, звонко прозвучавшие в начале XX века в авторизованных переводах Константина Бальмонта:
Симметрия, пропорция, гармония — слагаемые прекрасного
Таким образом, в конце XX века обретает свое второе рождение древняя библейская идея о возникновении Гармонии из Хаоса. В строгой естественно-ручной теории вновь оживают древние ведические Истины, звонко прозвучавшие в начале XX века в авторизованных переводах Константина Бальмонта:
И поэтому сказано не без причины — все слагающееся из противоположностей объединяется и сочетается некоей гармонией. Ибо гармония есть единое многого и согласие разногласного.Боэций
Душа следует своим собственным законам, тело — также своим, и они сообразуются в силу гармонии, предустановленной между всеми субстанциями, так как они все суть выражения одной и той же вселенной.Зерна учения о гармонии, брошенные Пифагором а Гераклитом в благодатную почву средиземноморской культуры, проросли в могучее древо гармонии, своими корнями сплотившее воедино все интеллектуальное наследие человечества. Учение о гармонии было подхвачено и развито Платоном, чья философия, будто скрепы-гармонии одиссеева корабля, пронизывает не только мировую философию, но и мировую культуру. Платон придал понятию гармонии универсальный смысл, распространив космологическую и математическую теории гармонии пифагорейцев на нравственный и духовный космос человека. Гармония для Платона есть основа прекрасного. В свою очередь такие качества как мера, симметрия, пропорция составляют единое целое гармонии. Из этих посылок естественным образом вытекает знаменитое изречение Платона о том, что "умеренность и соразмерность всюду становится красотой и добродетелью". Начиная с ранней классики взгляд на гармонию как согласие разногласного, лежащее в основе мироздания, как путеводную звезду на пути к тайнам мироздания отличается завидным постоянством. Такой взгляд на гармонию сохранял и в эпоху позднего эллинизма Цицерон: "Только мир свободен от всяких недостатков и во всех своих пропорциях и частях строен, закончен и совершенен"; и в последних лучах догоравшей античной культуры Боэций: "И поэтому сказано не без причины — все слагающееся из противоположностей объединяется и сочетаемся некоей гармонией"; и на рассвете эпохи Возрождения Альберти: "Ведь назначение и цель гармонии — упорядочить части, вообще говоря, разные по природе, неким совершенным отношением так, чтобы они одна другой соответствовали, создавая красоту"; и на пороге века Просвещения Лейбниц: "Душа следует своим законам, тело — также своим и они сообразуются в силу гармонии, предустановленной между всеми субстанциями, так как все они суть выражения одной и той же вселенной"; и в начале XX в. Пуанкаре: "Но то, что мы называем объективной реальностью, в конечном счете есть то, что .общо нескольким мыслящим существам и могло бы быть общо всем. Этой общею стороной может быть только гармония, выражаемая математическими законами. Следовательно, именно эта гармония и есть единственная объективная реальность, единственная истина, которой мы может достигнуть; а если я прибавлю, что универсальная гармония мира есть источник всякой красоты, то будет понятно, как мы должны ценить те медленные и тяжелые шаги вперед, которые мало-помалу открывают ее нам"; и в середине XX в. Эйнштейн: "Без веры во внутреннюю гармонию нашего мира, не могло бы быть никакой науки. Эта вера есть и всегда останется основным мотивом всякого научного творчества". К сожалению, у нас нет возможности остановиться подробнее на развитии учения о гармонии, в котором, как в капле воды, отражается все развитие человеческой мысли. Аристотель и Секст Эмпирик, Августин и Фома Аквинский, Дюрер и Леонардо да Винчи, Кеплер и Галилей, Гете и Шиллер, Кант и Гегель, Гейзенберг и Шредингер внесли свой вклад в это древнейшее учение. Мы же отметим три важных аспекта, которые выделяют в современных воззрениях на гармонию,- математический, эстетический и художественный. На ранних этапах развития учения о гармонии господствовало ее математическое понимание. Гармония трактовалась как соразмерность, пропорциональность отдельных частей, а также частей и целого. Такое внешнее, формальное толкование гармонии, выделяющее прежде всего количественную математическую сторону, было характерно Для пифагорейцев и мыслителей средневековья. В XVII веке пифагорейские "математические" взгляды на гармонию поднял на щит Иоганн Кеплер. В эпоху Возрождения математическое понимание гармонии постепенно вытесняется эстетическим. В отличие от математического эстетическое понимание гармонии является не просто количественным, а качественным, выражающим внутреннюю природу объекта. В эстетическом понимании гармонии получает развитие мысль Платона о связи гармонии с прекрасным. Поэтому эстетическая гармония связывалась с эстетическим еРезкиванием, с чувством прекрасного. В европейской этике красота природы становится неотделимой от РеДставления о ее гармонии.Г. В. Лейбниц
 Ле Корбюзье. Эскиз капеллы в Роншане
Более глубокое и диалектическое — художественное понимание гармонии вырабатывается в эстетике нового времени. Художественная гармония — это гармония искусства, это не только математическое соответствие между однородными элементами, но и единство противоположных эстетических категорий: прекрасного и безобразного, трагического и комического, возвышеного и низменного. Благодаря единству и борьбе этих противоречивых категорий художественная гармония приобретает движение и наполняется жизнью.
Итак, гармония — это сложное и многозначное понятие; поэтому гармония так близка и естествоиспытателю, и философу, и художнику.
Вот почему современные физики так часто говорят о гармонии природы, искренне веря, что сердцевину мироздания составляют простые и красивые математические закономерности и формулы. "Восприняв от античности идею о математическом истолковании порядка в природе,- пишет В. Гейзенберг,- современное естествознание осуществляет ее, однако, другим... способом... Наука нового времени показала, что в окружающем нас реальном мире неизменными являются не геометрические формы, а динамические законы... Гармонию пифагорейцев, которую еще Кеплер надеялся найти в орбитах небесных светил, естествознание со времен Ньютона ищет в математической структуре законов динамики, в уравнениях, формулирующих эти законы".
Вот почему художники так боготворят гармонию. "Поэт — сын гармонии,- говорил в своей речи "О назначении поэта" А. Блок,- и ему дана какая-то роль в мировой культуре. Три дела возложены на него: во-первых, освободить звуки из родной безначальной стихии, в которой они пребывают; во-вторых, привести эти звуки в гармонию, дать им форму; в-третьих, внести эту гармонию во внешний мир".
Поиски скрытой гармонии — высший удел и ученых, и художников. Это вечный путь человеческой культуры, путь, приносящий и ученым, и художникам муки и радости. А в конце пути, когда "ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже", сияет недосягаемая вершина — Гармония.
О трудном пути к этой вершине писано немало. Писал о нем и русский художник В. И. Суриков: "А какое время надо, чтобы картина утряслась так, чтобы переменить ничего нельзя было. Действительные размера каждого предмета найти нужно. Важно найти замбк" чтобы все части соединить. Это — математика". Имени0 математике, лежащей в основе скрытой гармонии искусства, и посвящены следующие три части книги.
Ле Корбюзье. Эскиз капеллы в Роншане
Более глубокое и диалектическое — художественное понимание гармонии вырабатывается в эстетике нового времени. Художественная гармония — это гармония искусства, это не только математическое соответствие между однородными элементами, но и единство противоположных эстетических категорий: прекрасного и безобразного, трагического и комического, возвышеного и низменного. Благодаря единству и борьбе этих противоречивых категорий художественная гармония приобретает движение и наполняется жизнью.
Итак, гармония — это сложное и многозначное понятие; поэтому гармония так близка и естествоиспытателю, и философу, и художнику.
Вот почему современные физики так часто говорят о гармонии природы, искренне веря, что сердцевину мироздания составляют простые и красивые математические закономерности и формулы. "Восприняв от античности идею о математическом истолковании порядка в природе,- пишет В. Гейзенберг,- современное естествознание осуществляет ее, однако, другим... способом... Наука нового времени показала, что в окружающем нас реальном мире неизменными являются не геометрические формы, а динамические законы... Гармонию пифагорейцев, которую еще Кеплер надеялся найти в орбитах небесных светил, естествознание со времен Ньютона ищет в математической структуре законов динамики, в уравнениях, формулирующих эти законы".
Вот почему художники так боготворят гармонию. "Поэт — сын гармонии,- говорил в своей речи "О назначении поэта" А. Блок,- и ему дана какая-то роль в мировой культуре. Три дела возложены на него: во-первых, освободить звуки из родной безначальной стихии, в которой они пребывают; во-вторых, привести эти звуки в гармонию, дать им форму; в-третьих, внести эту гармонию во внешний мир".
Поиски скрытой гармонии — высший удел и ученых, и художников. Это вечный путь человеческой культуры, путь, приносящий и ученым, и художникам муки и радости. А в конце пути, когда "ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже", сияет недосягаемая вершина — Гармония.
О трудном пути к этой вершине писано немало. Писал о нем и русский художник В. И. Суриков: "А какое время надо, чтобы картина утряслась так, чтобы переменить ничего нельзя было. Действительные размера каждого предмета найти нужно. Важно найти замбк" чтобы все части соединить. Это — математика". Имени0 математике, лежащей в основе скрытой гармонии искусства, и посвящены следующие три части книги.
II. Математика и музыка
Раздумывая об искусстве и науке, об их взаимных связях и, противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и что между ними размещается все, что человечество создало в области науки и искусства.Г. Нейгауз
 Наш разговор о многообразных отношениях между математикой и искусством мы не случайно начинаем с музыки, ибо связь математики и музыки представляется наиболее обусловленной как исторически, так и внутренне. Математика — самая абстрактная из наук, а музыка — наиболее отвлеченное из искусств, это высшие выразители науки и искусства.
Первые попытки математического осмысления искусства, так же как и сами истоки математики и искусства, теряются в глубине веков задолго до нашей эры. Воплощение математических законов просматривается в загадочном величии египетских пирамид. Пространственные формы пирамид настолько правильны и геометричны, что они вот уже пятое тысячелетие видятся скорее не плодом вдохновенного порыва художника, а результатом скрупулезных построений древнеегипетского математика. Другим интересным проявлением поисков математических закономерностей в области ваяния и зодчества является существование в древности так называемых "канонов", т. е. совокупности правил изображения человеческой фигуры. Создателем первого канона считается древнеегипетский архитектор и скульптор Имхотеп (XXVIII в. до н. э.), а Древняя Греция подарила миру великого ваятеля и теоретика искусства Поликлета (V в. до н. э.). "Сделал Поликлет также статую копьеносца (дорифор) — возмужалого юноши. Ее художники зовут Каноном и получают из нее, словно из какого-нибудь закона, основания своего искусства, и Поликлета считают единственным человеком, который из произведения искусства сделал его теорию". Так писал о Поликлете Плиний Старший (23(24)-79), римский писатель, ученый и государственный деятель, погибший в Помпее во время извержения Везувия, автор "Естественной истории" в 37 книгах — своеобразной энциклопедии естественнонаучных знаний античности.
Тем не менее названные примеры говорят скорее о случайном и неосознанном проникновении математики в пластические искусства (приписываемая Имхотепу книга канонов "Души Ра", согласно преданию, попросту упала с неба к северу от Мемфиса). А вот осмысленное и систематическое приложение к искусству математика нашла, конечно, в музыке, в трудах древнегреческого математика Пифагора, его многочисленных учеников последователей.
Наш разговор о многообразных отношениях между математикой и искусством мы не случайно начинаем с музыки, ибо связь математики и музыки представляется наиболее обусловленной как исторически, так и внутренне. Математика — самая абстрактная из наук, а музыка — наиболее отвлеченное из искусств, это высшие выразители науки и искусства.
Первые попытки математического осмысления искусства, так же как и сами истоки математики и искусства, теряются в глубине веков задолго до нашей эры. Воплощение математических законов просматривается в загадочном величии египетских пирамид. Пространственные формы пирамид настолько правильны и геометричны, что они вот уже пятое тысячелетие видятся скорее не плодом вдохновенного порыва художника, а результатом скрупулезных построений древнеегипетского математика. Другим интересным проявлением поисков математических закономерностей в области ваяния и зодчества является существование в древности так называемых "канонов", т. е. совокупности правил изображения человеческой фигуры. Создателем первого канона считается древнеегипетский архитектор и скульптор Имхотеп (XXVIII в. до н. э.), а Древняя Греция подарила миру великого ваятеля и теоретика искусства Поликлета (V в. до н. э.). "Сделал Поликлет также статую копьеносца (дорифор) — возмужалого юноши. Ее художники зовут Каноном и получают из нее, словно из какого-нибудь закона, основания своего искусства, и Поликлета считают единственным человеком, который из произведения искусства сделал его теорию". Так писал о Поликлете Плиний Старший (23(24)-79), римский писатель, ученый и государственный деятель, погибший в Помпее во время извержения Везувия, автор "Естественной истории" в 37 книгах — своеобразной энциклопедии естественнонаучных знаний античности.
Тем не менее названные примеры говорят скорее о случайном и неосознанном проникновении математики в пластические искусства (приписываемая Имхотепу книга канонов "Души Ра", согласно преданию, попросту упала с неба к северу от Мемфиса). А вот осмысленное и систематическое приложение к искусству математика нашла, конечно, в музыке, в трудах древнегреческого математика Пифагора, его многочисленных учеников последователей.
5. Пифагор и пифагорейское учение о числе
Греки совершили открытие, величайшее из когда-либо совершенных человеком: они открыли могущество разума.С берегов Средиземноморья — "колыбели европейской цивилизации", с тех давних времен, названных через много веков "весною человечества", дошло до нас имя Пифагора — математика, философа, мистика. Мы не знаем доподлинно портрета Пифагора, не сохранилось ни одной строки из его сочинений; его биография стала легендой, полной невероятных преувеличений, а самого Пифагора назвали "на одну десятую гением, на девять десятых выдумкой". По преданию, вид его был так величествен, что ученикам часто казалось, будто это сам бог Аполлон говорит с ними. Пифагор — едва ли не самый популярный ученый не только в античности, но и в наши дни. И дело, конечно, не в том, что "таблица Пифагора" смотрит на нас с любой тетрадки в клеточку. Дело в том, что "то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило все последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы". Так определяет роль Пифагора в современной науке американский математик М. Клайн. Что же известно о Пифагоре? Родился Пифагор на острове Самос, расположенном в Эгейском море у берегов Малой Азии, около 570 г. до н. э. Остров Самос известен пробитым под горою Кастро туннелем, по которому проходилводопровод, снабжавший город Самос питьевой водой. Туннель строился с двух сторон, причем расчеты, без которых в этом деле не обойтись, были настолько точными, что оба хода сошлись под горой с незначительной ошибкой. Самосский туннель, построенный около 530 г. до н. э., является едва ли не единственным замечательным подтверждением математической подготовки греческих строителей — современников Пифагора, свидетельствует о высоком уровне математики того времени и смелом ее применении. Отец Пифагора Мнесарх был резчиком по драгоценным камням. Будучи пытливым юношей, Пифагор отправился в путешествие по странам Востока, спускался в знаменитую пещеру Крита, с которой греки связывали миф о сотворении богов, был в Египте, где якобы попал в плен к персам и был увезен в Вавилон. Это несчастье сыграло счастливую роль в судьбе Пифагора: вавилонская наука, и в частности математика, была передовой наукой того времени, и у халдейских мудрецов было чему поучиться. И хотя о странствиях Пифагора, как и о всей его жизни, нет достоверных данных, взаимосвязь вавилонской математики и математики Пифагора (вспомним хотя бы, что знаменитая теорема Пифагора была известна без доказательства вавилонянам) указы-" вает на то, что Пифагор во многом воспринял восточную мудрость. Египетские жрецы и вавилонские халдеи привили также Пифагору пристрастие к восточным таинствам, магии и числовой мистике.М. Клайн
 Предполагаемый бюст Пифагора. Найден при раскопках Геркуланума близ Помпеи. Бронзовая копия с греческого оригинала. IV в. до н. э. (?)
Вернувшись на родину, Пифагор собирает вокруг себя единомышленников, приспособив для занятий философией одну из пещер, где проводит почти все дни и ночи. Однако вскоре он покидает родной город в знак протеста против деятельности правителя Самоса, тирана Поликрата, считая, что свободный человек не должен подчиняться произволу и деспотизму. Согласно преданию, на сороковом году жизни Пифагор поселился в южноиталийском городе Кротоне. Здесь он "сразу привлек всеобщее уважение как человек, много странствующий, многоопытный и дивно одаренный судьбою и природою: с виду он был величав и благороден, а красота и обаяние были у него и в голосе, и в обхождении, и во всем",- писал в "Жизни Пифагора" древнегреческий философ Порфирий (233-304) В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Система жизненных принципов и правил, проповедуемая Пифагором, и сейчас достойна подражания. Так, Пифагор учил: "беги от всякой хитрости, любым орудием отсекай от тела болезнь, от души — невежество, от утробы — роскошество, от семьи — ссору, от всего, что есть — неумеренность". День пифагорейцу надлежало заканчивать вопросом:
Предполагаемый бюст Пифагора. Найден при раскопках Геркуланума близ Помпеи. Бронзовая копия с греческого оригинала. IV в. до н. э. (?)
Вернувшись на родину, Пифагор собирает вокруг себя единомышленников, приспособив для занятий философией одну из пещер, где проводит почти все дни и ночи. Однако вскоре он покидает родной город в знак протеста против деятельности правителя Самоса, тирана Поликрата, считая, что свободный человек не должен подчиняться произволу и деспотизму. Согласно преданию, на сороковом году жизни Пифагор поселился в южноиталийском городе Кротоне. Здесь он "сразу привлек всеобщее уважение как человек, много странствующий, многоопытный и дивно одаренный судьбою и природою: с виду он был величав и благороден, а красота и обаяние были у него и в голосе, и в обхождении, и во всем",- писал в "Жизни Пифагора" древнегреческий философ Порфирий (233-304) В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Система жизненных принципов и правил, проповедуемая Пифагором, и сейчас достойна подражания. Так, Пифагор учил: "беги от всякой хитрости, любым орудием отсекай от тела болезнь, от души — невежество, от утробы — роскошество, от семьи — ссору, от всего, что есть — неумеренность". День пифагорейцу надлежало заканчивать вопросом:
 Звездчатый пятиугольник, или пентаграмма,- пифагорейский символ здравия и тайный опознавательный знак
Обет молчания, даваемый пифагорейцами, нашел отражение в символе "бык на языке", что на современный лад означает "держи язык за зубами". Вообще, пифагорейцы имели множество знаков и символов, которые были своего
рода заповедями, например: "через весы не шагай", т. е. не нарушай справедливости; "огня ножом не вороши", т. е. не задевай гневных людей обидными словами; "не ешь сердца", т. е. не подтачивай душу страстями или горем.
Но главным пифагорейским символом — символом здоровья и опознавательным знаком — была пентаграмма или пифагорейская звезда — звездчатый пятиугольник, образованный диагоналями правильного пятиугольника. Звездчатый пятиугольник обладает замечательными математическими свойствами, которые мы рассмотрим в главе 15. Он содержит все пропорции, известные пифагорейцам: арифметическую, геометрическую, гармоническую и так называемую золотую. Видимо, поэтому пентаграмма и была выбрана в качестве пифагорейского символа.
Нарисованная пентаграмма была тайным знаком, по которому пифагорейцы узнавали друг друга. Согласно легенде, когда один пифагореец умирал на чужбине и не мог расплатиться с гостеприимным хозяином дома, ухаживавшим за ним, он велел хозяину нарисовать на стене своего дома пентаграмму. "Если когда-нибудь мимо пройдет пифагореец, он обязательно сюда заглянет",- сказал умиравший. Действительно, через несколько лет другой странствующий пифа гореец увидел знак, расспросил о случившемся хозяина и щедро вознагради его.
Однако в первоначальном виде пифагорейский союз просуществовал недолго и к концу VI века (ок. 510 г. до н. э.) подвергся кровавой расправе. Пифагорейцы бежали из Кротона в другие города, что во многом способствовало распространению учения Пифагора по всей Греции и даже за ее пределы. Сам Пифагор удалился в город Метапонт, расположенный неподалеку от Кротона, где и провел остаток своей жизни.
Смерть Пифагора также окружена красивыми легендами. По одной из них, дом в Кротоне, где Пифагор собирался со своими учениками, был подожжен. Преданные друзья бросились в огонь и проложили в нем дорогу учителю, чтобы он по их телам вышел из огня, как по мосту. Друзья погибли, а сам Пифагор, будучи спасенным столь дорогой ценой, так затосковал, что лишил себя жизни. Умер Пифагор около 500 г. до н. э.
Подлинно новым и революционным в пифагорейской научной системе явилось учение о числе, которое мы рассмотрим в трех аспектах: философском, математическом и музыкальном. В числовых отношениях, т. е. в математике, видели пифагорейцы сущность мировой гармонии, ключ к разгадке всех тайн природы, окруженных ореолом мифологии. Вообще, развитие пифагореизма шло от мифологии через философию к науке. Пифагорейская наука была еще слишком близка к мифологии, чем и объясняется царившее в ней "мифологическое начало". Но то, что в математических свойствах пифагорейцы увидели сущность явлений природы, то, что в основе разнородных процессов они обнаружили некоторую пропорциональность, закономерность, выражаемую числом, было выдающимся научным завоеванием. "Подобно тому как число подчинено определенным законам, подчинена им и вселенная; этим впервые высказывается мысль о закономерен вселенной",- так характеризовал роль пифагорейского учения о числе Ф. Энгельс (т. 20, с. 503).
Примечательно, что отправным пунктом в пифагорейском учении о числе была музыка. Именно в музыке была первые обнаружена таинственная направляющая роль чисел в природе. По преданию, сам Пифагор установил, что приятные слуху созвучия получаются лишь в том случае, когда длины струн, издающих эти звуки, относятся как целые числа первой четверки: 1:2, 2:3, 3:4 (см. гл. 6). Это открытие потрясло Пифагора и долго вдохновляло его учеников на поиски новых числовых закономерностей в природе. По мнению выдающегося немецкого физика А. Зоммерфельда, день, когда было сделано это открытие, можно назвать днем рождения математической физики.
Вот как описывает этот день римский философ и сенатор Северин Боэций (480- 524): "И вот однажды, под влиянием какого-то божественного наития, проходя мимо кузниц, он слышит, что удары молотков из различных звуков образуют некое единое звучание. Тогда, пораженный, он подошел вплотную к тому, что долгое время искал, и после долгого размышления решил, что различие звуков обусловлено силами ударяющих, а для того чтобы уяснить это лучше, велел кузнецам поменяться молотками. Однако выяснилось, что свойство звуков не заключено в мышцах людей и продолжает сопровождать молотки, поменявшиеся мерами. Когда, следовательно, Пифагор это заметил, то исследовал вес молотков. Тих молотков было пять, причем обнаружилось, что один из них был вдвое больше Другого и эти два отвечали друг другу соответственно созвучию октавы. Вес вдвое большего был на 4/3 больше веса третьего, а именно того, с которым он звучал в кварту...
Вернувшись домой, Пифагор путем различного исследования стал выяснять, заключается ли в этих пропорциях вся причина созвучия (Трактат о музыке)".
Звездчатый пятиугольник, или пентаграмма,- пифагорейский символ здравия и тайный опознавательный знак
Обет молчания, даваемый пифагорейцами, нашел отражение в символе "бык на языке", что на современный лад означает "держи язык за зубами". Вообще, пифагорейцы имели множество знаков и символов, которые были своего
рода заповедями, например: "через весы не шагай", т. е. не нарушай справедливости; "огня ножом не вороши", т. е. не задевай гневных людей обидными словами; "не ешь сердца", т. е. не подтачивай душу страстями или горем.
Но главным пифагорейским символом — символом здоровья и опознавательным знаком — была пентаграмма или пифагорейская звезда — звездчатый пятиугольник, образованный диагоналями правильного пятиугольника. Звездчатый пятиугольник обладает замечательными математическими свойствами, которые мы рассмотрим в главе 15. Он содержит все пропорции, известные пифагорейцам: арифметическую, геометрическую, гармоническую и так называемую золотую. Видимо, поэтому пентаграмма и была выбрана в качестве пифагорейского символа.
Нарисованная пентаграмма была тайным знаком, по которому пифагорейцы узнавали друг друга. Согласно легенде, когда один пифагореец умирал на чужбине и не мог расплатиться с гостеприимным хозяином дома, ухаживавшим за ним, он велел хозяину нарисовать на стене своего дома пентаграмму. "Если когда-нибудь мимо пройдет пифагореец, он обязательно сюда заглянет",- сказал умиравший. Действительно, через несколько лет другой странствующий пифа гореец увидел знак, расспросил о случившемся хозяина и щедро вознагради его.
Однако в первоначальном виде пифагорейский союз просуществовал недолго и к концу VI века (ок. 510 г. до н. э.) подвергся кровавой расправе. Пифагорейцы бежали из Кротона в другие города, что во многом способствовало распространению учения Пифагора по всей Греции и даже за ее пределы. Сам Пифагор удалился в город Метапонт, расположенный неподалеку от Кротона, где и провел остаток своей жизни.
Смерть Пифагора также окружена красивыми легендами. По одной из них, дом в Кротоне, где Пифагор собирался со своими учениками, был подожжен. Преданные друзья бросились в огонь и проложили в нем дорогу учителю, чтобы он по их телам вышел из огня, как по мосту. Друзья погибли, а сам Пифагор, будучи спасенным столь дорогой ценой, так затосковал, что лишил себя жизни. Умер Пифагор около 500 г. до н. э.
Подлинно новым и революционным в пифагорейской научной системе явилось учение о числе, которое мы рассмотрим в трех аспектах: философском, математическом и музыкальном. В числовых отношениях, т. е. в математике, видели пифагорейцы сущность мировой гармонии, ключ к разгадке всех тайн природы, окруженных ореолом мифологии. Вообще, развитие пифагореизма шло от мифологии через философию к науке. Пифагорейская наука была еще слишком близка к мифологии, чем и объясняется царившее в ней "мифологическое начало". Но то, что в математических свойствах пифагорейцы увидели сущность явлений природы, то, что в основе разнородных процессов они обнаружили некоторую пропорциональность, закономерность, выражаемую числом, было выдающимся научным завоеванием. "Подобно тому как число подчинено определенным законам, подчинена им и вселенная; этим впервые высказывается мысль о закономерен вселенной",- так характеризовал роль пифагорейского учения о числе Ф. Энгельс (т. 20, с. 503).
Примечательно, что отправным пунктом в пифагорейском учении о числе была музыка. Именно в музыке была первые обнаружена таинственная направляющая роль чисел в природе. По преданию, сам Пифагор установил, что приятные слуху созвучия получаются лишь в том случае, когда длины струн, издающих эти звуки, относятся как целые числа первой четверки: 1:2, 2:3, 3:4 (см. гл. 6). Это открытие потрясло Пифагора и долго вдохновляло его учеников на поиски новых числовых закономерностей в природе. По мнению выдающегося немецкого физика А. Зоммерфельда, день, когда было сделано это открытие, можно назвать днем рождения математической физики.
Вот как описывает этот день римский философ и сенатор Северин Боэций (480- 524): "И вот однажды, под влиянием какого-то божественного наития, проходя мимо кузниц, он слышит, что удары молотков из различных звуков образуют некое единое звучание. Тогда, пораженный, он подошел вплотную к тому, что долгое время искал, и после долгого размышления решил, что различие звуков обусловлено силами ударяющих, а для того чтобы уяснить это лучше, велел кузнецам поменяться молотками. Однако выяснилось, что свойство звуков не заключено в мышцах людей и продолжает сопровождать молотки, поменявшиеся мерами. Когда, следовательно, Пифагор это заметил, то исследовал вес молотков. Тих молотков было пять, причем обнаружилось, что один из них был вдвое больше Другого и эти два отвечали друг другу соответственно созвучию октавы. Вес вдвое большего был на 4/3 больше веса третьего, а именно того, с которым он звучал в кварту...
Вернувшись домой, Пифагор путем различного исследования стал выяснять, заключается ли в этих пропорциях вся причина созвучия (Трактат о музыке)".
 Пифагор со своими учениками. Иллюстрация из книги Франкино Гафурио 'Теория музыки'. Милан. 1492. Гравюры изображают акустические опыты Пифагора и Филолая на сосудах, струнах и трубках, находящихся в отношениях 4:6: :8:9:12:16
Только что появившаяся на свет пифагорейская наука еще не могла отделить абстрактное понятие числа от конкретного материального объекта. Видя в числах сущность явлений, начало начал, пифагорейцы считали, что реальные тела состоят из "единиц бытия" — "математических атомов", различные комбинации которых и представляют конкретные объекты. Даже вселенная мыслилась ими как совокупность чисел. Сами же числа пифагорейцы представляли наглядно и материально: единица трактовалась как абсолютная и неделимая единичность, т. е. точка, "геометрический атом" или первооснова всех чисел; два — как уход в неопределенную даль, т. е. прямая линия, простирающаяся в одном измерении; три — треугольник, образующий плоскость двух измерений, и возврат к определенности; четыре — пирамида, дающая представление о пространстве трех измерений. Вообще, числа 1, 2, 3, 4 играли у пифагорейцев особую роль и образовывали тетрактис, или четверку. По преданию, клятва пифагорейцев гласила: "Клянусь именем Тетрактис, ниспосланной нашим душам. В ней источник и корни вечно цветущей природы". Особая роль тетрактиса, видимо, была навеяна законами музыкальных созвучий, после чего все объекты природы виделись пифагорейцам состоящими из четверок: четверка геометрических элементов — точка, линия, поверхность, тело; четверка физических элементов — земля, вода, огонь, воздух. (Учение Платона о четырех физических элементах, четырех стихиях, мы рассмотрим в главе 7.) Сумма же чисел, образующих тетрактис, равная десяти (10 = 1 + 2+ 3 + 4), считалась священным числом и олицетворяла всю вселенную.
Так родился знаменитый пифагорейский тезис: "Все вещи суть числа". Этот тезис, если забыть о его внутреннем содержании, а тем более если числа отождествлять с цифрами, многим представлялся попросту абсурдным. Далее, считая, что материальный мир состоит из чисел, т. е. из идей, пифагорейцы, сами того не сознавая, становились на позиции философского идеализма, и не случайно именно на почве пифагореизма возникло учение основоположника объективного идеализма в философии Платона. Наконец, интерес к числу часто носил у пифагорейцев религиозно-мистический характер[10]. Но всякое явление следует рассматривать в его историческом окружении "Идеалистическая мистификация чисел у пифагорейцев была следствием неразвитости науки и философии и строя мышления, близкого к мифологическому,- пишет современный болгарский философ Е. Данков.- Но за этой формой нельзя не видеть рационального содержания значение которого все яснее проступает на современном уровне развития научного познания".
Наиболее страстно и убежденно роль числа в познании мира определил знаменитый пифагореец V века до н. э. Филолай. В одном из сохранившихся фрагментов сочинения Филолая "О природе" говорится: "В число же никогда не проникает ложь, потому что она противна и ненавистна его природе, истина же родственна числу и неразрывно связана с ним с самого начала".
Заканчивая разговор о философских аспектах пифагорейского учения о числе, хочется вспомнить и слова великого Гёте. Будучи не только гениальным поэтом, но и выдающимся мыслителем и разносторонним ученым; Гёте стряхнул с пифагорейской мудрости идеалистическую пыль: "Числа не управляют миром, но показывают, как управляется мир".
Перейдем теперь к математической стороне пифагорейского учения о числе. Числа пифагорейцы изображали в виде точек (возможно, камешками, расположенными на песке), которые они группировали в геометрические фигуры. Так возникли числа, сегодня именуемые фигурными:
линейные числа (в современной терминологии это простые числа), т. е. числа, которые делятся на единицу и на самих себя и, следовательно, представимы только в виде последовательности точек, выстроенных в линию
Пифагор со своими учениками. Иллюстрация из книги Франкино Гафурио 'Теория музыки'. Милан. 1492. Гравюры изображают акустические опыты Пифагора и Филолая на сосудах, струнах и трубках, находящихся в отношениях 4:6: :8:9:12:16
Только что появившаяся на свет пифагорейская наука еще не могла отделить абстрактное понятие числа от конкретного материального объекта. Видя в числах сущность явлений, начало начал, пифагорейцы считали, что реальные тела состоят из "единиц бытия" — "математических атомов", различные комбинации которых и представляют конкретные объекты. Даже вселенная мыслилась ими как совокупность чисел. Сами же числа пифагорейцы представляли наглядно и материально: единица трактовалась как абсолютная и неделимая единичность, т. е. точка, "геометрический атом" или первооснова всех чисел; два — как уход в неопределенную даль, т. е. прямая линия, простирающаяся в одном измерении; три — треугольник, образующий плоскость двух измерений, и возврат к определенности; четыре — пирамида, дающая представление о пространстве трех измерений. Вообще, числа 1, 2, 3, 4 играли у пифагорейцев особую роль и образовывали тетрактис, или четверку. По преданию, клятва пифагорейцев гласила: "Клянусь именем Тетрактис, ниспосланной нашим душам. В ней источник и корни вечно цветущей природы". Особая роль тетрактиса, видимо, была навеяна законами музыкальных созвучий, после чего все объекты природы виделись пифагорейцам состоящими из четверок: четверка геометрических элементов — точка, линия, поверхность, тело; четверка физических элементов — земля, вода, огонь, воздух. (Учение Платона о четырех физических элементах, четырех стихиях, мы рассмотрим в главе 7.) Сумма же чисел, образующих тетрактис, равная десяти (10 = 1 + 2+ 3 + 4), считалась священным числом и олицетворяла всю вселенную.
Так родился знаменитый пифагорейский тезис: "Все вещи суть числа". Этот тезис, если забыть о его внутреннем содержании, а тем более если числа отождествлять с цифрами, многим представлялся попросту абсурдным. Далее, считая, что материальный мир состоит из чисел, т. е. из идей, пифагорейцы, сами того не сознавая, становились на позиции философского идеализма, и не случайно именно на почве пифагореизма возникло учение основоположника объективного идеализма в философии Платона. Наконец, интерес к числу часто носил у пифагорейцев религиозно-мистический характер[10]. Но всякое явление следует рассматривать в его историческом окружении "Идеалистическая мистификация чисел у пифагорейцев была следствием неразвитости науки и философии и строя мышления, близкого к мифологическому,- пишет современный болгарский философ Е. Данков.- Но за этой формой нельзя не видеть рационального содержания значение которого все яснее проступает на современном уровне развития научного познания".
Наиболее страстно и убежденно роль числа в познании мира определил знаменитый пифагореец V века до н. э. Филолай. В одном из сохранившихся фрагментов сочинения Филолая "О природе" говорится: "В число же никогда не проникает ложь, потому что она противна и ненавистна его природе, истина же родственна числу и неразрывно связана с ним с самого начала".
Заканчивая разговор о философских аспектах пифагорейского учения о числе, хочется вспомнить и слова великого Гёте. Будучи не только гениальным поэтом, но и выдающимся мыслителем и разносторонним ученым; Гёте стряхнул с пифагорейской мудрости идеалистическую пыль: "Числа не управляют миром, но показывают, как управляется мир".
Перейдем теперь к математической стороне пифагорейского учения о числе. Числа пифагорейцы изображали в виде точек (возможно, камешками, расположенными на песке), которые они группировали в геометрические фигуры. Так возникли числа, сегодня именуемые фигурными:
линейные числа (в современной терминологии это простые числа), т. е. числа, которые делятся на единицу и на самих себя и, следовательно, представимы только в виде последовательности точек, выстроенных в линию  (линейное число 5);
плоские числа — числа, представимые в виде произведения двух сомножителей
(линейное число 5);
плоские числа — числа, представимые в виде произведения двух сомножителей  (плоское число 6);
телесные числа, выражаемые произведением трех сомножителей
(плоское число 6);
телесные числа, выражаемые произведением трех сомножителей  (телесное число 8);
треугольные числа
(телесное число 8);
треугольные числа  (треугольные числа 1, 3, 6, 10);
квадратные числа
(треугольные числа 1, 3, 6, 10);
квадратные числа  (квадратные числа 1, 4, 9);
пятиугольные числа
(квадратные числа 1, 4, 9);
пятиугольные числа  (пятиугольные числа 1, 5, 12)
и т. д. Именно от фигурных чисел пошло выражение "возвести число в квадрат или куб".
Такое фигурное представление чисел часто помогало найти различные числовые закономерности. Например, написав последовательность квадратных чисел, легко увидеть (именно увидеть глазами!)
доказательство следующего математического утверждения:
(пятиугольные числа 1, 5, 12)
и т. д. Именно от фигурных чисел пошло выражение "возвести число в квадрат или куб".
Такое фигурное представление чисел часто помогало найти различные числовые закономерности. Например, написав последовательность квадратных чисел, легко увидеть (именно увидеть глазами!)
доказательство следующего математического утверждения:

 Аналогичное рассмотрение n-го треугольного числа приводит к равенству
Аналогичное рассмотрение n-го треугольного числа приводит к равенству
 Фигура (обозначенная черными точками), которая, будучи приложенной к основной фигуре (белые точки), образует ей подобную, была названа Аристотелем гномоном. Первоначально слово "гномон" означало солнечные часы — прибор, позволяющий по линиям, которые пересекает тень от вертикального столбика, разделять беспредельность времени на очевидные части. Число для пифагорейцев и есть такой гносеологический гномон, дающий возможность различать вещи и тем самым овладевать ими в сознании. Живые организмы растут именно методом гномона, что позволяет сохранять присущую этим организмам форму.
Вообще, с изучения фигурных чисел, т. е. сумм некоторого числа единиц-точек (камешков), поставленных в виде определенной фигуры, началось изучение сумм числовых рядов. Это в свою очередь позволило Архимеду (ок. 287-212 гг. до н. э.) развить методы нахождения площадей и объемов фигур и тел и вплотную подойти к созданию интегрального исчисления, появившегося, однако, лишь 2000 лет спустя.
Рассмотрение чисел привело пифагорейцев к рассмотрению отношений между ними, т. е. пропорций. Пропорция с равными средними членами определяет среднее значение. По преданию, Пифагору были известны три вида средних значений, которые называли "древними":
арифметическое среднее
Фигура (обозначенная черными точками), которая, будучи приложенной к основной фигуре (белые точки), образует ей подобную, была названа Аристотелем гномоном. Первоначально слово "гномон" означало солнечные часы — прибор, позволяющий по линиям, которые пересекает тень от вертикального столбика, разделять беспредельность времени на очевидные части. Число для пифагорейцев и есть такой гносеологический гномон, дающий возможность различать вещи и тем самым овладевать ими в сознании. Живые организмы растут именно методом гномона, что позволяет сохранять присущую этим организмам форму.
Вообще, с изучения фигурных чисел, т. е. сумм некоторого числа единиц-точек (камешков), поставленных в виде определенной фигуры, началось изучение сумм числовых рядов. Это в свою очередь позволило Архимеду (ок. 287-212 гг. до н. э.) развить методы нахождения площадей и объемов фигур и тел и вплотную подойти к созданию интегрального исчисления, появившегося, однако, лишь 2000 лет спустя.
Рассмотрение чисел привело пифагорейцев к рассмотрению отношений между ними, т. е. пропорций. Пропорция с равными средними членами определяет среднее значение. По преданию, Пифагору были известны три вида средних значений, которые называли "древними":
арифметическое среднее  геометрическое среднее
геометрическое среднее  гармоническое среднее
гармоническое среднее  Обратим внимание на то, что среднее гармоническое величин а, b, с есть среднее арифметическое обратных величин 1/а, 1/b, 1/с. Пропорции и средние значения пифагорейцы наполняли не только математическим, но и философским и эстетическим содержанием, объясняя с их помощью и музыкальные созвучия, и даже всю вселенную.
Обратим внимание на то, что среднее гармоническое величин а, b, с есть среднее арифметическое обратных величин 1/а, 1/b, 1/с. Пропорции и средние значения пифагорейцы наполняли не только математическим, но и философским и эстетическим содержанием, объясняя с их помощью и музыкальные созвучия, и даже всю вселенную.
Однако история науки, как и сама жизнь, полна неожиданных и драматических событий: среднее геометрическое таило в себе сокрушительный удар по всей пифагорейской системе; более того, нанести этот удар пифагорейцы, истинные рыцари науки, вынуждены были сами себе. Именно пифагорейцы обнаружили, что среднее геометрическое к числам 1 и 2 (в современных обозначениях
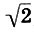 ) не выражается в виде отношения натуральных чисел, а других чисел древние греки не знали. Говоря языком геометрии, пифагорейцы установили, что диагональ квадрата, сторона которого равна 1, несоизмерима с этой стороной, т. е. отношение диагонали к стороне не выражается никаким целым или дробным числом. Выражаясь языком алгебры, пифагорейцы доказали, что уравнение m2=2n2 не имеет решений во множестве рациональных чисел[11], что и потребовало введения чисел новой природы — иррациональных.
Иррациональность отношения стороны и диагонали квадрата пифагорейцы объясняли тем, что оба этих отрезка состоят из бесчисленного множества точек и поэтому отношение сводится к отношению двух бесконечно больших целых чисел. Хотя эта мысль не выдерживает критики для геометрических объектов, находящихся в рациональных отношениях (ведь они также состоят из бесчисленного множества точек!), по отношению к иррациональным числам она является справедливой. Действительно, всякое иррациональное число можно с любой степенью точности представить в виде отношения двух целых чисел, причем чем больше будут эти числа, тем точнее их отношение будет выражать иррациональное число.
Открытие несоизмеримости (для диагонали квадрата со стороной 1 не было соответствующего числа!) опрокидывало всю философскую систему пифагорейцев, которые были убеждены, что "элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом". Это открытие долго держалось в тайне, а ученик Пифагора Гиппас из Метапонта за то, что он открыл недостойным участия в учениях природу пропорции и несоизмеримости, был изгнан из школы Пифагора. Позднее, когда Гиппас погиб во время кораблекрушения, его противники видели в этом наказание богов за разглашение тайны. Следует сказать, что пифагорейцы, не в пример иным ученым, после отчаянной борьбы против открытия, опрокидывавшего символ их "веры" признали свое поражение. Пытаясь выйти из тупика, они стали представлять величины не арифметически — числами, геометрически — отрезками. Так возникла геометрическая алгебра.
Между тем исторически именно это неосознанное открытие иррациональных чисел является наивысшим достижением пифагорейской школы; ему было суждено пережить тысячелетия и стать поворотным этапом в развитии математики, истоком современного математического анализа. С этого открытия начинается эра теоретической математики, ибо обнаружить несоизмеримые величины с помощью опыта невозможно.
Наконец, рассмотрим "музыкальную" сторону пифагорейского учения о числе. Как уже отмечалось, открытие математических закономерностей в музыкальных созвучиях послужило первым "экспериментальным" подтверждением пифагорейской философии числа. "Открытие Пифагора... было первым примером установления числовых связей в природе,- читаем мы в "Фейнмановских лекциях по физике".- Поистине должно быть было удивительно вдруг неожиданно обнаружить, что в природе есть факты, которые описываются простыми числовыми отношениями".
С этого времени музыка, точнее теория Музыки или учение о гармонии, занимает Почетное место в пифагорейской системе Знаний. "Музыкантов"-пифагорейцев интересует не столько музыкальное искусство, реальная музыка звуков, сколько е математические пропорции и соотношения, которые, как считалось, лежат в основе музыки. Многие греческие математики, в том числе Евклид (III в. до н. э.) и Клавдий Птолемей (85? -165?), посвятили музыкальным созвучиям и построению музыкальной шкалы специальные сочинения. Впрочем, поиски математических закономерностей в музыкальных созвучиях вели и через два тысячелетия такие великие математики, как Иоганн Кеплер, Готфрид Лейбниц, Леонард Эйлер.
) не выражается в виде отношения натуральных чисел, а других чисел древние греки не знали. Говоря языком геометрии, пифагорейцы установили, что диагональ квадрата, сторона которого равна 1, несоизмерима с этой стороной, т. е. отношение диагонали к стороне не выражается никаким целым или дробным числом. Выражаясь языком алгебры, пифагорейцы доказали, что уравнение m2=2n2 не имеет решений во множестве рациональных чисел[11], что и потребовало введения чисел новой природы — иррациональных.
Иррациональность отношения стороны и диагонали квадрата пифагорейцы объясняли тем, что оба этих отрезка состоят из бесчисленного множества точек и поэтому отношение сводится к отношению двух бесконечно больших целых чисел. Хотя эта мысль не выдерживает критики для геометрических объектов, находящихся в рациональных отношениях (ведь они также состоят из бесчисленного множества точек!), по отношению к иррациональным числам она является справедливой. Действительно, всякое иррациональное число можно с любой степенью точности представить в виде отношения двух целых чисел, причем чем больше будут эти числа, тем точнее их отношение будет выражать иррациональное число.
Открытие несоизмеримости (для диагонали квадрата со стороной 1 не было соответствующего числа!) опрокидывало всю философскую систему пифагорейцев, которые были убеждены, что "элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом". Это открытие долго держалось в тайне, а ученик Пифагора Гиппас из Метапонта за то, что он открыл недостойным участия в учениях природу пропорции и несоизмеримости, был изгнан из школы Пифагора. Позднее, когда Гиппас погиб во время кораблекрушения, его противники видели в этом наказание богов за разглашение тайны. Следует сказать, что пифагорейцы, не в пример иным ученым, после отчаянной борьбы против открытия, опрокидывавшего символ их "веры" признали свое поражение. Пытаясь выйти из тупика, они стали представлять величины не арифметически — числами, геометрически — отрезками. Так возникла геометрическая алгебра.
Между тем исторически именно это неосознанное открытие иррациональных чисел является наивысшим достижением пифагорейской школы; ему было суждено пережить тысячелетия и стать поворотным этапом в развитии математики, истоком современного математического анализа. С этого открытия начинается эра теоретической математики, ибо обнаружить несоизмеримые величины с помощью опыта невозможно.
Наконец, рассмотрим "музыкальную" сторону пифагорейского учения о числе. Как уже отмечалось, открытие математических закономерностей в музыкальных созвучиях послужило первым "экспериментальным" подтверждением пифагорейской философии числа. "Открытие Пифагора... было первым примером установления числовых связей в природе,- читаем мы в "Фейнмановских лекциях по физике".- Поистине должно быть было удивительно вдруг неожиданно обнаружить, что в природе есть факты, которые описываются простыми числовыми отношениями".
С этого времени музыка, точнее теория Музыки или учение о гармонии, занимает Почетное место в пифагорейской системе Знаний. "Музыкантов"-пифагорейцев интересует не столько музыкальное искусство, реальная музыка звуков, сколько е математические пропорции и соотношения, которые, как считалось, лежат в основе музыки. Многие греческие математики, в том числе Евклид (III в. до н. э.) и Клавдий Птолемей (85? -165?), посвятили музыкальным созвучиям и построению музыкальной шкалы специальные сочинения. Впрочем, поиски математических закономерностей в музыкальных созвучиях вели и через два тысячелетия такие великие математики, как Иоганн Кеплер, Готфрид Лейбниц, Леонард Эйлер.
 Титульный лист книги Грегора Райха 'Маргарита философи-ка'. Фрайбург. 1503
Идея музыкальных соотношений настолько увлекла пифагорейцев, что они пытались обнаружить их всюду. В конце концов эта идея приняла "космические масштабы" и переросла в идею "всеобщей гармонии". Пифагорейцы утвердились в том, что вся Вселенная устроена на основе музыкальных, т. е. простых числовых, соотношений, что движущиеся планеты издают "музыку небесных сфер", а обычная музыка является лишь "отзвуком" царящей всюду "всеобщей гармонии" (см. гл. 7).
Таким образом, музыка и астрономия были сведены пифагорейцами к анализу числовых закономерностей, т. е. к арифметике и геометрии. Все четыре дисциплины стали считаться математическими и называться одним словом — "математа". Пифагорейское отношение к музыке как точной науке сохранилось и в средние века. Так, квадривиум (буквально — пересечение четырех дорог) — повышенный курс светского образования в средневековых университетах — состоял из четырех предметов: музыки, арифметики, геометрии и астрономии. "Высшая наука — математика — подразделяется на следующие искусства: арифметику, музыку, геометрию и астрономию — это определение римского писателя VI века Кассиодора (ок. 487- ок. 578).- Арифметика — учение о количестве, выражаемом числом, музыка же — учение, которое рассматривает числа по отношению к явлениям наблюдаемым в звуке". Вместе с тривииумом, содержавшим грамматику, риторику и диалектику, квадривиум составлял так называемые "семь свободных искусств" Это был, по мнению Кассиодора, своп элементарных знаний, необходимых монахам для понимания Библии, которму суждено было на протяжении целого тысячелетия представлять систему средневекового образования.
Как видим, термины "наука" и "искусство" в далекие времена античности практически не различались. Пифагорейцы называли математику и музыку родными сестрами. С тех пор дороги математики и музыки разошлись настолько, что их сопоставление сейчас многим покажется просто недоразумением. А ведь музыка пронизана математикой, как и математика полна поэзии и музыки! Это прекрасно чувствовали древние греки, и доказательство тому — содержание следующей главы.
Титульный лист книги Грегора Райха 'Маргарита философи-ка'. Фрайбург. 1503
Идея музыкальных соотношений настолько увлекла пифагорейцев, что они пытались обнаружить их всюду. В конце концов эта идея приняла "космические масштабы" и переросла в идею "всеобщей гармонии". Пифагорейцы утвердились в том, что вся Вселенная устроена на основе музыкальных, т. е. простых числовых, соотношений, что движущиеся планеты издают "музыку небесных сфер", а обычная музыка является лишь "отзвуком" царящей всюду "всеобщей гармонии" (см. гл. 7).
Таким образом, музыка и астрономия были сведены пифагорейцами к анализу числовых закономерностей, т. е. к арифметике и геометрии. Все четыре дисциплины стали считаться математическими и называться одним словом — "математа". Пифагорейское отношение к музыке как точной науке сохранилось и в средние века. Так, квадривиум (буквально — пересечение четырех дорог) — повышенный курс светского образования в средневековых университетах — состоял из четырех предметов: музыки, арифметики, геометрии и астрономии. "Высшая наука — математика — подразделяется на следующие искусства: арифметику, музыку, геометрию и астрономию — это определение римского писателя VI века Кассиодора (ок. 487- ок. 578).- Арифметика — учение о количестве, выражаемом числом, музыка же — учение, которое рассматривает числа по отношению к явлениям наблюдаемым в звуке". Вместе с тривииумом, содержавшим грамматику, риторику и диалектику, квадривиум составлял так называемые "семь свободных искусств" Это был, по мнению Кассиодора, своп элементарных знаний, необходимых монахам для понимания Библии, которму суждено было на протяжении целого тысячелетия представлять систему средневекового образования.
Как видим, термины "наука" и "искусство" в далекие времена античности практически не различались. Пифагорейцы называли математику и музыку родными сестрами. С тех пор дороги математики и музыки разошлись настолько, что их сопоставление сейчас многим покажется просто недоразумением. А ведь музыка пронизана математикой, как и математика полна поэзии и музыки! Это прекрасно чувствовали древние греки, и доказательство тому — содержание следующей главы.
6. Пифагорова гамма
Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства ее должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы.Строго говоря, речь здесь пойдет о пифагоровом строе, а слово "гамма" вынесено в заголовок потому, что оно у всех ассоциируется с музыкой. Что же такое гамма и строй в музыке? Гаммой, или звукорядом, называется последовательность звуков (ступеней) некоторой музыкальной системы (лада), расположенных, начиная от основного звука (основного тона), в восходящем или нисходящем порядке. Название "гамма" происходит от греческой буквы Гγ (гамма), которой в средние века обозначали крайний нижний тон звукоряда, а затем и весь звукоряд. Важнейшей характеристикой музыкального звука является его высота, представляющая отражение в сознании частоты колебания звучащего тела, например струны. Чем больше частота колебаний струны, тем "выше" представляется нам звук. Каждый отдельно взятый звук не образует музыкальной системы и, если он не слишком громкий, не вызывает у нас особой реакции. Однако уже сочетание двух звуков в иных случаях получается приятным и благозвучным, а в других, наоборот "режет" ухо. Согласованное сочетание двух звуков называется консонансом, несогласованное — диссонансом. Ясно, что консонанс или диссонанс двух тонов определяются высотным расстоянием между этими тонами или интервалом. Интервалом между двумя тонами назовем порядковый номер ступени верхнего тона относительно нижнего в данном звукоряде, а интервальным коэффициентом I21 двух тонов — отношение частоты колебаний верхнего тона к частоте нижнего[12]:Плутарх
 (6.1)
Рассмотрим теперь некоторую совокупность звуков, нажав, например, на фортепиано последовательно несколько клавиш. Скорее всего, у нас получится бессвязный набор звуков, как говорится, ни складу ни ладу. В других случаях звуки вроде бы подходят, ладятся между собой, но их совокупность покажется оборванной, незаконченной. Эту последовательность так и хочется продолжить до определенной ноты, которая в данной системе звуков кажется наиболее устойчивой, основной и называется тоникой. Итак, звуки в музыкальной системе связаны между собой определенными зависимостями, одни из них являются неустойчивыми и тяготеют к другим — устойчивым.
Но не только тоника и совокупность Устойчивых и неустойчивых звуков определяют характер музыкальной системы. Легко убедиться, нажав подряд восемь белых клавиш от ноты до (гамма до мажор натуральный) и от ноты ля (ля минор натуральный), что эти гаммы звучат по-разному: первая — мажор — звучит бодро и светло, а вторая — минор — грустно и пасмурно[13]. Следовательно, существует и другая характеристика системы звуков — наклонение: мажорное или минорное. Таким образом, мы приходим к одно^ му из самых сложных понятий в теории музыки — понятию лада.
Ладом называется приятная для слуха взаимосвязь музыкальных звуков, определяемая зависимостью неустойчивых звуков от устойчивых, и прежде всего от основного устойчивого звука — тоники, и имеющая определенный характер звучания — наклонение. История музыкальной культуры знает множество ладов, свойственных разным народам и разным временам. Древние греки знали с десяток ладов, а лады некоторых восточных стран и Индии чрезвычайно сложны, своеобразны и непривычны для европейского слуха. Наиболее распространенные современные лады состоят из семи основных ступеней, каждая из которых может повышаться или понижаться, что дает еще пять дополнительных звуков. Таким образом, диатоническая (7-ступенная) гамма лада превращается в хроматическую (12-звуковую). Первой ступенью лада является тоника. Законы строения лада — это целая наука, краеугольный камень музыкознания, а изучению этих законов многие ученые и композиторы посвятили всю свою жизнь.
(6.1)
Рассмотрим теперь некоторую совокупность звуков, нажав, например, на фортепиано последовательно несколько клавиш. Скорее всего, у нас получится бессвязный набор звуков, как говорится, ни складу ни ладу. В других случаях звуки вроде бы подходят, ладятся между собой, но их совокупность покажется оборванной, незаконченной. Эту последовательность так и хочется продолжить до определенной ноты, которая в данной системе звуков кажется наиболее устойчивой, основной и называется тоникой. Итак, звуки в музыкальной системе связаны между собой определенными зависимостями, одни из них являются неустойчивыми и тяготеют к другим — устойчивым.
Но не только тоника и совокупность Устойчивых и неустойчивых звуков определяют характер музыкальной системы. Легко убедиться, нажав подряд восемь белых клавиш от ноты до (гамма до мажор натуральный) и от ноты ля (ля минор натуральный), что эти гаммы звучат по-разному: первая — мажор — звучит бодро и светло, а вторая — минор — грустно и пасмурно[13]. Следовательно, существует и другая характеристика системы звуков — наклонение: мажорное или минорное. Таким образом, мы приходим к одно^ му из самых сложных понятий в теории музыки — понятию лада.
Ладом называется приятная для слуха взаимосвязь музыкальных звуков, определяемая зависимостью неустойчивых звуков от устойчивых, и прежде всего от основного устойчивого звука — тоники, и имеющая определенный характер звучания — наклонение. История музыкальной культуры знает множество ладов, свойственных разным народам и разным временам. Древние греки знали с десяток ладов, а лады некоторых восточных стран и Индии чрезвычайно сложны, своеобразны и непривычны для европейского слуха. Наиболее распространенные современные лады состоят из семи основных ступеней, каждая из которых может повышаться или понижаться, что дает еще пять дополнительных звуков. Таким образом, диатоническая (7-ступенная) гамма лада превращается в хроматическую (12-звуковую). Первой ступенью лада является тоника. Законы строения лада — это целая наука, краеугольный камень музыкознания, а изучению этих законов многие ученые и композиторы посвятили всю свою жизнь.
 Парфенон — храм богини Афины Парфенос в Афинах. Возведенный в 447-438 до н. э. зодчими Иктином и Каллистра-том в ознаменование победы над персами, украшенный бессмертными работами скульптора Фидия, Парфенон третье тысячелетие несет в себе поразительную загадку гармонии и величия. Этот шедевр архитектуры, названный Ле Корбюзье грандиозной скульптурой, вписанной в прекрасный ландшафт Пирея, остается прекрасным даже в развалинах
Нас же будут в первую очередь интересовать математические закономерности, описывающие строение лада, т. е. музыкальный строй. Музыкальным строем называется математическое выражение определенной системы звуковысотных отношений. Помимо чисто теоретического интереса строй находит применение при настройке музыкальных инструментов с фиксированной высотой звуков, таких, как фортепиано или орган.
В заключение заметим, что наши эксперименты с нажатием клавиш на фортепиано могут закончиться самым редким и самым приятным феноменом, когда взятая система звуков будет не только принадлежать к какому-либо ладу, но и будет носить осмысленный характер. Такой художественно осмысленный последовательный ряд звуков разной высоты называется мелодией. Это как раз то, что мы так любим напевать в зависимости от нашего настроения — бодрого, грустного, веселого...
После такого кратчайшего экскурса в теоретическое музыкознание мы можем вернуться на берега солнечной Эллады во времена мудрого Пифагора. Попытаемся восстановить рассуждения Пифагора и его учеников при построении пифагорова строя, ибо именно этот строй определил на тысячелетия, если не навечно, все развитие музыкальной культуры, не только европейской, но и восточной. Мы уже говорили, что сам Пифагор не оставил никаких письменных работ, да и наследие пифагорейцев представляется безнадежной грудой развалин, т. е. собранием случайно уцелевших фрагментов и более поздних цитат. Бесспорно, развалины эти прекрасны и поныне поражают воображение, как развалины знаменитого Парфенона, однако многое в этих обломках бесследно утеряно и о целом часто можно только догадываться. И все-таки...
Монохорд — однострунный — был одним из первых музыкальных инструментов древних греков. Это был длинный ящик, необходимый для усиления звука, над которым натягивалась струна. Снизу струна поджималась передвижной подставкой для деления струны на две отдельно звучащие части. На деревянном ящике под струной имелась шкала делений, позволявшая точно установить, какая часть струны звучит. Конечно, как музыкальный инструмент монохорд покажется нам слишком примитивным, однако он был прекрасным физическим прибором и учебным пособием, на котором античные созерцатели постигали премудрости музыкальной грамоты.
Древние уверяли, что уже Пифагор Знал законы колебания струны монохорда и построения музыкальных созвучий (консонансов), однако запись об этих законах мы находим у пифагорейца Архита из Тарента (428-365 гг. до н. э.), жившего На полтора столетия позже Пифагора. Архит был, безусловно, самым выдающимся представителем пифагорейской школы, другом философа Платона и учителем математика Евдокса (ок. 408 — ок. 355 гг. до н. э.), государственным деятелем и полководцем. Многосторонность Архита поразительна: он решил знаменитую де-лосскую задачу об удвоении куба, заслуженно считался крупнейшим пифагорейским теоретиком музыки, первым упорядочил механику на основе математики и свел движения механизмов к геометрическим чертежам, работал над деревянной моделью летающего голубя. По мнению Ван дер Вардена, Архит является автором VIII книги "Начал" Евклида, в которой изложена арифметическая теория пропорций. Как государственный деятель Архит пользовался исключительным уважением: он семь лет подряд избирался стратегом*, хотя по закону стратеги выбирались лишь на один год. Путем искусных дипломатических маневров Архит вызволил из плена Платона и тем самым спас жизнь великому философу. "Славный Архит, земель, и морей, и песков исчислитель..." — писал Гораций.
* (Стратег — в древнегреческих городах-государствах военачальник, облеченный ши-кими военными и политическими полномочиями. )
"Законы Пифагора — Архита", на которых основывалась вся пифагорейская теория музыки, можно сформулировать так:
1- Высота тона (частота колебаний f) звучащей струны обратно пропорциональна ее длине l:
Парфенон — храм богини Афины Парфенос в Афинах. Возведенный в 447-438 до н. э. зодчими Иктином и Каллистра-том в ознаменование победы над персами, украшенный бессмертными работами скульптора Фидия, Парфенон третье тысячелетие несет в себе поразительную загадку гармонии и величия. Этот шедевр архитектуры, названный Ле Корбюзье грандиозной скульптурой, вписанной в прекрасный ландшафт Пирея, остается прекрасным даже в развалинах
Нас же будут в первую очередь интересовать математические закономерности, описывающие строение лада, т. е. музыкальный строй. Музыкальным строем называется математическое выражение определенной системы звуковысотных отношений. Помимо чисто теоретического интереса строй находит применение при настройке музыкальных инструментов с фиксированной высотой звуков, таких, как фортепиано или орган.
В заключение заметим, что наши эксперименты с нажатием клавиш на фортепиано могут закончиться самым редким и самым приятным феноменом, когда взятая система звуков будет не только принадлежать к какому-либо ладу, но и будет носить осмысленный характер. Такой художественно осмысленный последовательный ряд звуков разной высоты называется мелодией. Это как раз то, что мы так любим напевать в зависимости от нашего настроения — бодрого, грустного, веселого...
После такого кратчайшего экскурса в теоретическое музыкознание мы можем вернуться на берега солнечной Эллады во времена мудрого Пифагора. Попытаемся восстановить рассуждения Пифагора и его учеников при построении пифагорова строя, ибо именно этот строй определил на тысячелетия, если не навечно, все развитие музыкальной культуры, не только европейской, но и восточной. Мы уже говорили, что сам Пифагор не оставил никаких письменных работ, да и наследие пифагорейцев представляется безнадежной грудой развалин, т. е. собранием случайно уцелевших фрагментов и более поздних цитат. Бесспорно, развалины эти прекрасны и поныне поражают воображение, как развалины знаменитого Парфенона, однако многое в этих обломках бесследно утеряно и о целом часто можно только догадываться. И все-таки...
Монохорд — однострунный — был одним из первых музыкальных инструментов древних греков. Это был длинный ящик, необходимый для усиления звука, над которым натягивалась струна. Снизу струна поджималась передвижной подставкой для деления струны на две отдельно звучащие части. На деревянном ящике под струной имелась шкала делений, позволявшая точно установить, какая часть струны звучит. Конечно, как музыкальный инструмент монохорд покажется нам слишком примитивным, однако он был прекрасным физическим прибором и учебным пособием, на котором античные созерцатели постигали премудрости музыкальной грамоты.
Древние уверяли, что уже Пифагор Знал законы колебания струны монохорда и построения музыкальных созвучий (консонансов), однако запись об этих законах мы находим у пифагорейца Архита из Тарента (428-365 гг. до н. э.), жившего На полтора столетия позже Пифагора. Архит был, безусловно, самым выдающимся представителем пифагорейской школы, другом философа Платона и учителем математика Евдокса (ок. 408 — ок. 355 гг. до н. э.), государственным деятелем и полководцем. Многосторонность Архита поразительна: он решил знаменитую де-лосскую задачу об удвоении куба, заслуженно считался крупнейшим пифагорейским теоретиком музыки, первым упорядочил механику на основе математики и свел движения механизмов к геометрическим чертежам, работал над деревянной моделью летающего голубя. По мнению Ван дер Вардена, Архит является автором VIII книги "Начал" Евклида, в которой изложена арифметическая теория пропорций. Как государственный деятель Архит пользовался исключительным уважением: он семь лет подряд избирался стратегом*, хотя по закону стратеги выбирались лишь на один год. Путем искусных дипломатических маневров Архит вызволил из плена Платона и тем самым спас жизнь великому философу. "Славный Архит, земель, и морей, и песков исчислитель..." — писал Гораций.
* (Стратег — в древнегреческих городах-государствах военачальник, облеченный ши-кими военными и политическими полномочиями. )
"Законы Пифагора — Архита", на которых основывалась вся пифагорейская теория музыки, можно сформулировать так:
1- Высота тона (частота колебаний f) звучащей струны обратно пропорциональна ее длине l:
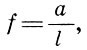 (6.2)
здесь а — коэффициент пропорциональности, зависящий от физических свойств струны (толщины, материала и т. п.).
2. Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т. е. как 1:2, 2:3, 3:4.
Эти интервалы — "совершенные консонансы", и их интервальные коэффициенты позже получили латинские названия* :
* (Названиями интервалов в музыке служат латинские числительные, которые указывают порядковый номер ступени звукоряда, составляющей интервал с исходной ступенью: октава — восьмая, квинта — пятая, кварта — четвертая и т. д.)
октава
(6.2)
здесь а — коэффициент пропорциональности, зависящий от физических свойств струны (толщины, материала и т. п.).
2. Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как целые числа, составляющие треугольное число 10 = 1 + 2 + 3 + 4, т. е. как 1:2, 2:3, 3:4.
Эти интервалы — "совершенные консонансы", и их интервальные коэффициенты позже получили латинские названия* :
* (Названиями интервалов в музыке служат латинские числительные, которые указывают порядковый номер ступени звукоряда, составляющей интервал с исходной ступенью: октава — восьмая, квинта — пятая, кварта — четвертая и т. д.)
октава
 квинт
квинт
 кварта
кварта

 Треугольное число 10
Было замечено также, что наиболее полное слияние тонов дает октава (2/1), затем идут квинта (3/2) и кварта (4/3), т. е. чем меньше число п в отношении вида
Треугольное число 10
Было замечено также, что наиболее полное слияние тонов дает октава (2/1), затем идут квинта (3/2) и кварта (4/3), т. е. чем меньше число п в отношении вида  тем созвучнее интервал.
"Второй закон Пифагора — Архита" и сейчас кажется удивительным. (В его истинной природе мы разберемся в главе 10.) Что же говорить о пифагорейцах, которых он просто привел в восторг! Здесь они нашли подтверждение всей своей философии: целые числа, более того, числа тетрактиса правят всем, даже музыкой! Пифагорейцы не заставили себя долго ждать и распространили закон музыкальных отношений всюду, где это возможно, в том числе и на строение вселенной (см. гл. 7).
Итак, если в качестве цены деления шкалы монохорда взять отрезок l, равный 1/12 длины струны монохорда l1, то вместе со всей струной монохорда длины l1 = 12l будут созвучны ее части длины l2 = 6l — звук на октаву выше (l2/l1 = l/2), l3 = 9l — звук на квинту выше (l3/l1 = 2/3) и l4 = 8l — звук на кварту выше (l4/l1 = 3/4). Это созвучие и определяющие его числа 6, 8, 9, 12 назывались тетрада (четверка). Пифагорейцы считали, что тетрада — это "та гамма, по которой поют сирены". При настройке античной лиры, ставшей символом музыки, четыре ее струны обязательно настраивались по правилу тетрады, а настройка остальных струн зависела от лада, в котором предстояло на ней играть.
Но для античного мыслителя было мало установить численные значения изучаемых величин. Пифагорейский глаз и ум привыкли не только измерять, но и соизмерять, т. е. раскрывать внутренние связи между изучаемыми предметами, другими словами, устанавливать пропорциональные отношения. Архит был истинным пифагорейцем, и он установил пропорциональные отношения между основным совершенным консонансом — октавой, квинтой и квартой. Решение это было получено Архитом в связи с желанием разделить октаву на благозвучные интервалы. Вероятно, Архит исходил из того интуитивно очевидного предположения, что вместе с тонами f1 и f2 = 2f1, дающими основной консонанс — октаву, должно дать консонанс и их среднее арифметическое f3 = (f1 + f2)/2. Но тогда длина струны l3 выразится через длины струн l1 и l2 согласно (6.2) следующим образом:
тем созвучнее интервал.
"Второй закон Пифагора — Архита" и сейчас кажется удивительным. (В его истинной природе мы разберемся в главе 10.) Что же говорить о пифагорейцах, которых он просто привел в восторг! Здесь они нашли подтверждение всей своей философии: целые числа, более того, числа тетрактиса правят всем, даже музыкой! Пифагорейцы не заставили себя долго ждать и распространили закон музыкальных отношений всюду, где это возможно, в том числе и на строение вселенной (см. гл. 7).
Итак, если в качестве цены деления шкалы монохорда взять отрезок l, равный 1/12 длины струны монохорда l1, то вместе со всей струной монохорда длины l1 = 12l будут созвучны ее части длины l2 = 6l — звук на октаву выше (l2/l1 = l/2), l3 = 9l — звук на квинту выше (l3/l1 = 2/3) и l4 = 8l — звук на кварту выше (l4/l1 = 3/4). Это созвучие и определяющие его числа 6, 8, 9, 12 назывались тетрада (четверка). Пифагорейцы считали, что тетрада — это "та гамма, по которой поют сирены". При настройке античной лиры, ставшей символом музыки, четыре ее струны обязательно настраивались по правилу тетрады, а настройка остальных струн зависела от лада, в котором предстояло на ней играть.
Но для античного мыслителя было мало установить численные значения изучаемых величин. Пифагорейский глаз и ум привыкли не только измерять, но и соизмерять, т. е. раскрывать внутренние связи между изучаемыми предметами, другими словами, устанавливать пропорциональные отношения. Архит был истинным пифагорейцем, и он установил пропорциональные отношения между основным совершенным консонансом — октавой, квинтой и квартой. Решение это было получено Архитом в связи с желанием разделить октаву на благозвучные интервалы. Вероятно, Архит исходил из того интуитивно очевидного предположения, что вместе с тонами f1 и f2 = 2f1, дающими основной консонанс — октаву, должно дать консонанс и их среднее арифметическое f3 = (f1 + f2)/2. Но тогда длина струны l3 выразится через длины струн l1 и l2 согласно (6.2) следующим образом:
 т. е. l3 есть среднее гармоническое l1 и l2 (см. 5.1). Легко обнаружить и обратное: среднее гармоническое для частот f1 и f2 переходит в среднее арифметическое для длин l1 и l2:
т. е. l3 есть среднее гармоническое l1 и l2 (см. 5.1). Легко обнаружить и обратное: среднее гармоническое для частот f1 и f2 переходит в среднее арифметическое для длин l1 и l2:
 Вспоминая, что
Вспоминая, что  мы вместе с Архитом приходим к важному выводу:
мы вместе с Архитом приходим к важному выводу:
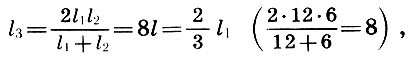 (6.3)
(6.3)
 (6.4)
т. е. квинта есть среднее гармоническое длин струн основного тона l1 и октавы l2, а кварта — среднее арифметическое l1 и l2.
Но произведение среднего арифметического на среднее гармоническое равно произведению исходных чисел:
(6.4)
т. е. квинта есть среднее гармоническое длин струн основного тона l1 и октавы l2, а кварта — среднее арифметическое l1 и l2.
Но произведение среднего арифметического на среднее гармоническое равно произведению исходных чисел:
 (6.5)
откуда, разделив обе части на l12, получаем второй важный вывод:
(6.5)
откуда, разделив обе части на l12, получаем второй важный вывод:
 (6.6)
или
(6.6)
или
 т. е. октава есть произведение квинты на кварту.
Разделив же (6.5) на l1l3, Архит получает и третью из основных пропорций -геометрическую:
т. е. октава есть произведение квинты на кварту.
Разделив же (6.5) на l1l3, Архит получает и третью из основных пропорций -геометрическую:
 (6.7)
которую называли "музыкальной": октава так относится к квинте, как кварта к основному тону.
(6.7)
которую называли "музыкальной": октава так относится к квинте, как кварта к основному тону.
 Деление струны монохорда (l1) на части, образующие с ней совершенные консонансы: октаву (l2), квинту (l3) и кварту (l4) и соотношения между ними. Интервалы, которые целая струна монохорда образует со своими частями, показаны красными стрелками
Легко получить еще два соотношения:
Деление струны монохорда (l1) на части, образующие с ней совершенные консонансы: октаву (l2), квинту (l3) и кварту (l4) и соотношения между ними. Интервалы, которые целая струна монохорда образует со своими частями, показаны красными стрелками
Легко получить еще два соотношения:
 (6.8)
т. е. октава делится на два неравных консонансных интервала — квинту и кварту. Интервал, дополняющий данный интервал до октавы, называется его обращением. Таким образом, квинта есть обращение кварты и наоборот.
Наконец, найдем интервальный коэффициент между струнами квинты l3 и кварты l4, который вместе со своим интервалом называется тоном (не нужно путать тон-интервал и тон-звук данной высоты):
(6.8)
т. е. октава делится на два неравных консонансных интервала — квинту и кварту. Интервал, дополняющий данный интервал до октавы, называется его обращением. Таким образом, квинта есть обращение кварты и наоборот.
Наконец, найдем интервальный коэффициент между струнами квинты l3 и кварты l4, который вместе со своим интервалом называется тоном (не нужно путать тон-интервал и тон-звук данной высоты):
 (6.9)
т. е. тон-интервал равен отношению квинты к кварте.
Заметим, что в отличие от обычного Расстояния на прямой r21 = х2 — x1 определяемого как разность координат конца и начала, интервальный коэффициент — вЫсотное расстояние — определен как отношение составляющих его тонов
(6.9)
т. е. тон-интервал равен отношению квинты к кварте.
Заметим, что в отличие от обычного Расстояния на прямой r21 = х2 — x1 определяемого как разность координат конца и начала, интервальный коэффициент — вЫсотное расстояние — определен как отношение составляющих его тонов  Тогда три тона f1 <f2 <f3, расположенных на равных расстояниях r и образующих арифметическую прогрессию x1, х2 = x1 + r, x3 = x1 + 2r. Поэтому интервальные коэффициенты складываются и вычитаются "геометрически", а сами интервалы — "арифметически", как обычные расстояния, а именно:
сумма двух интервалов равна произведению их интервальных коэффициентов:
Тогда три тона f1 <f2 <f3, расположенных на равных расстояниях r и образующих арифметическую прогрессию x1, х2 = x1 + r, x3 = x1 + 2r. Поэтому интервальные коэффициенты складываются и вычитаются "геометрически", а сами интервалы — "арифметически", как обычные расстояния, а именно:
сумма двух интервалов равна произведению их интервальных коэффициентов:
 (6.10)
разность двух интервалов равна частному их интервальных коэффициентов:
(6.10)
разность двух интервалов равна частному их интервальных коэффициентов:
 (6.11)
разделить интервал на n равных частей означает извлечь корень степени n из его интервального коэффициента:
(6.11)
разделить интервал на n равных частей означает извлечь корень степени n из его интервального коэффициента:
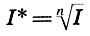 (6.12)
и т. д.
Чтобы перейти от интервальных коэффициентов к интервалам-расстояниям, достаточно ввести логарифмический интервал L = loga I и логарифмическую частоту F = loga f. Тогда, логарифмируя определение (6.1) и равенства (6.10) — (6.12) получаем привычное определение и правила действия с расстояниями:
(6.12)
и т. д.
Чтобы перейти от интервальных коэффициентов к интервалам-расстояниям, достаточно ввести логарифмический интервал L = loga I и логарифмическую частоту F = loga f. Тогда, логарифмируя определение (6.1) и равенства (6.10) — (6.12) получаем привычное определение и правила действия с расстояниями:
 (6.13)
В главе 9 при построении равномерно-темперированного строя особенно удобно будет взять логарифмы по основанию 2. Тогда интервал октавы f1 = 1, f2 = 2 перейдет в логарифмический интервал 0≤L≤1 (log2l=0, log22 = l).
Решение проблемы деления октавы подсказало Архиту сразу два доказательства иррациональности
(6.13)
В главе 9 при построении равномерно-темперированного строя особенно удобно будет взять логарифмы по основанию 2. Тогда интервал октавы f1 = 1, f2 = 2 перейдет в логарифмический интервал 0≤L≤1 (log2l=0, log22 = l).
Решение проблемы деления октавы подсказало Архиту сразу два доказательства иррациональности  . В самом деле, если попытаться разделить октаву на два равных интервала I, то, полагая в (6.8) I23 = I31 = I, имеем
. В самом деле, если попытаться разделить октаву на два равных интервала I, то, полагая в (6.8) I23 = I31 = I, имеем
 Но при таком соотношении длин струн прослушивается явный диссонанс. Поскольку же консонанс определяется отношением целых чисел вида (n+1):2, то напрашивается мысль, что число
Но при таком соотношении длин струн прослушивается явный диссонанс. Поскольку же консонанс определяется отношением целых чисел вида (n+1):2, то напрашивается мысль, что число  не может быть выражено отношением двух целых чисел, т. е. является иррациональным.
Второе доказательство иррациональности
не может быть выражено отношением двух целых чисел, т. е. является иррациональным.
Второе доказательство иррациональности  менее музыкально, но более математично. Чтобы найти квадратный корень числа, не являющегося полным квадратом, Архит разлагает его на два неравных сомножителя (2 = 1*2), затем образует из этих сомножителей среднее арифметическое 3/2 и среднее гармоническое 4/3 и составляет из этих чисел музыкальную пропорцию (6.7):
менее музыкально, но более математично. Чтобы найти квадратный корень числа, не являющегося полным квадратом, Архит разлагает его на два неравных сомножителя (2 = 1*2), затем образует из этих сомножителей среднее арифметическое 3/2 и среднее гармоническое 4/3 и составляет из этих чисел музыкальную пропорцию (6.7):

Произведение средних членов этой пропорции равно данному числу 2, а их разность
 меньше, чем разность нулевого приближения 2 — 1 = 1. Следовательно,
меньше, чем разность нулевого приближения 2 — 1 = 1. Следовательно, 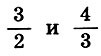 можно рассматривать как приближенные значения
можно рассматривать как приближенные значения  .
(3/2 с избытком, 4/3 с недостатком ] .
Проделав ту же процедуру над первыми приближениями, получим вторые приближения:
.
(3/2 с избытком, 4/3 с недостатком ] .
Проделав ту же процедуру над первыми приближениями, получим вторые приближения:
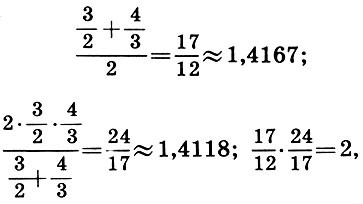 причем
причем
 а затем — и третьи приближения:
а затем — и третьи приближения:
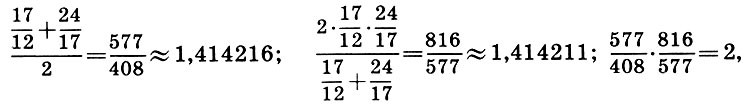 причем
1,414216-1,414211=0,000005.
причем
1,414216-1,414211=0,000005.
Поскольку данную процедуру можно повторять неограниченно, то ясно, что число
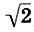 иррациональное. Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что чем больше целые числа в отношении, тем точнее они выражают иррациональное число (см. с. 96). Наконец, вспоминая, что значение
иррациональное. Попутно мы убеждаемся в справедливости пифагорейской мысли о том, что чем больше целые числа в отношении, тем точнее они выражают иррациональное число (см. с. 96). Наконец, вспоминая, что значение  равно 1,414213..., мы видим, что "музыкальный" метод Архита очень быстро сходится к точному значению
равно 1,414213..., мы видим, что "музыкальный" метод Архита очень быстро сходится к точному значению  и уже третье приближение дает пять верных знаков после запятой!
и уже третье приближение дает пять верных знаков после запятой!
Но вернемся к нашим интервалам. Итак, октава делится на два неравных консонанса квинту и кварту, а квинта — на консонанс кварту и диссонанс тон. Тон-интервал и был принят за интервал между соседними по высоте звуками (ступенями) при построении пифагоровой гаммы. Здесь и находится ключ к построению лада. По мнению советского музыковеда Л. А. Мазеля, интервал квинты, разделенный на кварту и тон, является основным музыкальным элементом. Выбрав тон в качестве основной ладообразующей ступеньки, античным теоретикам осталось только отложить от основного звука
 , затем — еще один тон
, затем — еще один тон  , а оставшийся интервал между вторым тоном и тоном кварты
, а оставшийся интервал между вторым тоном и тоном кварты 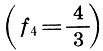 назвать полутоном
назвать полутоном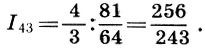 Название это вполне оправдано, так как деление тона-интервала пополам по формуле (6.12) дает
Название это вполне оправдано, так как деление тона-интервала пополам по формуле (6.12) дает  т. е. полутон практически равен половине тона*. Так была получена основа всей древнегреческой музыки — тетрахорд — четырехструнный звукоряд в пределах кварты.
* (Интервал, тона (полутона) в теории музыки принят в качестве единицы арифметического измерения интервалов, а сами интервалы тона и полутона в отличие от их интервальных коэффициентов называют большой и малой секундами.)
Ясно, что имеется только три возможности для положения полутона в пределах тетрахорда, что и определяло характер и название тетрахорда:
дорийский: полутон — тон — тон;
фригийский: тон — полутон — тон;
лидийский: тон — тон — полутон.
Названия тетрахордов указывают на соответствующие области Греции и Малой Азии, каждая из которых пела в своем ладу.
Конечно, четырех струн в пределах кварты было мало для ведения мелодии, поэтому тетрахорды соединялись. Мы уже выяснили, что октава состоит из двух кварт и тона; следовательно, в пределах октавы можно расположить два тетрахорда, разделенных интервалом в тон. Объединяя с помощью разделительного тона два одноименных тетрахорда, получили октаву, которую греки называли "гармония". Именно в античной теории музыки слово "гармония" обрело свое современное значение — согласие разногласного. Таких основных видов гармонии по числу тетрахордов получалось три:
т. е. полутон практически равен половине тона*. Так была получена основа всей древнегреческой музыки — тетрахорд — четырехструнный звукоряд в пределах кварты.
* (Интервал, тона (полутона) в теории музыки принят в качестве единицы арифметического измерения интервалов, а сами интервалы тона и полутона в отличие от их интервальных коэффициентов называют большой и малой секундами.)
Ясно, что имеется только три возможности для положения полутона в пределах тетрахорда, что и определяло характер и название тетрахорда:
дорийский: полутон — тон — тон;
фригийский: тон — полутон — тон;
лидийский: тон — тон — полутон.
Названия тетрахордов указывают на соответствующие области Греции и Малой Азии, каждая из которых пела в своем ладу.
Конечно, четырех струн в пределах кварты было мало для ведения мелодии, поэтому тетрахорды соединялись. Мы уже выяснили, что октава состоит из двух кварт и тона; следовательно, в пределах октавы можно расположить два тетрахорда, разделенных интервалом в тон. Объединяя с помощью разделительного тона два одноименных тетрахорда, получили октаву, которую греки называли "гармония". Именно в античной теории музыки слово "гармония" обрело свое современное значение — согласие разногласного. Таких основных видов гармонии по числу тетрахордов получалось три:


 Здесь 1 обозначает тон, 1/2 — полутон, разделительный тон обведен кружком. Эти античные гармонии сопоставимы с современными гаммами. В самом деле, каждый, знакомый с азами музыкальной грамоты, узнает в лидийской гармонии обычный натуральный мажор (2 тона — полутон, 3 тона — полутон, или на белых клавишах фортепиано до-ре-ми-фа-соль-ля-cи-дo), а в дорийской и фригийской — почти натуральный минор*.
* ("Почти" потому, что в сравнении с натуральным минором (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) у дорийской гаммы понижена вторая ступень, а у фригийской — повышена шестая.)
Здесь 1 обозначает тон, 1/2 — полутон, разделительный тон обведен кружком. Эти античные гармонии сопоставимы с современными гаммами. В самом деле, каждый, знакомый с азами музыкальной грамоты, узнает в лидийской гармонии обычный натуральный мажор (2 тона — полутон, 3 тона — полутон, или на белых клавишах фортепиано до-ре-ми-фа-соль-ля-cи-дo), а в дорийской и фригийской — почти натуральный минор*.
* ("Почти" потому, что в сравнении с натуральным минором (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) у дорийской гаммы понижена вторая ступень, а у фригийской — повышена шестая.)
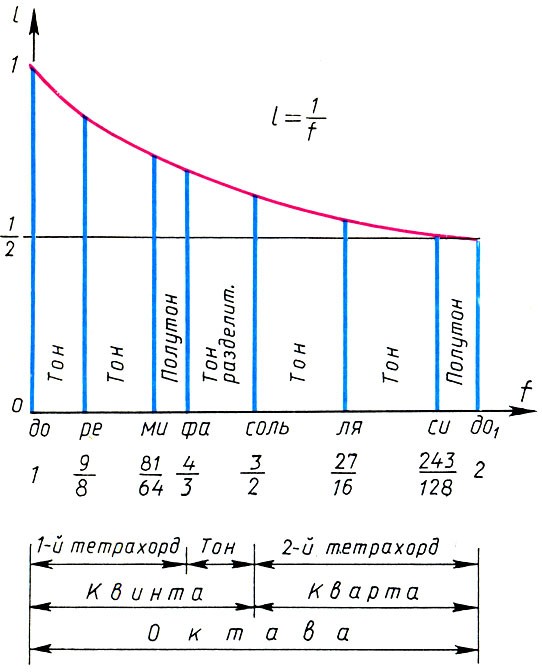 Пифагоров строй лидийской гаммы и его математические характеристики
Зная размеры интервалов, образующих, например, лидийскую гармонию и правила действия с ними, легко получить математическое выражение этой гаммы, т. е. построить ее пифагоров строй. Приняв частоту нижнего тона за единицу f1 = 1, oнаходим первый тетрахорд: f1 = 1, f2 = 9/8, f3 = 9/8*9/8=81/64, f4=4/3. Второй тетрахорд получается сдвигом первого на квинту: f5 = 3/2fl = 3/2, f6 = 3/2f2 = 27/16, f7 = 3/2f3 = 243/128, f8 = 3/2f4 = 2. Окончательно для интервальных коэффициентов имеем
Пифагоров строй лидийской гаммы и его математические характеристики
Зная размеры интервалов, образующих, например, лидийскую гармонию и правила действия с ними, легко получить математическое выражение этой гаммы, т. е. построить ее пифагоров строй. Приняв частоту нижнего тона за единицу f1 = 1, oнаходим первый тетрахорд: f1 = 1, f2 = 9/8, f3 = 9/8*9/8=81/64, f4=4/3. Второй тетрахорд получается сдвигом первого на квинту: f5 = 3/2fl = 3/2, f6 = 3/2f2 = 27/16, f7 = 3/2f3 = 243/128, f8 = 3/2f4 = 2. Окончательно для интервальных коэффициентов имеем
 (6.14)
Это и есть канон Пифагора. По преданию, канон Пифагора впервые нашел практическое применение при настройке лиры легендарного Орфея.
Существовал и другой способ расположения тетрахордов в октаве. Античные теоретики "склеивали" тетрахорды так, что верхний звук одного тетрахорда являлся нижним звуком второго. Тогда дополняющий до октавы тон помещали внизу или наверху такой системы. Если этот тон помещался внизу, то к названию тетрахорда прибавляли приставку гипо-(под-), а если наверху — приставку гипер- (над-). Так получалось еще 6 гармоний, среди которых две пары (гипо-фригийская — гиперлидийская и гиподорийская — гиперфригийская) оказывались совершенно одинаковыми. Отбросив две лишние гаммы, оставалось семь основных ладов. Эти лады имели огромное значение не только в античной музыке, но и через тысячу лет продолжали жить в средневековых ладах, а через две тысячи лет живут в современных натуральных ладах. Правда, средневековые монахи перепутали названия своих ладов в сравнении с античными, что часто порождает различные недоразумения. В таблице 1 собраны все основные античные лады, указан порядок следования в них интервалов, считая, что нижний звук расположен слева, а верхний — справа, приведены их древнегреческие и средневековые названия и указано их наклонение. Разделительный тон обведен кружком.
(6.14)
Это и есть канон Пифагора. По преданию, канон Пифагора впервые нашел практическое применение при настройке лиры легендарного Орфея.
Существовал и другой способ расположения тетрахордов в октаве. Античные теоретики "склеивали" тетрахорды так, что верхний звук одного тетрахорда являлся нижним звуком второго. Тогда дополняющий до октавы тон помещали внизу или наверху такой системы. Если этот тон помещался внизу, то к названию тетрахорда прибавляли приставку гипо-(под-), а если наверху — приставку гипер- (над-). Так получалось еще 6 гармоний, среди которых две пары (гипо-фригийская — гиперлидийская и гиподорийская — гиперфригийская) оказывались совершенно одинаковыми. Отбросив две лишние гаммы, оставалось семь основных ладов. Эти лады имели огромное значение не только в античной музыке, но и через тысячу лет продолжали жить в средневековых ладах, а через две тысячи лет живут в современных натуральных ладах. Правда, средневековые монахи перепутали названия своих ладов в сравнении с античными, что часто порождает различные недоразумения. В таблице 1 собраны все основные античные лады, указан порядок следования в них интервалов, считая, что нижний звук расположен слева, а верхний — справа, приведены их древнегреческие и средневековые названия и указано их наклонение. Разделительный тон обведен кружком.
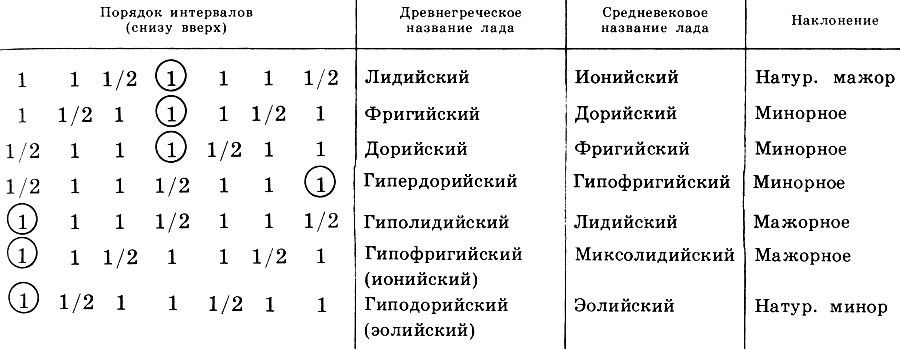 Таблица 1. Порядок следования интервалов тон (1) и полутон (1/2) в античных ладах (снизу вверх), древнегреческие и средневековые названия ладов и их наклонения
Если вспомнить, что сейчас господствуют только два лада — мажор и минор, то остается только удивляться, насколько утонченным было античное музыкальное сознание. Каждый лад греки наполняли определенным этико-эстетическим содержанием, его "этосом", устанавливая ясную связь между музыкальными образами и состояниями души. Музыке приписывали магические и даже врачебные Функции, но особенное значение придавалось музыке как средству воспитания.
Таблица 1. Порядок следования интервалов тон (1) и полутон (1/2) в античных ладах (снизу вверх), древнегреческие и средневековые названия ладов и их наклонения
Если вспомнить, что сейчас господствуют только два лада — мажор и минор, то остается только удивляться, насколько утонченным было античное музыкальное сознание. Каждый лад греки наполняли определенным этико-эстетическим содержанием, его "этосом", устанавливая ясную связь между музыкальными образами и состояниями души. Музыке приписывали магические и даже врачебные Функции, но особенное значение придавалось музыке как средству воспитания.
 Пляшущая менада. Рельеф
Так, развивая в работе "Государство" теорию идеального государства, Платон исключительное значение придает воспитательной роли музыки. Примечательно, что здесь Платон перекликается с другим выдающимся мыслителем, жившим на другом конце Земли за двести лет до Платона,- древнекитайским философом Конфуцием (ок. 551-479 гг. до н. э.), сказавшим: "Если хотите знать, как страна управляется и какова ее нравственность — прислушайтесь к ее музыке". Платон для мирной жизни оставляет один строгий дорийский лад, считая его подлинно греческим, мужественным, деятельным. Для чрезвычайного события, каковым, например, является война, Платон оставляет фригийский лад как наиболее страстный. Лидийский же лад он называет печальным, погребальным, соответствующим женской, а не мужской психике и потому неуместным в идеальном государстве. Остальные лады как слишком утонченные Платон также отбрасывает, неукоснительно проводя в воспитании принцип строгости и простоты. Безусловно, это не означает, что Платон плохо разбирался в музыке. Напротив, в музыке он находил чистый и возвышенный, "платонический" идеал прекрасного, идеал, лишенный вычурности, размягченности, грубых и разнузданных страстей.
Аристотель в "Политике" судит о ладах, пожалуй, еще строже Платона, признавая только дорийский лад как лад, способный тренировать психику. Тем не менее Аристотель делает подробную "этическую" классификацию ладов, различая пады, которые вызывают психическое равновесие (дорийский), напротив, нарушают зго (гипофригийский — "застольный" лад), возбуждают волю и стремление к действию (гиподорийский — лад греческой трагедии), вызывают восторженное и экстатическое состояние (фригийский, гиполидийский).
Прекрасное описание "этоса" греческих ладов мы находим в книге древнеримского писателя Апулея (ок. 124 — ?) "Флориды": "Жил когда-то флейтист по имени Антигенид. Сладостен был каждый звук в игре этого музыканта, все лады были знакомы ему, и он мог воссоздать для тебя, по твоему выбору, и простоту эолийского лада, и богатство ионийского, и грусть лидийского, и приподнятость фригийского, и воинственность дорийского".
Впрочем, стоп! Нет ли здесь противоречия? Дорийский лад называется воинственным, а ведь это, по существу, наш минор! Поскольку именно дорийский лад считался истинно греческим, то получается, что основной характер греческой музыки печальный, минорный. Для греков же дорийский лад является выражением бодрости, жизнерадостности и даже воинственности. Вот как объясняет это кажущееся противоречие выдающийся современный знаток античности, последний философ русского "серебряного века" профессор А. Ф. Лосев (1893-1988)[14]: "Греческое искусство — неизменное жизнеут-верждение. Благородная сдержанность и даже печаль не оставляют грека и тогда, когда он веселится, когда он бодро строит жизнь, когда он воюет и погибает. "Веселые" же лады так или иначе тяготеют к этому прекрасному, благородному, бодрому, важному и в то же время величественно-печальному ладу — дорийскому. Дорийский лад — это скульптурный стиль греческой музыки... Так задумчива, печальна и благородна вся греческая скульптура".
Ну а лидийский лад? Ведь это в точности наш мажор, тогда как Апулей называет его грустным, а Платон — погребальным! Что ж, в оценке лидийского лада с Платоном не соглашался уже Аристотель, находя в лидийском ладу наивную детскость и прелесть и относя его к ладам, вызывающим психическое равновесие. С течением времени лидийский лад утратил плачевный характер, и античные теоретики стали чаще говорить о "сладкой лидийской мелодии" или о "разнообразной лидийской мелодии".
Таким образом, мы видим, что вопрос об "этосе" ладов не решается однозначно и во многом определяется традицией применения того или иного лада. И в наше время слушатель, воспитанный, например, на тонкой и своеобразной индийской музыке, вообще не отличит мажора от минора, не говоря уж об их "этосе". Конечно, мажорный лад отличается более светлыми и радостными тонами и тому есть объективные причины, о которых мы расскажем в главе 10. Но реализация этих возможностей зависит от массы других факторов (темп, ритм, мелодический рисунок и т. д.), и поэтому есть много веселых, энергичных произведений в миноре и грустных, задумчивых — в мажоре. Вспомним хотя бы "Патетическую сонату" до минор Бетховена, этот огненно-страстный монолог Героя, зовущего на яростную схватку и даже на смерть. Многие художники подобрали многие эпитеты к этой сонате (хотя, пожалуй, лучший из них — патетическая — принадлежит самому Бетховену), но только грустной — минорной — ее назвать никак нельзя. Напротив, Ноктюрн № 2 соч. 9 ми бемоль мажор Шопена пронизан настроением нежной мечтательности. Это подернутые дымкой грусти воспоминания автора, но отнюдь не веселая — мажорная — пьеса. В заключение попытаемся сказать несколько слов об "этосе интервалов", ибо именно анализу музыкальных интервалов и посвящена настоящая глава. Попытаемся, потому что данный вопрос еще более спорный и неразработанный, чем "этос ладов". И все-таки...
До сих пор мы ничего не говорили о "самом совершенном консонансе" — приме (унисоне) (l2/l1 = 1, т. е. две струны издают звук одинаковой высоты), ибо с точки зрения математики этот интервал не представляет интереса. Однако в оркестре этот простейший интервал играет огромную роль, придавая данному звуку объемность и яркость. Вспомним хотя бы бесподобную игру в унисон ансамбля скрипачей Большого театра.
Следующий совершенный консонанс — октава. При одновременном звучании октава также дает впечатление объемности звука, а при последовательном — ощущение простора и широты. Прекрасной тому иллюстрацией является "Песня о Родине" композитора И. О. Дунаевского (1900-1955). В ее запеве ("От Москвы до самых до окраин...") дважды звучит восходящая октава (l1/l2 = 2), рисуя необъятные просторы нашей Родины. Здесь же после двух октав идет восходящая квинта. Квинта (l1/l2 = 3/2) также звучит широко, но более рельефно и динамично, чем октава.
Мелодии многих революционных песен и гимнов начинаются интервалом восходящей кварты (l1/l2 = 4/3), например "Интернационал", "Гимн Советского Союза", "Марсельеза". Здесь интервал кварты звучит решительно и активно, как призыв к действию.
Особый "этос" у интервала секунды: при одновременном звучании он диссонирует и неприятен, но при последовательном предыдущий звук как бы переливается в последующий, образуя естественное течение мелодии от одного звука к другому. В мелодии интервалы между двумя опорными звуками часто заполняются последовательными секундовыми интервалами. Например, песня "Во поле береза стояла" начинается интервалом квинты, заполненным последовательными секундами, что создает впечатление спокойного и величавого течения мелодии, как величавы и спокойны картины русской природы.
Пляшущая менада. Рельеф
Так, развивая в работе "Государство" теорию идеального государства, Платон исключительное значение придает воспитательной роли музыки. Примечательно, что здесь Платон перекликается с другим выдающимся мыслителем, жившим на другом конце Земли за двести лет до Платона,- древнекитайским философом Конфуцием (ок. 551-479 гг. до н. э.), сказавшим: "Если хотите знать, как страна управляется и какова ее нравственность — прислушайтесь к ее музыке". Платон для мирной жизни оставляет один строгий дорийский лад, считая его подлинно греческим, мужественным, деятельным. Для чрезвычайного события, каковым, например, является война, Платон оставляет фригийский лад как наиболее страстный. Лидийский же лад он называет печальным, погребальным, соответствующим женской, а не мужской психике и потому неуместным в идеальном государстве. Остальные лады как слишком утонченные Платон также отбрасывает, неукоснительно проводя в воспитании принцип строгости и простоты. Безусловно, это не означает, что Платон плохо разбирался в музыке. Напротив, в музыке он находил чистый и возвышенный, "платонический" идеал прекрасного, идеал, лишенный вычурности, размягченности, грубых и разнузданных страстей.
Аристотель в "Политике" судит о ладах, пожалуй, еще строже Платона, признавая только дорийский лад как лад, способный тренировать психику. Тем не менее Аристотель делает подробную "этическую" классификацию ладов, различая пады, которые вызывают психическое равновесие (дорийский), напротив, нарушают зго (гипофригийский — "застольный" лад), возбуждают волю и стремление к действию (гиподорийский — лад греческой трагедии), вызывают восторженное и экстатическое состояние (фригийский, гиполидийский).
Прекрасное описание "этоса" греческих ладов мы находим в книге древнеримского писателя Апулея (ок. 124 — ?) "Флориды": "Жил когда-то флейтист по имени Антигенид. Сладостен был каждый звук в игре этого музыканта, все лады были знакомы ему, и он мог воссоздать для тебя, по твоему выбору, и простоту эолийского лада, и богатство ионийского, и грусть лидийского, и приподнятость фригийского, и воинственность дорийского".
Впрочем, стоп! Нет ли здесь противоречия? Дорийский лад называется воинственным, а ведь это, по существу, наш минор! Поскольку именно дорийский лад считался истинно греческим, то получается, что основной характер греческой музыки печальный, минорный. Для греков же дорийский лад является выражением бодрости, жизнерадостности и даже воинственности. Вот как объясняет это кажущееся противоречие выдающийся современный знаток античности, последний философ русского "серебряного века" профессор А. Ф. Лосев (1893-1988)[14]: "Греческое искусство — неизменное жизнеут-верждение. Благородная сдержанность и даже печаль не оставляют грека и тогда, когда он веселится, когда он бодро строит жизнь, когда он воюет и погибает. "Веселые" же лады так или иначе тяготеют к этому прекрасному, благородному, бодрому, важному и в то же время величественно-печальному ладу — дорийскому. Дорийский лад — это скульптурный стиль греческой музыки... Так задумчива, печальна и благородна вся греческая скульптура".
Ну а лидийский лад? Ведь это в точности наш мажор, тогда как Апулей называет его грустным, а Платон — погребальным! Что ж, в оценке лидийского лада с Платоном не соглашался уже Аристотель, находя в лидийском ладу наивную детскость и прелесть и относя его к ладам, вызывающим психическое равновесие. С течением времени лидийский лад утратил плачевный характер, и античные теоретики стали чаще говорить о "сладкой лидийской мелодии" или о "разнообразной лидийской мелодии".
Таким образом, мы видим, что вопрос об "этосе" ладов не решается однозначно и во многом определяется традицией применения того или иного лада. И в наше время слушатель, воспитанный, например, на тонкой и своеобразной индийской музыке, вообще не отличит мажора от минора, не говоря уж об их "этосе". Конечно, мажорный лад отличается более светлыми и радостными тонами и тому есть объективные причины, о которых мы расскажем в главе 10. Но реализация этих возможностей зависит от массы других факторов (темп, ритм, мелодический рисунок и т. д.), и поэтому есть много веселых, энергичных произведений в миноре и грустных, задумчивых — в мажоре. Вспомним хотя бы "Патетическую сонату" до минор Бетховена, этот огненно-страстный монолог Героя, зовущего на яростную схватку и даже на смерть. Многие художники подобрали многие эпитеты к этой сонате (хотя, пожалуй, лучший из них — патетическая — принадлежит самому Бетховену), но только грустной — минорной — ее назвать никак нельзя. Напротив, Ноктюрн № 2 соч. 9 ми бемоль мажор Шопена пронизан настроением нежной мечтательности. Это подернутые дымкой грусти воспоминания автора, но отнюдь не веселая — мажорная — пьеса. В заключение попытаемся сказать несколько слов об "этосе интервалов", ибо именно анализу музыкальных интервалов и посвящена настоящая глава. Попытаемся, потому что данный вопрос еще более спорный и неразработанный, чем "этос ладов". И все-таки...
До сих пор мы ничего не говорили о "самом совершенном консонансе" — приме (унисоне) (l2/l1 = 1, т. е. две струны издают звук одинаковой высоты), ибо с точки зрения математики этот интервал не представляет интереса. Однако в оркестре этот простейший интервал играет огромную роль, придавая данному звуку объемность и яркость. Вспомним хотя бы бесподобную игру в унисон ансамбля скрипачей Большого театра.
Следующий совершенный консонанс — октава. При одновременном звучании октава также дает впечатление объемности звука, а при последовательном — ощущение простора и широты. Прекрасной тому иллюстрацией является "Песня о Родине" композитора И. О. Дунаевского (1900-1955). В ее запеве ("От Москвы до самых до окраин...") дважды звучит восходящая октава (l1/l2 = 2), рисуя необъятные просторы нашей Родины. Здесь же после двух октав идет восходящая квинта. Квинта (l1/l2 = 3/2) также звучит широко, но более рельефно и динамично, чем октава.
Мелодии многих революционных песен и гимнов начинаются интервалом восходящей кварты (l1/l2 = 4/3), например "Интернационал", "Гимн Советского Союза", "Марсельеза". Здесь интервал кварты звучит решительно и активно, как призыв к действию.
Особый "этос" у интервала секунды: при одновременном звучании он диссонирует и неприятен, но при последовательном предыдущий звук как бы переливается в последующий, образуя естественное течение мелодии от одного звука к другому. В мелодии интервалы между двумя опорными звуками часто заполняются последовательными секундовыми интервалами. Например, песня "Во поле береза стояла" начинается интервалом квинты, заполненным последовательными секундами, что создает впечатление спокойного и величавого течения мелодии, как величавы и спокойны картины русской природы.
А наиболее неприятным и неблагозвучным является интервал тритон или полуоктава (l1/l2 =
 ). Своей неблагозвучностью этот интервал "подсказал" Архиту "музыкальное доказательство" иррациональности
). Своей неблагозвучностью этот интервал "подсказал" Архиту "музыкальное доказательство" иррациональности  .
Не правда ли, удивительные открытия сделали мы в этой главе? В музыкальной гамме мы обнаружили все математические пропорции, а для доказательства иррациональности
.
Не правда ли, удивительные открытия сделали мы в этой главе? В музыкальной гамме мы обнаружили все математические пропорции, а для доказательства иррациональности 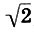 использовали музыкальную гамму. Мы нашли математический скелет музыкальной гаммы и увидели, насколько тонко (задолго до нашей эры!) древние греки чувствовали музыку. Но безудержный полет фантазии увлекал античных мыслителей все дальше, в заоблачные дали, в поиски всемирной "космической музыки". И хотя поиски эти оказались бесплодными, а античная космология с современной точки зрения кажется слишком наивной, не нужно спешить смеяться над нашими предшественниками; гораздо полезнее извлечь уроки из их опыта, о чем и говорится в эпиграфе к следующей главе.
использовали музыкальную гамму. Мы нашли математический скелет музыкальной гаммы и увидели, насколько тонко (задолго до нашей эры!) древние греки чувствовали музыку. Но безудержный полет фантазии увлекал античных мыслителей все дальше, в заоблачные дали, в поиски всемирной "космической музыки". И хотя поиски эти оказались бесплодными, а античная космология с современной точки зрения кажется слишком наивной, не нужно спешить смеяться над нашими предшественниками; гораздо полезнее извлечь уроки из их опыта, о чем и говорится в эпиграфе к следующей главе.
7. "Космическая музыка": от Платона до Кеплера
Современник, даже когда его влечет старина, склонен считать своих предков людьми простодушными и недалекими. Он замечает в них прежде всего то, чего им не хватало с современной точки зрения, и обычно не замечает того, чего ему самому не хватает по сравнению с ними.В наш бурный век космической тематикой вряд ли кого удивишь, тем более читателей, родившихся во время полетов человека в космос. "Космическая музыка" — это нечто вибрирующее, электронное из фильмов о летающих тарелках и инопланетянах — тоже стала привычной. Но вот то, что задолго до нашей эры, во времена, когда человечество "летало" только на восковых крыльях в мифах о Дедале и Икаре, была своя "космическая музыка", многим, возможно, покажется удивительным. По преданию, слово "космос", первоначально означавшее прекрасно устроенный, ввел в обиход Пифагор. "Скажи мне, ...разве есть что-либо стройное и прекрасное, что не было бы подражанием миру. Отсюда имя "Космос", которое греки дали ему",- вторил Пифагору через полтысячелетия Апулей. Из античности термин "космос" перешел в современную науку как синоним слова "вселенная". Итак, космос для пифагорейцев — это гармоничное, пропорциональное строение мира. Сами же пропорции, как мы уже видели, мыслились греками музыкально" поэтому и весь космос оказывался гармонично устроенным и музыкально звучащим телом. Согласно пифагорейским представлениям, планеты располагались на небесных сферах и совершали вместе с ними круговое вращение. Тогда, как и все движущиеся тела, вследствие трения об эфир они издавали звуки, которые соединялись в музыкальные созвучия. Так Рождалась чудесная музыка — "мировая Музыка", или "гармония сфер", без коброй мир бы распался. Сама же музыка — это первое из искусств, доставляющих людям радость,- являлась, по их Мнению, отражением гармонии, царящей сРеди небесных сфер.М. Алпатов
 Система мира по Филолаю
Учение о музыке сфер — самый туманный и вместе с тем поэтичный мотив пифагорейской эстетики. Он имел тысячи вариантов, оттенков и тысячелетнюю традицию, начиная от Пифагора и Платона до "Гармонии мира" Иоганна Кеплера, написанной уже в XVII веке. Разумеется, учение о "космической музыке" для нас, современников космических полетов, не более как красивая сказка, и расскажем мы эту сказку, чтобы показать, насколько сильным было музыкальное начало во всем античном мировоззрении. Кроме того, как и во всякой сказке, в этом учении рассыпаны зерна истины, позволяющие увидеть глубокие параллели в развитии человеческой мысли.
Первое письменное изложение пифагорейских идей появилось около 420 г. до н. э. в сочинении "О природе". "Природа, сущая в космосе, гармонично слажена из беспредельного и определяющих начал. Так устроен весь космос и все, что в нем" — так начинается эта книга, приписываемая Филолаю, ученику непосредственного ученика Пифагора — Гиппаса. Здесь же мы находим и первое письменное свидетельство о музыкально-числовом строении космоса.
По Филолаю, центром мироздания является некий Центральный Огонь, вокруг которого на десяти концентрических сферах в порядке удаления от него вращаются так называемая Противоземля, затем Земля, Луна, Солнце, пять планет (Меркурий, Венера, Марс, Юпитер, Сатурн — их последовательность Филолаем не указана)[15] и, наконец, Сфера неподвижных звезд. Центральный Огонь и Противоземля невидимы, ибо заслонены поверхностью Земли. Солнце, по Филолаю, только отражает свет и тепло Центрального Огня. Противоземля же введена им отчасти для объяснения солнечных затмений, отчасти для достижения требуемой числовой мистикой "священной десятки" — вместе с Противоземлей сфер получается десять. В пифагорейской системе Земля не является центром мироздания, а вместе с другими планетами движется вокруг Центрального Огня — прообраза Солнца. Вот почему, когда в XVI веке церковь развернула борьбу с гелиоцентрическим учением Коперника, это учение именовалось пифагорейским.
Внутреннее устройство пифагорейского космоса напоминало своеобразную музыкальную шкатулку: каждая из десяти движущихся сфер издавала некоторый звук. "Когда несутся Солнце, Луна и еще столь великое множество таких огромных светил со столь великой быстротою, невозможно, чтобы не возникал некоторый необыкновенный по силе звук",- утверждает неизвестный пифагорейский автор возможно Филолай. Высота звука определялась скоростью движения сферы, зависящей от расстояний между сферами, а последние находились в той же пропорции, что и интервалы музыкальной гаммы. Таким образом, колеблемый движением сфер эфир издает чудесную мировую музыку. Однако человеческое ухо не слышит этой ни с чем не сравнимой музыки. Как рожденный на берегу моря человек перестает в конце концов различать беспрестанный рокот волн, так и слух человека привык и не замечает гармонического звучания небесных сфер.
Итак, согласно пифагорейцам, небесная музыка изначально незримо живет в человеке. Вот почему человеческая душа охотно откликается на обычную земную музыку, которая является лишь подражанием небесной; вот почему из всех искусств музыке в античности отводилась исключительная роль.
В своем конспекте гегелевской "Истории философии" В. И. Ленин по поводу пифагорейского учения отмечает "связь зачатков научного мышления и фантазии &##225; lа религии, мифологии" (т. 29, с. 225). Особое внимание В. И. Ленин уделяет пифагорейскому учению о гармонии сфер, подчеркивая, что здесь имеется "намек на строение материи!" (т. 29, с. 224).
Дальнейшее развитие пифагорейское учение о гармонии сфер получило в трудах Платона. Платоновский диалог "Тимей", эта квинтэссенция древнего пифагорейства, является лучшим образцом античной космологии. Однако многое в "Тимее" изложено туманными и заумными намеками. Уже в древности эти места вызывали бесконечные споры, разночтения и комментарии, которые длятся и до сего времени.
Платон исходит из геоцентрической системы космоса: центром мироздания Для него является неподвижная Земля, вокруг которой на семи сферах[16] вращаются Луна, Солнце, Венера, Меркурий, Марс, Юпитер, Сатурн. Далее следует сФера неподвижных звезд. Как видим, несостоятельность Центрального Огня и Противоземли ко времени Платона была Уже осознана.
Система мира по Филолаю
Учение о музыке сфер — самый туманный и вместе с тем поэтичный мотив пифагорейской эстетики. Он имел тысячи вариантов, оттенков и тысячелетнюю традицию, начиная от Пифагора и Платона до "Гармонии мира" Иоганна Кеплера, написанной уже в XVII веке. Разумеется, учение о "космической музыке" для нас, современников космических полетов, не более как красивая сказка, и расскажем мы эту сказку, чтобы показать, насколько сильным было музыкальное начало во всем античном мировоззрении. Кроме того, как и во всякой сказке, в этом учении рассыпаны зерна истины, позволяющие увидеть глубокие параллели в развитии человеческой мысли.
Первое письменное изложение пифагорейских идей появилось около 420 г. до н. э. в сочинении "О природе". "Природа, сущая в космосе, гармонично слажена из беспредельного и определяющих начал. Так устроен весь космос и все, что в нем" — так начинается эта книга, приписываемая Филолаю, ученику непосредственного ученика Пифагора — Гиппаса. Здесь же мы находим и первое письменное свидетельство о музыкально-числовом строении космоса.
По Филолаю, центром мироздания является некий Центральный Огонь, вокруг которого на десяти концентрических сферах в порядке удаления от него вращаются так называемая Противоземля, затем Земля, Луна, Солнце, пять планет (Меркурий, Венера, Марс, Юпитер, Сатурн — их последовательность Филолаем не указана)[15] и, наконец, Сфера неподвижных звезд. Центральный Огонь и Противоземля невидимы, ибо заслонены поверхностью Земли. Солнце, по Филолаю, только отражает свет и тепло Центрального Огня. Противоземля же введена им отчасти для объяснения солнечных затмений, отчасти для достижения требуемой числовой мистикой "священной десятки" — вместе с Противоземлей сфер получается десять. В пифагорейской системе Земля не является центром мироздания, а вместе с другими планетами движется вокруг Центрального Огня — прообраза Солнца. Вот почему, когда в XVI веке церковь развернула борьбу с гелиоцентрическим учением Коперника, это учение именовалось пифагорейским.
Внутреннее устройство пифагорейского космоса напоминало своеобразную музыкальную шкатулку: каждая из десяти движущихся сфер издавала некоторый звук. "Когда несутся Солнце, Луна и еще столь великое множество таких огромных светил со столь великой быстротою, невозможно, чтобы не возникал некоторый необыкновенный по силе звук",- утверждает неизвестный пифагорейский автор возможно Филолай. Высота звука определялась скоростью движения сферы, зависящей от расстояний между сферами, а последние находились в той же пропорции, что и интервалы музыкальной гаммы. Таким образом, колеблемый движением сфер эфир издает чудесную мировую музыку. Однако человеческое ухо не слышит этой ни с чем не сравнимой музыки. Как рожденный на берегу моря человек перестает в конце концов различать беспрестанный рокот волн, так и слух человека привык и не замечает гармонического звучания небесных сфер.
Итак, согласно пифагорейцам, небесная музыка изначально незримо живет в человеке. Вот почему человеческая душа охотно откликается на обычную земную музыку, которая является лишь подражанием небесной; вот почему из всех искусств музыке в античности отводилась исключительная роль.
В своем конспекте гегелевской "Истории философии" В. И. Ленин по поводу пифагорейского учения отмечает "связь зачатков научного мышления и фантазии &##225; lа религии, мифологии" (т. 29, с. 225). Особое внимание В. И. Ленин уделяет пифагорейскому учению о гармонии сфер, подчеркивая, что здесь имеется "намек на строение материи!" (т. 29, с. 224).
Дальнейшее развитие пифагорейское учение о гармонии сфер получило в трудах Платона. Платоновский диалог "Тимей", эта квинтэссенция древнего пифагорейства, является лучшим образцом античной космологии. Однако многое в "Тимее" изложено туманными и заумными намеками. Уже в древности эти места вызывали бесконечные споры, разночтения и комментарии, которые длятся и до сего времени.
Платон исходит из геоцентрической системы космоса: центром мироздания Для него является неподвижная Земля, вокруг которой на семи сферах[16] вращаются Луна, Солнце, Венера, Меркурий, Марс, Юпитер, Сатурн. Далее следует сФера неподвижных звезд. Как видим, несостоятельность Центрального Огня и Противоземли ко времени Платона была Уже осознана.
 Система мира по Платону
На базе этой системы мироздания Платон развивает теорию небесного гептахорда — семиструнника, т. е. теорию семи подвижных сфер, настроенных в музыкальных отношениях. Согласно Платону, творец Вселенной — Демиург, создав вещество Вселенной, разделил его на две части: одна часть пошла на построение сферы неподвижных звезд, а вторая была математически строго разделена на семь частей для образования сфер Луны, Солнца и пяти планет. По этому поводу в "Тимее" Платона мы читаем: "Делить же он начал следующим образом: прежде всего отнял от целого одну долю, затем вторую — вдвое большую, третью — в полтора раза больше второй и в три раза больше первой, четвертую — вдвое больше второй, пятую — втрое больше третьей, шестую — в восемь раз больше первой, а седьмую — больше первой в двадцать семь раз". В результате получился ряд чисел
1 2 3 4 9 8 27, (7.1)
описывающий гармонию небесных сфер, или небесный гептахорд. Однако ни порядок расположения сфер, несущих светила, ни порядок отсчета чисел в ряде (7.1) Платоном указан не был. Поэтому на протяжении последующих двух тысячелетий члены платонова гептахорда имели самую разнообразную физическую интерпретацию.
Самым простым и соблазнительным было трактовать числа (7.1) как относительные расстояния от Земли до Луны, Солнца, Венеры, Меркурия, Марса, Юпитера и Сатурна соответственно. Тогда эти числа представляли и относительные высоты тонов, так как высота тона, издаваемого сферой, мыслилась пропорциональной скорости вращения сферы, а скорость вращения — пропорциональной расстоянию до неподвижной Земли. Таким образом, чем дальше находилась планета от Земли, тем больше была ее скорость и тем выше издаваемый ею тон. Скорее всего, эти рассуждения были навеяны простым опытом: камень, раскручиваемый на веревке, со свистом разрезает воздух и прекрасно демонстрирует все описанные закономерности. Правда, при такой трактовке относительное расстояние до Марса (9) получалось больше, чем до Юпитера (8), и, чтобы "исправить" эту ошибку, числа 9 и 8 в (7.1) просто переставили. Вот почему во многих текстах платонов гептахорд фигурирует в искаженном виде: 1, 2, 3, 4, 8, 9, 27.
И все-таки оставалось непонятным: откуда вообще взялся этот странный ряд чисел? Это загадка, которую исследователи, начиная с Аристотеля, чаще всего трактовали как некий курьез, если не просто глупость, не требующую даже разъяснений. "Однако,- как справедливо замечал А. Ф. Лосев,- такой антиисторический подход не может быть у современного исследователя, который, конечно, настолько далек от древнего пифагорейства, что даже не испытывает потребности его критиковать, а должен рассмотреть его со всеми объективно-историческими причинами, делающими его существование понятным".
Ключ к Платонову гептахорду, по-видимому, спрятан в самом пифагорейском понимании числа, а именно: единицы — как символа неделимого начала, двойки — как символа неопределенной бесконечности и тройки — как символа определенности. Но для Платона это слишком просто, и в качестве символа беспредельности он берет куб со стороной 2. Тогда его геометрические параметры (длина, площадь грани и объем) дают числа 2, 4, 8. А в качестве символа определенности Платон берет куб со стороной 3 и параметрами 3, 9, 27. Тогда взаимное переплетение этих двух троек чисел плюс начало всего — единица — и дают то единство "беспредельного и определяющих начал", о которых говорил Филолай.
Интересную реконструкцию платонова космоса совсем недавно, в 1985 г., предложил инженер С. В. Житомирский. Учитывая, что небесные сферы мыслились Платоном материально, т. е. обладали некоторой толщиной (такое представление сохранилось вплоть до Кеплера), Житомирский трактует числа (7.1) как толщины соответствующих сфер, причем отсчет начинает не от Земли, как это всегда было принято, а, наоборот, от сферы неподвижных звезд. Далее, вспоминая, что на изготовление последней сферы пошло столько же материала, сколько и на все
остальные, он полагает толщину сферы неподвижных звезд равной толщинам всех остальных сфер, т. е. 54 = 1 + 2 + 3 + 4 + 9 + 8 + 27. Таким образом получается реконструкция картины платонова космоса, которая согласуется с другими космологическими текстами Платона, а числа гептахорда (7.1) наполняются конкретным геометрическим содержанием:
Система мира по Платону
На базе этой системы мироздания Платон развивает теорию небесного гептахорда — семиструнника, т. е. теорию семи подвижных сфер, настроенных в музыкальных отношениях. Согласно Платону, творец Вселенной — Демиург, создав вещество Вселенной, разделил его на две части: одна часть пошла на построение сферы неподвижных звезд, а вторая была математически строго разделена на семь частей для образования сфер Луны, Солнца и пяти планет. По этому поводу в "Тимее" Платона мы читаем: "Делить же он начал следующим образом: прежде всего отнял от целого одну долю, затем вторую — вдвое большую, третью — в полтора раза больше второй и в три раза больше первой, четвертую — вдвое больше второй, пятую — втрое больше третьей, шестую — в восемь раз больше первой, а седьмую — больше первой в двадцать семь раз". В результате получился ряд чисел
1 2 3 4 9 8 27, (7.1)
описывающий гармонию небесных сфер, или небесный гептахорд. Однако ни порядок расположения сфер, несущих светила, ни порядок отсчета чисел в ряде (7.1) Платоном указан не был. Поэтому на протяжении последующих двух тысячелетий члены платонова гептахорда имели самую разнообразную физическую интерпретацию.
Самым простым и соблазнительным было трактовать числа (7.1) как относительные расстояния от Земли до Луны, Солнца, Венеры, Меркурия, Марса, Юпитера и Сатурна соответственно. Тогда эти числа представляли и относительные высоты тонов, так как высота тона, издаваемого сферой, мыслилась пропорциональной скорости вращения сферы, а скорость вращения — пропорциональной расстоянию до неподвижной Земли. Таким образом, чем дальше находилась планета от Земли, тем больше была ее скорость и тем выше издаваемый ею тон. Скорее всего, эти рассуждения были навеяны простым опытом: камень, раскручиваемый на веревке, со свистом разрезает воздух и прекрасно демонстрирует все описанные закономерности. Правда, при такой трактовке относительное расстояние до Марса (9) получалось больше, чем до Юпитера (8), и, чтобы "исправить" эту ошибку, числа 9 и 8 в (7.1) просто переставили. Вот почему во многих текстах платонов гептахорд фигурирует в искаженном виде: 1, 2, 3, 4, 8, 9, 27.
И все-таки оставалось непонятным: откуда вообще взялся этот странный ряд чисел? Это загадка, которую исследователи, начиная с Аристотеля, чаще всего трактовали как некий курьез, если не просто глупость, не требующую даже разъяснений. "Однако,- как справедливо замечал А. Ф. Лосев,- такой антиисторический подход не может быть у современного исследователя, который, конечно, настолько далек от древнего пифагорейства, что даже не испытывает потребности его критиковать, а должен рассмотреть его со всеми объективно-историческими причинами, делающими его существование понятным".
Ключ к Платонову гептахорду, по-видимому, спрятан в самом пифагорейском понимании числа, а именно: единицы — как символа неделимого начала, двойки — как символа неопределенной бесконечности и тройки — как символа определенности. Но для Платона это слишком просто, и в качестве символа беспредельности он берет куб со стороной 2. Тогда его геометрические параметры (длина, площадь грани и объем) дают числа 2, 4, 8. А в качестве символа определенности Платон берет куб со стороной 3 и параметрами 3, 9, 27. Тогда взаимное переплетение этих двух троек чисел плюс начало всего — единица — и дают то единство "беспредельного и определяющих начал", о которых говорил Филолай.
Интересную реконструкцию платонова космоса совсем недавно, в 1985 г., предложил инженер С. В. Житомирский. Учитывая, что небесные сферы мыслились Платоном материально, т. е. обладали некоторой толщиной (такое представление сохранилось вплоть до Кеплера), Житомирский трактует числа (7.1) как толщины соответствующих сфер, причем отсчет начинает не от Земли, как это всегда было принято, а, наоборот, от сферы неподвижных звезд. Далее, вспоминая, что на изготовление последней сферы пошло столько же материала, сколько и на все
остальные, он полагает толщину сферы неподвижных звезд равной толщинам всех остальных сфер, т. е. 54 = 1 + 2 + 3 + 4 + 9 + 8 + 27. Таким образом получается реконструкция картины платонова космоса, которая согласуется с другими космологическими текстами Платона, а числа гептахорда (7.1) наполняются конкретным геометрическим содержанием:
 Земля — Луна — Солнце — Венера — Меркурий — Марс — Юпитер — Сатурн — Небо звезд
Заметим, что и реконструкция Житомирского также страдает изъяном, так как Земля теперь растворилась в сфере Луны. Не будем более погружаться в бездну вопросов Платонова космоса, из которых уже два с половиной тысячелетия ищут выхода, и перейдем к музыкальной стороне учения Платона. Легко видеть, что платонов гептахорд содержит в себе все основные музыкальные интервалы: октаву (2/1), квинту (3/2), кварту (4/3), тон (9/8) и полутон
Земля — Луна — Солнце — Венера — Меркурий — Марс — Юпитер — Сатурн — Небо звезд
Заметим, что и реконструкция Житомирского также страдает изъяном, так как Земля теперь растворилась в сфере Луны. Не будем более погружаться в бездну вопросов Платонова космоса, из которых уже два с половиной тысячелетия ищут выхода, и перейдем к музыкальной стороне учения Платона. Легко видеть, что платонов гептахорд содержит в себе все основные музыкальные интервалы: октаву (2/1), квинту (3/2), кварту (4/3), тон (9/8) и полутон  . Объясняется это просто, ибо, как мы увидим в следующей главе, все тона пифагоровой гаммы получаются ходами вверх или вниз по квинтам (3/2), а квинта составлена из отношения тройки и двойки, т. е. из тех чисел, что и платонов гептахорд. С помощью полученных интервалов можно рассчитать строй любого лада. Неудивительно, что Платон утверждает, будто космос настроен в дорийском ладу, этом истинно национальном ладу древних греков, хотя остается непонятным, как получить строй дорийского лада из Платонова гептахорда. Не очень ясно также и то, что на самом деле представляет собой звучание Платонова гептахорда: гармонию или дисгармонию или даже какофонию сфер. Попробуйте решить для себя этот вопрос сами, сыграв гептахорд (7.1), скажем, от ноты До большой октавы: До-до-соль-до1-ре2-до2-ля3.
Впрочем, все это сегодня уже неважно. Для нас, людей XX века, важно другое: Платон мыслит мировое пространство неоднородным, как неодинаково натянуты струны единого музыкального инструмента. Но ведь эта мысль о неоднородности мирового пространства созвучна выводам из общей теории относительности Альберта Эйнштейна об искривленности пространства — времени и его неоднородности! Более двух тысячелетий, от Платона до Эйнштейна, мировое пространство мыслилось абсолютным и однородным! И вот за этот огромный промежуток времени, практически равный всей истории европейской цивилизации, наука, как и определено законами диалектики, совершает огромный виток по спирали и прежний вывод делается на базе самых современных научных знаний, а старая научная платформа кажется наивной и смешной! Сколько еще таких витков предстоит сделать науке?!
От внешнего строения космоса Платон в "Тимее" переходит к внутреннему его строению, т. е. строению материи. Это знаменитое учение Платона о четырех стихиях - основных компонентах мира и их атомах — Платоновых телах. Менее известно, что это учение также "музыкально", но, прежде чем остановиться на нем, следует сказать несколько слов о самом Платоне и его научных взглядах, что, видимо, поможет понять истоки этого экзотического учения.
. Объясняется это просто, ибо, как мы увидим в следующей главе, все тона пифагоровой гаммы получаются ходами вверх или вниз по квинтам (3/2), а квинта составлена из отношения тройки и двойки, т. е. из тех чисел, что и платонов гептахорд. С помощью полученных интервалов можно рассчитать строй любого лада. Неудивительно, что Платон утверждает, будто космос настроен в дорийском ладу, этом истинно национальном ладу древних греков, хотя остается непонятным, как получить строй дорийского лада из Платонова гептахорда. Не очень ясно также и то, что на самом деле представляет собой звучание Платонова гептахорда: гармонию или дисгармонию или даже какофонию сфер. Попробуйте решить для себя этот вопрос сами, сыграв гептахорд (7.1), скажем, от ноты До большой октавы: До-до-соль-до1-ре2-до2-ля3.
Впрочем, все это сегодня уже неважно. Для нас, людей XX века, важно другое: Платон мыслит мировое пространство неоднородным, как неодинаково натянуты струны единого музыкального инструмента. Но ведь эта мысль о неоднородности мирового пространства созвучна выводам из общей теории относительности Альберта Эйнштейна об искривленности пространства — времени и его неоднородности! Более двух тысячелетий, от Платона до Эйнштейна, мировое пространство мыслилось абсолютным и однородным! И вот за этот огромный промежуток времени, практически равный всей истории европейской цивилизации, наука, как и определено законами диалектики, совершает огромный виток по спирали и прежний вывод делается на базе самых современных научных знаний, а старая научная платформа кажется наивной и смешной! Сколько еще таких витков предстоит сделать науке?!
От внешнего строения космоса Платон в "Тимее" переходит к внутреннему его строению, т. е. строению материи. Это знаменитое учение Платона о четырех стихиях - основных компонентах мира и их атомах — Платоновых телах. Менее известно, что это учение также "музыкально", но, прежде чем остановиться на нем, следует сказать несколько слов о самом Платоне и его научных взглядах, что, видимо, поможет понять истоки этого экзотического учения.
 Платон (427-347). Римская мраморная копия с греческого оригинала. Ок. 370 до н. э
Платон (427-347 гг. до н. э.) — величайший философ античности, оказавший огромное влияние на развитие всей мировой культуры. Однако Платон был не только философом, создателем первой в истории человечества системы объективного идеализма, "линии Платона", по определению В. И. Ленина (т. 18, с. 131), но также и блестящим художником слова, организатором и теоретиком науки, ученым и гражданином города-государства Афины. После казни своего любимого учителя Сократа, болезненно переживая кризис афинской демократии, Платон покинул Афины и около двенадцати лет провел в путешествиях. Вернувшись на родину, Платон основал научную школу — Академию, которая разместилась на купленном для этой цели Платоном участке в роще близ Афин. Роща носила имя древнеаттического героя Академа, откуда и пошло название первой в истории человечества научной школы — Академии.
Платон и его ученики, платоники, были самой влиятельной после пифагорейцев группой мыслителей, а Платонова Академия в течение девяти столетий оставалась центром, влекущим к себе лучшие умы античности. Платон направлял и воодушевлял научную работу. Великие математики Теэтет и Евдокс были друзьями Платона, его учителями в математике и учениками в философии. Великий ученик Платона — Аристотель, будущий учитель и воспитатель Александра Македонского, двадцать лет жизни провел в благотворной атмосфере Академии. Хотя сам Платон и не был математиком, он придавал огромное значение изучению математики, живо интересовался ею и требовал от своих учеников основательных знаний математики, прежде чем посвятить их в свою философию. По преданию, на вратах Академии Платона было начертано: "Негеометр да не войдет!", а одному из начинающих философов, не знавшему математики, Платон сказал: "Уйди прочь! У тебя нет орудия для изучения философии..."
Не останавливаясь на философской системе Платона, отметим только, что, согласно Платону, существуют два мира: материальный несовершенный мир вещей и совершенный мир идей. Законы мира вещей несовершенны и преходящи, тогда как в мире идей господствуют абсолютные и неизменные истины, которые и надлежит изучать философу. Материальный мир есть не более как одна из несовершенных реализаций мира идей, и постигнуть реальный мир можно только с помощью математики идеального мира. То, что идеальный мир основан на математике, сомнений не вызывало. "Знание, к которому стремятся геометры, есть знание вечного, а не того, что тленно и преходяще",- утверждал Платон.
Таким образом, Платон ясно осознавал значение математизации науки, и это именно тот путь, по которому пошло развитие науки в античности и по которому оно продолжает идти сегодня. Однако следует четко различать: то, что Платон видел в математике инструмент познания законов природы, безусловно, верно, но что он считал истинным только мир идей, ложно. Это заблуждение Платона было вызвано тем очевидным фактом, что законы мира вещей открывались лишь путем абстрагирования и идеализации, путем "стирания случайных черт". Потому идеальный мир идей и казался Плауну истинным и непреходящим. Таким образом, идеализм Платона был связан с преувеличением роли разума и недооценки значения опыта.
Показательно, что в наше время стремительной математизации и широчайшего применения ЭВМ, время, когда стало возможным физический эксперимент заменить экспериментом вычислительным и буквально "увидеть" на экране дисплея ЭВМ то или иное физическое явление, некоторые философы-идеалисты пытаются поднять на щит учение Платона. Ответим сформулирован в статье Ю. А. Жданова "Философские проблемы современного естествознания": "В законах математики отражаются не свойства ума, а свойства всей материи, в том числе и ума. Вот почему эти законы имеют объективное содержание, вот почему они обладают эвристическим характером, вот почему на их основе можно строить научный прогноз и предсказание, проверяя их в последующем практикой". Напомним, что и в начале нашего столетия — времени рождения теории Эйнштейна и бурных потрясений в физике — Философы-идеалисты восклицали: "Материя исчезла, остались одни уравнения!" В. И. Ленин в своем труде "Материалы и эмпириокритицизм" подверг резкой критике эту идеалистическую трактовку математического знания, а гениальное ленинское предвидение "Электрон так жe неисчерпаем, как и атом" (т. 18, с. 277) подтверждается всем ходом развития физики элементарных частиц.
Но вернемся в Древнюю Грецию. Теперь нам будет понятно, откуда Платону пришла мысль отождествлять физические элементы (атомы четырех стихий) с геометрическими телами — правильными многогранниками: в геометрии Платон видел ключ к познанию природы. Впрочем, по порядку...
Многогранник называется правильным, если он лежит по одну сторону от плоскости любой его грани, т. е. является выпуклым, и все его грани есть равные правильные многоугольники. Простой подсчет суммы углов при вершине правильного многогранника показывает, что существует только пять правильных многогранников[17]. Доказательство этого факта имеется в XIII книге "Начал" Евклида, но сам факт был, безусловно, известен Платону, а правильные многогранники знали пифагорейцы задолго до Платона. Форму правильных тел, по-видимому, подсказала древним грекам сама природа: кристаллы поваренной соли имеют форму куба, кристаллы квасцов — октаэдра, а кристаллы пирита — додекаэдра. Последний, как показали раскопки в итальянских Альпах, был любимой игрушкой этрусских детей задолго до нашей эры.
Правильные многогранники всегда восхищали пытливые умы симметрией, простотой и мудростью своих форм. Леонардо да Винчи любил изготовлять из дерева каркасы правильных тел и преподносить их в виде подарка различным знаменитостям. К сожалению, мы не можем подробнее остановиться на массе любопытных геометрических свойств и физических приложений правильных тел. это выходит за рамки нашего разговор* а тем, кто заинтересуется ими, мы рекомендуем прочитать книгу К. Левитил "Геометрическая рапсодия".
Платон (427-347). Римская мраморная копия с греческого оригинала. Ок. 370 до н. э
Платон (427-347 гг. до н. э.) — величайший философ античности, оказавший огромное влияние на развитие всей мировой культуры. Однако Платон был не только философом, создателем первой в истории человечества системы объективного идеализма, "линии Платона", по определению В. И. Ленина (т. 18, с. 131), но также и блестящим художником слова, организатором и теоретиком науки, ученым и гражданином города-государства Афины. После казни своего любимого учителя Сократа, болезненно переживая кризис афинской демократии, Платон покинул Афины и около двенадцати лет провел в путешествиях. Вернувшись на родину, Платон основал научную школу — Академию, которая разместилась на купленном для этой цели Платоном участке в роще близ Афин. Роща носила имя древнеаттического героя Академа, откуда и пошло название первой в истории человечества научной школы — Академии.
Платон и его ученики, платоники, были самой влиятельной после пифагорейцев группой мыслителей, а Платонова Академия в течение девяти столетий оставалась центром, влекущим к себе лучшие умы античности. Платон направлял и воодушевлял научную работу. Великие математики Теэтет и Евдокс были друзьями Платона, его учителями в математике и учениками в философии. Великий ученик Платона — Аристотель, будущий учитель и воспитатель Александра Македонского, двадцать лет жизни провел в благотворной атмосфере Академии. Хотя сам Платон и не был математиком, он придавал огромное значение изучению математики, живо интересовался ею и требовал от своих учеников основательных знаний математики, прежде чем посвятить их в свою философию. По преданию, на вратах Академии Платона было начертано: "Негеометр да не войдет!", а одному из начинающих философов, не знавшему математики, Платон сказал: "Уйди прочь! У тебя нет орудия для изучения философии..."
Не останавливаясь на философской системе Платона, отметим только, что, согласно Платону, существуют два мира: материальный несовершенный мир вещей и совершенный мир идей. Законы мира вещей несовершенны и преходящи, тогда как в мире идей господствуют абсолютные и неизменные истины, которые и надлежит изучать философу. Материальный мир есть не более как одна из несовершенных реализаций мира идей, и постигнуть реальный мир можно только с помощью математики идеального мира. То, что идеальный мир основан на математике, сомнений не вызывало. "Знание, к которому стремятся геометры, есть знание вечного, а не того, что тленно и преходяще",- утверждал Платон.
Таким образом, Платон ясно осознавал значение математизации науки, и это именно тот путь, по которому пошло развитие науки в античности и по которому оно продолжает идти сегодня. Однако следует четко различать: то, что Платон видел в математике инструмент познания законов природы, безусловно, верно, но что он считал истинным только мир идей, ложно. Это заблуждение Платона было вызвано тем очевидным фактом, что законы мира вещей открывались лишь путем абстрагирования и идеализации, путем "стирания случайных черт". Потому идеальный мир идей и казался Плауну истинным и непреходящим. Таким образом, идеализм Платона был связан с преувеличением роли разума и недооценки значения опыта.
Показательно, что в наше время стремительной математизации и широчайшего применения ЭВМ, время, когда стало возможным физический эксперимент заменить экспериментом вычислительным и буквально "увидеть" на экране дисплея ЭВМ то или иное физическое явление, некоторые философы-идеалисты пытаются поднять на щит учение Платона. Ответим сформулирован в статье Ю. А. Жданова "Философские проблемы современного естествознания": "В законах математики отражаются не свойства ума, а свойства всей материи, в том числе и ума. Вот почему эти законы имеют объективное содержание, вот почему они обладают эвристическим характером, вот почему на их основе можно строить научный прогноз и предсказание, проверяя их в последующем практикой". Напомним, что и в начале нашего столетия — времени рождения теории Эйнштейна и бурных потрясений в физике — Философы-идеалисты восклицали: "Материя исчезла, остались одни уравнения!" В. И. Ленин в своем труде "Материалы и эмпириокритицизм" подверг резкой критике эту идеалистическую трактовку математического знания, а гениальное ленинское предвидение "Электрон так жe неисчерпаем, как и атом" (т. 18, с. 277) подтверждается всем ходом развития физики элементарных частиц.
Но вернемся в Древнюю Грецию. Теперь нам будет понятно, откуда Платону пришла мысль отождествлять физические элементы (атомы четырех стихий) с геометрическими телами — правильными многогранниками: в геометрии Платон видел ключ к познанию природы. Впрочем, по порядку...
Многогранник называется правильным, если он лежит по одну сторону от плоскости любой его грани, т. е. является выпуклым, и все его грани есть равные правильные многоугольники. Простой подсчет суммы углов при вершине правильного многогранника показывает, что существует только пять правильных многогранников[17]. Доказательство этого факта имеется в XIII книге "Начал" Евклида, но сам факт был, безусловно, известен Платону, а правильные многогранники знали пифагорейцы задолго до Платона. Форму правильных тел, по-видимому, подсказала древним грекам сама природа: кристаллы поваренной соли имеют форму куба, кристаллы квасцов — октаэдра, а кристаллы пирита — додекаэдра. Последний, как показали раскопки в итальянских Альпах, был любимой игрушкой этрусских детей задолго до нашей эры.
Правильные многогранники всегда восхищали пытливые умы симметрией, простотой и мудростью своих форм. Леонардо да Винчи любил изготовлять из дерева каркасы правильных тел и преподносить их в виде подарка различным знаменитостям. К сожалению, мы не можем подробнее остановиться на массе любопытных геометрических свойств и физических приложений правильных тел. это выходит за рамки нашего разговор* а тем, кто заинтересуется ими, мы рекомендуем прочитать книгу К. Левитил "Геометрическая рапсодия".
 Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Пачоли 'О божественной пропорции'. Венеция. 1509
Ко времени Платона в античной философии уже созрела концепция четырех элементов (стихий) — первооснов материального мира: огня, воздуха, воды ц земли. Огонь и землю Платон считает основными компонентами для образования космоса: "...всему, что имело произойти, надлежало, конечно, быть телесным, видимым и осязаемым. Но быть видимым ничто не может без посредства огня, точно так же и осязаемым ничто не может быть без чего-нибудь твердого, твердым же ничто не может быть без земли (Тимей)". Между основными стихиями помещаются две средние — вода и воздух, и все они связываются музыкальными отношениями. Атомам земли Платон придает форму куба, так как и земля, и куб отличаются неподвижностью и устойчивостью. Атомам воды — форму икосаэдра, так как вода отличается текучестью, а из всех правильных тел икосаэдр — наиболее "катящийся". Атомам воздуха — форму октаэдра, ибо воздух движется взад и вперед и октаэдр как бы направлен одновременно в разные стороны. Атомам огня — форму тетраэдра как наиболее острого, мечущегося в разные стороны. Не у дел остался пятый правильный многогранник — додекаэдр. Для него Платон вводит пятый элемент — "пятую сущность"[18] — мировой эфир, атомам которого придается форма додекаэдра как наиболее близкого к шару — самому с0' вершенному по форме телу. С тех пор правильные многогранники называются также платоновыми телами.
Далее, поскольку в музыкальных отмщениях греки видели основу "всеобщей гармонии", Платон устанавливает эти отношения не только для космических тел (гармония сфер), но и для самих элементов, из которых состоит космос. По Платону, отношение основных элементов — атомов земли к атомам огня — равно октаве (2/1), отношение атомов земли и воды, а также воздуха и огня равно кварте (4/3) и т. д. Несмотря на любовь Платона к геометрии, эти отношения не имеют никакой математической базы. Ими Не связаны ни число вершин Платоновых тел, ни объемы этих тел, вписанных одно в другое, ни число ребер или граней.
Заметим, что поиск музыкальных отношений в геометрических образах сильно увлекал античных исследователей. Не случайно из множества первоклассных открытий Архимед больше всего ценил открытие отношения объемов и площадей поверхностей цилиндра и вписанного в него шара, равного 3/2, т. е. квинте.
Но и в отжившем учении Платона об атомах четырех стихий есть своя внутренняя мудрость. Стремление свести сложные природные явления к простым неразложимым компонентам остается содержанием и современного естествознания. Сейчас известно чуть более ста атомов элементов, из которых состоят все встречающиеся в природе вещества. Сверхзадачей современной физики является выявление "кирпичиков мироздания" — элементарных частиц — первичных, неразложимых далее частиц, из которых состоит вся материя. Еще в начале XX века считалось, что таких частиц три: электрон, протон и нейтрон. Однако катастрофический рост числа открываемых элементарных частиц привел во второй половине XX века к пересмотру воззрений об их элементарности. Сегодня есть основания считать, что такие "экс-элементарные" частицы, как протоны, нейтроны, мезоны, гипероны и др., состоят из различных комбинаций трех типов кварков[19] (либо пар кварк — антикварк) — новых "кирпичиков мироздания". Не вдаваясь в дебри современной ядерной физики, отметим только, что, как и во времена Платона, принцип простоты является той нитью Ариадны, которая ведет сегодня физиков по темным лабиринтам микромира.
Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Пачоли 'О божественной пропорции'. Венеция. 1509
Ко времени Платона в античной философии уже созрела концепция четырех элементов (стихий) — первооснов материального мира: огня, воздуха, воды ц земли. Огонь и землю Платон считает основными компонентами для образования космоса: "...всему, что имело произойти, надлежало, конечно, быть телесным, видимым и осязаемым. Но быть видимым ничто не может без посредства огня, точно так же и осязаемым ничто не может быть без чего-нибудь твердого, твердым же ничто не может быть без земли (Тимей)". Между основными стихиями помещаются две средние — вода и воздух, и все они связываются музыкальными отношениями. Атомам земли Платон придает форму куба, так как и земля, и куб отличаются неподвижностью и устойчивостью. Атомам воды — форму икосаэдра, так как вода отличается текучестью, а из всех правильных тел икосаэдр — наиболее "катящийся". Атомам воздуха — форму октаэдра, ибо воздух движется взад и вперед и октаэдр как бы направлен одновременно в разные стороны. Атомам огня — форму тетраэдра как наиболее острого, мечущегося в разные стороны. Не у дел остался пятый правильный многогранник — додекаэдр. Для него Платон вводит пятый элемент — "пятую сущность"[18] — мировой эфир, атомам которого придается форма додекаэдра как наиболее близкого к шару — самому с0' вершенному по форме телу. С тех пор правильные многогранники называются также платоновыми телами.
Далее, поскольку в музыкальных отмщениях греки видели основу "всеобщей гармонии", Платон устанавливает эти отношения не только для космических тел (гармония сфер), но и для самих элементов, из которых состоит космос. По Платону, отношение основных элементов — атомов земли к атомам огня — равно октаве (2/1), отношение атомов земли и воды, а также воздуха и огня равно кварте (4/3) и т. д. Несмотря на любовь Платона к геометрии, эти отношения не имеют никакой математической базы. Ими Не связаны ни число вершин Платоновых тел, ни объемы этих тел, вписанных одно в другое, ни число ребер или граней.
Заметим, что поиск музыкальных отношений в геометрических образах сильно увлекал античных исследователей. Не случайно из множества первоклассных открытий Архимед больше всего ценил открытие отношения объемов и площадей поверхностей цилиндра и вписанного в него шара, равного 3/2, т. е. квинте.
Но и в отжившем учении Платона об атомах четырех стихий есть своя внутренняя мудрость. Стремление свести сложные природные явления к простым неразложимым компонентам остается содержанием и современного естествознания. Сейчас известно чуть более ста атомов элементов, из которых состоят все встречающиеся в природе вещества. Сверхзадачей современной физики является выявление "кирпичиков мироздания" — элементарных частиц — первичных, неразложимых далее частиц, из которых состоит вся материя. Еще в начале XX века считалось, что таких частиц три: электрон, протон и нейтрон. Однако катастрофический рост числа открываемых элементарных частиц привел во второй половине XX века к пересмотру воззрений об их элементарности. Сегодня есть основания считать, что такие "экс-элементарные" частицы, как протоны, нейтроны, мезоны, гипероны и др., состоят из различных комбинаций трех типов кварков[19] (либо пар кварк — антикварк) — новых "кирпичиков мироздания". Не вдаваясь в дебри современной ядерной физики, отметим только, что, как и во времена Платона, принцип простоты является той нитью Ариадны, которая ведет сегодня физиков по темным лабиринтам микромира.

 Теорему об отношении объемов и площадей поверхности цилиндра и вписанного в него шара Архимид считал своим высшим достижением. По завещанию Архимеда чертеж этих фигур был выполнен на его могильном камне
Теорему об отношении объемов и площадей поверхности цилиндра и вписанного в него шара Архимид считал своим высшим достижением. По завещанию Архимеда чертеж этих фигур был выполнен на его могильном камне
 Непреходящие математические свойства правильных многогранников (таблица) и их наивная физическая интерпретация по Платону
Еще более современным выглядит стремление Платона видеть элементы материи в виде правильных симметричных тел. Современная наука все глубже проникает в тайну того, что внешние проявления симметрии — от симметрии кристаллов и снежинок до симметрии молекул ДНК — есть следствие симметрии тех фундаментальных законов, которые управляют всеми процессами физического мира. Таким образом, то, что на заре цивилизации античные философы видели атомы в виде симметричных геометрических тел" должно вызывать не саркастическую усмешку, а, скорее, удивление.
Учения о четырех стихиях и гармонии сфер из античности перешли в средневековье. Народное творчество, фантазия средневековых алхимиков и воображение поэтов населили четыре Платоновы стихии мифическими существами — духами. Так появились подземные человечки — гномы или кобольды — духи земли; златокудрые русалки — ундины — с рыбьим хвостом вместо ног — духи воды; прекрасные существа, населяющие атмосферу, ростом не более дюйма с шапочкой из цветка на голове — сильфы или эльфы — духи воздуха; наконец, духи огня — саламандры, пляшущие в огне в виде ящериц. Страшные карлики-гномы охраняют подземные богатства, они сказочно богаты, любят дразнить людей, но чаще помогают им. Красавицы-ундины вечерами расчесывают на берегу свои пышные волосы. Однако они опасны, так как могут очаровать своей красотой и пением пылкого юношу и увлечь его в подводное царство. Танцы и музыка — любимое занятие эльфов, а если музыкант начнет играть мелодию эльфов, то он не сможет остановиться, пока не доиграет ее до конца. Знакомые с детства сказки Андерсена "Дюймовочка" и "Русалочка", сказка братьев Гримм "Белоснежка и семь гномов", комедия Шекспира "Сон в летнюю ночь", баллада Гёте "Лесной царь", поэма Жуковского "Ундина" и многие стихотворения многих авторов навеяны этими легендами. Так отжившая научная теория превращалась в красивую сказку.
Непреходящие математические свойства правильных многогранников (таблица) и их наивная физическая интерпретация по Платону
Еще более современным выглядит стремление Платона видеть элементы материи в виде правильных симметричных тел. Современная наука все глубже проникает в тайну того, что внешние проявления симметрии — от симметрии кристаллов и снежинок до симметрии молекул ДНК — есть следствие симметрии тех фундаментальных законов, которые управляют всеми процессами физического мира. Таким образом, то, что на заре цивилизации античные философы видели атомы в виде симметричных геометрических тел" должно вызывать не саркастическую усмешку, а, скорее, удивление.
Учения о четырех стихиях и гармонии сфер из античности перешли в средневековье. Народное творчество, фантазия средневековых алхимиков и воображение поэтов населили четыре Платоновы стихии мифическими существами — духами. Так появились подземные человечки — гномы или кобольды — духи земли; златокудрые русалки — ундины — с рыбьим хвостом вместо ног — духи воды; прекрасные существа, населяющие атмосферу, ростом не более дюйма с шапочкой из цветка на голове — сильфы или эльфы — духи воздуха; наконец, духи огня — саламандры, пляшущие в огне в виде ящериц. Страшные карлики-гномы охраняют подземные богатства, они сказочно богаты, любят дразнить людей, но чаще помогают им. Красавицы-ундины вечерами расчесывают на берегу свои пышные волосы. Однако они опасны, так как могут очаровать своей красотой и пением пылкого юношу и увлечь его в подводное царство. Танцы и музыка — любимое занятие эльфов, а если музыкант начнет играть мелодию эльфов, то он не сможет остановиться, пока не доиграет ее до конца. Знакомые с детства сказки Андерсена "Дюймовочка" и "Русалочка", сказка братьев Гримм "Белоснежка и семь гномов", комедия Шекспира "Сон в летнюю ночь", баллада Гёте "Лесной царь", поэма Жуковского "Ундина" и многие стихотворения многих авторов навеяны этими легендами. Так отжившая научная теория превращалась в красивую сказку.
(Гёте. "Фауст")
("Рай", песнь I)
 Боттичелли. Иллюстрация к 'Божественной комедии' Данте. 1492-1497. Данте, влекомый Беатриче, взирает на геоцентрическую систему мироздания
Заключительные аккорды "космической музыки" прозвучали в работах Иоганна Кеплера (1571 -1630) — выдающегося немецкого математика, физика, астронома. Следуя пифагорейско-платоновской традиции, Кеплер верил, что в основе мироздания лежат простые числовые соотношения и совершенные геометрические формы. Но Кеплер поставил и вопросы, достойные отцасовременного естествознания: почему планет (известных в то время) только шесть? Почему их орбиты имеют те, а не иные параметры?
Сначала молодой учитель математики Иоганн Кеплер тщетно ищет между параметрами планетных орбит простые числовые отношения. Но вдруг... Решая с учениками какую-то геометрическую задачу, он начертил на классной доске равносторонний треугольник со вписанной и описанной окружностями. Внезапно его
Боттичелли. Иллюстрация к 'Божественной комедии' Данте. 1492-1497. Данте, влекомый Беатриче, взирает на геоцентрическую систему мироздания
Заключительные аккорды "космической музыки" прозвучали в работах Иоганна Кеплера (1571 -1630) — выдающегося немецкого математика, физика, астронома. Следуя пифагорейско-платоновской традиции, Кеплер верил, что в основе мироздания лежат простые числовые соотношения и совершенные геометрические формы. Но Кеплер поставил и вопросы, достойные отцасовременного естествознания: почему планет (известных в то время) только шесть? Почему их орбиты имеют те, а не иные параметры?
Сначала молодой учитель математики Иоганн Кеплер тщетно ищет между параметрами планетных орбит простые числовые отношения. Но вдруг... Решая с учениками какую-то геометрическую задачу, он начертил на классной доске равносторонний треугольник со вписанной и описанной окружностями. Внезапно его
 'Космическая музыка': от Платона до Кеплера
озарила мысль, что планетные орбиты связаны между собой посредством геометрических фигур. Однако расчеты показали, что плоские геометрические фигуры не удовлетворяли этой идее. Новые разочарования... "И вот я снова устремился вперед. Зачем рассматривать фигуры
двух измерений для пригонки орбит в пространстве? Следует рассмотреть формы трех измерений...",- вспоминал впоследствии Кеплер. Новые поиски и новое озарение: существует только шесть планет и, следовательно, пять промежутков между ними. Но и Платоновых тел только пять! Как трудно было допустить, что это простое совпадение!.. "Я еще не имел ясной идеи о порядке, в котором следует расположить правильные тела... День и ночь я проводил за расчетами... Через несколько дней все стало на свои места." Какой накал страстей в этих записях Кеплера!
Вскоре двадцатичетырехлетний учитель издает маленькую книжку с вычур ным названием, как требовала мода того времени,- "Предвестник космографических исследований, содержащий тайну мироздания относительно чудесных пр°" порций между небесными кругами и истинных причин числа и размеров небесных сфер, а также периодических движений, изложенный с помощью пяти правильных тел Иоганном Кеплером из Вюртемберга, математиком достославной провинции Штирии", или "Mysterium Сosniographicum" ("Тайна мироздания"), как любил называть ее сам Кеплер. Книга эта содержала формулу открытия Кеплера: в сферу орбиты Сатурна Кеплер вписывает куб, в куб — сферу Юпитера, в сферу Юпитера — тетраэдр, и так далее последовательно вписываются друг в друга сферы Марса — додекаэдр, сфера Земля — икосаэдр, сфера Венеры — октаэдр и сфера Меркурия. В центре всей системы коперниканец Кеплер помещает Солнце*. Тайна мироздания кажется раскрытой! Вселенная устроена на основе единого геометрического принципа!
* (Для каждого правильного многогранника существует вписанная сфера, касающаяся центров каждой грани, и описанная сфера, проходящая через все вершины, причем центры этих сФер совпадают. Таким образом, все построенные Кеплером сферы имеют общий центр.)
Что же показали математические расчеты? Конечно, совпадение с данными Коперника по радиусам планетных орбит было поразительным, но все-таки не столь точным, как того хотелось бы педантичному Кеплеру[20].Особенно много хлопот доставила Кеплеру сфера Меркурия, которую в конце концов пришлось вписать в октаэдр так, чтобы -она касалась не граней, а середины ребер последнего. Остальные незначительные расхождения между теорией и опытными данными Кеплер объяснил тем, что реальные планетные сферы имеют некоторую толщину, что и позволило "выбрать" эти расхождения.
Однако червь сомнения поселился в Душе Кеплера. Можно сказать, что оставшиеся тридцать лет жизни Кеплер посвятил "спасению" своей теории от самого себя. Эта работа привела к открытию истинных астрономических законов — трех знаменитых законов Кеплера, на базе которых Ньютон построил свою теорию тяготения. Сам же Кеплер в полной мере не осознал своих настоящих открытий и до конца жизни более всего любил свою первую работу.
'Космическая музыка': от Платона до Кеплера
озарила мысль, что планетные орбиты связаны между собой посредством геометрических фигур. Однако расчеты показали, что плоские геометрические фигуры не удовлетворяли этой идее. Новые разочарования... "И вот я снова устремился вперед. Зачем рассматривать фигуры
двух измерений для пригонки орбит в пространстве? Следует рассмотреть формы трех измерений...",- вспоминал впоследствии Кеплер. Новые поиски и новое озарение: существует только шесть планет и, следовательно, пять промежутков между ними. Но и Платоновых тел только пять! Как трудно было допустить, что это простое совпадение!.. "Я еще не имел ясной идеи о порядке, в котором следует расположить правильные тела... День и ночь я проводил за расчетами... Через несколько дней все стало на свои места." Какой накал страстей в этих записях Кеплера!
Вскоре двадцатичетырехлетний учитель издает маленькую книжку с вычур ным названием, как требовала мода того времени,- "Предвестник космографических исследований, содержащий тайну мироздания относительно чудесных пр°" порций между небесными кругами и истинных причин числа и размеров небесных сфер, а также периодических движений, изложенный с помощью пяти правильных тел Иоганном Кеплером из Вюртемберга, математиком достославной провинции Штирии", или "Mysterium Сosniographicum" ("Тайна мироздания"), как любил называть ее сам Кеплер. Книга эта содержала формулу открытия Кеплера: в сферу орбиты Сатурна Кеплер вписывает куб, в куб — сферу Юпитера, в сферу Юпитера — тетраэдр, и так далее последовательно вписываются друг в друга сферы Марса — додекаэдр, сфера Земля — икосаэдр, сфера Венеры — октаэдр и сфера Меркурия. В центре всей системы коперниканец Кеплер помещает Солнце*. Тайна мироздания кажется раскрытой! Вселенная устроена на основе единого геометрического принципа!
* (Для каждого правильного многогранника существует вписанная сфера, касающаяся центров каждой грани, и описанная сфера, проходящая через все вершины, причем центры этих сФер совпадают. Таким образом, все построенные Кеплером сферы имеют общий центр.)
Что же показали математические расчеты? Конечно, совпадение с данными Коперника по радиусам планетных орбит было поразительным, но все-таки не столь точным, как того хотелось бы педантичному Кеплеру[20].Особенно много хлопот доставила Кеплеру сфера Меркурия, которую в конце концов пришлось вписать в октаэдр так, чтобы -она касалась не граней, а середины ребер последнего. Остальные незначительные расхождения между теорией и опытными данными Кеплер объяснил тем, что реальные планетные сферы имеют некоторую толщину, что и позволило "выбрать" эти расхождения.
Однако червь сомнения поселился в Душе Кеплера. Можно сказать, что оставшиеся тридцать лет жизни Кеплер посвятил "спасению" своей теории от самого себя. Эта работа привела к открытию истинных астрономических законов — трех знаменитых законов Кеплера, на базе которых Ньютон построил свою теорию тяготения. Сам же Кеплер в полной мере не осознал своих настоящих открытий и до конца жизни более всего любил свою первую работу.
 Космический кубок Кеплера, Иллюстрация Иоганна Кеплера из его книги 'Тайна мироздания'. Тюбинген. 1596
Не забыл Кеплер и о самой "музыке" сфер. Поискам гармонических соотношений посвящена одна из глав книги "Гармония мира" (1619), которую он считал своей вершиной: "жребий брошен. Я написал книгу либо для современников, либо для потомков..." Кеплер установил семь основных гармонических интервалов (консонансов): октаву (2/1), большую сексту (5/3), малую сексту (8/5), чистую квинту (3/2), чистую кварту (4/3), большую терцию (5/4) и малую терцию (6/5), из которых он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармонических соотношений "на небе", проделав огромную вычислительную работу, Кеплер наконец установил, что отношения экстремальных (наибольших и наименьших) угловых скоростей[21] для некоторых планет близки к гармоническим: Марс — 3/2, Юпитер — 6/5, Сатурн — 5/4. "Солнце гармонии засияло во всем блеске... Небесные движения есть не что иное, как ни на миг не прекращающаяся многоголосая музыка". И здесь Кеплера не оставляет буйная фантазия. Небольшие расхождения теории и эксперимента он объясняет тем, что небесный секстет должен звучать одинаково согласованно и в миноре, и в мажоре, а для этого ему необходимо иметь возможность перестраивать свои инструменты. Далее Кеплер утверждает, что Сатурн и Юпитер "поют" басом, Марс — тенором, Земля и Венера — альтом, а Меркурий — дискантом. Никаких математических "доказательств" здесь он не приводит. Да и сам Кеплер устал в поисках всеобщей гармонии: "Мой мозг устает, когда я пытаюсь понять, что я написал, и мне уже трудно восстановить связь между рисунками и текстом, которую я сам когда-то нашел..." Занималась заря нового естествознания: на смену фантазиям Кеплера шли уравнения Ньютона. Красивая сказка о музыке сфер доживала свой век, и работы Кеплера были ее лебединой песней.
Космический кубок Кеплера, Иллюстрация Иоганна Кеплера из его книги 'Тайна мироздания'. Тюбинген. 1596
Не забыл Кеплер и о самой "музыке" сфер. Поискам гармонических соотношений посвящена одна из глав книги "Гармония мира" (1619), которую он считал своей вершиной: "жребий брошен. Я написал книгу либо для современников, либо для потомков..." Кеплер установил семь основных гармонических интервалов (консонансов): октаву (2/1), большую сексту (5/3), малую сексту (8/5), чистую квинту (3/2), чистую кварту (4/3), большую терцию (5/4) и малую терцию (6/5), из которых он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармонических соотношений "на небе", проделав огромную вычислительную работу, Кеплер наконец установил, что отношения экстремальных (наибольших и наименьших) угловых скоростей[21] для некоторых планет близки к гармоническим: Марс — 3/2, Юпитер — 6/5, Сатурн — 5/4. "Солнце гармонии засияло во всем блеске... Небесные движения есть не что иное, как ни на миг не прекращающаяся многоголосая музыка". И здесь Кеплера не оставляет буйная фантазия. Небольшие расхождения теории и эксперимента он объясняет тем, что небесный секстет должен звучать одинаково согласованно и в миноре, и в мажоре, а для этого ему необходимо иметь возможность перестраивать свои инструменты. Далее Кеплер утверждает, что Сатурн и Юпитер "поют" басом, Марс — тенором, Земля и Венера — альтом, а Меркурий — дискантом. Никаких математических "доказательств" здесь он не приводит. Да и сам Кеплер устал в поисках всеобщей гармонии: "Мой мозг устает, когда я пытаюсь понять, что я написал, и мне уже трудно восстановить связь между рисунками и текстом, которую я сам когда-то нашел..." Занималась заря нового естествознания: на смену фантазиям Кеплера шли уравнения Ньютона. Красивая сказка о музыке сфер доживала свой век, и работы Кеплера были ее лебединой песней.
(Н. Заболоцкий)
 (7.2)
h — постоянная Планка.
В простейшем случае атома водорода, содержащего один электрон, энергия n-го энергетического уровня равна
(7.2)
h — постоянная Планка.
В простейшем случае атома водорода, содержащего один электрон, энергия n-го энергетического уровня равна
 (7.3)
R — постоянная Ридберга.
Здесь n = 1, 2, 3,... называется главным квантовым числом. Тогда совокупность частот, излучаемых атомом водорода при переходе с верхнего энергетического уровня на нижний (i>k), определяет спектр испускания данного атома и каждому такому переходу соответствует своя спектральная линия. Для атома водорода согласно формулам 7.2, 7.3 получаем совокупность спектральных линий с частотами
(7.3)
R — постоянная Ридберга.
Здесь n = 1, 2, 3,... называется главным квантовым числом. Тогда совокупность частот, излучаемых атомом водорода при переходе с верхнего энергетического уровня на нижний (i>k), определяет спектр испускания данного атома и каждому такому переходу соответствует своя спектральная линия. Для атома водорода согласно формулам 7.2, 7.3 получаем совокупность спектральных линий с частотами
 При переходе со второго, третьего и т. д. энергетических уровней ni = 2, 3, 4... на первый nk = 1 получается так называемая "спектральная серия Лаймана", для которой α21=3/4, α31=8/9, α41 = 15/16. Но ведь это кварта (3/4), тон (8/9) и полутон в чистом строе (15/16)! "Таким образом,- писал А. Эйнштейн,- мы открыли некоторое подобие между колебанием струны и атомом, испускающим излучение".
"То, что нам сегодня удается понять на языке спектров,- это истинная музыка атомных сфер, созвучие целочисленных отношений, все возрастающие порядок и гармония при всем их многообразии — так восторженно отзывался о квантовой теории немецкий физик и математик Арнольд Зоммерфельд (1868-1951).- ... Она представляет собой тот полный таинства инструмент, на котором природа исполняет спектральную музыку и ритмом которого она управляет строением атома и атомных ядер".
Итак, обыкновенная музыкальная гамма увлекла нас вслед за Пифагором, Платоном и Кеплером в путешествие по просторам космоса. Мы узнали, что "пифагорово пенье" услышали и физики XX века, но уже не в космосе, а в противоположной стихии — микромире. Но нам пора от "физических приложений" вновь вернуться к математическому содержанию музыкальной гаммы, которая таит в себе еще немало секретов.
При переходе со второго, третьего и т. д. энергетических уровней ni = 2, 3, 4... на первый nk = 1 получается так называемая "спектральная серия Лаймана", для которой α21=3/4, α31=8/9, α41 = 15/16. Но ведь это кварта (3/4), тон (8/9) и полутон в чистом строе (15/16)! "Таким образом,- писал А. Эйнштейн,- мы открыли некоторое подобие между колебанием струны и атомом, испускающим излучение".
"То, что нам сегодня удается понять на языке спектров,- это истинная музыка атомных сфер, созвучие целочисленных отношений, все возрастающие порядок и гармония при всем их многообразии — так восторженно отзывался о квантовой теории немецкий физик и математик Арнольд Зоммерфельд (1868-1951).- ... Она представляет собой тот полный таинства инструмент, на котором природа исполняет спектральную музыку и ритмом которого она управляет строением атома и атомных ядер".
Итак, обыкновенная музыкальная гамма увлекла нас вслед за Пифагором, Платоном и Кеплером в путешествие по просторам космоса. Мы узнали, что "пифагорово пенье" услышали и физики XX века, но уже не в космосе, а в противоположной стихии — микромире. Но нам пора от "физических приложений" вновь вернуться к математическому содержанию музыкальной гаммы, которая таит в себе еще немало секретов.
8. Математический строй музыки
Настоящая наука и настоящая музыка требуют однородного мыслительного процесса.В главе 6 мы получили пифагоров строй, т. е. математическое выражение интервальных коэффициентов, лидийской гаммы (6.14), или, в современной терминологии, пифагоров строй натурального мажора:А. Эйнштейн
 (8.1)
Здесь цифры внизу обозначают интервальные коэффициенты соседних ступеней гаммы; напомним, что 9/8 есть тон, а 256/243 — полутон. Мы обнаружили также, что основные консонансные интервалы в пределах октавы — квинта и кварта — являются соответственно средним арифметическим и средним гармоническим частот основного тона и октавы. Кроме того, октава, квинта, кварта и тон образуют геометрическую пропорцию:
октава/квинта = кварта/тон.
Таким образом, музыкальная гамма разделена на пропорциональные части; она буквально пронизана пропорциями, а пропорциональность, как мы знаем, является одним из объективных критериев красоты. Однако на этом математика музыкальной гаммы не кончается, а, скорее, только начинается.
Прежде всего из (8.1) видно, что расстояния между соседними ступенями пифагорова строя неодинаковы. Поэтому, во-первых, от ноты до можно было играть только в лидийском ладу, а чтобы сыграть от этой ноты, скажем, в дорийском ладу, необходимо было перестраивать почти все струны лиры. Во-вторых, от ноты ре получался уже не лидийский, а фригийский лад и, вообще, от каждой новой ноты начинался новый лад (не случайно в таблице 1 на с. 107 имеется семь ладов — по одному на каждую из семи нот октавы). Поэтому, чтобы сыграть мелодию в лидийском ладу от другой ноты (чего, безусловно, требовали ограниченные возможности человеческого голоса: один поет выше, другой — ниже), лиру также следовало перестраивать. (Конечно, если всю жизнь играть в одном ладу и одной тональности, то семи нот в октаве будет вполне достаточно. До сих пор прекрасно обходятся семью звуками некоторые гармошки и другие народные инструменты.)
Итак, для того, чтобы иметь возможность переходить из лада в лад и из тональности в тональность, строй должен быть равномерным, т. е. иметь одинаковые высотные расстояния (интервальные коэффициенты) между звуками. Казалось бы, что проще: нужно разделить каждый тон-интервал пополам на два полутона, т. е. получить еще пять дополнительных звуков, и шкала пифагорова строя станет равномерной. Но вот тут-то и таилась основная трудность.
(8.1)
Здесь цифры внизу обозначают интервальные коэффициенты соседних ступеней гаммы; напомним, что 9/8 есть тон, а 256/243 — полутон. Мы обнаружили также, что основные консонансные интервалы в пределах октавы — квинта и кварта — являются соответственно средним арифметическим и средним гармоническим частот основного тона и октавы. Кроме того, октава, квинта, кварта и тон образуют геометрическую пропорцию:
октава/квинта = кварта/тон.
Таким образом, музыкальная гамма разделена на пропорциональные части; она буквально пронизана пропорциями, а пропорциональность, как мы знаем, является одним из объективных критериев красоты. Однако на этом математика музыкальной гаммы не кончается, а, скорее, только начинается.
Прежде всего из (8.1) видно, что расстояния между соседними ступенями пифагорова строя неодинаковы. Поэтому, во-первых, от ноты до можно было играть только в лидийском ладу, а чтобы сыграть от этой ноты, скажем, в дорийском ладу, необходимо было перестраивать почти все струны лиры. Во-вторых, от ноты ре получался уже не лидийский, а фригийский лад и, вообще, от каждой новой ноты начинался новый лад (не случайно в таблице 1 на с. 107 имеется семь ладов — по одному на каждую из семи нот октавы). Поэтому, чтобы сыграть мелодию в лидийском ладу от другой ноты (чего, безусловно, требовали ограниченные возможности человеческого голоса: один поет выше, другой — ниже), лиру также следовало перестраивать. (Конечно, если всю жизнь играть в одном ладу и одной тональности, то семи нот в октаве будет вполне достаточно. До сих пор прекрасно обходятся семью звуками некоторые гармошки и другие народные инструменты.)
Итак, для того, чтобы иметь возможность переходить из лада в лад и из тональности в тональность, строй должен быть равномерным, т. е. иметь одинаковые высотные расстояния (интервальные коэффициенты) между звуками. Казалось бы, что проще: нужно разделить каждый тон-интервал пополам на два полутона, т. е. получить еще пять дополнительных звуков, и шкала пифагорова строя станет равномерной. Но вот тут-то и таилась основная трудность.
Дело в том, что половина тона
 в точности не равна полутону (256/243≈1,0545) (см. с. 105). Поэтому если в качестве единого масштаба строя взять полутон
в точности не равна полутону (256/243≈1,0545) (см. с. 105). Поэтому если в качестве единого масштаба строя взять полутон  т е заменить на него имеющиеся в (8.1) два полутона 256/243, то эти 12 новых полутонов приведут нас не точно в октаву (2), а чуточку выше:
т е заменить на него имеющиеся в (8.1) два полутона 256/243, то эти 12 новых полутонов приведут нас не точно в октаву (2), а чуточку выше:  Интервал между октавой, полученной шагами по 12-равномерным полутонам
Интервал между октавой, полученной шагами по 12-равномерным полутонам  и чистой октавой равен (9/8)6:2 ≈ 1,0136 и называется пифагоровой коммой*.
Представляя пифагорову комму в виде
и чистой октавой равен (9/8)6:2 ≈ 1,0136 и называется пифагоровой коммой*.
Представляя пифагорову комму в виде
 мы получим еще один важный результат: 12 квинт с точностью до пифагоровой коммы равны 7 октавам.
мы получим еще один важный результат: 12 квинт с точностью до пифагоровой коммы равны 7 октавам.
Но
 т. е. новый полутон содержал иррациональное число
т. е. новый полутон содержал иррациональное число  , которого пифагорейцы боялись как огня. Взять столь "некрасивое" число в качестве единицы измерения музыкальной гаммы было немыслимым для пифагорейцев: это противоречило всей философии целочисленных отношений. Поэтому пифагорейцы пошли другим путем: в качестве основы музыкальной гаммы они взяли квинту, "красивое" число 3/2.
* (Коммой (от греч. komma — отрезок) в музыкальной акустике называется интервал, не превышающий 1/9 целого тона. Пифагорова комма приблизительно равна 1/9 тона
, которого пифагорейцы боялись как огня. Взять столь "некрасивое" число в качестве единицы измерения музыкальной гаммы было немыслимым для пифагорейцев: это противоречило всей философии целочисленных отношений. Поэтому пифагорейцы пошли другим путем: в качестве основы музыкальной гаммы они взяли квинту, "красивое" число 3/2.
* (Коммой (от греч. komma — отрезок) в музыкальной акустике называется интервал, не превышающий 1/9 целого тона. Пифагорова комма приблизительно равна 1/9 тона  .)
Рассмотрим ряд, составленный из степеней числа 3/2:
.)
Рассмотрим ряд, составленный из степеней числа 3/2:

Оказывается, с помощью этого красивого симметричного ряда можно получить все интервальные коэффициенты пифагорова строя. Начнем с середины ряда
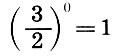 и все получаемые звуки будем сводить в одну октаву, умножая или деля их интервальные коэффициенты на нужные степени числа 2 (интервальный коэффициент октавы). Новые звуки будем обозначать либо ближайшим снизу основным звуком с добавлением слова "диез"
и все получаемые звуки будем сводить в одну октаву, умножая или деля их интервальные коэффициенты на нужные степени числа 2 (интервальный коэффициент октавы). Новые звуки будем обозначать либо ближайшим снизу основным звуком с добавлением слова "диез"  при движении по квинтам вверх, либо ближайшим сверху основным звуком с добавлением слова "бемоль"
при движении по квинтам вверх, либо ближайшим сверху основным звуком с добавлением слова "бемоль"  при движении по квинтам вниз. Это означает соответственно повышение или понижение основного звука. Итак,
при движении по квинтам вниз. Это означает соответственно повышение или понижение основного звука. Итак,
 (8.2)
Как видим, двигаясь по квинтам вверх и вниз от основного тона, мы получили все ступени пифагорова строя (8.1), каждая из которых в свою очередь может быть повышена, понижена, дважды повышена или понижена и т. д. Процесс этот, к сожалению, бесконечен. Точного октавного повторения основного тона (до) мы так и не получим. (Легко видеть, что си-диез и ре-бемоль-бемоль совпадают с основным тоном (до) опять же с точностью до пифагоровой коммы.) Следовательно, и точно разделить октаву на целое число частей этим методом мы не сможем.
Таким образом, желая разделить пять тонов в (8.1) на полутона, мы получили, по крайней мере, 10 промежуточных звуков. Новый пифагоров строй примет вид (интервальные коэффициенты новых звуков для краткости опущены)
(8.2)
Как видим, двигаясь по квинтам вверх и вниз от основного тона, мы получили все ступени пифагорова строя (8.1), каждая из которых в свою очередь может быть повышена, понижена, дважды повышена или понижена и т. д. Процесс этот, к сожалению, бесконечен. Точного октавного повторения основного тона (до) мы так и не получим. (Легко видеть, что си-диез и ре-бемоль-бемоль совпадают с основным тоном (до) опять же с точностью до пифагоровой коммы.) Следовательно, и точно разделить октаву на целое число частей этим методом мы не сможем.
Таким образом, желая разделить пять тонов в (8.1) на полутона, мы получили, по крайней мере, 10 промежуточных звуков. Новый пифагоров строй примет вид (интервальные коэффициенты новых звуков для краткости опущены)
 Какие из этих дополнительных звуков взять: с бемолями или диезами? Для музыкантов, играющих на инструментах с нефиксированной высотой звуков (скрипачей, например), эта проблема не стоит. Они берут и те и другие. В результате звучание скрипки становится более выразительным и контрастным, так как в ладе обостряются тяготения неустойчивых звуков к устойчивым. Этим во многом объясняется то "волшебное пение" скрипки, которое доступно только ей одной*.
* (Каким тонким является инструмент скрипка, убеждает простой пример из книги известного венгерского скрипача Карла Флеша "Искусство скрипичной игры": "Пусть на струне ля необходимо сыграть два звука ля и си-бемоль второй октавы. Разница между этими звуками равна 60 Гц. Расстояние на грифе — 2 мм, следовательно, на одно колебание струны приходится 1/30 мм. Предполагая, что ля взято чисто, и желая сыграть математически чисто си-бемоль, мы должны поставить палец в нужное место струны с точностью до 1/30 мм". Насколько же чувствительными должны быть слух и пальцы скрипача, чтобы отмерить расстояние с точностью до 1/30 мм (это 33 микрона)! )
Что касается инструментов с фиксированной высотой звуков, то введение десяти дополнительных звуков на семь основных слишком усложнило бы и сами инструменты, и игру на них. Тем более что и это не решало окончательно проблему и более тонкие построения требовали все новых и новых звуков. На сегодня в теории музыки известна масса строев с числом ступеней от 17 до 84! Но все они так и остались в кабинетах теоретиков. Практика же, руководствуясь мудрым критерием простоты (и красоты), оставила только пять дополнительных звуков: по одному в каждом из целых тонов. Они и стали черными (дополнительными) клавишами фортепиано.
Так в октаве стало 12 звуков. Поскольку каждая пара дополнительных звуков отличалась лишь на пифагорову комму (это легко проверить самостоятельно), то их попросту приравняли между собой (до-диез стал равен ре-бемолю и т. д.).
Такое приравнивание звуков с одинаковой высотой, но разными названиями в теории музыки называется энгармонизмом. Тонкости ладового звучания были принесены в жертву простоте. Инструменты же с числом звуков в октаве, превышающим 12, можно увидеть только в музеях. В московском Музее музыкальной культуры имени М. И. Глинки хранится рояль русского писателя, музыканта и музыковеда В. Ф. Одоевского (1804-1869), в каждой октаве которого имеется не 12, а 17 клавиш, настроенных согласно (8.2).
Квинтовая цепь пифагорова строя дала простой способ настройки инструментов с фиксированной высотой звуков: органов, клавесинов, фортепиано. От основного тона (сегодня по общему признанию им является звук ля первой октавы) откладывались семь октав — скелет музыкальной шкалы. Эти октавы заполнялись 12 звуками, полученными ходами по квинтам вверх и вниз. Какие из звуков взять за дополнительные — повышенные или пониженные,- особого значения не имело. Важно было другое: пифагорова комма оставалась внутри октавы. Ее можно было переместить в любое место октавы, но нельзя было сделать только одного: нельзя было от нее избавиться! И она продолжала портить кровь музыкантам на протяжении столетий. Почему?
Если взять пифагоров строй с пониженными дополнительными звуками:
Какие из этих дополнительных звуков взять: с бемолями или диезами? Для музыкантов, играющих на инструментах с нефиксированной высотой звуков (скрипачей, например), эта проблема не стоит. Они берут и те и другие. В результате звучание скрипки становится более выразительным и контрастным, так как в ладе обостряются тяготения неустойчивых звуков к устойчивым. Этим во многом объясняется то "волшебное пение" скрипки, которое доступно только ей одной*.
* (Каким тонким является инструмент скрипка, убеждает простой пример из книги известного венгерского скрипача Карла Флеша "Искусство скрипичной игры": "Пусть на струне ля необходимо сыграть два звука ля и си-бемоль второй октавы. Разница между этими звуками равна 60 Гц. Расстояние на грифе — 2 мм, следовательно, на одно колебание струны приходится 1/30 мм. Предполагая, что ля взято чисто, и желая сыграть математически чисто си-бемоль, мы должны поставить палец в нужное место струны с точностью до 1/30 мм". Насколько же чувствительными должны быть слух и пальцы скрипача, чтобы отмерить расстояние с точностью до 1/30 мм (это 33 микрона)! )
Что касается инструментов с фиксированной высотой звуков, то введение десяти дополнительных звуков на семь основных слишком усложнило бы и сами инструменты, и игру на них. Тем более что и это не решало окончательно проблему и более тонкие построения требовали все новых и новых звуков. На сегодня в теории музыки известна масса строев с числом ступеней от 17 до 84! Но все они так и остались в кабинетах теоретиков. Практика же, руководствуясь мудрым критерием простоты (и красоты), оставила только пять дополнительных звуков: по одному в каждом из целых тонов. Они и стали черными (дополнительными) клавишами фортепиано.
Так в октаве стало 12 звуков. Поскольку каждая пара дополнительных звуков отличалась лишь на пифагорову комму (это легко проверить самостоятельно), то их попросту приравняли между собой (до-диез стал равен ре-бемолю и т. д.).
Такое приравнивание звуков с одинаковой высотой, но разными названиями в теории музыки называется энгармонизмом. Тонкости ладового звучания были принесены в жертву простоте. Инструменты же с числом звуков в октаве, превышающим 12, можно увидеть только в музеях. В московском Музее музыкальной культуры имени М. И. Глинки хранится рояль русского писателя, музыканта и музыковеда В. Ф. Одоевского (1804-1869), в каждой октаве которого имеется не 12, а 17 клавиш, настроенных согласно (8.2).
Квинтовая цепь пифагорова строя дала простой способ настройки инструментов с фиксированной высотой звуков: органов, клавесинов, фортепиано. От основного тона (сегодня по общему признанию им является звук ля первой октавы) откладывались семь октав — скелет музыкальной шкалы. Эти октавы заполнялись 12 звуками, полученными ходами по квинтам вверх и вниз. Какие из звуков взять за дополнительные — повышенные или пониженные,- особого значения не имело. Важно было другое: пифагорова комма оставалась внутри октавы. Ее можно было переместить в любое место октавы, но нельзя было сделать только одного: нельзя было от нее избавиться! И она продолжала портить кровь музыкантам на протяжении столетий. Почему?
Если взять пифагоров строй с пониженными дополнительными звуками:
 то в таком строе все квинты будут звучать чисто (иметь интервальный коэффициент 3/2), кроме одной. Квинта си-соль-бемоль будет иметь интервальный коэффициент 1024/729:243/256≈1,4798, а не 1,5! От чистой квинты она, разумеется, отличается на пифагорову комму: 1,5/1,4798≈1,0136. Такая квинта на органе издавала пронзительный, неприятный звук, похожий на завывание волка, за что и была прозвана "волчьей квинтой" или просто "волком". Обращением "волчьей квинты" является "волчья кварта" соль-бемоль-си, которая также отличается от чистой кварты (4/3 = 1,333...) на пифагорову комму:
243/127:1024/729≈1,3515; 1,3515/1,3333≈1,0136. Можно сказать, что вся история развития музыкальных строев была историей борьбы с "волками". Но об этом — чуть позже.
А сейчас обратим внимание на второй существенный недостаток пифагорова строя. Его заметил еще во II веке древнегреческий ученый пифагореец Дидим. Дело в том, что пифагорова терция (81/64) при гармоническом, т. е. одновременном, исполнении обоих тонов, образующих терцию, звучит слишком напряженно. Дидим предложил заменить пифагорову терцию (81/64) так называемой "чистой терцией" (5/4 = 80/64), которая гармонически звучит значительно приятнее, хотя, как видим, лишь чуть-чуть отличается от пифагоровой терции. Разность пифагоровой и чистой терций (81/64:80/64 = 81/80≈1,0125) называется ди-димовой коммой и приблизительно равна 1/10 целого тона.
Однако идеи Дидима, как это не раз случалось с учеными Древней Греции, опередили историю почти на полторы тысячи лет. Они не нашли подходящей почвы для Развития, увяли, умерли и были воскрешены только в конце XV века...
то в таком строе все квинты будут звучать чисто (иметь интервальный коэффициент 3/2), кроме одной. Квинта си-соль-бемоль будет иметь интервальный коэффициент 1024/729:243/256≈1,4798, а не 1,5! От чистой квинты она, разумеется, отличается на пифагорову комму: 1,5/1,4798≈1,0136. Такая квинта на органе издавала пронзительный, неприятный звук, похожий на завывание волка, за что и была прозвана "волчьей квинтой" или просто "волком". Обращением "волчьей квинты" является "волчья кварта" соль-бемоль-си, которая также отличается от чистой кварты (4/3 = 1,333...) на пифагорову комму:
243/127:1024/729≈1,3515; 1,3515/1,3333≈1,0136. Можно сказать, что вся история развития музыкальных строев была историей борьбы с "волками". Но об этом — чуть позже.
А сейчас обратим внимание на второй существенный недостаток пифагорова строя. Его заметил еще во II веке древнегреческий ученый пифагореец Дидим. Дело в том, что пифагорова терция (81/64) при гармоническом, т. е. одновременном, исполнении обоих тонов, образующих терцию, звучит слишком напряженно. Дидим предложил заменить пифагорову терцию (81/64) так называемой "чистой терцией" (5/4 = 80/64), которая гармонически звучит значительно приятнее, хотя, как видим, лишь чуть-чуть отличается от пифагоровой терции. Разность пифагоровой и чистой терций (81/64:80/64 = 81/80≈1,0125) называется ди-димовой коммой и приблизительно равна 1/10 целого тона.
Однако идеи Дидима, как это не раз случалось с учеными Древней Греции, опередили историю почти на полторы тысячи лет. Они не нашли подходящей почвы для Развития, увяли, умерли и были воскрешены только в конце XV века...
 Орган Домского собора в Риге. '... У него одного существуют те потрясающие звуки, те громы, тот величественный, говорящий будто из вечности голос, которого выражение невозможно никакому другому инструменту, никакому оркестру',- писал об органе В. Стасов
...В XIV веке в Европе получает широкое распространение орган, ставший официальным инструментом католической церкви. С развитием органа развивается и многоголосие, которого не знала ни Древняя Греция, ни раннее средневековье. В течение столетий орган настраивался в пифагоровом строе. Никакого другого строя средневековье не знало. Но пифагоровы терции звучали на органе особенно жестко и не давали покоя музыкантам.
В XVI веке выдающийся итальянский композитор и музыкальный теоретик Джозеффо Царлино (1517-1590) воскресил идеи Дидима. Так родился новый квинтово-терцовый строй, названный чистым строем. Новое всегда с трудом пробивает себе дорогу. Учение Царлино подверглось резким нападкам. Любопытно, что среди тех, кто не признавал учения Царлино и вел с ним непримиримую борьбу, был Винченцо Галилей — выдающийся итальянский лютнист и отец великого революционера в науке Галилео Галилея. Почему чистая терция (5/4), ставшая наравне с квинтой полноправной хозяйкой нового строя, звучит приятнее пифагоровой, мы объясним в главе 10. Пока же отметим одну поразительную закономерность: интервальный коэффициент чистой терции (ее называют также большой терцией) есть среднее арифметическое интервальных коэффициентов основного тона (1) и квинты (3/2):
Орган Домского собора в Риге. '... У него одного существуют те потрясающие звуки, те громы, тот величественный, говорящий будто из вечности голос, которого выражение невозможно никакому другому инструменту, никакому оркестру',- писал об органе В. Стасов
...В XIV веке в Европе получает широкое распространение орган, ставший официальным инструментом католической церкви. С развитием органа развивается и многоголосие, которого не знала ни Древняя Греция, ни раннее средневековье. В течение столетий орган настраивался в пифагоровом строе. Никакого другого строя средневековье не знало. Но пифагоровы терции звучали на органе особенно жестко и не давали покоя музыкантам.
В XVI веке выдающийся итальянский композитор и музыкальный теоретик Джозеффо Царлино (1517-1590) воскресил идеи Дидима. Так родился новый квинтово-терцовый строй, названный чистым строем. Новое всегда с трудом пробивает себе дорогу. Учение Царлино подверглось резким нападкам. Любопытно, что среди тех, кто не признавал учения Царлино и вел с ним непримиримую борьбу, был Винченцо Галилей — выдающийся итальянский лютнист и отец великого революционера в науке Галилео Галилея. Почему чистая терция (5/4), ставшая наравне с квинтой полноправной хозяйкой нового строя, звучит приятнее пифагоровой, мы объясним в главе 10. Пока же отметим одну поразительную закономерность: интервальный коэффициент чистой терции (ее называют также большой терцией) есть среднее арифметическое интервальных коэффициентов основного тона (1) и квинты (3/2):
 (8.3)
А дополнение большой терции (5/4) до квинты (3/2) — малая терция (3/2:5/4 = 6/5) — является средним гармоническим основного тона и квинты:
(8.3)
А дополнение большой терции (5/4) до квинты (3/2) — малая терция (3/2:5/4 = 6/5) — является средним гармоническим основного тона и квинты:
 (8.4)
Оба этих интервала дают приятное звучание; таким образом, закон целочисленных отношений Пифагора расширяется, а внутри музыкальной гаммы появляются еще две пропорции!
Предполагают, что еще Архит умел выражать большую и малую терции как среднее арифметическое и гармоническое тона и квинты. Однако письменное свидетельство этому мы находим лишь в объемном труде "Универсальная гармония" Марена Мерсенна (1588-1648) — монаха францисканского ордена, французского математика, теоретика музыки и философа, учившегося в иезуитском колледже Ла Флеш вместе с Рене Декартом. Труд Мерсенна — нескончаемое исследование об интервалах, полное всеобъемлющих умозрений. На десяти страницах огромного формата автор глубокомысленно обсуждает, например, "является ли унисон консонансом", и попутно решает вопрос, "как бы человек мог поднять землю", и т. д. Однако, несмотря на чрезвычайную напыщенность, которая, впрочем, была неотъемлемой чертой всех сочинений того времени, работа Мерсенна содержала интересные идеи и прозрения. В частности это касалось консонантности и пропорций большой и малой терций. Сегодня большую и малую терции относят к группе несовершенных консонансов.
Но вернемся к работам Царлино. Выдающейся заслугой Царлино было не только выявление консонантности большой терции (5/4), но и построение "совершенной гармонии" — объединение большой терции и квинты в гармоническое трезвучие. Это был первый в истории музыки аккорд, а само трезвучие
(8.4)
Оба этих интервала дают приятное звучание; таким образом, закон целочисленных отношений Пифагора расширяется, а внутри музыкальной гаммы появляются еще две пропорции!
Предполагают, что еще Архит умел выражать большую и малую терции как среднее арифметическое и гармоническое тона и квинты. Однако письменное свидетельство этому мы находим лишь в объемном труде "Универсальная гармония" Марена Мерсенна (1588-1648) — монаха францисканского ордена, французского математика, теоретика музыки и философа, учившегося в иезуитском колледже Ла Флеш вместе с Рене Декартом. Труд Мерсенна — нескончаемое исследование об интервалах, полное всеобъемлющих умозрений. На десяти страницах огромного формата автор глубокомысленно обсуждает, например, "является ли унисон консонансом", и попутно решает вопрос, "как бы человек мог поднять землю", и т. д. Однако, несмотря на чрезвычайную напыщенность, которая, впрочем, была неотъемлемой чертой всех сочинений того времени, работа Мерсенна содержала интересные идеи и прозрения. В частности это касалось консонантности и пропорций большой и малой терций. Сегодня большую и малую терции относят к группе несовершенных консонансов.
Но вернемся к работам Царлино. Выдающейся заслугой Царлино было не только выявление консонантности большой терции (5/4), но и построение "совершенной гармонии" — объединение большой терции и квинты в гармоническое трезвучие. Это был первый в истории музыки аккорд, а само трезвучие
 (8.5)
ныне именуется мажорным и является основой всего гармонического языка музыки. Кроме того, Царлино обнаружил, что если отложить те же большую терцию и квинту вниз от основного тона, то окраска звучания аккорда существенно изменится. Светлые тона мажора подергиваются пасмурной дымкой иного звучания- минора. Приводя аккорд 2/3÷4/5÷1 к основному тону (умножая на 3/2, т. е. сдвигая вверх на квинту), получаем минорное трезвучие
(8.5)
ныне именуется мажорным и является основой всего гармонического языка музыки. Кроме того, Царлино обнаружил, что если отложить те же большую терцию и квинту вниз от основного тона, то окраска звучания аккорда существенно изменится. Светлые тона мажора подергиваются пасмурной дымкой иного звучания- минора. Приводя аккорд 2/3÷4/5÷1 к основному тону (умножая на 3/2, т. е. сдвигая вверх на квинту), получаем минорное трезвучие
 Так был открыт закон, известный сегодня каждому юному музыканту: смена большой терции на малую переводит мажорное трезвучие в минорное:
Так был открыт закон, известный сегодня каждому юному музыканту: смена большой терции на малую переводит мажорное трезвучие в минорное:
 (8.6)
Мажорное трезвучие было взято за основу чистого строя. Обрамляя мажорное трезвучие 1÷5/4÷3/2 такими же трезвучиями сверху и снизу
(8.6)
Мажорное трезвучие было взято за основу чистого строя. Обрамляя мажорное трезвучие 1÷5/4÷3/2 такими же трезвучиями сверху и снизу
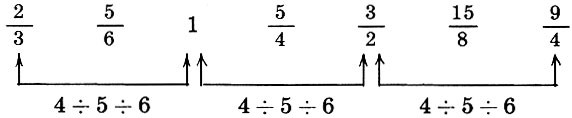 и сводя умножением и делением на 2 построенные звуки в одну октаву, получаем чистый строй лидийской гаммы (натурального мажора):
и сводя умножением и делением на 2 построенные звуки в одну октаву, получаем чистый строй лидийской гаммы (натурального мажора):
 (8.7)
Здесь кружками отмечены тоны, изменившиеся по сравнению с пифагоровым строем (8.1), цифры внизу обозначают интервалы между ступенями.
Как видим, числовые характеристики чистого строя более простые. Однако сам строй стал менее равномерным: в нем, кроме полутона 16/15, появились две разновидности целых тонов 9/8 и 10/9. Знакомые с музыкальной грамотой, конечно, увидели, что мажорные трезвучия (4÷5÷6) чистого строя построены на тонике (до), субдоминанте (фа) и доминанте (соль).
С помощью целых тонов 9/8 и 10/9 и полутона 16/15 легко построить чистый строй фригийской гаммы (см. табл. 1, с. 107), который понадобится нам в части IV:
(8.7)
Здесь кружками отмечены тоны, изменившиеся по сравнению с пифагоровым строем (8.1), цифры внизу обозначают интервалы между ступенями.
Как видим, числовые характеристики чистого строя более простые. Однако сам строй стал менее равномерным: в нем, кроме полутона 16/15, появились две разновидности целых тонов 9/8 и 10/9. Знакомые с музыкальной грамотой, конечно, увидели, что мажорные трезвучия (4÷5÷6) чистого строя построены на тонике (до), субдоминанте (фа) и доминанте (соль).
С помощью целых тонов 9/8 и 10/9 и полутона 16/15 легко построить чистый строй фригийской гаммы (см. табл. 1, с. 107), который понадобится нам в части IV:
 (8.8)
Мы не будем останавливаться на проблеме деления целых тонов чистого строя, тем более, что их теперь стало два. Отметим другое. Чистый строй в истории музыки сыграл короткую, но заметную роль. Его звучание стало намного ярче и богаче по сравнению с пифагоровым строем. Чистый строй способствовал формированию мажорного и минорного ладов, развитию музыкальной гармонии. Но...
Вместе с достоинствами пришли и недостатки. Все те же ненавистные музыкантам "волки" поселились теперь уже не на дополнительных, а на основных ступенях чистого строя! Легко проверить, что квинта между II и VI ступенями (ре-ля) является самым настоящим "волком": 5/3:9/8=40/27≈1,4815. Соответственно "волком" является и ее обращение — кварта (ля-ре1): 9/4:5/3=27/20= 1,35:
(8.8)
Мы не будем останавливаться на проблеме деления целых тонов чистого строя, тем более, что их теперь стало два. Отметим другое. Чистый строй в истории музыки сыграл короткую, но заметную роль. Его звучание стало намного ярче и богаче по сравнению с пифагоровым строем. Чистый строй способствовал формированию мажорного и минорного ладов, развитию музыкальной гармонии. Но...
Вместе с достоинствами пришли и недостатки. Все те же ненавистные музыкантам "волки" поселились теперь уже не на дополнительных, а на основных ступенях чистого строя! Легко проверить, что квинта между II и VI ступенями (ре-ля) является самым настоящим "волком": 5/3:9/8=40/27≈1,4815. Соответственно "волком" является и ее обращение — кварта (ля-ре1): 9/4:5/3=27/20= 1,35:
 Следовательно, настроив орган в чистом строе от ноты до, например, органист не мог уже перейти в тональности ро мажор и ре минор, т. е. в те тональности, где "волчья квинта" входит в тоническое трезвучие и встречается наиболее часто. Разумеется, приходилось исключать и те тональности, где эта квинта входила в доминанту и субдоминанту, которые также являются основными ступенями лада. Таким образом, органист оказывался что называется связанным по рукам: модуляции, т. е. переходы, в другие тональности были крайне ограничены и опасны, и это лишало музыку значительной части ее выразительных средств.
"Волки" продолжали донимать органистов. На фоне "совершенной гармонии" чистого строя это было особенно невыносимо. Забавный случай рассказывают о знаменитом французском композиторе и теоретике музыки, страстном приверженце чистого строя, Жане Рамо (1683 -1764). Однажды Рамо, желая отказаться от предлагаемой ему должности церковного органиста, "выпустил" из органа столько "волков", что своей игрой привел в ужас святых отцов и убедил их в своей "бесталанности". Святые отцы поспешили удалиться вместе со своими лестными предложениями.
Однако проблема оставалась. Выгнать "волков" из органа, т. е. найти закон построения нового музыкального строя, а значит, и рецепт новой настройки органа, наряду с музыкантами безрезультатно пытались и математики: Кеплер, Декарт, Лейбниц, Эйлер. О теории гармонии Эйлера шутливо говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов.
Но то, что не смог сделать изощренный ум математика, сделала обыкновенная смекалка простого органиста...
Следовательно, настроив орган в чистом строе от ноты до, например, органист не мог уже перейти в тональности ро мажор и ре минор, т. е. в те тональности, где "волчья квинта" входит в тоническое трезвучие и встречается наиболее часто. Разумеется, приходилось исключать и те тональности, где эта квинта входила в доминанту и субдоминанту, которые также являются основными ступенями лада. Таким образом, органист оказывался что называется связанным по рукам: модуляции, т. е. переходы, в другие тональности были крайне ограничены и опасны, и это лишало музыку значительной части ее выразительных средств.
"Волки" продолжали донимать органистов. На фоне "совершенной гармонии" чистого строя это было особенно невыносимо. Забавный случай рассказывают о знаменитом французском композиторе и теоретике музыки, страстном приверженце чистого строя, Жане Рамо (1683 -1764). Однажды Рамо, желая отказаться от предлагаемой ему должности церковного органиста, "выпустил" из органа столько "волков", что своей игрой привел в ужас святых отцов и убедил их в своей "бесталанности". Святые отцы поспешили удалиться вместе со своими лестными предложениями.
Однако проблема оставалась. Выгнать "волков" из органа, т. е. найти закон построения нового музыкального строя, а значит, и рецепт новой настройки органа, наряду с музыкантами безрезультатно пытались и математики: Кеплер, Декарт, Лейбниц, Эйлер. О теории гармонии Эйлера шутливо говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов.
Но то, что не смог сделать изощренный ум математика, сделала обыкновенная смекалка простого органиста...
9. Алгебра гармонии — темперация
...Звуки умертвив", Музыку я разъял, как труп. Поверил Я алгеброй гармонию...XVIII век в истории музыки начался решительной победой рационализма века Просвещения над антично-средневековым музыкальным целомудрием. К 1700 г. немецкий органист Андреас Веркмейстер (1645-1706) осуществил смелое и гениально простое решение: он отказался от совершенных и несовершенных консонансов — квинт, кварт и терций, оставив в первозданной консонантной красе лишь одну октаву, и попросту разделил ее (геометрически!) на 12 равных частей. В результате пифагорова комма, которую до того времени нетронутой передвигали с места на место, также разделилась на 12 равных частей и стала незаметной. Так в музыке восторжествовала темперация (лат. соразмерность), а новый двенадцатизвуковой строй был назван равномерно-темперированным. Но по порядку... Вначале, разумеется, были попытки улучшить чистый строй, который сохранял главный недостаток пифагорова строя: невозможность безболезненного перехода из тональности в тональность. Естественным желанием при решении этой проблемы было увеличить количество звуков в октаве. Посмотрим, что из этого выйдет. Пусть мы настроили октаву в чистом строе от ноты до малой октавы (1) согласно (8.7). Затем повторим ту же процедуру от ноты ре (9/8), для чего 9/8 умножим последовательно на все интервальные коэффициенты чистого строя (нижние цифры в (8.7)). Проделаем эти построения от всех 7 основных нот чистого строя; при этом новые ноты, которые мы будем получать в следующей (первой) октаве, также будем учитывать, ибо у них, разумеется, должны быть октавные повторения в исходной (малой) октаве. В результате наших вычислений получим (новые ноты написаны красным, октавные повторения нот — синим):А. Пушкин
 Как видим, 7 основных нот дали нам 11 дополнительных! Итог не слишком радостный. Но процесс образования новых нот все-таки затухает: нота ре дала 4 новых ноты, ми — 3, фа — 2, соль — ни одной (!), ля и си — по одной. Теперь ту же процедуру нужно проделать с новыми одиннадцатью нотами, ибо раз мы хотим сделать все ноты равноправными, то они не должны составлять исключение. Затем — с вновь полученными (самыми новыми) и т. д. К счастью, процесс все-таки замкнется, но какой ценой! В результате получим 84 ступени в октаве! Кто будет играть на столь сложном инструменте?!
Сейчас трудно сказать, кому первому пришла идея равномерно разделить октаву (а вместе с ней и пифагорову комму) на 12 равных частей. Идея эта была подготовлена самой логикой развития музыкального строя и, как говорят в таких случаях, носилась в воздухе. Но изложение этой идеи мы находим опять-таки в энциклопедическом труде Мерсенна "Универсальная гармония". Здесь Мерсенн дал математическое описание нового строя и рассчитал его интервальные коэффициенты. Суть нового метода заключалась в следующем.
Мы знаем, что и пифагоров, и чистый строй не замкнуты, т. е. звук, полученный в результате 12 ходов по квинтам вверх или вниз, не является точным октавным повторением исходного звука, а отличается от него на пифагорову комму. На протяжении столетий наибольшее, что позволяли себе теоретики музыки,- это перегонять комму по гамме с места на место. Комма нетронутой блуждала по гамме и время от времени заявляла о себе в завывании "волков". Так вот, Мерсенн предложил сузить полутона так, чтобы они точно укладывались в октаву. Тем самым он равномерно распределил пифагорову комму по всем 12 полутонам, и она как бы "растворилась" в гамме: стала незаметной.
Для того чтобы разделить октаву (2) на 12 равных частей, в качестве нового полутона необходимо взять по формуле (6.12) интервал
Как видим, 7 основных нот дали нам 11 дополнительных! Итог не слишком радостный. Но процесс образования новых нот все-таки затухает: нота ре дала 4 новых ноты, ми — 3, фа — 2, соль — ни одной (!), ля и си — по одной. Теперь ту же процедуру нужно проделать с новыми одиннадцатью нотами, ибо раз мы хотим сделать все ноты равноправными, то они не должны составлять исключение. Затем — с вновь полученными (самыми новыми) и т. д. К счастью, процесс все-таки замкнется, но какой ценой! В результате получим 84 ступени в октаве! Кто будет играть на столь сложном инструменте?!
Сейчас трудно сказать, кому первому пришла идея равномерно разделить октаву (а вместе с ней и пифагорову комму) на 12 равных частей. Идея эта была подготовлена самой логикой развития музыкального строя и, как говорят в таких случаях, носилась в воздухе. Но изложение этой идеи мы находим опять-таки в энциклопедическом труде Мерсенна "Универсальная гармония". Здесь Мерсенн дал математическое описание нового строя и рассчитал его интервальные коэффициенты. Суть нового метода заключалась в следующем.
Мы знаем, что и пифагоров, и чистый строй не замкнуты, т. е. звук, полученный в результате 12 ходов по квинтам вверх или вниз, не является точным октавным повторением исходного звука, а отличается от него на пифагорову комму. На протяжении столетий наибольшее, что позволяли себе теоретики музыки,- это перегонять комму по гамме с места на место. Комма нетронутой блуждала по гамме и время от времени заявляла о себе в завывании "волков". Так вот, Мерсенн предложил сузить полутона так, чтобы они точно укладывались в октаву. Тем самым он равномерно распределил пифагорову комму по всем 12 полутонам, и она как бы "растворилась" в гамме: стала незаметной.
Для того чтобы разделить октаву (2) на 12 равных частей, в качестве нового полутона необходимо взять по формуле (6.12) интервал  Следовательно, математическое выражение равномерно-темперированного строя будет предельно простым:
Следовательно, математическое выражение равномерно-темперированного строя будет предельно простым:
 (9.1)
Если воспользоваться логарифмическими частотами и логарифмическими интервалами (6.13), т. е. прологарифмировать (9.1) по основанию 2, то математический строй (9.1) примет наиболее простой вид (интервал логарифмической октавы 0≤L≤1 будет арифметически разделен на 12 равных логарифмических полутонов (1/12)):
(9.1)
Если воспользоваться логарифмическими частотами и логарифмическими интервалами (6.13), т. е. прологарифмировать (9.1) по основанию 2, то математический строй (9.1) примет наиболее простой вид (интервал логарифмической октавы 0≤L≤1 будет арифметически разделен на 12 равных логарифмических полутонов (1/12)):
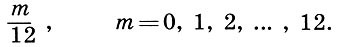 (9.2)
Проверим, что будет в новом строе с консонансами и прежде всего с квинтой. Темперированная квинта имеет интервальный коэффициент 27/12≈1,4983, который несущественно отличается от интервального коэффициента чистой квинты (3/2):
(9.2)
Проверим, что будет в новом строе с консонансами и прежде всего с квинтой. Темперированная квинта имеет интервальный коэффициент 27/12≈1,4983, который несущественно отличается от интервального коэффициента чистой квинты (3/2):
 То же справедливо и для кварты (4/3):
То же справедливо и для кварты (4/3):
 Эти расхождения улавливает лишь изощренный слух профессионала. Несколько хуже обстоят дела с терциями. Сравнивая темперированную большую терцию
24/12 =
Эти расхождения улавливает лишь изощренный слух профессионала. Несколько хуже обстоят дела с терциями. Сравнивая темперированную большую терцию
24/12 =  1,2599 с пифагоровой терцией (81/64 = 1,2656) и чистой терцией (5/4 = 1,25), имеем 1,2656/1,2599≈1,0044; 1,2599/1,25≈1,008. Как видим, здесь относительные ошибки соответственно в 4 и 8 раз больше, чем для квинты (примерно то же имеем для темперированной малой терции). Но и эти терции в музыкальном отношении вполне приемлемы.
Однако новая система Мерсенна была принята в штыки. Даже приятель Мерсенна по иезуитскому коллежу математик Декарт был возмущен надругательством над чистотой консонансов, а музыкантов, которые рискнут воспользоваться новой темперацией, назвал невеждами, не имеющими никакого представления о законах музыкальной науки. "Что касается Ваших музыкантов,- писал Мерсенну Декарт,- то какими умелыми Вы бы их ни делали, я должен сказать, что они или издеваются, или насмехаются, или никогда ничего не понимали в теории музыки". Чистота звучания и простота целочисленных отношений для консонансов, идущие от родоначальника европейской науки Пифагора, представлялись Декарту нерушимыми. Таким образом, потребовалось еще более полувека, чтобы новая система завоевала себе право на жизнь.
Путь Веркмейстера к равномерной темперации, разумеется, не был усыпан розами. К тому времени и в музыке сформировались два противоборствующих лагеря: теоретики, опиравшиеся в построении музыкальных систем на математику ("разум"), и практики, предпочитавшие полагаться на собственный слух ("ухо"). Любопытно, что среди сторонников "уха" были математики Декарт и Д'Аламбер, а среди сторонников "разума" — композитор Рамо. К счастью, Веркмейстер держался "золотой середины".
Как бы то ни было, но к концу XVII века вышли две его книги, содержавшие практическое изложение равномерной темперации. Первая из них называлась "Музыкальная темперация, или ясное математически правильное изложение того, как при помощи монохорда следует настраивать по хорошей темперации клавиры — органы, позитивы, регали, спинеты, для того чтобы в соответствии с сегодняшней манерой исполнения музыки все тональности звучали в приятной и сносной гармонии. К этому добавлено предваряющее сочинение о преимуществах совершенных и несовершенных музыкальных исчислений, пропорций и консонансов, которые надо учитывать при установлении этой темперации. Наряду с этим приложено гравированное на меди ясное и полное обозначение этой темперации на монохорде. Обнародовано Андреасом Веркмейстером, соборным органистом в Кведлинбурге. 1691 год". Название второй книги мы лучше опустим.
Итак, к началу XVIII века органы, настроенные Андреасом Веркмейстером, зазвучали в равномерно-темперированном строе. Преимущества нового строя были очевидны. Это был замкнутый энгармонический строй, состоящий из интервалов, вполне приемлемых для музыкального слуха и в гармоническом, и в мелодическом исполнении. В новом строе стали совершенно безболезненными переходы из тональности в тональность (модуляции), "волки" навсегда покинули орган. Простота нового строя также была его неоспоримым преимуществом.
Конечно, и в век Просвещения новое не всеми воспринималось восторженно. Выдающийся немецкий композитор Георг Фридрих Гендель (1685-1759) не принял новшества. Отказ от совершенных консонансов возмущал его. К счастью, равномерная темперация нашла сторонника в лице сверстника Генделя, великого немецкого композитора и органиста Иоганна Себастьяна Баха (1685-1750). В простоте и математической строгости равномерной темперации Бах гениально предвидел подлинный путь развития музыки. Предвидения Баха сбылись: равномерная темперация сегодня лежит в основе всей мировой музыки.
1,2599 с пифагоровой терцией (81/64 = 1,2656) и чистой терцией (5/4 = 1,25), имеем 1,2656/1,2599≈1,0044; 1,2599/1,25≈1,008. Как видим, здесь относительные ошибки соответственно в 4 и 8 раз больше, чем для квинты (примерно то же имеем для темперированной малой терции). Но и эти терции в музыкальном отношении вполне приемлемы.
Однако новая система Мерсенна была принята в штыки. Даже приятель Мерсенна по иезуитскому коллежу математик Декарт был возмущен надругательством над чистотой консонансов, а музыкантов, которые рискнут воспользоваться новой темперацией, назвал невеждами, не имеющими никакого представления о законах музыкальной науки. "Что касается Ваших музыкантов,- писал Мерсенну Декарт,- то какими умелыми Вы бы их ни делали, я должен сказать, что они или издеваются, или насмехаются, или никогда ничего не понимали в теории музыки". Чистота звучания и простота целочисленных отношений для консонансов, идущие от родоначальника европейской науки Пифагора, представлялись Декарту нерушимыми. Таким образом, потребовалось еще более полувека, чтобы новая система завоевала себе право на жизнь.
Путь Веркмейстера к равномерной темперации, разумеется, не был усыпан розами. К тому времени и в музыке сформировались два противоборствующих лагеря: теоретики, опиравшиеся в построении музыкальных систем на математику ("разум"), и практики, предпочитавшие полагаться на собственный слух ("ухо"). Любопытно, что среди сторонников "уха" были математики Декарт и Д'Аламбер, а среди сторонников "разума" — композитор Рамо. К счастью, Веркмейстер держался "золотой середины".
Как бы то ни было, но к концу XVII века вышли две его книги, содержавшие практическое изложение равномерной темперации. Первая из них называлась "Музыкальная темперация, или ясное математически правильное изложение того, как при помощи монохорда следует настраивать по хорошей темперации клавиры — органы, позитивы, регали, спинеты, для того чтобы в соответствии с сегодняшней манерой исполнения музыки все тональности звучали в приятной и сносной гармонии. К этому добавлено предваряющее сочинение о преимуществах совершенных и несовершенных музыкальных исчислений, пропорций и консонансов, которые надо учитывать при установлении этой темперации. Наряду с этим приложено гравированное на меди ясное и полное обозначение этой темперации на монохорде. Обнародовано Андреасом Веркмейстером, соборным органистом в Кведлинбурге. 1691 год". Название второй книги мы лучше опустим.
Итак, к началу XVIII века органы, настроенные Андреасом Веркмейстером, зазвучали в равномерно-темперированном строе. Преимущества нового строя были очевидны. Это был замкнутый энгармонический строй, состоящий из интервалов, вполне приемлемых для музыкального слуха и в гармоническом, и в мелодическом исполнении. В новом строе стали совершенно безболезненными переходы из тональности в тональность (модуляции), "волки" навсегда покинули орган. Простота нового строя также была его неоспоримым преимуществом.
Конечно, и в век Просвещения новое не всеми воспринималось восторженно. Выдающийся немецкий композитор Георг Фридрих Гендель (1685-1759) не принял новшества. Отказ от совершенных консонансов возмущал его. К счастью, равномерная темперация нашла сторонника в лице сверстника Генделя, великого немецкого композитора и органиста Иоганна Себастьяна Баха (1685-1750). В простоте и математической строгости равномерной темперации Бах гениально предвидел подлинный путь развития музыки. Предвидения Баха сбылись: равномерная темперация сегодня лежит в основе всей мировой музыки.
 Иоганн Себастьян Бах (1685- 1750). Последний прижизненный портрет И. С. Баха работы неизвестного художника
Для демонстрации возможностей нового строя Бах написал свое бессмертное произведение "Хорошо темперированный клавир", основной целью которого было ознакомить играющих на клавире со всеми двадцатью четырьмя (12-мажорными и 12-минорными) тональностями хроматической гаммы нового "хорошо согласованного" строя. Бах хотел показать равноценность всех тональностей при новой системе настройки клавира и вместе с тем выявить характерную окраску каждой тональности. На титульном листе "Хорошо темперированного клавира" значилось: "Для пользы и употребления жадного до учения музыкального юношества, как и для особого времяпрепровождения тех, кто уже преуспел в этом учении, составлено и изготовлено Иоганном Себастьяном Бахом — в настоящее время великокняжеским Ангальт-Кетенским капельмейстером и директором камерной музыки. В году 1722".
Разумеется, Бах слишком скромно оценивал свое произведение. Цикл прелюдий и фуг Баха занимает особое место в мире музыки. Это не просто один из бессмертных шедевров мировой музыки. Это настоящая энциклопедия полифонического искусства, его альфа и омега, настольная книга каждого мыслящего музыканта. Не случайно Бетховен называл "Хорошо темперированный клавир" своей "музыкальной библией", которую он изучал с раннего детства до глубокой старости. Да и сам Бах всю жизнь обращался к своему детищу и через 24 года написал вторую часть "Хорошо темперированного клавира", также состоящую из 24 прелюдий и фуг.
И все-таки является ли 12-звуковая равномерная темперация "абсолютной истиной" в музыке? Разумеется, нет! Спор Баха и Генделя продолжается. Музыкантов с особо тонким слухом раздражают "тупые" консонансы темперированного строя. Чайковский после отдыха на природе болезненно ощущал недостатки темперированной музыки, и прежде всего собственной. Известно, как мучился Скрябин, не находя в рояле чистых интервалов. В последние годы жизни Скрябин пытался сконструировать рояль с дополнительными тонами, но неожиданная смерть не позволила осуществить задуманное. Наш соотечественник и современник, крупнейший пианист XX века Святослав Рихтер признается, что он физически старается преодолеть темперацию рояля при помощи звукоизвлечения, придавая диезным и бемольным звукам, когда это нужно, различную тембровую окраску. Поиски новых равномерных темперации продолжаются. Разработаны 24-, 48- и 53-зву-ковые равномерные темперации. На каждую из них специально написана музыка и сконструированы музыкальные инструменты. Но все они практического распространения не получили. Возможно, новые темперации ждут еще нового Веркмейстера и нового Баха...
На этом можно было бы поставить точку. Но мы поставили многоточие, ибо у вдумчивого читателя должен возникнуть еще один вопрос: почему все-таки октава разделена именно на 12 частей? Это вопрос из области математики, и ответ на него содержится в решении задачи, которую мы сформулируем так.
Требуется разделить интервал октавы 1≤f≤2 на n геометрически равных частей 1 = f0≤f1≤f2≤...≤fn = 2, так, чтобы k-я точка деления приходилась на главный консонанс октавы — квинту, т. е. fk = 3/2 (0<k<n). Так как согласно (6.12) fk = 2k/n, то мы приходим к уравнению
Иоганн Себастьян Бах (1685- 1750). Последний прижизненный портрет И. С. Баха работы неизвестного художника
Для демонстрации возможностей нового строя Бах написал свое бессмертное произведение "Хорошо темперированный клавир", основной целью которого было ознакомить играющих на клавире со всеми двадцатью четырьмя (12-мажорными и 12-минорными) тональностями хроматической гаммы нового "хорошо согласованного" строя. Бах хотел показать равноценность всех тональностей при новой системе настройки клавира и вместе с тем выявить характерную окраску каждой тональности. На титульном листе "Хорошо темперированного клавира" значилось: "Для пользы и употребления жадного до учения музыкального юношества, как и для особого времяпрепровождения тех, кто уже преуспел в этом учении, составлено и изготовлено Иоганном Себастьяном Бахом — в настоящее время великокняжеским Ангальт-Кетенским капельмейстером и директором камерной музыки. В году 1722".
Разумеется, Бах слишком скромно оценивал свое произведение. Цикл прелюдий и фуг Баха занимает особое место в мире музыки. Это не просто один из бессмертных шедевров мировой музыки. Это настоящая энциклопедия полифонического искусства, его альфа и омега, настольная книга каждого мыслящего музыканта. Не случайно Бетховен называл "Хорошо темперированный клавир" своей "музыкальной библией", которую он изучал с раннего детства до глубокой старости. Да и сам Бах всю жизнь обращался к своему детищу и через 24 года написал вторую часть "Хорошо темперированного клавира", также состоящую из 24 прелюдий и фуг.
И все-таки является ли 12-звуковая равномерная темперация "абсолютной истиной" в музыке? Разумеется, нет! Спор Баха и Генделя продолжается. Музыкантов с особо тонким слухом раздражают "тупые" консонансы темперированного строя. Чайковский после отдыха на природе болезненно ощущал недостатки темперированной музыки, и прежде всего собственной. Известно, как мучился Скрябин, не находя в рояле чистых интервалов. В последние годы жизни Скрябин пытался сконструировать рояль с дополнительными тонами, но неожиданная смерть не позволила осуществить задуманное. Наш соотечественник и современник, крупнейший пианист XX века Святослав Рихтер признается, что он физически старается преодолеть темперацию рояля при помощи звукоизвлечения, придавая диезным и бемольным звукам, когда это нужно, различную тембровую окраску. Поиски новых равномерных темперации продолжаются. Разработаны 24-, 48- и 53-зву-ковые равномерные темперации. На каждую из них специально написана музыка и сконструированы музыкальные инструменты. Но все они практического распространения не получили. Возможно, новые темперации ждут еще нового Веркмейстера и нового Баха...
На этом можно было бы поставить точку. Но мы поставили многоточие, ибо у вдумчивого читателя должен возникнуть еще один вопрос: почему все-таки октава разделена именно на 12 частей? Это вопрос из области математики, и ответ на него содержится в решении задачи, которую мы сформулируем так.
Требуется разделить интервал октавы 1≤f≤2 на n геометрически равных частей 1 = f0≤f1≤f2≤...≤fn = 2, так, чтобы k-я точка деления приходилась на главный консонанс октавы — квинту, т. е. fk = 3/2 (0<k<n). Так как согласно (6.12) fk = 2k/n, то мы приходим к уравнению
 (9.3)
Но левая часть уравнения (9.3) есть число четное при любых n и k, тогда как правая — число нечетное. Таким образом, мы пришли к противоречию, которое доказывает, что уравнение (9.3) в целых числах решений не имеет. Одновременно мы можем сделать важный вывод: шкала равномерно-темперированного строя никогда точно не пройдет через квинту.
Будем искать в целых числах приближенные решения уравнения (9.3). Логарифмируя, представим это уравнение в виде
(9.3)
Но левая часть уравнения (9.3) есть число четное при любых n и k, тогда как правая — число нечетное. Таким образом, мы пришли к противоречию, которое доказывает, что уравнение (9.3) в целых числах решений не имеет. Одновременно мы можем сделать важный вывод: шкала равномерно-темперированного строя никогда точно не пройдет через квинту.
Будем искать в целых числах приближенные решения уравнения (9.3). Логарифмируя, представим это уравнение в виде
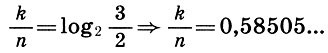 (9.4)
и, как говорят математики, найдем рациональные приближения иррационального числа 0,58505... Такие задачи в математике решаются с помощью цепных дробей, т. е. дробей вида
(9.4)
и, как говорят математики, найдем рациональные приближения иррационального числа 0,58505... Такие задачи в математике решаются с помощью цепных дробей, т. е. дробей вида
 (9.5)
Здесь a1, а2, а3, ... — натуральные числа. Известно, что всякое число а∈[0; 1] можно разложить в цепную дробь (9.5), которая будет бесконечной, если число а иррациональное. Рациональные выражения
(9.5)
Здесь a1, а2, а3, ... — натуральные числа. Известно, что всякое число а∈[0; 1] можно разложить в цепную дробь (9.5), которая будет бесконечной, если число а иррациональное. Рациональные выражения
 и т. д.
называются подходящими дробями цепной дроби (9.5), т. е. являются рациональными приближениями числа а.
Разложим число
и т. д.
называются подходящими дробями цепной дроби (9.5), т. е. являются рациональными приближениями числа а.
Разложим число  в цепную дробь. По определению логарифма имеем
в цепную дробь. По определению логарифма имеем
 (9.6)
Ясно, что х<1. Положим
(9.6)
Ясно, что х<1. Положим 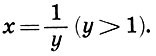 Тогда (9.6) примет вид
Тогда (9.6) примет вид
 (9.7)
Легко видеть, что 1<y<2,так как при этом
(9.7)
Легко видеть, что 1<y<2,так как при этом
 Поэтому положим
Поэтому положим
 Уравнение (9.7) преобразуется к виду
Уравнение (9.7) преобразуется к виду
 (9.8)
Очевидно, что 1<z<2, так как
(9.8)
Очевидно, что 1<z<2, так как  Следовательно, полагаем
Следовательно, полагаем
 Тогда уравнение (9.8) примет вид
Тогда уравнение (9.8) примет вид
 (9.9)
(9.9)
Так как
 , то для u получаем оценку 2<u<3. Поэтому в (9.9) делаем подстановку
, то для u получаем оценку 2<u<3. Поэтому в (9.9) делаем подстановку  и получаем
и получаем
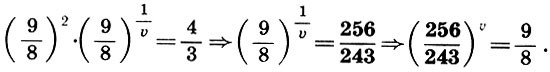 (9.10)
С помощью таблиц логарифмов или простой проверкой на микрокалькуляторе находим оценку для v:2<u<3. Наконец, сделаем еще одну замену
(9.10)
С помощью таблиц логарифмов или простой проверкой на микрокалькуляторе находим оценку для v:2<u<3. Наконец, сделаем еще одну замену  отчего (9.10) примет вид
отчего (9.10) примет вид
 или
или
 (9.11)
Для w справедлива оценка 3<w<4, поэтому
(9.11)
Для w справедлива оценка 3<w<4, поэтому  Не будем более испытывать терпение читателей (процесс разложения иррационального числа в цепную дробь все равно бесконечен). А в качестве компенсации за длинные выкладки обратим внимание на то, что в наших приближениях (9.6) — (9.11) все время фигурируют музыкальные интервалы: октава (2), квинта (3/2), кварта (4/3), тон (9/8),полутон (256/243) и даже пифагорова комма ((3/2)12:27)!
Построим теперь соответствующую цепную дробь:
Не будем более испытывать терпение читателей (процесс разложения иррационального числа в цепную дробь все равно бесконечен). А в качестве компенсации за длинные выкладки обратим внимание на то, что в наших приближениях (9.6) — (9.11) все время фигурируют музыкальные интервалы: октава (2), квинта (3/2), кварта (4/3), тон (9/8),полутон (256/243) и даже пифагорова комма ((3/2)12:27)!
Построим теперь соответствующую цепную дробь:
 и выпишем подходящие дроби:
и выпишем подходящие дроби:
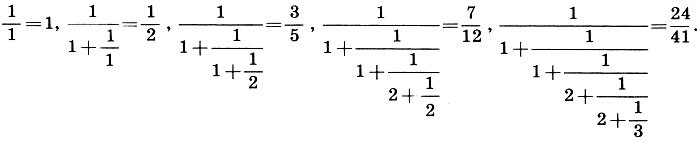 Первые три дроби 1; 0,5; 0,6 дают слишком грубое приближение к числу x = 0,58505... Четвертая дробь k/n = = 7/12 = 0,5833... является достаточно хорошим приближением. Она-то и положена в основу 12-звукового равномерно-темперированного строя (n = 12, k = 7, т. е. на седьмой ступени 12-звуковой гаммы находится темперированная квинта). Пятая дробь 24/41=0,58536 дает еще лучшее приближение. Таким образом, мы получаем еще одну равномерную темперацию, которая на 24-й ступени имеет практически идеальную квинту. Но ведь октава при этом делится на 41 ступень! Вряд ли кто отважится играть на столь сложном инструменте. Итак, именно 12-звуковая темперация является той "золотой серединой", которая обеспечивает достаточно чистое звучание консонансов при достаточной простоте музыкальной гаммы.
История создания равномерной темперации свидетельствует о том, как тесно порой переплетаются судьбы математики и музыки. Равномерная темперация в музыке появилась вслед за изобретением логарифмов и развитием алгебры иррациональных величин в математике. Без знания логарифмов провести расчеты равномерно-темперированного строя (8.8) было бы попросту невозможно. Логарифмы стали той "алгеброй гармонии", на которой выросла темперация.
И в заключение скажем несколько слов об одном любопытном и пока загадочном свойстве равномерной темперации. Согласно логике построения темперированной шкалы (9.1) все 12 мажорных, равно как и все 12 минорных, тональностей равномерно-темперированного строя должны звучать одинаково. Однако музыканты считают, что каждая тональность темперированного строя обладает своей неповторимой окраской. Так, композиторы единодушно сходятся в том, что до мажор характерен для светлого, солнечного настроения. Очень любил до мажор за жизнерадостность и оптимизм Бетховен. Вспомним 1-ю Симфонию и 1-й Концерт для фортепиано с оркестром Бетховена, написанные в до мажоре, которые как бы радостно перекликаются друг с другом; или его же 21-ю Сонату до мажор, названную за светлые и прозрачные тона именем богини утренней зари Авроры. Считается, что ми мажор выражает взволнованное, напряженное, мятущееся настроение. Поэтому именно ми мажор был так созвучен восторженной, страстно ищущей и терзаемой противоречиями душе Листа; в ми мажоре Листом написаны многие фортепианные произведения, транскрипции, "Фауст-симфония". В тональности фа диез мажор композиторы находят легкое, радостно возвышенное, романтическое настроение, столь характерное для творчества Шопена ("Баркарола", Экспромт соч. 36, Ноктюрн № 2 соч. 15). До минор считается тональностью мужественной печали, героико-трагических образов (вспомним огненный пафос "Патетической" сонаты Бетховена, знаменитый "революционный" этюд Шопена или шквальные кульминации 2-го Концерта для фортепиано с оркестром Рахманинова); ми бемоль минор - тональность глубоко трагических состояний. Например, Полонез № 2 соч. 26 — одно из самых скорбных творений Шопена.
Мы не можем сказать, отражают ли такого рода суждения какие-либо неизвестные пока объективные закономерности, или это дань устоявшейся традиции. Если мы имеем дело с традицией, то ее корни следует искать в пифагоровом строе. Действительно, в пифагоровом строе энгармонические звуки не только нетождественны, но и принципиально отличаются друг от друга по своим качествам и выразительности. В пифагоровом строе соль диез, например, находится на пифагорову комму выше, чем ля бемоль. Поэтому соль диез тяготеет к верхнему звуку ля и воспринимается светлее, чем ля бемоль, который направлен к нижнему звуку соль и потому кажется более мрачным. Следовательно, и все повышенные звуки восходящей линии квинтового ряда (диезные звуки) имеют светлый характер, тогда как пониженные (бемольные) звуки нисходящей линии квинтового ряда (см. (8.2)) несут мрачный оттенок. Итак, все та же пифагорова комма окрашивает бемольные и диезные звуки в противоположные цвета — темные и светлые. Теперь становится понятным, почему Шопен написал свой знаменитый траурный марш из 2-й Сонаты соч. 35 в си бемоль миноре - тональности с пятью бемолями, а "Баркаролу" — самое утонченное и поэтическое из своих произведений, ставшее символом интимной лирики в музыке,- в фа диез мажоре - тональности с шестью диезами. Вот почему похоронный марш из 12-й Сонаты написан Бетховеном в ля бемоль миноре - тональности с наибольшим числом, семью бемолями, хотя, по мнению знатоков, эта находка Бетховена во многом теряет в равномерно-темперированном строе фортепиано.
Так что же такое есть индивидуальная окраска тональностей: традиция, идущая от пифагорова строя, или неизвестная объективная закономерность? Окончательного ответа на этот вопрос пока не существует.
Вот так, вместо обещанной точки в конце параграфа мы вновь пришли к вопросительному знаку. Но ведь это и хорошо, ибо новые вопросы зовут нас в новые пути в неизвестное! А впереди у нас, пожалуй, главный вопрос всей второй части: в чем секрет "закона Пифагора"? Почему приятные для "уха" консонансные интервалы математически выражаются такими приятными для "разума" простыми целочисленными соотношениями 2/1, 3/2, 4/3, 5/4, 6/5?
Первые три дроби 1; 0,5; 0,6 дают слишком грубое приближение к числу x = 0,58505... Четвертая дробь k/n = = 7/12 = 0,5833... является достаточно хорошим приближением. Она-то и положена в основу 12-звукового равномерно-темперированного строя (n = 12, k = 7, т. е. на седьмой ступени 12-звуковой гаммы находится темперированная квинта). Пятая дробь 24/41=0,58536 дает еще лучшее приближение. Таким образом, мы получаем еще одну равномерную темперацию, которая на 24-й ступени имеет практически идеальную квинту. Но ведь октава при этом делится на 41 ступень! Вряд ли кто отважится играть на столь сложном инструменте. Итак, именно 12-звуковая темперация является той "золотой серединой", которая обеспечивает достаточно чистое звучание консонансов при достаточной простоте музыкальной гаммы.
История создания равномерной темперации свидетельствует о том, как тесно порой переплетаются судьбы математики и музыки. Равномерная темперация в музыке появилась вслед за изобретением логарифмов и развитием алгебры иррациональных величин в математике. Без знания логарифмов провести расчеты равномерно-темперированного строя (8.8) было бы попросту невозможно. Логарифмы стали той "алгеброй гармонии", на которой выросла темперация.
И в заключение скажем несколько слов об одном любопытном и пока загадочном свойстве равномерной темперации. Согласно логике построения темперированной шкалы (9.1) все 12 мажорных, равно как и все 12 минорных, тональностей равномерно-темперированного строя должны звучать одинаково. Однако музыканты считают, что каждая тональность темперированного строя обладает своей неповторимой окраской. Так, композиторы единодушно сходятся в том, что до мажор характерен для светлого, солнечного настроения. Очень любил до мажор за жизнерадостность и оптимизм Бетховен. Вспомним 1-ю Симфонию и 1-й Концерт для фортепиано с оркестром Бетховена, написанные в до мажоре, которые как бы радостно перекликаются друг с другом; или его же 21-ю Сонату до мажор, названную за светлые и прозрачные тона именем богини утренней зари Авроры. Считается, что ми мажор выражает взволнованное, напряженное, мятущееся настроение. Поэтому именно ми мажор был так созвучен восторженной, страстно ищущей и терзаемой противоречиями душе Листа; в ми мажоре Листом написаны многие фортепианные произведения, транскрипции, "Фауст-симфония". В тональности фа диез мажор композиторы находят легкое, радостно возвышенное, романтическое настроение, столь характерное для творчества Шопена ("Баркарола", Экспромт соч. 36, Ноктюрн № 2 соч. 15). До минор считается тональностью мужественной печали, героико-трагических образов (вспомним огненный пафос "Патетической" сонаты Бетховена, знаменитый "революционный" этюд Шопена или шквальные кульминации 2-го Концерта для фортепиано с оркестром Рахманинова); ми бемоль минор - тональность глубоко трагических состояний. Например, Полонез № 2 соч. 26 — одно из самых скорбных творений Шопена.
Мы не можем сказать, отражают ли такого рода суждения какие-либо неизвестные пока объективные закономерности, или это дань устоявшейся традиции. Если мы имеем дело с традицией, то ее корни следует искать в пифагоровом строе. Действительно, в пифагоровом строе энгармонические звуки не только нетождественны, но и принципиально отличаются друг от друга по своим качествам и выразительности. В пифагоровом строе соль диез, например, находится на пифагорову комму выше, чем ля бемоль. Поэтому соль диез тяготеет к верхнему звуку ля и воспринимается светлее, чем ля бемоль, который направлен к нижнему звуку соль и потому кажется более мрачным. Следовательно, и все повышенные звуки восходящей линии квинтового ряда (диезные звуки) имеют светлый характер, тогда как пониженные (бемольные) звуки нисходящей линии квинтового ряда (см. (8.2)) несут мрачный оттенок. Итак, все та же пифагорова комма окрашивает бемольные и диезные звуки в противоположные цвета — темные и светлые. Теперь становится понятным, почему Шопен написал свой знаменитый траурный марш из 2-й Сонаты соч. 35 в си бемоль миноре - тональности с пятью бемолями, а "Баркаролу" — самое утонченное и поэтическое из своих произведений, ставшее символом интимной лирики в музыке,- в фа диез мажоре - тональности с шестью диезами. Вот почему похоронный марш из 12-й Сонаты написан Бетховеном в ля бемоль миноре - тональности с наибольшим числом, семью бемолями, хотя, по мнению знатоков, эта находка Бетховена во многом теряет в равномерно-темперированном строе фортепиано.
Так что же такое есть индивидуальная окраска тональностей: традиция, идущая от пифагорова строя, или неизвестная объективная закономерность? Окончательного ответа на этот вопрос пока не существует.
Вот так, вместо обещанной точки в конце параграфа мы вновь пришли к вопросительному знаку. Но ведь это и хорошо, ибо новые вопросы зовут нас в новые пути в неизвестное! А впереди у нас, пожалуй, главный вопрос всей второй части: в чем секрет "закона Пифагора"? Почему приятные для "уха" консонансные интервалы математически выражаются такими приятными для "разума" простыми целочисленными соотношениями 2/1, 3/2, 4/3, 5/4, 6/5?
10. Математика колебания струны: тайное становится явным
Музыка есть таинственная арифметика души; она вычисляет, сама того не сознавая.Ноябрьским утром 1717 г. на ступенях парижской церкви святого Жана ле Рона был найден младенец. Его взяли на воспитание и в честь святого церкви окрестили Жаном ле Роном. Мальчик рано проявил блестящий ум и жадную любознательность и вскоре стал гордостью всей Франции. Это был Жан ле Рон Д'Аламбер (1717-1783) — выдающийся французский математик, философ, писатель, член Парижской, Петербургской и других академий. Круг интересов Д'Аламбера был необычайно широк: механика (принцип Д'Аламбера), гидродинамика (парадокс Д'Аламбера), математика (признак сходи мости Д'Аламбера), математическая физика (формула Д'Аламбера), философия теория музыки. Такой широты требовала и oабота вместе с Дени Дидро над созданием наменитой "Энциклопедии наук, искусств и ремесел", да и сам дух эпохи посвещения, когда к знаниям тянулись все, в том числе и "просвещенные деспоты" Фридрих II и Екатерина II. Последуя неоднократно приглашала Д'Аламбера быть воспитателем ее сына — цесаревича Павла, назначая при этом баснословное вознаграждение, но всегда получала деликатный, но твердый отказ.Г. Лейбниц
 Колебания струны длины l. Показаны два момента времени t1<t2. Масштаб по ординате U(х,t) сильно увеличен
В 1747 г. Д'Аламбер опубликовал статью "Исследования по вопросам о кривой, которую образует натянутая струнa, приведенная в колебание", где впервые задача о колебании струны сводилась к решению дифференциального уравнения в частных производных. И хотя эта тема выходит за рамки школьной математики но ведь в знаниях "держать себя в рамках" — значит погубить свою любознательность!), мы рассмотрим простое и поистине красивое уравнение, описывающее колебание струны, так называемое полновое уравнение, с которого началась новая ветвь математики — математическая физика:
Колебания струны длины l. Показаны два момента времени t1<t2. Масштаб по ординате U(х,t) сильно увеличен
В 1747 г. Д'Аламбер опубликовал статью "Исследования по вопросам о кривой, которую образует натянутая струнa, приведенная в колебание", где впервые задача о колебании струны сводилась к решению дифференциального уравнения в частных производных. И хотя эта тема выходит за рамки школьной математики но ведь в знаниях "держать себя в рамках" — значит погубить свою любознательность!), мы рассмотрим простое и поистине красивое уравнение, описывающее колебание струны, так называемое полновое уравнение, с которого началась новая ветвь математики — математическая физика:
 (10.1)
(10.1)
Здесь t — время; х — координата струны в положении равновесия; u = u(х, t) — неизвестная функция, выражающая отклонение точки с координатой х в момент времени t от положения равновесия; а2 — коэффициент пропорциональности, характеризующий упругие свойства струны
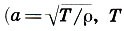 , T — сила натяжения струны, р — плотность однородной струны). Предполагается, что струна совершает малые колебания, происходящие в одной плоскости. Наконец, символы
, T — сила натяжения струны, р — плотность однородной струны). Предполагается, что струна совершает малые колебания, происходящие в одной плоскости. Наконец, символы  обозначают частную производную второго порядка, которая определяется как производная от производной
обозначают частную производную второго порядка, которая определяется как производная от производной  . Частные производные —
. Частные производные —  , как и обычная "школьная" производная
, как и обычная "школьная" производная  характеризует скорость изменения функции u(х,t) по каждой из переменных х или t в отдельности при условии, что другая переменная не изменяется (у функций одной переменной y = y(x) — одна производная, а у функции двух переменных u = u(х,t) — две частные производные
характеризует скорость изменения функции u(х,t) по каждой из переменных х или t в отдельности при условии, что другая переменная не изменяется (у функций одной переменной y = y(x) — одна производная, а у функции двух переменных u = u(х,t) — две частные производные  . Чтобы отличать частные производные от обыкновенных "школьных", пишут не прямую букву
. Чтобы отличать частные производные от обыкновенных "школьных", пишут не прямую букву  , а круглую
, а круглую  .
Волновое уравнение (10.1) есть не что иное, как следствие второго закона Ньютона. Левая часть (10.1) выражает вертикальное ускорение струны в точке х, а правая часть — отнесенную к массе струны силу, вызывающую это ускорение, которая тем больше, чем больше вогнутость струны
.
Волновое уравнение (10.1) есть не что иное, как следствие второго закона Ньютона. Левая часть (10.1) выражает вертикальное ускорение струны в точке х, а правая часть — отнесенную к массе струны силу, вызывающую это ускорение, которая тем больше, чем больше вогнутость струны  .
Д'Аламбер нашел общее решение уравнения (10.1)
.
Д'Аламбер нашел общее решение уравнения (10.1)
 (10.2)
которое содержит две произвольные функции φ(х,t) и ψ(х,t). Через пять лет Даниил Бернулли (1700-1782), математик, механик, физиолог и медик, почетный член Петербургской Академии наук, представитель славного рода Бернулли, который к настоящему времени подарил миру более 100 потомков, добившихся значительных результатов во всех сферах человеческой деятельности, и прежде всего в научной, получил другое общее решение уравнения (10.1)
(10.2)
которое содержит две произвольные функции φ(х,t) и ψ(х,t). Через пять лет Даниил Бернулли (1700-1782), математик, механик, физиолог и медик, почетный член Петербургской Академии наук, представитель славного рода Бернулли, который к настоящему времени подарил миру более 100 потомков, добившихся значительных результатов во всех сферах человеческой деятельности, и прежде всего в научной, получил другое общее решение уравнения (10.1)
 (10.3)
Сравнивая решения Д'Аламбера (10.2) и Д. Бернулли (10.3), мы, казалось бы, приходим к абсурду: одно и то же уравнение (10.1) имеет совершенно непохожие решения! Но никакого абсурда здесь нет, так уж устроены дифференциальные уравнения. Они обладают бесчисленным множеством решений, что легко видеть из (10.2), где функции φ(x — at) и ψ(x + at) произвольные. При достаточно общих предположениях относительно функций φ и ψ правая часть (10.2) может быть представлена рядом (10.3).
Выбор того или иного частного решения дифференциального уравнения диктуется условиями, в которых протекает процесс (это так называемые граничные условия), и условиями, которые имели место в начале процесса (так называемые начальные условия). Только совокупность дифференциального уравнения, начальных и граничных условий определяет решение той или иной физической задачи. С помощью общего решения (10.2) Д'Аламбер решил одну из таких задач: найти колебания бесконечной струны (т. е. при отсутствии граничных условий), которой в начальный момент времени t = 0 придали некоторую форму f(х) и сообщили некоторое ускорение g(x). Математически задача ставилась так: найти решение уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(x), u(х,0) = g(x), т. е. решить систему
(10.3)
Сравнивая решения Д'Аламбера (10.2) и Д. Бернулли (10.3), мы, казалось бы, приходим к абсурду: одно и то же уравнение (10.1) имеет совершенно непохожие решения! Но никакого абсурда здесь нет, так уж устроены дифференциальные уравнения. Они обладают бесчисленным множеством решений, что легко видеть из (10.2), где функции φ(x — at) и ψ(x + at) произвольные. При достаточно общих предположениях относительно функций φ и ψ правая часть (10.2) может быть представлена рядом (10.3).
Выбор того или иного частного решения дифференциального уравнения диктуется условиями, в которых протекает процесс (это так называемые граничные условия), и условиями, которые имели место в начале процесса (так называемые начальные условия). Только совокупность дифференциального уравнения, начальных и граничных условий определяет решение той или иной физической задачи. С помощью общего решения (10.2) Д'Аламбер решил одну из таких задач: найти колебания бесконечной струны (т. е. при отсутствии граничных условий), которой в начальный момент времени t = 0 придали некоторую форму f(х) и сообщили некоторое ускорение g(x). Математически задача ставилась так: найти решение уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(x), u(х,0) = g(x), т. е. решить систему
 (10.4)
Решение задачи (10.4) определяется формулой Д'Аламбера
(10.4)
Решение задачи (10.4) определяется формулой Д'Аламбера
 (10.5)
Формула (10.5) в простейшем случае g(x) = 0, т. е. когда струну тихонько оттянули и отпустили, не придавая ей дополнительного ускорения, принимает вид
(10.5)
Формула (10.5) в простейшем случае g(x) = 0, т. е. когда струну тихонько оттянули и отпустили, не придавая ей дополнительного ускорения, принимает вид
 и физически означает, что сообщенный струне при t=0 профиль f(x) будет распространяться влево и вправо со скоростью а. Это так называемые две бегущие волны, движущиеся в противоположных направлениях с одинаковой скоростью а.
и физически означает, что сообщенный струне при t=0 профиль f(x) будет распространяться влево и вправо со скоростью а. Это так называемые две бегущие волны, движущиеся в противоположных направлениях с одинаковой скоростью а.
 Начальное возмущение треугольной формы распадается на две бегущие волны. Профиль начального возмущения сохраняет свою форму, а его амплитуда уменьшается вдвое
На самом деле бесконечных струн не бывает. Струна имеет конечную длину l и, как правило, жестко закреплена на концах. Так возникают граничные условия: u(0,t) = 0 — струна закреплена слева (х = 0); и (l,t) = 0 — струна закреплена справа (х = l). Ясно, что в этом случае бегущие волны будут отражаться от концов, взаимодействовать друг с другом и образовывать более сложную картину колебаний.
Задача о колебании конечной струны была независимо решена Д'Аламбером и Эйлером, а еще через полвека Жозеф Фурье изобрел новый метод, позволявший решать эту и многие другие задачи математической физики. Задача о колебании конечной струны формулируется так: найти решение волнового уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(х), ut(x,0) = g(x) и граничным условиям u(0,t) = 0, u(l,t) = 0, т. е. решить систему
Начальное возмущение треугольной формы распадается на две бегущие волны. Профиль начального возмущения сохраняет свою форму, а его амплитуда уменьшается вдвое
На самом деле бесконечных струн не бывает. Струна имеет конечную длину l и, как правило, жестко закреплена на концах. Так возникают граничные условия: u(0,t) = 0 — струна закреплена слева (х = 0); и (l,t) = 0 — струна закреплена справа (х = l). Ясно, что в этом случае бегущие волны будут отражаться от концов, взаимодействовать друг с другом и образовывать более сложную картину колебаний.
Задача о колебании конечной струны была независимо решена Д'Аламбером и Эйлером, а еще через полвека Жозеф Фурье изобрел новый метод, позволявший решать эту и многие другие задачи математической физики. Задача о колебании конечной струны формулируется так: найти решение волнового уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(х), ut(x,0) = g(x) и граничным условиям u(0,t) = 0, u(l,t) = 0, т. е. решить систему
 (10.6)
Жан Батист Жозеф Фурье (1768-1830) не был кабинетным ученым. Он взлетел на гребне Великой французской революции 1789 г. и из сына провинциального портного, готовившегося принять монашеский постриг, превратился в друга императора Наполеона. В 1798 г. Фурье участвовал в египетском походе Наполеона, где его жизнь не раз подвергалась опасностям. По возвращении из Египта Фурье занимался административной деятельностью, но находил время и для математических исследований. В 1807 г. он написал свою бессмертную работу "Математическая теория тепла". Главный математический результат Фурье можно описать так: при некоторых ограничениях всякую функцию f (х) можно представить в виде ряда (бесконечной суммы чисел или функций), называемого ныне рядом Фурье:
(10.6)
Жан Батист Жозеф Фурье (1768-1830) не был кабинетным ученым. Он взлетел на гребне Великой французской революции 1789 г. и из сына провинциального портного, готовившегося принять монашеский постриг, превратился в друга императора Наполеона. В 1798 г. Фурье участвовал в египетском походе Наполеона, где его жизнь не раз подвергалась опасностям. По возвращении из Египта Фурье занимался административной деятельностью, но находил время и для математических исследований. В 1807 г. он написал свою бессмертную работу "Математическая теория тепла". Главный математический результат Фурье можно описать так: при некоторых ограничениях всякую функцию f (х) можно представить в виде ряда (бесконечной суммы чисел или функций), называемого ныне рядом Фурье:
 Фурье разработал метод решения уравнений типа (10.1), называемый методом разделения переменных Фурье.
Идея метода Фурье гениально проста. Решение уравнения (10.1) ищется в виде произведения двух функций X(х) и Т(t), каждая из которых зависит только от одной, "своей" переменной:
u(х,t) = X(x)T(t). (10.7)
Замена (10.7) расщепляет уравнение (10.1) на два дифференциальных уравнения в обыкновенных "школьных" производных:
Фурье разработал метод решения уравнений типа (10.1), называемый методом разделения переменных Фурье.
Идея метода Фурье гениально проста. Решение уравнения (10.1) ищется в виде произведения двух функций X(х) и Т(t), каждая из которых зависит только от одной, "своей" переменной:
u(х,t) = X(x)T(t). (10.7)
Замена (10.7) расщепляет уравнение (10.1) на два дифференциальных уравнения в обыкновенных "школьных" производных:
 (10.8)
где λ — неизвестный вспомогательный параметр. Решая уравнения (10.8) и удовлетворяя начальным и граничным условиям (10.6) (разумеется, мы опускаем все промежуточные выкладки, которых здесь, как и при выводе формулы Д'Аламбера (10.5), хватит на несколько страниц), находят окончательное решение задачи (10.6) о колебании конечной струны:
(10.8)
где λ — неизвестный вспомогательный параметр. Решая уравнения (10.8) и удовлетворяя начальным и граничным условиям (10.6) (разумеется, мы опускаем все промежуточные выкладки, которых здесь, как и при выводе формулы Д'Аламбера (10.5), хватит на несколько страниц), находят окончательное решение задачи (10.6) о колебании конечной струны:
 (10.9)
Выясним физический смысл решения (10.9), и прежде всего функций un(х,t), составляющих это решение. Для этого выполним искусственное преобразование:
(10.9)
Выясним физический смысл решения (10.9), и прежде всего функций un(х,t), составляющих это решение. Для этого выполним искусственное преобразование:
 (Здесь мы воспользовались формулой синуса суммы двух аргументов и тем, что
(Здесь мы воспользовались формулой синуса суммы двух аргументов и тем, что  Таким образом, un(х,t) можнс представить в виде
Таким образом, un(х,t) можнс представить в виде
 или
или
 (10.10)
Из формулы (10.10) видно, что каждое решение un представляет собой гармоническое колебание (т. е. колебание по закону синуса) с одной и той же частотой
(10.10)
Из формулы (10.10) видно, что каждое решение un представляет собой гармоническое колебание (т. е. колебание по закону синуса) с одной и той же частотой  и фазой φn. Амплитуда же колебаний Аn(х) для разных точек струны разная, т. е. зависит от координаты точки струны х. Из (10.10) видно, что при х = 0 и х = l Аn(0) = Аn(1) = 0, т. е. на концах струна неподвижна.
Итак, во времени колебания струны происходят с постоянной частотой ωn, амплитуда колебания для каждой точки струны своя. При этом все точки струны одновременно достигают своего максимального отклонения в ту или другую сторону и одновременно проходят положения равновесия. Такие колебания называются стоячими волнами.
Пользуясь выражением для амплитуды стоячей волны (10.10) и учитывая, что 0≤x≤l, найдем неподвижные точки стоячих волн:
и фазой φn. Амплитуда же колебаний Аn(х) для разных точек струны разная, т. е. зависит от координаты точки струны х. Из (10.10) видно, что при х = 0 и х = l Аn(0) = Аn(1) = 0, т. е. на концах струна неподвижна.
Итак, во времени колебания струны происходят с постоянной частотой ωn, амплитуда колебания для каждой точки струны своя. При этом все точки струны одновременно достигают своего максимального отклонения в ту или другую сторону и одновременно проходят положения равновесия. Такие колебания называются стоячими волнами.
Пользуясь выражением для амплитуды стоячей волны (10.10) и учитывая, что 0≤x≤l, найдем неподвижные точки стоячих волн:
 Неподвижные точки называются узлами стоячей волны. Ясно, что посередине между узлами расположены точки, в которых отклонения в стоячей волне достигают максимума. Эти точки называются пучностями стоячей волны.
Неподвижные точки называются узлами стоячей волны. Ясно, что посередине между узлами расположены точки, в которых отклонения в стоячей волне достигают максимума. Эти точки называются пучностями стоячей волны.
Сделаем общий вывод: колебание конечной струны представляет собой бесконечную сумму стоячих волн un(х,t), каждая из которых имеет постоянную частоту колебания
 и изменяющуюся по длине струны амплитуду
и изменяющуюся по длине струны амплитуду  В k-й стоячей волне имеется k
пучностей и (k + 1) узлов.
В k-й стоячей волне имеется k
пучностей и (k + 1) узлов.
Перейдем теперь к "музыкальному содержанию" решения (10.9) и прежде всего к частотам колебаний. Мы пришли к выводу, что струна колеблется не только всей своей длиной, но одновременно и отдельными частями: половинками, третями, четвертями и т. д. Следовательно, струна издает звук не только основной частоты
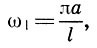 , но и призвуки частот
, но и призвуки частот  . Тон основной частоты струны ω1 называется основным тоном струны, а остальные тона, соответствующие частотам ω2, ω3, ..., ωk, ..., называются обертонами (верхними тонами) или гармониками. Основной тон струны принимается за первый обертон (первую гармонику). Именно обертоны, сливаясь в общем звучании с основным тоном, придают звуку музыкальную окраску, называемую тембром.
Различие тембров музыкальных звуков в основном объясняется составом и интенсивностью обертонов у разных источников звуков. Чем больше у звука обертонов, тем красивее, "богаче" он нам кажется. По тембру, т. е. по составу обертонов, мы отличаем звуки одной и той же высоты и одинаковой громкости, воспроизведенные на скрипке или фортепиано, голосом или на флейте. Разумеется, и сам инструмент способен давать различные тембровые окраски, что прежде всего относится к скрипке.
. Тон основной частоты струны ω1 называется основным тоном струны, а остальные тона, соответствующие частотам ω2, ω3, ..., ωk, ..., называются обертонами (верхними тонами) или гармониками. Основной тон струны принимается за первый обертон (первую гармонику). Именно обертоны, сливаясь в общем звучании с основным тоном, придают звуку музыкальную окраску, называемую тембром.
Различие тембров музыкальных звуков в основном объясняется составом и интенсивностью обертонов у разных источников звуков. Чем больше у звука обертонов, тем красивее, "богаче" он нам кажется. По тембру, т. е. по составу обертонов, мы отличаем звуки одной и той же высоты и одинаковой громкости, воспроизведенные на скрипке или фортепиано, голосом или на флейте. Разумеется, и сам инструмент способен давать различные тембровые окраски, что прежде всего относится к скрипке.
 Три первые стоячие волны (гармоники) колеблющейся струны. Колебания конечной струны U(х,t) представимы в виде суммы бесконечного числа стоячих волн usubn/sub(х,t)
У скрипачей есть особый способ необычного по тембру звукоизвлечения — игра флажолетами. Слегка дотрагиваясь пальцем до струны в узлах стоячих волн, но так, чтобы струна не соприкасалась с грифом, скрипач гасит одни обертоны и оставляет другие. В результате возникает мягкий, немного свистящий звук, напоминающий по тембру звучание старинного Деревянного духового инструмента — флажолета. Например, дотронувшись до струны точно посередине, скрипач гасит все гармоники, имеющие в этой точке пучности, и сохраняет только гармоники, имеющие в этой точке узлы, т. е. четные гармоники. Таким образом, самой низкой частотой станет второй обертон
Три первые стоячие волны (гармоники) колеблющейся струны. Колебания конечной струны U(х,t) представимы в виде суммы бесконечного числа стоячих волн usubn/sub(х,t)
У скрипачей есть особый способ необычного по тембру звукоизвлечения — игра флажолетами. Слегка дотрагиваясь пальцем до струны в узлах стоячих волн, но так, чтобы струна не соприкасалась с грифом, скрипач гасит одни обертоны и оставляет другие. В результате возникает мягкий, немного свистящий звук, напоминающий по тембру звучание старинного Деревянного духового инструмента — флажолета. Например, дотронувшись до струны точно посередине, скрипач гасит все гармоники, имеющие в этой точке пучности, и сохраняет только гармоники, имеющие в этой точке узлы, т. е. четные гармоники. Таким образом, самой низкой частотой станет второй обертон  .
Но это не будет по тембру звук точно на на октаву выше основного тона
.
Но это не будет по тембру звук точно на на октаву выше основного тона  , так как он будет составлен только из четных гармоник. Аналогично, дотронувшись до струны в точке l/3, скрипач оставит только гармоники, кратные трем: ω3, ω6, ..., и получит флажолет, не похожий на первый, даже если сделать ω2 = ω3. Игра флажолетами требует виртуозной точности. Ведь если мы не попадем точно в узел, то погасим вообще все гармоники и струна попросту не зазвучит!
Вот какую огромную роль играют в музыке слагаемые un(х,t) в решении (10.9). Их с полным правом называют звуковой краской музыканта. Но не только музыканты, а и создатели музыкальных инструментов проявляют постоянную заботу об этих слагаемых, от которых зависит тембр звука. Достаточно напомнить об особом "итальянском тембре" скрипок работ знаменитых итальянских мастеров XVI-XVIII веков, представителей нескольких поколений семей Амати, Гварнери, Страдивари.
Из решения (10.9), задавая нужным образом функции f(х) и g(x) и вычисляя интегралы, можно формально получить законы, которые экспериментально обнаружил английский ученый-энциклопедист Томас Юнг (1773 — 1829):
1. Если возбуждать струну в какой-либо точке, то в этой точке возникает пучность и не может образоваться узел.
2. Если затормозить струну в какой-либо точке, то в этой точке возникает узел и не может образоваться пучность.
Из первого закона Юнга следует, что если возбуждать струну, например, точно посередине, то в ней погасятся все гармоники, имеющие в этой точке узел, т. е. все четные обертоны. Значит, мы потеряем половину обертонов и звук станет блеклым. Ясно, что чем дальше от середины мы будем возбуждать струну, тем меньше первых, самых важных гармоник мы потеряем. Тембр звука от этого станет полнее и ярче. Вот почему смычок на скрипке, правая рука на гитаре, молоточки на фортепиано — все они возбуждают струну приблизительно на 1/7-1/10 доли струны от места ее закрепления. Делается это для того, чтобы не потревожить первые обертоны, а значит, не обеднить музыкальный звук. Что касается игры на скрипке флажолетами, то она основана на втором законе Юнга, который является обратным к первому закону.
Прежде чем расстаться с законами Юнга, скажем несколько слов об их создателе. Томас Юнг был удивительным человеком. " Всякий может делать то, что делают другие" — таков был девиз его жизни. И Юнг необычайно преуспел в исполнении этого нелегкого правила. Он был цирковым актером (акробатом и канатоходцем), авторитетным знатоком живописи, играл практически на всех су. Шествовавших в его время музыкальных инструментах, занимался расшифровкой египетских иероглифов, знал массу языков, в том числе латинский, греческий и арабский. И кроме всех этих "увлечений", Юнг получил блестящие результаты в науках: физике (волновая теория света), теории упругости (модуль упругости Юнга), оптике, акустике, астрономии, физиологии, медицине. Юнг написал около 60 глав научных приложений к знаменитой "Британской энциклопедии".
Рассмотрим подробнее основной тон струны. Вспоминая, что
, так как он будет составлен только из четных гармоник. Аналогично, дотронувшись до струны в точке l/3, скрипач оставит только гармоники, кратные трем: ω3, ω6, ..., и получит флажолет, не похожий на первый, даже если сделать ω2 = ω3. Игра флажолетами требует виртуозной точности. Ведь если мы не попадем точно в узел, то погасим вообще все гармоники и струна попросту не зазвучит!
Вот какую огромную роль играют в музыке слагаемые un(х,t) в решении (10.9). Их с полным правом называют звуковой краской музыканта. Но не только музыканты, а и создатели музыкальных инструментов проявляют постоянную заботу об этих слагаемых, от которых зависит тембр звука. Достаточно напомнить об особом "итальянском тембре" скрипок работ знаменитых итальянских мастеров XVI-XVIII веков, представителей нескольких поколений семей Амати, Гварнери, Страдивари.
Из решения (10.9), задавая нужным образом функции f(х) и g(x) и вычисляя интегралы, можно формально получить законы, которые экспериментально обнаружил английский ученый-энциклопедист Томас Юнг (1773 — 1829):
1. Если возбуждать струну в какой-либо точке, то в этой точке возникает пучность и не может образоваться узел.
2. Если затормозить струну в какой-либо точке, то в этой точке возникает узел и не может образоваться пучность.
Из первого закона Юнга следует, что если возбуждать струну, например, точно посередине, то в ней погасятся все гармоники, имеющие в этой точке узел, т. е. все четные обертоны. Значит, мы потеряем половину обертонов и звук станет блеклым. Ясно, что чем дальше от середины мы будем возбуждать струну, тем меньше первых, самых важных гармоник мы потеряем. Тембр звука от этого станет полнее и ярче. Вот почему смычок на скрипке, правая рука на гитаре, молоточки на фортепиано — все они возбуждают струну приблизительно на 1/7-1/10 доли струны от места ее закрепления. Делается это для того, чтобы не потревожить первые обертоны, а значит, не обеднить музыкальный звук. Что касается игры на скрипке флажолетами, то она основана на втором законе Юнга, который является обратным к первому закону.
Прежде чем расстаться с законами Юнга, скажем несколько слов об их создателе. Томас Юнг был удивительным человеком. " Всякий может делать то, что делают другие" — таков был девиз его жизни. И Юнг необычайно преуспел в исполнении этого нелегкого правила. Он был цирковым актером (акробатом и канатоходцем), авторитетным знатоком живописи, играл практически на всех су. Шествовавших в его время музыкальных инструментах, занимался расшифровкой египетских иероглифов, знал массу языков, в том числе латинский, греческий и арабский. И кроме всех этих "увлечений", Юнг получил блестящие результаты в науках: физике (волновая теория света), теории упругости (модуль упругости Юнга), оптике, акустике, астрономии, физиологии, медицине. Юнг написал около 60 глав научных приложений к знаменитой "Британской энциклопедии".
Рассмотрим подробнее основной тон струны. Вспоминая, что  , получим формулу для частоты основного тона:
, получим формулу для частоты основного тона:
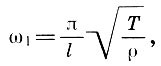 (10.11)
откуда легко увидеть законы колебания струны, которые экспериментально обнаружили еще древние греки и которые затем переоткрыл и описал в своей "Универсальной гармонии" Марен Мерсенн:
1. Для струн одинаковой плотности и одинакового натяжения частота колебания обратно пропорциональна длине струны (это не что иное, как "первый закон Пифагора — Архита"; см. с. 101).
2. При заданной длине и плотности струны ее частота пропорциональна корню квадратному из натяжения.
3. При заданной длине и натяжении частота струны обратно пропорциональна корню квадратному из ее плотности. (При постоянной плотности чем толще струна, тем меньше частота ее колебаний, т. е. тем ниже звук.)
Разумеется, все эти законы (по крайней мере, качественно) можно было установить на монохорде.
(10.11)
откуда легко увидеть законы колебания струны, которые экспериментально обнаружили еще древние греки и которые затем переоткрыл и описал в своей "Универсальной гармонии" Марен Мерсенн:
1. Для струн одинаковой плотности и одинакового натяжения частота колебания обратно пропорциональна длине струны (это не что иное, как "первый закон Пифагора — Архита"; см. с. 101).
2. При заданной длине и плотности струны ее частота пропорциональна корню квадратному из натяжения.
3. При заданной длине и натяжении частота струны обратно пропорциональна корню квадратному из ее плотности. (При постоянной плотности чем толще струна, тем меньше частота ее колебаний, т. е. тем ниже звук.)
Разумеется, все эти законы (по крайней мере, качественно) можно было установить на монохорде.
Но обратимся вновь к обертонам. Легко видеть, что частоты обертонов
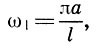
 относятся как числа натурального ряда:
относятся как числа натурального ряда:
 (10.12)
Таким образом, струна издает целый звукоряд тонов, называемый натуральным звукорядом. Теоретически натуральный звукоряд бесконечен. На практике же имеют значение первые 16 обертонов, так как остальные обертоны слишком мало отличаются друг от друга, обладают слишком малой энергией и фактически не слышны.
(10.12)
Таким образом, струна издает целый звукоряд тонов, называемый натуральным звукорядом. Теоретически натуральный звукоряд бесконечен. На практике же имеют значение первые 16 обертонов, так как остальные обертоны слишком мало отличаются друг от друга, обладают слишком малой энергией и фактически не слышны.
 Натуральный звукоряд. Полагая ω1 = l, частоты натурального звукоряда выражаются натуральным рядом чисел (ωn = n). Натуральный звукоряд содержит все консонансы и все интервалы чистого строя
Натуральный звукоряд. Полагая ω1 = l, частоты натурального звукоряда выражаются натуральным рядом чисел (ωn = n). Натуральный звукоряд содержит все консонансы и все интервалы чистого строя
В самом деле, из (10.12) следует, что интервальный коэффициент двух соседних гармоник ωn и ωn+1 равен
 (n = 1, 2, 3, ...). Поскольку
(n = 1, 2, 3, ...). Поскольку  то мы легко приходим к выводу: с ростом номера п интервал между соседними гармониками натурального звукоряда уменьшается и в пределе стремится к чистой приме (унисону).
На рисунке показаны первые 16 гармоник колеблющейся струны, образующие натуральный звукоряд. Цифры справа обозначают частоты гармоник, считая ω1 = 1, а красная линия (гипербола) отсекает часть струны 1/n, которая колеблется с частотой ωn = n. Мы видим, что второй обертон и основной тон составляют интервал октавы ω2/ω1 = 2. Третий и второй обертоны — интервал квинты: ω3/ω2 = 3/2. Четвертый и третий — кварты: ω4/ω3 = 4/3. Пятый и четвертый — большой терции: ω5/ω4 = 5/4. Шестой и пятый — малой терции: ω6/ω5 = 6/5. Но ведь это есть не что иное, как набор совершенных и несовершенных консонансов! Таким образом, мы пришли к разгадке "закона консонансов" — "второго закона Пифагора — Архита" (с. 101 — 102): консонантные интервалы, которые математически выражаются отношением
то мы легко приходим к выводу: с ростом номера п интервал между соседними гармониками натурального звукоряда уменьшается и в пределе стремится к чистой приме (унисону).
На рисунке показаны первые 16 гармоник колеблющейся струны, образующие натуральный звукоряд. Цифры справа обозначают частоты гармоник, считая ω1 = 1, а красная линия (гипербола) отсекает часть струны 1/n, которая колеблется с частотой ωn = n. Мы видим, что второй обертон и основной тон составляют интервал октавы ω2/ω1 = 2. Третий и второй обертоны — интервал квинты: ω3/ω2 = 3/2. Четвертый и третий — кварты: ω4/ω3 = 4/3. Пятый и четвертый — большой терции: ω5/ω4 = 5/4. Шестой и пятый — малой терции: ω6/ω5 = 6/5. Но ведь это есть не что иное, как набор совершенных и несовершенных консонансов! Таким образом, мы пришли к разгадке "закона консонансов" — "второго закона Пифагора — Архита" (с. 101 — 102): консонантные интервалы, которые математически выражаются отношением
вида
 (n = 1, 2, 3, 4, 5), определены самой природой колебания струны! Все консонансы заключены в первых шести гармониках, т. е. первых шести тонах натурального звукоряда, причем по мере удаления от первой гармоники (основного тона) степень консонантности интервала убывает. Итак, закон целочисленных отношений для консонантных интервалов
(n = 1, 2, 3, 4, 5), определены самой природой колебания струны! Все консонансы заключены в первых шести гармониках, т. е. первых шести тонах натурального звукоряда, причем по мере удаления от первой гармоники (основного тона) степень консонантности интервала убывает. Итак, закон целочисленных отношений для консонантных интервалов  , который, по преданию, был экспериментально открыт Пифагором на монохорде, является следствием математического решения задачи о колебании струны и непосредственно вытекает из решения (10.9).
Переходя к более высоким гармоникам, нетрудно обнаружить также два интервала тона чистого строя: ω9/ω8 = 9/8, ω10/ω9 = 10/9 и интервал полутона чистого строя: ω16/ω15 = 16/15. Таким образом, все интервалы чистого строя содержатся в натуральном звукоряде! Вот почему чистый строй более приятен в гармоническом звучании, чем пифагоров строй.
Но и сами тона чистого строя (8.7) почти полностью определены натуральным звукорядом. В самом деле, если рассмотреть октаву между 8-й и 16-й гармониками, принимая частоту 8-й гармоники за единицу (т. е. поделив все частоты на 8), то мы обнаружим в этой октаве все ступени чистого строя, кроме 4-й (4/3) и 6-й (5/3). Следовательно, чистый строй почти целиком содержится в натуральном звукоряде.
, который, по преданию, был экспериментально открыт Пифагором на монохорде, является следствием математического решения задачи о колебании струны и непосредственно вытекает из решения (10.9).
Переходя к более высоким гармоникам, нетрудно обнаружить также два интервала тона чистого строя: ω9/ω8 = 9/8, ω10/ω9 = 10/9 и интервал полутона чистого строя: ω16/ω15 = 16/15. Таким образом, все интервалы чистого строя содержатся в натуральном звукоряде! Вот почему чистый строй более приятен в гармоническом звучании, чем пифагоров строй.
Но и сами тона чистого строя (8.7) почти полностью определены натуральным звукорядом. В самом деле, если рассмотреть октаву между 8-й и 16-й гармониками, принимая частоту 8-й гармоники за единицу (т. е. поделив все частоты на 8), то мы обнаружим в этой октаве все ступени чистого строя, кроме 4-й (4/3) и 6-й (5/3). Следовательно, чистый строй почти целиком содержится в натуральном звукоряде.
 Однако это коварное "почти" до сих пор составляет одну из загадок музыки. В самом деле, почему именно 7, 11 и 13-й обертоны (14-й обертон является октавным повторением 7-го) не входят ни в один из музыкальных строев? Знаменитый "фальшивый" 7-й обертон третье столетие не дает покоя теоретикам музыки! С одной стороны, ясно, что неправильно называть этот звук фальшивым, ибо он дан самой природой, которую трудно упрекнуть в фальши. Но с другой стороны, все теоретики музыки, начиная с Рамо, были слишком большими музыкантами, чтобы включить седьмую гармонику в какую-либо музыкальную систему (седьмой звук явно "резал ухо"!). Впрочем, еще в XVIII веке французский музыкальный теоретик Балльер с присущей французу легкостью писал: "Разница между древностью и современностью заключается в том, что тогда начинали считать диссонансы с 5-го призвука, а теперь начинают их считать лишь с 7-го". Не пойдет ли развитие музыки так, что в новых музыкальных системах найдется место и 7, и 11, и 13-му обертонам?.. А пока молоточки фортепиано, следуя первому закону Юнга, ударяют на 1/8 длины струны, чтобы максимально снизить силу злополучного 7-го обертона.
Наконец, отметим еще одну важную особенность натурального звукоряда. Глядя на рисунок, мы видим, что 4, 5 и 6-я гармоники образуют мажорное звучание (до-ми-соль). А если к ним добавить еще и 1-ю, и 2-ю гармоники, то получится мажорное трезвучие в сопровождении октавного баса! Итак, мажорное трезвучие составлено из ближайших гармоник (4, 5 и 6-й) основного тона (баса мажорного трезвучия). Следовательно, оно не только консонирует, но и обладает акустическим единством, заложенным в самой природе колебания струны. Это дало основание одному из последних универсальных ученых — немецкому математику, физику, физиологу и психологу Герману Гельмгольцу (1821 — 1894) утверждать, что "мажорный аккорд наиболее натурален из всех аккордов".
Ну а минорное трезвучие? Споры о природе минора не затихают и по сей день. В них участвовали Рамо, Д'Аламбер, Руссо, Гёте, Гельмгольц, многие наши современники. На сегодня мнения сходятся в том, что поскольку в минорном трезвучии (до — ми-бемоль — соль) второй звук (ми-бемоль) лежит на полутон ниже пятой гармоники основного тона, то он образует с ней едва слышимый диссонанс, который и обусловливает некоторую "затененность", "нечто мрачное и неясное, необъяснимое для слушателя" (Гельмгольц). По o этой причине в музыке Баха, Генделя, Моцарта минорные произведения часто заканчиваются мажорным — наиболее натуральным, просветленным — аккордом.
Итак, в мажорной гамме третья ступень как бы тяготеет вверх, тогда как в минорной она тяготеет вниз. Движение же вверх воспринимается нами как восхождение к свету, просветление, радость. Напротив, движение вниз ассоциируется со спуском в темноту, затемнением, печалью. Эти объективные предпосылки поддерживаются, кроме того, определенной традицией применения мажора и минора. В тех же случаях, когда эти традиции нарушаются, мы встречаем разудалую песню "Яблочко", написанную в миноре, и молитву "Ave Maria", которую, несмотря на ее название — "Радуйся, Мария" — и мажорный лад, никак не назовешь веселой. К сожалению, смешивание объективных физико-математических законов строения мажора и минора с их субъективной эстетической оценкой породило вокруг них много ненужных споров.
В заключение остановимся еще на одной проблеме колеблющейся струны. До сих пор, следуя решению (10.9), мы пытались "разъять, как труп" колебания струны на простейшие гармонические составляющие. Но ведь на самом деле, опять же согласно (10.9), составляющие колебание струны гармоники складываются, образуя сложную картину колебаний. Характер этой картины зависит прежде всего от амплитуд гармоник. Решить эту задачу в общем виде не просто, поэтому остановимся на более простой задаче.
Пусть складываются два колебания постоянной и одинаковой амплитуды, равной для простоты единице, и разных частот ω1<ω2:
Однако это коварное "почти" до сих пор составляет одну из загадок музыки. В самом деле, почему именно 7, 11 и 13-й обертоны (14-й обертон является октавным повторением 7-го) не входят ни в один из музыкальных строев? Знаменитый "фальшивый" 7-й обертон третье столетие не дает покоя теоретикам музыки! С одной стороны, ясно, что неправильно называть этот звук фальшивым, ибо он дан самой природой, которую трудно упрекнуть в фальши. Но с другой стороны, все теоретики музыки, начиная с Рамо, были слишком большими музыкантами, чтобы включить седьмую гармонику в какую-либо музыкальную систему (седьмой звук явно "резал ухо"!). Впрочем, еще в XVIII веке французский музыкальный теоретик Балльер с присущей французу легкостью писал: "Разница между древностью и современностью заключается в том, что тогда начинали считать диссонансы с 5-го призвука, а теперь начинают их считать лишь с 7-го". Не пойдет ли развитие музыки так, что в новых музыкальных системах найдется место и 7, и 11, и 13-му обертонам?.. А пока молоточки фортепиано, следуя первому закону Юнга, ударяют на 1/8 длины струны, чтобы максимально снизить силу злополучного 7-го обертона.
Наконец, отметим еще одну важную особенность натурального звукоряда. Глядя на рисунок, мы видим, что 4, 5 и 6-я гармоники образуют мажорное звучание (до-ми-соль). А если к ним добавить еще и 1-ю, и 2-ю гармоники, то получится мажорное трезвучие в сопровождении октавного баса! Итак, мажорное трезвучие составлено из ближайших гармоник (4, 5 и 6-й) основного тона (баса мажорного трезвучия). Следовательно, оно не только консонирует, но и обладает акустическим единством, заложенным в самой природе колебания струны. Это дало основание одному из последних универсальных ученых — немецкому математику, физику, физиологу и психологу Герману Гельмгольцу (1821 — 1894) утверждать, что "мажорный аккорд наиболее натурален из всех аккордов".
Ну а минорное трезвучие? Споры о природе минора не затихают и по сей день. В них участвовали Рамо, Д'Аламбер, Руссо, Гёте, Гельмгольц, многие наши современники. На сегодня мнения сходятся в том, что поскольку в минорном трезвучии (до — ми-бемоль — соль) второй звук (ми-бемоль) лежит на полутон ниже пятой гармоники основного тона, то он образует с ней едва слышимый диссонанс, который и обусловливает некоторую "затененность", "нечто мрачное и неясное, необъяснимое для слушателя" (Гельмгольц). По o этой причине в музыке Баха, Генделя, Моцарта минорные произведения часто заканчиваются мажорным — наиболее натуральным, просветленным — аккордом.
Итак, в мажорной гамме третья ступень как бы тяготеет вверх, тогда как в минорной она тяготеет вниз. Движение же вверх воспринимается нами как восхождение к свету, просветление, радость. Напротив, движение вниз ассоциируется со спуском в темноту, затемнением, печалью. Эти объективные предпосылки поддерживаются, кроме того, определенной традицией применения мажора и минора. В тех же случаях, когда эти традиции нарушаются, мы встречаем разудалую песню "Яблочко", написанную в миноре, и молитву "Ave Maria", которую, несмотря на ее название — "Радуйся, Мария" — и мажорный лад, никак не назовешь веселой. К сожалению, смешивание объективных физико-математических законов строения мажора и минора с их субъективной эстетической оценкой породило вокруг них много ненужных споров.
В заключение остановимся еще на одной проблеме колеблющейся струны. До сих пор, следуя решению (10.9), мы пытались "разъять, как труп" колебания струны на простейшие гармонические составляющие. Но ведь на самом деле, опять же согласно (10.9), составляющие колебание струны гармоники складываются, образуя сложную картину колебаний. Характер этой картины зависит прежде всего от амплитуд гармоник. Решить эту задачу в общем виде не просто, поэтому остановимся на более простой задаче.
Пусть складываются два колебания постоянной и одинаковой амплитуды, равной для простоты единице, и разных частот ω1<ω2:
 Суммарное колебание, пользуясь формулами суммы синусов и косинуса половинного угла, представим в виде
Суммарное колебание, пользуясь формулами суммы синусов и косинуса половинного угла, представим в виде
 (10.13)
(10.13)
 При сложении двух колебаний, близких по частоте (ω1 = 8 и ω2 = 10), возникают биения — периодическое усиление и ослабление звука, происходящее с частотой биений ω = ω2 — ω1 = 2
При сложении двух колебаний, близких по частоте (ω1 = 8 и ω2 = 10), возникают биения — периодическое усиление и ослабление звука, происходящее с частотой биений ω = ω2 — ω1 = 2
Равенство (10.13), когда частоты ω1 и ω2 близки друг к другу с достаточной степенью точности, можно трактовать следующим образом: сумма двух гармонических колебаний частот ω1 и ω2 является "почти гармоническим" колебанием, частота которого есть среднее арифметическое данных частот
 , а амплитуда изменяется во времени с частотой ω2-ω1 и ограничена сверху функцией
, а амплитуда изменяется во времени с частотой ω2-ω1 и ограничена сверху функцией  , а снизу — функцией —
, а снизу — функцией —  . Легко видеть, что амплитуда суммарного колебания пульсирует с частотой ω2-ω1 от нуля до максимального значения и затем снова до нуля. По этой причине такие колебания называют биениями. Из (10.13) также видно, что максимальная амплитуда биений вдвое больше амплитуд составляющих колебаний.
Итак, при сложении двух близких по частоте колебаний возникают биения" т. е. почти гармонические колебания с частотой, равной средней частоте данных колебаний, и амплитудой, пульсирующей с частотой биений, которая равна разности частот данных колебаний. Издаваемый при биениях звук то периодически усиливается, то замирает.
Перейдем к музыкальной стороне явления биений. Известно, что всякое прерывистое раздражение нервов воспринимается сильнее, чем постоянное. Однако с увеличением частоты раздражений нерв не успевает следить за изменениями, отдельные раздражения сливаются между собой и становятся незаметными. Экспериментально установлено, что наиболее отчетливо слышны биения с частотой 4-5 Гц (колебаний в секунду). Биения с частотой около 15 Гц еще различимы, а при частоте около 30 Гц они начинают сливаться, но создают неприятное ощущение хрипловатости звучания.
Существует теория Гельмгольца, которая объясняет явления консонанса и диссонанса биениями, возникающими между гармониками двух звучащих основных тонов. Согласно теории Гельмгольца, от наличия биений, их частоты и громкости (амплитуды) зависит степень консонантности и диссонантности интервала. Поясним эту теорию на примере. В таблице 2 в качестве основного тона взяты нота до малой октавы, частота которой равна 131 Гц, и ее пять обертонов. Далее приведены первые пять обертонов для звуков до1, соль, фа, ми (чистого строя), ми (пифагорова строя) и до-диез (чистого строя), которые образуют с основным тоном до соответственно интервалы октавы, квинты, кварты, большой терции, пифагоровой терции и малой секунды.
. Легко видеть, что амплитуда суммарного колебания пульсирует с частотой ω2-ω1 от нуля до максимального значения и затем снова до нуля. По этой причине такие колебания называют биениями. Из (10.13) также видно, что максимальная амплитуда биений вдвое больше амплитуд составляющих колебаний.
Итак, при сложении двух близких по частоте колебаний возникают биения" т. е. почти гармонические колебания с частотой, равной средней частоте данных колебаний, и амплитудой, пульсирующей с частотой биений, которая равна разности частот данных колебаний. Издаваемый при биениях звук то периодически усиливается, то замирает.
Перейдем к музыкальной стороне явления биений. Известно, что всякое прерывистое раздражение нервов воспринимается сильнее, чем постоянное. Однако с увеличением частоты раздражений нерв не успевает следить за изменениями, отдельные раздражения сливаются между собой и становятся незаметными. Экспериментально установлено, что наиболее отчетливо слышны биения с частотой 4-5 Гц (колебаний в секунду). Биения с частотой около 15 Гц еще различимы, а при частоте около 30 Гц они начинают сливаться, но создают неприятное ощущение хрипловатости звучания.
Существует теория Гельмгольца, которая объясняет явления консонанса и диссонанса биениями, возникающими между гармониками двух звучащих основных тонов. Согласно теории Гельмгольца, от наличия биений, их частоты и громкости (амплитуды) зависит степень консонантности и диссонантности интервала. Поясним эту теорию на примере. В таблице 2 в качестве основного тона взяты нота до малой октавы, частота которой равна 131 Гц, и ее пять обертонов. Далее приведены первые пять обертонов для звуков до1, соль, фа, ми (чистого строя), ми (пифагорова строя) и до-диез (чистого строя), которые образуют с основным тоном до соответственно интервалы октавы, квинты, кварты, большой терции, пифагоровой терции и малой секунды.
 Таблица 2. Основные гармоники ноты до малой октавы и нот, образующих с до важнейшие интервалы
Понятно, что для октавы совпадают частоты гармоник, номера которых относятся как 2/1, для квинты — как 3/2 и т. д. (см. табл. 2). Сравнивая частоты первых гармоник, мы видим, что чем меньше становится интервал, тем ближе частоты основных тонов, тем различимее будут биения и, следовательно, тем меньше будет степень консонантности интервала. Поэтому самым консонантным интервалом является октава, затем идут квинта и кварта. Все три этих интервала не дают биений и относятся к совершенным консонансам. Терция дает в первых гармониках чуть более 30 биений, т. е. на пороге различимости, и поэтому относится к несовершенным консонансам. А вот малая секунда дает 9 биений (140-131 = 9) и поэтому является явным диссонансом. Заметим, что четвертая гармоника пифагоровой терции (663,2) и пятая гармоника основного тона (655) дают 8 биений (663-655 = 8). Эти биения и создают неприятное гармоническое звучание пифагоровой терции. Однако поскольку они происходят в старших гармониках, т. е. значительно слабее биений в первых гармониках, то ясно, что пифагорову терцию нельзя причислить к диссонансу наравне с малой секундой, где такие же биения происходят в первых гармониках.
Таким образом, мы выполнили обещание, данное на с. 130 и объяснили, почему пифагорова терция в гармоническом исполнении звучит напряженно по сравнению с чистой. Конечно, теория Гельмгольца не решает всех музыкальных загадок колеблющейся струны — таких как проблема 7-го обертона, например,- и здесь еще остается немало точек приложения для пытливого ума.
Не правда ли, какое удивительное разнообразие законов, свойств и загадок таит в себе простое колебание простой струны! Законы Пифагора — Архита (особенно "закон консонансов"), законы Мерсенна и законы Юнга, решения Д'Аламбера Д. Бернулли и Фурье, натуральный звукоряд и мажорное трезвучие, биения... Вот уже третье тысячелетие обыкновенная струна открывает человечеству свои необыкновенные тайны! И быть может, кто-то задумается следующий раз об этих тайнах, прежде чем ударить по струнам старенькой гитары.
Таблица 2. Основные гармоники ноты до малой октавы и нот, образующих с до важнейшие интервалы
Понятно, что для октавы совпадают частоты гармоник, номера которых относятся как 2/1, для квинты — как 3/2 и т. д. (см. табл. 2). Сравнивая частоты первых гармоник, мы видим, что чем меньше становится интервал, тем ближе частоты основных тонов, тем различимее будут биения и, следовательно, тем меньше будет степень консонантности интервала. Поэтому самым консонантным интервалом является октава, затем идут квинта и кварта. Все три этих интервала не дают биений и относятся к совершенным консонансам. Терция дает в первых гармониках чуть более 30 биений, т. е. на пороге различимости, и поэтому относится к несовершенным консонансам. А вот малая секунда дает 9 биений (140-131 = 9) и поэтому является явным диссонансом. Заметим, что четвертая гармоника пифагоровой терции (663,2) и пятая гармоника основного тона (655) дают 8 биений (663-655 = 8). Эти биения и создают неприятное гармоническое звучание пифагоровой терции. Однако поскольку они происходят в старших гармониках, т. е. значительно слабее биений в первых гармониках, то ясно, что пифагорову терцию нельзя причислить к диссонансу наравне с малой секундой, где такие же биения происходят в первых гармониках.
Таким образом, мы выполнили обещание, данное на с. 130 и объяснили, почему пифагорова терция в гармоническом исполнении звучит напряженно по сравнению с чистой. Конечно, теория Гельмгольца не решает всех музыкальных загадок колеблющейся струны — таких как проблема 7-го обертона, например,- и здесь еще остается немало точек приложения для пытливого ума.
Не правда ли, какое удивительное разнообразие законов, свойств и загадок таит в себе простое колебание простой струны! Законы Пифагора — Архита (особенно "закон консонансов"), законы Мерсенна и законы Юнга, решения Д'Аламбера Д. Бернулли и Фурье, натуральный звукоряд и мажорное трезвучие, биения... Вот уже третье тысячелетие обыкновенная струна открывает человечеству свои необыкновенные тайны! И быть может, кто-то задумается следующий раз об этих тайнах, прежде чем ударить по струнам старенькой гитары.
11. Пропорции музыкальной гаммы
Пройдут миллионы лет, и если музыка в нашем смысле будет еще существовать, то те же семь основных тонов нашей гаммы, в их мелодических и гармонических комбинациях, оживляемые ритмом, будут все еще служить источником новых музыкальных мыслей.Если окинуть взглядом 2500 лет истории европейской музыки, от Пифагора и до наших дней, то слова П. И. Чайковского, вынесенные в эпиграф, обретают особый смысл. В самом деле, каких только переворотов в мировоззрении, сознании и бытии человечества не произошло за это время! Но основа музыки — музыкальная гамма — остается практически неизменной. Музыкальная гамма даже в наш бурный век представляется незыблемым утесом в клокочущем море новых идей и теорий. Но в чем причина такого завидного долголетия музыкальной гаммы? Почему из всего обилия звуков с частотой от 16 до 20000 Гц, которые способно воспринимать наше ухо (в области до 4000 Гц мы отличаем звуки, отстоящие друг от друга по частоте всего на одно колебание в секунду, т. е. почти 4000 звуков!), в музыке используется всего 7 октав по 12 звуков, т. е. всего 84 звука[22]? Объяснить, почему музыкальный звукоряд содержит именно 7 октав, нетрудно. В самом деле, возьмем самую нижнюю ноту звукоряда — ля — субконтроктавы, частота которой равна 27,5 Гц, т. е. находится у нижней границы слышимости звуков. (Подходить ближе к границе слышимости не стоит, так как у каждого человека она своя и, значит, некоторые люди не услышат более низкие звуки.) Рассмотрим 8 октавных повторений этой ноты:П. Чайковский
 * (Частота ноты ля первой октавы — 440 Гц — является эталонной при настройке фортепиано и проверяется по камертону. Относительно этой ноты сохранилось интересное предание: в Древнем Египте около города Фивы находилась огромная статуя эфиопского Царя Мемнона. Статуя была повреждена во время землетрясения и каждое утро на рассвете якобы издавала звук ля,, который считался голосом Мемнона. Фивские музыканты приходили к статуе настраивать свои инструменты. К сожалению, в начале нашей эры голос Мемнона звучать перестал и проверить правоту предания невозможно.)
Легко видеть, что восьмая октава выходит далеко за границу четкой различимости высоких звуков (4000 Гц), и, таким образом, в диапазоне до 4000 Гц укладывается чуть более 7 октав. Выходить же за границу 4000 Гц нет смысла, так как звуки там плохо различаются по высоте и мелодия будет теряться.
Итак, в диапазоне от 16 до 4000 Гц укладывается чуть более 7 октав. Октав-ные звуки воспринимаются как подобные, родственные (это объясняется, как мы уже знаем, совпадением большого числа их гармоник) и служат своего рода масштабными метками в музыкальной шкале. Следовательно, построение музыкальной шкалы сводится к искусному делению октавы на составные части.
Почему октава разделена именно на 12 частей, мы уже объяснили в предыдущей главе. Как показала история развития музыки, только при таком делении октавы достигается та "строгая соразмеренная гармония всех частей, объединяемых тем, чему они принадлежат,- такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже". Эти слова, как мы знаем (с. 17), являются определением красоты по Альберти. Красота же вечна. Таким образом, именно в пропорциональном гармоничном делении октавы на составные части и заключается источник красоты музыкальной гаммы, а значит, и секрет ее трехтысячелетнего долголетия.
Мы уже отмечали некоторые пропорции музыкальной гаммы. Мы также знаем, что пропорциональность и симметрия являются объективными признаками красоты. Однако чем ближе всматриваешься в музыкальную гамму, тем полнее раскрываются все новые закономерности ее пропорционального строения, а значит, и объективные законы ее красоты. Остановимся подробнее на некоторых из этих закономерностей.
Рассмотрим вначале равномерно-темперированную 12-ступенную хроматическую гамму (9.1), имеющую наиболее простое строение:
* (Частота ноты ля первой октавы — 440 Гц — является эталонной при настройке фортепиано и проверяется по камертону. Относительно этой ноты сохранилось интересное предание: в Древнем Египте около города Фивы находилась огромная статуя эфиопского Царя Мемнона. Статуя была повреждена во время землетрясения и каждое утро на рассвете якобы издавала звук ля,, который считался голосом Мемнона. Фивские музыканты приходили к статуе настраивать свои инструменты. К сожалению, в начале нашей эры голос Мемнона звучать перестал и проверить правоту предания невозможно.)
Легко видеть, что восьмая октава выходит далеко за границу четкой различимости высоких звуков (4000 Гц), и, таким образом, в диапазоне до 4000 Гц укладывается чуть более 7 октав. Выходить же за границу 4000 Гц нет смысла, так как звуки там плохо различаются по высоте и мелодия будет теряться.
Итак, в диапазоне от 16 до 4000 Гц укладывается чуть более 7 октав. Октав-ные звуки воспринимаются как подобные, родственные (это объясняется, как мы уже знаем, совпадением большого числа их гармоник) и служат своего рода масштабными метками в музыкальной шкале. Следовательно, построение музыкальной шкалы сводится к искусному делению октавы на составные части.
Почему октава разделена именно на 12 частей, мы уже объяснили в предыдущей главе. Как показала история развития музыки, только при таком делении октавы достигается та "строгая соразмеренная гармония всех частей, объединяемых тем, чему они принадлежат,- такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже". Эти слова, как мы знаем (с. 17), являются определением красоты по Альберти. Красота же вечна. Таким образом, именно в пропорциональном гармоничном делении октавы на составные части и заключается источник красоты музыкальной гаммы, а значит, и секрет ее трехтысячелетнего долголетия.
Мы уже отмечали некоторые пропорции музыкальной гаммы. Мы также знаем, что пропорциональность и симметрия являются объективными признаками красоты. Однако чем ближе всматриваешься в музыкальную гамму, тем полнее раскрываются все новые закономерности ее пропорционального строения, а значит, и объективные законы ее красоты. Остановимся подробнее на некоторых из этих закономерностей.
Рассмотрим вначале равномерно-темперированную 12-ступенную хроматическую гамму (9.1), имеющую наиболее простое строение:
 (11.1)
Легко видеть, что ступени равномерно-темперированной гаммы (11.1) образуют геометрическую прогрессию со знаменателем
(11.1)
Легко видеть, что ступени равномерно-темперированной гаммы (11.1) образуют геометрическую прогрессию со знаменателем 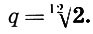 . Тогда
. Тогда
 или
или  (11.2)
Следовательно, каждая внутренняя ступень гаммы (11.1) является средним геометрическим своих соседей. Назовем это локальной геометрической симметрией с коэффициентом симметрии (отношением входящих в пропорцию членов)
(11.2)
Следовательно, каждая внутренняя ступень гаммы (11.1) является средним геометрическим своих соседей. Назовем это локальной геометрической симметрией с коэффициентом симметрии (отношением входящих в пропорцию членов)  .
Кроме того, гамма (11.1) обладает глобальной геометрической симметрией, т. е. произведения членов (11.1), равноудаленных от концов, равны квадрату среднего члена b6:
.
Кроме того, гамма (11.1) обладает глобальной геометрической симметрией, т. е. произведения членов (11.1), равноудаленных от концов, равны квадрату среднего члена b6:
 или
или  откуда имеем
откуда имеем
 (11.3)
(11.3)
Таким образом, седьмая ступень (11.1) b6=
 , так называемый тритон, равный увеличенной кварте или уменьшенной квинте, является средним геометрическим любой пары равноудаленных от концов ступеней. Назовем тритон b6=
, так называемый тритон, равный увеличенной кварте или уменьшенной квинте, является средним геометрическим любой пары равноудаленных от концов ступеней. Назовем тритон b6= , центром глобальной геометрической симметрии гаммы (11.1). Глобальная геометрическая симметрия связывает интервал и его обращение через интервальный коэффициент октавы.
Если прологарифмировать (11.1) — (11.3) по основанию 2, то эти соотношения примут наиболее простой вид
, центром глобальной геометрической симметрии гаммы (11.1). Глобальная геометрическая симметрия связывает интервал и его обращение через интервальный коэффициент октавы.
Если прологарифмировать (11.1) — (11.3) по основанию 2, то эти соотношения примут наиболее простой вид
 (11.4)
(11.4)
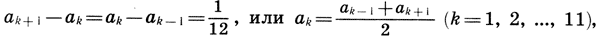 (11.5)
(11.5)
 (11.6)
Здесь ak = log2bk (k = 0, l, 2, ..., 12). Равенства (11.4) — (11.6) выражают тот простой факт, что логарифмическая октава [0; 1] разбита на 12 равных частей. Поэтому каждые три соседних члена (11.4) симметричны относительно среднего из них и отстоят от него на расстояние 1/12 (локальная симметрия), а середина логарифмической октавы а6=1/2 является центром ее глобальной симметрии, т. е. для каждого аn слева от а6 существует симметричный относительно а6 член a12-n справа от а6, так что расстояния a12-n — а6 и а6 — аn равны (n = 0, 1, 2, ..., 5).
Из равенств (11.1-3) или (11.4-6) очевидно, что при любых сдвигах (геометрических для (11.1) или арифметических для (11.4) структура равномерно-темперированной гаммы не нарушается, т. е. равномерно-темперированная гамма допускает модуляции в любые тональности. Эти возможности равномерной темперации, как отмечалось в главе 9, блестяще проиллюстрировал И. С. Бах в своем "Хорошо темперированном клавире".
Рассмотрим теперь лидийскую гамму пифагорова строя, или натуральный мажор (8.1), взяв в качестве дополнительных ступеней пониженные звуки (ре-бемоль, ми-бемоль, соль-бемоль, ля-бемоль, си-бемоль) и один повышенный звук (фа-диез) согласно (8.2):
(11.6)
Здесь ak = log2bk (k = 0, l, 2, ..., 12). Равенства (11.4) — (11.6) выражают тот простой факт, что логарифмическая октава [0; 1] разбита на 12 равных частей. Поэтому каждые три соседних члена (11.4) симметричны относительно среднего из них и отстоят от него на расстояние 1/12 (локальная симметрия), а середина логарифмической октавы а6=1/2 является центром ее глобальной симметрии, т. е. для каждого аn слева от а6 существует симметричный относительно а6 член a12-n справа от а6, так что расстояния a12-n — а6 и а6 — аn равны (n = 0, 1, 2, ..., 5).
Из равенств (11.1-3) или (11.4-6) очевидно, что при любых сдвигах (геометрических для (11.1) или арифметических для (11.4) структура равномерно-темперированной гаммы не нарушается, т. е. равномерно-темперированная гамма допускает модуляции в любые тональности. Эти возможности равномерной темперации, как отмечалось в главе 9, блестяще проиллюстрировал И. С. Бах в своем "Хорошо темперированном клавире".
Рассмотрим теперь лидийскую гамму пифагорова строя, или натуральный мажор (8.1), взяв в качестве дополнительных ступеней пониженные звуки (ре-бемоль, ми-бемоль, соль-бемоль, ля-бемоль, си-бемоль) и один повышенный звук (фа-диез) согласно (8.2):
 (11.7)
Структура пифагоровой гаммы (11.7) значительно сложнее. Однако при ближайшем рассмотрении можно обнаружить, что пифагорова гамма состоит из трех геометрических прогрессий, переплетенных между собой, подобно Платонову гептахорду (7.1), причем все три прогрессии имеют одинаковый знаменатель
(11.7)
Структура пифагоровой гаммы (11.7) значительно сложнее. Однако при ближайшем рассмотрении можно обнаружить, что пифагорова гамма состоит из трех геометрических прогрессий, переплетенных между собой, подобно Платонову гептахорду (7.1), причем все три прогрессии имеют одинаковый знаменатель  :
:
 Для этих прогрессий справедливы соотношения
Для этих прогрессий справедливы соотношения
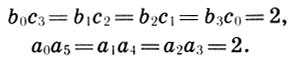 Учитывая расположение членов прогрессии в (11.7), приходим к выводу, что пифагоровагамма, также обладает глобальной геометрической симметрией. Следовательно,
Учитывая расположение членов прогрессии в (11.7), приходим к выводу, что пифагоровагамма, также обладает глобальной геометрической симметрией. Следовательно,  является центром глобальной симметрии пифагоровой гаммы.
является центром глобальной симметрии пифагоровой гаммы.
Но
 не является ступенью гаммы (11.7). Кроме того, в (11.7) осталась одна пара энгармонически неравных звуков соль-бемоль и фа-диез. Если в качестве энгармонически равного звука для соль-бемоль
не является ступенью гаммы (11.7). Кроме того, в (11.7) осталась одна пара энгармонически неравных звуков соль-бемоль и фа-диез. Если в качестве энгармонически равного звука для соль-бемоль  и фа-диез
и фа-диез  взять их среднее геометрическое
взять их среднее геометрическое  , то оно оказывается в точности равным центру глобальной симметрии
, то оно оказывается в точности равным центру глобальной симметрии  . Таким образом, мы получим 12-ступенную хроматическую пифагорову гамму с центром глобальной симметрии
. Таким образом, мы получим 12-ступенную хроматическую пифагорову гамму с центром глобальной симметрии  на седьмой ступени:
на седьмой ступени:
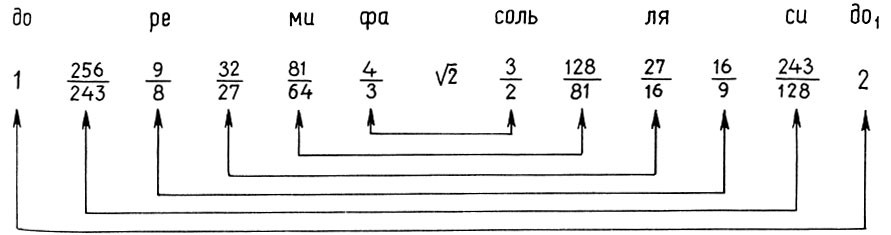 (11.8)
(11.8)
Легко проверить, что в гамме (11.8) можно взять чистые квинты на всех ступенях, кроме седьмой (
 ), которая даст "волчью" квинту. Кроме того, сам интервал тритона (
), которая даст "волчью" квинту. Кроме того, сам интервал тритона ( ), как мы знаем, является резким диссонансом. Оба этих качества составили тритону печальную славу. В средние века тритон называли "дьяволом в музыке", и до XVI века употреблять его в церковных песнопениях строго запрещалось.
Рассмотрим теперь диатоническую 7-ступенную гамму чистого строя (8.7):
), как мы знаем, является резким диссонансом. Оба этих качества составили тритону печальную славу. В средние века тритон называли "дьяволом в музыке", и до XVI века употреблять его в церковных песнопениях строго запрещалось.
Рассмотрим теперь диатоническую 7-ступенную гамму чистого строя (8.7):
 (11.9)
Мы знаем, что гамма чистого строя является наиболее благозвучной, а ее интервальные коэффициенты имеют самый простой вид. Но еще удивительнее то, что гамма (11.9) является и самой пропорциональной. В самом деле, среднее арифметическое и среднее гармоническое основного тона (1) и октавы (2) дают нам квинту и кварту:
(11.9)
Мы знаем, что гамма чистого строя является наиболее благозвучной, а ее интервальные коэффициенты имеют самый простой вид. Но еще удивительнее то, что гамма (11.9) является и самой пропорциональной. В самом деле, среднее арифметическое и среднее гармоническое основного тона (1) и октавы (2) дают нам квинту и кварту:
 Среднее арифметическое и среднее гармоническое основного тона и квинты образуют большую и малую терции:
Среднее арифметическое и среднее гармоническое основного тона и квинты образуют большую и малую терции:
 Наконец, взяв среднее арифметическое и среднее гармоническое основного тона и большой терции, мы получим оба интервала тона чистого строя:
Наконец, взяв среднее арифметическое и среднее гармоническое основного тона и большой терции, мы получим оба интервала тона чистого строя:
 Таким образом, все главные интервалы чистого строя получаются как последовательная цепь средних пропорциональных, началом которой является пропорциональное деление октавы на квинту и кварту.
Перейдем к хроматической гамме чистого строя. Для построения дополнительных ступеней хроматической гаммы отложим полутон чистого строя (16/15) вверх от 1, 2, 4, 5 и 6-й ступеней диатонической гаммы (11.9), т. е. умножим их интервальные коэффициенты на 16/15, а также из соображений симметрии отложим полутон вниз от 5-й ступени. В результате получим 13-ступенную гамму:
Таким образом, все главные интервалы чистого строя получаются как последовательная цепь средних пропорциональных, началом которой является пропорциональное деление октавы на квинту и кварту.
Перейдем к хроматической гамме чистого строя. Для построения дополнительных ступеней хроматической гаммы отложим полутон чистого строя (16/15) вверх от 1, 2, 4, 5 и 6-й ступеней диатонической гаммы (11.9), т. е. умножим их интервальные коэффициенты на 16/15, а также из соображений симметрии отложим полутон вниз от 5-й ступени. В результате получим 13-ступенную гамму:
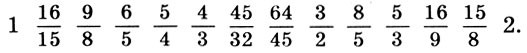
Интервальные коэффициенты 45/32 и 64/45 можно заменить на более простые 7/5 и 10/7, которые приближенно им равны
 и также обладают геометрической симметрией относительно
и также обладают геометрической симметрией относительно  . В результате входящие в хроматическую гамму чистого строя интервальные коэффициенты выразятся с помощью отношения натуральных чисел, не превосходящих 16, которые можно трактовать как частоты первых 16 гармоник основного тона (1), или первые 16 ступеней натурального звукоряда:
. В результате входящие в хроматическую гамму чистого строя интервальные коэффициенты выразятся с помощью отношения натуральных чисел, не превосходящих 16, которые можно трактовать как частоты первых 16 гармоник основного тона (1), или первые 16 ступеней натурального звукоряда:
 (11.10)
Заметим, что, как и в диатонической гамме (11.9), интервальные коэффициенты хроматической гаммы (11.10) не содержат 11-й и 13-й обертоны, а печально известный "фальшивый" 7-й обертон входит только в два коэффициента (7/5 = 1,4 и 10/7≈1,428), которые приближенно равны интервальному коэффициенту тритона
(11.10)
Заметим, что, как и в диатонической гамме (11.9), интервальные коэффициенты хроматической гаммы (11.10) не содержат 11-й и 13-й обертоны, а печально известный "фальшивый" 7-й обертон входит только в два коэффициента (7/5 = 1,4 и 10/7≈1,428), которые приближенно равны интервальному коэффициенту тритона  чья дурная слава известна в музыке не менее.
Взяв, как и в (11.8), в качестве энгармонически равного звука для соль-бемоль (7/5) и фа-диез (10/7) их среднее геометрическое
чья дурная слава известна в музыке не менее.
Взяв, как и в (11.8), в качестве энгармонически равного звука для соль-бемоль (7/5) и фа-диез (10/7) их среднее геометрическое  , мы придем к 12-ступенной хроматической гамме чистого строя интервальные коэффициенты которой имеют вид
, мы придем к 12-ступенной хроматической гамме чистого строя интервальные коэффициенты которой имеют вид
 (11.11)
На этот раз интервальные коэффициенты в (11.11) не образуют никаких прогрессий. Однако, нетрудно обнаружить, что гамма (11.11) также обладает глобальной геометрической симметрией относительно
(11.11)
На этот раз интервальные коэффициенты в (11.11) не образуют никаких прогрессий. Однако, нетрудно обнаружить, что гамма (11.11) также обладает глобальной геометрической симметрией относительно  , т. е.
, т. е.
 Гаммы (11.8) и (11.11) не обладают локальной геометрической симметрией, поэтому не допускают сдвигов без искажений. Последнее означает, что модуляции в другие тональности в пифагоровом и чистом строе затруднены.
Подведем некоторые итоги. Прежде всего мы видим, что музыкальные гаммы представляют собой строго упорядоченную совокупность звуков, отобранную из всего многообразия звуков, которые способно воспринимать и различать человеческое ухо. Именно закономерное построение гаммы, а следовательно и лада, позволяет на ее основе составлять и более сложные музыкальные конструкции, также носящие закономерный характер и называемые мелодией. Можно сказать, что гамма есть основная мелодия лада.
Отметим еще одно важное обстоятельство. В каждой из рассмотренных нами хроматических гамм: равномерно-темперированной (11.1), пифагоровой (11.8) и чистого строя (11.11) — точно выполнен один тип симметрии и только приблизительно другой. Так, равномерно-темперированная гамма (11.1) обладает локальной и глобальной геометрической симметрией, но в ней только приблизительно соблюдены пропорции деления октавы на квинту и кварту, большую и малую терции и т. д. Пифагорова гамма и гамма чистого строя обладают глобальной геометрической симметрией, но локальная симметрия в них выполнена только приблизительно. Зато в обеих гаммах точно соблюдено условие пропорционального деления октавы на квинту и кварту, а гамма чистого строя обладает еще двумя парами пропорций деления, что, видимо, и делает ее наиболее мелодичной из всех трех типов гамм.
Таким образом, в строении гаммы наряду с точной симметрией мы находим и приблизительную симметрию. (О загадках приблизительной симметрии и ее роли в науке и искусстве мы уже вели речь в главе 4.) Следовательно, в законах построения музыкальной гаммы отражается противоборство симметрии и асимметрии, олицетворяющих покой и движение, закономерное и случайное, вечное и сиюминутное. Именно диалектическое единство двух противоположных начал — симметрии и асимметрии — наполняет гамму подлинной гармонией, является источником вечной красоты и юного изящества музыкальной гаммы.
Последние три десятилетия поисками математических закономерностей в музыке усиленно занимается московский композитор М. А. Марутаев. Еще в студенческие годы М. Марутаева занимала мысль найти объяснение принципам музыкальной формы и ладогармонического языка. Результаты многолетних изысканий М. Марутаева легли в основу развитой им теории качественной симметрии чисел, позволившей автору определить меру нарушения симметрии в музыкальной гамме.
На основании теории качественной симметрии чисел Марутаев строит концепцию "универсальной гармонии", т. е., проще говоря, пытается решить одну из вечных загадок: найти "формулу красоты", "универсальную гармонию", которую искали еще древние греки и которая связала бы воедино законы природы и законы искусства.
К сожалению, и на сегодня это фантастическая задача, ибо человечеству пока не известны ни единые законы природы, ни тем более законы искусства.
Вот почему у концепции Марутаева много как пылких сторонников, так и ярых противников. Мы не будем останавливаться на концепции Марутаева, которая во многом спорна, а местами и просто содержит математические огрехи (но у кого хватит смелости объявить себя специалистом и в науке, и в искусстве?!), а отметим лишь некоторые любопытные факты, установленные Марутаевым.
Вновь обратимся к гаммам. Прежде всего заметим, что, хотя мы все время говорили о 12-ступенных хроматических гаммах, мы везде фактически включали в рассмотрение 13-ю ступень (октавное повторение основного тона), которая на самом деле является 1-й ступенью следующей октавы. Если в гаммах (11.1), (11.8) и (11.11) октавное повторение основного тона не рассматривать, то получается действительно 12-ступенные музыкальные ряды, которые Марутаев называет качественными музыкальными рядами, поскольку они состоят из оригинальных качеств:
1,37
Гаммы (11.8) и (11.11) не обладают локальной геометрической симметрией, поэтому не допускают сдвигов без искажений. Последнее означает, что модуляции в другие тональности в пифагоровом и чистом строе затруднены.
Подведем некоторые итоги. Прежде всего мы видим, что музыкальные гаммы представляют собой строго упорядоченную совокупность звуков, отобранную из всего многообразия звуков, которые способно воспринимать и различать человеческое ухо. Именно закономерное построение гаммы, а следовательно и лада, позволяет на ее основе составлять и более сложные музыкальные конструкции, также носящие закономерный характер и называемые мелодией. Можно сказать, что гамма есть основная мелодия лада.
Отметим еще одно важное обстоятельство. В каждой из рассмотренных нами хроматических гамм: равномерно-темперированной (11.1), пифагоровой (11.8) и чистого строя (11.11) — точно выполнен один тип симметрии и только приблизительно другой. Так, равномерно-темперированная гамма (11.1) обладает локальной и глобальной геометрической симметрией, но в ней только приблизительно соблюдены пропорции деления октавы на квинту и кварту, большую и малую терции и т. д. Пифагорова гамма и гамма чистого строя обладают глобальной геометрической симметрией, но локальная симметрия в них выполнена только приблизительно. Зато в обеих гаммах точно соблюдено условие пропорционального деления октавы на квинту и кварту, а гамма чистого строя обладает еще двумя парами пропорций деления, что, видимо, и делает ее наиболее мелодичной из всех трех типов гамм.
Таким образом, в строении гаммы наряду с точной симметрией мы находим и приблизительную симметрию. (О загадках приблизительной симметрии и ее роли в науке и искусстве мы уже вели речь в главе 4.) Следовательно, в законах построения музыкальной гаммы отражается противоборство симметрии и асимметрии, олицетворяющих покой и движение, закономерное и случайное, вечное и сиюминутное. Именно диалектическое единство двух противоположных начал — симметрии и асимметрии — наполняет гамму подлинной гармонией, является источником вечной красоты и юного изящества музыкальной гаммы.
Последние три десятилетия поисками математических закономерностей в музыке усиленно занимается московский композитор М. А. Марутаев. Еще в студенческие годы М. Марутаева занимала мысль найти объяснение принципам музыкальной формы и ладогармонического языка. Результаты многолетних изысканий М. Марутаева легли в основу развитой им теории качественной симметрии чисел, позволившей автору определить меру нарушения симметрии в музыкальной гамме.
На основании теории качественной симметрии чисел Марутаев строит концепцию "универсальной гармонии", т. е., проще говоря, пытается решить одну из вечных загадок: найти "формулу красоты", "универсальную гармонию", которую искали еще древние греки и которая связала бы воедино законы природы и законы искусства.
К сожалению, и на сегодня это фантастическая задача, ибо человечеству пока не известны ни единые законы природы, ни тем более законы искусства.
Вот почему у концепции Марутаева много как пылких сторонников, так и ярых противников. Мы не будем останавливаться на концепции Марутаева, которая во многом спорна, а местами и просто содержит математические огрехи (но у кого хватит смелости объявить себя специалистом и в науке, и в искусстве?!), а отметим лишь некоторые любопытные факты, установленные Марутаевым.
Вновь обратимся к гаммам. Прежде всего заметим, что, хотя мы все время говорили о 12-ступенных хроматических гаммах, мы везде фактически включали в рассмотрение 13-ю ступень (октавное повторение основного тона), которая на самом деле является 1-й ступенью следующей октавы. Если в гаммах (11.1), (11.8) и (11.11) октавное повторение основного тона не рассматривать, то получается действительно 12-ступенные музыкальные ряды, которые Марутаев называет качественными музыкальными рядами, поскольку они состоят из оригинальных качеств:
1,37
 (1.12)
(1.12)
 (1.13)
(1.13)
 (1.14)
Легко видеть, что качественная равномерно-темперированная гамма (11.12) сохраняет свойство глобальной геометрической симметрии, центр которой сместился из точки
(1.14)
Легко видеть, что качественная равномерно-темперированная гамма (11.12) сохраняет свойство глобальной геометрической симметрии, центр которой сместился из точки  ≈1,41 в точку 211/24≈1,37:
≈1,41 в точку 211/24≈1,37:
 А вот для качественных гамм пифагорова и чистого строя глобальная геометрическая симметрия нарушится и будет выполняться только приблизительно. В самом деле, вычисляя среднее геометрическое для равноудаленных от концов членов ряда (11.13)
А вот для качественных гамм пифагорова и чистого строя глобальная геометрическая симметрия нарушится и будет выполняться только приблизительно. В самом деле, вычисляя среднее геометрическое для равноудаленных от концов членов ряда (11.13)
 и ряда (11.14)
и ряда (11.14)
 мы видим, что эти числа слегка различаются, однако их среднее арифметическое с точностью до 5 знаков совпадает между собой и с точностью до 4 знаков — 211/24
мы видим, что эти числа слегка различаются, однако их среднее арифметическое с точностью до 5 знаков совпадает между собой и с точностью до 4 знаков — 211/24
 Итак, число 1,37 является центром глобальной геометрической симметрии (точной для (11.12) и приблизительной для (11.13) и (11.14)) 12-ступенных музыкальных гамм. Далее, Марутаев напоминает, что в ботанике известен идеальный угол расхождения листьев, равный 137°30'. Это математически рассчитанный угол, на который должны поворачиваться листья при их винтовом расположении вдоль стебля, так чтобы получать наибольшее количество вертикально падающего света. Удивительным оказывается и тот факт, что идеальный угол получается при двух последовательных делениях по золотому сечению угла 360°.
Итак, число 1,37 является центром глобальной геометрической симметрии (точной для (11.12) и приблизительной для (11.13) и (11.14)) 12-ступенных музыкальных гамм. Далее, Марутаев напоминает, что в ботанике известен идеальный угол расхождения листьев, равный 137°30'. Это математически рассчитанный угол, на который должны поворачиваться листья при их винтовом расположении вдоль стебля, так чтобы получать наибольшее количество вертикально падающего света. Удивительным оказывается и тот факт, что идеальный угол получается при двух последовательных делениях по золотому сечению угла 360°.
Особую роль играет число 137 и в физике, где оно является безразмерной комбинацией фундаментальных постоянных природы. Вот что по поводу этого числа пишет один из крупнейших современных физиков, лауреат Нобелевской премии англичанин Поль Дирак, возглавлявший в 60-е гг. XX века в Кембридже знаменитую лукасовскую кафедру — ту самую, которую в 60-е гг. XVII века профессор Исаак Барроу уступил своему 26-летнему ученику Исааку Ньютону: "В природе существует несколько фундаментальных констант: заряд электрона (е), постоянная Планка, деленная на 2π(
 =h/2π), и скорость света (с). Из этих фундаментальных констант можно вывести число, которое не обладает размерностью: с/е2. На основании экспериментальных данных установлено, что это число имеет величину 137 или весьма близкую к 137. Далее, нам неизвестно, почему оно имеет именно это значение, а не какое-нибудь иное. Для объяснения этого факта выдвигались различные идеи, однако никакой приемлемой теории не существует. Все же можно быть вполне уверенным в том, что физики когда-нибудь решат эту проблему и объяснят, почему это число имеет именно такое значение. Возможно, создадут такую физическую теорию, которая будет работать, если
=h/2π), и скорость света (с). Из этих фундаментальных констант можно вывести число, которое не обладает размерностью: с/е2. На основании экспериментальных данных установлено, что это число имеет величину 137 или весьма близкую к 137. Далее, нам неизвестно, почему оно имеет именно это значение, а не какое-нибудь иное. Для объяснения этого факта выдвигались различные идеи, однако никакой приемлемой теории не существует. Все же можно быть вполне уверенным в том, что физики когда-нибудь решат эту проблему и объяснят, почему это число имеет именно такое значение. Возможно, создадут такую физическую теорию, которая будет работать, если 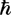 *с/е2 равно 137, и не будет работать, если оно имеет любое другое значение".
Еще один пример из физики. При распаде урана образуются осколки неравной массы. Кривая распределения осколков по массам имеет два максимума при массовых числах порядка 102 и 140 (это наиболее вероятные массовые числа осколков при распаде урана). Взяв отношение этих максимумов, имеем 140/102≈1,37.
Наконец, Марутаев приводит многочисленные примеры анализа музыкальных произведений по их метрическим параметрам, в которых встречается число 1,37. Рассматриваются сонатные или трехчастные формы. Протяженность музыкального произведения во времени можно характеризовать, например, числом восьмых долей или числом тактов, если размеры тактов (т. е. число восьмых долей в такте) не изменяются. Тогда протяженность трехчастной формы можно представить в виде Т = а + b + с, где а, b, с — числа тактов (восьмых долей) в экспозиции, разработке (средней части) и репризе соответственно. Оказалось, что во многих известных произведениях выдающихся композиторов: Моцарта (Соната № 12, ч. 1), Бетховена (соната № 14 "Лунная"), Дебюсси ("Детский уголок", пьеса № 1), Шостаковича (Фуга № 1, оп. 87) — имеет место соотношение
*с/е2 равно 137, и не будет работать, если оно имеет любое другое значение".
Еще один пример из физики. При распаде урана образуются осколки неравной массы. Кривая распределения осколков по массам имеет два максимума при массовых числах порядка 102 и 140 (это наиболее вероятные массовые числа осколков при распаде урана). Взяв отношение этих максимумов, имеем 140/102≈1,37.
Наконец, Марутаев приводит многочисленные примеры анализа музыкальных произведений по их метрическим параметрам, в которых встречается число 1,37. Рассматриваются сонатные или трехчастные формы. Протяженность музыкального произведения во времени можно характеризовать, например, числом восьмых долей или числом тактов, если размеры тактов (т. е. число восьмых долей в такте) не изменяются. Тогда протяженность трехчастной формы можно представить в виде Т = а + b + с, где а, b, с — числа тактов (восьмых долей) в экспозиции, разработке (средней части) и репризе соответственно. Оказалось, что во многих известных произведениях выдающихся композиторов: Моцарта (Соната № 12, ч. 1), Бетховена (соната № 14 "Лунная"), Дебюсси ("Детский уголок", пьеса № 1), Шостаковича (Фуга № 1, оп. 87) — имеет место соотношение
 Так что же это такое: открытие "универсальной гармонии" или игра чисел? Почти наверняка — второе. Однако не нужно спешить обвинять автора в числовых спекуляциях. Вспомним кружочки противоположного цвета в мудром символе Ин-Ян: каждое доброе дело содержит крупицу зла и даже зло несет в себе частицу доброты. В нашем случае мудрый древнекитайский символ говорит: даже неправильная научная теория является шагом вперед на пути к истине.
Не нужно забывать' и исторический пример Пифагора, которого со всех сторон и во все времена обвиняли в числовых спекуляциях, но тем не менее сегодня общепризнано, что закон целочисленных отношений для консонансов является первым физическим законом, получившим математическое описание. Исследования Марутаева, безусловно, продвигают нас хотя бы на шаг вперед на трудном пути постижения математических тайн музыки. Впрочем, так их оценивает и сам автор. Что же касается "универсальной гармонии", то она представляется нам столь же непостижимой, как "абсолютная истина" или "перпетуум-мобиле".
Так что же это такое: открытие "универсальной гармонии" или игра чисел? Почти наверняка — второе. Однако не нужно спешить обвинять автора в числовых спекуляциях. Вспомним кружочки противоположного цвета в мудром символе Ин-Ян: каждое доброе дело содержит крупицу зла и даже зло несет в себе частицу доброты. В нашем случае мудрый древнекитайский символ говорит: даже неправильная научная теория является шагом вперед на пути к истине.
Не нужно забывать' и исторический пример Пифагора, которого со всех сторон и во все времена обвиняли в числовых спекуляциях, но тем не менее сегодня общепризнано, что закон целочисленных отношений для консонансов является первым физическим законом, получившим математическое описание. Исследования Марутаева, безусловно, продвигают нас хотя бы на шаг вперед на трудном пути постижения математических тайн музыки. Впрочем, так их оценивает и сам автор. Что же касается "универсальной гармонии", то она представляется нам столь же непостижимой, как "абсолютная истина" или "перпетуум-мобиле".
12. Математический анализ музыки
Чрезвычайная бедность, шаткость и разрозненность существующих основ музыкальной эстетики побуждает нас пытливо всматриваться во всякое закономерное явление, относящееся к этой области, в надежде приподнять хотя бы уголок изидовой завесы, скрывающей от нашего умственного взора таинственные творческие законы природы...До сих пор в нашем разговоре о музыке мы фактически не выходили за пределы одной октавы. С одной стороны, это хорошо, ибо говорит о том, сколь много мудрости в простоте знакомых каждому семи нот октавы. Но с другой стороны, безусловно, непростительно по отношению к музыке в целом, ибо музыка — это прежде" всего мелодия, это песня души. Ведь, как сказал Пушкин,Э. Розенов
 (12.1)
Поскольку х есть часть целого, т. е. величина положительная, а второй корень (12.1) отрицателен, то приходим к единственному значению корня:
(12.1)
Поскольку х есть часть целого, т. е. величина положительная, а второй корень (12.1) отрицателен, то приходим к единственному значению корня:
 (12.2)
где величина φ является коэффициентом золотого сечения. Тогда
(12.2)
где величина φ является коэффициентом золотого сечения. Тогда
 (12.3)
причем Ф = 1/φ
Для меньшей части имеем а — х = а(1 — φ) = аφ2, причем аφ + φ2 = а. Разделив теперь величину аφ в золотой пропорции, получим
(12.3)
причем Ф = 1/φ
Для меньшей части имеем а — х = а(1 — φ) = аφ2, причем аφ + φ2 = а. Разделив теперь величину аφ в золотой пропорции, получим
 причем аφ2 + аφ3 = аφ. Легко видеть, что большая часть второй золотой пропорции у = аφ2 совпадает с меньшей частью первой а — х = аφ2. Итак, при последовательном делении целого а в золотой пропорции имеет место геометрическая прогрессия (ряд золотого сечения) со знаменателем φ, каждый член которой равен сумме двух последующих членов прогрессии:
причем аφ2 + аφ3 = аφ. Легко видеть, что большая часть второй золотой пропорции у = аφ2 совпадает с меньшей частью первой а — х = аφ2. Итак, при последовательном делении целого а в золотой пропорции имеет место геометрическая прогрессия (ряд золотого сечения) со знаменателем φ, каждый член которой равен сумме двух последующих членов прогрессии:
 (12.4)
Огромная роль золотого сечения в пространственных искусствах (скульптуре, архитектуре, живописи) известна с античных времен и имеет немало объяснений. Например, такое: линия глаз, на которой человек привык концентрировать свое внимание, слушая собеседника, делит длину лица в отношении золотого сечения. Поэтому при взгляде на любой предмет мы невольно направляем глаза в точку золотого деления, которая кажется нам привычной, естественной, а потому и красивой. Что касается искусств, развивающихся во времени (поэзия, музыка), то здесь неизвестны аналогичные природные предпосылки закона золотого сечения. Но тем более удивительным оказывается действие этого закона в поэзии и музыке, которое, по-видимому, первым обнаружил Розенов.
(12.4)
Огромная роль золотого сечения в пространственных искусствах (скульптуре, архитектуре, живописи) известна с античных времен и имеет немало объяснений. Например, такое: линия глаз, на которой человек привык концентрировать свое внимание, слушая собеседника, делит длину лица в отношении золотого сечения. Поэтому при взгляде на любой предмет мы невольно направляем глаза в точку золотого деления, которая кажется нам привычной, естественной, а потому и красивой. Что касается искусств, развивающихся во времени (поэзия, музыка), то здесь неизвестны аналогичные природные предпосылки закона золотого сечения. Но тем более удивительным оказывается действие этого закона в поэзии и музыке, которое, по-видимому, первым обнаружил Розенов.
 Последовательное деление единичного отрезка в золотом сечении
Последовательное деление единичного отрезка в золотом сечении
 Ряд золотого сечения
Розенов проанализировал "популярнейшие и наиболее излюбленные произведения гениальных авторов Баха, Моцарта, Бетховена, Шопена, Вагнера, Глинки, а также произведения народного творчества наиболее древнего происхождения, живучесть которых является достаточным доказательством их эстетической ценности и широкой популярности". Остановимся на анализе Хроматической фантазии и фуги И. С. Баха, которые объединены общей тональностью ре минор и контрастны по жанру и образу. Хроматическая фантазия с фугой ре минор - одно из величайших творений Баха, образец совершенства формы и содержания, "могущественнейшее клавесинное произведение" (А. Н. Серов).
Хроматическая фантазия написана в размере 4/4, имеет 79 тактов, т. е. 79*4 = 316 четвертных долей. Итак, "целое" а = 316. Фантазия состоит из двух ясно различимых по характеру частей, отделенных друг от друга паузой. Первая часть, прелюдия, заканчивается на арпеджированном доминантовом трезвучии с разрешением на 2-й четверти 49-го такта, на которой стоит знак ферматы (удлинение звука), и затем идет пауза. Таким образом, первая часть фактически заканчивается на 3-й четверти 49-го такта, т. е. на 195-й (48*4 + 3) четверти (а1 =195). Вторая часть, пишет Розенов, "состоит из ряда в высшей степени выразительных колорированных речитативов, то развивающихся по силе, энергии и размаху До гигантской мощи, то нежных и жалобных, то сердитых и запальчивых, то впадающих в необычную для той эпохи романтическую мечтательность". На вторую часть приходится 121 четверть (а2 = а-а1 = 316 — 195 = 121). Вычисляя "теоретическую" длину первой части с помощью коэффициента золотого сечения, мы с поражающей точностью находим а1= аφ = 0,316-0,618 = 195,3! Итак, Хроматическая фантазия разделена на первую и вторую части в золотой пропорции :
Ряд золотого сечения
Розенов проанализировал "популярнейшие и наиболее излюбленные произведения гениальных авторов Баха, Моцарта, Бетховена, Шопена, Вагнера, Глинки, а также произведения народного творчества наиболее древнего происхождения, живучесть которых является достаточным доказательством их эстетической ценности и широкой популярности". Остановимся на анализе Хроматической фантазии и фуги И. С. Баха, которые объединены общей тональностью ре минор и контрастны по жанру и образу. Хроматическая фантазия с фугой ре минор - одно из величайших творений Баха, образец совершенства формы и содержания, "могущественнейшее клавесинное произведение" (А. Н. Серов).
Хроматическая фантазия написана в размере 4/4, имеет 79 тактов, т. е. 79*4 = 316 четвертных долей. Итак, "целое" а = 316. Фантазия состоит из двух ясно различимых по характеру частей, отделенных друг от друга паузой. Первая часть, прелюдия, заканчивается на арпеджированном доминантовом трезвучии с разрешением на 2-й четверти 49-го такта, на которой стоит знак ферматы (удлинение звука), и затем идет пауза. Таким образом, первая часть фактически заканчивается на 3-й четверти 49-го такта, т. е. на 195-й (48*4 + 3) четверти (а1 =195). Вторая часть, пишет Розенов, "состоит из ряда в высшей степени выразительных колорированных речитативов, то развивающихся по силе, энергии и размаху До гигантской мощи, то нежных и жалобных, то сердитых и запальчивых, то впадающих в необычную для той эпохи романтическую мечтательность". На вторую часть приходится 121 четверть (а2 = а-а1 = 316 — 195 = 121). Вычисляя "теоретическую" длину первой части с помощью коэффициента золотого сечения, мы с поражающей точностью находим а1= аφ = 0,316-0,618 = 195,3! Итак, Хроматическая фантазия разделена на первую и вторую части в золотой пропорции :
 Но на этом чудеса гениального творения Баха только начинаются. Построив ряд золотого сечения (12.4) при а = 316, имеем
316 195,3 120,7 74,6 46,1 28,5 17,6.
Каково же должно быть наше удивление, когда мы обнаружим, что на 124-й четверти находится кульминация первой части и стоит знак ферматы, а на 77-й четверти от начала второй части имеет место кульминация второй части! Таким образом, кульминация обеих частей с небольшой погрешностью, легко объяснимой растяжимостью темпов, делит эти части по закону золотого сечения. Далее, каждый из полученных четырех разделов Хроматической фантазии имеет характерные особенности, которые также с потрясающей точностью приходятся на точки золотого деления этих разделов! Наконец, Розенов нашел и более мелкие деления Хроматической фантазии в золотой пропорции, на которых мы не будем останавливаться.
Итак, Хроматическая фантазия, произведение свободного по форме жанра, буквально соткано из золотых пропорций! Пожалуй, эстетическое впечатление от математического анализа Хроматической фантазии имеет не меньшую силу, чем прослушивание бессмертного творения Баха. А взятые вместе — чувственное впечатление и рациональный анализ, безусловно, позволяют еще на один шаг приблизиться к сокровенным тайникам гения.
Но на этом чудеса гениального творения Баха только начинаются. Построив ряд золотого сечения (12.4) при а = 316, имеем
316 195,3 120,7 74,6 46,1 28,5 17,6.
Каково же должно быть наше удивление, когда мы обнаружим, что на 124-й четверти находится кульминация первой части и стоит знак ферматы, а на 77-й четверти от начала второй части имеет место кульминация второй части! Таким образом, кульминация обеих частей с небольшой погрешностью, легко объяснимой растяжимостью темпов, делит эти части по закону золотого сечения. Далее, каждый из полученных четырех разделов Хроматической фантазии имеет характерные особенности, которые также с потрясающей точностью приходятся на точки золотого деления этих разделов! Наконец, Розенов нашел и более мелкие деления Хроматической фантазии в золотой пропорции, на которых мы не будем останавливаться.
Итак, Хроматическая фантазия, произведение свободного по форме жанра, буквально соткано из золотых пропорций! Пожалуй, эстетическое впечатление от математического анализа Хроматической фантазии имеет не меньшую силу, чем прослушивание бессмертного творения Баха. А взятые вместе — чувственное впечатление и рациональный анализ, безусловно, позволяют еще на один шаг приблизиться к сокровенным тайникам гения.
 Главные золотые сечения Хроматической фантазии И. С. Баха. Цифры обозначают число четвертей теоретического ряда золотого сечения (а = 316). Справа дано описание соответствующих характерных мест нотного текста фантазии
Перейдем к анализу фуги. Фуга (от лат. fuga — бег) является наиболее совершенной формой многоголосной музыки (полифонии). Фуга строится на многократных проведениях (повторениях) основной музыкальной темы в разных голосах. Проведения основной темы обычно перемежаются в фуге с промежуточными вставками, называемыми интермедиями. Таким образом, фуга в отличие от фантазии имеет четко определенный закон построения. Но тем не менее точность "математического" построения фуги ре минор просто поражает!
Фуга ре минор состоит из семи пар проведений и интермедий и двух самостоятельных проведений. Из семи пар "проведение-интермедия" пять пар строго подчиняются закону золотого сечения. Те же две пары "проведение-интермедия", для которых закон золотого деления не выполнен, являются своеобразными центрами симметрии относительно обрамляющих их разделов фуги и с каждым из них находятся в золотой пропорции! Именно для того, чтобы выделить эти два центра симметрии, Бах специально допускает в их строении отклонения от золотого деления и делает эти две пары "проведение-интермедия" симметричными.
На рисунке приведена схема строения фуги ре минор. Здесь же указано число четвертей в каждом разделе фуги (целые числа) и даны теоретические значения членов золотой пропорции (дробные числа). Как видим, все пять пар "проведение-интермедия" с изумительной точностью разделены в золотой пропорции (абсолютные ошибки колеблются в диапазоне от 0,05 до 0,15 четверти, относительные ошибки — от 0,02% до 0,7%). Таким относительным погрешностям могут позавидовать многие из современных инженерных расчетов! В более крупных разделах абсолютные ошибки, естественно, возрастают. Но и при делении самого большого раздела (91 четверть) эти ошибки не превышают 1,25 четверти. Не следует, однако, забывать, что мы имеем дело с художественным произведением. Отметим, что в фуге ре минор существуют также и более мелкие, и более крупные соотношения золотого сечения, на которых мы просто не останавливаемся.
Итак, простой математический анализ, не выходящий за рамки арифметики, позволяет совершенно иными глазами взглянуть на музыкальное произведение, увидеть его скрытую внутреннюю красоту, которую мы только ощущаем, слушая произведение, и которую мы "видим", проводя его математический анализ. Вот как сказал об этом Розенов: "При взгляде на схемы Хроматической фантазии и фуги... невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силой художественной чуткости до такой степени точности законы природного творчества".
Главные золотые сечения Хроматической фантазии И. С. Баха. Цифры обозначают число четвертей теоретического ряда золотого сечения (а = 316). Справа дано описание соответствующих характерных мест нотного текста фантазии
Перейдем к анализу фуги. Фуга (от лат. fuga — бег) является наиболее совершенной формой многоголосной музыки (полифонии). Фуга строится на многократных проведениях (повторениях) основной музыкальной темы в разных голосах. Проведения основной темы обычно перемежаются в фуге с промежуточными вставками, называемыми интермедиями. Таким образом, фуга в отличие от фантазии имеет четко определенный закон построения. Но тем не менее точность "математического" построения фуги ре минор просто поражает!
Фуга ре минор состоит из семи пар проведений и интермедий и двух самостоятельных проведений. Из семи пар "проведение-интермедия" пять пар строго подчиняются закону золотого сечения. Те же две пары "проведение-интермедия", для которых закон золотого деления не выполнен, являются своеобразными центрами симметрии относительно обрамляющих их разделов фуги и с каждым из них находятся в золотой пропорции! Именно для того, чтобы выделить эти два центра симметрии, Бах специально допускает в их строении отклонения от золотого деления и делает эти две пары "проведение-интермедия" симметричными.
На рисунке приведена схема строения фуги ре минор. Здесь же указано число четвертей в каждом разделе фуги (целые числа) и даны теоретические значения членов золотой пропорции (дробные числа). Как видим, все пять пар "проведение-интермедия" с изумительной точностью разделены в золотой пропорции (абсолютные ошибки колеблются в диапазоне от 0,05 до 0,15 четверти, относительные ошибки — от 0,02% до 0,7%). Таким относительным погрешностям могут позавидовать многие из современных инженерных расчетов! В более крупных разделах абсолютные ошибки, естественно, возрастают. Но и при делении самого большого раздела (91 четверть) эти ошибки не превышают 1,25 четверти. Не следует, однако, забывать, что мы имеем дело с художественным произведением. Отметим, что в фуге ре минор существуют также и более мелкие, и более крупные соотношения золотого сечения, на которых мы просто не останавливаемся.
Итак, простой математический анализ, не выходящий за рамки арифметики, позволяет совершенно иными глазами взглянуть на музыкальное произведение, увидеть его скрытую внутреннюю красоту, которую мы только ощущаем, слушая произведение, и которую мы "видим", проводя его математический анализ. Вот как сказал об этом Розенов: "При взгляде на схемы Хроматической фантазии и фуги... невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силой художественной чуткости до такой степени точности законы природного творчества".

 Строение фуги ре минор И. С. Баха. Целые числа указывают число четвертей в фуге, дробные — теоретические значения золотых сечений. Золотые пропорции в более крупных частях фуги отмечены фигурными скобками, центры симметрии — кружками. П — проведение, И — интермедия
Далее Розенов, "дабы показать, что приведенный пример не является у Баха исключительным", рассматривает многочисленные прелюдии и фуги из "Хорошо темперированного клавира" Баха, а также оперу Моцарта "Дон-Жуан", финал знаменитой "Лунной" сонаты Бетховена, Фантазию фа минор Шопена, вступление к опере "Тристан и Изольда" Вагнера, увертюру к опере "Руслан и Людмила" Глинки и многие народные песни. Во всех этих произведениях Розенов с замечательной точностью обнаруживает действие закона золотого сечения. "Приведенные мною примеры проявления закона золотого сечения настолько характерны и замечательны,- пишет Розенов,- что исключают всякую возможность отрицания эстетического значения этого закона в музыке". Не правда ли, здесь мы имеем тот самый случай, когда "цифры могут представлять собой культурную и эстетическую ценность"? (См. высказывание Н. Винера в эпиграфе к первой части книги.)
Но помимо установления самого факта наличия закона золотого сечения в музыкальных произведениях и его огромного эстетического значения в музыке математический анализ музыки (даже такой элементарный) позволяет сделать некоторые выводы о характерных особенностях творчества самих композиторов. Так, сравнивая проявление закона золотого сечения у Баха и Бетховена, Розенов пишет: "Мы находим у Баха сравнительно более детальную и органическую сплоченность. Закон золотого деления проявляется у него с поразительной точностью в соотношениях крупных и мелких частей как в строгих, так и в свободных формах, что, несомненно, соответствует с характером этого гениального мастера-труженика, сильным, здоровым и уравновешенным, с его глубоко сосредоточенным отношением к работе и детально отделанной манерою письма. У Бетховена проявление закона золотого сечения глубоко логично по отношению к размерам частей формы, но главным образом указывает на силу темперамента этого автора по точности совпадения всех моментов высшего напряжения чувств и разрешения подготовленного ожидания с моментами золотых сечений. У Шопена внутренняя формальная связь сравнительно слабее и проявляется не сплошь, а лишь местами. По силе темперамента он сходен с Бетховеном, но проявление это более внешне и касается чаще изящной нарядности изложения мысли, нежели его внутренней логики. У Моцарта темперамент проявляется сравнительно слабее, закон золотого сечения направлен у него особенно часто к подчеркиванию драматических элементов (психологических контрастов, противопоставлений характеров) и трагических положений. У Глинки мы находим применение данного закона только лишь в широких масштабах при полном почти отсутствии мелочных соответствий, встречающихся так часто у Баха и Шопена".
Вот к каким глубоким эстетическим выводам приводит простейший математический анализ музыки! Слова Розенова о том, что закон золотого сечения "может, по-видимому, явиться в дальнейшем немаловажным вкладом в экспериментальную эстетику", оказались пророческими. А сама экспериментальная эстетика сегодня обрела наконец права гражданства и уверенно набирает силу.
Из начала XX столетия перенесемся теперь в его вторую половину и перейдем к современным исследованиям по экспериментальной эстетике. Начиная с 1952 г. интересные работы по применению математических методов в исследованиях искусства — литературы, живописи, музыки — публикует видный немецкий ученый Вильгельм Фукс. Фукс — прежде всего физик, работающий в области физики плазмы. Однако у этого ученого-энциклопедиста есть и хобби — исследования в области экспериментальной эстетики, часть из которых собрана в интереснейшей монографии Фукса "По всем правилам искусства". В своих работах по экспериментальной эстетике Фукс стремился показать, что точные методы могут быть эффективно применены к исследованию культурного наследия человечества. Хотя со времен Галилея и Ньютона математическое описание стало великим путем познания природы, применение математического метода к искусству до сих пор вызывало недоверие, сарказм или просто неприязнь. Повинна в этом, скорее всего, все та же инерция мышления, "благодаря" которой в свое время отвергались анатомия и демографическая статистика, считавшиеся уделом лишь Бога и короля. Однако, как отмечает Фукс, "выдающиеся успехи точных наук в присущих им сферах привели к тому, что теперь все более соблазнительной представляется идея испытать методы этих наук и в других областях". В силу известного нам свойства математики "называть разные вещи одним и тем же именем" такие исследования помогли бы выявить общие закономерности в разнородных, на первый взгляд, явлениях культуры. Тем не менее сама постановка подобной проблемы была столь нова и необычна, что Фукс вполне справедливо задавал сам себе вопросы: "Можно ли применять абстрактный аппарат точных наук к явлениям культуры? И если да, то имеет ли это смысл? Будут ли получены при этом результаты, столь же объективные, как и в естественных науках? Удастся ли помимо голых чисел, результатов измерений и статистической обработки фактического материала выявить некий род объективных закономерностей, регулярностей, характерных форм явлений?"
Нам представляется, что работы Фукса дали, бесспорно, положительный ответ на эти вопросы, и мы надеемся, что рассматриваемые далее примеры, относящиеся к математическому анализу музыки, будут тому блестящим доказательством.
Вновь обратимся к анализу высоты музыкальных звуков, которому посвящена практически вся вторая часть книги. На примере многочисленных скрипичных произведений Фукс исследовал, как разные авторы в разные эпохи использовали звуковой материал скрипки. Диапазон звучания скрипки простирается от ноты соль малой октавы до ноты до пятой октавы. Считая энгармонически равные звуки (до-диез = ре-бемоль и т. п.) за один звук, в диапазоне соль-до5мы имеем 54 звука. Пронумеруем их, т. е. каждому звуку скрипки поставим в соответствие число i = 1, 2, ..., 54: соль ⇔ i = l, соль-диез = ля-бемоль ⇔ i = , ля ⇔ i = 3 ..., до5 ⇔ i = 54. Подсчитав общее число звуков N в данном произведении, легко найти относительную частоту появления i-ro звука по формуле
Строение фуги ре минор И. С. Баха. Целые числа указывают число четвертей в фуге, дробные — теоретические значения золотых сечений. Золотые пропорции в более крупных частях фуги отмечены фигурными скобками, центры симметрии — кружками. П — проведение, И — интермедия
Далее Розенов, "дабы показать, что приведенный пример не является у Баха исключительным", рассматривает многочисленные прелюдии и фуги из "Хорошо темперированного клавира" Баха, а также оперу Моцарта "Дон-Жуан", финал знаменитой "Лунной" сонаты Бетховена, Фантазию фа минор Шопена, вступление к опере "Тристан и Изольда" Вагнера, увертюру к опере "Руслан и Людмила" Глинки и многие народные песни. Во всех этих произведениях Розенов с замечательной точностью обнаруживает действие закона золотого сечения. "Приведенные мною примеры проявления закона золотого сечения настолько характерны и замечательны,- пишет Розенов,- что исключают всякую возможность отрицания эстетического значения этого закона в музыке". Не правда ли, здесь мы имеем тот самый случай, когда "цифры могут представлять собой культурную и эстетическую ценность"? (См. высказывание Н. Винера в эпиграфе к первой части книги.)
Но помимо установления самого факта наличия закона золотого сечения в музыкальных произведениях и его огромного эстетического значения в музыке математический анализ музыки (даже такой элементарный) позволяет сделать некоторые выводы о характерных особенностях творчества самих композиторов. Так, сравнивая проявление закона золотого сечения у Баха и Бетховена, Розенов пишет: "Мы находим у Баха сравнительно более детальную и органическую сплоченность. Закон золотого деления проявляется у него с поразительной точностью в соотношениях крупных и мелких частей как в строгих, так и в свободных формах, что, несомненно, соответствует с характером этого гениального мастера-труженика, сильным, здоровым и уравновешенным, с его глубоко сосредоточенным отношением к работе и детально отделанной манерою письма. У Бетховена проявление закона золотого сечения глубоко логично по отношению к размерам частей формы, но главным образом указывает на силу темперамента этого автора по точности совпадения всех моментов высшего напряжения чувств и разрешения подготовленного ожидания с моментами золотых сечений. У Шопена внутренняя формальная связь сравнительно слабее и проявляется не сплошь, а лишь местами. По силе темперамента он сходен с Бетховеном, но проявление это более внешне и касается чаще изящной нарядности изложения мысли, нежели его внутренней логики. У Моцарта темперамент проявляется сравнительно слабее, закон золотого сечения направлен у него особенно часто к подчеркиванию драматических элементов (психологических контрастов, противопоставлений характеров) и трагических положений. У Глинки мы находим применение данного закона только лишь в широких масштабах при полном почти отсутствии мелочных соответствий, встречающихся так часто у Баха и Шопена".
Вот к каким глубоким эстетическим выводам приводит простейший математический анализ музыки! Слова Розенова о том, что закон золотого сечения "может, по-видимому, явиться в дальнейшем немаловажным вкладом в экспериментальную эстетику", оказались пророческими. А сама экспериментальная эстетика сегодня обрела наконец права гражданства и уверенно набирает силу.
Из начала XX столетия перенесемся теперь в его вторую половину и перейдем к современным исследованиям по экспериментальной эстетике. Начиная с 1952 г. интересные работы по применению математических методов в исследованиях искусства — литературы, живописи, музыки — публикует видный немецкий ученый Вильгельм Фукс. Фукс — прежде всего физик, работающий в области физики плазмы. Однако у этого ученого-энциклопедиста есть и хобби — исследования в области экспериментальной эстетики, часть из которых собрана в интереснейшей монографии Фукса "По всем правилам искусства". В своих работах по экспериментальной эстетике Фукс стремился показать, что точные методы могут быть эффективно применены к исследованию культурного наследия человечества. Хотя со времен Галилея и Ньютона математическое описание стало великим путем познания природы, применение математического метода к искусству до сих пор вызывало недоверие, сарказм или просто неприязнь. Повинна в этом, скорее всего, все та же инерция мышления, "благодаря" которой в свое время отвергались анатомия и демографическая статистика, считавшиеся уделом лишь Бога и короля. Однако, как отмечает Фукс, "выдающиеся успехи точных наук в присущих им сферах привели к тому, что теперь все более соблазнительной представляется идея испытать методы этих наук и в других областях". В силу известного нам свойства математики "называть разные вещи одним и тем же именем" такие исследования помогли бы выявить общие закономерности в разнородных, на первый взгляд, явлениях культуры. Тем не менее сама постановка подобной проблемы была столь нова и необычна, что Фукс вполне справедливо задавал сам себе вопросы: "Можно ли применять абстрактный аппарат точных наук к явлениям культуры? И если да, то имеет ли это смысл? Будут ли получены при этом результаты, столь же объективные, как и в естественных науках? Удастся ли помимо голых чисел, результатов измерений и статистической обработки фактического материала выявить некий род объективных закономерностей, регулярностей, характерных форм явлений?"
Нам представляется, что работы Фукса дали, бесспорно, положительный ответ на эти вопросы, и мы надеемся, что рассматриваемые далее примеры, относящиеся к математическому анализу музыки, будут тому блестящим доказательством.
Вновь обратимся к анализу высоты музыкальных звуков, которому посвящена практически вся вторая часть книги. На примере многочисленных скрипичных произведений Фукс исследовал, как разные авторы в разные эпохи использовали звуковой материал скрипки. Диапазон звучания скрипки простирается от ноты соль малой октавы до ноты до пятой октавы. Считая энгармонически равные звуки (до-диез = ре-бемоль и т. п.) за один звук, в диапазоне соль-до5мы имеем 54 звука. Пронумеруем их, т. е. каждому звуку скрипки поставим в соответствие число i = 1, 2, ..., 54: соль ⇔ i = l, соль-диез = ля-бемоль ⇔ i = , ля ⇔ i = 3 ..., до5 ⇔ i = 54. Подсчитав общее число звуков N в данном произведении, легко найти относительную частоту появления i-ro звука по формуле
 где ni — частота i-то звука, т. е. число появлений i-го звука в произведении. Например, в струнном квартете ми-бемоль мажор Бетховена, в партии первой скрипки N = 3796, а нота соль первой октавы (i = l) встречается 23 раза (n1 =23). Следовательно, ее относительная частота W1= 23/3796 = 0,006. Ясно, что если самые верхние звуки из диапазона звучания скрипки в произведении не используются, то их частота будет равна нулю. Совокупность (i, Wi) i = l, 2, ..., k называется статистическим распределением, а ломаная линия, отрезки которой соединяют точки статистического распределения, называется полигоном относительных частот. Заметим, что поскольку n1 + n2 + ... + nk = N, то W1 + W2 + ... + Wk = (n1 + n2 +... + nk)/N=l, т. е. сумма всех относительных частот статистического распределения равна 1.
где ni — частота i-то звука, т. е. число появлений i-го звука в произведении. Например, в струнном квартете ми-бемоль мажор Бетховена, в партии первой скрипки N = 3796, а нота соль первой октавы (i = l) встречается 23 раза (n1 =23). Следовательно, ее относительная частота W1= 23/3796 = 0,006. Ясно, что если самые верхние звуки из диапазона звучания скрипки в произведении не используются, то их частота будет равна нулю. Совокупность (i, Wi) i = l, 2, ..., k называется статистическим распределением, а ломаная линия, отрезки которой соединяют точки статистического распределения, называется полигоном относительных частот. Заметим, что поскольку n1 + n2 + ... + nk = N, то W1 + W2 + ... + Wk = (n1 + n2 +... + nk)/N=l, т. е. сумма всех относительных частот статистического распределения равна 1.
 Полигоны относительных частот высоты звуков в партии первой скрипки. Уже по внешнему виду статистических распределений можно заключить, что композиторы-додекафонисты Берг и Веберн применяли совершенно иные правила композиции, чем Бетховен и Рихард Штраус
На рисунке построены полигоны относительных частот высоты звуков в партии первой скрипки для четырех музыкальных произведений: струнного квартета ми-бемоль мажор Бетховена (1809) (партия первой скрипки); симфонической поэмы Рихарда Штрауса "Тиль Уленшпигель" (1890) (партия первой скрипки); первой части скрипичного концерта Берга (1935) и струнного трио Веберна (1927) (партия скрипки). Одного взгляда на рисунок достаточно для того, чтобы понять: первые два произведения — Бетховена и Р. Штрауса, при всем их различии, принадлежат к одному типу музыки, а два последних — Берга и Веберна — к совершенно другому типу (хотя они также отличаются, между собой). Знатоки музыки воспримут этот факт как должное: ведь по отношению к Бетховену и Р. Штраусу Берг и Веберн — представители принципиально иного направления в музыке, так называемой додекафонной* или атональной музыки. Поскольку атональная музыка отрицает главную роль тоники и устойчивых звуков в ладу и считает все звуки равноправными, то и статистическое распределение высот звуков в атональной музыке должно быть более гладким по сравнению с тональной музыкой, где одни звуки являются явно предпочтительными (пики на полигоне относительных частот), а другие употребляются редко ("провалы" на полигоне).
* (Додекафония (от греч. dodeka — двенадцать и phone — звук) — метод музыкальной композиции, основанный на отрицании ладовых связей между звуками. В додекафонии все 12 звуков хроматической гаммы считаются абсолютно равными (откуда и происходит название) без различия устойчивых и неустойчивых звуков и без выделения тоники. Поэтому додекафонию называют также атональной музыкой. Метод додекафонии был разработан и внедрен австрийским композитором Арнольдом Шёнбергом (1874-1951). Альбан Берг (1885-1935) и Антон фон Веберн (1883- 1945) — ученики и последователи Шёнберга.)
Итак, тот факт, что Берг и Веберн — представители одного направления в музыке, а Бетховен и Р. Штраус — другого, нашел яркое выражение в статистических распределениях высот звуков у этих композиторов. Заметим, что Берг и Веберн, будучи пылкими последователями Шёнберга, сочиняли свою музыку по сходным и весьма строгим формальным правилам. Поэтому их статистические распределения так похожи, хотяу с другой стороны, и различаются тонкими деталями, которые характеризуют индивидуальные черты каждого композитора. Таким образом, уже простая статистика высот звуков позволяет выявить, с одной стороны, принадлежность автора к тому или иному направлению в музыке, а с другой — увидеть тонкие черты различия, характерные для конкретных произведений и конкретных композиторов. Однако пока мы ограничивались лишь качественными выводами. Посмотрим, нельзя ли извлечь из статистических распределений какие-либо количественные характеристики.
Всякое статистическое распределение (xi, Wi) i = l, 2, ..., k обладает двумя важнейшими числовыми характеристиками: эмпирической средней и эмпирической дисперсией. Эмпирической средней
Полигоны относительных частот высоты звуков в партии первой скрипки. Уже по внешнему виду статистических распределений можно заключить, что композиторы-додекафонисты Берг и Веберн применяли совершенно иные правила композиции, чем Бетховен и Рихард Штраус
На рисунке построены полигоны относительных частот высоты звуков в партии первой скрипки для четырех музыкальных произведений: струнного квартета ми-бемоль мажор Бетховена (1809) (партия первой скрипки); симфонической поэмы Рихарда Штрауса "Тиль Уленшпигель" (1890) (партия первой скрипки); первой части скрипичного концерта Берга (1935) и струнного трио Веберна (1927) (партия скрипки). Одного взгляда на рисунок достаточно для того, чтобы понять: первые два произведения — Бетховена и Р. Штрауса, при всем их различии, принадлежат к одному типу музыки, а два последних — Берга и Веберна — к совершенно другому типу (хотя они также отличаются, между собой). Знатоки музыки воспримут этот факт как должное: ведь по отношению к Бетховену и Р. Штраусу Берг и Веберн — представители принципиально иного направления в музыке, так называемой додекафонной* или атональной музыки. Поскольку атональная музыка отрицает главную роль тоники и устойчивых звуков в ладу и считает все звуки равноправными, то и статистическое распределение высот звуков в атональной музыке должно быть более гладким по сравнению с тональной музыкой, где одни звуки являются явно предпочтительными (пики на полигоне относительных частот), а другие употребляются редко ("провалы" на полигоне).
* (Додекафония (от греч. dodeka — двенадцать и phone — звук) — метод музыкальной композиции, основанный на отрицании ладовых связей между звуками. В додекафонии все 12 звуков хроматической гаммы считаются абсолютно равными (откуда и происходит название) без различия устойчивых и неустойчивых звуков и без выделения тоники. Поэтому додекафонию называют также атональной музыкой. Метод додекафонии был разработан и внедрен австрийским композитором Арнольдом Шёнбергом (1874-1951). Альбан Берг (1885-1935) и Антон фон Веберн (1883- 1945) — ученики и последователи Шёнберга.)
Итак, тот факт, что Берг и Веберн — представители одного направления в музыке, а Бетховен и Р. Штраус — другого, нашел яркое выражение в статистических распределениях высот звуков у этих композиторов. Заметим, что Берг и Веберн, будучи пылкими последователями Шёнберга, сочиняли свою музыку по сходным и весьма строгим формальным правилам. Поэтому их статистические распределения так похожи, хотяу с другой стороны, и различаются тонкими деталями, которые характеризуют индивидуальные черты каждого композитора. Таким образом, уже простая статистика высот звуков позволяет выявить, с одной стороны, принадлежность автора к тому или иному направлению в музыке, а с другой — увидеть тонкие черты различия, характерные для конкретных произведений и конкретных композиторов. Однако пока мы ограничивались лишь качественными выводами. Посмотрим, нельзя ли извлечь из статистических распределений какие-либо количественные характеристики.
Всякое статистическое распределение (xi, Wi) i = l, 2, ..., k обладает двумя важнейшими числовыми характеристиками: эмпирической средней и эмпирической дисперсией. Эмпирической средней  называется среднее арифметическое значений хi, статистического распределения с учетом их частот п" т. е.
называется среднее арифметическое значений хi, статистического распределения с учетом их частот п" т. е.
 (12.5)
(12.5)
Эмпирическая средняя характеризует "среднюю величину" значений статистического распределения. Однако помимо "средней величины" важно знать, насколько "разбросаны" значения ж, относительно этой средней величины, т. е. какова дисперсия (от лат. dispersus — рассыпанный) статистического рарпределения. Назовем разность xi —
 отклонением значения xi от эмпирической средней
отклонением значения xi от эмпирической средней  . Легко видеть, что сумма всех отклонений с учетом их частот ni, равна нулю:
. Легко видеть, что сумма всех отклонений с учетом их частот ni, равна нулю:
 и, значит, не может быть взята в качестве характеристики рассеяния параметров статистического распределения. Поэтому в качестве характеристики разброса параметров xi берут среднее арифметическое квадратов отклонений. Итак, эмпирической дисперсией D называется среднее арифметическое квадратов отклонений значений хi, от их эмпирической средней
и, значит, не может быть взята в качестве характеристики рассеяния параметров статистического распределения. Поэтому в качестве характеристики разброса параметров xi берут среднее арифметическое квадратов отклонений. Итак, эмпирической дисперсией D называется среднее арифметическое квадратов отклонений значений хi, от их эмпирической средней  с учетом частот ni, т. е.
с учетом частот ni, т. е.
 (12.6)
Для вычисления эмпирической дисперсии существует также более практичная формула
(12.6)
Для вычисления эмпирической дисперсии существует также более практичная формула
 (12.7)
т. е. эмпирическая дисперсия равна эмпирическому среднему квадратов значений статистического распределения минус квадрат эмпирической средней. Наконец, чтобы характеристики рассеяния имели ту же размерность, что и значения xi статистического распределения, вместо дисперсии рассматривают среднее квадратическое отклонение
(12.7)
т. е. эмпирическая дисперсия равна эмпирическому среднему квадратов значений статистического распределения минус квадрат эмпирической средней. Наконец, чтобы характеристики рассеяния имели ту же размерность, что и значения xi статистического распределения, вместо дисперсии рассматривают среднее квадратическое отклонение
 (12.8)
Среднее квадратическое отклонение показывает, насколько узко или насколько широко распределены вокруг эмпирического среднего
(12.8)
Среднее квадратическое отклонение показывает, насколько узко или насколько широко распределены вокруг эмпирического среднего  значения статистического распределения xi.
значения статистического распределения xi.
 Таблица 3. Статистическое распределение (xi = i, Wi) высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена. Для расчета дисперсии приведены также значения xi2 = i2
В качестве примера найдем эмпирическую среднюю, эмпирическую дисперсию и среднее квадратическое отклонение для статистического распределения высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена (см. с. 168). Выпишем значения xi = i, xi2 = i2 и Wi (i=l, 2, ..., 54) в виде таблицы 3. Легко проверить, что
Таблица 3. Статистическое распределение (xi = i, Wi) высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена. Для расчета дисперсии приведены также значения xi2 = i2
В качестве примера найдем эмпирическую среднюю, эмпирическую дисперсию и среднее квадратическое отклонение для статистического распределения высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена (см. с. 168). Выпишем значения xi = i, xi2 = i2 и Wi (i=l, 2, ..., 54) в виде таблицы 3. Легко проверить, что
 Подставляя данные таблицы 3 в формулы (12.6), (12.7) и (12.8), находим
Подставляя данные таблицы 3 в формулы (12.6), (12.7) и (12.8), находим
 Итак, для струнного квартета Бетховена эмпирическая средняя
Итак, для струнного квартета Бетховена эмпирическая средняя  = 19,25, т. е. "средним" звуком произведения является ре-бемоль второй октавы. Это еще мало о чем говорит. Вторая характеристика — среднее квадратическое отклонение — означает, что средний разброс звуков в произведении относительно ре-бемоль составляет ± 8 звуков, т. е. наиболее употребимые звуки произведения находятся в диапазоне 11≤i≤27, или от фа1 до ля2. Среднее квадратическое отклонение высоты звуков музыкального произведения оказалось чрезвычайно эффективной характеристикой, позволяющей найти общие закономерности в развитии всей музыки. Остановимся на этом подробнее.
Как уже отмечали, основной целью работ Фукса было не просто найти какие-либо числовые характеристики произведений искусства, а выявить на основании этих характеристик закономерности общего порядка. С этой целью Фуксом были составлены статистические распределения высоты звуков в партиях первой скрипки большого числа произведений за период почти в пятьсот лет. Были определены числовые характеристики этих распределений, и прежде всего среднее квадратическое отклонение. Анализ поведения среднего квадратического отклонения дал блестящий результат: среднее квадратическое отклонение за последние 500 лет истории европейской музыки монотонно возрастает. Это уже есть не что иное, как закон развития музыки!
В таблице 4 приведены результаты исследований Фукса. Здесь представлены произведения, написанные с 1530 г. по 1960 г. Для каждого произведения было составлено статистическое распределение высоты звуков в партии первой скрипки, аналогичное таблице 3. Затем были определены средние квадратические отклонения в этих распределениях (найденное нами значение σ = 7,8 для струнного квартета ми-бемоль мажор Бетховена находится в соответствующем месте таблицы 4). Наконец, для каждого периода в истории развития музыки было вычислено среднее арифметическое о средних квадратических отклонений отдельных произведений. Разбиение на периоды проведено в соответствии с существовавшими в музыке направлениями. Так, в таблице 4 полифония строгого стиля представленапроизведениями Вилларта, Модены, Палестрины, Хаслера, Шейна и Розенмюллера; полифония свободного стиля (барокко) — произведениями Коре л ли, Вивальди и Баха; классицизм — произведениями Моцарта, Бетховена и Шпора; романтизм — произведениями Шуберта, Шумана, Брамса, Р. Штрауса и Чайковского; неоромантизм — произведениями Хиндемита, Бартока и Эгка; додекафония — произведениями Шёнберга, Веберна, Берга и Ноно. Поэтому естественно, что одни периоды в таблице 4 далеко отстоят друг от друга, а другие — пересекаются. Достаточно одного взгляда на первый и последний столбцы таблицы 4, чтобы увидеть закономерность: за прошедшие 500 лет значение
= 19,25, т. е. "средним" звуком произведения является ре-бемоль второй октавы. Это еще мало о чем говорит. Вторая характеристика — среднее квадратическое отклонение — означает, что средний разброс звуков в произведении относительно ре-бемоль составляет ± 8 звуков, т. е. наиболее употребимые звуки произведения находятся в диапазоне 11≤i≤27, или от фа1 до ля2. Среднее квадратическое отклонение высоты звуков музыкального произведения оказалось чрезвычайно эффективной характеристикой, позволяющей найти общие закономерности в развитии всей музыки. Остановимся на этом подробнее.
Как уже отмечали, основной целью работ Фукса было не просто найти какие-либо числовые характеристики произведений искусства, а выявить на основании этих характеристик закономерности общего порядка. С этой целью Фуксом были составлены статистические распределения высоты звуков в партиях первой скрипки большого числа произведений за период почти в пятьсот лет. Были определены числовые характеристики этих распределений, и прежде всего среднее квадратическое отклонение. Анализ поведения среднего квадратического отклонения дал блестящий результат: среднее квадратическое отклонение за последние 500 лет истории европейской музыки монотонно возрастает. Это уже есть не что иное, как закон развития музыки!
В таблице 4 приведены результаты исследований Фукса. Здесь представлены произведения, написанные с 1530 г. по 1960 г. Для каждого произведения было составлено статистическое распределение высоты звуков в партии первой скрипки, аналогичное таблице 3. Затем были определены средние квадратические отклонения в этих распределениях (найденное нами значение σ = 7,8 для струнного квартета ми-бемоль мажор Бетховена находится в соответствующем месте таблицы 4). Наконец, для каждого периода в истории развития музыки было вычислено среднее арифметическое о средних квадратических отклонений отдельных произведений. Разбиение на периоды проведено в соответствии с существовавшими в музыке направлениями. Так, в таблице 4 полифония строгого стиля представленапроизведениями Вилларта, Модены, Палестрины, Хаслера, Шейна и Розенмюллера; полифония свободного стиля (барокко) — произведениями Коре л ли, Вивальди и Баха; классицизм — произведениями Моцарта, Бетховена и Шпора; романтизм — произведениями Шуберта, Шумана, Брамса, Р. Штрауса и Чайковского; неоромантизм — произведениями Хиндемита, Бартока и Эгка; додекафония — произведениями Шёнберга, Веберна, Берга и Ноно. Поэтому естественно, что одни периоды в таблице 4 далеко отстоят друг от друга, а другие — пересекаются. Достаточно одного взгляда на первый и последний столбцы таблицы 4, чтобы увидеть закономерность: за прошедшие 500 лет значение  возросло от 3,7 до 10,8, т. е. по мере развития музыки значение σвозрастает.
возросло от 3,7 до 10,8, т. е. по мере развития музыки значение σвозрастает.
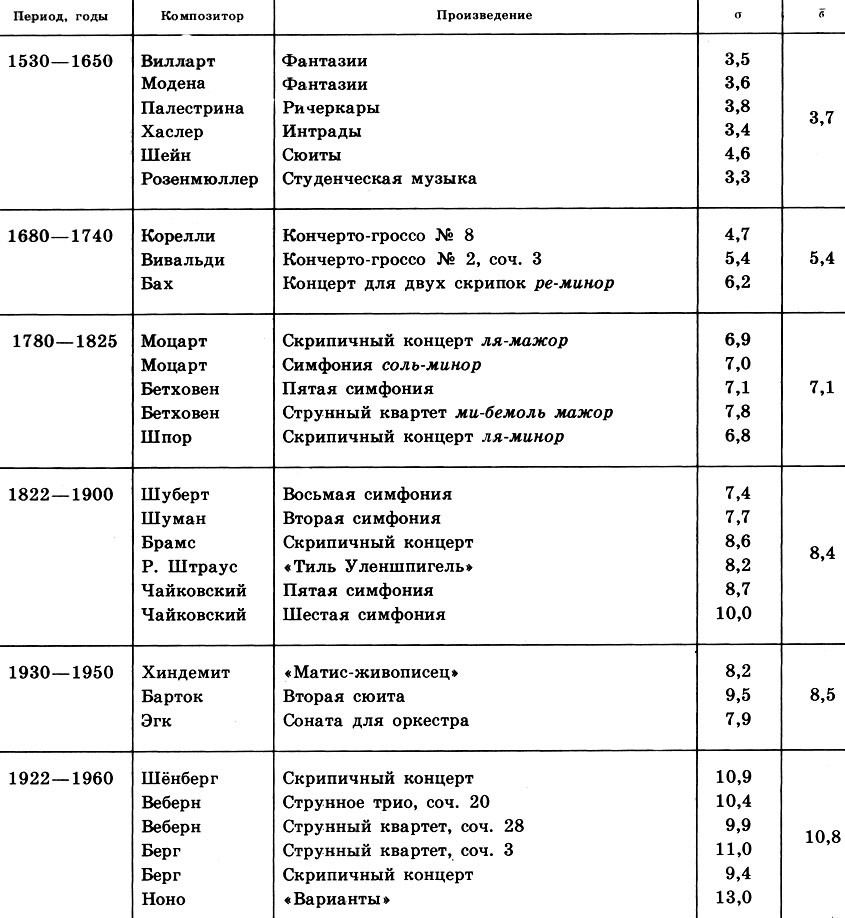 Таблица 4. Усредненные значения о среднего квадратического отклонения высоты звуков музыкального произведения отражают определенный закон развития музыки: за последние 500 лет значение а монотонно возрастает
"Естественно,- отмечал Фукс,- музыковед в связи с нашими распределениями частот может поставить много критически окрашенных вопросов. Так, степень важности партии первой скрипки может быть очень различной в разных частях сочинения: в одной части она может решающим образом определять мелодию, ритм и гармонию, а в других местах сочинения играть роль, в музыкальном отношении подчиненную. Вопросы подобного рода, а также и другие важные обстоятельства должны, естественно, учитываться в тех ветвях музыковедения, которые связаны с количест венными исследованиями". Все это, разумеется, так, и у математического музыковедения непочатый край проблем. Не нельзя не видеть подкупающей простоты и универсальности найденных (пусть простейших) математических закономерностей. Зная эти закономерности, можно, например, подсчитать значение σ для произведения какого-то неизвестного нам автора и, пользуясь данными таблицы 4, отнести это произведение к тому или иному музыкальному направлению. Это будет уже некая "музыкальная криминалистика", построенная на базе математики. В подобной всеобщности и заключается могущество математического метода.
Таблица 4. Усредненные значения о среднего квадратического отклонения высоты звуков музыкального произведения отражают определенный закон развития музыки: за последние 500 лет значение а монотонно возрастает
"Естественно,- отмечал Фукс,- музыковед в связи с нашими распределениями частот может поставить много критически окрашенных вопросов. Так, степень важности партии первой скрипки может быть очень различной в разных частях сочинения: в одной части она может решающим образом определять мелодию, ритм и гармонию, а в других местах сочинения играть роль, в музыкальном отношении подчиненную. Вопросы подобного рода, а также и другие важные обстоятельства должны, естественно, учитываться в тех ветвях музыковедения, которые связаны с количест венными исследованиями". Все это, разумеется, так, и у математического музыковедения непочатый край проблем. Не нельзя не видеть подкупающей простоты и универсальности найденных (пусть простейших) математических закономерностей. Зная эти закономерности, можно, например, подсчитать значение σ для произведения какого-то неизвестного нам автора и, пользуясь данными таблицы 4, отнести это произведение к тому или иному музыкальному направлению. Это будет уже некая "музыкальная криминалистика", построенная на базе математики. В подобной всеобщности и заключается могущество математического метода.
 Матрицы переходов в парти первой скрипки (площадь ее ответствующего кружка прс порциональна частоте переход от одного звука к другому). Легко видеть, насколько закономерен характер переходов музыке Баха и Бетховена и насколько он близок к случайному в музыке Веберна
Сделаем еще один, последний, шаг в нашем кратком знакомстве с математическим анализом музыки. Очевидно, что статистические распределения высоты звуков показывают лишь, сколько раз данный звук встречается в музыкальном произведении. Но ведь главным элементом музыки является мелодия — художественно осмысленная последовательность звуков в произведении. Информация же о последовательном расположении звуков в статистическом распределении высот теряется. Получить такую информацию нетрудно с помощью так называемых матриц перехода. Матрица перехода представляет из себя квадратную таблицу, по горизонтальной и вертикальной осям которой отложены все звуки из диапазона звучания музыкального произведения. На пересечении строк и столбцов матрицы перехода ставится частота, с которой в данном произведении совершается переход от одного звука к другому.
На рисунке показаны матрицы переходов, составленные Фуксом, для знакомых нам произведений (взяты партии первой скрипки): концерта для двух скрипок ре-минор Баха, струнного квартета ми-бемоль мажор Бетховена и струнного трио Веберна. Четвертая матрица представляет частоты перехода для случайной последовательности звуков, которая была образована из того же звукового материала, что и сочинение Веберна. Для наглядности частота переходов характеризуется не цифрами, а площадью кружка (чем больше частота перехода, тем больше площадь соответствующего кружка). Простое сопоставление приведенных матриц убеждает в том, насколько строгими и закономерными являются переходы у Баха и Бетховена и насколько они близки к случайным у Веберна. Эти закономерности также можно описать численно с помощью так называемых коэффициентов корреляции, которые служат своеобразной "мерой беспорядка". Для последовательности случайных чисел, т. е. при полном беспорядке, коэффициент корреляции практически равен нулю. Наоборот, при сильной зависимости между элементами коэффициент корреляции близок к единице. В приведенных примерах коэффициент корреляции k для "случайной музыки" равен 0,03 (для трио Веберна й = 0,06), т. е. музыка Веберна близка к "случайной музыке". Напротив, в концерте для двух скрипок Баха k = 0,61, а в струнном квартете Бетховена k = 0,76, т. е. музыка Бетховена является наиболее "закономерной".
Свой анализ матриц перехода Фукс заканчивает следующим замечанием: "Для читателей, интересующихся музыкой, стоит заметить, что из всех возможных переходов используется только небольшая их часть: у Баха 23%, у Бетховена 16% и у Веберна 24% всех возможных связей в рассматриваемом диапазоне звуков. Однако уже из этих простых фактов, к которым можно было бы добавить и другие, вытекает следующее заключение. Возможности музыки, использующей классические инструменты — сочиненной по правилам контрапункта, додекафонной музыки или по каким-нибудь другим правилам,- еще никоим образом не исчерпаны".
Продолжая мысль Фукса, мы можем в заключение сказать, что возможности математических методов анализа музыки и произведений искусства вообще не только не исчерпаны, но представляют собой почти нетронутую целину для исследователя. Экспериментальная эстетика ждет еще своего Ньютона.
Матрицы переходов в парти первой скрипки (площадь ее ответствующего кружка прс порциональна частоте переход от одного звука к другому). Легко видеть, насколько закономерен характер переходов музыке Баха и Бетховена и насколько он близок к случайному в музыке Веберна
Сделаем еще один, последний, шаг в нашем кратком знакомстве с математическим анализом музыки. Очевидно, что статистические распределения высоты звуков показывают лишь, сколько раз данный звук встречается в музыкальном произведении. Но ведь главным элементом музыки является мелодия — художественно осмысленная последовательность звуков в произведении. Информация же о последовательном расположении звуков в статистическом распределении высот теряется. Получить такую информацию нетрудно с помощью так называемых матриц перехода. Матрица перехода представляет из себя квадратную таблицу, по горизонтальной и вертикальной осям которой отложены все звуки из диапазона звучания музыкального произведения. На пересечении строк и столбцов матрицы перехода ставится частота, с которой в данном произведении совершается переход от одного звука к другому.
На рисунке показаны матрицы переходов, составленные Фуксом, для знакомых нам произведений (взяты партии первой скрипки): концерта для двух скрипок ре-минор Баха, струнного квартета ми-бемоль мажор Бетховена и струнного трио Веберна. Четвертая матрица представляет частоты перехода для случайной последовательности звуков, которая была образована из того же звукового материала, что и сочинение Веберна. Для наглядности частота переходов характеризуется не цифрами, а площадью кружка (чем больше частота перехода, тем больше площадь соответствующего кружка). Простое сопоставление приведенных матриц убеждает в том, насколько строгими и закономерными являются переходы у Баха и Бетховена и насколько они близки к случайным у Веберна. Эти закономерности также можно описать численно с помощью так называемых коэффициентов корреляции, которые служат своеобразной "мерой беспорядка". Для последовательности случайных чисел, т. е. при полном беспорядке, коэффициент корреляции практически равен нулю. Наоборот, при сильной зависимости между элементами коэффициент корреляции близок к единице. В приведенных примерах коэффициент корреляции k для "случайной музыки" равен 0,03 (для трио Веберна й = 0,06), т. е. музыка Веберна близка к "случайной музыке". Напротив, в концерте для двух скрипок Баха k = 0,61, а в струнном квартете Бетховена k = 0,76, т. е. музыка Бетховена является наиболее "закономерной".
Свой анализ матриц перехода Фукс заканчивает следующим замечанием: "Для читателей, интересующихся музыкой, стоит заметить, что из всех возможных переходов используется только небольшая их часть: у Баха 23%, у Бетховена 16% и у Веберна 24% всех возможных связей в рассматриваемом диапазоне звуков. Однако уже из этих простых фактов, к которым можно было бы добавить и другие, вытекает следующее заключение. Возможности музыки, использующей классические инструменты — сочиненной по правилам контрапункта, додекафонной музыки или по каким-нибудь другим правилам,- еще никоим образом не исчерпаны".
Продолжая мысль Фукса, мы можем в заключение сказать, что возможности математических методов анализа музыки и произведений искусства вообще не только не исчерпаны, но представляют собой почти нетронутую целину для исследователя. Экспериментальная эстетика ждет еще своего Ньютона.
III. Математика и архитектура
О смертный! как мечта из камня я прекрасна! .......................................... В лазури царствую я сфинксом непостижимым; Как лебедь, я бела и холодна, как снег; Презрев движение, любуюсь неподвижным; Вовек я не смеюсь, не плачу я вовек.Ш. Бодлер
 Архитектура — удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника и искусство. Только соразмерное, гармоническое единство этих начал делает возводимое человеком сооружение памятником архитектуры, неподвластным времени, подобно памятникам литературы, ваяния, музыки. Если же какой-то из элементов зодчества — наука, техника или искусство — начинает подавлять остальные, то истинная архитектура скатывается на одно из тупиковых направлений, именуемых функционализмом, техницизмом, эклектизмом или еще каким-нибудь "измом".
Но архитектура не только древнейшая сфера человеческой деятельности, не только "искусство строить", как определял ее еще Альберти, но и результат такой деятельности. Архитектура — это совокупность зданий и сооружений, это пространство, созданное человеком и необходимое для его жизни и деятельности. Эта искусственная среда, воздвигнутая человеческими руками, является непременным условием существования и развития общества. Вот почему архитектура зарождается вместе с человеком и сопровождает человечество на всем его историческом пути. По образному выражению Гоголя, "...архитектура — тоже летопись мира: она говорит, когда уже молчат и песни, и предания и когда уже ничто не говорит о погибшем народе. Пусть же она хоть отрывками является среди наших городов в таком виде, в каком она была при отжившем уже народе, чтобы при взгляде на нее осенила нас мысль о минувшей жизни, и погрузила бы нас в его быт, в его привычки и степень понимания, и вызывала бы у нас благодарность за его существование, бывшее ступенью нашего собственного возвышения". Да, зодчество — это и "каменная летопись истории". Без греческих и римских развалин, без узких средневековых улочек и таинственных замков, без кружева готических соборов и очарования древнерусских храмов наши представления о прошедших эпохах были бы невообразимо бедными.
Архитектура бифункциональна: она призвана отвечать не только эстетическим, но и утилитарным требованиям, она должна создавать не только прекрасное, но и полезное. Интуиция и расчет — непременные спутники зодчего.
Архитектура триедина: она извечно сочетает в себе логику ученого, ремесло мастера и вдохновение художника. "Прочность — польза — красота" — такова знаменитая формула единого архитектурного целого, выведенная два тысячелетия тому назад древнеримским теоретиком зодчества Витрувием (I в. до н. э.). Вот почему архитектура как нельзя более отвечает теме нашего разговора: взаимодействие науки и искусства, математика и искусство.
Роль математики в формировании "прочности" и "пользы" архитектуры очевидна. Она такова же, какова роль математики в естествознании и технике, в которых со времен Галилея "царице всех наук" принадлежат только первые
роли. Вот почему мы почти не будем касаться этой темы, которая могла бы составить содержание увлекательной книги. Нас же будет интересовать "неочевидный" вклад математики в красоту архитектуры, т. е. для нас архитектура будет прежде всего искусством. Но и в этой "надводной" части архитектурного айсберга математике, и прежде всего геометрии, принадлежит выдающаяся роль, о чем и пойдет речь в настоящей части книги.
Архитектура — удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника и искусство. Только соразмерное, гармоническое единство этих начал делает возводимое человеком сооружение памятником архитектуры, неподвластным времени, подобно памятникам литературы, ваяния, музыки. Если же какой-то из элементов зодчества — наука, техника или искусство — начинает подавлять остальные, то истинная архитектура скатывается на одно из тупиковых направлений, именуемых функционализмом, техницизмом, эклектизмом или еще каким-нибудь "измом".
Но архитектура не только древнейшая сфера человеческой деятельности, не только "искусство строить", как определял ее еще Альберти, но и результат такой деятельности. Архитектура — это совокупность зданий и сооружений, это пространство, созданное человеком и необходимое для его жизни и деятельности. Эта искусственная среда, воздвигнутая человеческими руками, является непременным условием существования и развития общества. Вот почему архитектура зарождается вместе с человеком и сопровождает человечество на всем его историческом пути. По образному выражению Гоголя, "...архитектура — тоже летопись мира: она говорит, когда уже молчат и песни, и предания и когда уже ничто не говорит о погибшем народе. Пусть же она хоть отрывками является среди наших городов в таком виде, в каком она была при отжившем уже народе, чтобы при взгляде на нее осенила нас мысль о минувшей жизни, и погрузила бы нас в его быт, в его привычки и степень понимания, и вызывала бы у нас благодарность за его существование, бывшее ступенью нашего собственного возвышения". Да, зодчество — это и "каменная летопись истории". Без греческих и римских развалин, без узких средневековых улочек и таинственных замков, без кружева готических соборов и очарования древнерусских храмов наши представления о прошедших эпохах были бы невообразимо бедными.
Архитектура бифункциональна: она призвана отвечать не только эстетическим, но и утилитарным требованиям, она должна создавать не только прекрасное, но и полезное. Интуиция и расчет — непременные спутники зодчего.
Архитектура триедина: она извечно сочетает в себе логику ученого, ремесло мастера и вдохновение художника. "Прочность — польза — красота" — такова знаменитая формула единого архитектурного целого, выведенная два тысячелетия тому назад древнеримским теоретиком зодчества Витрувием (I в. до н. э.). Вот почему архитектура как нельзя более отвечает теме нашего разговора: взаимодействие науки и искусства, математика и искусство.
Роль математики в формировании "прочности" и "пользы" архитектуры очевидна. Она такова же, какова роль математики в естествознании и технике, в которых со времен Галилея "царице всех наук" принадлежат только первые
роли. Вот почему мы почти не будем касаться этой темы, которая могла бы составить содержание увлекательной книги. Нас же будет интересовать "неочевидный" вклад математики в красоту архитектуры, т. е. для нас архитектура будет прежде всего искусством. Но и в этой "надводной" части архитектурного айсберга математике, и прежде всего геометрии, принадлежит выдающаяся роль, о чем и пойдет речь в настоящей части книги.
13. Архитектура = (наука + техника)*искусство
Все [в архитектуре] ... должно делать, принимая во внимание прочность, пользу и красоту.М. Витрувий
Архитектура, что за вещь? Она есть строение естественное и художественное."Возвышенное чудо мира! Дух мой возносится в священном восторге, когда с удивлением взираю на твое неизмеримое великолепие. Своею немой бесконечностью ты пробуждаешь мысль за мыслью и не даешь успокоиться восхищенной душе". Так восторженно писал об архитектурном облике собора Св. Петра в Риме Вильгельм Генрих Ваккенродер. Однако, если бы Ваккенродер был знаком с инженерной (внутренней) красотой собора, которая прячется за красотою его внешних архитектурных форм, ему бы пришлось повторить свой взволнованный монолог дважды. В самом деле, строительство каменного купола собора диаметром 42 м представляло собой сложнейшую техническую задачу. Достаточно сказать, что за всю историю человечества построено только 4 сооружения, имеющих каменные купола диаметром более 40 м! Это Пантеон в Риме (123), собор Санта-Мария дель Фьоре во Флоренции (1434), собор Св. Петра в Риме (1590) и мавзолей Гол-Гумбаз в Биджапуре (Индия, 1656)[23]. Фундамент собора Св. Петра был заложен в 1506 г., сооружение купола закончено в 1590 г., а грандиозный ансамбль площади собора со знаменитой 4-рядной колоннадой был завершен в 1663 г. На протяжении этих 150 лет строительством собора руководили такие замечательные художники и архитекторы, как Браманте, Рафаэль, Микеланджело, Виньола, Бернини. Хотя Микеланджело было 72 года, когда в 1547 г. он был назначен на должность архитектора собора, великий Буонарроти фактически заново разработал проект купола собора и еще 17 лет вплоть до своей смерти плодотворно руководил строительством этого грандиозного сооружения.Ф. Каржавин
 Собор Св. Петра в Риме (Ватикан). 1506-1663. Одно из лучших мировых купольных сооружений, главный храм католической церкви. В 42-метровом каменном куполе собора навеки материализовалась неиссякаемая энергия его создателя — великого Микеланджело
История строительства и дальнейшего существования собора полна драматических событий. Так, в 1740 г., через 150 лет после сооружения купола, некоторые трещины, неизбежно возникающие в кладке, расширились до угрожающих размеров. Это событие стимулировало новые теоретические исследования. В 1748 г. профессор экспериментальной философии (т. е. физики) университета в Падуе Джиованни Полени, опираясь на работы математика Стирлинга и механика Ла Гира, математически доказал, что купол собора находится в состоянии статического равновесия и появившиеся трещины угрозы не представляют. Прошедшие с тех пор 200 лет являются лучшим подтверждением справедливости математических расчетов Полени. К сожалению, теория каменных куполов была полностью завершена только в XX веке, когда такие купола превратились в отжившую конструкцию и их перестали строить.
История собора Св. Петра в Риме (а подобную историю имеет каждое выдающееся архитектурное сооружение) убеждает в том, что зодчество представляет собой сложный узел научных, технических и эстетических проблем. Архитектура парадоксально соединяет в себе результаты строительной деятельности и художественного творчества, инженерный расчет, научное знание и художественное озарение.
"Прочность — польза — красота",- говорит формула архитектуры Витрувия. Прочность не случайно стоит в ней на первом месте. Вся история архитектуры есть история созидания прочности, история борьбы с действием всемогущей силы тяготения. Недаром самый первый строительный кодекс, составленный в царствование вавилонского царя Хаммурапи за 1800 лет до нашей эры, гласит: "Если строитель построил дом для человека, и работа его не крепка, и дом, построенный им, обвалился и убил владельца, то строитель сей должен быть казнен". (Эта запись вытесана на колонне, ныне хранящейся в парижском Лувре.) Мелькали годы, проходили эпохи, менялись строительные материалы, а значит, и конструкции архитектурных сооружений, но всегда соображения прочности были определяющими в выборе новой архитектурной конструкции.
Но если относительно "прочности" у архитекторов никогда сомнений не возникало, то "польза" и "красота" являются предметом постоянных дискуссий. Впрочем, дискуссии о красоте и целесообразности (пользе) не являются привилегией одних только архитекторов. Это общеэстетическая проблема, уходящая корнями в седую древность. "Прекрасно то, что хорошо служит данной цели",- учит Сократ. "Дома строят для того, чтобы в них жить, а не для того, чтобы ими любоваться",- вторил Сократу через 2000 лет Фрэнсис Бэкон. Увлечение формулой Бэкона еще через 300 лет привело к тому, что безликие фасады со скоростью произрастания сорняков расплодились по всему земному шару. Невозможно стало отличить не только два новых дома, но и два новых района и даже два новых города. Архитектурная безликость стала притчей во языцех, сделав возможными смешные коллизии типа той, что произошла в пьесе Э. Брагинского и Э. Рязанова "С легким паром!". Надо сказать, что на сегодняшний день ошибочность увлечения одной только пользой в архитектуре осознана всеми и делаются серьезные шаги по преодолению этого заблуждения.
Есть и другая крайность во взглядах На соотношение пользы и красоты. Известный нам Джон Рескин говорил: "Искусство — это то, что бесполезно. Как только вещь становится полезной, она более не может быть красивой". Англичанина Рескина поддерживал француз Теофил Готье: "По-настоящему прекрасным является только то, что ничему не служит". По-видимому, те же взгляды на соотношение пользы и красоты имели и фараоны Древнего царства, жившие за ,4500 лет до Рескина и Готье. Во всяком случае, построенные ими пирамиды останутся в истории человечества непревзойденным образцом самого грандиозного и самого бесполезного сооружения. Только в условиях рабовладельческого строя возможна была такая бессмысленная трата человеческой энергии, когда сто тысяч рабов в течение двадцати лет возводили гробницу для одного из смертных — фараона Хеопса. Внутренний, полезный объем пирамиды настолько ничтожен, что ее вообще с трудом можно отнести к архитектурному сооружению.
Зато прочность пирамид недосягаема. Желая прославить своего фараона в веках, древнеегипетские зодчие из всех геометрических тел выбрали именно пирамиду. Выбор этот не случаен, ибо в условиях земного тяготения пирамида является наиболее устойчивой конструкцией, способной существовать в веках без риска обвалиться или рассыпаться. Главное правило устойчивости конструкции — уменьшение ее массы по мере увеличения высоты над землей — выражено в пирамиде с предельной ясностью и симметрией. Рациональность, "полезность" геометрической формы пирамиды заставляют забыть о ее утилитарной бесполезности. Именно эта геометрически оправданная форма пирамиды, подчеркнутая ее циклопическими размерами и точной системой пропорций, придает пирамиде ни с чем не сравнимую выразительность, особую красоту и величие, вызывает ощущение вечности, бессмертия, мудрости и покоя.
"Сорок веков смотрят на вас с высоты этих пирамид" — эти красивые слова генерал Бонапарт произнес перед сражением при египетских пирамидах 21 июля 1798 г. Однако отнюдь не философские размышления, а сиюминутные честолюбивые планы вызывал у генерала вид четырехтысячелетних сооружений. Для генерала Бонапарта предстоящее сражение было еще одним шагом на пути к короне императора Наполеона...
А пирамиды продолжают бесстрастно взирать на проходящих у их подножия людей, прославляя в веках мудрость, мастерство и вдохновение древнеегипетских зодчих.
Собор Св. Петра в Риме (Ватикан). 1506-1663. Одно из лучших мировых купольных сооружений, главный храм католической церкви. В 42-метровом каменном куполе собора навеки материализовалась неиссякаемая энергия его создателя — великого Микеланджело
История строительства и дальнейшего существования собора полна драматических событий. Так, в 1740 г., через 150 лет после сооружения купола, некоторые трещины, неизбежно возникающие в кладке, расширились до угрожающих размеров. Это событие стимулировало новые теоретические исследования. В 1748 г. профессор экспериментальной философии (т. е. физики) университета в Падуе Джиованни Полени, опираясь на работы математика Стирлинга и механика Ла Гира, математически доказал, что купол собора находится в состоянии статического равновесия и появившиеся трещины угрозы не представляют. Прошедшие с тех пор 200 лет являются лучшим подтверждением справедливости математических расчетов Полени. К сожалению, теория каменных куполов была полностью завершена только в XX веке, когда такие купола превратились в отжившую конструкцию и их перестали строить.
История собора Св. Петра в Риме (а подобную историю имеет каждое выдающееся архитектурное сооружение) убеждает в том, что зодчество представляет собой сложный узел научных, технических и эстетических проблем. Архитектура парадоксально соединяет в себе результаты строительной деятельности и художественного творчества, инженерный расчет, научное знание и художественное озарение.
"Прочность — польза — красота",- говорит формула архитектуры Витрувия. Прочность не случайно стоит в ней на первом месте. Вся история архитектуры есть история созидания прочности, история борьбы с действием всемогущей силы тяготения. Недаром самый первый строительный кодекс, составленный в царствование вавилонского царя Хаммурапи за 1800 лет до нашей эры, гласит: "Если строитель построил дом для человека, и работа его не крепка, и дом, построенный им, обвалился и убил владельца, то строитель сей должен быть казнен". (Эта запись вытесана на колонне, ныне хранящейся в парижском Лувре.) Мелькали годы, проходили эпохи, менялись строительные материалы, а значит, и конструкции архитектурных сооружений, но всегда соображения прочности были определяющими в выборе новой архитектурной конструкции.
Но если относительно "прочности" у архитекторов никогда сомнений не возникало, то "польза" и "красота" являются предметом постоянных дискуссий. Впрочем, дискуссии о красоте и целесообразности (пользе) не являются привилегией одних только архитекторов. Это общеэстетическая проблема, уходящая корнями в седую древность. "Прекрасно то, что хорошо служит данной цели",- учит Сократ. "Дома строят для того, чтобы в них жить, а не для того, чтобы ими любоваться",- вторил Сократу через 2000 лет Фрэнсис Бэкон. Увлечение формулой Бэкона еще через 300 лет привело к тому, что безликие фасады со скоростью произрастания сорняков расплодились по всему земному шару. Невозможно стало отличить не только два новых дома, но и два новых района и даже два новых города. Архитектурная безликость стала притчей во языцех, сделав возможными смешные коллизии типа той, что произошла в пьесе Э. Брагинского и Э. Рязанова "С легким паром!". Надо сказать, что на сегодняшний день ошибочность увлечения одной только пользой в архитектуре осознана всеми и делаются серьезные шаги по преодолению этого заблуждения.
Есть и другая крайность во взглядах На соотношение пользы и красоты. Известный нам Джон Рескин говорил: "Искусство — это то, что бесполезно. Как только вещь становится полезной, она более не может быть красивой". Англичанина Рескина поддерживал француз Теофил Готье: "По-настоящему прекрасным является только то, что ничему не служит". По-видимому, те же взгляды на соотношение пользы и красоты имели и фараоны Древнего царства, жившие за ,4500 лет до Рескина и Готье. Во всяком случае, построенные ими пирамиды останутся в истории человечества непревзойденным образцом самого грандиозного и самого бесполезного сооружения. Только в условиях рабовладельческого строя возможна была такая бессмысленная трата человеческой энергии, когда сто тысяч рабов в течение двадцати лет возводили гробницу для одного из смертных — фараона Хеопса. Внутренний, полезный объем пирамиды настолько ничтожен, что ее вообще с трудом можно отнести к архитектурному сооружению.
Зато прочность пирамид недосягаема. Желая прославить своего фараона в веках, древнеегипетские зодчие из всех геометрических тел выбрали именно пирамиду. Выбор этот не случаен, ибо в условиях земного тяготения пирамида является наиболее устойчивой конструкцией, способной существовать в веках без риска обвалиться или рассыпаться. Главное правило устойчивости конструкции — уменьшение ее массы по мере увеличения высоты над землей — выражено в пирамиде с предельной ясностью и симметрией. Рациональность, "полезность" геометрической формы пирамиды заставляют забыть о ее утилитарной бесполезности. Именно эта геометрически оправданная форма пирамиды, подчеркнутая ее циклопическими размерами и точной системой пропорций, придает пирамиде ни с чем не сравнимую выразительность, особую красоту и величие, вызывает ощущение вечности, бессмертия, мудрости и покоя.
"Сорок веков смотрят на вас с высоты этих пирамид" — эти красивые слова генерал Бонапарт произнес перед сражением при египетских пирамидах 21 июля 1798 г. Однако отнюдь не философские размышления, а сиюминутные честолюбивые планы вызывал у генерала вид четырехтысячелетних сооружений. Для генерала Бонапарта предстоящее сражение было еще одним шагом на пути к короне императора Наполеона...
А пирамиды продолжают бесстрастно взирать на проходящих у их подножия людей, прославляя в веках мудрость, мастерство и вдохновение древнеегипетских зодчих.
(В. Брюсов)

 Пирамида фараона Хеопса в Гизе. XXVIII в. до н. э. Первоначальная высота пирамиды — 147 м. Это самая большая из древнеегипетских пирамид и вплоть до XIX в.- самое высокое из рукотворных сооружений
Разговор о египетских пирамидах незаметно привел нас к важнейшей проблеме архитектурной теории: проблеме соотношения конструкции и архитектурной формы. Только единство конструкции и наружной формы придает строению качество, именуемое архитектурной истиной. Диалектическое единство внутренней конструкции и внешней формы является главнейшим правилом образования архитектурных форм. Суть этой проблемы точно схвачена в афоризме французского архитектора Огюста Перре (1874-1954): "Тот, кто прячет колонну, столб или какую-либо несущую часть, допускает ошибку; тот, кто делает ложную колонну, совершает преступление".
Пирамида фараона Хеопса в Гизе. XXVIII в. до н. э. Первоначальная высота пирамиды — 147 м. Это самая большая из древнеегипетских пирамид и вплоть до XIX в.- самое высокое из рукотворных сооружений
Разговор о египетских пирамидах незаметно привел нас к важнейшей проблеме архитектурной теории: проблеме соотношения конструкции и архитектурной формы. Только единство конструкции и наружной формы придает строению качество, именуемое архитектурной истиной. Диалектическое единство внутренней конструкции и внешней формы является главнейшим правилом образования архитектурных форм. Суть этой проблемы точно схвачена в афоризме французского архитектора Огюста Перре (1874-1954): "Тот, кто прячет колонну, столб или какую-либо несущую часть, допускает ошибку; тот, кто делает ложную колонну, совершает преступление".
 Развитие стоечно-балочной конструкции в архитектуре. Храм Амона в Карнаке (Египет). XV в. до н. э
Конструкция древнеегипетской пирамиды является самой простой, прочной и устойчивой. Вес каждого верхнего блока пирамиды по всей поверхности передается нижним блокам. Форма пирамиды представляет полное единство с ее конструкцией. Однако такая конструкция не создает внутреннего объема и, по существу, не является архитектурной конструкцией.
Развитие стоечно-балочной конструкции в архитектуре. Храм Амона в Карнаке (Египет). XV в. до н. э
Конструкция древнеегипетской пирамиды является самой простой, прочной и устойчивой. Вес каждого верхнего блока пирамиды по всей поверхности передается нижним блокам. Форма пирамиды представляет полное единство с ее конструкцией. Однако такая конструкция не создает внутреннего объема и, по существу, не является архитектурной конструкцией.
 Развитие стоечно-балочной конструкции в архитектуре. Схема действия веса балки на опоры
Развитие стоечно-балочной конструкции в архитектуре. Схема действия веса балки на опоры
 Развитие стоечно-балочной конструкции в архитектуре. Комплекс Стонхендж (Англия). XX-XVIII вв. до н. э
Простейшей и древнейшей архитектурной конструкцией является стоечно-балочная система. Ее прототипом был дольмен — культовое сооружение, состоящее из двух вертикально поставленных камней, на которые наши предки водрузили третий горизонтальный камень. Назначение дольмена до конца не выяснено. Но ясно одно: дольмен — это гимн челочка о преодолении силы тяжести, это Вступление к грандиозной архитектурной симфонии будущего.
Развитие стоечно-балочной конструкции в архитектуре. Комплекс Стонхендж (Англия). XX-XVIII вв. до н. э
Простейшей и древнейшей архитектурной конструкцией является стоечно-балочная система. Ее прототипом был дольмен — культовое сооружение, состоящее из двух вертикально поставленных камней, на которые наши предки водрузили третий горизонтальный камень. Назначение дольмена до конца не выяснено. Но ясно одно: дольмен — это гимн челочка о преодолении силы тяжести, это Вступление к грандиозной архитектурной симфонии будущего.
 Развитие стоечно-балочной конструкции в архитектуре. Кариатиды храма Эрехтейнов (Греция). V в. до н. э
Со временем дольмен перерос в кромлех — сооружение, служившее, по всей видимости, для жертвоприношений и ритуальных торжеств. Кромлех состоял из огромных отдельно стоящих камней, которые накрывались горизонтальными камнями и образовывали одну или несколько концентрических окружностей. Самый значительный и загадочный кромлех сохранился в местечке Стонхендж (Англия) и относится к XX-XVII векам до н. э. Есть основания считать, что он был и древней астрономической обсерваторией.
В дальнейшем оставалось только придать каменному столбу кромлеха форму лотоса или изящной женской фигуры — кариатиды (по-гречески "девушки"), и стоечно-балочная конструкция превращалась в произведение искусства. Такое чудесное превращение мы видим в колоннах древнеегипетского храма бога Амона в Карнаке (XV в. до н. э.) или в кариатидах древнегреческого храма Эрехтейон на афинском Акрополе (421 — 406 гг. до н. э.).
Разумеется, стоечно-балочная конструкция проигрывала пирамиде в устойчивости и распределении веса, но она позволяла создавать внутренние объемы и, безусловно, явилась выдающимся завоеванием человеческой мысли. Главным же недостатком такой конструкции было то, что камень плохо работает на изгиб. Каменный брус сечением 10 X10 см и длиной 1 м 34 см обламывается под действием собственного веса. Вот почему в храме Амона в Карнаке мы видим такой лес колонн. Зато камень прекрасно работает на сжатие. Это свойство камня и дало жизнь новой архитектурной конструкции — арке, а затем и своду.
Родившись в Месопотамии и Персии, арочно-сводчатая конструкция была доведена римлянами до совершенства и стала основой древнеримской архитектуры. Арочно-сводчатая конструкция позволяла римлянам возводить гигантские сооружения. Это амфитеатр Флавиев (Колизей — от лат. colosseus — колоссальный; 75-80 гг.) — самое высокое (48 м) из сохранившихся сооружений античного Рима, вмещавшее 56 тысяч зрителей. Три яруса арок Колизея являются необходимым элементом его конструкции и неотъемлемой частью его архитектурной формы. Построенный за 10 лет, впоследствии Колизей в течение многих веков использовался как каменоломня. Это гигантские термы (бани) Каракаллы (нач. III в.) и Диоклетиана (нач. IV в.) в Риме, вмещавшие одновременно до 3 тысяч посетителей. Римские термы имели мощные цилиндрические и крестовые своды огромной высоты, были пышно украшены мозаикой, скульптурой, росписями, имели залы для омовения, массажа, сухого потения, гимнастических упражнений и даже библиотеки и походили скорее на дворцы. Это система арочных водоводов-акведуков (пролет арок — от 5 до 25 м, высота — более 40 м, общая протяженность — до 60 км), которые стали неотъемлемой частью римского пейзажа. И наконец, вершина древнеримского строительного искусства — Пантеон — храм всех богов. Мы уже отмечали, что в "классе каменных куполов" 43-метровый купол Пантеона в истории зодчества остался недосягаемым. Но Пантеон не только вершина научных и технических достижений древнеримских строителей, а и шедевр архитектурного искусства. В интерьере Пантеона достигнута завораживающая гармония между высотой и диаметром сооружения, которая имеет простое математическое выражение: высота стен Пантеона равна радиусу полусферы его купола, т. е. весь Пантеон как бы наброшен на 43-метровый шар. Цельность и величественность Пантеона оказали огромное влияние на многие поколения архитекторов.
Развитие стоечно-балочной конструкции в архитектуре. Кариатиды храма Эрехтейнов (Греция). V в. до н. э
Со временем дольмен перерос в кромлех — сооружение, служившее, по всей видимости, для жертвоприношений и ритуальных торжеств. Кромлех состоял из огромных отдельно стоящих камней, которые накрывались горизонтальными камнями и образовывали одну или несколько концентрических окружностей. Самый значительный и загадочный кромлех сохранился в местечке Стонхендж (Англия) и относится к XX-XVII векам до н. э. Есть основания считать, что он был и древней астрономической обсерваторией.
В дальнейшем оставалось только придать каменному столбу кромлеха форму лотоса или изящной женской фигуры — кариатиды (по-гречески "девушки"), и стоечно-балочная конструкция превращалась в произведение искусства. Такое чудесное превращение мы видим в колоннах древнеегипетского храма бога Амона в Карнаке (XV в. до н. э.) или в кариатидах древнегреческого храма Эрехтейон на афинском Акрополе (421 — 406 гг. до н. э.).
Разумеется, стоечно-балочная конструкция проигрывала пирамиде в устойчивости и распределении веса, но она позволяла создавать внутренние объемы и, безусловно, явилась выдающимся завоеванием человеческой мысли. Главным же недостатком такой конструкции было то, что камень плохо работает на изгиб. Каменный брус сечением 10 X10 см и длиной 1 м 34 см обламывается под действием собственного веса. Вот почему в храме Амона в Карнаке мы видим такой лес колонн. Зато камень прекрасно работает на сжатие. Это свойство камня и дало жизнь новой архитектурной конструкции — арке, а затем и своду.
Родившись в Месопотамии и Персии, арочно-сводчатая конструкция была доведена римлянами до совершенства и стала основой древнеримской архитектуры. Арочно-сводчатая конструкция позволяла римлянам возводить гигантские сооружения. Это амфитеатр Флавиев (Колизей — от лат. colosseus — колоссальный; 75-80 гг.) — самое высокое (48 м) из сохранившихся сооружений античного Рима, вмещавшее 56 тысяч зрителей. Три яруса арок Колизея являются необходимым элементом его конструкции и неотъемлемой частью его архитектурной формы. Построенный за 10 лет, впоследствии Колизей в течение многих веков использовался как каменоломня. Это гигантские термы (бани) Каракаллы (нач. III в.) и Диоклетиана (нач. IV в.) в Риме, вмещавшие одновременно до 3 тысяч посетителей. Римские термы имели мощные цилиндрические и крестовые своды огромной высоты, были пышно украшены мозаикой, скульптурой, росписями, имели залы для омовения, массажа, сухого потения, гимнастических упражнений и даже библиотеки и походили скорее на дворцы. Это система арочных водоводов-акведуков (пролет арок — от 5 до 25 м, высота — более 40 м, общая протяженность — до 60 км), которые стали неотъемлемой частью римского пейзажа. И наконец, вершина древнеримского строительного искусства — Пантеон — храм всех богов. Мы уже отмечали, что в "классе каменных куполов" 43-метровый купол Пантеона в истории зодчества остался недосягаемым. Но Пантеон не только вершина научных и технических достижений древнеримских строителей, а и шедевр архитектурного искусства. В интерьере Пантеона достигнута завораживающая гармония между высотой и диаметром сооружения, которая имеет простое математическое выражение: высота стен Пантеона равна радиусу полусферы его купола, т. е. весь Пантеон как бы наброшен на 43-метровый шар. Цельность и величественность Пантеона оказали огромное влияние на многие поколения архитекторов.
 Схема усилий в полуциркульной арке
Схема усилий в полуциркульной арке
 Арочно-сводчатая конструкция в древнеримской архитектуре. Амфитеатр Флавиев (Колизей). Рим. 70-80
Арочно-сводчатая конструкция в древнеримской архитектуре. Амфитеатр Флавиев (Колизей). Рим. 70-80
 Акведук 'Гардский мост' близ Нима. Франция. I-II вв.
Акведук 'Гардский мост' близ Нима. Франция. I-II вв.
 Пантеон (интерьер). Рим. 123 н. э. Здание освещается через 9-метровое отверстие в центре полусферического купола
Пантеон (интерьер). Рим. 123 н. э. Здание освещается через 9-метровое отверстие в центре полусферического купола
 Пантеон (внешний вид). Рим. 123 н. э. Здание освещается через 9-метровое отверстие в центре полусферического купола
Итак, арки и своды произвели целую революцию в архитектуре. С того момента, как в арке устанавливался так называемый замковый камень, арка становилась самонесущей конструкцией. (Поэтому процесс установления замкового камня часто сопровождался религиозной церемонией, а сам камень старались как-то украсить.)
Пантеон (внешний вид). Рим. 123 н. э. Здание освещается через 9-метровое отверстие в центре полусферического купола
Итак, арки и своды произвели целую революцию в архитектуре. С того момента, как в арке устанавливался так называемый замковый камень, арка становилась самонесущей конструкцией. (Поэтому процесс установления замкового камня часто сопровождался религиозной церемонией, а сам камень старались как-то украсить.)
 Математика и архитектура
Математика и архитектура
 Математика и архитектура
Римские арки, своды и купола были неизменно полуциркульными. Здесь, видимо, сказывалось влияние пифагорейской философии, считавшей круг и сферу идеальными фигурами, а также, безусловно, простота построения. Как бы то ни было, с появлением арочно-сводчатой конструкции в архитектуру прямых линий и плоскостей пришли окружности, сферы и круговые цилиндры, что сделало геометрический язык архитектуры значительно богаче. Однако полуциркульная арка или полусферический купол давали сильный боковой распор, что ясно видно из схемы сил, действующих в арке. Боковые усилия приходилось гасить толщиной стен и устройством дополнительных контрфорсов (толщина стен Пантеона достигала 7 метров!), а это влекло огромный расход строительных материалов.
Рим пал, растоптанный варварами, а вместе с Римом пало и рабовладение. Средневековые мастера уже не могли себе позволить гасить огромные распоры от полуциркульных сводов семиметровыми стенами. Камень был дорог, да и каменотесам нужно было платить. Благо, вместе с пленниками-сарацинами крестоносцы привезли в Европу секреты возведения стрельчатых арок. Так новая конструкция породила новую архитектуру — готику.
Стрельчатая арка по сравнению с полуциркульной является более совершенной конструкцией: она вызывает меньший боковой распор, а следовательно, и меньший расход камня. Очевидно также, что стрельчатая арка имеет более сложную геометрическую форму по сравнению с полуциркульной, которая строится одним движением циркуля. Таким образом, на примере трех конструкций — стоечно-балочной, арочной и стрельчатой — мы видим, что по мере совершенствования конструкции усложняется и ее геометрия. Современная архитектура подтверждает эту закономерность.
Математика и архитектура
Римские арки, своды и купола были неизменно полуциркульными. Здесь, видимо, сказывалось влияние пифагорейской философии, считавшей круг и сферу идеальными фигурами, а также, безусловно, простота построения. Как бы то ни было, с появлением арочно-сводчатой конструкции в архитектуру прямых линий и плоскостей пришли окружности, сферы и круговые цилиндры, что сделало геометрический язык архитектуры значительно богаче. Однако полуциркульная арка или полусферический купол давали сильный боковой распор, что ясно видно из схемы сил, действующих в арке. Боковые усилия приходилось гасить толщиной стен и устройством дополнительных контрфорсов (толщина стен Пантеона достигала 7 метров!), а это влекло огромный расход строительных материалов.
Рим пал, растоптанный варварами, а вместе с Римом пало и рабовладение. Средневековые мастера уже не могли себе позволить гасить огромные распоры от полуциркульных сводов семиметровыми стенами. Камень был дорог, да и каменотесам нужно было платить. Благо, вместе с пленниками-сарацинами крестоносцы привезли в Европу секреты возведения стрельчатых арок. Так новая конструкция породила новую архитектуру — готику.
Стрельчатая арка по сравнению с полуциркульной является более совершенной конструкцией: она вызывает меньший боковой распор, а следовательно, и меньший расход камня. Очевидно также, что стрельчатая арка имеет более сложную геометрическую форму по сравнению с полуциркульной, которая строится одним движением циркуля. Таким образом, на примере трех конструкций — стоечно-балочной, арочной и стрельчатой — мы видим, что по мере совершенствования конструкции усложняется и ее геометрия. Современная архитектура подтверждает эту закономерность.
 Собор в Реймсе. Витражи центрального нефа и апсида. 1211 — 1427
Собор в Реймсе. Витражи центрального нефа и апсида. 1211 — 1427
 Готическая архитектура. Новая конструкция, породившая и новую, устремленную ввысь, архитектурную форму. Собор в Амьене. Западный фасад. 1220-1288
Готическая архитектура. Новая конструкция, породившая и новую, устремленную ввысь, архитектурную форму. Собор в Амьене. Западный фасад. 1220-1288
 Аркбутаны собора в Ле Мане с высоты птичьего полета. 1217-1254
Аркбутаны собора в Ле Мане с высоты птичьего полета. 1217-1254
 Схема усилий в аркбутане и контрфорсе
Стрельчатая арка привнесла в готическую архитектуру два конструктивных новшества. Во-первых, стрельчатые своды
Собор в Шартре. Аркбутаны. 1134-1260.
стали выполнять на нервюрах — каменных ребрах, несущих независимые друг от друга части свода — распалубки. Нервюры служат как бы скелетом свода, они воспринимают на себя основную нагрузку. В результате конструкция свода становится более гибкой: она может выдерживать те деформации, которые для монолитного свода окажутся губительными. Таким образом, нервюры явились прототипом современной каркасной конструкции.
Во-вторых, боковой распор от стрельчатого свода средневековые зодчие решили гасить не в самих стенах, несущих этот свод, а вне их. Для этого за пределами внутреннего пространства готического собора ставились специальные опоры — контрфорсы, нагрузка на которые передавалась с помощью арочных конструкций — аркбутанов. Аркбутаны, словно растопырившиеся ребра рыбьего скелета, окружали снаружи готический собор.
Зато внутренним опорам и стенам готического собора оставалась лишь одна вертикальная нагрузка — вот почему их можно было делать более тонкими и изящными. Со временем центральные устои готического храма превратились в пучок нервюр, которые, словно преодолев земное притяжение, стремительно возносились к небу. Стрельчатая форма арок подчеркивала это безудержное стремление ввысь. Самые высокие своды имели соборы Северной Франции: собор в Амьене (1288 г., 43 м) и собор в Бове (1347 г., 48 м). Своды готического собора будто парили далеко в вышине, освещенные вибрирующими потоками света от цветных витражей. Поскольку вертикальную нагрузку готического храма нес пучок нервюр, центральные стены как несущие конструкции оказались ненужными, и их заменили цветными витражами. Вы слышите, как перекликаются готические конструкции XII-XV веков с современными архитектурными конструкциями, у которых на грузку взял на себя тонкий железобетонный каркас, а стены стали стеклянными?
Однако потребовалось еще не одно столетие, чтобы каркас преодолел силу, куда более значительную, чем земное тяготение,- силу инерции человеческого мышления. Слишком привычным и естественным было видеть основу архитектурной конструкции в толстых стенах, несущих основную нагрузку. Правда, было и еще одно сдерживающее обстоятельство: нужен был новый материал для каркаса, более технологичный и дешевый, чем камень. Такой материал появился лишь в XIX веке. Это был металл.
XIX век можно назвать "железным веком" в истории человечества: железные дороги и паровые машины, первый железный мост через Темзу (1816), первые застекленные металлические крыши (типа крыши московского ГУМа), металлические купола, быстро побившие недосягаемые древнеримские рекорды, и металлические пролеты, превысившие к концу века 100-метровый рубеж. В 1889 г. к открытию Всемирной выставки в Париже как символ победоносного шествия металла в технике и архитектуре была построена знаменитая Эйфелева башня по проекту французского инженера Гюстава Эйфеля (1832-1923). Она сразу вдвое перекрыла все рекорды по преодолению высоты, взметнувшись вверх на 312,6 метра! Так был побит самый долговечный рекорд в истории человечества: ведь пирамида Хеопса в течение 45 веков оставалась самым высоким творением рук человека. Первоначальная высота пирамиды Хеопса была 147 м, хотя к настоящему времени ее верхушка обвалилась и пирамида стала на 10 м ниже. Шпили готических соборов лишь приближались к этой отметке. Самым высоким в Англии был собор в Солисбери (1258 г., 123 м), а во Франции — Страсбургский собор (1439 г., 142 м). Башня собора в Бове, построенная в 1569 г., лишь на 8 метров и только на 4 года побила рекорд высоты пирамиды Хеопса, а затем рухнула. Крест собора Св. Петра в Риме был поднят на высоту 138 м. Только в XIX веке шпиль Ульмского собора поднялся на 12 метров выше пирамиды Хеопса. И вот в конце XIX века принципиально новая конструкция из принципиально нового материала дает принципиально новый результат!
Однако объявлять Эйфелеву башню произведением искусства парижане не спешили. "Здесь нет искусства, один металл!" — возмущались они. "Я бежал из Парижа, а затем покинул Францию, потому что меня навязчиво преследовал вид Эйфелевой башни,- писал Ги де Мопассан.- Вообразите же, что скажут отдаленные потомки о нашем поколении, если только вспышка народного гнева не повалит эту высоченную и тощую пирамиду железных лестниц".
Но не отдаленные потомки, а уже следующее поколение Парижан не мыслило себе родного города без Эйфелевой башни. И конечно же, бессмертие принесла Эйфелевой башне не ее конструкция, которая сегодня кажется архаичной, а пропорциональность и гармоническое единство ее форм, т. е. как раз то, что и делает строительную конструкцию произведением архитектурного искусства.
"Век железа" в архитектуре оказался недолгим. С новым XX веком пришел и новый необычный материал — железобетон, совершивший подлинную революцию в зодчестве. "Первая ласточка" новой архитектуры появилась в 1903 г. Это был жилой дом архитектора О. Перре в Париже — железобетонный каркас с большими остекленными проемами. Перре доказал, что возведение домов из кирпича и камня с массивными стенами необязательно. Так начался "век железобетона". Железобетон открывал невиданные возможности перед архитекторами: он был дешев, обладал необходимой прочностью, мог непрерывно переходить из одной формы в другую. Неудивительно, что зодчие спешили проверить новый материал на перекрытиях, сооружение которых всегда представляло одну из важнейших технических проблем. Скорлупа обычного куриного яйца была для архитекторов эталоном прочной и легкой конструкции. Отношение диаметра большого куриного яйца к толщине скорлупы равно в среднем 130. Такое соотношение между диаметром пролета и его толщиной казалось недостижимым. Например, для Пантеона в Риме оно равнялось 11, т. е. было на порядок меньше. И вот железобетонные "скорлупки" опрокидывают все традиционные представления и оставляют далеко позади рекорды куриного яйца. Наглядное представление о динамике этого важного в архитектуре параметра дает таблица 5.
Схема усилий в аркбутане и контрфорсе
Стрельчатая арка привнесла в готическую архитектуру два конструктивных новшества. Во-первых, стрельчатые своды
Собор в Шартре. Аркбутаны. 1134-1260.
стали выполнять на нервюрах — каменных ребрах, несущих независимые друг от друга части свода — распалубки. Нервюры служат как бы скелетом свода, они воспринимают на себя основную нагрузку. В результате конструкция свода становится более гибкой: она может выдерживать те деформации, которые для монолитного свода окажутся губительными. Таким образом, нервюры явились прототипом современной каркасной конструкции.
Во-вторых, боковой распор от стрельчатого свода средневековые зодчие решили гасить не в самих стенах, несущих этот свод, а вне их. Для этого за пределами внутреннего пространства готического собора ставились специальные опоры — контрфорсы, нагрузка на которые передавалась с помощью арочных конструкций — аркбутанов. Аркбутаны, словно растопырившиеся ребра рыбьего скелета, окружали снаружи готический собор.
Зато внутренним опорам и стенам готического собора оставалась лишь одна вертикальная нагрузка — вот почему их можно было делать более тонкими и изящными. Со временем центральные устои готического храма превратились в пучок нервюр, которые, словно преодолев земное притяжение, стремительно возносились к небу. Стрельчатая форма арок подчеркивала это безудержное стремление ввысь. Самые высокие своды имели соборы Северной Франции: собор в Амьене (1288 г., 43 м) и собор в Бове (1347 г., 48 м). Своды готического собора будто парили далеко в вышине, освещенные вибрирующими потоками света от цветных витражей. Поскольку вертикальную нагрузку готического храма нес пучок нервюр, центральные стены как несущие конструкции оказались ненужными, и их заменили цветными витражами. Вы слышите, как перекликаются готические конструкции XII-XV веков с современными архитектурными конструкциями, у которых на грузку взял на себя тонкий железобетонный каркас, а стены стали стеклянными?
Однако потребовалось еще не одно столетие, чтобы каркас преодолел силу, куда более значительную, чем земное тяготение,- силу инерции человеческого мышления. Слишком привычным и естественным было видеть основу архитектурной конструкции в толстых стенах, несущих основную нагрузку. Правда, было и еще одно сдерживающее обстоятельство: нужен был новый материал для каркаса, более технологичный и дешевый, чем камень. Такой материал появился лишь в XIX веке. Это был металл.
XIX век можно назвать "железным веком" в истории человечества: железные дороги и паровые машины, первый железный мост через Темзу (1816), первые застекленные металлические крыши (типа крыши московского ГУМа), металлические купола, быстро побившие недосягаемые древнеримские рекорды, и металлические пролеты, превысившие к концу века 100-метровый рубеж. В 1889 г. к открытию Всемирной выставки в Париже как символ победоносного шествия металла в технике и архитектуре была построена знаменитая Эйфелева башня по проекту французского инженера Гюстава Эйфеля (1832-1923). Она сразу вдвое перекрыла все рекорды по преодолению высоты, взметнувшись вверх на 312,6 метра! Так был побит самый долговечный рекорд в истории человечества: ведь пирамида Хеопса в течение 45 веков оставалась самым высоким творением рук человека. Первоначальная высота пирамиды Хеопса была 147 м, хотя к настоящему времени ее верхушка обвалилась и пирамида стала на 10 м ниже. Шпили готических соборов лишь приближались к этой отметке. Самым высоким в Англии был собор в Солисбери (1258 г., 123 м), а во Франции — Страсбургский собор (1439 г., 142 м). Башня собора в Бове, построенная в 1569 г., лишь на 8 метров и только на 4 года побила рекорд высоты пирамиды Хеопса, а затем рухнула. Крест собора Св. Петра в Риме был поднят на высоту 138 м. Только в XIX веке шпиль Ульмского собора поднялся на 12 метров выше пирамиды Хеопса. И вот в конце XIX века принципиально новая конструкция из принципиально нового материала дает принципиально новый результат!
Однако объявлять Эйфелеву башню произведением искусства парижане не спешили. "Здесь нет искусства, один металл!" — возмущались они. "Я бежал из Парижа, а затем покинул Францию, потому что меня навязчиво преследовал вид Эйфелевой башни,- писал Ги де Мопассан.- Вообразите же, что скажут отдаленные потомки о нашем поколении, если только вспышка народного гнева не повалит эту высоченную и тощую пирамиду железных лестниц".
Но не отдаленные потомки, а уже следующее поколение Парижан не мыслило себе родного города без Эйфелевой башни. И конечно же, бессмертие принесла Эйфелевой башне не ее конструкция, которая сегодня кажется архаичной, а пропорциональность и гармоническое единство ее форм, т. е. как раз то, что и делает строительную конструкцию произведением архитектурного искусства.
"Век железа" в архитектуре оказался недолгим. С новым XX веком пришел и новый необычный материал — железобетон, совершивший подлинную революцию в зодчестве. "Первая ласточка" новой архитектуры появилась в 1903 г. Это был жилой дом архитектора О. Перре в Париже — железобетонный каркас с большими остекленными проемами. Перре доказал, что возведение домов из кирпича и камня с массивными стенами необязательно. Так начался "век железобетона". Железобетон открывал невиданные возможности перед архитекторами: он был дешев, обладал необходимой прочностью, мог непрерывно переходить из одной формы в другую. Неудивительно, что зодчие спешили проверить новый материал на перекрытиях, сооружение которых всегда представляло одну из важнейших технических проблем. Скорлупа обычного куриного яйца была для архитекторов эталоном прочной и легкой конструкции. Отношение диаметра большого куриного яйца к толщине скорлупы равно в среднем 130. Такое соотношение между диаметром пролета и его толщиной казалось недостижимым. Например, для Пантеона в Риме оно равнялось 11, т. е. было на порядок меньше. И вот железобетонные "скорлупки" опрокидывают все традиционные представления и оставляют далеко позади рекорды куриного яйца. Наглядное представление о динамике этого важного в архитектуре параметра дает таблица 5.
 Таблица 5. Динамика отношения диаметра оболочки к ее толщине в истории архитектуры
Таблица 5. Динамика отношения диаметра оболочки к ее толщине в истории архитектуры

 Радиобашня (впоследствии телебашня) Шухова на Шаболовке (Москва. 1922) и линейчатое свойство однополостного гиперболоида
Строительство железобетонных покрытий требовало опалубки, удерживающей жидкий бетон и придающей ему лучшую форму. Опалубку же удобнее всего делать из прямых досок. Простейшие поверхности, образованные движением прямой в пространстве и называемые линейчатыми поверхностями — цилиндры и конусы,- были известны давно. Еще древние римляне сооружали цилиндрические своды. А существуют ли другие линейчатые поверхности? Ответ на этот вопрос архитекторам подсказали математики, которые обнаружили еще два типа линейчатых поверхностей:
однополостный гиперболоид:
Радиобашня (впоследствии телебашня) Шухова на Шаболовке (Москва. 1922) и линейчатое свойство однополостного гиперболоида
Строительство железобетонных покрытий требовало опалубки, удерживающей жидкий бетон и придающей ему лучшую форму. Опалубку же удобнее всего делать из прямых досок. Простейшие поверхности, образованные движением прямой в пространстве и называемые линейчатыми поверхностями — цилиндры и конусы,- были известны давно. Еще древние римляне сооружали цилиндрические своды. А существуют ли другие линейчатые поверхности? Ответ на этот вопрос архитекторам подсказали математики, которые обнаружили еще два типа линейчатых поверхностей:
однополостный гиперболоид:
 (13.1)
гиперболический параболоид:
(13.1)
гиперболический параболоид:
 (13.2)
Канонические уравнения этих поверхностей (13.1) и (13.2) легко представить в виде
(13.2)
Канонические уравнения этих поверхностей (13.1) и (13.2) легко представить в виде
 откуда и видно, что они образованы двумя семействами прямых в пространстве (в уравнение прямой переменные х, у, z входят только в первых степенях).
Архитекторы воспользовались открытием математиков. Форму однополостного гиперболоида имеют градирни — устройства для охлаждения воды атмосферным воздухом. Линейчатое свойство однополостного гиперболоида положено в основу конструкции Шаболовской радиобашни в Москве, построенной по проекту замечательного русского советского инженера, почетного академика В. Г. Шухова (1853- 1939). Башня Шухова состоит из нескольких поставленных друг на друга частей однополостных гиперболоидов, причем каждая часть сделана из двух семейств прямолинейных балок, соединенных в точках пересечения.
Если однополостный гиперболоид отдает должное "пользе" в архитектуре, то гиперболический параболоид (архитекторы называют его красивым сокращенным именем гипар) благодаря своей выразительной и элегантной форме служит "красоте". Архитектурные возможности гипаров открыл инженер Феликс Кандела — испанский патриот, сражавшийся против фашистской диктатуры Франко, в 1939 г. вынужденный эмигрировать в Мексику. Кандела с блеском продемонстрировал выразительные свойства гипаров на различных сооружениях — от промышленных зданий до ресторанов, ночных клубов и церквей. Объединяло столь функционально несхожие сооружения одно: в них математическая поверхность становилась произведением архитектурного искусства. Линейчатое свойство гипаров позволяет разрезать их по прямолинейным образующим и составлять из нескольких гипаров экзотические конструкции. Именно так поступил в 1958 г. Ле Корбюзье, построив причудливый павильон фирмы "Филипс" на Международной выставке в Брюсселе.
Точно сказал о внутренней красоте гипаров один из ее приверженцев — американский инженер Вейдлингер: "Красота форм достигается не средствами "косметики", а вытекает из сущности конструкции. Сама по себе форма является почти эпюрой[24] усилий, которые она должна воспринять". А для людей, которые видят только внешнюю красоту гипаров, они напоминают крылья огромных фантастических птиц, опустившихся на нашу Землю лишь отдохнуть и в каждое мгновение готовых взмахнуть крыльями-гипарами и улететь в свои неведомые миры. Именно эта "вторая реальность", "поэтическое дыхание" и преобразуют математическую поверхность, строительную конструкцию в искусство, именуемое архитектурой.
Ни один из видов искусств так тесно не связан с геометрией, как архитектура. "Окружающий нас мир — это мир геометрии чистой, истинной, безупречной в наших глазах. Все вокруг — геометрия. Никогда мы не видим так ясно таких форм, как круг, прямоугольник, угол, цилиндр, гипар, выполненных с такой тщательностью и так уверенно". Эти восторженные слова о геометрии принадлежат Ле Корбюзье.
откуда и видно, что они образованы двумя семействами прямых в пространстве (в уравнение прямой переменные х, у, z входят только в первых степенях).
Архитекторы воспользовались открытием математиков. Форму однополостного гиперболоида имеют градирни — устройства для охлаждения воды атмосферным воздухом. Линейчатое свойство однополостного гиперболоида положено в основу конструкции Шаболовской радиобашни в Москве, построенной по проекту замечательного русского советского инженера, почетного академика В. Г. Шухова (1853- 1939). Башня Шухова состоит из нескольких поставленных друг на друга частей однополостных гиперболоидов, причем каждая часть сделана из двух семейств прямолинейных балок, соединенных в точках пересечения.
Если однополостный гиперболоид отдает должное "пользе" в архитектуре, то гиперболический параболоид (архитекторы называют его красивым сокращенным именем гипар) благодаря своей выразительной и элегантной форме служит "красоте". Архитектурные возможности гипаров открыл инженер Феликс Кандела — испанский патриот, сражавшийся против фашистской диктатуры Франко, в 1939 г. вынужденный эмигрировать в Мексику. Кандела с блеском продемонстрировал выразительные свойства гипаров на различных сооружениях — от промышленных зданий до ресторанов, ночных клубов и церквей. Объединяло столь функционально несхожие сооружения одно: в них математическая поверхность становилась произведением архитектурного искусства. Линейчатое свойство гипаров позволяет разрезать их по прямолинейным образующим и составлять из нескольких гипаров экзотические конструкции. Именно так поступил в 1958 г. Ле Корбюзье, построив причудливый павильон фирмы "Филипс" на Международной выставке в Брюсселе.
Точно сказал о внутренней красоте гипаров один из ее приверженцев — американский инженер Вейдлингер: "Красота форм достигается не средствами "косметики", а вытекает из сущности конструкции. Сама по себе форма является почти эпюрой[24] усилий, которые она должна воспринять". А для людей, которые видят только внешнюю красоту гипаров, они напоминают крылья огромных фантастических птиц, опустившихся на нашу Землю лишь отдохнуть и в каждое мгновение готовых взмахнуть крыльями-гипарами и улететь в свои неведомые миры. Именно эта "вторая реальность", "поэтическое дыхание" и преобразуют математическую поверхность, строительную конструкцию в искусство, именуемое архитектурой.
Ни один из видов искусств так тесно не связан с геометрией, как архитектура. "Окружающий нас мир — это мир геометрии чистой, истинной, безупречной в наших глазах. Все вокруг — геометрия. Никогда мы не видим так ясно таких форм, как круг, прямоугольник, угол, цилиндр, гипар, выполненных с такой тщательностью и так уверенно". Эти восторженные слова о геометрии принадлежат Ле Корбюзье.

 Вечерний зал в Акапулько (Мексика) архитектора Канде-ла и линейчатое свойство гиперболического параболоида
Но в отличие от "абстрактной", "математической" геометрии "архитектурная" геометрия наполнена собственным эстетическим содержанием. Дело в том, что образы "математической" геометрии бестелесны: они не имеют толщины, не имеют веса и потому свободно парят в нашем воображении. Иное дело — образы "архитектурной" геометрии. Они созданы из конкретного материала: они весомы, они живут в поле земного тяготения. Геометрическую фигуру, например пирамиду, мы можем поворачивать в нашем воображении в любую сторону — от этого ее свойства не изменяются. Но попробуйте мысленно повернуть вершиной вниз пирамиду Хеопса, и вам сразу станет не по себе: пирамида начнет качаться из стороны в сторону и разваливаться на куски. Причина здесь очевидна: на пирамиду Хеопса даже в нашем воображении действует земное притяжение. И для того чтобы обеспечить своему сооружению бессмертие, древнеегипетский зодчий гениально воплотил в каменной пирамиде важнейшее правило устойчивости и прочности конструкции — расширение книзу. Так пирамида в архитектуре закономерно стала олицетворением устойчивости и прочности, вечности и покоя. В этом ее эстетическое содержание. Художественное выражение закономерностей архитектурного сооружения или конструкции называется архитектоникой или просто тектоникой. Можно сказать, что пирамида является символом тектоники всей классической архитектуры, ее эстетическим флагом.
Современное зодчество бросило вызов классической тектонике. Получив в свое распоряжение особо прочные материалы и конструкции, оно стремится перевернуть вверх ногами "пирамиду архитектоники". Современная архитектура, будто преодолев силы тяготения, парит в воздухе. Человечество всегда мечтало о легкой и воздушной архитектуре, и вот в XX веке эти мечты обретают плоть. Горизонтальные плоскости, будто летящие в пространстве ("Дом над водопадом" в Бер-Ране, США, арх. Ф. Райт, 1936 г.); гигантские нависающие объемы (Клуб им. И. В. Русакова в Москве, арх. К. Мельников, 1929 г.); V-образные опоры, оторвавшие здание от земли ("Лучезарный дом" в Марселе, арх. Ле Корбюзье, 1952 г.); стены, превращенные в витражи, в которые любуются золотые купола Кремлевских соборов (Кремлевский Дворец съездов, арх. М. Посохин и др., 1961 г.); причудливые линии козырьков и сводов-оболочек в форме гипаров (церковь де ла Виргин Милагроза в Мехико, инж. Ф. Кандела, 1955 г.)- все это приметы современной архитектоники и ставшие классикой примеры современной архитектуры. Все эти приметы, собранные вместе, легко обнаружить в здании Штаб-квартиры ЮНЕСКО в Париже (арх. П. Нерви и др., 1957 г.), которое и было задумано как символ современной архитектуры.
А вот и символ современной архитектоники — проект музея современного искусства в столице Венесуэлы Каракасе. Проект создан лауреатом Ленинской премии мира, бразильским архитектором Оскаром Нимейром и представляет собой огромную пирамиду из стекла и бетона, стоящую "вверх ногами". Конечно, главное в проекте Нимейера — это вызов классической каменной тектонике, стремление выразить новые возможности новой архитектуры в новой, пусть даже парадоксальной форме. Право на жизнь новых идей доказывается в проекте Нимейера "методом от противного".
Проект Нимейера остался неосуществленным, но его смелые тектонические идеи дали свои всходы. Вот здание фирмы "Эссо" в Риме, построенное в 1980 г. архитекторами Дж. Лафуэнте и Г. Ребеккини. Здание напоминает три пирамиды в Гизе (см. с. 180), перевернутые "вверх ногами"; оно явно перекликается со знаменитым проектом Нимейера, хотя конструктивно решено по-своему. Веер стальных опор является конструктивным и эмоциональным стержнем здания, которое напоминает, скорее, не дом, а какой-то сложный механизм. Благодаря новым тектоническим идеям, цельности и геометричности всей композиции здание "Эссо" производит сильное впечатление, хотя, разумеется, и стоит особняком в архитектуре второй половины XX века.
Вечерний зал в Акапулько (Мексика) архитектора Канде-ла и линейчатое свойство гиперболического параболоида
Но в отличие от "абстрактной", "математической" геометрии "архитектурная" геометрия наполнена собственным эстетическим содержанием. Дело в том, что образы "математической" геометрии бестелесны: они не имеют толщины, не имеют веса и потому свободно парят в нашем воображении. Иное дело — образы "архитектурной" геометрии. Они созданы из конкретного материала: они весомы, они живут в поле земного тяготения. Геометрическую фигуру, например пирамиду, мы можем поворачивать в нашем воображении в любую сторону — от этого ее свойства не изменяются. Но попробуйте мысленно повернуть вершиной вниз пирамиду Хеопса, и вам сразу станет не по себе: пирамида начнет качаться из стороны в сторону и разваливаться на куски. Причина здесь очевидна: на пирамиду Хеопса даже в нашем воображении действует земное притяжение. И для того чтобы обеспечить своему сооружению бессмертие, древнеегипетский зодчий гениально воплотил в каменной пирамиде важнейшее правило устойчивости и прочности конструкции — расширение книзу. Так пирамида в архитектуре закономерно стала олицетворением устойчивости и прочности, вечности и покоя. В этом ее эстетическое содержание. Художественное выражение закономерностей архитектурного сооружения или конструкции называется архитектоникой или просто тектоникой. Можно сказать, что пирамида является символом тектоники всей классической архитектуры, ее эстетическим флагом.
Современное зодчество бросило вызов классической тектонике. Получив в свое распоряжение особо прочные материалы и конструкции, оно стремится перевернуть вверх ногами "пирамиду архитектоники". Современная архитектура, будто преодолев силы тяготения, парит в воздухе. Человечество всегда мечтало о легкой и воздушной архитектуре, и вот в XX веке эти мечты обретают плоть. Горизонтальные плоскости, будто летящие в пространстве ("Дом над водопадом" в Бер-Ране, США, арх. Ф. Райт, 1936 г.); гигантские нависающие объемы (Клуб им. И. В. Русакова в Москве, арх. К. Мельников, 1929 г.); V-образные опоры, оторвавшие здание от земли ("Лучезарный дом" в Марселе, арх. Ле Корбюзье, 1952 г.); стены, превращенные в витражи, в которые любуются золотые купола Кремлевских соборов (Кремлевский Дворец съездов, арх. М. Посохин и др., 1961 г.); причудливые линии козырьков и сводов-оболочек в форме гипаров (церковь де ла Виргин Милагроза в Мехико, инж. Ф. Кандела, 1955 г.)- все это приметы современной архитектоники и ставшие классикой примеры современной архитектуры. Все эти приметы, собранные вместе, легко обнаружить в здании Штаб-квартиры ЮНЕСКО в Париже (арх. П. Нерви и др., 1957 г.), которое и было задумано как символ современной архитектуры.
А вот и символ современной архитектоники — проект музея современного искусства в столице Венесуэлы Каракасе. Проект создан лауреатом Ленинской премии мира, бразильским архитектором Оскаром Нимейром и представляет собой огромную пирамиду из стекла и бетона, стоящую "вверх ногами". Конечно, главное в проекте Нимейера — это вызов классической каменной тектонике, стремление выразить новые возможности новой архитектуры в новой, пусть даже парадоксальной форме. Право на жизнь новых идей доказывается в проекте Нимейера "методом от противного".
Проект Нимейера остался неосуществленным, но его смелые тектонические идеи дали свои всходы. Вот здание фирмы "Эссо" в Риме, построенное в 1980 г. архитекторами Дж. Лафуэнте и Г. Ребеккини. Здание напоминает три пирамиды в Гизе (см. с. 180), перевернутые "вверх ногами"; оно явно перекликается со знаменитым проектом Нимейера, хотя конструктивно решено по-своему. Веер стальных опор является конструктивным и эмоциональным стержнем здания, которое напоминает, скорее, не дом, а какой-то сложный механизм. Благодаря новым тектоническим идеям, цельности и геометричности всей композиции здание "Эссо" производит сильное впечатление, хотя, разумеется, и стоит особняком в архитектуре второй половины XX века.
 Современная архитектура — это геометрия, парящая в воздухе. Дом над водопадом в Бер-Ране. США. Арх. Ф. Райт. 1936
Современная архитектура — это геометрия, парящая в воздухе. Дом над водопадом в Бер-Ране. США. Арх. Ф. Райт. 1936
 Клуб им. И. В. Русакова в Москве. Арх. К. Мельников. 1929
Клуб им. И. В. Русакова в Москве. Арх. К. Мельников. 1929
Все вокруг — геометрия. Дух геометрического и математического порядка станет властителем архитектурных судеб.Ле Корбюзье
Архитектура — это способность нашего сознания закреплять в материальных формах чувство эпохи. Произведение искусства — это инобытие человека-творца, либо нашего современника, либо человека другой эпохи, либо художника, вовсе нам неизвестного. Художественное творчество есть момент глубочайшего откровения, это страстная и искренняя исповедь, быть может, это — Нагорная проповедь.Ле Корбюзье
 Здание ЮНЕСКО в Париже — классика современной архитектуры. Арх. М. Брейер, Б. Зерфюсс, П. Нерви. 1957
Возможно, "перевернутая пирамида" Оскара Нимейера или "падающие дома", проект которых разработан советским архитектором Г. Б. Борисовским, в будущем станут привычными элементами архитектурного пейзажа. Ведь стала же таким элементом V-образная опора, которая в соперничестве с античной колонной сужается, а не расширяется книзу! Несмотря на свое противоречие с законами старой, доброй классической тектоники, V-образная опора, форма которой непосредственно следует из эпюры распределения нагрузок в конструкции, сумела отстоять свое место под солнцем. Так формы "чистой" геометрии обретают в геометрии архитектурнойновое эстетическое звучание.
Наш краткий обзор некоторых страниц истории архитектуры дает достаточно ясное представление о том, насколько тесно взаимосвязаны в ней наука, техника и искусство, как важна для архитектуры гармония определяющих ее начал: "прочности — пользы — красоты", как сказал Витрувий, или "конструкции — функции — формы", как любят говорить современные архитекторы. Вся история архитектуры — это история поисков гармонического единства "функции — конструкции — формы", это история непрерывного восхождения на пути к вершине, имя которой "прочность — польза — красота ".
Здание ЮНЕСКО в Париже — классика современной архитектуры. Арх. М. Брейер, Б. Зерфюсс, П. Нерви. 1957
Возможно, "перевернутая пирамида" Оскара Нимейера или "падающие дома", проект которых разработан советским архитектором Г. Б. Борисовским, в будущем станут привычными элементами архитектурного пейзажа. Ведь стала же таким элементом V-образная опора, которая в соперничестве с античной колонной сужается, а не расширяется книзу! Несмотря на свое противоречие с законами старой, доброй классической тектоники, V-образная опора, форма которой непосредственно следует из эпюры распределения нагрузок в конструкции, сумела отстоять свое место под солнцем. Так формы "чистой" геометрии обретают в геометрии архитектурнойновое эстетическое звучание.
Наш краткий обзор некоторых страниц истории архитектуры дает достаточно ясное представление о том, насколько тесно взаимосвязаны в ней наука, техника и искусство, как важна для архитектуры гармония определяющих ее начал: "прочности — пользы — красоты", как сказал Витрувий, или "конструкции — функции — формы", как любят говорить современные архитекторы. Вся история архитектуры — это история поисков гармонического единства "функции — конструкции — формы", это история непрерывного восхождения на пути к вершине, имя которой "прочность — польза — красота ".
 Здание фирмы 'Эссо' в Риме — предвестник новой архитектоники. Арх. Дж. Лафунте, Г. Ре-беккини. 1980
И все-таки одному из начал — красоте — зодчие придают особое значение, ибо без красоты, без искусства архитектуры вообще нет, остаются только серые безликие строения. Памятник архитектуры может стать непрочным и бесполезным (таковым сейчас стал двадцатидвухглавый красавец Преображенский собор на острове Кижи — жемчужина древнерусского деревянного зодчества), но памятник архитектуры не может быть некрасивым, ибо в таком случае он из памятника превращается в строение. Вот почему в формуле архитектуры, данной известным советским архитектором, лауреатом Государственных премий Ф. А. Новиковым, искусство стоит не слагаемым, а сомножителем: архитектура = (наука + техника) — искусство. Вот почему с этой формулы начинается настоящий параграф: она с математической откровенностью говорит, что если множитель "искусство" окажется равным нулю, то и весь результат — "архитектура" — будет равен нулю. И сколько бы мы ни увеличивали стоящие в скобках слагаемые, как бы ни были глубоки научные изыскания и сколь современна ни была бы строительная техника, их детище окажется мертвым, равным нулю, пока его не оживит волшебный сомножитель искусства. Вот об этом сомножителе в формуле архитектуры и пойдет речь далее.
Здание фирмы 'Эссо' в Риме — предвестник новой архитектоники. Арх. Дж. Лафунте, Г. Ре-беккини. 1980
И все-таки одному из начал — красоте — зодчие придают особое значение, ибо без красоты, без искусства архитектуры вообще нет, остаются только серые безликие строения. Памятник архитектуры может стать непрочным и бесполезным (таковым сейчас стал двадцатидвухглавый красавец Преображенский собор на острове Кижи — жемчужина древнерусского деревянного зодчества), но памятник архитектуры не может быть некрасивым, ибо в таком случае он из памятника превращается в строение. Вот почему в формуле архитектуры, данной известным советским архитектором, лауреатом Государственных премий Ф. А. Новиковым, искусство стоит не слагаемым, а сомножителем: архитектура = (наука + техника) — искусство. Вот почему с этой формулы начинается настоящий параграф: она с математической откровенностью говорит, что если множитель "искусство" окажется равным нулю, то и весь результат — "архитектура" — будет равен нулю. И сколько бы мы ни увеличивали стоящие в скобках слагаемые, как бы ни были глубоки научные изыскания и сколь современна ни была бы строительная техника, их детище окажется мертвым, равным нулю, пока его не оживит волшебный сомножитель искусства. Вот об этом сомножителе в формуле архитектуры и пойдет речь далее.
14. Пропорция — математика архитектурной гармонии
Гармония — вот что лежит в основе всех видов искусства на всем протяжении человеческой истории.И. Жолтовский
Ты ползал вокруг могучих развалин, чтобы вымолить у них тайну пропорции.И. В. Гёте
 Церковь Покрова Богородицы на Hep ли. 1165. Весенним половодьем церковь плывет над водой, будто сказочное видение
Весенним половодьем белым видением из сказочного града Китежа встает над водой, залившей луга, церковь Покрова Богородицы... "Сей же великий князь Андрей, аще печалию о скончавшемся сыне объят быв, и скорбяше, обаче более в богоугодныя дела поощряшеся... на реке Клязьме, в лугу, нача здати церковь во имя Пресвятыя Богородицы Честнаго ея Покрова, на устьи реки Нерли... и помо-щию Пресвятыя Богоматере оную церковь единым летом соверши",- сказано в житии великого князя Андрея Боголюбского о постройке храма в лето 1165. Более восьмисот раз разливалась с тех пор тихая Нерль, и кажется, будто церковь Покрова родилась вместе с речкой, ее лугами и перелесками, а не стоит на искусственном холме, на мощном десятиметровом фундаменте, созданном руками человека... В чем красота и очарование церкви Покрова на Нерли? Ведь она имеет скромные размеры (высота от основания до маковки — 24 м), ее архитектурные формы крайне просты, а белокаменные украшения сдержаны и лаконичны. И тем не менее церковь по праву считается жемчужиной русской архитектуры. Почему?
Ответить на этот вопрос лучше всего словами выдающегося советского зодчего, автора гостиницы "Москва", Казанского вокзала, академика А. В. Щусева (1873- 1949): "Пожалуй, самым трудным и вместе с тем обязательным в архитектурном творчестве является простота. Простота форм обязывает придавать прекрасные пропорции и соотношения, которые сообщили бы им необходимую гармонию".
Но и за 300 лет до Щусева представитель другой эпохи и другого архитектурного направления, французский зодчий Франсуа Блондель (1618-1686) в своем "Курсе архитектуры" восторженно писал о пропорциях: "Удовлетворение, которое мы испытываем, глядя на прекрасное произведение искусства, проистекает оттого, что в нем соблюдены правила и мера, ибо удовольствие в нас вызывают единственно лишь пропорции. Если же они отсутствуют, то, сколько бы мы ни украшали здание, эти наружные украшения не заменят нам внутреннюю красоту и привлекательность, коль скоро их нет, и, пожалуй, можно сказать, что уродство становится еще ненавистнее и невыносимее, чем пышнее наружные украшения, чем дороже или роскошнее материал... Дабы подкрепить наше утверждение, я заявляю, что красота, возникающая из меры и пропорции, вовсе не требует дорогих материалов и изящной работы, дабы вызвать восхищение, напротив, она сверкает и делается все ощутимее, проступая сквозь грязь и хаос материала и его обработки. Нам приятно смотреть на некоторые соотношения тех готических зданий, красота которых, очевидно, возникла из симметрии и пропорций между целым и частями и внутри отдельных частей, и видна, невзирая на уродливые трещины и скрывающие их украшения".
Огромную роль пропорций прекрасно осознавали древнегреческие и древнеегипетские зодчие. Более того, по мнению другого французского архитектора и теоретика Виолле-ле-Дюка (1814 — 1879), "большое достоинство греческих зодчих состояло в том, что у них были выработаны законы пропорциональности в архитектуре и что греки им подчинялись, несчастье нашего времени составляет убеждение, что архитектурное произведение может быть создано, руководствуясь одним лишь воображением, одной лишь фантазией, подчиняясь единственно так называемому вкусу, одним словом так, как создается туалет красивой женщины".
В чем же заключается сила архитектурных пропорций? В том, что архитектурные пропорции — это математика зодчего. А математика — это универсальный язык науки (см. с. 40), поэтому мы можем сказать, что пропорции — это универсальный язык архитектуры, язык всеобъемлющий и всесильный, как всеобъемлюща и всесильна математика. Обратим внимание на то, что не случайно в высказываниях архитекторов о пропорциях так часто встречаются слова "внутренняя красота", "простота", "всеобщность", т. е. те же слова, которыми в главе 2 мы описывали качества математики.
Уже Платон глубоко понимал не только математическую, но и эстетическую сущность пропорции, позволяющей связывать целое и его части. Об этом свидетельствует следующий отрывок из цитированного нами "Тимея": "Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться связь, которая скрепила бы их. Это наилучшим образом может выполнить пропорция, ибо если три числа обладают тем свойством, что среднее так относится к меньшему, как большее к среднему, и, наоборот, меньшее так относится к среднему, как среднее к большему, то последнее и первое и будет средним, а среднее первым и последним".
Этот отрывок, как и все у Платона, не сразу поддается пониманию. Однако он станет совершенно прозрачным, если его перевести на язык математики. Вводя обозначения: а — большее ("последнее") число, х — среднее число ("связь"), у — меньшее ("первое") число,- имеем х:у = =а:x, или у:х = х: а, или ау = х2. С легкой руки Луки Пачоли (см. с. 209) считалось, что под х и у Платон понимал части целого а, т. е. что х + у = а, и поэтому Платон говорил о золотой пропорции (12.1) а:х = х:(а — х). Отсюда пошло мнение, что античные пропорции основаны на золотом сечении. Однако, как считает сегодня архитектор И. Ш. Шевелев, такое мнение не обосновано и речь у Платона идет о геометрической пропорции общего вида а:х = х:у, откуда следует совершенно иная теория античных пропорций (см. гл. 16).
Пропорции являются важным и надежным средством зодчего для достижения хрупкого и тонко сбалансированного равновесия между целым и его частями, имя которому — гармония. Напомним, что по сравнению с композитором или скульптором архитектор находится в более сложном положении, ибо на пути к гармонии он должен заботиться не только о "красоте", но также и о "пользе", и "прочности". Еще Гораций в послании к братьям Пизонам "Наука поэзии" в образной форме говорил о том, как непросто красиво и целесообразно соединять части в единое целое, что взятые вместе "части": лицо женщины, грива льва, тигровая шкура или павлиний хвост, которые сами по себе являются своеобразными эталонами красоты,- не только не дают нам прекрасного "целого"- гармонии, но представляют, по крайней мере, странное зрелище.
Церковь Покрова Богородицы на Hep ли. 1165. Весенним половодьем церковь плывет над водой, будто сказочное видение
Весенним половодьем белым видением из сказочного града Китежа встает над водой, залившей луга, церковь Покрова Богородицы... "Сей же великий князь Андрей, аще печалию о скончавшемся сыне объят быв, и скорбяше, обаче более в богоугодныя дела поощряшеся... на реке Клязьме, в лугу, нача здати церковь во имя Пресвятыя Богородицы Честнаго ея Покрова, на устьи реки Нерли... и помо-щию Пресвятыя Богоматере оную церковь единым летом соверши",- сказано в житии великого князя Андрея Боголюбского о постройке храма в лето 1165. Более восьмисот раз разливалась с тех пор тихая Нерль, и кажется, будто церковь Покрова родилась вместе с речкой, ее лугами и перелесками, а не стоит на искусственном холме, на мощном десятиметровом фундаменте, созданном руками человека... В чем красота и очарование церкви Покрова на Нерли? Ведь она имеет скромные размеры (высота от основания до маковки — 24 м), ее архитектурные формы крайне просты, а белокаменные украшения сдержаны и лаконичны. И тем не менее церковь по праву считается жемчужиной русской архитектуры. Почему?
Ответить на этот вопрос лучше всего словами выдающегося советского зодчего, автора гостиницы "Москва", Казанского вокзала, академика А. В. Щусева (1873- 1949): "Пожалуй, самым трудным и вместе с тем обязательным в архитектурном творчестве является простота. Простота форм обязывает придавать прекрасные пропорции и соотношения, которые сообщили бы им необходимую гармонию".
Но и за 300 лет до Щусева представитель другой эпохи и другого архитектурного направления, французский зодчий Франсуа Блондель (1618-1686) в своем "Курсе архитектуры" восторженно писал о пропорциях: "Удовлетворение, которое мы испытываем, глядя на прекрасное произведение искусства, проистекает оттого, что в нем соблюдены правила и мера, ибо удовольствие в нас вызывают единственно лишь пропорции. Если же они отсутствуют, то, сколько бы мы ни украшали здание, эти наружные украшения не заменят нам внутреннюю красоту и привлекательность, коль скоро их нет, и, пожалуй, можно сказать, что уродство становится еще ненавистнее и невыносимее, чем пышнее наружные украшения, чем дороже или роскошнее материал... Дабы подкрепить наше утверждение, я заявляю, что красота, возникающая из меры и пропорции, вовсе не требует дорогих материалов и изящной работы, дабы вызвать восхищение, напротив, она сверкает и делается все ощутимее, проступая сквозь грязь и хаос материала и его обработки. Нам приятно смотреть на некоторые соотношения тех готических зданий, красота которых, очевидно, возникла из симметрии и пропорций между целым и частями и внутри отдельных частей, и видна, невзирая на уродливые трещины и скрывающие их украшения".
Огромную роль пропорций прекрасно осознавали древнегреческие и древнеегипетские зодчие. Более того, по мнению другого французского архитектора и теоретика Виолле-ле-Дюка (1814 — 1879), "большое достоинство греческих зодчих состояло в том, что у них были выработаны законы пропорциональности в архитектуре и что греки им подчинялись, несчастье нашего времени составляет убеждение, что архитектурное произведение может быть создано, руководствуясь одним лишь воображением, одной лишь фантазией, подчиняясь единственно так называемому вкусу, одним словом так, как создается туалет красивой женщины".
В чем же заключается сила архитектурных пропорций? В том, что архитектурные пропорции — это математика зодчего. А математика — это универсальный язык науки (см. с. 40), поэтому мы можем сказать, что пропорции — это универсальный язык архитектуры, язык всеобъемлющий и всесильный, как всеобъемлюща и всесильна математика. Обратим внимание на то, что не случайно в высказываниях архитекторов о пропорциях так часто встречаются слова "внутренняя красота", "простота", "всеобщность", т. е. те же слова, которыми в главе 2 мы описывали качества математики.
Уже Платон глубоко понимал не только математическую, но и эстетическую сущность пропорции, позволяющей связывать целое и его части. Об этом свидетельствует следующий отрывок из цитированного нами "Тимея": "Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться связь, которая скрепила бы их. Это наилучшим образом может выполнить пропорция, ибо если три числа обладают тем свойством, что среднее так относится к меньшему, как большее к среднему, и, наоборот, меньшее так относится к среднему, как среднее к большему, то последнее и первое и будет средним, а среднее первым и последним".
Этот отрывок, как и все у Платона, не сразу поддается пониманию. Однако он станет совершенно прозрачным, если его перевести на язык математики. Вводя обозначения: а — большее ("последнее") число, х — среднее число ("связь"), у — меньшее ("первое") число,- имеем х:у = =а:x, или у:х = х: а, или ау = х2. С легкой руки Луки Пачоли (см. с. 209) считалось, что под х и у Платон понимал части целого а, т. е. что х + у = а, и поэтому Платон говорил о золотой пропорции (12.1) а:х = х:(а — х). Отсюда пошло мнение, что античные пропорции основаны на золотом сечении. Однако, как считает сегодня архитектор И. Ш. Шевелев, такое мнение не обосновано и речь у Платона идет о геометрической пропорции общего вида а:х = х:у, откуда следует совершенно иная теория античных пропорций (см. гл. 16).
Пропорции являются важным и надежным средством зодчего для достижения хрупкого и тонко сбалансированного равновесия между целым и его частями, имя которому — гармония. Напомним, что по сравнению с композитором или скульптором архитектор находится в более сложном положении, ибо на пути к гармонии он должен заботиться не только о "красоте", но также и о "пользе", и "прочности". Еще Гораций в послании к братьям Пизонам "Наука поэзии" в образной форме говорил о том, как непросто красиво и целесообразно соединять части в единое целое, что взятые вместе "части": лицо женщины, грива льва, тигровая шкура или павлиний хвост, которые сами по себе являются своеобразными эталонами красоты,- не только не дают нам прекрасного "целого"- гармонии, но представляют, по крайней мере, странное зрелище.
Но сами шедевры древней архитектуры безмолвно взывали к обратному: античные пропорции основаны на иррациональных отношениях! В самом деле, ведь "точную соразмерность" частей и целого можно достигнуть и другим путем — геометрическим. Например, построив квадрат со стороной АВ и измерив шнуром его диагональ АС, нетрудно было получить иррациональную пропорцию АВ/АС = 1/
 , даже не зная иррациональных чисел. Далее, отложив с помощью шнура на продолжении стороны АВ диагональ AC = AD, легко было построить прямоугольник с иррациональным отношением сторон DE/AD = 1/
, даже не зная иррациональных чисел. Далее, отложив с помощью шнура на продолжении стороны АВ диагональ AC = AD, легко было построить прямоугольник с иррациональным отношением сторон DE/AD = 1/ . Повторив эту операцию несколько раз, можно получить систему прямоугольников с иррациональными отношениями сторон. Ясно, что прямоугольник AHKN на рисунке (б) состоит из двух квадратов. Таким образом, мы получаем еще один практически удобный способ получения иррациональных отношений — систему двух квадратов. Два квадрата, приставленных один к другому, дают иррациональные отношения ВС/АС = 1/√5, АВ/АС = 2/√5, а с помощью двух операций циркулем или шнурком, как показано на рисунке (в), в них можно получить и золотое сечение ЕВ/АЕ = АЕ/АВ = (√5 — 1)/2 = φ, АВ/АЕ = АЕ/ЕВ=1/φ = (√5 + 1)/2 = Φ (см. (12.1)-(12.3)).
Помимо гипотез, построенных на изучении геометрических свойств античных памятников, были и "материальные" свидетельства того, что древние пользовались иррациональными пропорциями. История сохранила имена древнейших математиков и зодчих — Имхотепа и Хесиры, живших в XXVIII веке до н. э., — строителей первой в истории Древнего Египта пирамиды фараона Джосера в Саккаре. Это были высокочтимые люди, о чем свидетельствуют древнеегипетские иероглифы: "Визирь фараона Нижнего Египта, первый после фараона Верхнего Египта, управитель великой палаты, почетный гражданин, великий жрец Гелиополиса, Имхотеп, строитель и скульптор"; "Хесира, начальник Дестиутса и начальник Бута, начальник врачей, писец фараона, приближенный фараона, жрец Гора, главный архитектор фараона, Верховный начальник десятки Юга и резчик". Хесира был похоронен вблизи пирамиды Джосера. Стены его гробницы украшали рельефы на досках. Поистине потрясающе, что древние доски, которым почти 5000 лет, прекрасно сохранились и выставлены сегодня в Египетском музее в Каире. На двух панелях изображены фигуры владельца гробницы, которые считаются лучшими образцами рельефного портрета в древнеегипетском искусстве. Но для нас эти рельефы интересны прежде всего потому, что в руках у Хесиры, помимо прибора для письма, изображены две палки — два эталона меры. Если теперь взять линейку, измерить Длины этих палок и найти их отношение, то мы обнаружим, что они относятся как 1/√5 = 0,447!
. Повторив эту операцию несколько раз, можно получить систему прямоугольников с иррациональными отношениями сторон. Ясно, что прямоугольник AHKN на рисунке (б) состоит из двух квадратов. Таким образом, мы получаем еще один практически удобный способ получения иррациональных отношений — систему двух квадратов. Два квадрата, приставленных один к другому, дают иррациональные отношения ВС/АС = 1/√5, АВ/АС = 2/√5, а с помощью двух операций циркулем или шнурком, как показано на рисунке (в), в них можно получить и золотое сечение ЕВ/АЕ = АЕ/АВ = (√5 — 1)/2 = φ, АВ/АЕ = АЕ/ЕВ=1/φ = (√5 + 1)/2 = Φ (см. (12.1)-(12.3)).
Помимо гипотез, построенных на изучении геометрических свойств античных памятников, были и "материальные" свидетельства того, что древние пользовались иррациональными пропорциями. История сохранила имена древнейших математиков и зодчих — Имхотепа и Хесиры, живших в XXVIII веке до н. э., — строителей первой в истории Древнего Египта пирамиды фараона Джосера в Саккаре. Это были высокочтимые люди, о чем свидетельствуют древнеегипетские иероглифы: "Визирь фараона Нижнего Египта, первый после фараона Верхнего Египта, управитель великой палаты, почетный гражданин, великий жрец Гелиополиса, Имхотеп, строитель и скульптор"; "Хесира, начальник Дестиутса и начальник Бута, начальник врачей, писец фараона, приближенный фараона, жрец Гора, главный архитектор фараона, Верховный начальник десятки Юга и резчик". Хесира был похоронен вблизи пирамиды Джосера. Стены его гробницы украшали рельефы на досках. Поистине потрясающе, что древние доски, которым почти 5000 лет, прекрасно сохранились и выставлены сегодня в Египетском музее в Каире. На двух панелях изображены фигуры владельца гробницы, которые считаются лучшими образцами рельефного портрета в древнеегипетском искусстве. Но для нас эти рельефы интересны прежде всего потому, что в руках у Хесиры, помимо прибора для письма, изображены две палки — два эталона меры. Если теперь взять линейку, измерить Длины этих палок и найти их отношение, то мы обнаружим, что они относятся как 1/√5 = 0,447!
 Примеры геометрического построения иррациональных отношений. Диагональ квадрата (а). Система прямоугольников с иррациональными отношениями сторон (б). Золотое сечение в системе 'двойной квадрат' (в). Помпейскйй пропорциональный циркуль, установленный на золотое сечение (г)
Примеры геометрического построения иррациональных отношений. Диагональ квадрата (а). Система прямоугольников с иррациональными отношениями сторон (б). Золотое сечение в системе 'двойной квадрат' (в). Помпейскйй пропорциональный циркуль, установленный на золотое сечение (г)
 Зодчий Хесира. Фрагмент деревянной панели из гробницы Хесиры в Саккаре. XXVIII в. до н. э. Рельеф Хесиры — не только лучший образец древнеегипетского рельефного портрета, не только древнейшее в мире художественное произведение на дереве, но и научное свидетельство о древнеегипетской системе архитектурного пропорционирования
Существует и еще одно удивительное свидетельство мудрости древних. В Неаполе, в Национальном музее, хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных подлине ножек, скрепленных винтом наподобие ножниц, и позволяет (минуя вычисления!) для любого отрезка получать отрезок, находящийся с ним в заданном отношении. Действие пропорционального циркуля основано на подобии треугольников и не требует особых комментариев (г). Так вот, помпейский циркуль наглухо закреплен в отношении золотого сечения! Это легко проверить, зная размеры циркуля, которые на рисунке (г) указаны в миллиметрах.
Кроме помпейского, особый интерес представляет циркуль из Музея терм в Риме. Он также имеет длину вполовину римского фута — 146 мм, но настроен на другую иррациональную пропорцию (больший отрезок — 92 мм, меньший — 52 мм):
Зодчий Хесира. Фрагмент деревянной панели из гробницы Хесиры в Саккаре. XXVIII в. до н. э. Рельеф Хесиры — не только лучший образец древнеегипетского рельефного портрета, не только древнейшее в мире художественное произведение на дереве, но и научное свидетельство о древнеегипетской системе архитектурного пропорционирования
Существует и еще одно удивительное свидетельство мудрости древних. В Неаполе, в Национальном музее, хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных подлине ножек, скрепленных винтом наподобие ножниц, и позволяет (минуя вычисления!) для любого отрезка получать отрезок, находящийся с ним в заданном отношении. Действие пропорционального циркуля основано на подобии треугольников и не требует особых комментариев (г). Так вот, помпейский циркуль наглухо закреплен в отношении золотого сечения! Это легко проверить, зная размеры циркуля, которые на рисунке (г) указаны в миллиметрах.
Кроме помпейского, особый интерес представляет циркуль из Музея терм в Риме. Он также имеет длину вполовину римского фута — 146 мм, но настроен на другую иррациональную пропорцию (больший отрезок — 92 мм, меньший — 52 мм):
 Геометрически эта пропорция означает отношение отрезка AD ко всей диагонали АС (см. с. 199). Как считает архитектор П. Ш. Шевелев, именно с помощью такого циркуля мог быть построен чертеж Парфенона.
Но, несмотря на многие доказательства, авторитет Витрувия (возможно, и неправильно понятого), авторитет модульной системы в архитектуре, был столь велик, что мысль о геометрическом построении иррациональных пропорций древними оформилась лишь к XX веку. Но как именно, по какой системе древние строили свои замечательные пропорции? Это по-прежнему оставалось тайной, и здесь теоретики архитектуры могли довольствоваться лишь гипотезами. Стремление познать тайны древних пропорций было огромным. Еще бы: ведь это дало бы ключ к созданию новых шедевров!
Естественно, что каждый автор стремился проверить свою теорию на пропорциях Парфенона. Парфенон был и остается совершеннейшим из архитектурных сооружений, архитектурной скульптурой, мраморным сводом законов античного зодчества. Уникальность и бессмертие Парфенона осознавали уже в античности. Вот как писал о Парфеноне в I веке древнегреческий писатель, историк и философ Плутарх (ок. 46 — ок. 127): "Так вырастали эти строения, гордые в своем величии, непревзойденные по своей волшебной красоте. Такими они были потому, что мастера старались превзойти друг друга, каждый из них свое ремесло превращал в художественное творчество... И так эти здания словно дышат молодостью, из века в век защищающей их от зуба времени. Можно сказать, что от этих творений веет ароматом каменных цветов и в них живет душа, которая никогда не стареет".
Теорий античных пропорций, и в частности пропорций Парфенона, становилось все больше. Наконец, к середине XX века их стало столько, что сами архитекторы перестали понимать, какие же из этих теорий справедливы и есть ли среди них таковые. Некоторые архитекторы вообще потеряли веру в пропорции. Вот, например, выдержка из книги архитектора Г. Б. Борисовского " Наука, техника, искусство":
"Все исследователи, почти как правило, дают анализ пропорций Парфенона,
стараясь привлечь его в качестве авторитетного свидетеля правоты их теории. Это делают Тирш, Цейзинг, Жолтовский, Гримм и др. Все ищут в нем именно тот порядок, который они отстаивают своей теорией. Если сопоставить эти анализы, то обнаружится несколько странная ситуация.
Тирш еще в прошлом столетии заявил: пропорции Парфенона построены на подобии. Вот чертеж, неоспоримо доказывающий это. (Чудесно,- говорят все.)
Цейзинг уверяет: в основе пропорций Парфенона лежит золотое сечение. Вот чертеж, это подтверждающий. (Все в восхищении.)
Жолтовский считает: Парфенон зиждется на золотом сечении. И дает совершенно иной чертеж, неоспоримо подтверждающий это. (Все в восторге.)
Гримм утверждает то же, что Цейзинг и Жолтовский, и приводит другой чертеж, не менее убедительный, хотя и совсем не похожий на два предыдущих. (Все в изумлении.)
Хэмбридж утверждает: пропорции Парфенона складываются из динамических прямоугольников. Вот чертеж, неоспоримо это доказывающий. (Все аплодируют.)
Мессель заявляет: пропорции Парфенона основаны на членении окружности. Вот чертеж, убеждающий нас в этом. (Аплодисменты, переходящие в овацию.)
Не так давно архитектор И. Шевелев опубликовал статью и небольшую книгу, в которой утверждает, что пропорции Парфенона основаны на соотношении 1:√5, и представляет чертеж с расчетом, убедительно это подтверждающим. (Аплодисментов пока не слышно.)
Явно здесь что-то не так ..."
Действительно, глядя на различные чертежи пропорций Парфенона, кажется, что между ними нет ничего общего. Между тем здесь все "так". Различные анализы пропорций Парфенона — это различные доказательства "теоремы Парфенона", которая, как и теорема Пифагора, имеет много доказательств. Но от этого "теорема Парфенона" не становится хуже (или вовсе перестает существовать, как кажется Борисовскому), а, напротив, предстает перед нами во всем своем богатстве и красоте. Ибо множество доказательств свидетельствует о большом числе конкретных реализаций, о "всеобщности" доказываемого, а всеобщность является одним из признаков красоты науки (см. с. 29, 30).
Геометрически эта пропорция означает отношение отрезка AD ко всей диагонали АС (см. с. 199). Как считает архитектор П. Ш. Шевелев, именно с помощью такого циркуля мог быть построен чертеж Парфенона.
Но, несмотря на многие доказательства, авторитет Витрувия (возможно, и неправильно понятого), авторитет модульной системы в архитектуре, был столь велик, что мысль о геометрическом построении иррациональных пропорций древними оформилась лишь к XX веку. Но как именно, по какой системе древние строили свои замечательные пропорции? Это по-прежнему оставалось тайной, и здесь теоретики архитектуры могли довольствоваться лишь гипотезами. Стремление познать тайны древних пропорций было огромным. Еще бы: ведь это дало бы ключ к созданию новых шедевров!
Естественно, что каждый автор стремился проверить свою теорию на пропорциях Парфенона. Парфенон был и остается совершеннейшим из архитектурных сооружений, архитектурной скульптурой, мраморным сводом законов античного зодчества. Уникальность и бессмертие Парфенона осознавали уже в античности. Вот как писал о Парфеноне в I веке древнегреческий писатель, историк и философ Плутарх (ок. 46 — ок. 127): "Так вырастали эти строения, гордые в своем величии, непревзойденные по своей волшебной красоте. Такими они были потому, что мастера старались превзойти друг друга, каждый из них свое ремесло превращал в художественное творчество... И так эти здания словно дышат молодостью, из века в век защищающей их от зуба времени. Можно сказать, что от этих творений веет ароматом каменных цветов и в них живет душа, которая никогда не стареет".
Теорий античных пропорций, и в частности пропорций Парфенона, становилось все больше. Наконец, к середине XX века их стало столько, что сами архитекторы перестали понимать, какие же из этих теорий справедливы и есть ли среди них таковые. Некоторые архитекторы вообще потеряли веру в пропорции. Вот, например, выдержка из книги архитектора Г. Б. Борисовского " Наука, техника, искусство":
"Все исследователи, почти как правило, дают анализ пропорций Парфенона,
стараясь привлечь его в качестве авторитетного свидетеля правоты их теории. Это делают Тирш, Цейзинг, Жолтовский, Гримм и др. Все ищут в нем именно тот порядок, который они отстаивают своей теорией. Если сопоставить эти анализы, то обнаружится несколько странная ситуация.
Тирш еще в прошлом столетии заявил: пропорции Парфенона построены на подобии. Вот чертеж, неоспоримо доказывающий это. (Чудесно,- говорят все.)
Цейзинг уверяет: в основе пропорций Парфенона лежит золотое сечение. Вот чертеж, это подтверждающий. (Все в восхищении.)
Жолтовский считает: Парфенон зиждется на золотом сечении. И дает совершенно иной чертеж, неоспоримо подтверждающий это. (Все в восторге.)
Гримм утверждает то же, что Цейзинг и Жолтовский, и приводит другой чертеж, не менее убедительный, хотя и совсем не похожий на два предыдущих. (Все в изумлении.)
Хэмбридж утверждает: пропорции Парфенона складываются из динамических прямоугольников. Вот чертеж, неоспоримо это доказывающий. (Все аплодируют.)
Мессель заявляет: пропорции Парфенона основаны на членении окружности. Вот чертеж, убеждающий нас в этом. (Аплодисменты, переходящие в овацию.)
Не так давно архитектор И. Шевелев опубликовал статью и небольшую книгу, в которой утверждает, что пропорции Парфенона основаны на соотношении 1:√5, и представляет чертеж с расчетом, убедительно это подтверждающим. (Аплодисментов пока не слышно.)
Явно здесь что-то не так ..."
Действительно, глядя на различные чертежи пропорций Парфенона, кажется, что между ними нет ничего общего. Между тем здесь все "так". Различные анализы пропорций Парфенона — это различные доказательства "теоремы Парфенона", которая, как и теорема Пифагора, имеет много доказательств. Но от этого "теорема Парфенона" не становится хуже (или вовсе перестает существовать, как кажется Борисовскому), а, напротив, предстает перед нами во всем своем богатстве и красоте. Ибо множество доказательств свидетельствует о большом числе конкретных реализаций, о "всеобщности" доказываемого, а всеобщность является одним из признаков красоты науки (см. с. 29, 30).
 Различные методы анализа пропорций Парфенона: Жолтовский (а), Хэмбидж (б), Мессель (в), Шевелев (г)
В самом деле, Тирш говорит о подобии. Но подобие — это геометрическое выражение пропорциональности.
Цейзинг и Жолтовский уточняют: в пропорциях Парфенона имеется золотое сечение. В частности, в золотой пропорции соотносятся главные вертикальные размеры портика: высота ВС поддерживающих частей (основание и колонны) и высота АС поддерживаемых частей (антаблемент и фронтон).
Гримм, воспитанный на целочисленных музыкальных пропорциях Возрождения, считает, что главные вертикали Парфенона находятся в отношении малой сексты (8/5). Казалось бы, совершенно иной, "музыкальный", подход. Но и здесь нет противоречия с Цейзингом и Жолтовским, ибо 8/5, как будет показано в следующей главе, есть отношение двух членов ряда Фибоначчи и является одним из рациональных приближений коэффициента золотого сечения Ф (8/5 = 1,600; Φ ≈ 1,618). Гримм правильно заметил, что золотое сечение в главных вертикалях Парфенона выдержано лишь приблизительно, и этим уточнил Цейзинга и Жолтовского.
Различные методы анализа пропорций Парфенона: Жолтовский (а), Хэмбидж (б), Мессель (в), Шевелев (г)
В самом деле, Тирш говорит о подобии. Но подобие — это геометрическое выражение пропорциональности.
Цейзинг и Жолтовский уточняют: в пропорциях Парфенона имеется золотое сечение. В частности, в золотой пропорции соотносятся главные вертикальные размеры портика: высота ВС поддерживающих частей (основание и колонны) и высота АС поддерживаемых частей (антаблемент и фронтон).
Гримм, воспитанный на целочисленных музыкальных пропорциях Возрождения, считает, что главные вертикали Парфенона находятся в отношении малой сексты (8/5). Казалось бы, совершенно иной, "музыкальный", подход. Но и здесь нет противоречия с Цейзингом и Жолтовским, ибо 8/5, как будет показано в следующей главе, есть отношение двух членов ряда Фибоначчи и является одним из рациональных приближений коэффициента золотого сечения Ф (8/5 = 1,600; Φ ≈ 1,618). Гримм правильно заметил, что золотое сечение в главных вертикалях Парфенона выдержано лишь приблизительно, и этим уточнил Цейзинга и Жолтовского.
Но все эти исследования носили эмпирический характер и не давали целостной системы античного пропорционирования. Первой такой попыткой была система динамических прямоугольников американского искусствоведа Хэмбиджа. Прямоугольники с иррациональным отношением сторон Хэмбидж называет динамическими, связывая с ними идею роста, движения и гармонии в природе и искусстве. Особую роль Хэмбидж отводит прямоугольнику с отношением сторон
 . Хэмбидж разбивает фасад Парфенона на ряд динамических прямоугольников (l:√5) и квадратов (1:1). Здесь все ново и спорно: и подход, и метод, и чертеж. Но что будет с интересующими нас главными вертикалями? Выражая вертикальные элементы х, у, z через ширину основания а:х — а/2√5, у = а/4√5, z = а/4, легко видеть, что главные вертикали Парфенона по-прежнему находятся в золотой пропорции
. Хэмбидж разбивает фасад Парфенона на ряд динамических прямоугольников (l:√5) и квадратов (1:1). Здесь все ново и спорно: и подход, и метод, и чертеж. Но что будет с интересующими нас главными вертикалями? Выражая вертикальные элементы х, у, z через ширину основания а:х — а/2√5, у = а/4√5, z = а/4, легко видеть, что главные вертикали Парфенона по-прежнему находятся в золотой пропорции  Метод пропорционирования немецкого теоретика Месселя основан на десятикрат ном делении окружности. Мессель считает, что обычный циркуль (или шнур) являлся основным рабочим инструментом античного и средневекового зодчего. Подход Месселя также оригинален и также спорен во всех аспектах, кроме одного — математического. Действительно, как мы увидим в следующей главе, при делении окружности на десять частей можно получить весь ряд золотого сечения (12.4)! Поэтому В1С1:С1А1 = Φ ≈ВС:СА, т. е. интересующие нас главные вертикали Парфенона приблизительно находятся в золотой пропорции.
В главе 16 мы подробнее познакомимся с системой пропорционирования Шевелева и покажем, что в этой системе для главных вертикалей также приближенно выполняется золотая пропорция.
Заметим, что во всех случаях приближенного выполнения пропорции золотого сечения ошибка не превышает 1%. К сожалению, существующие обмеры Парфенона выполнены примерно с такой же точностью и поэтому не могут служить критерием истинности теории. Но и более тщательные обмеры Парфенона нужно будет осторожно применять в качестве критерия истины, ибо при строительстве сооружения 2500 лет назад, разумеется, могли быть допущены отклонения от замысла автора.
Вот почему главным критерием истинности той или иной гипотезы будет оставаться ее логическая непротиворечивость, ее математическая целостность. Этим требованиям, по нашему мнению, наиболее полно удовлетворяет система Шевелева, которая не получила еще должного признания. Система Шевелева позволяет из одного размера — ширины стилобата (верхней ступени основания) — получить все размеры Парфенона в диапазоне от 69,5 м (длина стилобата) до 16 см (высота шейки капители)! Таким образом, именно в системе Шевелева выполняется принцип гармонии Гераклита: "из всего — единое, из единого — все".
Итак, главный вопрос о том, какой системой пропорций пользовался гениальный создатель Парфенона зодчий Иктин, пока остается открытым. Заметим, что мы остановились только на соотношении двух главных вертикалей Парфенона. В золотой пропорции соотносятся и многие другие элементы Парфенона, однако подробный анализ пропорций этого великого архитектурного памятника занял бы объем, по крайней мере равный объему всей этой книги. Мы же в нашем кратком обозрении убедились, что разговор об архитектурных пропорциях неизбежно приводит к золотой, или, как ее называли во времена Возрождения, божественной пропорции. Поэтому нам необходимо подробнее познакомиться с математическими свойствами этого интереснейшего феномена.
Метод пропорционирования немецкого теоретика Месселя основан на десятикрат ном делении окружности. Мессель считает, что обычный циркуль (или шнур) являлся основным рабочим инструментом античного и средневекового зодчего. Подход Месселя также оригинален и также спорен во всех аспектах, кроме одного — математического. Действительно, как мы увидим в следующей главе, при делении окружности на десять частей можно получить весь ряд золотого сечения (12.4)! Поэтому В1С1:С1А1 = Φ ≈ВС:СА, т. е. интересующие нас главные вертикали Парфенона приблизительно находятся в золотой пропорции.
В главе 16 мы подробнее познакомимся с системой пропорционирования Шевелева и покажем, что в этой системе для главных вертикалей также приближенно выполняется золотая пропорция.
Заметим, что во всех случаях приближенного выполнения пропорции золотого сечения ошибка не превышает 1%. К сожалению, существующие обмеры Парфенона выполнены примерно с такой же точностью и поэтому не могут служить критерием истинности теории. Но и более тщательные обмеры Парфенона нужно будет осторожно применять в качестве критерия истины, ибо при строительстве сооружения 2500 лет назад, разумеется, могли быть допущены отклонения от замысла автора.
Вот почему главным критерием истинности той или иной гипотезы будет оставаться ее логическая непротиворечивость, ее математическая целостность. Этим требованиям, по нашему мнению, наиболее полно удовлетворяет система Шевелева, которая не получила еще должного признания. Система Шевелева позволяет из одного размера — ширины стилобата (верхней ступени основания) — получить все размеры Парфенона в диапазоне от 69,5 м (длина стилобата) до 16 см (высота шейки капители)! Таким образом, именно в системе Шевелева выполняется принцип гармонии Гераклита: "из всего — единое, из единого — все".
Итак, главный вопрос о том, какой системой пропорций пользовался гениальный создатель Парфенона зодчий Иктин, пока остается открытым. Заметим, что мы остановились только на соотношении двух главных вертикалей Парфенона. В золотой пропорции соотносятся и многие другие элементы Парфенона, однако подробный анализ пропорций этого великого архитектурного памятника занял бы объем, по крайней мере равный объему всей этой книги. Мы же в нашем кратком обозрении убедились, что разговор об архитектурных пропорциях неизбежно приводит к золотой, или, как ее называли во времена Возрождения, божественной пропорции. Поэтому нам необходимо подробнее познакомиться с математическими свойствами этого интереснейшего феномена.
15. Тайны золотого сечения
Геометрия владеет двумя сокровищами: одно из них — это теорема Пифагора, а другое — деление отрезка в среднем и крайнем отношении ... Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень.Пятиконечной звезде — около 3000 лет. Ее первые изображения донесли до нас вавилонские глиняные таблички. Из Древней Вавилонии в Средиземноморье, как полагают, звездчатый пятиугольник перевез Пифагор и сделал его символом жизни и здоровья, а также тайным опознавательным знаком. В средние века пентаграмма "предохраняла" от "нечистой силы", что, впрочем, не мешало называть ее "лапой ведьмы". Вспомним гётевского "Фауста":И. Кеплер
 (15.1)
т. е. "целое" (АВ) так относится к большей части (AD), как большая часть к меньшей (DB). Иначе говоря, точка D делит отрезок АВ в золотом сечении.
(15.1)
т. е. "целое" (АВ) так относится к большей части (AD), как большая часть к меньшей (DB). Иначе говоря, точка D делит отрезок АВ в золотом сечении.
 Точное деление окружности на 5 равных частей, описанное в 'Альмагесте' Птолемея. Ок 150 до н. э. (а). Приближенное построение пятиугольника по заданной стороне из 'Руководства к измерению' Дюрера 1525 (б). Цифрами обозначены последовательные положение ножки циркуля
Принимая сторону исходного правильного пятиугольника за единицу AF = AD = 1, полагая DB = x и, следовательно АВ = 1 + х, из (15.1) приходим к уравнению (12.1) при а = 1:
Точное деление окружности на 5 равных частей, описанное в 'Альмагесте' Птолемея. Ок 150 до н. э. (а). Приближенное построение пятиугольника по заданной стороне из 'Руководства к измерению' Дюрера 1525 (б). Цифрами обозначены последовательные положение ножки циркуля
Принимая сторону исходного правильного пятиугольника за единицу AF = AD = 1, полагая DB = x и, следовательно АВ = 1 + х, из (15.1) приходим к уравнению (12.1) при а = 1:
 которое имеет единственный положительный корень
которое имеет единственный положительный корень
 Поскольку
Поскольку
 (проверьте это), то мы окончательно находим: x = DB = AE = EF =...= φ, AD = DC = CB = AF = ... = 1, ED = EG = ...= = 1 — φ = φ2.
(проверьте это), то мы окончательно находим: x = DB = AE = EF =...= φ, AD = DC = CB = AF = ... = 1, ED = EG = ...= = 1 — φ = φ2.
 Ряд золотого сечения 1, φ, φ2, φ3, ... в последовательности звездчатых пятиугольников (а) и звездчатых десятиугольников (б)
Повторяя наши рассуждения для треугольника DGH, в котором DG = y, легко видеть, что стороны внутренней звезды будут равны φ3, а стороны ее внутреннего правильного пятиугольника — φ4. И т. д.
Таким образом, последовательность правильных пятиугольников и вписанных в них звезд образует ряд золотого сечения (12.4) при а=1:
Ряд золотого сечения 1, φ, φ2, φ3, ... в последовательности звездчатых пятиугольников (а) и звездчатых десятиугольников (б)
Повторяя наши рассуждения для треугольника DGH, в котором DG = y, легко видеть, что стороны внутренней звезды будут равны φ3, а стороны ее внутреннего правильного пятиугольника — φ4. И т. д.
Таким образом, последовательность правильных пятиугольников и вписанных в них звезд образует ряд золотого сечения (12.4) при а=1:
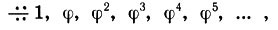 причем стороны правильных пятиугольников образуют ряд четных степеней:
причем стороны правильных пятиугольников образуют ряд четных степеней:
 а стороны звезд — ряд нечетных степеней:
а стороны звезд — ряд нечетных степеней:
 Наконец, если продолжить стороны правильного пятиугольника до пересечения, то получим звезду, сторона которой х находится со стороной исходного пятиугольника AF = 1 в золотом отношении, т. е. 1/х = φ ⇒ 1/φ = (√5 + 1)/2 = Φ
Итак, ряд золотого сечения можно неограниченно продолжить и в сторону увеличения, и в общем виде ряд золотого сечения будет иметь вид
Наконец, если продолжить стороны правильного пятиугольника до пересечения, то получим звезду, сторона которой х находится со стороной исходного пятиугольника AF = 1 в золотом отношении, т. е. 1/х = φ ⇒ 1/φ = (√5 + 1)/2 = Φ
Итак, ряд золотого сечения можно неограниченно продолжить и в сторону увеличения, и в общем виде ряд золотого сечения будет иметь вид
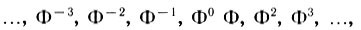 или
или
 (15.2)
Ряд (15.2) является геометрической прогрессией со знаменателем Ф. Однако из бесконечного множества геометрических прогрессий ряд (15.2) отличается уникальным свойством, называемым аддитивным свойством: сумма двух соседних членов ряда равна следующему члену ряда:
(15.2)
Ряд (15.2) является геометрической прогрессией со знаменателем Ф. Однако из бесконечного множества геометрических прогрессий ряд (15.2) отличается уникальным свойством, называемым аддитивным свойством: сумма двух соседних членов ряда равна следующему члену ряда:
 В самом деле, поскольку 1 + Φ = Φ2 (проверьте это), то
В самом деле, поскольку 1 + Φ = Φ2 (проверьте это), то
 (15.3)
Именно благодаря аддитивному свойству ряд золотого сечения играет важную роль в архитектуре, о чем мы подробнее поговорим чуть позже. А пока заметим, что вместо ряда (15.2) удобнее рассматривать две его "половинки":
возрастающую геометрическую прогрессию со знаменателем Φ≈1,618033988:
(15.3)
Именно благодаря аддитивному свойству ряд золотого сечения играет важную роль в архитектуре, о чем мы подробнее поговорим чуть позже. А пока заметим, что вместо ряда (15.2) удобнее рассматривать две его "половинки":
возрастающую геометрическую прогрессию со знаменателем Φ≈1,618033988:
 (15.4)
и убывающую геометрическую прогрессию со знаменателем φ = Φ-1≈0,618033988:
(15.4)
и убывающую геометрическую прогрессию со знаменателем φ = Φ-1≈0,618033988:
 (15.5)
Аддитивное свойство ряда (15.5) прекрасно иллюстрируется последовательностью вписанных друг в друга правильных пятиугольников и пятиконечных звезд (см. с. 206): AD = AE + ED (1 = φ + φ2), DG = DK + KG (φ = φ2 + φ3) и т. д.
Итак, правильный пятиугольник и пятиконечная звезда, образованная его диагоналями, обладают массой интересных свойств:
1. Пересекающиеся диагонали правильного пятиугольника делят друг друга в золотой пропорции
(15.5)
Аддитивное свойство ряда (15.5) прекрасно иллюстрируется последовательностью вписанных друг в друга правильных пятиугольников и пятиконечных звезд (см. с. 206): AD = AE + ED (1 = φ + φ2), DG = DK + KG (φ = φ2 + φ3) и т. д.
Итак, правильный пятиугольник и пятиконечная звезда, образованная его диагоналями, обладают массой интересных свойств:
1. Пересекающиеся диагонали правильного пятиугольника делят друг друга в золотой пропорции
 2. Сторона правильного пятиугольника, сторона вписанной в него пятиконечной звезды и сторона образованного звездой внутреннего пятиугольника также относятся в золотой пропорции
2. Сторона правильного пятиугольника, сторона вписанной в него пятиконечной звезды и сторона образованного звездой внутреннего пятиугольника также относятся в золотой пропорции
 3. Стороны правильных пятиугольников и вписанных в них звезд образуют ряд золотого сечения (15.5), который является бесконечно убывающей геометрической прогрессией со знаменателем ф и обладает аддитивным свойством (φn = φn+1 + φn+2, n = 0, 1, 2, ...).
4. Отрезки пятиконечной звезды АВ = Φ, AD = 1, АЕ = φ и ED = φ2 связаны между собой всеми видами "древних" средних (5.1), а именно:
3. Стороны правильных пятиугольников и вписанных в них звезд образуют ряд золотого сечения (15.5), который является бесконечно убывающей геометрической прогрессией со знаменателем ф и обладает аддитивным свойством (φn = φn+1 + φn+2, n = 0, 1, 2, ...).
4. Отрезки пятиконечной звезды АВ = Φ, AD = 1, АЕ = φ и ED = φ2 связаны между собой всеми видами "древних" средних (5.1), а именно:
 — арифметическое среднее;
— арифметическое среднее;
 — геометрическое среднее;
— геометрическое среднее;
 — гармоническое среднее.
В общем случае для четырех последовательных членов ряда (15.5) φn, φn+1, φn+2, φn+3 нетрудно доказать справедливость соотношения
— гармоническое среднее.
В общем случае для четырех последовательных членов ряда (15.5) φn, φn+1, φn+2, φn+3 нетрудно доказать справедливость соотношения
 5. Из всех равнобедренных треугольников только треугольник, у которого углы при основании (72°) вдвое больше угла при вершине (36°), обладает особым свойством: биссектриса угла при основании делит противоположную сторону в золотом сечении. Такой треугольник (например, ΔАВС на с. 206) получил название "возвышенного".
Подведем некоторый итог: мы выполнили обещание, данное на с. 204 и показали, что пятиконечная звезда (пентаграмма) наряду с золотой пропорцией содержит все "древние" средние. Такое необычайно пропорциональное строение пентаграммы, красота ее внутреннего математического строения, по-видимому, и являются основой красоты ее внешней формы. Можно только догадываться, в какой восторг приводило пифагорейцев столь редкое обилие математических свойств в одной геометрической фигуре. Поэтому неудивительно, что именно пентаграмма была выбрана пифагорейцами в качестве символа жизни и здоровья.
Разделим теперь окружность на 10 равных частей. Это легко сделать с помощью описанного нами метода Птолемея (см. с. 205), в котором отрезок ОА дает сторону правильного десятиугольника (докажите это). Соединяя подряд точки деления окружности, получим правильный десятиугольник, а соединяя точки деления через две,- звездчатый десятиугольник. Внутри звездчатого десятиугольника вновь образуется правильный десятиугольник, в который можно вписать новый звездчатый десятиугольник, и т. д. (см. рисунок на с. 206).
Проведя радиусы в вершины десятиугольников, легко увидеть (именно увидеть глазами) целое созвездие пятиконечных звезд. А зная свойства последних, мы предчувствуем обилие золотых пропорций. Действительно, прежде всего заметим, что треугольник АОВ является возвышенным, поэтому АВ:ОВ = φ, т. е. сторона правильного десятиугольника а10 относится к радиусу описанной окружности R в золотой пропорции а10:R = φ.
Далее, считая радиус исходной окружности R = l и учитывая свойства пятиконечной звезды, легко обнаружить весь ряд золотого сечения (15.5) в последовательности вписанных друг в друга звездчатых десятиугольников. В частности, на рисунке (б) ВС = φ, ОС = фφ2, поэтому ВС/ОС = 1/φ = Φ (тем самым мы погасили еще один "долг" и доказали, что на рисунке ( в, с. 202) B1C1/C1A1 = 0). Попутно мы чисто геометрическим путем доказали равенство
5. Из всех равнобедренных треугольников только треугольник, у которого углы при основании (72°) вдвое больше угла при вершине (36°), обладает особым свойством: биссектриса угла при основании делит противоположную сторону в золотом сечении. Такой треугольник (например, ΔАВС на с. 206) получил название "возвышенного".
Подведем некоторый итог: мы выполнили обещание, данное на с. 204 и показали, что пятиконечная звезда (пентаграмма) наряду с золотой пропорцией содержит все "древние" средние. Такое необычайно пропорциональное строение пентаграммы, красота ее внутреннего математического строения, по-видимому, и являются основой красоты ее внешней формы. Можно только догадываться, в какой восторг приводило пифагорейцев столь редкое обилие математических свойств в одной геометрической фигуре. Поэтому неудивительно, что именно пентаграмма была выбрана пифагорейцами в качестве символа жизни и здоровья.
Разделим теперь окружность на 10 равных частей. Это легко сделать с помощью описанного нами метода Птолемея (см. с. 205), в котором отрезок ОА дает сторону правильного десятиугольника (докажите это). Соединяя подряд точки деления окружности, получим правильный десятиугольник, а соединяя точки деления через две,- звездчатый десятиугольник. Внутри звездчатого десятиугольника вновь образуется правильный десятиугольник, в который можно вписать новый звездчатый десятиугольник, и т. д. (см. рисунок на с. 206).
Проведя радиусы в вершины десятиугольников, легко увидеть (именно увидеть глазами) целое созвездие пятиконечных звезд. А зная свойства последних, мы предчувствуем обилие золотых пропорций. Действительно, прежде всего заметим, что треугольник АОВ является возвышенным, поэтому АВ:ОВ = φ, т. е. сторона правильного десятиугольника а10 относится к радиусу описанной окружности R в золотой пропорции а10:R = φ.
Далее, считая радиус исходной окружности R = l и учитывая свойства пятиконечной звезды, легко обнаружить весь ряд золотого сечения (15.5) в последовательности вписанных друг в друга звездчатых десятиугольников. В частности, на рисунке (б) ВС = φ, ОС = фφ2, поэтому ВС/ОС = 1/φ = Φ (тем самым мы погасили еще один "долг" и доказали, что на рисунке ( в, с. 202) B1C1/C1A1 = 0). Попутно мы чисто геометрическим путем доказали равенство
 которое легко доказать и алгебраически, вспоминая формулу суммы бесконечно убывающей геометрической прогрессии
которое легко доказать и алгебраически, вспоминая формулу суммы бесконечно убывающей геометрической прогрессии
 В нашем случае а1=φ2, q = φ, поэтому
В нашем случае а1=φ2, q = φ, поэтому  Заметим, что обнаруженное нами созвездие вложенных друг в друга пятиконечных звезд позволило сразу увидеть ряд золотого сечения при десятикратном делении окружности и избавило от громоздких алгебраических выкладок.
Теперь становится понятным, почему именно десятикратное деление окружности было выбрано Месселем в качестве метода архитектурного пропорционирования. При десятикратном делении окружности легко получить весь ряд золотого сечения (15.5), который играет огромную роль в архитектурных пропорциях.
Рассмотренные нами геометрические свойства золотого сечения в числе других были с восторгом описаны в 1509 г. в книге монаха ордена францисканцев Луки Пачоли (ок. 1445 — ок. 1514) "О божественной пропорции". Пачоли приводит лишь тринадцать свойств золотого сечения (дабы почтить двенадцать апостолов и их учителя Христа), отмечая, что для перечисления всех свойств золотого сечения не хватило бы чернил и бумаги. Каждому свойству золотого сечения Пачоли ставит особый эпитет, говоря "...о его третьем исключительном свойстве... о его четвертом невыразимом свойстве... о его десятом возвышенном свойстве... о его двенадцатом почти сверхъестественном свойстве...". Пачоли преподавал в различных университетах Италии и был талантливым педагогом. Любопытно, что хорошо известная каждому современному школьнику задача о трубах, наполняющих бассейн, описана в книге Пачоли "Сумма арифметики, геометрии, учения о пропорциях и отношениях", изданной в 1494 г.
Заметим, что обнаруженное нами созвездие вложенных друг в друга пятиконечных звезд позволило сразу увидеть ряд золотого сечения при десятикратном делении окружности и избавило от громоздких алгебраических выкладок.
Теперь становится понятным, почему именно десятикратное деление окружности было выбрано Месселем в качестве метода архитектурного пропорционирования. При десятикратном делении окружности легко получить весь ряд золотого сечения (15.5), который играет огромную роль в архитектурных пропорциях.
Рассмотренные нами геометрические свойства золотого сечения в числе других были с восторгом описаны в 1509 г. в книге монаха ордена францисканцев Луки Пачоли (ок. 1445 — ок. 1514) "О божественной пропорции". Пачоли приводит лишь тринадцать свойств золотого сечения (дабы почтить двенадцать апостолов и их учителя Христа), отмечая, что для перечисления всех свойств золотого сечения не хватило бы чернил и бумаги. Каждому свойству золотого сечения Пачоли ставит особый эпитет, говоря "...о его третьем исключительном свойстве... о его четвертом невыразимом свойстве... о его десятом возвышенном свойстве... о его двенадцатом почти сверхъестественном свойстве...". Пачоли преподавал в различных университетах Италии и был талантливым педагогом. Любопытно, что хорошо известная каждому современному школьнику задача о трубах, наполняющих бассейн, описана в книге Пачоли "Сумма арифметики, геометрии, учения о пропорциях и отношениях", изданной в 1494 г.
 Джакопо де Барбари. Портрет Луки Пачоли. Ок. 1510. Справа изображен ученик Пачоли Гвидобальдо д'Урбино. Возможно, это автопортрет художника. В левом верхнем углу подвешен ромбокубооктаэдр — одно из тел Архимеда. Справа на старинном фолианте стоит додекаэдр
Рассмотрим теперь ряд золотого сечения (15.4)
Джакопо де Барбари. Портрет Луки Пачоли. Ок. 1510. Справа изображен ученик Пачоли Гвидобальдо д'Урбино. Возможно, это автопортрет художника. В левом верхнем углу подвешен ромбокубооктаэдр — одно из тел Архимеда. Справа на старинном фолианте стоит додекаэдр
Рассмотрим теперь ряд золотого сечения (15.4)
 и, пользуясь аддитивным свойством ряда, будем выражать степени Φn через Φ:
и, пользуясь аддитивным свойством ряда, будем выражать степени Φn через Φ:
 Легко видеть, что коэффициенты при Φ, также как и первые слагаемые, образуют последовательность натуральных чисел:
Легко видеть, что коэффициенты при Φ, также как и первые слагаемые, образуют последовательность натуральных чисел:
 (15.7)
Последовательности, в которых каждый член определяется как некоторая функция предыдущих, называются рекуррентными или возвратными.
Последовательность (15.6) имеет древнюю историю. Она впервые была описана в 1202 г. в "Книге об абаке" итальянским купцом и математиком Леонардо из Пизы, известным более по его прозвищу — Фибоначчи — сын доброй природы. С тех пор последовательность (15.6) называется рядом Фибоначчи, а ее члены — числами Фибоначчи. "Книга об абаке" Фибоначчи была своего рода математической энциклопедией средневековья и сыграла заметную роль в развитии математики в Европе. Значительную часть этого трактата составляли задачи, одна из которых гласила:
"Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца своего рождения. Так как первая пара в первом месяце дает потомство, удвой, и в этом месяце окажется 2 пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; ..." И т. д. В заключение Фибоначчи пишет: "...мы складываем первое число со вторым, т. е. 1 и 2; и второе с третьим; и третье с четвертым; и четвертое с пятым; и так одно за другим, пока не сложим десятое с одиннадцатым, т. е. 144 с 233; и мы получим общее число упомянутых (пар.- А. В.) кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев".
Заметим, что свое решение Фибоначчи дал для взрослой пары кроликов. Если же решать задачу для новорожденной пары, то мы получим полный ряд Фибоначчи (15.6) и к концу года будем иметь 233 пары кроликов.
Но какое отношение задача о размножении кроликов имеет к золотому сечению? А вот какое. Если мы возьмем отношение последующего члена ряда (15.6) к предыдущему
(15.7)
Последовательности, в которых каждый член определяется как некоторая функция предыдущих, называются рекуррентными или возвратными.
Последовательность (15.6) имеет древнюю историю. Она впервые была описана в 1202 г. в "Книге об абаке" итальянским купцом и математиком Леонардо из Пизы, известным более по его прозвищу — Фибоначчи — сын доброй природы. С тех пор последовательность (15.6) называется рядом Фибоначчи, а ее члены — числами Фибоначчи. "Книга об абаке" Фибоначчи была своего рода математической энциклопедией средневековья и сыграла заметную роль в развитии математики в Европе. Значительную часть этого трактата составляли задачи, одна из которых гласила:
"Сколько пар кроликов в один год от одной пары рождается?
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца своего рождения. Так как первая пара в первом месяце дает потомство, удвой, и в этом месяце окажется 2 пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; ..." И т. д. В заключение Фибоначчи пишет: "...мы складываем первое число со вторым, т. е. 1 и 2; и второе с третьим; и третье с четвертым; и четвертое с пятым; и так одно за другим, пока не сложим десятое с одиннадцатым, т. е. 144 с 233; и мы получим общее число упомянутых (пар.- А. В.) кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев".
Заметим, что свое решение Фибоначчи дал для взрослой пары кроликов. Если же решать задачу для новорожденной пары, то мы получим полный ряд Фибоначчи (15.6) и к концу года будем иметь 233 пары кроликов.
Но какое отношение задача о размножении кроликов имеет к золотому сечению? А вот какое. Если мы возьмем отношение последующего члена ряда (15.6) к предыдущему 
, то весьма скоро обнаружим, что это отношение с ростом k стремится к коэффициенту золотого сечения Φ. В самом деле,

 Поэтому, глядя на рисунок, нетрудно убедиться (хотя не так-то просто доказать!), что
Поэтому, глядя на рисунок, нетрудно убедиться (хотя не так-то просто доказать!), что
 (15.8)
и наоборот,
(15.8)
и наоборот,
 (15.9)
Процесс асимптотического приближения отношения Uk+1/Uk к Φ напоминает затухающие колебания маятника.
(15.9)
Процесс асимптотического приближения отношения Uk+1/Uk к Φ напоминает затухающие колебания маятника.
 'Генеалогическое древо кроликов' в задаче Фибоначчи. Общее число пар кроликов, так же как и число новорожденных пар, образует последовательность чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, ...
Рассмотрим цепную дробь
'Генеалогическое древо кроликов' в задаче Фибоначчи. Общее число пар кроликов, так же как и число новорожденных пар, образует последовательность чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, ...
Рассмотрим цепную дробь
 Обозначая эту дробь через х>0, нетрудно увидеть то же самое х в знаменателе первой дроби. Поэтому
Обозначая эту дробь через х>0, нетрудно увидеть то же самое х в знаменателе первой дроби. Поэтому
 откуда находим уравнение для х:
откуда находим уравнение для х:
 которое имеет единственный положительный корень
которое имеет единственный положительный корень
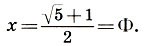 Итак, коэффициент золотого сечения Φ можно представить в виде цепной дроби
Итак, коэффициент золотого сечения Φ можно представить в виде цепной дроби
 (15.10)
(15.10)
 Для ряда Фибоначчи [Uk] отношение Uk+1/Uk последующего члена ряда к предыдущему с ростом k стремится к коэффициенту золотого сечения Φ = (√5 + 1)/2
Выпишем подходящие дроби (см. с. 136) Цепной дроби (15.10):
Для ряда Фибоначчи [Uk] отношение Uk+1/Uk последующего члена ряда к предыдущему с ростом k стремится к коэффициенту золотого сечения Φ = (√5 + 1)/2
Выпишем подходящие дроби (см. с. 136) Цепной дроби (15.10):
 Как видим, подходящие дроби, которые являются рациональными приближениями иррационального числа Φ, равны отношениям соседних чисел Фибоначчи
Как видим, подходящие дроби, которые являются рациональными приближениями иррационального числа Φ, равны отношениям соседних чисел Фибоначчи  Поэтому
Поэтому
 Итак, отношение двух соседних чисел Фибоначчи является рациональным приближением коэффициента золотого сечения, т. е.
Итак, отношение двух соседних чисел Фибоначчи является рациональным приближением коэффициента золотого сечения, т. е.

Именно таким рациональным приближением числа Φ и является интервальный коэффициент малой сексты (обращение большой терции
 , которым Гримм выражал отношение главных вертикалей Парфенона; см. с. 202). Другим примером рационального приближения числа Ф является отношение числа четвертей во второй и четвертой паре "проведение — интермедия" в фуге ре минор Баха (см. с. 165), которое в точности равно отношению
, которым Гримм выражал отношение главных вертикалей Парфенона; см. с. 202). Другим примером рационального приближения числа Ф является отношение числа четвертей во второй и четвертой паре "проведение — интермедия" в фуге ре минор Баха (см. с. 165), которое в точности равно отношению  . Еще раз обратим внимание на потрясающую точность (относительная погрешность составляет 0,06%!), с которой у Баха выполнен закон золотого сечения.
В 1843 г., через 641 год после открытия ряда Фибоначчи, определяемого рекуррентно через сумму двух предыдущих членов ряда, французский математик Ж. Бине нашел формулу для вычисления n-го члена ряда Фибоначчи как функции его номера:
. Еще раз обратим внимание на потрясающую точность (относительная погрешность составляет 0,06%!), с которой у Баха выполнен закон золотого сечения.
В 1843 г., через 641 год после открытия ряда Фибоначчи, определяемого рекуррентно через сумму двух предыдущих членов ряда, французский математик Ж. Бине нашел формулу для вычисления n-го члена ряда Фибоначчи как функции его номера:
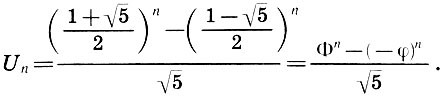 (15.11)
Пользуясь формулой Бине (15.11) нетрудно доказать, что
(15.11)
Пользуясь формулой Бине (15.11) нетрудно доказать, что

 Наконец, укажем еще одно представление коэффициента золотого сечения Φ, полученное в начале нашего века:
Наконец, укажем еще одно представление коэффициента золотого сечения Φ, полученное в начале нашего века:
 (15.12)
Не правда ли, все формулы (15.10)- (15.12) отличаются особой красотой, простотой и изяществом!
(15.12)
Не правда ли, все формулы (15.10)- (15.12) отличаются особой красотой, простотой и изяществом!
 Боттичелли. Рождение Венеры. Ок. 1483-1484. Нет живописи более поэтичной, чем живопись Боттичелли, и нет у великого Сандро картины более знаменитой, чем его 'Венера'. Неповторимо нервное изящество боттичеллиевских линий и болезненная хрупкость его вытянутых фигур. Неповторима младенческая чистота Венеры и кроткая печаль ее взора. Неповторим льнущий к телу клубок золотых волос Венеры, в котором, как в клубке змей, таится роковое коварство этого безгрешного существа. Но для неоплатоника Боттичелли его Венера, так же как и для неопифагорейца Поликлета его Дорифор,- это воплощение идеи универсальной гармонии золотого сечения, господствующего в природе
Боттичелли. Рождение Венеры. Ок. 1483-1484. Нет живописи более поэтичной, чем живопись Боттичелли, и нет у великого Сандро картины более знаменитой, чем его 'Венера'. Неповторимо нервное изящество боттичеллиевских линий и болезненная хрупкость его вытянутых фигур. Неповторима младенческая чистота Венеры и кроткая печаль ее взора. Неповторим льнущий к телу клубок золотых волос Венеры, в котором, как в клубке змей, таится роковое коварство этого безгрешного существа. Но для неоплатоника Боттичелли его Венера, так же как и для неопифагорейца Поликлета его Дорифор,- это воплощение идеи универсальной гармонии золотого сечения, господствующего в природе
 Пропорциональный анализ Венеры убеждает нас в этом
Итак, ряд золотого сечения (15.4), (15.5) и тесно связанный с ним ряд Фибоначчи (15.6) обладают массой исключительных математических свойств, которые каким-то поразительным образом сошлись в этих феноменах. Но золотое сечение и числа Фибоначчи имеют не менее удивительные приложения не только в искусстве (с чем мы немного познакомились в гл. 4 и гл. 12), но и в живой природе. К настоящему времени накоплено множество фактов, показывающих, что ряд Фибоначчи проявляется в формах живой природы как закон единообразного роста. Ряд Фибоначчи обнаружен и в расположении семян подсолнечника или сосновой шишки, и в распределении листьев и хвои на деревьях, и в расположении стеблей. Возьмите линейку и измерьте длину трех фаланг среднего пальца и пясти. Поделив эти числа на длину первой фаланги, вы с поразительной точностью обнаружите 4 члена ряда золотого сечения (15.4):
Пропорциональный анализ Венеры убеждает нас в этом
Итак, ряд золотого сечения (15.4), (15.5) и тесно связанный с ним ряд Фибоначчи (15.6) обладают массой исключительных математических свойств, которые каким-то поразительным образом сошлись в этих феноменах. Но золотое сечение и числа Фибоначчи имеют не менее удивительные приложения не только в искусстве (с чем мы немного познакомились в гл. 4 и гл. 12), но и в живой природе. К настоящему времени накоплено множество фактов, показывающих, что ряд Фибоначчи проявляется в формах живой природы как закон единообразного роста. Ряд Фибоначчи обнаружен и в расположении семян подсолнечника или сосновой шишки, и в распределении листьев и хвои на деревьях, и в расположении стеблей. Возьмите линейку и измерьте длину трех фаланг среднего пальца и пясти. Поделив эти числа на длину первой фаланги, вы с поразительной точностью обнаружите 4 члена ряда золотого сечения (15.4):
 Но самым удивительным, пожалуй, является то, что точка, питающая новую жизнь,- пуп человека — делит тело человека в золотом сечении.
Что стоит за этими и многими другими фактами — игра чисел или некоторый универсальный закон природы? Хочется верить, во второе, ибо жизнь — это не хаос случайностей, а претворение генетически определенных законов. Видимо, действием закона золотого сечения в природе и объясняются интригующие проявления этого закона в искусстве. По крайней мере, автор стоит на "природнической" точке зрения на прекрасное и в законах искусства видит отражение законов красоты природы (хотя и те и другие законы пока еще не познаны).
Почему же закон золотого сечения так часто проявляется в архитектуре? Этому есть, на наш взгляд, вполне рациональное, математическое объяснение. Мы знаем, что для достижения гармонии в произведении искусства (в том числе и в архитектурном произведении) должен выполняться принцип Гераклита: "из всего — единое, из единого — все". В самом деле, гармония в архитектурном произведении зависит не столько от размеров самого сооружения, сколько от соотношений между размерами составляющих его частей. Для того чтобы выполнялся основной принцип гармонии "все во всем", взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение, т. е. архитектурное "целое" а и его части а1, а2, а3, а4, ... должны находиться в одинаковых отношениях
Но самым удивительным, пожалуй, является то, что точка, питающая новую жизнь,- пуп человека — делит тело человека в золотом сечении.
Что стоит за этими и многими другими фактами — игра чисел или некоторый универсальный закон природы? Хочется верить, во второе, ибо жизнь — это не хаос случайностей, а претворение генетически определенных законов. Видимо, действием закона золотого сечения в природе и объясняются интригующие проявления этого закона в искусстве. По крайней мере, автор стоит на "природнической" точке зрения на прекрасное и в законах искусства видит отражение законов красоты природы (хотя и те и другие законы пока еще не познаны).
Почему же закон золотого сечения так часто проявляется в архитектуре? Этому есть, на наш взгляд, вполне рациональное, математическое объяснение. Мы знаем, что для достижения гармонии в произведении искусства (в том числе и в архитектурном произведении) должен выполняться принцип Гераклита: "из всего — единое, из единого — все". В самом деле, гармония в архитектурном произведении зависит не столько от размеров самого сооружения, сколько от соотношений между размерами составляющих его частей. Для того чтобы выполнялся основной принцип гармонии "все во всем", взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение, т. е. архитектурное "целое" а и его части а1, а2, а3, а4, ... должны находиться в одинаковых отношениях
 Отсюда a = a1p, а1 =а2р, а2 = а3p, ..., или a1 = qa, a2 = q2a, a3 = g3a, ... (q = l/p), т. е. "целое" а и его части a1, а2, а3, ... должны образовывать геометрическую прогрессию
Отсюда a = a1p, а1 =а2р, а2 = а3p, ..., или a1 = qa, a2 = q2a, a3 = g3a, ... (q = l/p), т. е. "целое" а и его части a1, а2, а3, ... должны образовывать геометрическую прогрессию
 (15.13)
Но части архитектурного целого должны "сходиться" в целое, т. е., разделив "целое" а на части а1 и а2, необходимо, чтобы
(15.13)
Но части архитектурного целого должны "сходиться" в целое, т. е., разделив "целое" а на части а1 и а2, необходимо, чтобы
 Учитывая (15.13), условие (15.14) примет вид
Учитывая (15.13), условие (15.14) примет вид
 т. е. единственное положительное значение для q равно коэффициенту золотого сечения φ.
Итак, из всех геометрических прогрессий (15.13) только ряд золотого сечения обладает аддитивным свойством (15.14), поэтому только при делении "целого" a на части а1 и а2 в золотой пропорции выполняется принцип "все во всем" и одновременно части "сходятся" в целое.
т. е. единственное положительное значение для q равно коэффициенту золотого сечения φ.
Итак, из всех геометрических прогрессий (15.13) только ряд золотого сечения обладает аддитивным свойством (15.14), поэтому только при делении "целого" a на части а1 и а2 в золотой пропорции выполняется принцип "все во всем" и одновременно части "сходятся" в целое.
 Пропорции храма Василия Блаженного в Москве определяются восемью членами ряда золотого сечения: 1, φ, φ2, φ3, φ4, φ5, φ6, φ7
При этом соотношения (15.13) и (15.14) принимают вид (12.4)
Пропорции храма Василия Блаженного в Москве определяются восемью членами ряда золотого сечения: 1, φ, φ2, φ3, φ4, φ5, φ6, φ7
При этом соотношения (15.13) и (15.14) принимают вид (12.4)
 Это и есть знакомый нам ряд золотого сечения.
Подробным анализом пропорций некоторых архитектурных шедевров разных эпох, стилей и разных народов мы займемся в следующих двух главах. Но сейчас нам хочется закончить разговор о золотом сечении одним примером, показывающим, насколько органично входит оно в архитектурные пропорции. В качестве примера рассмотрим пропорциональный строй одной из жемчужин древнерусской архитектуры — храма Василия Блаженного в Москве. За "целое" а = 1 принята высота храма. Пропорции храма определяются восемью членами ряда золотого сечения:
Это и есть знакомый нам ряд золотого сечения.
Подробным анализом пропорций некоторых архитектурных шедевров разных эпох, стилей и разных народов мы займемся в следующих двух главах. Но сейчас нам хочется закончить разговор о золотом сечении одним примером, показывающим, насколько органично входит оно в архитектурные пропорции. В качестве примера рассмотрим пропорциональный строй одной из жемчужин древнерусской архитектуры — храма Василия Блаженного в Москве. За "целое" а = 1 принята высота храма. Пропорции храма определяются восемью членами ряда золотого сечения:
 Многие из членов ряда неоднократно повторяются в пропорциях этого затейливого архитектурного сооружения, но всегда благодаря аддитивному свойству золотого сечения мы уверены в том, что части сойдутся в целое, т. е.
Многие из членов ряда неоднократно повторяются в пропорциях этого затейливого архитектурного сооружения, но всегда благодаря аддитивному свойству золотого сечения мы уверены в том, что части сойдутся в целое, т. е.
 Таким образом, аддитивное свойство золотого сечения делает эту геометрическую пропорцию единственной и неповторимой.
Таким образом, аддитивное свойство золотого сечения делает эту геометрическую пропорцию единственной и неповторимой.
16. Пропорции: от Парфенона до Нотр-Дама
...Вся наша Франция заключена в наших соборах, как и вся Греция сжата в одном Парфеноне."Человек — мера всех вещей..." Этот знаменитый афоризм древнегреческого философа-софиста Протагора (ок. 490 — ок. 420 до н. э.) является ключом к разгадке тайны пропорций Парфенона, его поразительной гармонии и спокойствия. Как это ни парадоксально, но между живыми линиями человеческого тела и застывшими на тысячелетия каменными очертаниями древнего сооружения существует глубокая связь, выраженная в математических законах пропорциональности. Но по порядку... Мы уже знаем о многих теориях античных пропорций, пытавшихся объяснить гармонию Парфенона на основе золотого сечения (см. гл. 14). Такой подход понятен ввиду особой роли золотого сечения как в природе, так и в искусстве, роли, которая во многом еще остается загадочной. Кроме того, апологеты золотого сечения ссылались на некоторые высказывания Платона о пропорциях. Однако эти высказывания великого философа, видимо, понимались слишком узко (см. с. 195). В главе 14 мы показали, что многие внешне различные теории пропорций Парфенона математически приводят к золотому сечению в отдельных элементах этого архитектурного шедевра. Но целостной теории на базе золотого сечения все-таки не получалось. Некоторых исследователей отсутствие единой теории античных пропорций вообще разуверило в принципе пропорциональности. Пессимисты подняли на щит высказывание великого теоретика пропорций XX века Ле Корбюзье о том, что "Парфенон — это более, чем архитектура, это — скульптура". Они объявили математическое исследование пропорций Парфенона кощунством. Действительно, тщательное изучение показало, что в Парфеноне, как и в человеческом теле, нет прямых линий. Линии Парфенона наполнены жизнью и пластикой. Однако это отнюдь не означает, что в них нет пропорциональной зависимости, той самой, которую так одержимо искали и находили в теле человека Поликлет, Леонардо да Винчи, Дюрер и др. А оптимисты продолжают поиск законов строения архитектурных шедевров, поиск тех вечных истин, которые, возможно, являются общими законами формообразования и в природе, и в искусстве. Оригинальную теорию разрабатывает в течение последних двадцати лет архитектор И. Ш. Шевелев. Это теория парных мер, которая настолько естественна, что просто удивительно, почему она до середины XX века никому не пришла в голову. Парные меры - это два эталона длины а и Ь, которые позволяли устанавливать одинаковые отношения между отдельными парами архитектурного сооружения a:b = na:nb (n = 1, 2, 3, ...). Какие же величины выступали в качестве парных мер? Сама история развития математики указывает на то, что это были геометрические объекты: сторона и диагональ прямоугольника. В самом деле, математика начиналась с геометрии, а слово "геометрия" означает землемерие. Основной задачей последнего было измерение площадей земельных участков. Древнейшим методом измерения площадей был метод приложения, суть которого состояла в следующем. К измеряемому прямоугольнику прикладывается эталон площади (как правило, квадрат). В прямоугольнике, образованном стороной эталона и стороной измеряемого участка, проводилась диагональ до пересечения с продолжением второй стороны эталона.О. Роден
 Измерение площади прямоугольного участка 'методом приложения'
Получалось три прямоугольника. Два из них, через которые прошла диагональ, подобны, а третий равновелик эталону (докажите это). Сторона равновеликого прямоугольника и служила линейной мерой для определения площади. Так измерение площади сводилось к простому подсчету числа линейных мер в стороне измеряемого прямоугольника. Так сторона и диагональ прямоугольника становились основными инструментами древних землемеров-математиков.
Из всего множества прямоугольников квадрат и двойной квадрат обладают тем практическим преимуществом, что требует для построения прямого угла не три, а две меры (в двойном квадрате большая сторона получается двукратным отложением малой). Так появились парные меры 1:√2 и 1:√5 (см. с. 199).
Знания, накопленные в геометрии, использовались и в архитектуре. Древние зодчие были прекрасными математиками. Но в отличие от землемерия архитектура обладает третьим измерением — высотой. Поэтому стороны и диагональ прямоугольника, проведенные на земле, пришлось заменить мерными палками, которыми можно было оперировать и в третьем измерении. Парную меру двойного квадрата 1:√5 мы и видим в руках древнеегипетского зодчего Хесиры (см. с. 200).
Измерение площади прямоугольного участка 'методом приложения'
Получалось три прямоугольника. Два из них, через которые прошла диагональ, подобны, а третий равновелик эталону (докажите это). Сторона равновеликого прямоугольника и служила линейной мерой для определения площади. Так измерение площади сводилось к простому подсчету числа линейных мер в стороне измеряемого прямоугольника. Так сторона и диагональ прямоугольника становились основными инструментами древних землемеров-математиков.
Из всего множества прямоугольников квадрат и двойной квадрат обладают тем практическим преимуществом, что требует для построения прямого угла не три, а две меры (в двойном квадрате большая сторона получается двукратным отложением малой). Так появились парные меры 1:√2 и 1:√5 (см. с. 199).
Знания, накопленные в геометрии, использовались и в архитектуре. Древние зодчие были прекрасными математиками. Но в отличие от землемерия архитектура обладает третьим измерением — высотой. Поэтому стороны и диагональ прямоугольника, проведенные на земле, пришлось заменить мерными палками, которыми можно было оперировать и в третьем измерении. Парную меру двойного квадрата 1:√5 мы и видим в руках древнеегипетского зодчего Хесиры (см. с. 200).
 Геометрические свойства системы двух квадратов. Исходный двойной квадрат показан красным, прямоугольники золотого сечения — синим. Рисунок демонстрирует также аддитивное свойство прямоугольников системы двойного квадрата
Парная мера 1:√5 встречается во множестве древних сооружений, разделенных между собой веками и тысячами километров: пирамиды Джосера, Хеопса, Хефрена и Миккерина, пропорции Парфенона и Эрехтейона, церковь Покрова на Нерли и храм Вознесения в Коломенском, древние храмы Киева и Новгорода...
Разумеется, причина популярности этой парной меры не только в том, что для построения прямого угла с ее помощью требуются именно две, а не три меры. Истинная причина заключена в разнообразии математических свойств двойного квадрата.
В самом деле, возьмем квадрат со стороной 1, построим двойной квадрат (т. е. прямоугольник со сторонами 1 и 2), проведем в нем диагональ и опишем ею полуокружность (см. рис. ). Так мы построим новый двойной квадрат с малой стороной √5. Продлив стороны исходного двойного квадрата до пересечения со сторонами нового, мы получим целую гамму пропорций, содержащую практически все коэффициенты пропорциональности от
Геометрические свойства системы двух квадратов. Исходный двойной квадрат показан красным, прямоугольники золотого сечения — синим. Рисунок демонстрирует также аддитивное свойство прямоугольников системы двойного квадрата
Парная мера 1:√5 встречается во множестве древних сооружений, разделенных между собой веками и тысячами километров: пирамиды Джосера, Хеопса, Хефрена и Миккерина, пропорции Парфенона и Эрехтейона, церковь Покрова на Нерли и храм Вознесения в Коломенском, древние храмы Киева и Новгорода...
Разумеется, причина популярности этой парной меры не только в том, что для построения прямого угла с ее помощью требуются именно две, а не три меры. Истинная причина заключена в разнообразии математических свойств двойного квадрата.
В самом деле, возьмем квадрат со стороной 1, построим двойной квадрат (т. е. прямоугольник со сторонами 1 и 2), проведем в нем диагональ и опишем ею полуокружность (см. рис. ). Так мы построим новый двойной квадрат с малой стороной √5. Продлив стороны исходного двойного квадрата до пересечения со сторонами нового, мы получим целую гамму пропорций, содержащую практически все коэффициенты пропорциональности от  до 1 с шагом 0,1:
до 1 с шагом 0,1:

и т. д. Заметим: двойной квадрат тесно связан с золотым сечением. Так, в результате наших построений мы получили два прямоугольника золотого сечения, выделенные синим цветом:
 и
и  .
.
Ну а какое отношение математика двойного квадрата имеет к архитектуре? Широкое распространение в архитектуре пропорции двойного квадрата, как и пропорции золотого сечения, получили благодаря свойству, которое по аналогии с золотым сечением можно назвать аддитивным свойством площадей. Дело в том, что каждое архитектурное произведение или его часть можно вписать в прямоугольник. Так вот, прямоугольники системы двойного квадрата могут без остатка разлагаться на другие прямоугольники этой же системы. Это и есть аддитивное свойство площадей системы двух квадратов, аналогичное линейному аддитивному свойству золотого сечения. Например, прямоугольник золотого сечения (
 +1) одной линией можно разделить на два прямоугольника, стороны которых будут относиться как 1:2 и 2:
+1) одной линией можно разделить на два прямоугольника, стороны которых будут относиться как 1:2 и 2: , а прямоугольник со сторонами 2 и
, а прямоугольник со сторонами 2 и  легко разложить на "золотой" прямоугольник (
легко разложить на "золотой" прямоугольник ( -1):2 и двойной квадрат 1:2. Прямоугольник 1:2 четырьмя линиями разбивается на шесть прямоугольников: два неравных прямоугольника 1:2, два равных прямоугольника 2: √5 и два неравных "золотых" прямоугольника (√5 — 1): 2. И т. д. Таким образом, система двух квадратов дает поразительное разнообразие разбиений целого на части, находящиеся в тех же пропорциональных отношениях. Так, благодаря аддитивному свойству площадей системы двух квадратов достигается взаимосвязь целого и его частей, осуществляется основной принцип гармонии: "из всего — единое, из единого — все".
Заметим, что получаемые в системе Двух квадратов прямоугольники с отношением сторон
-1):2 и двойной квадрат 1:2. Прямоугольник 1:2 четырьмя линиями разбивается на шесть прямоугольников: два неравных прямоугольника 1:2, два равных прямоугольника 2: √5 и два неравных "золотых" прямоугольника (√5 — 1): 2. И т. д. Таким образом, система двух квадратов дает поразительное разнообразие разбиений целого на части, находящиеся в тех же пропорциональных отношениях. Так, благодаря аддитивному свойству площадей системы двух квадратов достигается взаимосвязь целого и его частей, осуществляется основной принцип гармонии: "из всего — единое, из единого — все".
Заметим, что получаемые в системе Двух квадратов прямоугольники с отношением сторон  :2≈1,118 близки к квадратам, а само отношение √5:2 представляет так называемую функцию золотого сечения, введенную архитектором Жолтовским. В терминах ряда золотого сечения (15.5) функция золотого сечения определяется как отношение
:2≈1,118 близки к квадратам, а само отношение √5:2 представляет так называемую функцию золотого сечения, введенную архитектором Жолтовским. В терминах ряда золотого сечения (15.5) функция золотого сечения определяется как отношение
 Поскольку
Поскольку  , то мы легко получаем
, то мы легко получаем
 Прямоугольник с отношением сторон
Прямоугольник с отношением сторон  :2 Жолтовский называл "живым квадратом", считая, что он должен заменить в архитектуре математический квадрат, который не встречается в природе и не радует глаз своей пропорцией (1:1). Будучи большим энтузиастом золотого сечения и его функции, Жолтовский нашел многочисленные примеры этих пропорций в архитектурных шедеврах, в том числе и в Парфеноне (см. с. 202). Итак, среди многих пропорций, обладающих аддитивным свойством площадей, двойной квадрат содержит и такие "выдающиеся" пропорции, как золотое сечение и функцию золотого сечения.
Теория парных мер родилась в 60-е годы. Однако, кроме мерных палок Хесиры, эта теория реальных подтверждений не имела и, по существу, оставалась гипотезой, построенной на математических рассуждениях. Правда, пропорциональные циркули (см. с. 199) также представляют собой парные меры. Но это меры, с помощью которых строился чертеж архитектурного сооружения, а не само сооружение. И вот в 1970 г. теория парных мер получила еще одно блестящее доказательство. При археологических раскопках в Новгороде экспедицией члена-корреспондента АН СССР А. В. Арциховского был найден обломок мерной трости конца XII века. Мерная трость представляет собой брусок прямоугольного сечения, на трех гранях которого нанесены три различные шкалы. 24 деления каждой из шкал дают разные сажени: тмутараканскую (Ст= 142,1 см), мерную (См = 175,6 см) и косую новгородскую (Кн = 200,9 см). Но ведь это не что иное, как парные меры системы двух квадратов! В самом деле, Ст : См = 1:(
:2 Жолтовский называл "живым квадратом", считая, что он должен заменить в архитектуре математический квадрат, который не встречается в природе и не радует глаз своей пропорцией (1:1). Будучи большим энтузиастом золотого сечения и его функции, Жолтовский нашел многочисленные примеры этих пропорций в архитектурных шедеврах, в том числе и в Парфеноне (см. с. 202). Итак, среди многих пропорций, обладающих аддитивным свойством площадей, двойной квадрат содержит и такие "выдающиеся" пропорции, как золотое сечение и функцию золотого сечения.
Теория парных мер родилась в 60-е годы. Однако, кроме мерных палок Хесиры, эта теория реальных подтверждений не имела и, по существу, оставалась гипотезой, построенной на математических рассуждениях. Правда, пропорциональные циркули (см. с. 199) также представляют собой парные меры. Но это меры, с помощью которых строился чертеж архитектурного сооружения, а не само сооружение. И вот в 1970 г. теория парных мер получила еще одно блестящее доказательство. При археологических раскопках в Новгороде экспедицией члена-корреспондента АН СССР А. В. Арциховского был найден обломок мерной трости конца XII века. Мерная трость представляет собой брусок прямоугольного сечения, на трех гранях которого нанесены три различные шкалы. 24 деления каждой из шкал дают разные сажени: тмутараканскую (Ст= 142,1 см), мерную (См = 175,6 см) и косую новгородскую (Кн = 200,9 см). Но ведь это не что иное, как парные меры системы двух квадратов! В самом деле, Ст : См = 1:( — 1) = 0,809, Ст:Кн = 1:√2 = 0,707. (Подробнее о древнерусских парных мерах и системах пропорционирования мы поговорим в следующей главе.) Так мерная трость[26], а вместе с ней и парные меры из математических абстракций перешли в область реального. Так в нетрадиционной области — теории архитектуры — еще раз проявилось удивительное свойство математики совершать открытия "на кончике пера". Так геометрия двойного квадрата связала воедино мерные палки Хесиры, античные пропорциональные циркули и новгородскую мерную трость.
Вернемся, наконец, к теории пропорций Парфенона, к афоризму Протагора: "человек — мера всех вещей". Для древнегреческой философии, искусства и религии всегда было характерно очеловечивание сил природы — антропоморфизм. Даже греческие боги были подвержены человеческим слабостям и страстям. Архитектура в антропоморфизме греков не составляла исключения. Вот что по этому поводу писал тонкий знаток античной архитектуры, профессор Н. И. Врунов: "Ордер классического греческого храма является также главным носителем человеческого начала: он осуществляет на языке архитектуры образ монументализированного человека-героя... Самая форма дорической колонны вызывает ассоциации, связанные с человеческим телом. Прежде всего — вертикализм колонны. Вертикаль — главная ось человеческого тела, основная характерная особенность внешнего облика человека, главное его отличие от облика животного".
Но какой именно математической зависимостью связаны пропорции дорической колонны и человеческого тела? В поисках ответа на этот вопрос роковую роль сыграло следующее высказывание Витрувия: "Желая сделать так, чтобы они (колонны.- А. В.) были пригодны к поддержанию тяжести и обладали правильным и красивым обличьем, они измерили след мужской ступни по отношению к человеческому росту, и, найдя, что ступня составляет шестую его долю, применили это соотношение к колоннаде, и, сообразно с толщиной основания ее ствола, вывели ее высоту в 6 раз больше, включая сюда и капитель. Таким образом, дорийская колонна стала воспроизводить в зданиях пропорции, крепость и красоту мужского тела". Итак, по Витрувию, справедливы отношения: (стопа человека): (высота его тела) = (диаметр колонны): (общая высота колонны) = 1:6. Между тем обмеры дорических колонн упрямо противоречили Витрувию. Неумолимые цифры заставили Брунова отказаться от своих прежних воззрений: "Нельзя утверждать, что дорическая колонна повторяет пропорции тела человека, потому что людей таких пропорций, как колонны Парфенона, не существует". Разгадка была где-то рядом, но ее нашел только в 60-е годы архитектор Шевелев. Вот его решение.
— 1) = 0,809, Ст:Кн = 1:√2 = 0,707. (Подробнее о древнерусских парных мерах и системах пропорционирования мы поговорим в следующей главе.) Так мерная трость[26], а вместе с ней и парные меры из математических абстракций перешли в область реального. Так в нетрадиционной области — теории архитектуры — еще раз проявилось удивительное свойство математики совершать открытия "на кончике пера". Так геометрия двойного квадрата связала воедино мерные палки Хесиры, античные пропорциональные циркули и новгородскую мерную трость.
Вернемся, наконец, к теории пропорций Парфенона, к афоризму Протагора: "человек — мера всех вещей". Для древнегреческой философии, искусства и религии всегда было характерно очеловечивание сил природы — антропоморфизм. Даже греческие боги были подвержены человеческим слабостям и страстям. Архитектура в антропоморфизме греков не составляла исключения. Вот что по этому поводу писал тонкий знаток античной архитектуры, профессор Н. И. Врунов: "Ордер классического греческого храма является также главным носителем человеческого начала: он осуществляет на языке архитектуры образ монументализированного человека-героя... Самая форма дорической колонны вызывает ассоциации, связанные с человеческим телом. Прежде всего — вертикализм колонны. Вертикаль — главная ось человеческого тела, основная характерная особенность внешнего облика человека, главное его отличие от облика животного".
Но какой именно математической зависимостью связаны пропорции дорической колонны и человеческого тела? В поисках ответа на этот вопрос роковую роль сыграло следующее высказывание Витрувия: "Желая сделать так, чтобы они (колонны.- А. В.) были пригодны к поддержанию тяжести и обладали правильным и красивым обличьем, они измерили след мужской ступни по отношению к человеческому росту, и, найдя, что ступня составляет шестую его долю, применили это соотношение к колоннаде, и, сообразно с толщиной основания ее ствола, вывели ее высоту в 6 раз больше, включая сюда и капитель. Таким образом, дорийская колонна стала воспроизводить в зданиях пропорции, крепость и красоту мужского тела". Итак, по Витрувию, справедливы отношения: (стопа человека): (высота его тела) = (диаметр колонны): (общая высота колонны) = 1:6. Между тем обмеры дорических колонн упрямо противоречили Витрувию. Неумолимые цифры заставили Брунова отказаться от своих прежних воззрений: "Нельзя утверждать, что дорическая колонна повторяет пропорции тела человека, потому что людей таких пропорций, как колонны Парфенона, не существует". Разгадка была где-то рядом, но ее нашел только в 60-е годы архитектор Шевелев. Вот его решение.
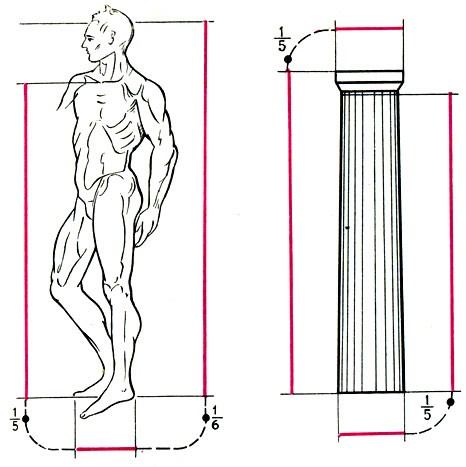 Отношение длины стопы человека к длине его тела от основания шеи до стопы 1:5 — ключ к пропорциональному строю Парфенона (по Шевелеву)
Со времен Поликлета установлено, что если стопу человека принять за единицу измерения — фут (греческий фут = 30,89 см), то рост человека составит 6 футов, а голова вместе с шеей — 1 фут. В этом можно убедиться, глядя на рисунок на следующей странице. Следовательно, на оставшуюся часть тела приходится 5 футов. Именно эта часть и олицетворяет "крепость и красоту мужского тела". В самом деле, в "человеческой колонне" шея — самое слабое место. Груз взваливают на плечи, и даже атланты сгибают шеи и принимают тяжесть на поднятые к голове руки. Эта простая мысль и привела Шевелева к тому, что ствол колонны, несущий тяжесть, должен ассоциироваться не с полным ростом человека, а с его наиболее крепкой частью от стоп до основания шеи. Все сразу стало на свои места. Возникла цепочка пропорций, выполнявшихся с прекрасной точностью:(нижний диаметр колонны):(высота ствола колонны)=(ширина капители по абаке):(высота колонны с капителью) = (стопа человека):(высота человека от стоп до основания шеи)=1:5. Далее, поскольку "подобное в мириады раз прекраснее того, что неподобно" (Витрувий), отношение 1:5 было распространено на всю соразмерность колоннады в целом: (высота колоннады = колонна + антаблемент):(длина храма по стилобату)=1:5.
Мы употребили немало терминов, относящихся к классическому ордеру. Ордер (от лат. ordo — порядок) — это тип архитектурной композиции, названный так Витрувием и основанный на художественной переработке стоечно-балочной конструкции (см. с. 181). Огромную роль в развитии европейской архитектуры сыграли родившиеся в Древней Греции классические ордеры: дорический, ионический и коринфский. Название ордера происходит от названия соответствующей области Древней Греции или Малой Азии. Все последующие архитектурные стили, не говоря уже о зодчестве Возрождения и классицизма, развивались под влиянием классического ордера. Наиболее древний — дорический — ордер (ордер Парфенона) отличается торжественной монументальностью форм, строгостью пропорций и лаконизмом деталей.
Отношение длины стопы человека к длине его тела от основания шеи до стопы 1:5 — ключ к пропорциональному строю Парфенона (по Шевелеву)
Со времен Поликлета установлено, что если стопу человека принять за единицу измерения — фут (греческий фут = 30,89 см), то рост человека составит 6 футов, а голова вместе с шеей — 1 фут. В этом можно убедиться, глядя на рисунок на следующей странице. Следовательно, на оставшуюся часть тела приходится 5 футов. Именно эта часть и олицетворяет "крепость и красоту мужского тела". В самом деле, в "человеческой колонне" шея — самое слабое место. Груз взваливают на плечи, и даже атланты сгибают шеи и принимают тяжесть на поднятые к голове руки. Эта простая мысль и привела Шевелева к тому, что ствол колонны, несущий тяжесть, должен ассоциироваться не с полным ростом человека, а с его наиболее крепкой частью от стоп до основания шеи. Все сразу стало на свои места. Возникла цепочка пропорций, выполнявшихся с прекрасной точностью:(нижний диаметр колонны):(высота ствола колонны)=(ширина капители по абаке):(высота колонны с капителью) = (стопа человека):(высота человека от стоп до основания шеи)=1:5. Далее, поскольку "подобное в мириады раз прекраснее того, что неподобно" (Витрувий), отношение 1:5 было распространено на всю соразмерность колоннады в целом: (высота колоннады = колонна + антаблемент):(длина храма по стилобату)=1:5.
Мы употребили немало терминов, относящихся к классическому ордеру. Ордер (от лат. ordo — порядок) — это тип архитектурной композиции, названный так Витрувием и основанный на художественной переработке стоечно-балочной конструкции (см. с. 181). Огромную роль в развитии европейской архитектуры сыграли родившиеся в Древней Греции классические ордеры: дорический, ионический и коринфский. Название ордера происходит от названия соответствующей области Древней Греции или Малой Азии. Все последующие архитектурные стили, не говоря уже о зодчестве Возрождения и классицизма, развивались под влиянием классического ордера. Наиболее древний — дорический — ордер (ордер Парфенона) отличается торжественной монументальностью форм, строгостью пропорций и лаконизмом деталей.
 Основные элементы дорического ордера, видимые на главном фасаде Парфенона, и их выражение через ширину стилобата: а = 100 фут. = 30,87 м
Итак, в дорической колонне воспроизведены пропорции несущей части мужского тела 1:5. В том же отношении находятся и крайние размеры всего Парфенона — высота колоннады и длина храма. Но вспомним Платона: "невозможно, чтобы две вещи совершенным образом соединились без третьей...", которая является их средним геометрическим (см. с. 195)[27]. Следовательно, пропорции Парфенона должны определяться еще одной величиной — средним геометрическим чисел 1 и 5, т. е.
Основные элементы дорического ордера, видимые на главном фасаде Парфенона, и их выражение через ширину стилобата: а = 100 фут. = 30,87 м
Итак, в дорической колонне воспроизведены пропорции несущей части мужского тела 1:5. В том же отношении находятся и крайние размеры всего Парфенона — высота колоннады и длина храма. Но вспомним Платона: "невозможно, чтобы две вещи совершенным образом соединились без третьей...", которая является их средним геометрическим (см. с. 195)[27]. Следовательно, пропорции Парфенона должны определяться еще одной величиной — средним геометрическим чисел 1 и 5, т. е.  Ho ведь √5 есть не что иное, как диагональ двойного квадрата! Таким образом именно парная мера 1:√5 являлся ключом к пропорциональному строению всего Парфенона! Вслед за Шевелевым нам остается только убедиться в справедливости этой гипотезы. В самом деле, между крайними размерами — высотой колоннады и длиной храма — должно лежать и их среднее геометрическое — ширина сооружения. Размеры Парфенона подтверждают это:
Ho ведь √5 есть не что иное, как диагональ двойного квадрата! Таким образом именно парная мера 1:√5 являлся ключом к пропорциональному строению всего Парфенона! Вслед за Шевелевым нам остается только убедиться в справедливости этой гипотезы. В самом деле, между крайними размерами — высотой колоннады и длиной храма — должно лежать и их среднее геометрическое — ширина сооружения. Размеры Парфенона подтверждают это:
 (16.1)
Поскольку ширина стилобата точно равна 100 греческим футам, то естественно предположить, что именно этот размер был выбран за исходный размер Парфенона. Итак, если ширина стилобата равна а, то согласно (16.1) его длина b = a√5, a высота колоннады а1 = а:√5. Так же и шаг колонн связывает всю колоннаду в единое целое и является средним геометрическим диаметра колонны и высоты ее ствола:
(16.1)
Поскольку ширина стилобата точно равна 100 греческим футам, то естественно предположить, что именно этот размер был выбран за исходный размер Парфенона. Итак, если ширина стилобата равна а, то согласно (16.1) его длина b = a√5, a высота колоннады а1 = а:√5. Так же и шаг колонн связывает всю колоннаду в единое целое и является средним геометрическим диаметра колонны и высоты ее ствола:
 (16.2)
Высота колоннады а1 складывается из высот колонны и антаблемента либо из высот нагрузки а2 и ствола колонны а3, т. е. а1 = а2 + а3. Последние две высоты также относятся как 1:√5, откуда легко получить выражение а3 через а1.
(16.2)
Высота колоннады а1 складывается из высот колонны и антаблемента либо из высот нагрузки а2 и ствола колонны а3, т. е. а1 = а2 + а3. Последние две высоты также относятся как 1:√5, откуда легко получить выражение а3 через а1.
 Зная высоту ствола колонны а3, из (16.2) находим шаг колоннады b = а3:√5 и диаметр колонны b2 = b1:√5.
Далее. В композиции главного фасада Парфенона можно выделить две пары связанных между собой элементов. Первая пара — это два горизонтальных каменных пояса: нагрузка а2 и стереобат а4. Эта пара связана числом членений: стереобат и нагрузка содержат по четыре элемента. (Возможно, число элементов в этих парах навеяно учением о четырех стихиях, ибо Парфенон является воплощением в камне всей античной философии.) Вторую пару образуют стволы колонн а3 и фронтон а5. Обе пары связаны все тем же законом пропорциональности 1:√5:
Зная высоту ствола колонны а3, из (16.2) находим шаг колоннады b = а3:√5 и диаметр колонны b2 = b1:√5.
Далее. В композиции главного фасада Парфенона можно выделить две пары связанных между собой элементов. Первая пара — это два горизонтальных каменных пояса: нагрузка а2 и стереобат а4. Эта пара связана числом членений: стереобат и нагрузка содержат по четыре элемента. (Возможно, число элементов в этих парах навеяно учением о четырех стихиях, ибо Парфенон является воплощением в камне всей античной философии.) Вторую пару образуют стволы колонн а3 и фронтон а5. Обе пары связаны все тем же законом пропорциональности 1:√5:
 (16.4)
Таким образом, "главный фасад оказался зарифмован через строку,- пишет Шевелев.- Причем движение от меньшего к большему (от стереобата к нагрузке), определенное пропорциональной связью первой пары, уравновешено движением от меньшего к большему второй пары (фронтон — ствол колонны), которое противоположно направлено".
(16.4)
Таким образом, "главный фасад оказался зарифмован через строку,- пишет Шевелев.- Причем движение от меньшего к большему (от стереобата к нагрузке), определенное пропорциональной связью первой пары, уравновешено движением от меньшего к большему второй пары (фронтон — ствол колонны), которое противоположно направлено".
Перейдем к оставшимся вертикальным Размерам Парфенона. Высота капители а7 и диаметр колонны b2 опять же соотносятся как 1:
 , откуда а7=b2:
, откуда а7=b2: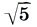 = а:5
= а:5 (
( + 1). Зная а7, легко выразить высоту антаблемента: а6 = а2 — а7 = 4а:5
+ 1). Зная а7, легко выразить высоту антаблемента: а6 = а2 — а7 = 4а:5 (
( + 1). Наконец, антаблемент а6 и капитель а7 разделены одинаково, зеркально-симметрично, в отношении 1:1:
+ 1). Наконец, антаблемент а6 и капитель а7 разделены одинаково, зеркально-симметрично, в отношении 1:1: на части х, х, х:
на части х, х, х: и y, y, y:
и y, y, y: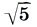 соответственно. Тогда из условия x+x+x:
соответственно. Тогда из условия x+x+x: = a6 и у+у+у:
= a6 и у+у+у: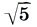 = а7 находим: x = k2a6, y = k2a7, k2 =
= а7 находим: x = k2a6, y = k2a7, k2 =  :(2
:(2 + 1), т. е. находим высоты составляющих антаблемент частей — архитрава а8 = k2a6, фриза а10 = k2а6 и карниза a12 = k2a6:
+ 1), т. е. находим высоты составляющих антаблемент частей — архитрава а8 = k2a6, фриза а10 = k2а6 и карниза a12 = k2a6: , а также высоты элементов капители — абака a9 = k2a7, эхина a11 =k2a7 и шейки а13 = k2а7:
, а также высоты элементов капители — абака a9 = k2a7, эхина a11 =k2a7 и шейки а13 = k2а7: .
Таковы лишь основные идеи пропорционального деления основных элементов Парфенона.
.
Таковы лишь основные идеи пропорционального деления основных элементов Парфенона.
 Пропорциональное дерево Парфенона (по Шевелеву). Все размеры храма от длины стилобата b = 69,5 м до высоты шейки а13 = 0,158 м выражаются через ширину стилобата: а = 100 фут. = 30,87 м
А более пытливому исследователю Парфенон открывает и свои более сокровенные тайны. Оказывается, что угловые колонны в Парфеноне толще остальных, рядовых, и сближены с ними. Отношение верхнего диаметра к нижнему в угловых колоннах менее контрастно, чем в рядовых. Такая расстановка колонн логична: ведь и в жизни сильных людей ставят на флангах. Но дело не столько в этом. Дело в том, что угловые колонны смотрятся на фоне яркого неба Эллады. Солнечные лучи дифрагируют, огибают угловые колонны. Поэтому если их сделать одинаковыми с рядовыми колоннами, которые смотрятся на темном фоне целлы — святилища храма, то угловые колонны будут казаться тоньше. Итак, в конструкцию Парфенона введены так называемые оптические поправки.
Древние греки прекрасно знали особенности оптического восприятия человеческого глаза: строго вертикальные и параллельные колонны кажутся распадающимися, а горизонтальная балка — прогнувшейся книзу.
Пропорциональное дерево Парфенона (по Шевелеву). Все размеры храма от длины стилобата b = 69,5 м до высоты шейки а13 = 0,158 м выражаются через ширину стилобата: а = 100 фут. = 30,87 м
А более пытливому исследователю Парфенон открывает и свои более сокровенные тайны. Оказывается, что угловые колонны в Парфеноне толще остальных, рядовых, и сближены с ними. Отношение верхнего диаметра к нижнему в угловых колоннах менее контрастно, чем в рядовых. Такая расстановка колонн логична: ведь и в жизни сильных людей ставят на флангах. Но дело не столько в этом. Дело в том, что угловые колонны смотрятся на фоне яркого неба Эллады. Солнечные лучи дифрагируют, огибают угловые колонны. Поэтому если их сделать одинаковыми с рядовыми колоннами, которые смотрятся на темном фоне целлы — святилища храма, то угловые колонны будут казаться тоньше. Итак, в конструкцию Парфенона введены так называемые оптические поправки.
Древние греки прекрасно знали особенности оптического восприятия человеческого глаза: строго вертикальные и параллельные колонны кажутся распадающимися, а горизонтальная балка — прогнувшейся книзу.
Но даже оптические поправки в Парфеноне подчинены закону
 Действительно, нижний диаметр угловых колонн больше "теоретического диаметра" b2 = a:5(
Действительно, нижний диаметр угловых колонн больше "теоретического диаметра" b2 = a:5( + l) = 190,79 см на 2,96 см, а у рядовых — меньше на 1,32 см. Взяв отношение этих поправок, мы с изумлением обнаруживаем: 1,32:2,96 = 0,446 ≈ 1:(
+ l) = 190,79 см на 2,96 см, а у рядовых — меньше на 1,32 см. Взяв отношение этих поправок, мы с изумлением обнаруживаем: 1,32:2,96 = 0,446 ≈ 1:( = 0,447!
= 0,447!
 Оптические иллюзии восприятия. Так выглядел бы Парфенон, если бы его линии были строго горизонтальны и вертикальны (а). Таков Парфенон в действительности (б). Парфенон, каким мы его видим благодаря оптическим поправкам (в). Наклоны и искривления прямых сильно преувеличены
Раз уж мы заговорили об отличии "теоретических" размеров Парфенона от истинных, следует расставить все точки над i. Разумеется, совпадение "теоретических" размеров (см. (16.1) — (16.4) и рис. на с. 222) с реальными размерами Парфенона не является абсолютным. Относительные расхождения теории с действительностью колеблются в пределах от 05% до 1,6%. Наибольшее расхождение получается для высоты антаблемента — 3,5%. Это и понятно, ибо высота антаблемента — единственный размер в "пропорциональном дереве Парфенона", полученный не с помощью закона пропорциональности 1:(
Оптические иллюзии восприятия. Так выглядел бы Парфенон, если бы его линии были строго горизонтальны и вертикальны (а). Таков Парфенон в действительности (б). Парфенон, каким мы его видим благодаря оптическим поправкам (в). Наклоны и искривления прямых сильно преувеличены
Раз уж мы заговорили об отличии "теоретических" размеров Парфенона от истинных, следует расставить все точки над i. Разумеется, совпадение "теоретических" размеров (см. (16.1) — (16.4) и рис. на с. 222) с реальными размерами Парфенона не является абсолютным. Относительные расхождения теории с действительностью колеблются в пределах от 05% до 1,6%. Наибольшее расхождение получается для высоты антаблемента — 3,5%. Это и понятно, ибо высота антаблемента — единственный размер в "пропорциональном дереве Парфенона", полученный не с помощью закона пропорциональности 1:( , а выражением через другие размеры. Таким образом, антаблемент является наиболее слабым местом в теории Шевелева, и эта слабость теории автоматически проявилась в математической оценке погрешностей. Впрочем, как нам кажется, и такая точность в расстояниях между горизонтальными линиями сооружения (3,5 см на 1 м) является желанным эталоном для некоторых современных строителей.
Заканчивая наш анализ пропорций Парфенона, естественно поставить вопросы: является ли теория Шевелева окончательной теорией Парфенона? Таков ли на самом деле был план построения чертежа Парфенона мудрым Иктином? Ответы на эти вопросы, возможно, даст время. Ибо, как это ни парадоксально, но чем дальше мы уходим от древних, тем лучше мы их узнаем. В этом убеждает нас весь ход развития исторической науки.
И последнее. Внимательный читатель должен задать еще один вопрос: а как теория Шевелева стыкуется с "теориями золотого сечения Парфенона", рассмотренными нами в главе 14? Напомним, что там мы привели к общему знаменателю разнообразные теории пропорций Парфенона, Цейзинга, Жолтовского, Гримма, Хэмбриджа и Месселя и показали, что все они, несмотря на внешнее различие, дают золотое сечение в главных вертикалях Парфенона, т. е. в отношении несущих частей с1 к несомым с2 (см. с. 202). А как обстоит дело с этим отношением в теории Шевелева? Из рисунка ясно, что
, а выражением через другие размеры. Таким образом, антаблемент является наиболее слабым местом в теории Шевелева, и эта слабость теории автоматически проявилась в математической оценке погрешностей. Впрочем, как нам кажется, и такая точность в расстояниях между горизонтальными линиями сооружения (3,5 см на 1 м) является желанным эталоном для некоторых современных строителей.
Заканчивая наш анализ пропорций Парфенона, естественно поставить вопросы: является ли теория Шевелева окончательной теорией Парфенона? Таков ли на самом деле был план построения чертежа Парфенона мудрым Иктином? Ответы на эти вопросы, возможно, даст время. Ибо, как это ни парадоксально, но чем дальше мы уходим от древних, тем лучше мы их узнаем. В этом убеждает нас весь ход развития исторической науки.
И последнее. Внимательный читатель должен задать еще один вопрос: а как теория Шевелева стыкуется с "теориями золотого сечения Парфенона", рассмотренными нами в главе 14? Напомним, что там мы привели к общему знаменателю разнообразные теории пропорций Парфенона, Цейзинга, Жолтовского, Гримма, Хэмбриджа и Месселя и показали, что все они, несмотря на внешнее различие, дают золотое сечение в главных вертикалях Парфенона, т. е. в отношении несущих частей с1 к несомым с2 (см. с. 202). А как обстоит дело с этим отношением в теории Шевелева? Из рисунка ясно, что
 Поэтому
Поэтому
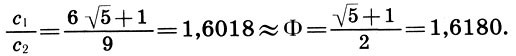 (16.5)
Итак, мы выполнили обещание, данное на с. 203, и показали, что и теория Шевелева, столь не похожая на все остальные теории Парфенона, там, где оно есть, с большой точностью дает золотое сечение. Точные обмеры показывают, что в самом Парфеноне закон золотого сечения выполнен приблизительно.
(16.5)
Итак, мы выполнили обещание, данное на с. 203, и показали, что и теория Шевелева, столь не похожая на все остальные теории Парфенона, там, где оно есть, с большой точностью дает золотое сечение. Точные обмеры показывают, что в самом Парфеноне закон золотого сечения выполнен приблизительно.
(Для поклонников золотого сечения покажем, что в теории Шевелева таковое имеется и в чистом виде. Например, отношение а1 :(a2 + a5) = l:2k1 = (
 + 2):2 = Φ. Этот факт еще раз говорит только о том, что двойной квадрат 1:
+ 2):2 = Φ. Этот факт еще раз говорит только о том, что двойной квадрат 1: тесно связан с золотым сечением.)
Прежде чем окончательно расстаться с Парфеноном, заметим, что и пропорции этого шедевра, и дорический ордер, в котором он выполнен, были не единственными архитектурными канонами, созданными гениальными древними греками. Неподалеку от Парфенона, на том же священном для древних и для современной цивилизации Акрополе, возвышается и другой бессмертный шедевр — храм Афины и Посейдона-Эрехтея — Эрехтейон, построенный чуть позже Парфенона, в 421 — 406 гг. до н. э. Но как не похоже это изящное и изысканное асимметричное сооружение, исполненное в ионическом ордере, на спокойный, строгий и симметрично уравновешенный Парфенон! Сколь отличны их пропорции! Достаточно сказать, что колонны Эрехтейона "вдвое стройнее": в них отношение диаметра основания к высоте равно 1:10. Но пропорции Эрехтейона — это еще одна увлекательная страница в архитектуре античности. А нас уже ждут гулкие своды готики.
Из светлого и жизнеобильного мира Древней Эллады перенесемся сквозь полтора тысячелетия в сумрачную эпоху европейского средневековья. Как все переменилось! Иная культура, иная философия, иная религия, иная архитектура... Вместо озаренной улыбкой античной любви к жизни и человеку — философия "умерщвления плоти", презрения земных радостей, аскетизма. Любые ростки свободной мысли, всякий вольный полет фантазии проходили через безжалостное прокрустово ложе церковных канонов. Но и в этих условиях
тесно связан с золотым сечением.)
Прежде чем окончательно расстаться с Парфеноном, заметим, что и пропорции этого шедевра, и дорический ордер, в котором он выполнен, были не единственными архитектурными канонами, созданными гениальными древними греками. Неподалеку от Парфенона, на том же священном для древних и для современной цивилизации Акрополе, возвышается и другой бессмертный шедевр — храм Афины и Посейдона-Эрехтея — Эрехтейон, построенный чуть позже Парфенона, в 421 — 406 гг. до н. э. Но как не похоже это изящное и изысканное асимметричное сооружение, исполненное в ионическом ордере, на спокойный, строгий и симметрично уравновешенный Парфенон! Сколь отличны их пропорции! Достаточно сказать, что колонны Эрехтейона "вдвое стройнее": в них отношение диаметра основания к высоте равно 1:10. Но пропорции Эрехтейона — это еще одна увлекательная страница в архитектуре античности. А нас уже ждут гулкие своды готики.
Из светлого и жизнеобильного мира Древней Эллады перенесемся сквозь полтора тысячелетия в сумрачную эпоху европейского средневековья. Как все переменилось! Иная культура, иная философия, иная религия, иная архитектура... Вместо озаренной улыбкой античной любви к жизни и человеку — философия "умерщвления плоти", презрения земных радостей, аскетизма. Любые ростки свободной мысли, всякий вольный полет фантазии проходили через безжалостное прокрустово ложе церковных канонов. Но и в этих условиях
(В. Брюсов)
 Виллар де Оннекур. Рисунки из альбома. 1235. Париж. Национальная библиотека. Попытки геометризированного рисования человека и животных, приведшие к полному отрицанию естественных пропорций
Виллар де Оннекур. Рисунки из альбома. 1235. Париж. Национальная библиотека. Попытки геометризированного рисования человека и животных, приведшие к полному отрицанию естественных пропорций
 Виллар де Оннекур. Рисунки из альбома. 1235. Париж. Национальная библиотека. Попытки геометризированного рисования человека
Но истину нельзя удержать в узде: стало достоянием человечества учение Пифагора, обрели жизнь и теоретические изыскания мастеров-каменотесов. Наиболее ранние из них мы находим в альбоме французского зодчего XIII века Вил л ара де Оннекура. Альбом содержит ряд геометрических конструкций, позволявших моделировать архитектурные формы, а также размышления автора о пропорциях человеческого тела. Сколь отличны эти рисунки от работ античных мастеров! Если древние греки пытались постичь законы пропорционального строения человеческого тела, а затем перенести эти законы на архитектурные сооружения, то средневековые мастера, наоборот, пытаются втиснуть живые линии в рамки простейших геометрических фигур, полностью игнорируя естественные пропорции. Вот голова мужчины, вписанная в сетку квадратов и их диагоналей (см. рис.). Это отнюдь не шарж или шутка, а прорисовка с витражей знаменитого Реймского собора. Человеческое тело не является более "мерой всех вещей". Такой мерой становится система геометрических фигур. Именно сетка геометрических линий является тем скелетом, на котором строится тело здания.
К концу XV века было издано несколько книг, посвященных секретам строительного мастерства средневековых зодчих. Вот строки из книги "О камне", написанной в 1486 г. немецким мастером Матхаусом Роцирером: "Если хочешь начертить план башни на точной геометрической основе по примеру каменотесов, начерти квадрат, обозначь его углы буквами а, Ь, с, d ... затем разделилинию а — b на две равные части и обозначь середину буквой е и таким же образом раздели три оставшиеся стороны квадрата. Затем поверни меньший квадрат так, как показано на рисунке". Система квадратов, описанная здесь, очевидна.
Виллар де Оннекур. Рисунки из альбома. 1235. Париж. Национальная библиотека. Попытки геометризированного рисования человека
Но истину нельзя удержать в узде: стало достоянием человечества учение Пифагора, обрели жизнь и теоретические изыскания мастеров-каменотесов. Наиболее ранние из них мы находим в альбоме французского зодчего XIII века Вил л ара де Оннекура. Альбом содержит ряд геометрических конструкций, позволявших моделировать архитектурные формы, а также размышления автора о пропорциях человеческого тела. Сколь отличны эти рисунки от работ античных мастеров! Если древние греки пытались постичь законы пропорционального строения человеческого тела, а затем перенести эти законы на архитектурные сооружения, то средневековые мастера, наоборот, пытаются втиснуть живые линии в рамки простейших геометрических фигур, полностью игнорируя естественные пропорции. Вот голова мужчины, вписанная в сетку квадратов и их диагоналей (см. рис.). Это отнюдь не шарж или шутка, а прорисовка с витражей знаменитого Реймского собора. Человеческое тело не является более "мерой всех вещей". Такой мерой становится система геометрических фигур. Именно сетка геометрических линий является тем скелетом, на котором строится тело здания.
К концу XV века было издано несколько книг, посвященных секретам строительного мастерства средневековых зодчих. Вот строки из книги "О камне", написанной в 1486 г. немецким мастером Матхаусом Роцирером: "Если хочешь начертить план башни на точной геометрической основе по примеру каменотесов, начерти квадрат, обозначь его углы буквами а, Ь, с, d ... затем разделилинию а — b на две равные части и обозначь середину буквой е и таким же образом раздели три оставшиеся стороны квадрата. Затем поверни меньший квадрат так, как показано на рисунке". Система квадратов, описанная здесь, очевидна.
 Чертежи для конструирования готических башен из книги Матхауса Роцирера 'О камне'. Регенсбург. 1486 (а)
Чертежи для конструирования готических башен из книги Матхауса Роцирера 'О камне'. Регенсбург. 1486 (а)
 Система квадрирования из книги Лоренца Лахера 'Наставления мастера Лахера'. Нюрнберг. 1516 (б)
Система квадрирования из книги Лоренца Лахера 'Наставления мастера Лахера'. Нюрнберг. 1516 (б)
 Система триангулирования Миланского собора. Иллюстрация из 'Комментариев к Витрувию' Цезаря Чезарино. Милан. 1521
Система триангулирования Миланского собора. Иллюстрация из 'Комментариев к Витрувию' Цезаря Чезарино. Милан. 1521
 Миланский собор. 1386-1858. Этот самый большой из всех готических соборов мира вмещает 40 000 молящихся. Строительство собора началось в 1386, шпиль был сооружен в 1756-1779, главный фасад завершен в 1805-1813, а последний шпиль — в 1858. Таким образом, собор строился 572 года!
Миланский собор. 1386-1858. Этот самый большой из всех готических соборов мира вмещает 40 000 молящихся. Строительство собора началось в 1386, шпиль был сооружен в 1756-1779, главный фасад завершен в 1805-1813, а последний шпиль — в 1858. Таким образом, собор строился 572 года!
 Витражи королевской капеллы Сен-Шапель-жемчужины французской высокой готики. Париж. 1240-1248
Витражи королевской капеллы Сен-Шапель-жемчужины французской высокой готики. Париж. 1240-1248
 Равносторонний треугольник — основа пропорциональной сетки капеллы Сен-Шапель (по Виолле-ле-Дюку)
Однако протест всесильных лож, требовавших строжайшего запрета на разглашение тайн строительства, помешал Роциреру продолжить публикацию своих трудов. Более того, из сохранившихся документов известно, что за нежелание подчиняться уставу строитель собора мастер Вольфган Роцирер, дядя Матхауса Роцирера, а с ним и резчик Микаэл Лой в 1514 г. были приговорены к смертной казни.
Равносторонний треугольник — основа пропорциональной сетки капеллы Сен-Шапель (по Виолле-ле-Дюку)
Однако протест всесильных лож, требовавших строжайшего запрета на разглашение тайн строительства, помешал Роциреру продолжить публикацию своих трудов. Более того, из сохранившихся документов известно, что за нежелание подчиняться уставу строитель собора мастер Вольфган Роцирер, дядя Матхауса Роцирера, а с ним и резчик Микаэл Лой в 1514 г. были приговорены к смертной казни.
 Пропорции западного фасада собора Парижской Богоматери
Показательны и строки из завещания сыну другого немецкого мастера Лоренца Лахера, написанного в 1516 г.: "Впиши один в другой три квадрата — и ты получишь длину и ширину, это та единая основа, к которой сводятся почти все необходимые нам чертежи".
Пропорции западного фасада собора Парижской Богоматери
Показательны и строки из завещания сыну другого немецкого мастера Лоренца Лахера, написанного в 1516 г.: "Впиши один в другой три квадрата — и ты получишь длину и ширину, это та единая основа, к которой сводятся почти все необходимые нам чертежи".
 Собор Парижской Богоматери (Нотр-Дам де Пари). Западный фасад. 1163-1257
Но была у средневековых мастеров и другая система пропорционального построения — система триангулирования. Противоположность мнений сторонников систем "ад квадратум" и "ад триангулам" со всей остротой проявилась в дискуссии, состоявшейся во время строительства Миланского собора. По причине огромных размеров собора, заложенного в 1386 г., при его строительстве возникли серьезные затруднения. Миланские зодчие пригласили иностранных коллег. В 1389 г. из Парижа был вызван мастер Николас де Бонавентура. В 1391 г. миланский мастер Джиованни был направлен для консультаций в Германию к мастеру Кельнского собора. В 1394 г. из германского города Ульма прибыл в Милан Ульрих фон Энсинген, а в 1399 г.- из Парижа Жан Миньо. В этот период положение с собором стало критическим. 11 января 1400 г. состоялось собрание всех архитекторов, на котором возник серьезный спор между Миньо и итальянскими зодчими. Разногласия во мнениях составили 54 пункта, среди которых был и пункт о системах пропорционирования. Сторонники системы триангулирования победили. На чертеже, сделанном в 1521 г. Чезаре Чезарино с оригинала 1395 г., мы видим, что в основе пропорций собора лежат равносторонние треугольники (см. рис. на с. 230).
Собор Парижской Богоматери (Нотр-Дам де Пари). Западный фасад. 1163-1257
Но была у средневековых мастеров и другая система пропорционального построения — система триангулирования. Противоположность мнений сторонников систем "ад квадратум" и "ад триангулам" со всей остротой проявилась в дискуссии, состоявшейся во время строительства Миланского собора. По причине огромных размеров собора, заложенного в 1386 г., при его строительстве возникли серьезные затруднения. Миланские зодчие пригласили иностранных коллег. В 1389 г. из Парижа был вызван мастер Николас де Бонавентура. В 1391 г. миланский мастер Джиованни был направлен для консультаций в Германию к мастеру Кельнского собора. В 1394 г. из германского города Ульма прибыл в Милан Ульрих фон Энсинген, а в 1399 г.- из Парижа Жан Миньо. В этот период положение с собором стало критическим. 11 января 1400 г. состоялось собрание всех архитекторов, на котором возник серьезный спор между Миньо и итальянскими зодчими. Разногласия во мнениях составили 54 пункта, среди которых был и пункт о системах пропорционирования. Сторонники системы триангулирования победили. На чертеже, сделанном в 1521 г. Чезаре Чезарино с оригинала 1395 г., мы видим, что в основе пропорций собора лежат равносторонние треугольники (см. рис. на с. 230).
 Пропорции: от Парфенона до Нотр-Дама
Среди сторонников системы триангулирования также велись споры относительно того, из каких треугольников должна состоять пропорциональная сетка готического собора: равносторонних, "египетских" и т. д. Мы не будем углубляться в эти теоретические премудрости, а только заметим, что и сторонники системы "ад триангулам", и приверженцы схемы "ад квадратум" оставили потомкам первоклассные архитектурные памятники. В качестве примера укажем на две жемчужины французской столицы: королевскую капеллу Сен Шапель (1243-1248) и знаменитый Нотр-Дам де Пари - собор Парижской Богоматери (1163-1257).
Капелла Сен Шапель — вершина высокой готики, образец совершенной гармонии и безукоризненной формы. Интерьер капеллы ошеломляет даже знатоков готического искусства: потоки теплого света, струящиеся из ее витражей, мощным аккордом вливаются в застывшую симфонию изысканных архитектурных форм капеллы. Согласно исследованиям Виолле-ле-Дюка, пропорциональная сетка капеллы построена на равносторонних треугольниках.
Собор Парижской Богоматери — самый величественный и самый популярный памятник ранней готики. В гордой размеренности западного фасада собора горизонтальные линии еще соперничают с вертикальными. Еще не исчезла стена фасада (ведь это только начало готики), но она уже приобрела легкость и даже прозрачность. Как показал французский историк архитектуры Огюст Шуази, пропорциональную основу западного фасада собора Нотр-Дам составляет квадрат, а высота башен фасада равна половине стороны этого квадрата...
Пропорции: от Парфенона до Нотр-Дама
Среди сторонников системы триангулирования также велись споры относительно того, из каких треугольников должна состоять пропорциональная сетка готического собора: равносторонних, "египетских" и т. д. Мы не будем углубляться в эти теоретические премудрости, а только заметим, что и сторонники системы "ад триангулам", и приверженцы схемы "ад квадратум" оставили потомкам первоклассные архитектурные памятники. В качестве примера укажем на две жемчужины французской столицы: королевскую капеллу Сен Шапель (1243-1248) и знаменитый Нотр-Дам де Пари - собор Парижской Богоматери (1163-1257).
Капелла Сен Шапель — вершина высокой готики, образец совершенной гармонии и безукоризненной формы. Интерьер капеллы ошеломляет даже знатоков готического искусства: потоки теплого света, струящиеся из ее витражей, мощным аккордом вливаются в застывшую симфонию изысканных архитектурных форм капеллы. Согласно исследованиям Виолле-ле-Дюка, пропорциональная сетка капеллы построена на равносторонних треугольниках.
Собор Парижской Богоматери — самый величественный и самый популярный памятник ранней готики. В гордой размеренности западного фасада собора горизонтальные линии еще соперничают с вертикальными. Еще не исчезла стена фасада (ведь это только начало готики), но она уже приобрела легкость и даже прозрачность. Как показал французский историк архитектуры Огюст Шуази, пропорциональную основу западного фасада собора Нотр-Дам составляет квадрат, а высота башен фасада равна половине стороны этого квадрата...
(О. Мандельштам)
17. Пропорции: от Покрова на Нерли до Модулора ле Корбюзье
И однажды возникло из грезы, Из молящейся этой души, Как трава, как вода, как березы, Диво дивное в русской глуши.Н. Рубцов
Настало время поисков пропорций. Утверждается дух архитектуры.В 1784 г. смиренный отец боголюбовской монашеской братии испросил разрешения у преосвященнейшего Виктора, архипастыря владимирского, благословления на разборку для монастырских потреб обветшавшей и полузаброшенной церковки. Разрешение было милостиво жаловано, но, как говорится, жизнь распорядилась по-своему: заказчики и подрядчики не сошлись в цене. Работы не начались, а там о них и вовсе забыли. Так волею судьбы остался жив памятник, который обошли стороной полчища Батыя и Мамая, пощадили столетия и пожарища бесконечных войн, шедевр древнерусского зодчества церковь Покрова Богородицы на Нерли. В ясные летние дни среди зелени заливных лугов ее стройная белизна, отраженная гладью старицы Клязьмы, дышит поэзией сказки. Лишь в короткие минуты заката белая свеча церкви загорается тревожно-багряным пламенем. В суровые зимы бескрайняя снежная пелена, будто заботливая мать, укутывает и прячет свое замерзшее дитя. "Во всей русской поэзии, давшей миру столько непревзойденных шедевров, нет, быть может, памятника более лирического, чем церковь Покрова на Нерли, ибо этот архитектурный памятник воспринимается как поэма, запечатленная в камне. Поэма русской природы, тихой грусти и созерцания" (Л. Любимов). Прежде чем приблизиться к тайне очарования древнерусской архитектуры, нам необходимо познакомиться с системой мер, существовавшей в Древней Руси. Мы уже отмечали (с. 198), что в разных местах земного шара, в разные времена и у разных народов эталоны длины были в принципе одинаковыми: они так или иначе происходили от человеческого тела. Эти так называемые антропометрические меры обладали ценнейшим для архитектуры качеством, о котором с введением метрической системы мер забыли, но к которому в XX веке вернулся Ле Корбюзье. Дело в том, что антропометрические меры в силу своего происхождения соразмерны человеку и поэтому удобны для конструирования искусственной среды обитания людей — архитектурных сооружений. Более того, в "человечьих" мерах заложены пропорции, отобранные самой природой, такие, как деление пополам, золотое сечение, функция золотого сечения. Следовательно, в антропометрических мерах естественным образом заложена гармония природы. Основной строительной мерой в Древней Руси была сажень, равная размаху рук в стороны. Сажень делилась на 2 полусажени, полусажень — на 2 локтя - расстояние от кончиков пальцев до локтя, локоть — на 2 пяди — расстояние между вытянутыми в противоположные стороны большим пальцем и мизинцем. Все четко и логично. Однако чем пристальнее историки изучали древнерусские летописи, тем больше становилось саженей, а когда их число перевалило за десять, голова у историков пошла кругом. Необходимо стало навести математический порядок в древнерусской системе мер. Это сделали историк, академик Б. А. Рыбаков и архитектор И. Ш. Шевелев. Начало антропометрическим мерам дает рост человека а. Главной из всех видов саженей является мерная, или маховая, сажень См, которая равна размаху рук человека в стороны. Изучение пропорций человеческого тела показывает, что См = 1,03а. Другой важной мерой у всех народов являлся двойной шаг, который равен высоте туловища от стоп до основания шеи. Последнее расстояние, как мы знаем (с. 220), равно 5/6а. Таким образом, двойной шаг, или малая (тмутараканская) сажень, Ст = 5/6а = 0,833а. Но главный сюрприз кроется в отношении этих двух основных размеров:Ле Корбюзье
 (17.1)
Следовательно, малая сажень Ст относится к мерной См как сторона двойного квадрата к его диагонали без малой стороны:
(17.1)
Следовательно, малая сажень Ст относится к мерной См как сторона двойного квадрата к его диагонали без малой стороны:
 Из (17.1) ясно, что отношение мерной полусажени См/2 к малой сажени Ст равно золотому сечению:
Из (17.1) ясно, что отношение мерной полусажени См/2 к малой сажени Ст равно золотому сечению:
 (17.2)
Итак, в установленном самой природой отношении полуразмаха рук (RS) к высоте туловища (LQ), т. е. в отношении двух основных мер Древней Руси, заключено золотое сечение, столь распространенное в древнерусской архитектуре.
Рост человека: а = АВ
Мерная сажень: Сн = AC = CN = 1,03a
Малая (тмутараканская) сажень:
(17.2)
Итак, в установленном самой природой отношении полуразмаха рук (RS) к высоте туловища (LQ), т. е. в отношении двух основных мер Древней Руси, заключено золотое сечение, столь распространенное в древнерусской архитектуре.
Рост человека: а = АВ
Мерная сажень: Сн = AC = CN = 1,03a
Малая (тмутараканская) сажень:  Сажень без чети:
Сажень без чети:  Косая новгородская сажень:
Косая новгородская сажень:  Косая великая сажень:
Косая великая сажень:  Соотношения между саженями:
Соотношения между саженями: 
 — золотое сечение
— золотое сечение
 — функция золотого сечения
— функция золотого сечения
 Основные древнерусские меры длины и геометрическая взаимосвязь между ними
Основные древнерусские меры длины и геометрическая взаимосвязь между ними
Построив квадраты на малой Ст и мерной См саженях и проведя в них диагонали, мы получаем еще два типа саженей: косую новгородскую сажень
 и великую косую сажень
и великую косую сажень . В отличие от первых двух саженей (малой и мерной), выражающих природные меры, косые сажени получены чисто геометрическим путем. Ясно, что
. В отличие от первых двух саженей (малой и мерной), выражающих природные меры, косые сажени получены чисто геометрическим путем. Ясно, что
 (17.3)
Наконец, существовала еще одна сажень, получаемая геометрическим путем. Это так называемая сажень без чети Сч, равная диагонали AM половины квадрата, построенного на мерной сажени См. У этой сажени не было соответствующей косой пары, и поэтому ее называли саженью без пары, без четы, или без чети. Из треугольника АСМ следует, что
(17.3)
Наконец, существовала еще одна сажень, получаемая геометрическим путем. Это так называемая сажень без чети Сч, равная диагонали AM половины квадрата, построенного на мерной сажени См. У этой сажени не было соответствующей косой пары, и поэтому ее называли саженью без пары, без четы, или без чети. Из треугольника АСМ следует, что  , откуда
, откуда
 (17.4)
т. е. отношение сажени без чети Сч к мерной сажени См равно функции золотого сечения (см. с. 219).
Таковы лишь основные типы саженей, существовавших в древнерусской метрологии. Новгородская мерная трость, найденная в 1970 г. (см. с. 219), позволила уточнить их размеры. Новгородские меры XII века соответствуют росту человека: а = 170,5 см. Тогда См = 175,6 см, Ст = 142,1 см, Кн= 200,9 см, Кв= 248,3 см, Сч= 196,3 см. Если же рост человека принять равным 6 греческим футам: а = 6*30,87 = 185,22 см, то для основных саженей (мерной и малой) получим значения: См = 190,8 см и Ст = 154,3 см. Именно эти меры наиболее часто встречаются в древнерусских храмах XI века, строительство которых, по-видимому, велось византийскими мастерами. Так, вместе с христианством Русь наследовала византийскую систему мер, которая в свою очередь взросла на античной средиземноморской культуре. Абсолютные размеры саженей в России с течением времени сильно колебались вплоть до введения метрической системы мер в 1918 г. Но важно то, что пропорциональные отношения между парными саженями сохранялись. Эти пропорции становились пропорциями архитектурных сооружений.
(17.4)
т. е. отношение сажени без чети Сч к мерной сажени См равно функции золотого сечения (см. с. 219).
Таковы лишь основные типы саженей, существовавших в древнерусской метрологии. Новгородская мерная трость, найденная в 1970 г. (см. с. 219), позволила уточнить их размеры. Новгородские меры XII века соответствуют росту человека: а = 170,5 см. Тогда См = 175,6 см, Ст = 142,1 см, Кн= 200,9 см, Кв= 248,3 см, Сч= 196,3 см. Если же рост человека принять равным 6 греческим футам: а = 6*30,87 = 185,22 см, то для основных саженей (мерной и малой) получим значения: См = 190,8 см и Ст = 154,3 см. Именно эти меры наиболее часто встречаются в древнерусских храмах XI века, строительство которых, по-видимому, велось византийскими мастерами. Так, вместе с христианством Русь наследовала византийскую систему мер, которая в свою очередь взросла на античной средиземноморской культуре. Абсолютные размеры саженей в России с течением времени сильно колебались вплоть до введения метрической системы мер в 1918 г. Но важно то, что пропорциональные отношения между парными саженями сохранялись. Эти пропорции становились пропорциями архитектурных сооружений.
О том, что меры древнерусскими строителями применялись парами, свидетельствует, например, новгородская грамота XVI века, которая так описывает размеры Софийского храма в Новгороде: "а внутри главы, где окна,- 12 сажен, а от Спасова образа ото лбу до моста церковного — 15 сажен мерных". (Обмеры показывают, что упоминаемые сажени соотносятся как
 :2.) О применении парных мер говорит и новгородская мерная трость, в которой малая сажень Ст использовалась либо в паре с мерной саженью См(Ст:См = 1:(
:2.) О применении парных мер говорит и новгородская мерная трость, в которой малая сажень Ст использовалась либо в паре с мерной саженью См(Ст:См = 1:( — 1)), либо с косой новгородской Кн(Ст:Кн = 1:√2). Если же на новгородской трости брались мерные полусажени в паре с малой саженью, то эта пара давала золотое сечение (См/2:Ст=φ). Итак, красота пропорций древнерусской архитектуры заложена в самой системе древнерусских мер, дающей такие важнейшие пропорции, как золотое сечение, функция золотого сечения, отношение двойного квадрата.
Но помимо всех этих пропорций, которые от самой природы перешли в систему мер, а затем и в архитектурные памятники, был у древнерусских мастеров и еще один секрет. Именно этот секрет позволял придавать каждому древнему сооружению неповторимую прелесть, "нюанс", как говорят архитекторы. Секрет этот раскрыт в рядной записи плотника Федора на постройку деревянной церкви Усть-Кулуйского погоста (кон. XVII в.), где сказано: "А рубить мне, Федору, в высоту до порога 9 рядов, а от полу до поволоки — как мера и красота скажет..."
"Как мера и красота скажет..." Эта замечательная формула безвестного русского плотника выражает суть диалектики взаимодействия рационального (мера) и чувственного (красота) начал в достижении прекрасного, союз математики (мера) и искусства (красота) в создании архитектурных памятников.
Перейдем, наконец, к анализу пропорций церкви Покрова на Нерли. Этот архитектурный шедевр для русского человека значит столько же, сколько Парфенон для грека. Поэтому неудивительно, что пропорциональный строй небольшой церкви анализировался многими исследователями и каждый из них старался дать свою "окончательную" разгадку тайны ее очарования. Рассмотрим кратко и мы пропорции церкви Покрова на Нерли с двух точек зрения.
Согласно архитектору Шевелеву, в основе пропорционального строения церкви Покрова лежит отношение сажени без чети к мерной сажени, которое является функцией золотого сечения (Сч:См = √5:2), а сам план церкви был построен следующим образом. Вначале размечался прямоугольник длиной 3 сажени без чети и шириной 3 мерные сажени, который очерчивал столбы, несущие барабан и своды. Поскольку 3Сч: 3См = √5:2 = 1,118, то стороны этого прямоугольника относятся к функции золотого сечения, а сам прямоугольник является почти квадратом, или, в терминологии Жолтовского, "живым квадратом". Проведя в исходном прямоугольнике диагонали, зодчий получал центр храма, а отложив на диагоналях от вершин к центру по 1 мерной сажени,- подкупольный прямоугольник и размеры несущих столбов. Так было построено ядро плана, определявшее все дальнейшие горизонтальные и вертикальные размеры сооружения. Мерная сажень строителей церкви Покрова равнялась См = 1,79 м.
Отмерив от Центра храма на восток 3См и на запад 3Сч, мастер получал длину внешнего прямоугольника, равную
— 1)), либо с косой новгородской Кн(Ст:Кн = 1:√2). Если же на новгородской трости брались мерные полусажени в паре с малой саженью, то эта пара давала золотое сечение (См/2:Ст=φ). Итак, красота пропорций древнерусской архитектуры заложена в самой системе древнерусских мер, дающей такие важнейшие пропорции, как золотое сечение, функция золотого сечения, отношение двойного квадрата.
Но помимо всех этих пропорций, которые от самой природы перешли в систему мер, а затем и в архитектурные памятники, был у древнерусских мастеров и еще один секрет. Именно этот секрет позволял придавать каждому древнему сооружению неповторимую прелесть, "нюанс", как говорят архитекторы. Секрет этот раскрыт в рядной записи плотника Федора на постройку деревянной церкви Усть-Кулуйского погоста (кон. XVII в.), где сказано: "А рубить мне, Федору, в высоту до порога 9 рядов, а от полу до поволоки — как мера и красота скажет..."
"Как мера и красота скажет..." Эта замечательная формула безвестного русского плотника выражает суть диалектики взаимодействия рационального (мера) и чувственного (красота) начал в достижении прекрасного, союз математики (мера) и искусства (красота) в создании архитектурных памятников.
Перейдем, наконец, к анализу пропорций церкви Покрова на Нерли. Этот архитектурный шедевр для русского человека значит столько же, сколько Парфенон для грека. Поэтому неудивительно, что пропорциональный строй небольшой церкви анализировался многими исследователями и каждый из них старался дать свою "окончательную" разгадку тайны ее очарования. Рассмотрим кратко и мы пропорции церкви Покрова на Нерли с двух точек зрения.
Согласно архитектору Шевелеву, в основе пропорционального строения церкви Покрова лежит отношение сажени без чети к мерной сажени, которое является функцией золотого сечения (Сч:См = √5:2), а сам план церкви был построен следующим образом. Вначале размечался прямоугольник длиной 3 сажени без чети и шириной 3 мерные сажени, который очерчивал столбы, несущие барабан и своды. Поскольку 3Сч: 3См = √5:2 = 1,118, то стороны этого прямоугольника относятся к функции золотого сечения, а сам прямоугольник является почти квадратом, или, в терминологии Жолтовского, "живым квадратом". Проведя в исходном прямоугольнике диагонали, зодчий получал центр храма, а отложив на диагоналях от вершин к центру по 1 мерной сажени,- подкупольный прямоугольник и размеры несущих столбов. Так было построено ядро плана, определявшее все дальнейшие горизонтальные и вертикальные размеры сооружения. Мерная сажень строителей церкви Покрова равнялась См = 1,79 м.
Отмерив от Центра храма на восток 3См и на запад 3Сч, мастер получал длину внешнего прямоугольника, равную 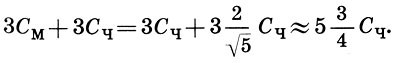 . А отложив этот размер в мерных саженях,- его ширину 53/4См. Таким образом, внешний прямоугольник плана церкви подобен ядру плана и также является "живым квадратом". Диагональ подкупольного прямоугольника определила диаметр центральной абсиды (подкупольного алтарного выступа) и диаметр барабана храма. Короткая сторона подкупольного прямоугольника задавала диаметры боковых абсид.
Наконец, высота основания храма — четверика, читаемая по высоте тонких колонок,- равна удвоенной длине ядра плана, т. е. 2*3Сч = 6Сч, а высота барабана с шлемовидной главой[29] — удвоенной ширине ядра, т. е. 2*3См = 6См. Таким образом, главные вертикальные размеры храма — высота основания и высота завершения — также относятся в функции золотого сечения. Сам же четверик представляет собой "почти куб", основанием которого является "почти квадрат", а высота почти равна сторонам основания. Итак, в построении четверика храма явно виден принцип приблизительной симметрии, который так часто встречается в природе и искусстве (см. гл. 4). Можно указать и на более мелкие членения храма, относящиеся в функции золотого сечения, т. е. в отношении сажени без чети к мерной сажени. Например, каменный поясок, венчающий колончатый фриз, который охватывает всю церковь и является ее важной архитектурной деталью, делит высоту четверика в функции золотого сечения.
Рассмотрим теперь ихнографию храма Покрова на Нерли, какой ее видит знаток древнерусской архитектуры К. Н. Афанасьев. Согласно Витрувию, "ихнография есть надлежащее и последовательное применение циркуля и линейки для получения очертаний плана". Как считает Афанасьев, исходным размером церкви Покрова является меньшая сторона подкупольного прямоугольника, равная 10 греческим футам: а = 10 греч. фут. = 308,7 см. Тогда большая сторона подкупольного прямоугольника получается как диагональ двойного квадрата со стороной а/2. Таким образом, подкупольный прямоугольник является "живым квадратом", стороны которого соотносятся в функции золотого сечения. Толщина столбов определяется отношением золотого сечения к модулю а/2. Дальнейшие построения ясны из рисунка. Так строится ядро плана. Остальные размеры плана получаются аналогичными построениями, опираясь в основном на модуль а/2.
. А отложив этот размер в мерных саженях,- его ширину 53/4См. Таким образом, внешний прямоугольник плана церкви подобен ядру плана и также является "живым квадратом". Диагональ подкупольного прямоугольника определила диаметр центральной абсиды (подкупольного алтарного выступа) и диаметр барабана храма. Короткая сторона подкупольного прямоугольника задавала диаметры боковых абсид.
Наконец, высота основания храма — четверика, читаемая по высоте тонких колонок,- равна удвоенной длине ядра плана, т. е. 2*3Сч = 6Сч, а высота барабана с шлемовидной главой[29] — удвоенной ширине ядра, т. е. 2*3См = 6См. Таким образом, главные вертикальные размеры храма — высота основания и высота завершения — также относятся в функции золотого сечения. Сам же четверик представляет собой "почти куб", основанием которого является "почти квадрат", а высота почти равна сторонам основания. Итак, в построении четверика храма явно виден принцип приблизительной симметрии, который так часто встречается в природе и искусстве (см. гл. 4). Можно указать и на более мелкие членения храма, относящиеся в функции золотого сечения, т. е. в отношении сажени без чети к мерной сажени. Например, каменный поясок, венчающий колончатый фриз, который охватывает всю церковь и является ее важной архитектурной деталью, делит высоту четверика в функции золотого сечения.
Рассмотрим теперь ихнографию храма Покрова на Нерли, какой ее видит знаток древнерусской архитектуры К. Н. Афанасьев. Согласно Витрувию, "ихнография есть надлежащее и последовательное применение циркуля и линейки для получения очертаний плана". Как считает Афанасьев, исходным размером церкви Покрова является меньшая сторона подкупольного прямоугольника, равная 10 греческим футам: а = 10 греч. фут. = 308,7 см. Тогда большая сторона подкупольного прямоугольника получается как диагональ двойного квадрата со стороной а/2. Таким образом, подкупольный прямоугольник является "живым квадратом", стороны которого соотносятся в функции золотого сечения. Толщина столбов определяется отношением золотого сечения к модулю а/2. Дальнейшие построения ясны из рисунка. Так строится ядро плана. Остальные размеры плана получаются аналогичными построениями, опираясь в основном на модуль а/2.
 Пропорции церкви Покрова Богородицы на Hepли. Построение плана с помощью парных мер по Шевелеву (а). Геометрическое построение ядра плана по Афанасьеву (б). Некоторые пропорциональные членения западного фасада (в)
Заметим, что вместе с функцией золотого сечения закон золотого сечения также определяет пропорциональный строй церкви Покрова. Это неудивительно, ибо данные отношения связаны геометрией двойного квадрата. Как установил Афанасьев, закону золотого сечения подчинены прежде всего главные вертикали храма, определяющие его силуэт: высота основания, равная высоте тонких колонок четверика, и высота барабана. Диаметр барабана относится к его высоте также в золотой пропорции. Эти пропорции видны с любых точек зрения. Переходя к западному фасаду, ряд золотого сечения можно продолжить: плечи храма относятся к диаметру барабана в золотой пропорции. Итак, принимая высоту белокаменной части церкви (от цоколя до купола) за единицу, мы получаем ряд золотого сечения: 1, φ, φ2, φ3, φ4, который определяет силуэт архитектурного сооружения. Этот ряд можно продолжить и в более мелких деталях. (Разумеется, западный фасад с точки зрения золотой пропорции не составляет исключения и взят нами лишь в качестве примера.)
Подведем некоторые итоги. Мы видим, что непостижимая, казалось бы, гармония храма Покрова подчинена математически строгим законам пропорциональности. План церкви построен на пропорциях функции золотого сечения — "живых квадратах", а ее силуэт определяется рядом золотого сечения. Эта цепь математических закономерностей и становится волшебной мелодией взаимосвязанных архитектурных форм. Конечно, законы пропорциональности определяют только "скелет" сооружения, который должен быть правильным и соразмерным, как скелет здорового человека. Но помимо математических законов меры в недрах архитектурного шедевра непременно заложены и непознанные законы красоты: "как мера и красота скажет..."! Именно диалектика взаимодействия законов меры и законов красоты, которые часто проявляются в отклонениях от законов меры, и создает неповторимый образ архитектурного шедевра.
Заметим, что с точки зрения геометрии рассмотренные нами реконструкции пропорционального строения церкви Покрова аналогичны. Они согласуются между собой и дают в плане три вписанных друг в друга "живых квадрата", отношение сторон которых √5:2 определяет весь пропорциональный строй храма. Однако с точки зрения истории архитектуры эти реконструкции отличаются принципиально. Первая из них основана на древнерусской системе мер и, следовательно, предполагает, что церковь Покрова была построена русскими зодчими. Вторая же в качестве основного размера имеет греческую меру и потому дает основание считать, что церковь строилась приглашенными из Византии мастерами... Кто и как создал жемчужину русской архитектуры? Возможно, мы еще узнаем ответ и на этот вопрос...
Церковь Покрова была построена в 1165 г. А через 73 года она стала свидетельницей небывалой в истории России беды: полчища Батыя, превратив в пепелище Рязань, Коломну и Москву, осадили Владимир. Русскому государству, истерзанному княжескими раздорами, был нанесен смертельный удар, оправиться от которого в полной мере Россия смогла только через 200 лет, к концу XV века.
Пропорции церкви Покрова Богородицы на Hepли. Построение плана с помощью парных мер по Шевелеву (а). Геометрическое построение ядра плана по Афанасьеву (б). Некоторые пропорциональные членения западного фасада (в)
Заметим, что вместе с функцией золотого сечения закон золотого сечения также определяет пропорциональный строй церкви Покрова. Это неудивительно, ибо данные отношения связаны геометрией двойного квадрата. Как установил Афанасьев, закону золотого сечения подчинены прежде всего главные вертикали храма, определяющие его силуэт: высота основания, равная высоте тонких колонок четверика, и высота барабана. Диаметр барабана относится к его высоте также в золотой пропорции. Эти пропорции видны с любых точек зрения. Переходя к западному фасаду, ряд золотого сечения можно продолжить: плечи храма относятся к диаметру барабана в золотой пропорции. Итак, принимая высоту белокаменной части церкви (от цоколя до купола) за единицу, мы получаем ряд золотого сечения: 1, φ, φ2, φ3, φ4, который определяет силуэт архитектурного сооружения. Этот ряд можно продолжить и в более мелких деталях. (Разумеется, западный фасад с точки зрения золотой пропорции не составляет исключения и взят нами лишь в качестве примера.)
Подведем некоторые итоги. Мы видим, что непостижимая, казалось бы, гармония храма Покрова подчинена математически строгим законам пропорциональности. План церкви построен на пропорциях функции золотого сечения — "живых квадратах", а ее силуэт определяется рядом золотого сечения. Эта цепь математических закономерностей и становится волшебной мелодией взаимосвязанных архитектурных форм. Конечно, законы пропорциональности определяют только "скелет" сооружения, который должен быть правильным и соразмерным, как скелет здорового человека. Но помимо математических законов меры в недрах архитектурного шедевра непременно заложены и непознанные законы красоты: "как мера и красота скажет..."! Именно диалектика взаимодействия законов меры и законов красоты, которые часто проявляются в отклонениях от законов меры, и создает неповторимый образ архитектурного шедевра.
Заметим, что с точки зрения геометрии рассмотренные нами реконструкции пропорционального строения церкви Покрова аналогичны. Они согласуются между собой и дают в плане три вписанных друг в друга "живых квадрата", отношение сторон которых √5:2 определяет весь пропорциональный строй храма. Однако с точки зрения истории архитектуры эти реконструкции отличаются принципиально. Первая из них основана на древнерусской системе мер и, следовательно, предполагает, что церковь Покрова была построена русскими зодчими. Вторая же в качестве основного размера имеет греческую меру и потому дает основание считать, что церковь строилась приглашенными из Византии мастерами... Кто и как создал жемчужину русской архитектуры? Возможно, мы еще узнаем ответ и на этот вопрос...
Церковь Покрова была построена в 1165 г. А через 73 года она стала свидетельницей небывалой в истории России беды: полчища Батыя, превратив в пепелище Рязань, Коломну и Москву, осадили Владимир. Русскому государству, истерзанному княжескими раздорами, был нанесен смертельный удар, оправиться от которого в полной мере Россия смогла только через 200 лет, к концу XV века.
 Церковь Вознесения в селе Коломенском (ныне Москва). 1532. Шедевр древнерусского зодчества, один из первых каменных шатровых храмов на Руси
В 1530 г. в царской усадьбе — селе Коломенском под Москвой — родился будущий царь пробуждающейся России Иван Грозный. А через два года здесь же, в Коломенском, на крутом берегу Москвы-реки, было завершено строительство церкви, поставленной в память об этом событии. Зодчие будто предвидели рождение небывало грозного царя: церковь тоже была небывалой. В ней все", и высота (почти 62 м), и каменный шатер, и устремленная ввысь форма — было невиданным. Новый храм словно символизировал прорыв России в свободное от татарского ига будущее. "...Бе же церковь та велми чюдна высотою и красотою и светлостию, такова не бывала прежде на Руси",- писал о ней летописец. Весь пропорциональный строй церкви, все ее безудержное стремление ввысь как нельзя более соответствовали названию — храм Вознесения.
Но для нас храм Вознесения интересен еще и тем, что он является не только гимном расправляющей крылья России, но и архитектурным гимном геометрии.
Ни один из рассмотренных архитектурных шедевров, в том числе и Парфенон, не настолько пронизан геометрией, не настолько прост и лаконичен в своей размерной структуре, как храм Вознесения в Коломенском. Соразмерности храма с предельной ясностью определены двумя парными мерами: горизонтальные — малой (тмутараканской) саженью Ст и косой новгородской саженью Кн (Ст:Кн = 1:√2), вертикальные — малой саженью Ст и мерной саженью См (Ст:См = 1:(√5 — 1)) и их комбинацией См:2Ст= (√5 — 1):2 = φ, дающей золотое сечение. Таким образом, храм Вознесения является также прекрасным примером применения московскими мастерами измерительного инструмента типа новгородской мерной трости, созданной, как мы помним, для работы именно этими двумя парами мер (см. с. 220). Рассмотрим пропорциональ-ный анализ храма, сделанный архитектором Шевелевым.
В основу плана церкви Вознесения положен квадрат ABCD со стороной в 10 малых сажень: а = АВ = 10Ст. Ясно, что диагонали квадрата равны 10 косым новгородским саженям: AC = BD = 10√2СТ = 10Кн. Так с помощью парных мер Ст и Кн осуществлялся контроль правильности построения исходного квадрата. Окружность радиуса R = 5Kн, описывающая квадрат, определяет положение всех 12 наружных углов плана храма. Вписав через середины сторон в квадрат ABCD новый квадрат и сделав построения, мы получим внешний контур плана — 20-уголъник. Выступающие над исходным квадратом части называются притворами, их ширина равна а/2 = 5Ст. Выразив радиус описанной окружности R в мерных саженях и отложив эту величину в малых саженях, строители получали сторону квадрата b, определяющего внутреннее пространство храма:
Церковь Вознесения в селе Коломенском (ныне Москва). 1532. Шедевр древнерусского зодчества, один из первых каменных шатровых храмов на Руси
В 1530 г. в царской усадьбе — селе Коломенском под Москвой — родился будущий царь пробуждающейся России Иван Грозный. А через два года здесь же, в Коломенском, на крутом берегу Москвы-реки, было завершено строительство церкви, поставленной в память об этом событии. Зодчие будто предвидели рождение небывало грозного царя: церковь тоже была небывалой. В ней все", и высота (почти 62 м), и каменный шатер, и устремленная ввысь форма — было невиданным. Новый храм словно символизировал прорыв России в свободное от татарского ига будущее. "...Бе же церковь та велми чюдна высотою и красотою и светлостию, такова не бывала прежде на Руси",- писал о ней летописец. Весь пропорциональный строй церкви, все ее безудержное стремление ввысь как нельзя более соответствовали названию — храм Вознесения.
Но для нас храм Вознесения интересен еще и тем, что он является не только гимном расправляющей крылья России, но и архитектурным гимном геометрии.
Ни один из рассмотренных архитектурных шедевров, в том числе и Парфенон, не настолько пронизан геометрией, не настолько прост и лаконичен в своей размерной структуре, как храм Вознесения в Коломенском. Соразмерности храма с предельной ясностью определены двумя парными мерами: горизонтальные — малой (тмутараканской) саженью Ст и косой новгородской саженью Кн (Ст:Кн = 1:√2), вертикальные — малой саженью Ст и мерной саженью См (Ст:См = 1:(√5 — 1)) и их комбинацией См:2Ст= (√5 — 1):2 = φ, дающей золотое сечение. Таким образом, храм Вознесения является также прекрасным примером применения московскими мастерами измерительного инструмента типа новгородской мерной трости, созданной, как мы помним, для работы именно этими двумя парами мер (см. с. 220). Рассмотрим пропорциональ-ный анализ храма, сделанный архитектором Шевелевым.
В основу плана церкви Вознесения положен квадрат ABCD со стороной в 10 малых сажень: а = АВ = 10Ст. Ясно, что диагонали квадрата равны 10 косым новгородским саженям: AC = BD = 10√2СТ = 10Кн. Так с помощью парных мер Ст и Кн осуществлялся контроль правильности построения исходного квадрата. Окружность радиуса R = 5Kн, описывающая квадрат, определяет положение всех 12 наружных углов плана храма. Вписав через середины сторон в квадрат ABCD новый квадрат и сделав построения, мы получим внешний контур плана — 20-уголъник. Выступающие над исходным квадратом части называются притворами, их ширина равна а/2 = 5Ст. Выразив радиус описанной окружности R в мерных саженях и отложив эту величину в малых саженях, строители получали сторону квадрата b, определяющего внутреннее пространство храма:
 Разумеется, коломенские мастера не вычисляли никаких радикалов! Они просто прикладывали мерную трость разными сторонами и автоматически переходили из одной меры в другую. План церкви построен. А мы выразим еще сторону квадрата с, охватывающего притворы: с = √7/2а (треугольник, из которого находится с/2, на чертеже не показан, чтобы не портить красоту центральной симметрии плана; найдите его). Зная а, b, с, легко выразить все остальные размеры плана и соотношения между ними.
Перейдем к объемам и вертикальным членениям храма. Церковь Вознесения со всех сторон окружена крытой галереей, поднятой над уровнем земли и называемой гульбищем. Гульбище делалось на уровне перекрытия подклета — полуподвального помещения, используемого в хозяйственных целях. Вход в церковь устраивался с гульбища, на которое в храме Вознесения ведут три крыльца, и, таким образом, вертикальные размеры церкви с гульбищем воспринимаются от уровня последнего.
Основной объем храма составляет 20-гранная призма, поставленная на подклет. Ее высота равна стороне исходного квадрата а. Таким образом, ядром основного объема является куб — четверик а×а×а (а=10Ст), украшенный гранями притворов. Вместе с подклетом высота 20-гранной призмы равна диагонали исходного квадрата а√2 = 10√2Ст = 10Кн. Итак, сторона и диагональ исходного квадрата (ядра плана) полностью определяют вертикальные размеры основного объема (ядра основания).
Двадцатигранная призма основного объема через затейливый пояс кокошников переходит в восьмигранную призму — восьмерик. Восьмерик также вписан к куб d×d×d(d = 9Cт). Затем восьмерик переходит в восьмигранный шатер, высота которого h = d√2 = 9√2Ст = 9Кн, т. е. шатер вписан в прямоугольный параллелепипед 9Ст×9Ст×9Кн. Площадь верхнего сечения шатра уменьшена в 16 раз, а его линейные размеры — в 4 раза. Поскольку 1/4 сажени равна локтю, то, следовательно, верхнее сечение вписано в квадрат где Лт — малый (тмутараканский) локоть (4Лт = Ст). Наконец, через венчающий карниз шатер завершается восьмигранным барабаном, сечение которого на малый полулокоть превышает верхнее сечение шатра. Барабан чуть нависает над шатром и вписан в куб f×f×f (f = 9,5Лт), а вместе с главкой, взятой без яблока (см. рис. на с. 242), барабан вписан в прямоугольный параллелепипед f×f×√2f.
Итак, мы видим как сторона ядра плана а, измеренная то малой саженью, то косой новгородской, рождает все главные вертикали храма. Заметим, что общая высота церкви от верха цоколя до яблока, на котором стоит крест, равна 4а = 40Ст, т. е. также простейшим образом выражается через исходный размер а. И еще одно важное отношение. Пояс кокошников, через который четверик основания переходит восьмерик шатра, делит храм на две части — основание и завершение. Высота основания h1≈14Cт, а высота завершения h2≈14Kн, откуда h1:h2 = Cт:Kн = 1:√2, т. е. главные вертикальные членения храма также относятся как малая и косая новгородская сажени.
Разумеется, коломенские мастера не вычисляли никаких радикалов! Они просто прикладывали мерную трость разными сторонами и автоматически переходили из одной меры в другую. План церкви построен. А мы выразим еще сторону квадрата с, охватывающего притворы: с = √7/2а (треугольник, из которого находится с/2, на чертеже не показан, чтобы не портить красоту центральной симметрии плана; найдите его). Зная а, b, с, легко выразить все остальные размеры плана и соотношения между ними.
Перейдем к объемам и вертикальным членениям храма. Церковь Вознесения со всех сторон окружена крытой галереей, поднятой над уровнем земли и называемой гульбищем. Гульбище делалось на уровне перекрытия подклета — полуподвального помещения, используемого в хозяйственных целях. Вход в церковь устраивался с гульбища, на которое в храме Вознесения ведут три крыльца, и, таким образом, вертикальные размеры церкви с гульбищем воспринимаются от уровня последнего.
Основной объем храма составляет 20-гранная призма, поставленная на подклет. Ее высота равна стороне исходного квадрата а. Таким образом, ядром основного объема является куб — четверик а×а×а (а=10Ст), украшенный гранями притворов. Вместе с подклетом высота 20-гранной призмы равна диагонали исходного квадрата а√2 = 10√2Ст = 10Кн. Итак, сторона и диагональ исходного квадрата (ядра плана) полностью определяют вертикальные размеры основного объема (ядра основания).
Двадцатигранная призма основного объема через затейливый пояс кокошников переходит в восьмигранную призму — восьмерик. Восьмерик также вписан к куб d×d×d(d = 9Cт). Затем восьмерик переходит в восьмигранный шатер, высота которого h = d√2 = 9√2Ст = 9Кн, т. е. шатер вписан в прямоугольный параллелепипед 9Ст×9Ст×9Кн. Площадь верхнего сечения шатра уменьшена в 16 раз, а его линейные размеры — в 4 раза. Поскольку 1/4 сажени равна локтю, то, следовательно, верхнее сечение вписано в квадрат где Лт — малый (тмутараканский) локоть (4Лт = Ст). Наконец, через венчающий карниз шатер завершается восьмигранным барабаном, сечение которого на малый полулокоть превышает верхнее сечение шатра. Барабан чуть нависает над шатром и вписан в куб f×f×f (f = 9,5Лт), а вместе с главкой, взятой без яблока (см. рис. на с. 242), барабан вписан в прямоугольный параллелепипед f×f×√2f.
Итак, мы видим как сторона ядра плана а, измеренная то малой саженью, то косой новгородской, рождает все главные вертикали храма. Заметим, что общая высота церкви от верха цоколя до яблока, на котором стоит крест, равна 4а = 40Ст, т. е. также простейшим образом выражается через исходный размер а. И еще одно важное отношение. Пояс кокошников, через который четверик основания переходит восьмерик шатра, делит храм на две части — основание и завершение. Высота основания h1≈14Cт, а высота завершения h2≈14Kн, откуда h1:h2 = Cт:Kн = 1:√2, т. е. главные вертикальные членения храма также относятся как малая и косая новгородская сажени.
 Пропорциональный строй церкви Вознесения в Коломенском (по Шевелеву)
Но пропорции храма Вознесения определены не одной, а двумя математическими закономерностями. Помимо пропорции Ст:Кн= 1:√2, определяющей основание, статическое начало храма, есть в нем и другая тема — тема развития вверх, вознесения, которая определена пропорциональной цепью: Ст:См = 1:(√5 — 1), а также пропорцией золотого сечения: См:2Ст=φ. В проведении этой темы соблюден знакомый нам по Парфенону принцип встречного движения пропорций. Две разные пропорциональные цепи накладываются друг на друга, сталкиваются и противоборствуют. В этом столкновении двух противоборствующих начал — горизонтального и вертикального — и заключается архитектурный образ церкви Вознесения. Не останавливаясь на математическом анализе этих двух систем, предоставим слово автору прекрасного эстетического анализа церкви Вознесения, искусствоведу А. Циресу. "В образе этой церкви,- пишет Цирес,- сплетаются два основных лейтмотива: мотив острого, полного столкновений и диссонансов динамизма и мотив гармонически спокойной красоты... Сложный ритм арок нижних галерей... идет, учащаясь от краев к центру,... теснит арки от краев к углам основного массива церкви и к ее середине,... подсказывает смену горизонтального движения движением, направленным ввысь... Так снизу вверх идет последовательное смягчение кристаллизма и нарастание компактности объема, вплоть до его стянутости в крепкий узел, венчающий всю объемную композицию главкой".
Но закончить разговор о пропорциях церкви Вознесения в Коломенском нам хочется словами автора математического анализа ее пропорций, Шевелева. "Подчеркнем выразительнейшую деталь размерной структуры, наиболее ярко показывающую особенность логики древнего мастера, стремящегося особенно точно выразить в метрологии главное. Так же как 10 саженей определили, по существу, весь храм, его ядро, так же и 10 локтей определили символ и венчание церкви — крест (10СтХ10СтХ10Ст — четверик; 10СтХ10СтХ10Кн — призма четверика; 10ЛтХ10Лт — соразмерность креста, ибо в нем заключен для зодчего и смысловой символ соединения, и символ торжества вертикали, и символ храма, и символ пропорции, построившей этот образ)".
Пропорциональный строй церкви Вознесения в Коломенском (по Шевелеву)
Но пропорции храма Вознесения определены не одной, а двумя математическими закономерностями. Помимо пропорции Ст:Кн= 1:√2, определяющей основание, статическое начало храма, есть в нем и другая тема — тема развития вверх, вознесения, которая определена пропорциональной цепью: Ст:См = 1:(√5 — 1), а также пропорцией золотого сечения: См:2Ст=φ. В проведении этой темы соблюден знакомый нам по Парфенону принцип встречного движения пропорций. Две разные пропорциональные цепи накладываются друг на друга, сталкиваются и противоборствуют. В этом столкновении двух противоборствующих начал — горизонтального и вертикального — и заключается архитектурный образ церкви Вознесения. Не останавливаясь на математическом анализе этих двух систем, предоставим слово автору прекрасного эстетического анализа церкви Вознесения, искусствоведу А. Циресу. "В образе этой церкви,- пишет Цирес,- сплетаются два основных лейтмотива: мотив острого, полного столкновений и диссонансов динамизма и мотив гармонически спокойной красоты... Сложный ритм арок нижних галерей... идет, учащаясь от краев к центру,... теснит арки от краев к углам основного массива церкви и к ее середине,... подсказывает смену горизонтального движения движением, направленным ввысь... Так снизу вверх идет последовательное смягчение кристаллизма и нарастание компактности объема, вплоть до его стянутости в крепкий узел, венчающий всю объемную композицию главкой".
Но закончить разговор о пропорциях церкви Вознесения в Коломенском нам хочется словами автора математического анализа ее пропорций, Шевелева. "Подчеркнем выразительнейшую деталь размерной структуры, наиболее ярко показывающую особенность логики древнего мастера, стремящегося особенно точно выразить в метрологии главное. Так же как 10 саженей определили, по существу, весь храм, его ядро, так же и 10 локтей определили символ и венчание церкви — крест (10СтХ10СтХ10Ст — четверик; 10СтХ10СтХ10Кн — призма четверика; 10ЛтХ10Лт — соразмерность креста, ибо в нем заключен для зодчего и смысловой символ соединения, и символ торжества вертикали, и символ храма, и символ пропорции, построившей этот образ)".
 Модулор Ле Корбюзье. Рисунок Ле Корбюзье. 'Модулор — это измерительный прибор, в основе которого лежат человеческий рост и математика' (Ле Корбюзье)
Нам остается только добавить, что село Коломенское давно уже стало частью современной Москвы и тем, кто не знает этого, мы рекомендуем сойти на одноименной станции метро и воочию убедиться в гениальности безвестных русских мастеров. Ну а те, кто знаком с храмом Вознесения, быть может, захотят теперь взглянуть на него другими глазами, увидеть в нем не только причудливую игру воображения художника, но и мудрый расчет изощренного ума мастера.
Коль скоро речь у нас зашла о метро, то перенесемся, наконец, в современный XX век. Время поисков пропорций и сегодня не кануло в Лету, напротив, по мнению Ле Корбюзье, оно только настало.
Мы уже отмечали (с. 220), что антропометрические меры благодаря своему происхождению оказались как нельзя лучше приспособлены для конструирования архитектурной среды. Мы только что убедились в том, что антропометрические меры содержали в себе замечательные пропорции, позволявшие древним мастерам создавать прекрасные памятники архитектуры.
7 апреля 1795 г. во Франции была введена метрическая система мер, в разработке которой участвовали такие крупнейшие ученые, как Лаплас, Монж, Кондорсе. За единицу длины — метр — была принята 1/10 000 000 часть 1/4 длины парижского географического меридиана. Метрическая система обладала бесспорными преимуществами и все шире раздвигала границы своего существования. Однако метр никоим образом не был связан с человеком, и, по мнению Ле Корбюзье, для архитектуре это имело самые серьезные последствия^ "Принимая участие в постройке хижин, жилых домов, храмов, предназначенных для потребностей человека, метр, по-видимому, ввел в них чужие и чуждые единицы измерения и, если мы присмотримся к нему ближе, может быть обвинен в дезориентации современной архитектуры и ее искажении... Архитектура, построенная на метрических измерениях, сбилась с правильного пути".
Но главная причина, толкавшая зодчих XX века на поиски новых систем измерений в архитектуре, была все-таки не в недостатках метрической системы мер. Английская архитектура с постоянством продолжала пользоваться футами и дюймами, но и у нее возникли те же проблемы. Дело было в том, что вместе с XX веком в архитектуру пришли невиданные объемы и темпы строительства. Проектирование архитектурной среды стало преимущественно типовым, а сама архитектура — индустриальной. В этих условиях строительные элементы необходимо было стандартизировать и унифицировать. Кроме того, архитекторам хотелось бы примирить непримиримое: красоту и стандарт. Требовалось найти такие методы пропорционирования, которые обладали бы максимальной гибкостью, простотой и универсальностью. "Если бы появился какой-нибудь линейный измеритель, подобный системам музыкальной записи, не облегчился бы ряд проблем, связанных со строительством?" — спрашивал Ле Корбюзье. И в 1949 г. он сам отвечает на этот вопрос, предложив в качестве такого измерителя систему модульной унификации — модулор.
Идея построения модулора гениально проста. Модулор — это ряд золотого сечения (15.2):
Модулор Ле Корбюзье. Рисунок Ле Корбюзье. 'Модулор — это измерительный прибор, в основе которого лежат человеческий рост и математика' (Ле Корбюзье)
Нам остается только добавить, что село Коломенское давно уже стало частью современной Москвы и тем, кто не знает этого, мы рекомендуем сойти на одноименной станции метро и воочию убедиться в гениальности безвестных русских мастеров. Ну а те, кто знаком с храмом Вознесения, быть может, захотят теперь взглянуть на него другими глазами, увидеть в нем не только причудливую игру воображения художника, но и мудрый расчет изощренного ума мастера.
Коль скоро речь у нас зашла о метро, то перенесемся, наконец, в современный XX век. Время поисков пропорций и сегодня не кануло в Лету, напротив, по мнению Ле Корбюзье, оно только настало.
Мы уже отмечали (с. 220), что антропометрические меры благодаря своему происхождению оказались как нельзя лучше приспособлены для конструирования архитектурной среды. Мы только что убедились в том, что антропометрические меры содержали в себе замечательные пропорции, позволявшие древним мастерам создавать прекрасные памятники архитектуры.
7 апреля 1795 г. во Франции была введена метрическая система мер, в разработке которой участвовали такие крупнейшие ученые, как Лаплас, Монж, Кондорсе. За единицу длины — метр — была принята 1/10 000 000 часть 1/4 длины парижского географического меридиана. Метрическая система обладала бесспорными преимуществами и все шире раздвигала границы своего существования. Однако метр никоим образом не был связан с человеком, и, по мнению Ле Корбюзье, для архитектуре это имело самые серьезные последствия^ "Принимая участие в постройке хижин, жилых домов, храмов, предназначенных для потребностей человека, метр, по-видимому, ввел в них чужие и чуждые единицы измерения и, если мы присмотримся к нему ближе, может быть обвинен в дезориентации современной архитектуры и ее искажении... Архитектура, построенная на метрических измерениях, сбилась с правильного пути".
Но главная причина, толкавшая зодчих XX века на поиски новых систем измерений в архитектуре, была все-таки не в недостатках метрической системы мер. Английская архитектура с постоянством продолжала пользоваться футами и дюймами, но и у нее возникли те же проблемы. Дело было в том, что вместе с XX веком в архитектуру пришли невиданные объемы и темпы строительства. Проектирование архитектурной среды стало преимущественно типовым, а сама архитектура — индустриальной. В этих условиях строительные элементы необходимо было стандартизировать и унифицировать. Кроме того, архитекторам хотелось бы примирить непримиримое: красоту и стандарт. Требовалось найти такие методы пропорционирования, которые обладали бы максимальной гибкостью, простотой и универсальностью. "Если бы появился какой-нибудь линейный измеритель, подобный системам музыкальной записи, не облегчился бы ряд проблем, связанных со строительством?" — спрашивал Ле Корбюзье. И в 1949 г. он сам отвечает на этот вопрос, предложив в качестве такого измерителя систему модульной унификации — модулор.
Идея построения модулора гениально проста. Модулор — это ряд золотого сечения (15.2):
 (17.1)
умноженный на два коэффициента. Первый коэффициент k1 равен росту человека; умножая (17.1) на k1, Корбюзье получает так называемый красный ряд. Второй коэффициент k2 равен расстоянию от земли до конца поднятой руки человека (это большая сажень в древнерусской системе мер)- При умножении (17.1) на k2 получается синий ряд. Осталось только выбрать числовые значения коэффициентов. Желая примирить в моду лоре английскую и французскую системы мер, а также следуя античной традиции, согласно которой рост человека равен 6 футам, Корбюзье взял в качестве k1 6 английских футов, т. е. k1 = 6*30,48 = 182,88 см. Значение k2 принято равным 226,0 см. Так были получены красный ряд:
(17.1)
умноженный на два коэффициента. Первый коэффициент k1 равен росту человека; умножая (17.1) на k1, Корбюзье получает так называемый красный ряд. Второй коэффициент k2 равен расстоянию от земли до конца поднятой руки человека (это большая сажень в древнерусской системе мер)- При умножении (17.1) на k2 получается синий ряд. Осталось только выбрать числовые значения коэффициентов. Желая примирить в моду лоре английскую и французскую системы мер, а также следуя античной традиции, согласно которой рост человека равен 6 футам, Корбюзье взял в качестве k1 6 английских футов, т. е. k1 = 6*30,48 = 182,88 см. Значение k2 принято равным 226,0 см. Так были получены красный ряд:
 (17.2)
и синий ряд:
(17.2)
и синий ряд:
 (17.3)
Значение k2 было выбрано еще и так, чтобы между красным и синим рядами существовала простая связь:
(17.3)
Значение k2 было выбрано еще и так, чтобы между красным и синим рядами существовала простая связь:
 (17.4)
Следовательно, синий ряд фактически есть удвоение красного ряда.
Будучи геометрическими прогрессиями, члены обоих рядов модулора образуют цепь равных отношений: an+1:an = bn+1:bn = Φ, т. е. в моду лоре воплощается принцип гармонии: "из всего — единое, из единого — все". Благодаря аддитивному свойству золотого сечения "части" модулора сходятся в "целое". Наконец, абсолютные значения шкал модулора происходят от человека и потому хорошо приспособлены для проектирования архитектурной среды. Так, по мнению автора, модулор вносит порядок, стандарт в производство и в то же время связывает все его элементы законами гармонии.
(17.4)
Следовательно, синий ряд фактически есть удвоение красного ряда.
Будучи геометрическими прогрессиями, члены обоих рядов модулора образуют цепь равных отношений: an+1:an = bn+1:bn = Φ, т. е. в моду лоре воплощается принцип гармонии: "из всего — единое, из единого — все". Благодаря аддитивному свойству золотого сечения "части" модулора сходятся в "целое". Наконец, абсолютные значения шкал модулора происходят от человека и потому хорошо приспособлены для проектирования архитектурной среды. Так, по мнению автора, модулор вносит порядок, стандарт в производство и в то же время связывает все его элементы законами гармонии.
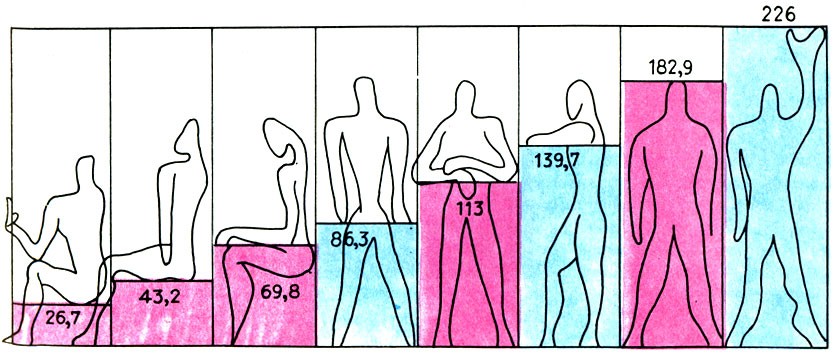 Числа красной и синей шкал модулора — действительные размеры, соответствующие определенным положениям тела человека. Рисунок Ле Корбюзье
Числа красной и синей шкал модулора — действительные размеры, соответствующие определенным положениям тела человека. Рисунок Ле Корбюзье
 Капелла в Роншане. 1958 (б). Эти два антипода в творчестве великого зодчего, две различные философии в архитектуре связаны воедино гаммой архитектурных пропорций — модулором
Капелла в Роншане. 1958 (б). Эти два антипода в творчестве великого зодчего, две различные философии в архитектуре связаны воедино гаммой архитектурных пропорций — модулором
 Ле Корбюзье. 'Лучезарный дом' в Марселе. 1947-1952 (а). Эти два антипода в творчестве великого зодчего, две различные философии в архитектуре связаны воедино гаммой архитектурных пропорций — модулором
Однако "погоня за двумя зайцами" (желание иметь хорошие числа и в метрах, и в футах) вылилась в серьезный недостаток: размеры модулора оказались несоразмерными со средним ростом человека. Широкого распространения модулор не получил. Но идеи стандарта и гармонии, заложенные в модулоре, не перестают волновать архитекторов. Вечный поиск совершенной гармонии продолжается. Недавно советским, архитектором Я. Д. Гликиным разработана универсальная система пропорциональности, которая, как показывает автор, вбирает в себя все известные до сего времени системы пропорционирования: системы триангулирования на египетском и на равностороннем треугольнике; системы Вйтрувия, Альберти, Хэмбриджа, Месселя, Шевелева; систему древнерусских мер и модулор Ле Корбюзье.
Что же объединяет все системы пропорциональности? Дело в том, что любая пропорциональная система — это основа, скелет архитектурного сооружения, это та гамма, а точнее, тот лад, в котором будет звучать архитектурная музыка. Именно это свойство модулора Ле Корбюзье имел в виду Альберт Эйнштейн, давая ему восторженную оценку: "Модулор — это гамма пропорций, которая делает плохое трудным, а хорошее — легким". Но гамма — это еще не мелодия, не музыка. Это хорошо осознавал и сам Корбюзье: "Модулор — это гамма. Музыкант располагает гаммой и создает музыку по своим способностям — банальную или прекрасную". В самом деле, как гамма уже третье тысячелетие дает возможность композитору создавать бесконечное разнообразие мелодий, так и система пропорционирования — модулор — нисколько не стесняет в творчестве архитектора. Сам
Корбюзье блестяще доказал это, построив с помощью своего модулора и знаменитый "Лучезарный дом" в Марселе, и не менее знаменитую капеллу в Роншане. Эти два произведения великого зодчего — два антипода, две разные философии в архитектуре. С одной стороны, воплощение здравого смысла, ясного, прямолинейного и рационального. С другой — нечто иррациональное, пластическое, скульптурное, сказочное. Единственное, что объединяет эти два выдающихся памятника зодчества — это модулор, архитектурная гамма пропорций, общая для обоих произведений Ле Корбюзье.
Но почему великий Эйнштейн систему пропорционирования в архитектуре — модулор — сравнивает с музыкальной гаммой? Почему его великий соотечественник Гёте называет архитектуру отзвучавшей музыкой? Что общего между архитектурой и музыкой? Это и будет последний вопрос, на который мы попытаемся ответить в этой части книги.
Ле Корбюзье. 'Лучезарный дом' в Марселе. 1947-1952 (а). Эти два антипода в творчестве великого зодчего, две различные философии в архитектуре связаны воедино гаммой архитектурных пропорций — модулором
Однако "погоня за двумя зайцами" (желание иметь хорошие числа и в метрах, и в футах) вылилась в серьезный недостаток: размеры модулора оказались несоразмерными со средним ростом человека. Широкого распространения модулор не получил. Но идеи стандарта и гармонии, заложенные в модулоре, не перестают волновать архитекторов. Вечный поиск совершенной гармонии продолжается. Недавно советским, архитектором Я. Д. Гликиным разработана универсальная система пропорциональности, которая, как показывает автор, вбирает в себя все известные до сего времени системы пропорционирования: системы триангулирования на египетском и на равностороннем треугольнике; системы Вйтрувия, Альберти, Хэмбриджа, Месселя, Шевелева; систему древнерусских мер и модулор Ле Корбюзье.
Что же объединяет все системы пропорциональности? Дело в том, что любая пропорциональная система — это основа, скелет архитектурного сооружения, это та гамма, а точнее, тот лад, в котором будет звучать архитектурная музыка. Именно это свойство модулора Ле Корбюзье имел в виду Альберт Эйнштейн, давая ему восторженную оценку: "Модулор — это гамма пропорций, которая делает плохое трудным, а хорошее — легким". Но гамма — это еще не мелодия, не музыка. Это хорошо осознавал и сам Корбюзье: "Модулор — это гамма. Музыкант располагает гаммой и создает музыку по своим способностям — банальную или прекрасную". В самом деле, как гамма уже третье тысячелетие дает возможность композитору создавать бесконечное разнообразие мелодий, так и система пропорционирования — модулор — нисколько не стесняет в творчестве архитектора. Сам
Корбюзье блестяще доказал это, построив с помощью своего модулора и знаменитый "Лучезарный дом" в Марселе, и не менее знаменитую капеллу в Роншане. Эти два произведения великого зодчего — два антипода, две разные философии в архитектуре. С одной стороны, воплощение здравого смысла, ясного, прямолинейного и рационального. С другой — нечто иррациональное, пластическое, скульптурное, сказочное. Единственное, что объединяет эти два выдающихся памятника зодчества — это модулор, архитектурная гамма пропорций, общая для обоих произведений Ле Корбюзье.
Но почему великий Эйнштейн систему пропорционирования в архитектуре — модулор — сравнивает с музыкальной гаммой? Почему его великий соотечественник Гёте называет архитектуру отзвучавшей музыкой? Что общего между архитектурой и музыкой? Это и будет последний вопрос, на который мы попытаемся ответить в этой части книги.
18. Архитектура — математика — музыка
Вообще архитектура есть застывшая музыка.Ф. Шеллинг
Один благородный философ говорил о зодчестве как о застывшей музыке и за то не раз подвергался насмешкам. Мы думаем, что мы лучше всего передадим эту прекрасную мысль, назвав архитектуру отзвучавшей мелодией.С легкой руки великого Гёте афоризм об архитектуре и музыке немецкого философа, идейного вождя немецкого романтизма Фридриха Шеллинга (1775-1854) стал настолько популярным, что сегодня, забыв имя настоящего автора, его настойчиво вкладывают в уста создателя "Фауста". Парадоксальность высказывания Шеллинга, соединившего в себе две столь далекие друг от друга области искусства — архитектуру и музыку, делает его еще более привлекательным. А ведь сопоставление архитектуры и музыки в большей степени закономерно, чем парадоксально, и поистине замечательно, что связующим звеном между архитектурой и музыкой выступает математика.И. В. Гёте
 Гравюра из книги Франкино Гафурио 'Теория музыки'. Мы видим атрибуты музыки — органные трубы и струны, связанные отношениями 6:4:3, а также атрибут архитектуры — циркуль, который, возможно, указывает на применение этих отношений в архитектуре
В чем же проявляется общность архитектуры, музыки и математики? Прежде всего — в максимальной абстрактности этих форм человеческой деятельности. Архитектура является наиболее абстрактным из пластических искусств, т. е. искусств, существующих в пространстве и воспринимаемых зрением. Назначение зрения — воспринимать предметы внешнего мира, а назначение пластических искусств — воспроизводить с той или иной мерой чувственной достоверности эти предметы. Однако архитектура не отображает реально существующие объекты, а создает некоторые абстрактные формы, которые являются плодом фантазии ее творца. Конечно, нам известны колонны в форме лотоса в древнеегипетской архитектуре или древнегреческие атланты и кариатиды, растительные мотивы коринфских капителей или звериные маски во владимиро-суздальском зодчестве. Но все это лишь элементы, украшения, архитектурная скульптура, но не сама архитектура в целом.
Музыка на первый взгляд является антиподом архитектуры. В противоположность архитектуре музыка развивается во времени, а не в пространстве; музыка обращена к слуху. Однако роднит эти два искусства та же абстрактность формы. В самом деле, на слух мы воспринимаем звуковую информацию из внешнего мира. Но музыка не воспроизводит словесную речь, она ничего не описывает и обычно не изображает природные звуки и звукосочетания. Музыкальная форма абстрактна, она рождается в голове ее создателя и практически не имеет аналогов во внешнем мире.
Так же и математика. Будучи наукой, целью которой является выработка и систематизация объективных знаний о действительности, математика не имеет' материального предмета изучения во внешнем мире. Математика — предельно абстрактная наука, но именно это качество наделяет ее силой, позволяет математике стать универсальным языком науки. Впрочем, эти качества математики мы уже обсуждали в главе 2.
Как и математика, архитектура и музыка от объектов реального мира через многие ступени абстракции поднимаются до совершенных высочайших идеальных образов. И разница между этими сферами творческой деятельности здесь проявляется лишь в том, что в математике абстрактные образы логические, в музыке — чувственные, а в архитектуре, пожалуй, и те и другие, ибо архитектура вбирает в себя качества и науки, и искусства. Ни математик, ни композитор, ни архитектор не могут непосредственно сравнить результаты своего творчества с конкретными явлениями внешнего мира. И лишь одна путеводная звезда — логика развития науки или искусства — направляет их путь. Но разумеется, ни архитектурные, ни музыкальные, ни математические абстракции — это не химеры, существующие в своем ирреальном мире, а те идеализации, которые, отбрасывая преходящее, частное, отражают природу глубже, вернее, полнее.
Итак, архитектура и музыка являются искусствами неизобразительными и неописательными. Архитектурная и музыкальная формы абстрактны, и поэтому в них яснее, нежели в других искусствах, проявляются такие законы построения формы, как симметрия, пропорциональность, гармония, равенство, повторы частей и т. д. Лишенные внутренних законов построения, эти абстрактные формы будут лишены и тех внешних ориентиров, которые так необходимы при их восприятии. Именно объективным системнымхарактером внутренних законов построения музыкальной формы объясняется то, что "музыка вызывает сходные мысли в разных головах" (Бодлер). То же в полной мере относится и к архитектуре.
Но откуда и архитектуре, и музыке взять законы построения формы, "законы красоты", которые бы стали их фундаментом? Для тех, кто стоит на "природнической" точке зрения на красоту, этой проблемы не существует. Разумеется, у природы. Но ведь законы природы, законы гармоничного, целесообразного и прекрасного устройства мироздания описываются математикой! Вспомним "непостижимую эффективность математики в естественных науках" (с. 44), вспомним слова Гейзенберга: "Понимание всего богато окрашенного многообразия явлений достигается путем осознания присущего всем явлениям объединяющего принципа форм, выражаемого на языке математики. Таким же образом устанавливается тесная взаимосвязь между тем, что воспринимается как прекрасное, и тем, что доступно пониманию лишь с помощью интеллекта".
Особенно ценно, что к тому же выводу о необходимости существования в основе архитектуры и музыки "объединяющего принципа формы" приходят не только представители естественных наук (что вполне естественно), но и служители мира искусств. Вот слова архитектора, академика Щусева: "Наряду с меняющимися формами природы и жизни есть и нечто вечное, а именно — закон красоты и гармонии, который проявляется одинаково в жизни природы и человека. Именно этот закон дает возможность построить теорию пропорций и пластических форм, а в музыке — теорию соотношения звуковых ладов". А вот мнение музыковеда, профессора Мазеля: "Без высотной (ладовой) организации музыки невозможно выработать некоторый "музыкальный язык", понятный широкому кругу людей. Без какой-либо ладовой системы, существующей во внутреннем слухе поющих, напев не мог бы запомниться и передаваться".
Но что же является этим загадочным "объединяющим принципом формы", который должен лежать в основе архитектуры и музыки? Как нам кажется, именно математика стала тем фундаментом, тем "законом красоты и гармонии", на котором строятся абстрактные формы архитектуры и музыки.
Поясним эту мысль на знакомых нам примерах. В главе 11 мы задавались вопросом: почему из 4000 звуков, хорошо различимых человеком, в музыке используются лишь около 90? Да только потому, что в основу музыки положена строгая математическая организация звуков. Только организовав звуки в октавы, только упорядочив их внутри каждой октавы, человек смог навести в мире звуков порядок, который стал "радовать глаз и разум" (в нашем случае — "слух и разум"). Только после построения гаммы стало возможным выработать "музыкальный язык" и передавать "музыкальные мысли" — мелодии на этом языке. Таким образом, музыкальная гамма — это основа музыкального языка, заложенная по законам математики. Ну а что сказать на этом языке, зависит от таланта, вкуса, душевного богатства композитора.
Что представляет собой гамма внутри октавы, каково ее математическое строение? Этим вопросом мы занимались практически на протяжении всей второй части. В главе 9 мы показали, что равномерно-темперированная гамма — основа сегодняшней музыки — есть не что иное, как геометрическая прогрессия со знаменателем
Гравюра из книги Франкино Гафурио 'Теория музыки'. Мы видим атрибуты музыки — органные трубы и струны, связанные отношениями 6:4:3, а также атрибут архитектуры — циркуль, который, возможно, указывает на применение этих отношений в архитектуре
В чем же проявляется общность архитектуры, музыки и математики? Прежде всего — в максимальной абстрактности этих форм человеческой деятельности. Архитектура является наиболее абстрактным из пластических искусств, т. е. искусств, существующих в пространстве и воспринимаемых зрением. Назначение зрения — воспринимать предметы внешнего мира, а назначение пластических искусств — воспроизводить с той или иной мерой чувственной достоверности эти предметы. Однако архитектура не отображает реально существующие объекты, а создает некоторые абстрактные формы, которые являются плодом фантазии ее творца. Конечно, нам известны колонны в форме лотоса в древнеегипетской архитектуре или древнегреческие атланты и кариатиды, растительные мотивы коринфских капителей или звериные маски во владимиро-суздальском зодчестве. Но все это лишь элементы, украшения, архитектурная скульптура, но не сама архитектура в целом.
Музыка на первый взгляд является антиподом архитектуры. В противоположность архитектуре музыка развивается во времени, а не в пространстве; музыка обращена к слуху. Однако роднит эти два искусства та же абстрактность формы. В самом деле, на слух мы воспринимаем звуковую информацию из внешнего мира. Но музыка не воспроизводит словесную речь, она ничего не описывает и обычно не изображает природные звуки и звукосочетания. Музыкальная форма абстрактна, она рождается в голове ее создателя и практически не имеет аналогов во внешнем мире.
Так же и математика. Будучи наукой, целью которой является выработка и систематизация объективных знаний о действительности, математика не имеет' материального предмета изучения во внешнем мире. Математика — предельно абстрактная наука, но именно это качество наделяет ее силой, позволяет математике стать универсальным языком науки. Впрочем, эти качества математики мы уже обсуждали в главе 2.
Как и математика, архитектура и музыка от объектов реального мира через многие ступени абстракции поднимаются до совершенных высочайших идеальных образов. И разница между этими сферами творческой деятельности здесь проявляется лишь в том, что в математике абстрактные образы логические, в музыке — чувственные, а в архитектуре, пожалуй, и те и другие, ибо архитектура вбирает в себя качества и науки, и искусства. Ни математик, ни композитор, ни архитектор не могут непосредственно сравнить результаты своего творчества с конкретными явлениями внешнего мира. И лишь одна путеводная звезда — логика развития науки или искусства — направляет их путь. Но разумеется, ни архитектурные, ни музыкальные, ни математические абстракции — это не химеры, существующие в своем ирреальном мире, а те идеализации, которые, отбрасывая преходящее, частное, отражают природу глубже, вернее, полнее.
Итак, архитектура и музыка являются искусствами неизобразительными и неописательными. Архитектурная и музыкальная формы абстрактны, и поэтому в них яснее, нежели в других искусствах, проявляются такие законы построения формы, как симметрия, пропорциональность, гармония, равенство, повторы частей и т. д. Лишенные внутренних законов построения, эти абстрактные формы будут лишены и тех внешних ориентиров, которые так необходимы при их восприятии. Именно объективным системнымхарактером внутренних законов построения музыкальной формы объясняется то, что "музыка вызывает сходные мысли в разных головах" (Бодлер). То же в полной мере относится и к архитектуре.
Но откуда и архитектуре, и музыке взять законы построения формы, "законы красоты", которые бы стали их фундаментом? Для тех, кто стоит на "природнической" точке зрения на красоту, этой проблемы не существует. Разумеется, у природы. Но ведь законы природы, законы гармоничного, целесообразного и прекрасного устройства мироздания описываются математикой! Вспомним "непостижимую эффективность математики в естественных науках" (с. 44), вспомним слова Гейзенберга: "Понимание всего богато окрашенного многообразия явлений достигается путем осознания присущего всем явлениям объединяющего принципа форм, выражаемого на языке математики. Таким же образом устанавливается тесная взаимосвязь между тем, что воспринимается как прекрасное, и тем, что доступно пониманию лишь с помощью интеллекта".
Особенно ценно, что к тому же выводу о необходимости существования в основе архитектуры и музыки "объединяющего принципа формы" приходят не только представители естественных наук (что вполне естественно), но и служители мира искусств. Вот слова архитектора, академика Щусева: "Наряду с меняющимися формами природы и жизни есть и нечто вечное, а именно — закон красоты и гармонии, который проявляется одинаково в жизни природы и человека. Именно этот закон дает возможность построить теорию пропорций и пластических форм, а в музыке — теорию соотношения звуковых ладов". А вот мнение музыковеда, профессора Мазеля: "Без высотной (ладовой) организации музыки невозможно выработать некоторый "музыкальный язык", понятный широкому кругу людей. Без какой-либо ладовой системы, существующей во внутреннем слухе поющих, напев не мог бы запомниться и передаваться".
Но что же является этим загадочным "объединяющим принципом формы", который должен лежать в основе архитектуры и музыки? Как нам кажется, именно математика стала тем фундаментом, тем "законом красоты и гармонии", на котором строятся абстрактные формы архитектуры и музыки.
Поясним эту мысль на знакомых нам примерах. В главе 11 мы задавались вопросом: почему из 4000 звуков, хорошо различимых человеком, в музыке используются лишь около 90? Да только потому, что в основу музыки положена строгая математическая организация звуков. Только организовав звуки в октавы, только упорядочив их внутри каждой октавы, человек смог навести в мире звуков порядок, который стал "радовать глаз и разум" (в нашем случае — "слух и разум"). Только после построения гаммы стало возможным выработать "музыкальный язык" и передавать "музыкальные мысли" — мелодии на этом языке. Таким образом, музыкальная гамма — это основа музыкального языка, заложенная по законам математики. Ну а что сказать на этом языке, зависит от таланта, вкуса, душевного богатства композитора.
Что представляет собой гамма внутри октавы, каково ее математическое строение? Этим вопросом мы занимались практически на протяжении всей второй части. В главе 9 мы показали, что равномерно-темперированная гамма — основа сегодняшней музыки — есть не что иное, как геометрическая прогрессия со знаменателем  Но ведь именно в геометрической прогрессии достигается соразмерность частей и целого, именуемая гармонией. Таким образом, гамма в пределах октавы также есть упорядоченная по законам математики последовательность звуков, которая в силу октавного подобия звуков является основой основ музыки. Не случайно Пифагор придавал огромное значение построению именно этой части музыкальной шкалы (см. эпиграф к гл. 6).
То же самое мы наблюдаем и в архитектуре. Из бесконечного многообразия соотношений между частями и целым в архитектурных шедеврах непременно заложена какая-то математическая закономерность, позволяющая отобрать и упорядочить эти отношения. В основе построения архитектурной формы лежит некоторый математический закон — закон пропорционального строения этой формы. В качестве такого закона в силу особых математических свойств (см. гл. 15) часто выступает геометрическая прогрессия — ряд золотого сечения или его производная — модулор Ле Корбюзье, а также функция золотого сечения или парные меры 1:√2 или 1:√5 Эти математические закономерности гармонизируют размеры сооружения, определяют его соразмерную структуру. Разумеется, как в музыке, так и в архитектуре пропорциональная шкала — это только "эстетический фундамент" архитектурного произведения, который никак не сдерживает творческой фантазии автора.
Заметим, что проблема гармонизации частей и целого давно уже перестала быть прерогативой лишь музыки или архитектуры. Повышение эстетических качеств промышленных изделий, придание им красивой формы и одновременно их стандартизация — одна из важнейших задач технической эстетики. Естественно, что решается эта задача на базе того же математического аппарата.
Чтобы связать части целого единым пропорциональным отношением, строятся так называемые ряды предпочтительных чисел (R), которые являются не чем иным, как геометрическими прогрессиями. В качестве знаменателей таких прогрессий выбирают степени числа 10. При этом сами степени в свою очередь образуют геометрическую прогрессию со знаменателем: 1/2: 1/5, 1/10, 1/20, 1/40. Так получаются инвариантные гармонические ряды:
Но ведь именно в геометрической прогрессии достигается соразмерность частей и целого, именуемая гармонией. Таким образом, гамма в пределах октавы также есть упорядоченная по законам математики последовательность звуков, которая в силу октавного подобия звуков является основой основ музыки. Не случайно Пифагор придавал огромное значение построению именно этой части музыкальной шкалы (см. эпиграф к гл. 6).
То же самое мы наблюдаем и в архитектуре. Из бесконечного многообразия соотношений между частями и целым в архитектурных шедеврах непременно заложена какая-то математическая закономерность, позволяющая отобрать и упорядочить эти отношения. В основе построения архитектурной формы лежит некоторый математический закон — закон пропорционального строения этой формы. В качестве такого закона в силу особых математических свойств (см. гл. 15) часто выступает геометрическая прогрессия — ряд золотого сечения или его производная — модулор Ле Корбюзье, а также функция золотого сечения или парные меры 1:√2 или 1:√5 Эти математические закономерности гармонизируют размеры сооружения, определяют его соразмерную структуру. Разумеется, как в музыке, так и в архитектуре пропорциональная шкала — это только "эстетический фундамент" архитектурного произведения, который никак не сдерживает творческой фантазии автора.
Заметим, что проблема гармонизации частей и целого давно уже перестала быть прерогативой лишь музыки или архитектуры. Повышение эстетических качеств промышленных изделий, придание им красивой формы и одновременно их стандартизация — одна из важнейших задач технической эстетики. Естественно, что решается эта задача на базе того же математического аппарата.
Чтобы связать части целого единым пропорциональным отношением, строятся так называемые ряды предпочтительных чисел (R), которые являются не чем иным, как геометрическими прогрессиями. В качестве знаменателей таких прогрессий выбирают степени числа 10. При этом сами степени в свою очередь образуют геометрическую прогрессию со знаменателем: 1/2: 1/5, 1/10, 1/20, 1/40. Так получаются инвариантные гармонические ряды:
 что каждый предыдущий ряд "вложен" во все последующие. Кроме того, поскольку 103/10 = 106/20 = 1012/40 = 1,9951≈2, то в ряду R10 происходит удвоение чисел через каждые 3 члена, в ряду R20 — через 6 членов, а в ряду R40 — через 12 членов. Исходя из этого свойства значения предпочтительных чисел " округляются.
Отметим одну любопытную деталь. Так как
что каждый предыдущий ряд "вложен" во все последующие. Кроме того, поскольку 103/10 = 106/20 = 1012/40 = 1,9951≈2, то в ряду R10 происходит удвоение чисел через каждые 3 члена, в ряду R20 — через 6 членов, а в ряду R40 — через 12 членов. Исходя из этого свойства значения предпочтительных чисел " округляются.
Отметим одну любопытную деталь. Так как  то с достаточной степенью точности можно сказать, что ряд R40 лежит в основе равномерно-темперированного строя:
то с достаточной степенью точности можно сказать, что ряд R40 лежит в основе равномерно-темперированного строя:

Преимущества гармонизации с помощью ряда предпочтительных чисел (геометрической прогрессии) перед обычным рядом чисел (арифметической прогрессией) очевидны из простого примера. Если стороны прямоугольника а и b увеличивать в геометрической прогрессии (аn = aqn, bn = bqn), то пропорции прямоугольника будут сохраняться:
 более того,
более того,  Арифметическая прогрессия (an = a + nq, b = a + nq) не сохраняет пропорции прямоугольника:
Арифметическая прогрессия (an = a + nq, b = a + nq) не сохраняет пропорции прямоугольника:  , причем
, причем  т. е. форма прямоугольника будет приближаться к квадрату. Свойство геометрической прогрессии сохранять пропорции ее членов было использовано еще в 1805 г. во Франции для упорядочения типографских шрифтов.
т. е. форма прямоугольника будет приближаться к квадрату. Свойство геометрической прогрессии сохранять пропорции ее членов было использовано еще в 1805 г. во Франции для упорядочения типографских шрифтов.
 Изменение сторон прямоугольника с помощью геометрической прогрессии сохраняет его пропорции (а), а с помощью арифметической прогрессии искажает их (б)
Отметим еще одну геометрическую прогрессию, имеющую непосредственное отношение к этой книге. Сегодня во многих странах, в том числе и в нашей, применяется стандарт, введенный в начале века немецким ученым Портсманом. Портсман выбрал отношение сторон прямоугольного листа бумаги а:b из условия, чтобы при складывании (фальцовке) эта пропорция сохранялась, т. е. a:b = b:a/2 (см. рис.). Решая это элементарное уравнение, находим: а:b = √2. В качестве исходного формата был выбран лист площадью 1 м2 со сторонами 1189X841 мм (√:1), а затем найдены и его доли: 1/2 м2 = 841Х594 мм; 1/4 м2 = 594Х Х420 мм; 1/8 м2 = 420Х297 мм; 1/16 м2 = 297X210 мм — лист для пишущей машинки; 1/32 м2 = 210X148 мм; 1/64 м2 = 148X105 мм — формат почтовой открытки. Так был построен основной ряд форматов бумаги RA. Существуют также и производные от этого ряда.
Изменение сторон прямоугольника с помощью геометрической прогрессии сохраняет его пропорции (а), а с помощью арифметической прогрессии искажает их (б)
Отметим еще одну геометрическую прогрессию, имеющую непосредственное отношение к этой книге. Сегодня во многих странах, в том числе и в нашей, применяется стандарт, введенный в начале века немецким ученым Портсманом. Портсман выбрал отношение сторон прямоугольного листа бумаги а:b из условия, чтобы при складывании (фальцовке) эта пропорция сохранялась, т. е. a:b = b:a/2 (см. рис.). Решая это элементарное уравнение, находим: а:b = √2. В качестве исходного формата был выбран лист площадью 1 м2 со сторонами 1189X841 мм (√:1), а затем найдены и его доли: 1/2 м2 = 841Х594 мм; 1/4 м2 = 594Х Х420 мм; 1/8 м2 = 420Х297 мм; 1/16 м2 = 297X210 мм — лист для пишущей машинки; 1/32 м2 = 210X148 мм; 1/64 м2 = 148X105 мм — формат почтовой открытки. Так был построен основной ряд форматов бумаги RA. Существуют также и производные от этого ряда.
 Построение основного формата бумаги RA с помощью геометрической прогрессии (q = √2), сохраняющей пропорции прямоугольного листа при фальцовке
Как видим, математические вопросы гармонизации частей и целого увели нас далеко и от музыки, и от архитектуры. Как тут не вспомнить высказывание английского естествоиспытателя, соратника Чарльза Дарвина — Томаса Гексли (1825-1895) о том, что математика, подобно жернову, перемалывает то, что под него засыпают. Однако если вдуматься, то все это имеет самое прямое отношение к нашей теме, ибо как на стандартном листе бумаги можно написать все что угодно, так и с помощью гармонизированной шкалы звуков (музыкальная гамма) или шкалы пропорций (модулор Ле Корбюзье) можно создать бессмертное произведение, а можно и...
Но вернемся к архитектуре и музыке. Музыка развивается во времени, она не стоит на месте, подвижна, она меняется каждое мгновение. Но если прозвучавшую музыку целиком охватить в памяти, то в нашем сознании станут проступать закономерности ее архитектурного строения: симметрия, пропорциональность, соразмерность частей и целого — гармония, ритм и т. д.
Именно законы общего построения музыки, которые выявляются памятью только в отзвучавшей мелодии, своеобразный глобальный ритм музыки и роднят ее с архитектурой. Именно "отзвучавшую музыку", ее глобальный ритм, ее архитектуру мы изучали в главе 12, когда рассматривали целиком всю хроматическую фантазию и всю фугу ре минор Баха и находили в их строении, в больших и малых формах пропорции золотого сечения, законы симметрии (см. с. 164).
С другой стороны, локальный ритм музыки, звучащие сию минуту музыкальные фразы сближают музыку с поэзией. И как связь музыкального произведения с поэтическим словом или сценическим действием делает образное содержание произведения более богатым и многогранным, так и связь произведения архитектуры с пластикой скульптуры и живописи (росписи стен, мозаики, барельефы, скульптурные группы) — синтез искусств — позволяет достигнуть многостороннего эмоционального воздействия, небывалого по силе и полноте чувств.
Архитектура во времени неизменна. Но подвижен человек, и, перемещаясь, он воспринимает архитектуру динамично. Меняя свое положение в архитектурной среде, глядя на памятник архитектуры с разных точек зрения, человек по-разному воспринимает его пластические формы; они оживают, и "застывшая музыка" начинает издавать волшебные звуки. "Искусство архитектуры заключается в том, чтобы заставить звучать опоры",- говорил французский архитектор О. Перре. Мысль эта отнюдь не парадоксальна: опора, несущая тяжесть, была и остается главной темой архитектурной симфонии, как вечен сам закон тяготения.
Но архитектура динамична даже тогда, когда воспринимающий ее человек неподвижен. Меняется положение солнца, и изменяется светотеневая пластика архитектурных форм. Днем и ночью, в предрассветном тумане и в лучах заходящего солнца, укутанные мягким снегом и омытые грозовыми дождями памятники зодчества поют неповторимые чарующие песнопения.
Итак, неподвижная архитектура, подобно звучащей музыке, постигается нами во времени. Однако процессы восприятия архитектуры и музыки существенно отличаются друг от друга. Музыка, как и само время, развивается только в одном направлении; ее нельзя повернуть вспять, остановить или ускорить по воле слушателя. Напротив, при рассмотрении памятника архитектуры мы не связаны никакой наперед заданной последовательностью, мы вольны приблизиться к архитектурному сооружению или отойти от него, зайти слева и справа, остановиться. Поэтому в музыке композитор имеет возможность управлять процессом эстетического восприятия, он может заранее подготовить слушателя к кульминации или для усиления выразительности допустить диссонанс и тут же разрешить его в консонанс.
Архитектор лишен таких возможностей. Архитектурный диссонанс не может организованно разрешиться в консонанс и будет постоянно довлеть на зрителя. В отличие от музыки, которая может быть веселой и задумчивой, торжественной и траурной, архитектура — это искусственная среда, в которой человеку предстоит жить и работать, и она должна доставлять ему только радость. Правда, есть и обратные примеры. Стендаль признавался: "Я бы разучился смеяться через неделю, если бы жил в палаццо Арконати". Немало унылых памятников архитектурной какофонии окружают нас и сегодня. И все-таки по своей эстетической направленности архитектура призвана быть искусством положительных эмоций, она должна вбирать в себя все лучшие духовные ценности человечества и нести их людям. "Архитектура включает в себя всю культуру эпохи, в архитектуре проявляется дух времени",- писал Ле Корбюзье, чье высказывание дополняют слова Луначарского: "Всякому великому времени соответствует великая архитектура".
Есть в архитектуре и еще одно движение — внутреннее. Оно несет в себе один из парадоксов искусства архитектуры — движение, застывшее в вечном покое. В дорических колоннах Парфенона чувствуется невозмутимая и величавая поступь героя, а в ионическом ордере Эрехтейона — легкий шаг античной красавицы. В готике все устремлено вверх: на головокружительную высоту взлетают пучки тонких нервюр и распадаются там в паутину сводов, тянутся вверх стрельчатые окна витражей, зубчатые шпили и башенки. Среди зелени лесов и полей кружится хоровод древнерусских церквей...
Так неподвижная архитектура оживает при ее восприятии, а подвижная музыка застывает в нашей памяти.
И в заключение — немного истории, ибо сопоставление архитектуры и музыки имеет давнюю традицию и началось задолго до Шеллинга и Гёте. o Как музыка в античную эпоху считалась дочерью математики, так и архитектура мыслителям Возрождения казалась дочерью музыки.
Ренессанс... Новая весна человечества... Возрождался интерес к античному духовному наследию, живой античной мысли и жизнеобильному античному искусству, бесплодные штудии божественного (studio divina) сменялись пытливым изучением человеческого (studio humana)...
Построение основного формата бумаги RA с помощью геометрической прогрессии (q = √2), сохраняющей пропорции прямоугольного листа при фальцовке
Как видим, математические вопросы гармонизации частей и целого увели нас далеко и от музыки, и от архитектуры. Как тут не вспомнить высказывание английского естествоиспытателя, соратника Чарльза Дарвина — Томаса Гексли (1825-1895) о том, что математика, подобно жернову, перемалывает то, что под него засыпают. Однако если вдуматься, то все это имеет самое прямое отношение к нашей теме, ибо как на стандартном листе бумаги можно написать все что угодно, так и с помощью гармонизированной шкалы звуков (музыкальная гамма) или шкалы пропорций (модулор Ле Корбюзье) можно создать бессмертное произведение, а можно и...
Но вернемся к архитектуре и музыке. Музыка развивается во времени, она не стоит на месте, подвижна, она меняется каждое мгновение. Но если прозвучавшую музыку целиком охватить в памяти, то в нашем сознании станут проступать закономерности ее архитектурного строения: симметрия, пропорциональность, соразмерность частей и целого — гармония, ритм и т. д.
Именно законы общего построения музыки, которые выявляются памятью только в отзвучавшей мелодии, своеобразный глобальный ритм музыки и роднят ее с архитектурой. Именно "отзвучавшую музыку", ее глобальный ритм, ее архитектуру мы изучали в главе 12, когда рассматривали целиком всю хроматическую фантазию и всю фугу ре минор Баха и находили в их строении, в больших и малых формах пропорции золотого сечения, законы симметрии (см. с. 164).
С другой стороны, локальный ритм музыки, звучащие сию минуту музыкальные фразы сближают музыку с поэзией. И как связь музыкального произведения с поэтическим словом или сценическим действием делает образное содержание произведения более богатым и многогранным, так и связь произведения архитектуры с пластикой скульптуры и живописи (росписи стен, мозаики, барельефы, скульптурные группы) — синтез искусств — позволяет достигнуть многостороннего эмоционального воздействия, небывалого по силе и полноте чувств.
Архитектура во времени неизменна. Но подвижен человек, и, перемещаясь, он воспринимает архитектуру динамично. Меняя свое положение в архитектурной среде, глядя на памятник архитектуры с разных точек зрения, человек по-разному воспринимает его пластические формы; они оживают, и "застывшая музыка" начинает издавать волшебные звуки. "Искусство архитектуры заключается в том, чтобы заставить звучать опоры",- говорил французский архитектор О. Перре. Мысль эта отнюдь не парадоксальна: опора, несущая тяжесть, была и остается главной темой архитектурной симфонии, как вечен сам закон тяготения.
Но архитектура динамична даже тогда, когда воспринимающий ее человек неподвижен. Меняется положение солнца, и изменяется светотеневая пластика архитектурных форм. Днем и ночью, в предрассветном тумане и в лучах заходящего солнца, укутанные мягким снегом и омытые грозовыми дождями памятники зодчества поют неповторимые чарующие песнопения.
Итак, неподвижная архитектура, подобно звучащей музыке, постигается нами во времени. Однако процессы восприятия архитектуры и музыки существенно отличаются друг от друга. Музыка, как и само время, развивается только в одном направлении; ее нельзя повернуть вспять, остановить или ускорить по воле слушателя. Напротив, при рассмотрении памятника архитектуры мы не связаны никакой наперед заданной последовательностью, мы вольны приблизиться к архитектурному сооружению или отойти от него, зайти слева и справа, остановиться. Поэтому в музыке композитор имеет возможность управлять процессом эстетического восприятия, он может заранее подготовить слушателя к кульминации или для усиления выразительности допустить диссонанс и тут же разрешить его в консонанс.
Архитектор лишен таких возможностей. Архитектурный диссонанс не может организованно разрешиться в консонанс и будет постоянно довлеть на зрителя. В отличие от музыки, которая может быть веселой и задумчивой, торжественной и траурной, архитектура — это искусственная среда, в которой человеку предстоит жить и работать, и она должна доставлять ему только радость. Правда, есть и обратные примеры. Стендаль признавался: "Я бы разучился смеяться через неделю, если бы жил в палаццо Арконати". Немало унылых памятников архитектурной какофонии окружают нас и сегодня. И все-таки по своей эстетической направленности архитектура призвана быть искусством положительных эмоций, она должна вбирать в себя все лучшие духовные ценности человечества и нести их людям. "Архитектура включает в себя всю культуру эпохи, в архитектуре проявляется дух времени",- писал Ле Корбюзье, чье высказывание дополняют слова Луначарского: "Всякому великому времени соответствует великая архитектура".
Есть в архитектуре и еще одно движение — внутреннее. Оно несет в себе один из парадоксов искусства архитектуры — движение, застывшее в вечном покое. В дорических колоннах Парфенона чувствуется невозмутимая и величавая поступь героя, а в ионическом ордере Эрехтейона — легкий шаг античной красавицы. В готике все устремлено вверх: на головокружительную высоту взлетают пучки тонких нервюр и распадаются там в паутину сводов, тянутся вверх стрельчатые окна витражей, зубчатые шпили и башенки. Среди зелени лесов и полей кружится хоровод древнерусских церквей...
Так неподвижная архитектура оживает при ее восприятии, а подвижная музыка застывает в нашей памяти.
И в заключение — немного истории, ибо сопоставление архитектуры и музыки имеет давнюю традицию и началось задолго до Шеллинга и Гёте. o Как музыка в античную эпоху считалась дочерью математики, так и архитектура мыслителям Возрождения казалась дочерью музыки.
Ренессанс... Новая весна человечества... Возрождался интерес к античному духовному наследию, живой античной мысли и жизнеобильному античному искусству, бесплодные штудии божественного (studio divina) сменялись пытливым изучением человеческого (studio humana)...
(В. Брюсов)
 Пифагор (справа), аллегория Арифметики и Боэций. Гравюра из книги Грегора Райха 'Маргарита философика'. В средневековой Европе Пифагор считался изобретателем счетной доски абака, а Боэций — создателем новой нумерации
Мы знаем (гл. 14) о том, какое огромное влияние на зодчих Возрождения оказал трактат Витрувия "Десять книг об архитектуре". Но мы также знаем, что архитектурная энциклопедия Витрувия стала источником многих заблуждений, происходивших чаще всего от неправильного толкования мыслей автора. Так случилось с архитектурой и музыкой.
Ссылаясь на авторитет Витрувия, архитекторы Возрождения выдвинули тезис о том, что наиболее приятными для созерцания должны быть те прямоугольники, стороны которых относятся как числа в благозвучных (консонантных) интервалах, т. е. как октава 2:1, квинта 3:2, кварта 4:3, а также большая 5:4 и малая 6:5 терции и их обращения — малая 8:5 и большая 5:3 сексты. В 1485 г. во Флоренции был издан трактат "Десять книг о зодчестве". Его автором был славный представитель архитектуры Раннего Возрождения, итальянский ученый, писатель и музыкант Леон Баттиста Альберти, умерший за 13 лет до того, как его детище увидело свет. "Десять книг" Альберти было вторым после "Десяти книг" Витрувия всеобъемлющим сочинением по архитектуре. В нем мы читаем: "И конечно, вновь и вновь следует повторить изречение Пифагора: "нет сомнений, что природа во всем остается себе подобной". Дело обстоит так: существуют числа, благодаря которым гармония звуков пленяет слух, эти же числа преисполняют и глаза, и дух чудесным наслаждением. Мы должны воспользоваться пропорциями, взятыми у музыкантов, кои величайшие мастера в этом виде чисел". Поскольку приятные слуху музыкальные интервалы описываются отношением целых чисел, то, согласно Альберти, и приятные глазу архитектурные формы также должны находиться в целочисленных "музыкальных" пропорциях.
В XVI веке архитектора Альберти поддержал математик Джероламо Кардано (1501 -1576), известный сегодня как автор формулы решения кубичного уравнения, которую, впрочем, как великую тайну ему открыл Никколо Тарталья (ок. 1499 — 1557). Как истинный представитель точного знания Кардано утверждал, что приятные для слуха и глаза целочисленные (музыкальные) отношения являются таковыми, поскольку они легкопостижимы разумом. Авторство музыкальной аналогии в архитектуре Кардано также приписывал незыблемому авторитету Витрувия.
В действительности интерес Витрувия к музыке ограничивался вопросами конструирования резонаторов для античных театров, а также правильной настройкой струн в катапультах и боевых машинах, которые находились в ведении архитекторов того времени. Правда, Витрувий дал в качестве прекрасных пропорций три "музыкальных" отношения 2:1, 3:2, 5:3. Но наряду с ними он рассматривал и такое отнюдь не музыкальное отношение, как отношение диагонали к стороне квадрата √2:1.
Как бы то ни было, но музыкальная аналогия прочно вошла в сознание архитекторов Возрождения. На первый взгляд, кажется странным, что теоретические воззрения зодчих Возрождения в большей мере определялись не трудами самих архитекторов, а математическими разработками по теории музыки. Но если вдуматься, то это, скорее, следовало из универсального характера математики: хорошо известные в музыке "математические законы красоты" (законы целочисленных консонантных отношений и законы среднепропорциональных) архитекторы Возрождения пытались перенести на свою почву. Не говорит ли эта попытка "пройти" из музыки в архитектуру с помощью математики о безграничной вере мыслителей Возрождения в универсальное могущество математики?!
Огромную роль в развитии музыкальной аналогии в архитектуре сыграл трактат Северина Боэция "О музыке", который вобрал в себя все античные теории музыкальной гармонии и фактически сохранил их для потомков. Автор другого выдающегося трактата по математической теории музыки — итальянский композитор XVI века Джузеппе Царлино — нам также знаком. Как мы знаем (с. 129), среди современников-музыкантов идеи Царлино должного признания не получили. Зато математические выкладки Царлино и его мысль о том, что консонантные (приятные для слуха) интервалы получаются как среднее арифметическое и среднее гармоническое, запали в душу современников-архитекторов и применялись ими для получения "консонантных" (приятных для глаза) пропорций.
Пифагор (справа), аллегория Арифметики и Боэций. Гравюра из книги Грегора Райха 'Маргарита философика'. В средневековой Европе Пифагор считался изобретателем счетной доски абака, а Боэций — создателем новой нумерации
Мы знаем (гл. 14) о том, какое огромное влияние на зодчих Возрождения оказал трактат Витрувия "Десять книг об архитектуре". Но мы также знаем, что архитектурная энциклопедия Витрувия стала источником многих заблуждений, происходивших чаще всего от неправильного толкования мыслей автора. Так случилось с архитектурой и музыкой.
Ссылаясь на авторитет Витрувия, архитекторы Возрождения выдвинули тезис о том, что наиболее приятными для созерцания должны быть те прямоугольники, стороны которых относятся как числа в благозвучных (консонантных) интервалах, т. е. как октава 2:1, квинта 3:2, кварта 4:3, а также большая 5:4 и малая 6:5 терции и их обращения — малая 8:5 и большая 5:3 сексты. В 1485 г. во Флоренции был издан трактат "Десять книг о зодчестве". Его автором был славный представитель архитектуры Раннего Возрождения, итальянский ученый, писатель и музыкант Леон Баттиста Альберти, умерший за 13 лет до того, как его детище увидело свет. "Десять книг" Альберти было вторым после "Десяти книг" Витрувия всеобъемлющим сочинением по архитектуре. В нем мы читаем: "И конечно, вновь и вновь следует повторить изречение Пифагора: "нет сомнений, что природа во всем остается себе подобной". Дело обстоит так: существуют числа, благодаря которым гармония звуков пленяет слух, эти же числа преисполняют и глаза, и дух чудесным наслаждением. Мы должны воспользоваться пропорциями, взятыми у музыкантов, кои величайшие мастера в этом виде чисел". Поскольку приятные слуху музыкальные интервалы описываются отношением целых чисел, то, согласно Альберти, и приятные глазу архитектурные формы также должны находиться в целочисленных "музыкальных" пропорциях.
В XVI веке архитектора Альберти поддержал математик Джероламо Кардано (1501 -1576), известный сегодня как автор формулы решения кубичного уравнения, которую, впрочем, как великую тайну ему открыл Никколо Тарталья (ок. 1499 — 1557). Как истинный представитель точного знания Кардано утверждал, что приятные для слуха и глаза целочисленные (музыкальные) отношения являются таковыми, поскольку они легкопостижимы разумом. Авторство музыкальной аналогии в архитектуре Кардано также приписывал незыблемому авторитету Витрувия.
В действительности интерес Витрувия к музыке ограничивался вопросами конструирования резонаторов для античных театров, а также правильной настройкой струн в катапультах и боевых машинах, которые находились в ведении архитекторов того времени. Правда, Витрувий дал в качестве прекрасных пропорций три "музыкальных" отношения 2:1, 3:2, 5:3. Но наряду с ними он рассматривал и такое отнюдь не музыкальное отношение, как отношение диагонали к стороне квадрата √2:1.
Как бы то ни было, но музыкальная аналогия прочно вошла в сознание архитекторов Возрождения. На первый взгляд, кажется странным, что теоретические воззрения зодчих Возрождения в большей мере определялись не трудами самих архитекторов, а математическими разработками по теории музыки. Но если вдуматься, то это, скорее, следовало из универсального характера математики: хорошо известные в музыке "математические законы красоты" (законы целочисленных консонантных отношений и законы среднепропорциональных) архитекторы Возрождения пытались перенести на свою почву. Не говорит ли эта попытка "пройти" из музыки в архитектуру с помощью математики о безграничной вере мыслителей Возрождения в универсальное могущество математики?!
Огромную роль в развитии музыкальной аналогии в архитектуре сыграл трактат Северина Боэция "О музыке", который вобрал в себя все античные теории музыкальной гармонии и фактически сохранил их для потомков. Автор другого выдающегося трактата по математической теории музыки — итальянский композитор XVI века Джузеппе Царлино — нам также знаком. Как мы знаем (с. 129), среди современников-музыкантов идеи Царлино должного признания не получили. Зато математические выкладки Царлино и его мысль о том, что консонантные (приятные для слуха) интервалы получаются как среднее арифметическое и среднее гармоническое, запали в душу современников-архитекторов и применялись ими для получения "консонантных" (приятных для глаза) пропорций.
 Палладио. Вилла Ротонда в Виченце. 1581. Воплощение идеи симметрии, математической строгости и музыкальных пропорций в архитектуре Ренессанса
Палладио. Вилла Ротонда в Виченце. 1581. Воплощение идеи симметрии, математической строгости и музыкальных пропорций в архитектуре Ренессанса
 Леонардо да Винчи. План собора, основанный на правильной восьмиконечной звезде, обладает поворотной симметрией 8-го порядка и отнюдь 'не музыкальной' системой пропорций √2:1
Музыкальная система пропорционирования нашла живой отклик в творчестве выдающегося итальянского архитектора Андреа Палладио (1508 -1580)- автора трактата "Четыре книги об архитектуре". Созданные Палладио типы городского дворца, церкви, виллы благодаря своей завершенности, сочетанию строгой упорядоченности и пластики получили распространение не только в Италии XVI века, но и составили целое направление — палладианство — в европейском зодчестве XVII-XVIII веков. Идея всепроникающей музыкальной гармонии, структурно-математическое понимание красоты, идея симметрии как неотъемлемого качества красоты наиболее полно воплощены Палладио в вилле Ротонда. С высоты птичьего полета в этом каноне архитектуры Ренессанса хорошо видны как поворотная симметрия 4-го порядка всего здания, так и зеркальная симметрия его фасадов, а также ощущается музыка простых целочисленных пропорций.
Вообще, убеждение в том, что архитектура — это наука и что красота здания определяется симметрией и математическими законами гармонии, можно считать главной аксиомой архитектуры Возрождения. Мыслители Возрождения были неоплатониками. Они верили в то, что платонов гептахорд (7.1), который содержит все консонансы, определяет гармонию мироздания, а значит, и единую гармонию всех искусств, а значит, и архитектуры.
И все-таки Палладио был больше архитектором, нежели философом-неоплатоником. Именно поэтому Палладио включил прямоугольник, стороны которого равны стороне и диагонали квадрата, т. е. прямоугольник с иррациональным соотношением сторон √2:1, в список семи форм,
рекомендуемых для планирования комнат. А ведь одного этого прямоугольника достаточно для того, чтобы полностью разрушить музыкальную аналогию в архитектуре.
В самом деле, как мы помним, интервал тритона √2:1 является острейшим диссонансом в музыке и назывался "дьяволом в музыке". С другой стороны, мы знаем, насколько широко парная мера √2:1 применялась в архитектуре. Знали это и архитекторы Возрождения. И не только из сочинений Витрувия. Достаточно вспомнить проект собора, выполненный Леонардо да Винчи и основанный на последовательности восьмиконечных звезд. Разбиение окружности на 8 равных частей порождает угол в 45°, а восьмиконечная звезда — систему равнобедренных прямоугольных треугольников, т. е. треугольников с соотношением √2:1.
Таким образом, красота архитектурных форм явно не умещалась в прокрустово ложе целочисленных отношений. Это понимали архитекторы Позднего Возрождения, и это было для них такой же трагедией, какой открытие несоизмеримости было для их кумиров — пифагорейцев. "Можно сказать, что Ренессанс вообще раздирается этим ужасающим противоречием: возрожденцам хотелось видеть и изображать живое и одушевленное трехмерное тело и в то же самое время им хотелось все свести на арифметику целых чисел" (А. Лосев. "Эстетика Возрождения").
Тем не менее музыкальная аналогия в архитектуре оставалась очень популярной и продолжала жить в творчестве архитекторов-палладианцев XVII и XVIII веков. А попытки примирить музыку архитектуры с иррациональными отношениями не прекращаются и в XX веке. Так, одни исследователи пропорций обращают внимание на то, что золотое сечение Φ = 1,618... достаточно хорошо аппроксимируется (приближенно выражается) отношениями членов ряда Фибоначчи (15.6): 5/3-1,666... и 8/5-1,6 (это большая и малая сексты в музыкальной терминологии). Действительно, без наложения друг на друга эти три пропорции отличить практически невозможно, и, таким образом, с точки зрения эстетического восприятия споры о преимуществах той или иной пропорции кажутся академическими. Другие объясняют "приятность для глаза" диссонантных иррациональных отношений тем, что при восприятии архитектурной формы глаз соизмеряет не линейные размеры, а площади поверхности. Тогда два квадрата с "немузыкальным" отношением сторон √2:1 дают "музыкальное" отношение площадей 2:1 (октаву). Квадраты с немыслимым в музыке соотношением сторон √3:√2 дадут в площадях квинту 3:2 и т. д.
Мы не будем вдаваться в обсуждение вопроса, почему одни отношения приятны для слуха или для глаза, а другие — нет. Несмотря на давнюю историю, вопрос этот на карте науки остается почти абсолютно белым пятном. Напомним, что консонансы в музыке Гельмгольц объяснял отсутствием неприятных биений между обертонами составляющих их гармоник (см. с. 151). Однако в настоящее время в теории Гельмгольца обнаружено много изъянов и восприятие консонансов не считается чисто физиологическим явлением. Тем более нет каких-либо установившихся соображений для объяснения эстетики восприятия тех или иных пропорций. "Не углубляясь еще дальше в эту спорную область, хотелось бы подчеркнуть большое значение какой бы то ни было теории в архитектурном проектировании". Этими словами известный английский математик и знаток искусства Дан Пидоу в книге "Геометрия и искусство" закончил обсуждение проблемы эстетики восприятия музыкальных пропорций в архитектуре. Конечно, нам следовало бы внять его мудрому примеру, но хочется сказать еще два слова вот о чем.
Леонардо да Винчи. План собора, основанный на правильной восьмиконечной звезде, обладает поворотной симметрией 8-го порядка и отнюдь 'не музыкальной' системой пропорций √2:1
Музыкальная система пропорционирования нашла живой отклик в творчестве выдающегося итальянского архитектора Андреа Палладио (1508 -1580)- автора трактата "Четыре книги об архитектуре". Созданные Палладио типы городского дворца, церкви, виллы благодаря своей завершенности, сочетанию строгой упорядоченности и пластики получили распространение не только в Италии XVI века, но и составили целое направление — палладианство — в европейском зодчестве XVII-XVIII веков. Идея всепроникающей музыкальной гармонии, структурно-математическое понимание красоты, идея симметрии как неотъемлемого качества красоты наиболее полно воплощены Палладио в вилле Ротонда. С высоты птичьего полета в этом каноне архитектуры Ренессанса хорошо видны как поворотная симметрия 4-го порядка всего здания, так и зеркальная симметрия его фасадов, а также ощущается музыка простых целочисленных пропорций.
Вообще, убеждение в том, что архитектура — это наука и что красота здания определяется симметрией и математическими законами гармонии, можно считать главной аксиомой архитектуры Возрождения. Мыслители Возрождения были неоплатониками. Они верили в то, что платонов гептахорд (7.1), который содержит все консонансы, определяет гармонию мироздания, а значит, и единую гармонию всех искусств, а значит, и архитектуры.
И все-таки Палладио был больше архитектором, нежели философом-неоплатоником. Именно поэтому Палладио включил прямоугольник, стороны которого равны стороне и диагонали квадрата, т. е. прямоугольник с иррациональным соотношением сторон √2:1, в список семи форм,
рекомендуемых для планирования комнат. А ведь одного этого прямоугольника достаточно для того, чтобы полностью разрушить музыкальную аналогию в архитектуре.
В самом деле, как мы помним, интервал тритона √2:1 является острейшим диссонансом в музыке и назывался "дьяволом в музыке". С другой стороны, мы знаем, насколько широко парная мера √2:1 применялась в архитектуре. Знали это и архитекторы Возрождения. И не только из сочинений Витрувия. Достаточно вспомнить проект собора, выполненный Леонардо да Винчи и основанный на последовательности восьмиконечных звезд. Разбиение окружности на 8 равных частей порождает угол в 45°, а восьмиконечная звезда — систему равнобедренных прямоугольных треугольников, т. е. треугольников с соотношением √2:1.
Таким образом, красота архитектурных форм явно не умещалась в прокрустово ложе целочисленных отношений. Это понимали архитекторы Позднего Возрождения, и это было для них такой же трагедией, какой открытие несоизмеримости было для их кумиров — пифагорейцев. "Можно сказать, что Ренессанс вообще раздирается этим ужасающим противоречием: возрожденцам хотелось видеть и изображать живое и одушевленное трехмерное тело и в то же самое время им хотелось все свести на арифметику целых чисел" (А. Лосев. "Эстетика Возрождения").
Тем не менее музыкальная аналогия в архитектуре оставалась очень популярной и продолжала жить в творчестве архитекторов-палладианцев XVII и XVIII веков. А попытки примирить музыку архитектуры с иррациональными отношениями не прекращаются и в XX веке. Так, одни исследователи пропорций обращают внимание на то, что золотое сечение Φ = 1,618... достаточно хорошо аппроксимируется (приближенно выражается) отношениями членов ряда Фибоначчи (15.6): 5/3-1,666... и 8/5-1,6 (это большая и малая сексты в музыкальной терминологии). Действительно, без наложения друг на друга эти три пропорции отличить практически невозможно, и, таким образом, с точки зрения эстетического восприятия споры о преимуществах той или иной пропорции кажутся академическими. Другие объясняют "приятность для глаза" диссонантных иррациональных отношений тем, что при восприятии архитектурной формы глаз соизмеряет не линейные размеры, а площади поверхности. Тогда два квадрата с "немузыкальным" отношением сторон √2:1 дают "музыкальное" отношение площадей 2:1 (октаву). Квадраты с немыслимым в музыке соотношением сторон √3:√2 дадут в площадях квинту 3:2 и т. д.
Мы не будем вдаваться в обсуждение вопроса, почему одни отношения приятны для слуха или для глаза, а другие — нет. Несмотря на давнюю историю, вопрос этот на карте науки остается почти абсолютно белым пятном. Напомним, что консонансы в музыке Гельмгольц объяснял отсутствием неприятных биений между обертонами составляющих их гармоник (см. с. 151). Однако в настоящее время в теории Гельмгольца обнаружено много изъянов и восприятие консонансов не считается чисто физиологическим явлением. Тем более нет каких-либо установившихся соображений для объяснения эстетики восприятия тех или иных пропорций. "Не углубляясь еще дальше в эту спорную область, хотелось бы подчеркнуть большое значение какой бы то ни было теории в архитектурном проектировании". Этими словами известный английский математик и знаток искусства Дан Пидоу в книге "Геометрия и искусство" закончил обсуждение проблемы эстетики восприятия музыкальных пропорций в архитектуре. Конечно, нам следовало бы внять его мудрому примеру, но хочется сказать еще два слова вот о чем.
В 1830-1834 гг. немецкий физиолог Эрнст Вебер (1795-1878) на основании многочисленных экспериментов установил, что человек воспринимает не абсолютный, а относительный прирост силы раздражителя (света, звука, груза, давящего на кожу, и т. д.), т. е. dR/R, где R — сила раздражителя, dR — прирост этой силы. Каждый по своему жизненному опыту знает, что, например, электрическая лампочка, включенная днем, не вызывает у нас никакой реакции, так как по отношению к солнечному свету прирост этой силы раздражения слишком мал(
 , так как R велико). Зато в темноте нас слепит даже зажженная спичка (здесь
, так как R велико). Зато в темноте нас слепит даже зажженная спичка (здесь  так как R≈0). R
20 лет спустя немецкий физик, психолог, философ и писатель Густав Фехнер (1801 -1887) математически обработал результаты экспериментов Вебера, т. е. на языке математики записал факт, установленный Вебером: приращение интенсивности ощущения dE пропорционально относительному приращению силы раздраения dR/R
так как R≈0). R
20 лет спустя немецкий физик, психолог, философ и писатель Густав Фехнер (1801 -1887) математически обработал результаты экспериментов Вебера, т. е. на языке математики записал факт, установленный Вебером: приращение интенсивности ощущения dE пропорционально относительному приращению силы раздраения dR/R
 (18.1)
здесь а — коэффициент пропорциональности. Получилось простейшее дифференциальное уравнение, решая которое Фехнер нашел связь между интенсивностью ощущения Е и силой раздражения R, действующей на какой-либо орган чувств:
(18.1)
здесь а — коэффициент пропорциональности. Получилось простейшее дифференциальное уравнение, решая которое Фехнер нашел связь между интенсивностью ощущения Е и силой раздражения R, действующей на какой-либо орган чувств:
 (18.2)
или
(18.2)
или
 (18.3)
здесь R0 — сила начального раздражения.
Формулы (18.1) — (18.3) и есть математическое выражение основного психофизического закона — закона Вебера — Фехнера.
(18.3)
здесь R0 — сила начального раздражения.
Формулы (18.1) — (18.3) и есть математическое выражение основного психофизического закона — закона Вебера — Фехнера.
 Согласно закону Вебера — Фехнера, для того, чтобы интенсивность ощущений Е нарастала в арифметической прогрессии, вызывающая их сила раздражения R должна нарастать в геометрической прогрессии
Что же мы можем извлечь из закона Вебера — Фехнера? Естественно предположить, что нам будет приятно, если наши ощущения в процессе восприятия музыки или архитектуры будут нарастать равномерно, т. е. в арифметической прогрессии. Положим Еn = Е0 + αn (n = 0, 1, 2, ...; α — разность арифметической прогрессии). Тогда согласно (18.3) вызывающая эти ощущения сила раздражения должна нарастать по закону
Согласно закону Вебера — Фехнера, для того, чтобы интенсивность ощущений Е нарастала в арифметической прогрессии, вызывающая их сила раздражения R должна нарастать в геометрической прогрессии
Что же мы можем извлечь из закона Вебера — Фехнера? Естественно предположить, что нам будет приятно, если наши ощущения в процессе восприятия музыки или архитектуры будут нарастать равномерно, т. е. в арифметической прогрессии. Положим Еn = Е0 + αn (n = 0, 1, 2, ...; α — разность арифметической прогрессии). Тогда согласно (18.3) вызывающая эти ощущения сила раздражения должна нарастать по закону
 т. е. сила раздражения Rn должна нарастать в геометрической прогрессии со знаменателем q = eα/a.
Но ведь и гамма равномерно-темперированного строя (9.1), и ряд золотого сечения (15.4) или (15.5), и красная (17.2) и синяя (17.3) шкалы модулора Ле Корбюзье являются геометрическими прогрессиями! Следовательно, все эти "раздражители"- наших органов чувств обеспечивают равномерное возрастание (или убывание) наших ощущений. Таким образом, именно закон Вебера — Фехнера, скорее всего, и является тем математическим законом, который лежит в основе основ как музыки (музыкальная гамма), так и архитектуры (шкала пропорциональностей), той "математикой", которая связывает и музыку, и архитектуру!
Подтверждением этому могли бы стать экспериментальные значения коэффициента α/а, полученные в результате психофизических опытов. Поскольку для равномерно-темперированной гаммы q = =
т. е. сила раздражения Rn должна нарастать в геометрической прогрессии со знаменателем q = eα/a.
Но ведь и гамма равномерно-темперированного строя (9.1), и ряд золотого сечения (15.4) или (15.5), и красная (17.2) и синяя (17.3) шкалы модулора Ле Корбюзье являются геометрическими прогрессиями! Следовательно, все эти "раздражители"- наших органов чувств обеспечивают равномерное возрастание (или убывание) наших ощущений. Таким образом, именно закон Вебера — Фехнера, скорее всего, и является тем математическим законом, который лежит в основе основ как музыки (музыкальная гамма), так и архитектуры (шкала пропорциональностей), той "математикой", которая связывает и музыку, и архитектуру!
Подтверждением этому могли бы стать экспериментальные значения коэффициента α/а, полученные в результате психофизических опытов. Поскольку для равномерно-темперированной гаммы q = =  = 1,06, а для ряда золотого сечения q = 1,618 (q = eα/a), то легко находим: для музыкальной гаммы α/а = 0,058, а для ряда золотого сечения α/а = 0,482. Если эти значения совпадут с экспериментальными, то это и будет хотя бы в первом приближении объяснением, почему именно 12-ступенная гамма и золотое сечение в течение тысячелетий продолжают радовать наши слух, глаз и разум.
Насколько это справедливо, покажут будущие исследования. Хочется верить, что законы красоты все-таки будут разгаданы, и, памятуя традиции Баха и Моцарта (см. с. 149), закончить последнюю главу об архитектуре и музыке мажорным аккордом.
= 1,06, а для ряда золотого сечения q = 1,618 (q = eα/a), то легко находим: для музыкальной гаммы α/а = 0,058, а для ряда золотого сечения α/а = 0,482. Если эти значения совпадут с экспериментальными, то это и будет хотя бы в первом приближении объяснением, почему именно 12-ступенная гамма и золотое сечение в течение тысячелетий продолжают радовать наши слух, глаз и разум.
Насколько это справедливо, покажут будущие исследования. Хочется верить, что законы красоты все-таки будут разгаданы, и, памятуя традиции Баха и Моцарта (см. с. 149), закончить последнюю главу об архитектуре и музыке мажорным аккордом.
IV. Математика и живопись
Мне хочется, чтобы живописец был как можно больше сведущ во всех свободных искусствах, но прежде всего я желаю, чтобы он узнал геометрию.Л. Б. Альберти
 "Ну это уж слишком! — рассердится уставший читатель.- Да, архитектура — наполовину наука, наполовину искусство, и потому "математическое начало" в ней естественно. Да, музыка слагается из колебаний среды и, следовательно, подчиняется законам акустики, которая полностью математизирована. Но какая математика нужна художнику, которому, кроме холста и красок, вообще ничего не нужно!? Примером "математики в живописи" может служить разве что картина Богданова-Бельского "Устный счет"!"
В этой части книги мы попытаемся убедить сердитого читателя в том, что он глубоко не прав.
Раздел называется "Математика и живопись", хотя, быть может, правильнее его следовало бы назвать "Математика и изобразительные искусства". Последние, как известно, объединяют живопись, скульптуру и графику. Тем не менее речь в этом разделе пойдет прежде всего о живописи: с одной стороны, потому, что живопись является ведущей составляющей изобразительного искусства, а с другой — потому, что именно в живописи заключены основные математические проблемы изобразительного искусства.
К сожалению, говоря о живописи, мы оставим в стороне ее основное изобразительное средство — цвет. Причин тому две: во-первых, ограниченные размеры книги, а во-вторых, сложность проблемы. Вопрос о цветовой гамме — совокупности взаимосвязанных цветов и их оттенков, "эстетике цвета" и "математике цвета" — во многом остается загадочным. Между тем еще Ньютон, разложивший солнечный свет на семь цветовых составляющих, заметил, что частоты v границ цветов солнечного спектра относятся как частоты самой симметричной фригийской гаммы чистого строя (8.8):
"Ну это уж слишком! — рассердится уставший читатель.- Да, архитектура — наполовину наука, наполовину искусство, и потому "математическое начало" в ней естественно. Да, музыка слагается из колебаний среды и, следовательно, подчиняется законам акустики, которая полностью математизирована. Но какая математика нужна художнику, которому, кроме холста и красок, вообще ничего не нужно!? Примером "математики в живописи" может служить разве что картина Богданова-Бельского "Устный счет"!"
В этой части книги мы попытаемся убедить сердитого читателя в том, что он глубоко не прав.
Раздел называется "Математика и живопись", хотя, быть может, правильнее его следовало бы назвать "Математика и изобразительные искусства". Последние, как известно, объединяют живопись, скульптуру и графику. Тем не менее речь в этом разделе пойдет прежде всего о живописи: с одной стороны, потому, что живопись является ведущей составляющей изобразительного искусства, а с другой — потому, что именно в живописи заключены основные математические проблемы изобразительного искусства.
К сожалению, говоря о живописи, мы оставим в стороне ее основное изобразительное средство — цвет. Причин тому две: во-первых, ограниченные размеры книги, а во-вторых, сложность проблемы. Вопрос о цветовой гамме — совокупности взаимосвязанных цветов и их оттенков, "эстетике цвета" и "математике цвета" — во многом остается загадочным. Между тем еще Ньютон, разложивший солнечный свет на семь цветовых составляющих, заметил, что частоты v границ цветов солнечного спектра относятся как частоты самой симметричной фригийской гаммы чистого строя (8.8):
 Тем самым вместе с дисперсией света Ньютон открыл и удивительную аналогию между цветом и музыкой, послужившую толчком к развитию цветомузыки. В наше время с изобретением цветного телевидения бурное развитие получила наука о количественном измерении цвета — колориметрия. Однако все эти вопросы для нас останутся в стороне.
Тем самым вместе с дисперсией света Ньютон открыл и удивительную аналогию между цветом и музыкой, послужившую толчком к развитию цветомузыки. В наше время с изобретением цветного телевидения бурное развитие получила наука о количественном измерении цвета — колориметрия. Однако все эти вопросы для нас останутся в стороне.
 Н. Богданов-Бельский. Устный счет. 1895. На картине изображен известный педагог, профессор С. А. Рачинский, сменивший университетскую кафедру на место учителя в сельской школе
Остановимся на другом важнейшем изобразительном средстве живописи — рисунке, который, по словам Вазари, является "отцом живописи". Рисунок играет важнейшую роль в определении очертаний предметов, их форм, объемов и взаимного расположения в пространстве. Таким образом, рисунок является "скелетом живописи", ее конструктивной основой и именно в нем заложены геометрические законы живописи. Вот почему все, что мы будем говорить о "математическом содержании живописи", будет как частный случай относиться и к графике — "одноцветной живописи", а в той части, где речь будет идти о пропорциях,- и к скульптуре. Заметим, что в скульптуре, основанной на принципе объемного трехмерного изображения предмета, само собой отпадает основная математическая проблема живописи — проблема изображения трехмерного пространства на двумерной плоскости картины, проблема перспективы.
Говоря о живописи, мы не будем касаться и таких средств языка живописи, как сюжет, композиция, колорит, светотень, контраст, фактура, тон, валёр, рефлекс, лессировка и т. д. Список этот можно продолжить: он говорит лишь о неисчерпаемых возможностях художественного образа. Однако, сколько бы мы ни продолжали этот список, сколько бы ни уточняли и ни утончали его составляющие, он не поможет нам понять закономерности языка живописи, раскрыть логику взаимосвязи и характер "содружества" тех или иных выразительных средств. Логика живописного произведения откроется нам лишь в том случае, если мы освободимся от частностей, вычленим лишь самую суть, предельно абстрагируемся, и как вершина такой абстракции встанет перед нами геометрия живописи.
Во вступлении ко второй части (с. 88) мы говорили о том, что поиски математических закономерностей в области изобразительных искусств имеют едва ли не древнейшую традицию. Блестящим тому подтверждением служит знаменитый канон Имхотепа, жившего в Древнем Египте в XXVIII веке до н. э., т. е. более чем за 2000 лет до того, как Пифагор открыл законы целочисленных отношений в музыке. Однако в отличие от объективных "законов Пифагора в музыке", которые справедливы и сегодня, "законы Имхотепа в ваянии" субъективны, и потому на смену им приходили столь же субъективные каноны Поликлета, Лисиппа и др. Тем не менее все эти каноны были попыткой найти объективные математические закономерности в строении человека — "законы красоты" человека.
Другой важнейшей математической темой в живописи, которая также на протяжении тысячелетий стимулировала поиски и дарила находки как художникам, так и ученым, является проблема построения перспективы. Эти две темы и составят предмет последней части книги.
Н. Богданов-Бельский. Устный счет. 1895. На картине изображен известный педагог, профессор С. А. Рачинский, сменивший университетскую кафедру на место учителя в сельской школе
Остановимся на другом важнейшем изобразительном средстве живописи — рисунке, который, по словам Вазари, является "отцом живописи". Рисунок играет важнейшую роль в определении очертаний предметов, их форм, объемов и взаимного расположения в пространстве. Таким образом, рисунок является "скелетом живописи", ее конструктивной основой и именно в нем заложены геометрические законы живописи. Вот почему все, что мы будем говорить о "математическом содержании живописи", будет как частный случай относиться и к графике — "одноцветной живописи", а в той части, где речь будет идти о пропорциях,- и к скульптуре. Заметим, что в скульптуре, основанной на принципе объемного трехмерного изображения предмета, само собой отпадает основная математическая проблема живописи — проблема изображения трехмерного пространства на двумерной плоскости картины, проблема перспективы.
Говоря о живописи, мы не будем касаться и таких средств языка живописи, как сюжет, композиция, колорит, светотень, контраст, фактура, тон, валёр, рефлекс, лессировка и т. д. Список этот можно продолжить: он говорит лишь о неисчерпаемых возможностях художественного образа. Однако, сколько бы мы ни продолжали этот список, сколько бы ни уточняли и ни утончали его составляющие, он не поможет нам понять закономерности языка живописи, раскрыть логику взаимосвязи и характер "содружества" тех или иных выразительных средств. Логика живописного произведения откроется нам лишь в том случае, если мы освободимся от частностей, вычленим лишь самую суть, предельно абстрагируемся, и как вершина такой абстракции встанет перед нами геометрия живописи.
Во вступлении ко второй части (с. 88) мы говорили о том, что поиски математических закономерностей в области изобразительных искусств имеют едва ли не древнейшую традицию. Блестящим тому подтверждением служит знаменитый канон Имхотепа, жившего в Древнем Египте в XXVIII веке до н. э., т. е. более чем за 2000 лет до того, как Пифагор открыл законы целочисленных отношений в музыке. Однако в отличие от объективных "законов Пифагора в музыке", которые справедливы и сегодня, "законы Имхотепа в ваянии" субъективны, и потому на смену им приходили столь же субъективные каноны Поликлета, Лисиппа и др. Тем не менее все эти каноны были попыткой найти объективные математические закономерности в строении человека — "законы красоты" человека.
Другой важнейшей математической темой в живописи, которая также на протяжении тысячелетий стимулировала поиски и дарила находки как художникам, так и ученым, является проблема построения перспективы. Эти две темы и составят предмет последней части книги.
19. "Законы красоты" человека
Человек — мера всех вещей.Во все времена, от наскальной живописи в Сахаре до полотен Сальвадора Дали, человек был и остается главной темой изобразительного искусства. "Виллендорфская Венера" или Венера Милосская, царь Хаммурапи или бог Аполлон, Сикстинская мадонна или девушка с персиками — для художника все они прежде всего были образами человека. Более того, в предыдущей части мы увидели, что образ человека, его пропорции нашли воплощение и в архитектурных произведениях от античных й древнерусских храмов до ультрасовременных сооружений Ле Корбюзье. Настало время подробнее поговорить об этих пропорциях — "законах красоты" человека[30]. С древнейших времен пропорции человека составляли предмет изучения художника, его "математическую лабораторию". На первых порах художником руководило, быть может, не столько стремление "дойти до самой сути", сколько необходимость в каких-то объективных — числовых или геометрических — формах передать свой опыт и свое мировоззрение преемникам. Так в искусстве возникали каноны. Известны три древнеегипетских канона : первый канон эпохи Древнего царства, приписываемый Имхотепу (XXVIII в. до н. э.), слагает рост человека из 6 ступеней ноги; второй — эпохи Среднего и Нового царства (XXI-XII вв. до н. э.) разбивает каждую ступню еще на три части и таким образом составляет рост человека из 18 единиц; третий канон позднего периода[31] (XI-IV вв. до н. э.) складывает рост человека из 21 части с четвертью. Текст египетских канонов не сохранился, хотя в дошедшем до нас каталоге храмовой библиотеки в Эдфу под шестым номером значится трактат "Предписание для стенной живописи и канон пропорций". Легко видеть, как с течением времени усложнялся древнеегипетский канон, хотя и на такие ничтожные для современника "уточнения" потребовалось ни много ни мало 2500 лет! Да, мерно, как воды Нила, текло время в Древнем Египте. И столь же неторопливым, статичным было египетское искусство. Более того, следование раз и навсегда принятым канонам, в том числе и художественным, неизменность всего сущего были своего рода философией древнеегипетского общества. И эта философия оцепенения мастерски воплощена древним художником в камне. Впрочем, для нас важно другое: почти за 3000 лет до н. э. изобразительное искусство подверглось математическому анализу и анализ этот был весьма объективен, коль скоро он устраивал древнеегипетских художников на протяжении тысячелетий. Только в математических закономерностях и можно было на века сохранить художественные каноны. Вера египтян в универсальность математического знания отражена в одном из математических папирусов, который начинается словами: "Точное сложение — врата в знание всех вещей и мрачных тайн". А вера в универсальность канона доходила до того, что один и тот же канон египтяне применяли как в живописи, так и в архитектуре. Сетка квадратов, применявшаяся с равным успехом и в ваянии, и в зодчестве, была у египтян математической основой, организующей изображение. Меняться могли лишь абсолютные размеры этой сетки, само же изображение, его пропорции оставались неизменными.Протагор
 Сетка квадратов 211/4 X14 — канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве
Сетка квадратов 211/4 X14 — канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве
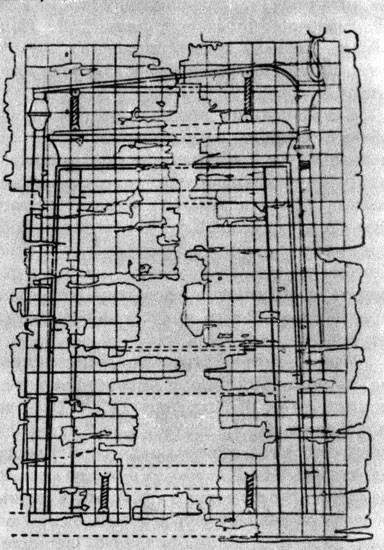 Сетка квадратов 211/4X14 — канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве
Но и внутри сетки положение фигуры строго регламентировалось математическими законами. Рассмотрим одно геометрическое построение, которое, как полагают, было известно древним египтянам. Стороны квадрата ABCD разделим в золотой пропорции точками Еi (i = 1, 2,..., 8). (Это легко сделать, разбив данный квадрат на четыре квадрата и в каждом двойном квадрате выполнив построения, указанные на рисунке, с. 265.) Из вершины квадрата проведем в точки деления по две "диагонали". В результате образуется восьмиконечная звезда, внутри которой заключены два малых квадрата, образующих звездчатый восьмиугольник. Соединяя через одну точки пересечения малых квадратов, построим меньший квадрат со сторонами, параллельными сторонам исходного квадрата. В последнем квадрате всю процедуру можно повторить. Таким образом, получится созвездие вписанных друг в друга восьмиконечных звезд, столь же красивое, как и созвездия пятиконечных и десятиконечных звезд, которые мы наблюдали на рисунках (с. 206).
Не будем перегружать рисунок дополнительными построениями и лишать любителей математики удовольствия самим найти на чертеже две гаммы треугольников, подобных прямоугольным треугольникам АВЕ2 и AFH. Отметим лишь, принимая сторону исходного квадрата за единицу, главное. В ΔАВЕ2 АВ = 1, BЕ2 = φ, АЕ2 = √1 + φ2 = ψ. В ΔABF ~ ΔАВЕ2
AF = 1/ψ, BF = φ/ψ, AB = 1. Из ΔABF и ΔBFG, имеющих общую сторону BF, можно найти элементы ΔBFG: BF = φ/ψ, FG = φ/2ψ ,BG = ψ/2, а значит, и элементы ΔAFH: AF = 1/ψ, FH = 1/2ψ, АH = ψ/2φ. (Напомним, что φ = (√5 — 1)/2 и при выводе соотношений в треугольниках используется аддитивное свойство ряда золотого сечения: 1 = φ + φ2, φ = φ2 + φ3, ... .)
Продолжая рассмотрение подобных треугольников, легко увидеть, что отношения соответствующих элементов треугольников, подобных ΔABE2, образуют бесконечно убывающую геометрическую прогрессию :
Сетка квадратов 211/4X14 — канон древнеегипетского искусства, применявшийся как в живописи, так и в зодчестве
Но и внутри сетки положение фигуры строго регламентировалось математическими законами. Рассмотрим одно геометрическое построение, которое, как полагают, было известно древним египтянам. Стороны квадрата ABCD разделим в золотой пропорции точками Еi (i = 1, 2,..., 8). (Это легко сделать, разбив данный квадрат на четыре квадрата и в каждом двойном квадрате выполнив построения, указанные на рисунке, с. 265.) Из вершины квадрата проведем в точки деления по две "диагонали". В результате образуется восьмиконечная звезда, внутри которой заключены два малых квадрата, образующих звездчатый восьмиугольник. Соединяя через одну точки пересечения малых квадратов, построим меньший квадрат со сторонами, параллельными сторонам исходного квадрата. В последнем квадрате всю процедуру можно повторить. Таким образом, получится созвездие вписанных друг в друга восьмиконечных звезд, столь же красивое, как и созвездия пятиконечных и десятиконечных звезд, которые мы наблюдали на рисунках (с. 206).
Не будем перегружать рисунок дополнительными построениями и лишать любителей математики удовольствия самим найти на чертеже две гаммы треугольников, подобных прямоугольным треугольникам АВЕ2 и AFH. Отметим лишь, принимая сторону исходного квадрата за единицу, главное. В ΔАВЕ2 АВ = 1, BЕ2 = φ, АЕ2 = √1 + φ2 = ψ. В ΔABF ~ ΔАВЕ2
AF = 1/ψ, BF = φ/ψ, AB = 1. Из ΔABF и ΔBFG, имеющих общую сторону BF, можно найти элементы ΔBFG: BF = φ/ψ, FG = φ/2ψ ,BG = ψ/2, а значит, и элементы ΔAFH: AF = 1/ψ, FH = 1/2ψ, АH = ψ/2φ. (Напомним, что φ = (√5 — 1)/2 и при выводе соотношений в треугольниках используется аддитивное свойство ряда золотого сечения: 1 = φ + φ2, φ = φ2 + φ3, ... .)
Продолжая рассмотрение подобных треугольников, легко увидеть, что отношения соответствующих элементов треугольников, подобных ΔABE2, образуют бесконечно убывающую геометрическую прогрессию :
 (19.1)
а отношения соответствующих элементов треугольников, подобных ΔAFH, образуют прогрессию:
(19.1)
а отношения соответствующих элементов треугольников, подобных ΔAFH, образуют прогрессию:
 (19.2)
Кроме того, имеют место комбинации двух основных типов прогрессий, а именно прогрессии вида
(19.2)
Кроме того, имеют место комбинации двух основных типов прогрессий, а именно прогрессии вида
 (19.3)
Итак, построения рисунка дают нам не только ряд золотого сечения (19.2), но и гамму геометрических прогрессий вида
(19.3)
Итак, построения рисунка дают нам не только ряд золотого сечения (19.2), но и гамму геометрических прогрессий вида
 (19.4)
соответствующие члены которых также находятся в золотой пропорции.
Любопытно, что в
(19.4)
соответствующие члены которых также находятся в золотой пропорции.
Любопытно, что в  Заметим также, что в
Заметим также, что в
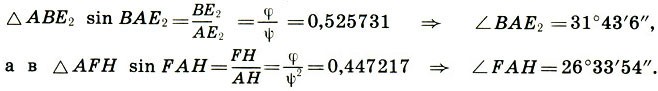 Таким образом, меньшие углы в треугольниках ΔВЕ2 и AFH почти равны; следовательно, эти треугольники почти подобны, а углы исходного квадрата делятся "диагоналями" почти точно на три части. Итак рассмотренное построение дает нам прекрасный пример приблизительной симметрии (см. гл. 4).
Таким образом, меньшие углы в треугольниках ΔВЕ2 и AFH почти равны; следовательно, эти треугольники почти подобны, а углы исходного квадрата делятся "диагоналями" почти точно на три части. Итак рассмотренное построение дает нам прекрасный пример приблизительной симметрии (см. гл. 4).
 Созвездие восьмиконечных звезд, вписанных в квадрат, содержит целую гамму золотых пропорций и использовалось древнеегипетскими художниками в пропорциях человека
Созвездие восьмиконечных звезд, вписанных в квадрат, содержит целую гамму золотых пропорций и использовалось древнеегипетскими художниками в пропорциях человека
 Математическое построение древнеегипетских рисунков на базе восьми пропорциональных величин (по Ф. де Кора). Фигурки жреца (а) и богини Ночи (б)
Интересно, что... Впрочем, достаточно. Оставим радость открытия любителям математики, тем более что у любителей искусства, видимо, давно уже созрел вопрос: "А какое отношение вся эта геометрия и алгебра имеют к теме нашего разговора — пропорциям человека?" А вот какое.
По мнению французского египтолога Фурнье де Кора, восемь величин из ряда (19.4), а именно
Математическое построение древнеегипетских рисунков на базе восьми пропорциональных величин (по Ф. де Кора). Фигурки жреца (а) и богини Ночи (б)
Интересно, что... Впрочем, достаточно. Оставим радость открытия любителям математики, тем более что у любителей искусства, видимо, давно уже созрел вопрос: "А какое отношение вся эта геометрия и алгебра имеют к теме нашего разговора — пропорциям человека?" А вот какое.
По мнению французского египтолога Фурнье де Кора, восемь величин из ряда (19.4), а именно
 (19.5)
определяют весь пропорциональный строй древнеегипетской живописи. Этот вывод де Кора основан на кропотливом изучении пропорции многих памятников изобразительного искусства Древнего Египта. На рисунке мы видим, что местоположение всех основных элементов фигур — уровень глаз, носа, рта, шеи, плеч, пояса и т. д.- с удивительной точностью определяется пропорциональными величинами (19.5), умноженными на общую длину фигурки (Н). Пользуясь (19.5) и соотношениями φn = φn+1 + φn+2, легко доказать равенства типа 2А1 + А8 = 1, А1 + А2 + А6 = 1, А1 + 2А3 = 1, А6 + А8 = А3, А3 + A8 = A2, А3 + А6 = А1, и т. д.
Конечно, ряд (19.4) дает настолько богатую гамму пропорций, что при достаточном числе членов она может быть точнее миллиметровой линейки. Математику, разумеется, не понравится, что в (19.5) пропущены члены φ, φ/ψ, φ2/ψ и φ4 отчего теория де Кора теряет в логической стройности. Да, по прошествии четырех тысячелетий трудно установить, какой именно системой пропорций пользовался древнеегипетский художник. Поэтому так много различных теорий пропорций. Но бесспорно другое: древнеегипетский художник применял жестко детерминированную систему математических правил, которая на века определила стиль древнеегипетского изобразительного искусства. Эта математика рисунка, ставшая каноном, на века сковала искусство Древнего Египта.
Описание египетского канона позднего периода и любопытную историю, связанную с ним, мы находим у древнегреческого историка Диодора Сицилийского (ок. 90-21 гг. до н. э.). По преданию, отец Пифагора Мнесарх построил на родном острове Самос храм в честь Аполлона Пифийского, статую для которого поручили изваять прославленным греческим скульпторам. "Из древних скульпторов наибольшею славою пользовались у них Телекл и Феодор, сыновья Река, которые соорудили для самосцев статую Аполлона Пифийского. Рассказывают, что одна половина этой статуи была приготовлена Телеклом на Самосе, другая же часть была сделана его братом Феодором в Эфесе. Будучисложенными, эти части настолько соответствовали одна другой, что казалось, будто все произведение исполнено одним мастером. Однако этот род работы никогда не применяется у греков, но большей частью употребляется у египтян... У них соразмерность статуи определяется не на глаз, но они после того, как высекут камни и обработают, разделив их на части, берут пропорцию от мельчайших до наибольших частей; рост тела они делят на 211/4 — часть и так дают все соразмерности живого человека. Поэтому после того, как работники сговорятся о размерах, то, разделивши между собой труд, обрабатывают согласно заданной величине так точно, что работа их наполняет изумлением". Возможно, что эта история, рассказанная Диодором, не более чем легенда. Но важен в ней даже не факт совпадения сложенных изваяний, сколько сама постановка такого вопроса. В этой истории, даже если она и легенда, отражена безграничная вера древних греков в могущество математики, которую с равным успехом можно применять не только в инженерных расчетах (вспомним о самосском туннеле, с. 89), но и в искусстве ваяния. Создавая свои бессмертные творения, древние не боялись "алгеброй разрушить гармонию" и твердо верили: математика поможет там, где, по словам Дюрера, "рука из-за спешки обманет тебя".
(19.5)
определяют весь пропорциональный строй древнеегипетской живописи. Этот вывод де Кора основан на кропотливом изучении пропорции многих памятников изобразительного искусства Древнего Египта. На рисунке мы видим, что местоположение всех основных элементов фигур — уровень глаз, носа, рта, шеи, плеч, пояса и т. д.- с удивительной точностью определяется пропорциональными величинами (19.5), умноженными на общую длину фигурки (Н). Пользуясь (19.5) и соотношениями φn = φn+1 + φn+2, легко доказать равенства типа 2А1 + А8 = 1, А1 + А2 + А6 = 1, А1 + 2А3 = 1, А6 + А8 = А3, А3 + A8 = A2, А3 + А6 = А1, и т. д.
Конечно, ряд (19.4) дает настолько богатую гамму пропорций, что при достаточном числе членов она может быть точнее миллиметровой линейки. Математику, разумеется, не понравится, что в (19.5) пропущены члены φ, φ/ψ, φ2/ψ и φ4 отчего теория де Кора теряет в логической стройности. Да, по прошествии четырех тысячелетий трудно установить, какой именно системой пропорций пользовался древнеегипетский художник. Поэтому так много различных теорий пропорций. Но бесспорно другое: древнеегипетский художник применял жестко детерминированную систему математических правил, которая на века определила стиль древнеегипетского изобразительного искусства. Эта математика рисунка, ставшая каноном, на века сковала искусство Древнего Египта.
Описание египетского канона позднего периода и любопытную историю, связанную с ним, мы находим у древнегреческого историка Диодора Сицилийского (ок. 90-21 гг. до н. э.). По преданию, отец Пифагора Мнесарх построил на родном острове Самос храм в честь Аполлона Пифийского, статую для которого поручили изваять прославленным греческим скульпторам. "Из древних скульпторов наибольшею славою пользовались у них Телекл и Феодор, сыновья Река, которые соорудили для самосцев статую Аполлона Пифийского. Рассказывают, что одна половина этой статуи была приготовлена Телеклом на Самосе, другая же часть была сделана его братом Феодором в Эфесе. Будучисложенными, эти части настолько соответствовали одна другой, что казалось, будто все произведение исполнено одним мастером. Однако этот род работы никогда не применяется у греков, но большей частью употребляется у египтян... У них соразмерность статуи определяется не на глаз, но они после того, как высекут камни и обработают, разделив их на части, берут пропорцию от мельчайших до наибольших частей; рост тела они делят на 211/4 — часть и так дают все соразмерности живого человека. Поэтому после того, как работники сговорятся о размерах, то, разделивши между собой труд, обрабатывают согласно заданной величине так точно, что работа их наполняет изумлением". Возможно, что эта история, рассказанная Диодором, не более чем легенда. Но важен в ней даже не факт совпадения сложенных изваяний, сколько сама постановка такого вопроса. В этой истории, даже если она и легенда, отражена безграничная вера древних греков в могущество математики, которую с равным успехом можно применять не только в инженерных расчетах (вспомним о самосском туннеле, с. 89), но и в искусстве ваяния. Создавая свои бессмертные творения, древние не боялись "алгеброй разрушить гармонию" и твердо верили: математика поможет там, где, по словам Дюрера, "рука из-за спешки обманет тебя".
 Курос из Теней ('Аполлон Тенейский'). Ок. 560 до н. э. Тождественность пропорций Аполлона Тенейского и египетского канона ваяния позднего периода еще раз доказывает факт влияния древнеегипетского искусства на раннее греческое искусство периода архаики
На рисунке изображен египетский канон, описанный у Диодора. Высота фигуры разделена точно на 21 — части, причем одно целое деление соответствует длине среднего пальца. Высота фигуры без головного убора составляет 19 частей. Рядом расположена греческая скульптура Аполлона Тенейского, относящаяся к середине VI века до н. э.- так называемому архаическому (от греч. "архайос" — древний) периоду греческого искусства. Точное совпадение пропорций этих двух фигур является математическим доказательством достаточно очевидной истины: греческое искусство периода архаики взросло на почве древнеегипетского искусства. Конечно, художественные образы этих фигур совершенно различны. Аполлон Тенейский, юноша-атлет (курос), светится жизнью и радостью: еще мгновение — и он сойдет с места навстречу новому искусству Эллады. Однако его пропорции- "математика Аполлона" — полностью сохраняют влияние древнеегипетского канона.
Греческое искусство развивалось очень динамично. Уже через 100 лет после Аполлона Тенейского, в середине V века до н. э., греческая цивилизация достигает своего апогея. Наступает период наивысшего расцвета искусства Древней Греции, именуемый периодом высокой классики. Возвышенные идеалы классики, вера в духовное, нравственное и физическое совершенство свободного эллина нашли отражение в скульптурах Поликлета, творившего во второй половине V века. Поликлет был не только гениальным скульптором, автором "Дорифора", "Дуадумена" и "Раненой амазонки", но и выдающимся теоретиком искусства.
Свои теоретические воззрения о пропорциях человека Поликлет изложил в трактате "Канон". Трактат этот, увы, не сохранился. Но как бы предчувствуя бренность написанного и бессмертие изваянного, Поликлет создает статую, в которой в бронзе воплощает свои теоретические воззрения. (Статуя эта также не сохранилась, но, к счастью, сохранилась ее римская мраморная копия.) Вот почему прославленная статуя юноши-копьеносца "Дорифор" имеет также и другое название — "Канон".
К сожалению, мы опять-таки не знаем, в каких конкретных математических отношениях выражался канон Поликлета. Но знание философских воззрений Поликлета, а главное — его скульптура помогают восстановить эти отношения. Поликлет был пифагорейцем, следовательно, он был неплохим математиком и, безусловно, был знаком с золотой пропорцией, которую пифагорейцы считали верхом совершенства. Можно только догадываться, какое изумление и радость испытал пифагореец Поликлет, когда обнаружил, что золотая пропорция присуща не только абстрактной геометрической фигуре, главному пифагорейскому символу — пятиконечной звезде, но и естественным образом входит в пропорции человека. Человеческое тело оказалось благодатным материалом для философа-пифагорейца: как нам известно, золотая пропорция пронизывает тело человека от малых размеров (три фаланги среднего пальца) до самых больших (см. с. 214). Анализ пропорций "Дорифора" и других скульптур Поликлета подтверждает наши предположения: в скульптурах Поликлета с большой точностью выдержаны пропорции ряда золотого сечения (см. с. 207)
1, φ, φ2, φ3, φ4, φ5, φ6.
Заметим, что в самом методе построения пропорций Поликлета есть принципиальное отличие от метода пропорционирования египтян. Египтяне исходили из какой-то условной единицы измерения, например длины среднего пальца, которую затем целое число раз "укладывали" в ту или иную часть изображения человека. Поликлет же рост человека принимает за единицу, затем фиксирует определенную часть тела, какова бы она ни была по размерам, и находит их отношение. Такое отношение могло выражаться не только отношением целых чисел, как у египтян, но и быть иррациональным числом, как в случае золотого сечения.
Таким образом, открытие золотой пропорции в строении человека, которое, по-видимому, принадлежит Поликлету, можно считать вслед за открытием закона целочисленных отношений в музыке вторым важнейшим событием в "математической теории искусств".
Курос из Теней ('Аполлон Тенейский'). Ок. 560 до н. э. Тождественность пропорций Аполлона Тенейского и египетского канона ваяния позднего периода еще раз доказывает факт влияния древнеегипетского искусства на раннее греческое искусство периода архаики
На рисунке изображен египетский канон, описанный у Диодора. Высота фигуры разделена точно на 21 — части, причем одно целое деление соответствует длине среднего пальца. Высота фигуры без головного убора составляет 19 частей. Рядом расположена греческая скульптура Аполлона Тенейского, относящаяся к середине VI века до н. э.- так называемому архаическому (от греч. "архайос" — древний) периоду греческого искусства. Точное совпадение пропорций этих двух фигур является математическим доказательством достаточно очевидной истины: греческое искусство периода архаики взросло на почве древнеегипетского искусства. Конечно, художественные образы этих фигур совершенно различны. Аполлон Тенейский, юноша-атлет (курос), светится жизнью и радостью: еще мгновение — и он сойдет с места навстречу новому искусству Эллады. Однако его пропорции- "математика Аполлона" — полностью сохраняют влияние древнеегипетского канона.
Греческое искусство развивалось очень динамично. Уже через 100 лет после Аполлона Тенейского, в середине V века до н. э., греческая цивилизация достигает своего апогея. Наступает период наивысшего расцвета искусства Древней Греции, именуемый периодом высокой классики. Возвышенные идеалы классики, вера в духовное, нравственное и физическое совершенство свободного эллина нашли отражение в скульптурах Поликлета, творившего во второй половине V века. Поликлет был не только гениальным скульптором, автором "Дорифора", "Дуадумена" и "Раненой амазонки", но и выдающимся теоретиком искусства.
Свои теоретические воззрения о пропорциях человека Поликлет изложил в трактате "Канон". Трактат этот, увы, не сохранился. Но как бы предчувствуя бренность написанного и бессмертие изваянного, Поликлет создает статую, в которой в бронзе воплощает свои теоретические воззрения. (Статуя эта также не сохранилась, но, к счастью, сохранилась ее римская мраморная копия.) Вот почему прославленная статуя юноши-копьеносца "Дорифор" имеет также и другое название — "Канон".
К сожалению, мы опять-таки не знаем, в каких конкретных математических отношениях выражался канон Поликлета. Но знание философских воззрений Поликлета, а главное — его скульптура помогают восстановить эти отношения. Поликлет был пифагорейцем, следовательно, он был неплохим математиком и, безусловно, был знаком с золотой пропорцией, которую пифагорейцы считали верхом совершенства. Можно только догадываться, какое изумление и радость испытал пифагореец Поликлет, когда обнаружил, что золотая пропорция присуща не только абстрактной геометрической фигуре, главному пифагорейскому символу — пятиконечной звезде, но и естественным образом входит в пропорции человека. Человеческое тело оказалось благодатным материалом для философа-пифагорейца: как нам известно, золотая пропорция пронизывает тело человека от малых размеров (три фаланги среднего пальца) до самых больших (см. с. 214). Анализ пропорций "Дорифора" и других скульптур Поликлета подтверждает наши предположения: в скульптурах Поликлета с большой точностью выдержаны пропорции ряда золотого сечения (см. с. 207)
1, φ, φ2, φ3, φ4, φ5, φ6.
Заметим, что в самом методе построения пропорций Поликлета есть принципиальное отличие от метода пропорционирования египтян. Египтяне исходили из какой-то условной единицы измерения, например длины среднего пальца, которую затем целое число раз "укладывали" в ту или иную часть изображения человека. Поликлет же рост человека принимает за единицу, затем фиксирует определенную часть тела, какова бы она ни была по размерам, и находит их отношение. Такое отношение могло выражаться не только отношением целых чисел, как у египтян, но и быть иррациональным числом, как в случае золотого сечения.
Таким образом, открытие золотой пропорции в строении человека, которое, по-видимому, принадлежит Поликлету, можно считать вслед за открытием закона целочисленных отношений в музыке вторым важнейшим событием в "математической теории искусств".
 Рисунок Леонардо да Винчи из анатомических рукописей, связавший совершенные геометрические фигуры с пропорциями человека, стал своеобразным символом синтеза математики и искусства
Разумеется, в рамках этой главы невозможно даже кратко остановиться на всех теориях пропорций человека, имеющих тысячелетнюю традицию и массу вариаций. Желая ярче передать тот или иной образ, художник намеренно усиливал одни пропорции и сглаживал другие и таким образом создавал свой собственный канон. Так, уже через сто лет после Поликлета, в IV веке до н. э., в Древней Греции сложился другой, более "утонченный" канон скульптора Лисиппа, бывшего придворным художником Александра Македонского. Как писал Плиний, Лисипп изображал людей не "какими они есть", но "какими они кажутся". Впрочем, вопрос о том, какие пропорции и насколько соответствуют тому или иному художественному образу, является вопросом искусствоведения, и нам не следует погружаться в него. Однако имена двух гениальных художников и мыслителей, двух титанов эпохи Возрождения — Леонардо да Винчи и Альбрехта Дюрера — мы не можем обойти здесь молчанием.
В построении пропорций человека Леонардо да Винчи исходит прежде всего из анализа многочисленных измерений самого человека, из его анатомии, а не из каких-то "высших" соображений, как это делали средневековые художники. Жажда научного знания, основанного на опыте и только опыте, отражает переворот в мышлении эпохи Возрождения, знаменует начало экспериментального естествознания. Стремление как можно глубже изучить пропорции и вообще строение человека, столь необходимые Леонардо-художнику, переросло в страсть к науке анатомии Леонардо-ученого, Составленные им анатомические тетради явились вершиной анатомии того времени и по сей день остаются непревзойденным образцом синтеза науки и искусства.
Свои исследования Леонардо не успел (а может, и не хотел) систематизировать, и они остались рассыпанными в виде рукописных набросков, в которых говорится буквально обо всем на свете, а текст перемежается великолепными рисунками. Мы остановимся лишь на одном наиболее популярном рисунке Леонардо на тему о пропорциях. Вот отрывок текста, которым Леонардо сопровождает рисунок: "Если ты раздвинешь ноги настолько, что убавишься в росте на 1/14, и если ты тогда разведешь руки и поднимешь их так, что коснешься средними пальцами макушки головы, то должен ты знать, что центром круга, описанного концами вытянутых членов, будет пупок и что пространство между ногами образует равносторонний треугольник. А пролет распростертых рук человека равен его росту". Заметим, что идея этого рисунка восходит к известному нам сочинению Витрувия.
Свое высшее развитие учение о пропорциях человека получило в трудах Дюрера. С немецкой скрупулезностью проводит Дюрер свои измерения и в конце концов доводит разбиение человеческого тела до 1/1800 части его длины, т. е. до величины, не превышающей одного миллиметра! По мнению А. Лосева, столь тщательное измерение "стало самоцелью и каким-то измерительным спортом!". Ни до, ни после Дюрера учение о пропорциях не доводилось до такой степени точности. Но главное, пожалуй, было в другом: Дюрер отказался от создания какого-либо "идеального" канона, а разработал не менее 26 различных типов пропорций человека.
Обратимся к трактату Дюрера "Четыре книги о пропорциях". "Если я намереваюсь сделать изображение человека,- читаем мы,- то прежде всего я поступаю таким образом: я беру линейку длиннее, чем фигура, и провожу на ней прямую линию такой длины, какой должна быть изображенная фигура, так, чтобы один конец касался макушки головы, а другой подошв... И я старательно делю всю длину, которую я обозначаю цифрой 1, на части от двух до пятидесяти или ста частей, сколько мне нужно, наношу их точками на линейку возле длинной линии, провожу из них линии вверх до высоты макушки и обозначаю их цифрами 2, 3, 4 и т. д. Таким образом, меньшие цифры будут обозначать более длинные части, а большие — короткие. Так, половина всей длины будет 2, треть — 3, четверть — 4 и т. д.". Затем Дюрер указывает "важнейшие расчленяющие линии": "верхнюю я называю макушкою, следующую под нею — лбом, следующую — бровями, затем идут нос, подбородок и далее плечевые мускулы, шейная впадина, верх груди..." и так далее вплоть до подошвы.
Рисунок Леонардо да Винчи из анатомических рукописей, связавший совершенные геометрические фигуры с пропорциями человека, стал своеобразным символом синтеза математики и искусства
Разумеется, в рамках этой главы невозможно даже кратко остановиться на всех теориях пропорций человека, имеющих тысячелетнюю традицию и массу вариаций. Желая ярче передать тот или иной образ, художник намеренно усиливал одни пропорции и сглаживал другие и таким образом создавал свой собственный канон. Так, уже через сто лет после Поликлета, в IV веке до н. э., в Древней Греции сложился другой, более "утонченный" канон скульптора Лисиппа, бывшего придворным художником Александра Македонского. Как писал Плиний, Лисипп изображал людей не "какими они есть", но "какими они кажутся". Впрочем, вопрос о том, какие пропорции и насколько соответствуют тому или иному художественному образу, является вопросом искусствоведения, и нам не следует погружаться в него. Однако имена двух гениальных художников и мыслителей, двух титанов эпохи Возрождения — Леонардо да Винчи и Альбрехта Дюрера — мы не можем обойти здесь молчанием.
В построении пропорций человека Леонардо да Винчи исходит прежде всего из анализа многочисленных измерений самого человека, из его анатомии, а не из каких-то "высших" соображений, как это делали средневековые художники. Жажда научного знания, основанного на опыте и только опыте, отражает переворот в мышлении эпохи Возрождения, знаменует начало экспериментального естествознания. Стремление как можно глубже изучить пропорции и вообще строение человека, столь необходимые Леонардо-художнику, переросло в страсть к науке анатомии Леонардо-ученого, Составленные им анатомические тетради явились вершиной анатомии того времени и по сей день остаются непревзойденным образцом синтеза науки и искусства.
Свои исследования Леонардо не успел (а может, и не хотел) систематизировать, и они остались рассыпанными в виде рукописных набросков, в которых говорится буквально обо всем на свете, а текст перемежается великолепными рисунками. Мы остановимся лишь на одном наиболее популярном рисунке Леонардо на тему о пропорциях. Вот отрывок текста, которым Леонардо сопровождает рисунок: "Если ты раздвинешь ноги настолько, что убавишься в росте на 1/14, и если ты тогда разведешь руки и поднимешь их так, что коснешься средними пальцами макушки головы, то должен ты знать, что центром круга, описанного концами вытянутых членов, будет пупок и что пространство между ногами образует равносторонний треугольник. А пролет распростертых рук человека равен его росту". Заметим, что идея этого рисунка восходит к известному нам сочинению Витрувия.
Свое высшее развитие учение о пропорциях человека получило в трудах Дюрера. С немецкой скрупулезностью проводит Дюрер свои измерения и в конце концов доводит разбиение человеческого тела до 1/1800 части его длины, т. е. до величины, не превышающей одного миллиметра! По мнению А. Лосева, столь тщательное измерение "стало самоцелью и каким-то измерительным спортом!". Ни до, ни после Дюрера учение о пропорциях не доводилось до такой степени точности. Но главное, пожалуй, было в другом: Дюрер отказался от создания какого-либо "идеального" канона, а разработал не менее 26 различных типов пропорций человека.
Обратимся к трактату Дюрера "Четыре книги о пропорциях". "Если я намереваюсь сделать изображение человека,- читаем мы,- то прежде всего я поступаю таким образом: я беру линейку длиннее, чем фигура, и провожу на ней прямую линию такой длины, какой должна быть изображенная фигура, так, чтобы один конец касался макушки головы, а другой подошв... И я старательно делю всю длину, которую я обозначаю цифрой 1, на части от двух до пятидесяти или ста частей, сколько мне нужно, наношу их точками на линейку возле длинной линии, провожу из них линии вверх до высоты макушки и обозначаю их цифрами 2, 3, 4 и т. д. Таким образом, меньшие цифры будут обозначать более длинные части, а большие — короткие. Так, половина всей длины будет 2, треть — 3, четверть — 4 и т. д.". Затем Дюрер указывает "важнейшие расчленяющие линии": "верхнюю я называю макушкою, следующую под нею — лбом, следующую — бровями, затем идут нос, подбородок и далее плечевые мускулы, шейная впадина, верх груди..." и так далее вплоть до подошвы.
 Пропорции фигурки младенца из трактата Дюрера 'Четыре книги о пропорциях'
Пропорции фигурки младенца из трактата Дюрера 'Четыре книги о пропорциях'
 Рисунки из 'Четырех книг о пропорциях' Дюрера. В своем трактате художник пытался найти совокупность геометрических преобразований, позволяющую охватить все многообразие человеческих лиц
Хотя Дюрер и отмечает, что таковых линий "можно сделать больше или меньше", большая тщательность в анализе фигуры человека современному читателю кажется просто немыслимой. Далее следуют промеры указанных линий, которые Даются для различных типов фигур: от мужских и женских фигур до фигурки младенца. Последняя дает ясное представление о том, сколь филигранными были геометрические построения Дюрера. В третьей книге трактата Дюрер показывает, "как можно изменять или искажать эти вышеописанные размеры... благодаря чему фигура становится неузнаваемой...". Предложенный Дюрером для этой цели "измените ль" представляет собой не что иное, как систему подобных треугольников. При этом Дюрер ясно осознает, что если пропорционально изменить все размеры фигуры, то ее вид останется прежним. И напротив, "если увеличить одни части и уменьшить другие, вид вещи станет иным".
Но если пропорции человеческой фигуры еще можно как-то классифицировать, то лицо человека никак не укладывалось у Дюрера в жесткие рамки пропорциональной сетки. Дюрер изобретает массу геометрических способов, которыми можно до неузнаваемости трансформировать изображение лица. Однако чем большим становится набор таких способов, тем яснее видно, что их число уходит в бесконечность. Дюрер-художник интуитивно осознает это: в его трактате не раз проскальзывает фраза о том, что "контуры человеческой фигуры нельзя начертить при помощи циркуля и линейки". И в то же время Дюрер-геометр упрямо продолжает поиски универсального геометрического метода в построении изображения человека.
На рисунке приведены некоторые из геометрических преобразований Дюрера. В первой строке слева показано исходное "правильное" лицо. Вторая строка слева представляет собой геометрические преобразования, которые в математике называются аффинными. Аффинное преобразование, или отображение,- это такое взаимно однозначное отображение, при котором параллельные прямые исходной плоскости (верхняя строка) переходят в параллельные прямые на плоскости отображения (вторая строка). Рисунки справа дают пример более сложных геометрических преобразований.
Глядя по прошествии 500 лет на геометрические построения Дюрера, хорошо видно, как в его исследованиях назрела потребность в точной науке о непрерывных процессах, науке о проявлении прерывного в непрерывном, науке о бесконечно большом числе бесконечно малых изменений. Такая наука родилась лишь через полтора века после Дюрера в трудах Ньютона и Лейбница, когда вместе с понятием производной "в математику вошли движение и диалектика" (Ф. Энгельс, т. 20, с. 573). Таким образом, творчество Дюрера еще раз убеждает нас в том, что пути науки и искусства связаны тысячами нитей. В геометрических поисках Дюрера мы видим, как одно из величайших завоеваний человеческой мысли — дифференциальное исчисление — зрело не только в лоне науки, но и в недрах искусства.
А как развивалась теория пропорций человека после Дюрера? В XVII веке движение вошло не только в науку, но и в искусство. На смену застывшим формам объекта, где царствовали покой и пропорция, в искусстве пробуждается интерес к изменчивому, как солнечный луч, субъекту, его настроению и мироощущению. Голландским люминаристам XVII века и французским импрессионистам XIX века уже не нужны были пропорции, ибо форма, объект растворялись в их полотнах в потоках воздуха, цвета и света. Искусство XX века еще более динамично: оно разрушает все каноны, часто не успевая провозгласить свои. Сегодня каждый художник стремится создать свой собственный канон, что порождает бесконечные споры об искусстве. Тот же "канон Ильи Глазунова" расколол наших современников на сторонников и противников, что, впрочем, не мешает и тем и другим в едином строю опоясывать Манеж с выставками художника.
Рисунки из 'Четырех книг о пропорциях' Дюрера. В своем трактате художник пытался найти совокупность геометрических преобразований, позволяющую охватить все многообразие человеческих лиц
Хотя Дюрер и отмечает, что таковых линий "можно сделать больше или меньше", большая тщательность в анализе фигуры человека современному читателю кажется просто немыслимой. Далее следуют промеры указанных линий, которые Даются для различных типов фигур: от мужских и женских фигур до фигурки младенца. Последняя дает ясное представление о том, сколь филигранными были геометрические построения Дюрера. В третьей книге трактата Дюрер показывает, "как можно изменять или искажать эти вышеописанные размеры... благодаря чему фигура становится неузнаваемой...". Предложенный Дюрером для этой цели "измените ль" представляет собой не что иное, как систему подобных треугольников. При этом Дюрер ясно осознает, что если пропорционально изменить все размеры фигуры, то ее вид останется прежним. И напротив, "если увеличить одни части и уменьшить другие, вид вещи станет иным".
Но если пропорции человеческой фигуры еще можно как-то классифицировать, то лицо человека никак не укладывалось у Дюрера в жесткие рамки пропорциональной сетки. Дюрер изобретает массу геометрических способов, которыми можно до неузнаваемости трансформировать изображение лица. Однако чем большим становится набор таких способов, тем яснее видно, что их число уходит в бесконечность. Дюрер-художник интуитивно осознает это: в его трактате не раз проскальзывает фраза о том, что "контуры человеческой фигуры нельзя начертить при помощи циркуля и линейки". И в то же время Дюрер-геометр упрямо продолжает поиски универсального геометрического метода в построении изображения человека.
На рисунке приведены некоторые из геометрических преобразований Дюрера. В первой строке слева показано исходное "правильное" лицо. Вторая строка слева представляет собой геометрические преобразования, которые в математике называются аффинными. Аффинное преобразование, или отображение,- это такое взаимно однозначное отображение, при котором параллельные прямые исходной плоскости (верхняя строка) переходят в параллельные прямые на плоскости отображения (вторая строка). Рисунки справа дают пример более сложных геометрических преобразований.
Глядя по прошествии 500 лет на геометрические построения Дюрера, хорошо видно, как в его исследованиях назрела потребность в точной науке о непрерывных процессах, науке о проявлении прерывного в непрерывном, науке о бесконечно большом числе бесконечно малых изменений. Такая наука родилась лишь через полтора века после Дюрера в трудах Ньютона и Лейбница, когда вместе с понятием производной "в математику вошли движение и диалектика" (Ф. Энгельс, т. 20, с. 573). Таким образом, творчество Дюрера еще раз убеждает нас в том, что пути науки и искусства связаны тысячами нитей. В геометрических поисках Дюрера мы видим, как одно из величайших завоеваний человеческой мысли — дифференциальное исчисление — зрело не только в лоне науки, но и в недрах искусства.
А как развивалась теория пропорций человека после Дюрера? В XVII веке движение вошло не только в науку, но и в искусство. На смену застывшим формам объекта, где царствовали покой и пропорция, в искусстве пробуждается интерес к изменчивому, как солнечный луч, субъекту, его настроению и мироощущению. Голландским люминаристам XVII века и французским импрессионистам XIX века уже не нужны были пропорции, ибо форма, объект растворялись в их полотнах в потоках воздуха, цвета и света. Искусство XX века еще более динамично: оно разрушает все каноны, часто не успевая провозгласить свои. Сегодня каждый художник стремится создать свой собственный канон, что порождает бесконечные споры об искусстве. Тот же "канон Ильи Глазунова" расколол наших современников на сторонников и противников, что, впрочем, не мешает и тем и другим в едином строю опоясывать Манеж с выставками художника.
 Рисунок человека, выполненный ЭВМ в исследовательском отделе фирмы 'Боинг'. Система топологических правил, введенных в ЭВМ, позволяет нарисовать различные стадии движения человека
Так что же, теория пропорций стала отжившим рудиментом искусства? Автору так не кажется. Да, в своем "арифметическом" выражении теория пропорций себя исчерпала. Да, человек — мера всех вещей — настолько разнообразен, что его нельзя втиснуть в рамки дискретных канонов. Но пропорции живы, как жив и сам человек.
Теория пропорций сегодня не умерла, а лишь замерла в ожидании качественно нового скачка, в ожидании перехода от "арифметического" к "аналитическому" и даже "компьютерному" выражению. Почва для такого скачка сегодня созрела: есть современный математический аппарат, позволяющий описать контуры человека не "на уровне циркуля и линейки"; есть современные ЭВМ с их графопостроителями и дисплеями. Нужно содружество художников и математиков.
Примеры такого содружества есть. В исследовательском отделе американской фирмы "Боинг" выполнен рисунок на ЭВМ. Рисунок математически сконструирован по стандартным дюреровским пропорциям человека и ряду топологических правил, определяющих работу суставов и обеспечивающих непрерывность контура человека при его перемещениях. Таким образом, этот "машинный человечек" может двигаться, а сама ЭВМ может создать целый мультфильм. Однако эта увлекательная тема — искусство и ЭВМ — выходит за рамки нашей книги.
Рисунок человека, выполненный ЭВМ в исследовательском отделе фирмы 'Боинг'. Система топологических правил, введенных в ЭВМ, позволяет нарисовать различные стадии движения человека
Так что же, теория пропорций стала отжившим рудиментом искусства? Автору так не кажется. Да, в своем "арифметическом" выражении теория пропорций себя исчерпала. Да, человек — мера всех вещей — настолько разнообразен, что его нельзя втиснуть в рамки дискретных канонов. Но пропорции живы, как жив и сам человек.
Теория пропорций сегодня не умерла, а лишь замерла в ожидании качественно нового скачка, в ожидании перехода от "арифметического" к "аналитическому" и даже "компьютерному" выражению. Почва для такого скачка сегодня созрела: есть современный математический аппарат, позволяющий описать контуры человека не "на уровне циркуля и линейки"; есть современные ЭВМ с их графопостроителями и дисплеями. Нужно содружество художников и математиков.
Примеры такого содружества есть. В исследовательском отделе американской фирмы "Боинг" выполнен рисунок на ЭВМ. Рисунок математически сконструирован по стандартным дюреровским пропорциям человека и ряду топологических правил, определяющих работу суставов и обеспечивающих непрерывность контура человека при его перемещениях. Таким образом, этот "машинный человечек" может двигаться, а сама ЭВМ может создать целый мультфильм. Однако эта увлекательная тема — искусство и ЭВМ — выходит за рамки нашей книги.
20. Перспектива — геометрия живописи
Все проблемы Перспективы можно пояснить при помощи пяти терминов Математики: точка, линия, угол, поверхность и тело.В первом наскальном изображении первый первобытный художник столкнулся с непростой математической задачей: отобразить трехмерный оригинал на двумерную плоскость "картины". Сама природа помогла ему в решении этой задачи, ибо, как заметил Леонардо да Винчи, "первая картина состояла из одной-единственной линии, которая окружала тень человека, отброшенную солнцем на стену". Почему художник не довольствовался трехмерной скульптурой, а стремился к двумерному изображению оригинала, понять нетрудно: плоская поверхность пещеры или стены храма, глиняной таблички или папируса, пергамена или бумаги была удобным носителем графической информации. В последних случаях такую поверхность можно было попросту свернуть в рулон и унести с собой. Люди издревле научились отображать всевозможные объекты окружающего их трехмерного мира на двумерную плоскость картины. Однако по мере развития такого искусства отображения все чаще возникал вопрос: насколько точно и насколько убедительно эти плоские образы отражают реальные трехмерные прообразы? На эти вопросы призвана была ответить наука, и прежде всего геометрия. И она по мере сил отвечала на них, хотя решение столь простой на первый взгляд задачи растянулось на тысячелетия. В этой главе мы рассмотрим с точки зрения геометрии, какие основные возможности имеются в решении задачи отображения трехмерного пространства на двумерную плоскость. А в главе 22 мы увидим, как эти возможности реализовы-вались в искусстве живописи. Раздел геометрии, в котором изучаются различные методы изображения пространственных форм на плоскости, называется начертательной геометрией. В основе начертательной геометрии лежит метод проекций, сущность которого такова. В пространстве выбирают фиксированную точку S — центр проектирования и плоскость проекций К (картинную плоскость), не проходящую через S. Для получения изображения — проекции[32] — объекта на плоскость К через центр проекций S и каждую точку А, В, С,... объекта проводят проектирующие лучи до пересечения с плоскостью К. Совокупность точек пересечения проектирующих лучей с картинной плоскостью и даст изображение (проекцию) объекта, которое называют центральной проекцией. Представим теперь, что центр проектирования S уходит в бесконечность. Тогда проектирующие лучи становятся параллельными между собой. Считая центр проектирования расположенным в бесконечно удаленной точке S∞ , мы, таким образом, приходим к важному частному случаю центрального проектирования — параллельному проектированию. Наконец, важным частным случаем параллельных проекций являются ортогональные проекции, когда проектирующие лучи ортогональны К, т. е. образуют прямые углы с плоскостью проекций К. При построении проекций некоторые свойства оригинала сохраняются и на его проекции. Такими неизменными свойствами — инвариантами — при центральном проектировании обладают: 1) точки (проекция точки — точка); 2) прямые; 3) свойство точки принадлежать прямой. При параллельном проектировании помимо того сохраняются следующие свойства: 4) параллельность прямых; 5) отношение отрезков прямых; 6) метрические свойства плоских фигур, параллельных картинной плоскости (плоские фигуры, параллельные картинной плоскости, проектируются на эту плоскость без искажений). Обратим внимание на то, что свойство параллельности прямых при центральном проектировании не сохраняется.Леонардо да Винчи
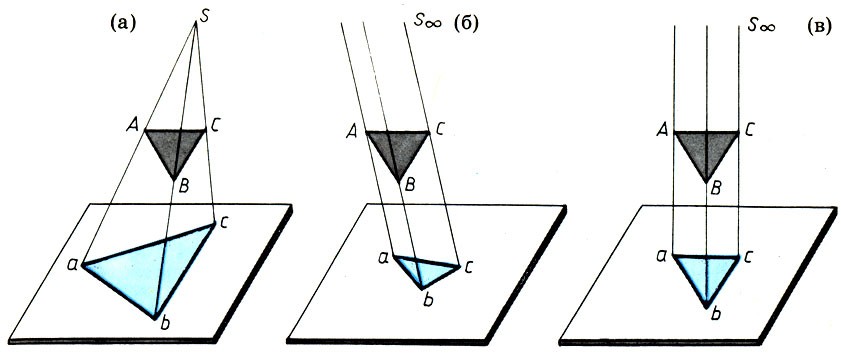 Важнейшие виды проекций: центральные (а), параллельные (б) и ортогональные (в)
Приложение начертательной геометрии к технике выдвинуло требование "обратимости" чертежа, т. е. возможности точного определения пространственной фигуры по плоскому чертежу, или, говоря языком математики, взаимно однозначности отображения пространства на плоскость. Рассмотренные проекции являются однозначными, но не взаимно однозначными отображениями, т. е. каждой точке пространства соответствует единственная точка плоскости, но не наоборот. Нетрудно убедиться и в том, что для определения положения точки в пространстве по ее чертежу необходимо иметь две проекции точки, полученные из двух центров или при двух направлениях проектирования. Эта гениально простая мысль и составляет основу начертательной геометрии, заложенную выдающимся французским математиком, активным деятелем Великой французской революции, другом и советником Наполеона Гаспаром Монжем (1746-1818).
Суть метода Монжа можно изложить двумя предложениями, как это сделал член-корреспондент АН СССР Б. Н. Делоне: "Пространственный объект проектируется ортогонально (т. е. перпендикулярами) на плоскость и также проектируется на некоторую другую ей перпендикулярную плоскость, и затем одна из этих плоскостей поворачивается вокруг прямой пересечения этих плоскостей, пока не совместится с другой. В результате на одной и той же плоскости оказываются две различные проекции (вида) рассматриваемого объекта, по которым уже можно, методами Монжа, восстановить размеры, углы и т. д., имеющиеся у данного пространственного объекта в натуре."
Несмотря на то что ортогональные проекции известны человечеству с незапамятных времен (вся живопись Древнего Египта есть не что иное, как ортогональные проекции на плоскость рисунка), простая мысль использовать две ортогональные проекции для получения взаимно однозначного отображения пространства на плоскость пришла Монжу лишь в конце XVIII века. Имея огромное практическое значение в теории фортификации, метод Монжа еще в течение 15 лет оберегался как военная тайна. Простота метода Монжа ошеломила современников. Познакомившись с его идеями, Лагранж, перемежая иронию с восторгом, воскликнул: "До слушания лекции Монжа я не знал, что мне известна начертательная геометрия!"
На рисунке показаны различные типы проекции одного и того же прямоугольного параллелепипеда с отношением сторон 1:2:3. Метод ортогональных проекций Монжа иллюстрирует рисунок а. Заметим, что третья проекция с точки зрения математики является лишней, но ею часто пользуются, чтобы создать более полное представление о пространственном теле. Как отмечалось, при ортогональном проектировании сохраняются истинные размеры контуров тела.
Однако ортогональные проекции не дают целостного впечатления о форме пространственного объекта. Более наглядное представление о форме тела дают аксонометрические проекции[33] — частный вид параллельных проекций, отображающих на плоскость К все точки пространственного объекта вместе с декартовой системой координат, к которой этот объект отнесен. На рисунке б построена аксонометрическая проекция нашего параллелепипеда. Мы видим, что в аксонометрии происходят искажения линейных размеров, различные по разным осям. Согласно основной теореме аксонометрии — теореме Польке, три произвольных отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных отрезков, выходящих из некоторой точки пространства, Следовательно, аксонометрические оси и коэффициенты искажения по ним (отношение длины по аксонометрической оси к истинной длине по соответствующей оси) могут быть выбраны произвольно. (В нашей аксонометрии углы между осями равны 120°, а коэффициенты искажения — 1.)
Наконец, на рисунке в построена центральная проекция нашего параллелепипеда. Сопоставляя все три проекции, мы видим, что перспектива наиболее адекватно, т. е. "похоже", передает видимый нами объект. Это замечательное свойство центральной проекции и снискало ей славу в искусстве живописи, где она получила особое название — перспектива (от лат. perspicio — ясно вижу). Перспективные проекции, являются и наиболее трудными из рассмотренных нами, поэтому остановимся на перспективе более подробно.
Прежде всего заметим, что реально существующий мир и видимый нами мир — не одно и то же. В самом деле, вспомним всем хорошо знакомый пример: рельсы железной дороги кажутся нам сходящимися на горизонте, хотя мы прекрасно знаем, что это не так и ни один машинист, увидев такую картину, не бросится останавливать поезд.
Важнейшие виды проекций: центральные (а), параллельные (б) и ортогональные (в)
Приложение начертательной геометрии к технике выдвинуло требование "обратимости" чертежа, т. е. возможности точного определения пространственной фигуры по плоскому чертежу, или, говоря языком математики, взаимно однозначности отображения пространства на плоскость. Рассмотренные проекции являются однозначными, но не взаимно однозначными отображениями, т. е. каждой точке пространства соответствует единственная точка плоскости, но не наоборот. Нетрудно убедиться и в том, что для определения положения точки в пространстве по ее чертежу необходимо иметь две проекции точки, полученные из двух центров или при двух направлениях проектирования. Эта гениально простая мысль и составляет основу начертательной геометрии, заложенную выдающимся французским математиком, активным деятелем Великой французской революции, другом и советником Наполеона Гаспаром Монжем (1746-1818).
Суть метода Монжа можно изложить двумя предложениями, как это сделал член-корреспондент АН СССР Б. Н. Делоне: "Пространственный объект проектируется ортогонально (т. е. перпендикулярами) на плоскость и также проектируется на некоторую другую ей перпендикулярную плоскость, и затем одна из этих плоскостей поворачивается вокруг прямой пересечения этих плоскостей, пока не совместится с другой. В результате на одной и той же плоскости оказываются две различные проекции (вида) рассматриваемого объекта, по которым уже можно, методами Монжа, восстановить размеры, углы и т. д., имеющиеся у данного пространственного объекта в натуре."
Несмотря на то что ортогональные проекции известны человечеству с незапамятных времен (вся живопись Древнего Египта есть не что иное, как ортогональные проекции на плоскость рисунка), простая мысль использовать две ортогональные проекции для получения взаимно однозначного отображения пространства на плоскость пришла Монжу лишь в конце XVIII века. Имея огромное практическое значение в теории фортификации, метод Монжа еще в течение 15 лет оберегался как военная тайна. Простота метода Монжа ошеломила современников. Познакомившись с его идеями, Лагранж, перемежая иронию с восторгом, воскликнул: "До слушания лекции Монжа я не знал, что мне известна начертательная геометрия!"
На рисунке показаны различные типы проекции одного и того же прямоугольного параллелепипеда с отношением сторон 1:2:3. Метод ортогональных проекций Монжа иллюстрирует рисунок а. Заметим, что третья проекция с точки зрения математики является лишней, но ею часто пользуются, чтобы создать более полное представление о пространственном теле. Как отмечалось, при ортогональном проектировании сохраняются истинные размеры контуров тела.
Однако ортогональные проекции не дают целостного впечатления о форме пространственного объекта. Более наглядное представление о форме тела дают аксонометрические проекции[33] — частный вид параллельных проекций, отображающих на плоскость К все точки пространственного объекта вместе с декартовой системой координат, к которой этот объект отнесен. На рисунке б построена аксонометрическая проекция нашего параллелепипеда. Мы видим, что в аксонометрии происходят искажения линейных размеров, различные по разным осям. Согласно основной теореме аксонометрии — теореме Польке, три произвольных отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельную проекцию трех равных и взаимно перпендикулярных отрезков, выходящих из некоторой точки пространства, Следовательно, аксонометрические оси и коэффициенты искажения по ним (отношение длины по аксонометрической оси к истинной длине по соответствующей оси) могут быть выбраны произвольно. (В нашей аксонометрии углы между осями равны 120°, а коэффициенты искажения — 1.)
Наконец, на рисунке в построена центральная проекция нашего параллелепипеда. Сопоставляя все три проекции, мы видим, что перспектива наиболее адекватно, т. е. "похоже", передает видимый нами объект. Это замечательное свойство центральной проекции и снискало ей славу в искусстве живописи, где она получила особое название — перспектива (от лат. perspicio — ясно вижу). Перспективные проекции, являются и наиболее трудными из рассмотренных нами, поэтому остановимся на перспективе более подробно.
Прежде всего заметим, что реально существующий мир и видимый нами мир — не одно и то же. В самом деле, вспомним всем хорошо знакомый пример: рельсы железной дороги кажутся нам сходящимися на горизонте, хотя мы прекрасно знаем, что это не так и ни один машинист, увидев такую картину, не бросится останавливать поезд.
 Ортогональные (а), аксонометрические (б) и центральные проекции (в) прямоугольного параллелепипеда с отношением сторон 1:2:3
Объяснение этому "парадоксу" было известно еще до нашей эры. В своем сочинении "Оптика" Евклид постулировал, что мы воспринимаем предметы, когда исходящие от них прямолинейные лучи света сходятся в нашем глазу. Таким образом, всю систему лучей зрения можно представить в виде "пирамиды зрения", вершина которой находится в глазу, а основанием служит рассматриваемый объект. В предложении 4 "Оптики" Евклид доказал, что из двух предметов одинакового размера более удаленный, т. е. видимый под меньшим углом зрения, кажется меньшим. Итак, почему дальние предметы кажутся меньшими, было понятно. Оставалось сделать еще один шаг — рассмотреть картину как сечение пирамиды зрения картинной плоскостью. Однако на этот шаг человечеству потребовалось более 1500 лет.
Мучительно долго ожидали идеи Евклида своего часа, и только в XIV веке могучий поток Возрождения подхватил их. Филиппо Брунеллёски (1377-1446), итальянский архитектор и ученый, автор выдающегося инженерного сооружения — грандиозного 42-метрового каменного купола над хором флорентийского собора Санта-Мария дель Фьоре, ставшего символом Флоренции,- сделал оставшийся шаг. Брунеллёски рассек пирамиду зрения Евклида картинной плоскостью и получил на ней центральную проекцию объекта, или перспективу. Перспектива, таким образом, была не просто объективным геометрическим методом построения изображения, но и "физиологическим" методом, т. е. методом, учитывающим закономерности работы человеческого глаза. Именно поэтому перспектива давала изображения, столь замечательно "похожие" на видимую глазом натуру.
Вслед за Брунеллёски поднимается мощная волна работ по перспективе. Титаны Возрождения не замыкаются в геометрических построениях, а воплощают теоретические разработки в своих бессмертных полотнах. Геометрия и живопись идут рука об руку. Вместе с трактатами "О живописи" Леона Баттисты Альберти, "О живописной перспективе" Пьеро делла Франчески[34] (ок. 1420-1492), "Трактатом о перспективе" Леонардо да Винчи, "Руководством к измерению" Альбрехта Дюрера, "Шестью книгами о перспективе" Гвидо Убальди (1545-1607) рождаются и такие памятники перспективе, как "Бичевание Христа" Пьеро делла Франчески, "Тайная вечеря" Леонардо да Винчи, "Обручение Марии" Рафаэля, "Меланхолия" и "Св. Иероним" Дюрера...
Но вернемся к нашему примеру с железной дорогой. Посмотрим, как изобразятся на плоскости картины "рельсы" — прямые, ортогональные плоскости картины, и "шпалы"- равноотстоящие прямые, параллельные этой плоскости. Пусть точка зрения S есть центр проекций, который определяет положение глаза художника; Т — горизонтальная плоскость, на которой лежат изображаемые объекты; К — плоскость картины (К1.Т). Из точки S мы смотрим[35] на "точки закрепления рельс к шпалам" А1, А2, А3, ... и В1, В2, В3,... Точки пересечения лучей зрения SAi и SBi с плоскостью К дают нам изображения (проекции) этих точек а1, а2, а3,... и b1, b2, b3,... на картине К. Очевидно, что точки, лежащие в основании картины, tt — линии пересечения плоскостей К и Т — при проектировании переходят сами в себя, т. е. линейные размеры в основании картины не искажаются.
Ясно, что по мере удаления точек Аi и Bi в бесконечность лучи SAi и SBi становятся все более пологими и все ближе подходят друг к другу (так как угол зрения, под которым мы видим равные отрезки AiBi, уменьшается), пока наконец не сольются, заняв предельное положение SS∞. Можно считать, что луч SS∞ пересекается с обоими "рельсами" (и вообще, с любой прямой, параллельной "рельсам") в бесконечно удаленной точке Sx, которая проектируется в главную точку картины О. Точка О лежит на прямой hh, называемой линией горизонта, которая есть линия пересечения картинной плоскости К и плоскости, проходящей через точку S параллельно плоскости Т. Расстояние SS' = 00' называется высотой точки зрения.
Ортогональные (а), аксонометрические (б) и центральные проекции (в) прямоугольного параллелепипеда с отношением сторон 1:2:3
Объяснение этому "парадоксу" было известно еще до нашей эры. В своем сочинении "Оптика" Евклид постулировал, что мы воспринимаем предметы, когда исходящие от них прямолинейные лучи света сходятся в нашем глазу. Таким образом, всю систему лучей зрения можно представить в виде "пирамиды зрения", вершина которой находится в глазу, а основанием служит рассматриваемый объект. В предложении 4 "Оптики" Евклид доказал, что из двух предметов одинакового размера более удаленный, т. е. видимый под меньшим углом зрения, кажется меньшим. Итак, почему дальние предметы кажутся меньшими, было понятно. Оставалось сделать еще один шаг — рассмотреть картину как сечение пирамиды зрения картинной плоскостью. Однако на этот шаг человечеству потребовалось более 1500 лет.
Мучительно долго ожидали идеи Евклида своего часа, и только в XIV веке могучий поток Возрождения подхватил их. Филиппо Брунеллёски (1377-1446), итальянский архитектор и ученый, автор выдающегося инженерного сооружения — грандиозного 42-метрового каменного купола над хором флорентийского собора Санта-Мария дель Фьоре, ставшего символом Флоренции,- сделал оставшийся шаг. Брунеллёски рассек пирамиду зрения Евклида картинной плоскостью и получил на ней центральную проекцию объекта, или перспективу. Перспектива, таким образом, была не просто объективным геометрическим методом построения изображения, но и "физиологическим" методом, т. е. методом, учитывающим закономерности работы человеческого глаза. Именно поэтому перспектива давала изображения, столь замечательно "похожие" на видимую глазом натуру.
Вслед за Брунеллёски поднимается мощная волна работ по перспективе. Титаны Возрождения не замыкаются в геометрических построениях, а воплощают теоретические разработки в своих бессмертных полотнах. Геометрия и живопись идут рука об руку. Вместе с трактатами "О живописи" Леона Баттисты Альберти, "О живописной перспективе" Пьеро делла Франчески[34] (ок. 1420-1492), "Трактатом о перспективе" Леонардо да Винчи, "Руководством к измерению" Альбрехта Дюрера, "Шестью книгами о перспективе" Гвидо Убальди (1545-1607) рождаются и такие памятники перспективе, как "Бичевание Христа" Пьеро делла Франчески, "Тайная вечеря" Леонардо да Винчи, "Обручение Марии" Рафаэля, "Меланхолия" и "Св. Иероним" Дюрера...
Но вернемся к нашему примеру с железной дорогой. Посмотрим, как изобразятся на плоскости картины "рельсы" — прямые, ортогональные плоскости картины, и "шпалы"- равноотстоящие прямые, параллельные этой плоскости. Пусть точка зрения S есть центр проекций, который определяет положение глаза художника; Т — горизонтальная плоскость, на которой лежат изображаемые объекты; К — плоскость картины (К1.Т). Из точки S мы смотрим[35] на "точки закрепления рельс к шпалам" А1, А2, А3, ... и В1, В2, В3,... Точки пересечения лучей зрения SAi и SBi с плоскостью К дают нам изображения (проекции) этих точек а1, а2, а3,... и b1, b2, b3,... на картине К. Очевидно, что точки, лежащие в основании картины, tt — линии пересечения плоскостей К и Т — при проектировании переходят сами в себя, т. е. линейные размеры в основании картины не искажаются.
Ясно, что по мере удаления точек Аi и Bi в бесконечность лучи SAi и SBi становятся все более пологими и все ближе подходят друг к другу (так как угол зрения, под которым мы видим равные отрезки AiBi, уменьшается), пока наконец не сольются, заняв предельное положение SS∞. Можно считать, что луч SS∞ пересекается с обоими "рельсами" (и вообще, с любой прямой, параллельной "рельсам") в бесконечно удаленной точке Sx, которая проектируется в главную точку картины О. Точка О лежит на прямой hh, называемой линией горизонта, которая есть линия пересечения картинной плоскости К и плоскости, проходящей через точку S параллельно плоскости Т. Расстояние SS' = 00' называется высотой точки зрения.
 Построение перспективного изображения прямых, перпендикулярных и параллельных картинной плоскости
Таким образом, мы приходим к основной теореме теории перспективы: семейство бесконечных параллельных прямых на плоскости Т, не параллельных основанию картины, изображается семейством пересекающихся отрезков на плоскости К, причем точка пересечения этих отрезков — точка схода - лежит на линии горизонта hh. Различным направлениям на плоскости Т соответствуют различные точки схода на линии горизонта. Следовательно, линия горизонта есть геометрическое место точек схода для всевозможных направлений на плоскости Т. Прямые плоскости T, параллельные основанию картины, точки схода не имеют и проектируются на плоскости К в прямые, параллельные основанию картины ("шпалы" на рисунке).
Разумеется, получать проекции точек объекта на картинной плоскости с помощью пространственных построений, как это сделано на рисунке, трудно и неудобно. Поэтому еще архитекторами Возрождения был разработан способ построения перспективы, названный способом архитекторов, позволяющий с помощью точек схода и линии горизонта непосредственно переходить с горизонтальной плоскости Т на плоскость картины К. Для построения точки схода F линии L по способу архитекторов из проекции точки зрения S' проводят линию L' параллельно L до пересечения с основанием картины в точке F'. Точка F' есть проекция точки схода F на основание картины. Восстанавливая из F' перпендикуляр до линии горизонта, находим саму точку схода F. (Доказательство справедливости этого построения очевидно из рисунка, а обоснование остальных построений способа архитекторов мы дадим в конце следующей главы.)
Перспектива открыла перед живописцами небывалые возможности. Впервые у художников появился геометрический метод изображения не отдельного предмета, а всего видимого трехмерного пространства, всего окружающего мира. Невиданные возможности перспективы наиболее ярко раскрывались в изображении интерьера. Вот почему художники Возрождения так любили изображать интерьер (вспомним "Афинскую школу" Рафаэля и "Тайную вечерю" Леонардо да Винчи, см. с. 55 и 308).
В самом деле, полностью изобразить интерьер комнаты, например, в аксонометрии просто невозможно. Для этого нужно считать стены комнаты и ее потолок прозрачными. Можно, конечно, дать ортогональные проекции стен, пола и потолка, но это будет чертеж комнаты. Иное дело — перспектива. Она чудесным образом раскрывает перед нами всю комнату, позволяя увидеть одновременно и ее стены, и пол, и потолок.
На рисунке в способом архитекторов построена перспектива "математической" комнаты в форме куба, имеющей окно, дверь, две балки на потолке и пол, выложенный квадратными плитами. Вынутая стена ABCD комнаты совпадает с плоскостью картины К и передается на ней без искажений (естественно, сохраняются и все размеры на ABCD, такие, как х, у, z и т. д.). Глаз художника расположен напротив центра комнаты, т. е. главная точка картины находится в центре квадрата ABCD. В главной точке картины пересекаются все прямые, перпендикулярные плоскости картины. Для построения перспективы берем план пола комнаты и, проводя из проекции точки зрения S' прямые, параллельные диагоналям пола, находим проекции точек схода F1' и F2' диагоналей. Перенося эти точки на линию горизонта hh, получаем точки схода диагоналей F1 и F2. В этих точках на перспективе пересекаются диагонали пола и параллельные им (на плане) прямые. Дальнейшее построение перспективы пола и стен комнаты, а также горизонтальных границ окна и двери понятно из рисунка.
Разметка вертикальных линий окна точками А2, А3, А4 делается следующим образом. Берем отрезок A1A5, задающий вертикальные линии окна, и его перспективное изображение а1а5. Затем откладываем из точки а1 отрезок A1A5 параллельно линии горизонта и проводим через точки А5 и а5 прямую до пересечения с линией горизонта в точке V. Прямые, проходящие через точку V и точки А1, А2, ... , А5 отрезка A1A5, разделят перспективу этого отрезка а1a5 в том же отношении. Аналогично размечаются вертикальные линии двери. Перспектива нашей "математической" комнаты готова.
Заметим, что проблема правильного построения перспективы "клетчатого" пола долго не давалась художникам Возрождения. Вот почему, решив эту геометрическую задачу, мастера Возрождения так любили изображать квадраты пола на своих полотнах (см. например, "Афинскую школу" и "Обручение Марии" Рафаэля, с. 310). Квадратные плиты были своеобразной координатной сеткой на плоскости пола и придавали глубине картины особую выразительность.
Заканчивая короткое знакомство с геометрическими основами теории перспективы, покажем, как построить перспективу прямоугольного параллелепипеда, расположенного под углом к плоскости картины К. Для простоты будем считать, что переднее ребро параллелепипеда лежит в плоскости картины. Пространственные построения здесь неудобны (см. рисунок в на с. 277), поэтому перспективу параллелепипеда найдем способом архитекторов, используя только основание параллелепипеда — прямоугольник ABCD, лежащий в горизонтальной плоскости Т.
Построение перспективного изображения прямых, перпендикулярных и параллельных картинной плоскости
Таким образом, мы приходим к основной теореме теории перспективы: семейство бесконечных параллельных прямых на плоскости Т, не параллельных основанию картины, изображается семейством пересекающихся отрезков на плоскости К, причем точка пересечения этих отрезков — точка схода - лежит на линии горизонта hh. Различным направлениям на плоскости Т соответствуют различные точки схода на линии горизонта. Следовательно, линия горизонта есть геометрическое место точек схода для всевозможных направлений на плоскости Т. Прямые плоскости T, параллельные основанию картины, точки схода не имеют и проектируются на плоскости К в прямые, параллельные основанию картины ("шпалы" на рисунке).
Разумеется, получать проекции точек объекта на картинной плоскости с помощью пространственных построений, как это сделано на рисунке, трудно и неудобно. Поэтому еще архитекторами Возрождения был разработан способ построения перспективы, названный способом архитекторов, позволяющий с помощью точек схода и линии горизонта непосредственно переходить с горизонтальной плоскости Т на плоскость картины К. Для построения точки схода F линии L по способу архитекторов из проекции точки зрения S' проводят линию L' параллельно L до пересечения с основанием картины в точке F'. Точка F' есть проекция точки схода F на основание картины. Восстанавливая из F' перпендикуляр до линии горизонта, находим саму точку схода F. (Доказательство справедливости этого построения очевидно из рисунка, а обоснование остальных построений способа архитекторов мы дадим в конце следующей главы.)
Перспектива открыла перед живописцами небывалые возможности. Впервые у художников появился геометрический метод изображения не отдельного предмета, а всего видимого трехмерного пространства, всего окружающего мира. Невиданные возможности перспективы наиболее ярко раскрывались в изображении интерьера. Вот почему художники Возрождения так любили изображать интерьер (вспомним "Афинскую школу" Рафаэля и "Тайную вечерю" Леонардо да Винчи, см. с. 55 и 308).
В самом деле, полностью изобразить интерьер комнаты, например, в аксонометрии просто невозможно. Для этого нужно считать стены комнаты и ее потолок прозрачными. Можно, конечно, дать ортогональные проекции стен, пола и потолка, но это будет чертеж комнаты. Иное дело — перспектива. Она чудесным образом раскрывает перед нами всю комнату, позволяя увидеть одновременно и ее стены, и пол, и потолок.
На рисунке в способом архитекторов построена перспектива "математической" комнаты в форме куба, имеющей окно, дверь, две балки на потолке и пол, выложенный квадратными плитами. Вынутая стена ABCD комнаты совпадает с плоскостью картины К и передается на ней без искажений (естественно, сохраняются и все размеры на ABCD, такие, как х, у, z и т. д.). Глаз художника расположен напротив центра комнаты, т. е. главная точка картины находится в центре квадрата ABCD. В главной точке картины пересекаются все прямые, перпендикулярные плоскости картины. Для построения перспективы берем план пола комнаты и, проводя из проекции точки зрения S' прямые, параллельные диагоналям пола, находим проекции точек схода F1' и F2' диагоналей. Перенося эти точки на линию горизонта hh, получаем точки схода диагоналей F1 и F2. В этих точках на перспективе пересекаются диагонали пола и параллельные им (на плане) прямые. Дальнейшее построение перспективы пола и стен комнаты, а также горизонтальных границ окна и двери понятно из рисунка.
Разметка вертикальных линий окна точками А2, А3, А4 делается следующим образом. Берем отрезок A1A5, задающий вертикальные линии окна, и его перспективное изображение а1а5. Затем откладываем из точки а1 отрезок A1A5 параллельно линии горизонта и проводим через точки А5 и а5 прямую до пересечения с линией горизонта в точке V. Прямые, проходящие через точку V и точки А1, А2, ... , А5 отрезка A1A5, разделят перспективу этого отрезка а1a5 в том же отношении. Аналогично размечаются вертикальные линии двери. Перспектива нашей "математической" комнаты готова.
Заметим, что проблема правильного построения перспективы "клетчатого" пола долго не давалась художникам Возрождения. Вот почему, решив эту геометрическую задачу, мастера Возрождения так любили изображать квадраты пола на своих полотнах (см. например, "Афинскую школу" и "Обручение Марии" Рафаэля, с. 310). Квадратные плиты были своеобразной координатной сеткой на плоскости пола и придавали глубине картины особую выразительность.
Заканчивая короткое знакомство с геометрическими основами теории перспективы, покажем, как построить перспективу прямоугольного параллелепипеда, расположенного под углом к плоскости картины К. Для простоты будем считать, что переднее ребро параллелепипеда лежит в плоскости картины. Пространственные построения здесь неудобны (см. рисунок в на с. 277), поэтому перспективу параллелепипеда найдем способом архитекторов, используя только основание параллелепипеда — прямоугольник ABCD, лежащий в горизонтальной плоскости Т.
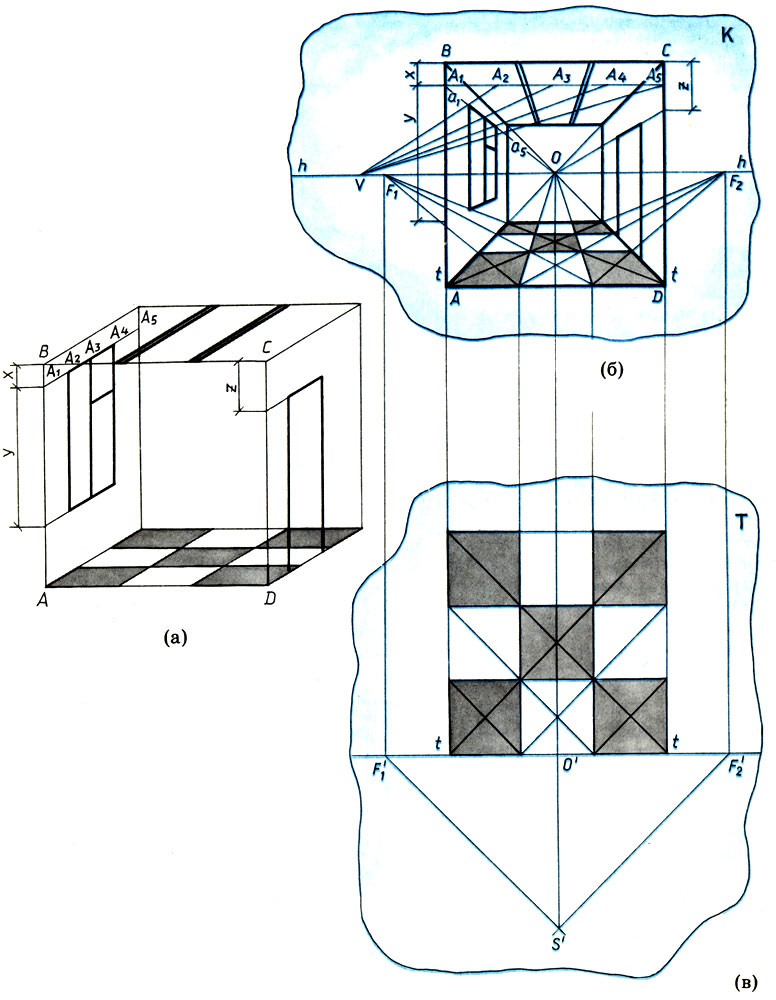 Построение перспективы интерьера комнаты способом архитекторов: (а) — аксонометрия комнаты; (б) — перспектива комнаты; (в) — план пола комнаты и проекция точки зрения
Построение перспективы интерьера комнаты способом архитекторов: (а) — аксонометрия комнаты; (б) — перспектива комнаты; (в) — план пола комнаты и проекция точки зрения
 Прямая (а) и обратная (в) перспективы прямоугольного параллелепипеда, расположенного под углом к картинной плоскости (б)
Прежде всего на плоскости картины К проводим линию основания tt и линию горизонта hh, которая выбирается по усмотрению художника (это высота точки зрения художника). Затем, проводя прямые S'F1' и S'F2' параллельные CD и СВ, строим точки схода F1 и F2 этих линий. Делая построения, понятные из рисунков а, б, получаем перспективу abcd основания ABCD. Далее, восставляя из точек а, b, с, d перпендикуляры и откладывая из точки а высоту параллелепипеда (так как переднее ребро параллелепипеда лежит в плоскости картины, то его размеры в перспективе сохраняются), получаем вершину параллелепипеда а'. Наконец, соединяя точку а' с точками схода F1 и F2, а также соединяя образуемые при этом точки b' и d' с соответствующими точками схода, получаем перспективу всего параллелепипеда.
Вообразим теперь, что, проводя линию горизонта hh, мы ошиблись и она оказалась у нас не выше, а ниже основания картины (рис. в на с. 282). В точности повторяя все предыдущие построения, мы получим обратную перспективу а, b, с, d прямоугольника ABCD.
Вместо привычного в прямой перспективе сокращения видимых размеров предмета по мере удаления его от наблюдателя в обратной перспективе происходит увеличение этих размеров. Заметим, что обратную перспективу a1b1c1d1 прямоугольника ABCD можно увидеть, если посмотреть на прямую перспективу abed этого прямоугольника из-за картины, да еще и "вверх ногами" (в этом легко убедиться, перевернув книгу и посмотрев на abed на свет с другой стороны страницы).
Если далее повторить все те же построения с высотами параллелепипеда, по-прежнему сохраняя его высоту в плоскости картины, то мы получим обратную перспективу всего параллелепипеда. Еще раз обратим внимание на "странность" обратной перспективы: видимые размеры фигуры в обратной перспективе по мере удаления от глаза наблюдателя не сокращаются (как в прямой перспективе), а увеличиваются.
До тех пор пока ваши построения обратной перспективы носили чисто геометрический характер, в них, может быть, и не было бы ничего странного, кроме замеченного расхождения обратной перспективы с нашим зрительным опытом. Но уж совсем удивительным оказывается то, что именно обратная перспектива является геометрической основой древнерусской живописи. Такая странная геометрия живописи Древней Руси до сих пор не дает покоя ее исследователям. Некоторые называют ее просто "ошибочным приемом". Другие связывают "потустороннее" геометрическое происхождение обратной перспективы (вспомните наш взгляд из-за картины) с тем "потусторонним" неземным ирреальным миром, который призвана была изображать древнерусская икона. Наконец, есть и третий, как нам кажется, наиболее реалистичный и научный взгляд на обратную перспективу. Но обо всем этом речь пойдет несколько позже.
Итак, перспектива — это очень просто. Это чистая геометрия. Так что же, овладев геометрией перспективы, каждый может стать художником? К сожалению, нет. Математически точная перспектива — это еще не живопись, а только чертеж, хотя бы и такой прекрасный, как воспроизведенный здесь нами. Перспектива — это только геометрическая основа живописи. Но эта основа мертва, до тех пор пока художник не вложит в нее частичку своей души, не сделает ее живописью. При этом в чем-то можно и поступиться геометрией (что часто и делали художники) во имя жизни самого искусства живописи.
Как мы видели, построение перспективных изображений — дело довольно сложное. Поэтому наряду с разработкой строгих математических основ теории перспективы художники Возрождения старались дать своим собратьям и простые практические методы построения перспективы. Остроумное устройство для построения перспективы описывает А. Дюрер в трактате "Руководство к измерению". На стене закреплена проушина (это "глаз" художника), через которую продет шнур, идущий последовательно от точки к точке предмета (это "луч зрения"). Шнур проходит через раму, которая закрывается дверцей с натянутой на ней бумагой. Рама имеет подвижные нити — горизонтальную и вертикальную, позволяющие фиксировать координаты точки пересечения "луча зрения" с открытой рамой и переносить их на бумагу (для этого шнур убирают, закрывают дверцу с бумагой и отмечают на ней соответствующую точку). Свой метод Дюрер иллюстрирует прекрасной гравюрой, которая, несмотря на свое "техническое" содержание, сама является произведением искусства.
Прямая (а) и обратная (в) перспективы прямоугольного параллелепипеда, расположенного под углом к картинной плоскости (б)
Прежде всего на плоскости картины К проводим линию основания tt и линию горизонта hh, которая выбирается по усмотрению художника (это высота точки зрения художника). Затем, проводя прямые S'F1' и S'F2' параллельные CD и СВ, строим точки схода F1 и F2 этих линий. Делая построения, понятные из рисунков а, б, получаем перспективу abcd основания ABCD. Далее, восставляя из точек а, b, с, d перпендикуляры и откладывая из точки а высоту параллелепипеда (так как переднее ребро параллелепипеда лежит в плоскости картины, то его размеры в перспективе сохраняются), получаем вершину параллелепипеда а'. Наконец, соединяя точку а' с точками схода F1 и F2, а также соединяя образуемые при этом точки b' и d' с соответствующими точками схода, получаем перспективу всего параллелепипеда.
Вообразим теперь, что, проводя линию горизонта hh, мы ошиблись и она оказалась у нас не выше, а ниже основания картины (рис. в на с. 282). В точности повторяя все предыдущие построения, мы получим обратную перспективу а, b, с, d прямоугольника ABCD.
Вместо привычного в прямой перспективе сокращения видимых размеров предмета по мере удаления его от наблюдателя в обратной перспективе происходит увеличение этих размеров. Заметим, что обратную перспективу a1b1c1d1 прямоугольника ABCD можно увидеть, если посмотреть на прямую перспективу abed этого прямоугольника из-за картины, да еще и "вверх ногами" (в этом легко убедиться, перевернув книгу и посмотрев на abed на свет с другой стороны страницы).
Если далее повторить все те же построения с высотами параллелепипеда, по-прежнему сохраняя его высоту в плоскости картины, то мы получим обратную перспективу всего параллелепипеда. Еще раз обратим внимание на "странность" обратной перспективы: видимые размеры фигуры в обратной перспективе по мере удаления от глаза наблюдателя не сокращаются (как в прямой перспективе), а увеличиваются.
До тех пор пока ваши построения обратной перспективы носили чисто геометрический характер, в них, может быть, и не было бы ничего странного, кроме замеченного расхождения обратной перспективы с нашим зрительным опытом. Но уж совсем удивительным оказывается то, что именно обратная перспектива является геометрической основой древнерусской живописи. Такая странная геометрия живописи Древней Руси до сих пор не дает покоя ее исследователям. Некоторые называют ее просто "ошибочным приемом". Другие связывают "потустороннее" геометрическое происхождение обратной перспективы (вспомните наш взгляд из-за картины) с тем "потусторонним" неземным ирреальным миром, который призвана была изображать древнерусская икона. Наконец, есть и третий, как нам кажется, наиболее реалистичный и научный взгляд на обратную перспективу. Но обо всем этом речь пойдет несколько позже.
Итак, перспектива — это очень просто. Это чистая геометрия. Так что же, овладев геометрией перспективы, каждый может стать художником? К сожалению, нет. Математически точная перспектива — это еще не живопись, а только чертеж, хотя бы и такой прекрасный, как воспроизведенный здесь нами. Перспектива — это только геометрическая основа живописи. Но эта основа мертва, до тех пор пока художник не вложит в нее частичку своей души, не сделает ее живописью. При этом в чем-то можно и поступиться геометрией (что часто и делали художники) во имя жизни самого искусства живописи.
Как мы видели, построение перспективных изображений — дело довольно сложное. Поэтому наряду с разработкой строгих математических основ теории перспективы художники Возрождения старались дать своим собратьям и простые практические методы построения перспективы. Остроумное устройство для построения перспективы описывает А. Дюрер в трактате "Руководство к измерению". На стене закреплена проушина (это "глаз" художника), через которую продет шнур, идущий последовательно от точки к точке предмета (это "луч зрения"). Шнур проходит через раму, которая закрывается дверцей с натянутой на ней бумагой. Рама имеет подвижные нити — горизонтальную и вертикальную, позволяющие фиксировать координаты точки пересечения "луча зрения" с открытой рамой и переносить их на бумагу (для этого шнур убирают, закрывают дверцу с бумагой и отмечают на ней соответствующую точку). Свой метод Дюрер иллюстрирует прекрасной гравюрой, которая, несмотря на свое "техническое" содержание, сама является произведением искусства.
 Перспективный чертеж церкви Покрова Богородицы на Нерли — геометрия, переходящая JB искусство
Как происходило дальнейшее развитие теории перспективы? Уже наше короткое знакомство с перспективой убеждает в том, что по перспективному изображению весьма трудно судить об истинных размерах предмета. Желая преодолеть эту трудность, математик и архитектор из Лиона Жерар Дезарг (1593-1662) в работе "Общий метод изображения предметов в перспективе" предложил использовать при построении перспективы метод координат. Изображение предмета предлагалось выполнять совместно с системой координат, относительно которой он ориентирован в пространстве. Метод Дезарга положил начало новому самостоятельному методу изображения, впоследствии названному аксонометрическим.
Дезарг обратил внимание и на другую особенность, возникающую при построении перспективы. Как мы видели, при центральном проектировании прямые, параллельные в горизонтальной плоскости Т, могут переходить в пересекающиеся прямые в картинной плоскости К (см. на с. 281). При этом точка схода параллельных прямых в картинной плоскости (точка О на рисунке) не имеет своего прообраза в плоскости Т. Желая избавиться от тацой особенности, Дезарг предложил дополнить обычную евклидову плоскость (плоскость с конечными точками) бесконечно удаленными точками, названными несобственными точками. Сколько бесконечно удаленных точек следовало ввести на плоскости Т? Очевидно, сколько есть направлений для параллельных прямых, так как естественно считать, что все параллельные друг другу прямые пересекаются в одной бесконечно удаленной точке. Ясно, что таких точек бесконечно много. Совокупность бесконечно удаленных точек на плоскости Т образует бесконечно удаленную прямую, которая на картинной плоскости К переходит в линию горизонта. Плоскость, дополненная бесконечно удаленными точками и бесконечно удаленной прямой, получила название расширенной, или проективной плоскости.
Далее Дезарг предложил стереть различия между собственными и несобственными элементами расширенной плоскости. Это значительно упрощало и обобщало многие рассуждения. В самом деле, в таком случае на расширенной плоскости исчезало само понятие параллельности прямых, так как параллельные прямые можно было считать пересекающимися в бесконечно удаленной точке. Но тогда автоматически устранялась и та особенность центрального проектирования, с которой все и началось: на расширенной плоскости пересекающиеся прямые (в том числе и пересекающиеся в несобственной точке, т. е. параллельные) проектировались в пересекающиеся. Таким образом, на расширенной плоскости центральные проекции дополнялись еще одним инвариантом (см. с. 275) — свойством прямых пересекаться.
Перспективный чертеж церкви Покрова Богородицы на Нерли — геометрия, переходящая JB искусство
Как происходило дальнейшее развитие теории перспективы? Уже наше короткое знакомство с перспективой убеждает в том, что по перспективному изображению весьма трудно судить об истинных размерах предмета. Желая преодолеть эту трудность, математик и архитектор из Лиона Жерар Дезарг (1593-1662) в работе "Общий метод изображения предметов в перспективе" предложил использовать при построении перспективы метод координат. Изображение предмета предлагалось выполнять совместно с системой координат, относительно которой он ориентирован в пространстве. Метод Дезарга положил начало новому самостоятельному методу изображения, впоследствии названному аксонометрическим.
Дезарг обратил внимание и на другую особенность, возникающую при построении перспективы. Как мы видели, при центральном проектировании прямые, параллельные в горизонтальной плоскости Т, могут переходить в пересекающиеся прямые в картинной плоскости К (см. на с. 281). При этом точка схода параллельных прямых в картинной плоскости (точка О на рисунке) не имеет своего прообраза в плоскости Т. Желая избавиться от тацой особенности, Дезарг предложил дополнить обычную евклидову плоскость (плоскость с конечными точками) бесконечно удаленными точками, названными несобственными точками. Сколько бесконечно удаленных точек следовало ввести на плоскости Т? Очевидно, сколько есть направлений для параллельных прямых, так как естественно считать, что все параллельные друг другу прямые пересекаются в одной бесконечно удаленной точке. Ясно, что таких точек бесконечно много. Совокупность бесконечно удаленных точек на плоскости Т образует бесконечно удаленную прямую, которая на картинной плоскости К переходит в линию горизонта. Плоскость, дополненная бесконечно удаленными точками и бесконечно удаленной прямой, получила название расширенной, или проективной плоскости.
Далее Дезарг предложил стереть различия между собственными и несобственными элементами расширенной плоскости. Это значительно упрощало и обобщало многие рассуждения. В самом деле, в таком случае на расширенной плоскости исчезало само понятие параллельности прямых, так как параллельные прямые можно было считать пересекающимися в бесконечно удаленной точке. Но тогда автоматически устранялась и та особенность центрального проектирования, с которой все и началось: на расширенной плоскости пересекающиеся прямые (в том числе и пересекающиеся в несобственной точке, т. е. параллельные) проектировались в пересекающиеся. Таким образом, на расширенной плоскости центральные проекции дополнялись еще одним инвариантом (см. с. 275) — свойством прямых пересекаться.
 Дюрер. Устройство для изображения предметов в перспективе. Гравюра. Ок. 1520
Поведение точек и прямых на расширенной плоскости управлялось лишь двумя аксиомами:
1) две различные точки на расширенной плоскости определяют прямую, и притом только одну, которой они принадлежат;
2) две различные прямые на расширенной плоскости определяют точку, и притом только одну, через которую они проходят.
Нет параллельных прямых! Нет знаменитого пятого постулата Евклида, который 2000 лет не давал покоя математикам! Геометрия расширенной плоскости — это геометрия точек, прямых и пересечений. Любая теорема о конфигурации этих элементов на расширенной плоскости оставалась справедливой и для любой центральной проекции этой конфигурации. Отсюда и пошло название новой геометрии — проективная геометрия.
Так, в недрах искусства живописи родилась новая наука — проективная геометрия — еще одно свидетельство тесных уз между наукой и искусством.
Новые идеи оказались чрезвычайно плодотворными и позволили Дезаргу получить ряд первоклассных результатов, в том числе и знаменитую теорему, носящую его имя. Однако идеи Дезарга опередили его время. Его сочинения отпугивали современников сжатостью изложения и многочисленностью новых обозначений. О Дезарге и его методе просто забыли...
Пути науки неисповедимы. Судьбе угодно было распорядиться так, чтобы ровно через 150 лет после смерти Дезарга его идеи возродил его жесоотечественник. Однако произошло это не в родной Франции, а в далекой России, в глухом провинциальном городе Саратове...
Дюрер. Устройство для изображения предметов в перспективе. Гравюра. Ок. 1520
Поведение точек и прямых на расширенной плоскости управлялось лишь двумя аксиомами:
1) две различные точки на расширенной плоскости определяют прямую, и притом только одну, которой они принадлежат;
2) две различные прямые на расширенной плоскости определяют точку, и притом только одну, через которую они проходят.
Нет параллельных прямых! Нет знаменитого пятого постулата Евклида, который 2000 лет не давал покоя математикам! Геометрия расширенной плоскости — это геометрия точек, прямых и пересечений. Любая теорема о конфигурации этих элементов на расширенной плоскости оставалась справедливой и для любой центральной проекции этой конфигурации. Отсюда и пошло название новой геометрии — проективная геометрия.
Так, в недрах искусства живописи родилась новая наука — проективная геометрия — еще одно свидетельство тесных уз между наукой и искусством.
Новые идеи оказались чрезвычайно плодотворными и позволили Дезаргу получить ряд первоклассных результатов, в том числе и знаменитую теорему, носящую его имя. Однако идеи Дезарга опередили его время. Его сочинения отпугивали современников сжатостью изложения и многочисленностью новых обозначений. О Дезарге и его методе просто забыли...
Пути науки неисповедимы. Судьбе угодно было распорядиться так, чтобы ровно через 150 лет после смерти Дезарга его идеи возродил его жесоотечественник. Однако произошло это не в родной Франции, а в далекой России, в глухом провинциальном городе Саратове...
21. В плену, в Саратове: рождение проективной геометрии
В деревню, к тетке, в глушь, в Саратов! Там будешь горе горевать...1812 год. Ноябрь. Истерзанная Бородинским сражением, испуганная московскими пожарами, измученная отсутствием продовольствия и фуража, "великая армия" Наполеона отступала. Впрочем, не отступала — бежала. Так и не дождавшись ключей от Москвы, не сумев пробиться в южные районы России, император молча скакал по им же разоренной Смоленской дороге. Из-за бескормицы начался падеж лошадей, приходилось бросать артиллерию. Лошади, еще месяц назад оглашавшие ржанием гулкие соборы Московского Кремля, валялись теперь вдоль дороги с раздутыми боками. Непрерывные атаки отрядов атамана Платова и Дениса Давыдова повергали в паническое оцепенение некогда грозную гвардию. Крепчали морозы, и таяла на глазах "великая армия" Наполеона. 3 (15) ноября авангарды генералов М. Милорадовича и Д. Голицына под местечком Красным близ Смоленска внезапно столкнулись с самим Наполеоном. Три дня шли кровопролитные бои, приведшие к разгрому лучших войск Наполеона. Французы потеряли 6 тысяч убитыми и ранеными, 26 тысяч пленными. Армия фактически была брошена императором, голодные и обмороженные солдаты прятались по лесам и далее спасались кто как может. Это была прелюдия к развязке на реке Березине. Среди оставленных умирать на красном снегу под красным был и двадцатитрехлетний сублейтенант инженерных войск Жан Виктор Понселе. К счастью, дозорный отряд казаков заметил, что молодой "французик" еще дышит. Мундир офицера корпуса инженеров спас ему жизнь. Его подобрали и доставили в русский штаб для допроса. Затем последовал мучительный 1000-верстный переход вглубь России. Почти пять месяцев нескончаемые вереницы полураздетых и полуживых военнопленных брели по бескрайним заснеженным равнинам. Морозы были так крепки, что ртуть застывала в термометрах. Люди падали и замерзали, не имея сил подняться. В марте 1813 г. Понселе с оставшимися в живых товарищами по несчастью оказался на берегах Волги, в губернском городе Саратове. Русский народ всегда был велик состраданием. В обмороженных французах сердобольные волжане увидели не бывших врагов, а нынешних страдальцев. Их обогрели, откормили. Яркое апрельское солнце, молодость и жажда жизни победили. Они выжили. Пленных не обременяли работами. Доподлинно известно лишь то, что они разбили прекрасную дубовую аллею у загородного дома саратовского губернатора. Возможно, один из немногих ныне уцелевших дубов был посажен руками Понселе. Со временем те, кто владел ремеслом, открыли лавки; другие подвизались на ниве воспитания: саратовские красавицы не упускали случая взять уроки модных парижских танцев. Жизнь вошла в свое русло. Понселе занялся науками. Книг, разумеется, не было, письменные принадлежности — самые скудные. Поэтому прежде всего он восстановил по памяти все, что знал по математике,- от арифметики до математического анализа и высшей геометрии. Вокруг Понселе собирается кружок единомышленников — таких же, как и он, воспитанников Политехнической школы в Париже либо мечтающих выдержать туда экзамен, если когда-нибудь они снова увидят родную Францию. Занятия математикой скрашивали долгие вечера. Любопытно признание самого Понселе в том, что практически все сложные математические выкладки, которые он изучал, стерлись в его памяти, тогда как общие фундаментальные принципы остались в ней такими же ясными, как и много лет назад. Именно за этими занятиями математикой Понселе и пришел к своему гениальному творению — созданию проективной геометрии. То, что в саратовском плену Понселе вспомнил прежде всего о геометрии, разумеется, не было случайным. Вся французская наука того времени была пронизана духом геометрии. Во главе Политехнической школы, которую Наполеон называл наседкой, несущей ему золотые яйца, стоял отец начертательной геометрии Гаспар Монж. Да и сам император оставил в геометрии несколько теорем, носящих его имя. Саратовский плен оказался недолгим. 25 марта (6 апреля) 1814 г. Наполеон подписал в Фонтебло отречение от престола и был сослан на остров Эльба. А в сентябре того же года пленники вернулись на родину. Понселе возвратился во Францию с семью записными книжками, хранившими его блестящие идеи. Именно "материал семи рукописных записных книжек, написанных в Саратове, в русском плену (с 1813 по 1814 г.), вместе с разными другими записями, старыми и новыми", и составил основу классического труда молодого офицера — "Трактат о проектных свойствах фигур". Первое издание трактата вышло в 1822 г. Второму изданию, вышедшему сорок лет спустя, была предпослана "апология" — описание давних приключений автора, имевших самый счастливый конец[36]. С выходом в свет трактата Понселе проективная геометрия стала самостоятельной наукой. Заслуга Понселе заключалась в выделении проективных свойств фигур (Понселе понимал их как свойства, которые остаются неизменными при любом центральном проектировании фигуры с одной плоскости на другую) в отдельный класс и установлении соответствий между метрическими и проективными свойствами этих фигур. Помимо точек и прямых проективными свойствами oбладают, например, линии второго порядка (окружности, эллипсы, параболы и гиперболы). Понселе были сформулированы также принцип непрерывности и принцип двойственности. Первый принцип позволил рассмотреть всякого рода исключения и особые случаи с более широкой точки зрения (например, параллельность прямых как пересечение их в бесконечно удаленной точке) и дать геометрический аналог мнимым числам в геометрии. С помощью второго принципа стало возможным в два раза увеличивать число теорем проективной геометрии, не прилагая при этом никаких усилий. Истинное значение проективных свойств геометрии было осознано лишь в конце XIХ века, когда немецкий математик Феликс Клейн (1849-1925) доказал, что обычная геометрия Евклида, и "необычная" геометрия Лобачевского могут быть ассмотрены в рамках проективной геометрии. Так было установлено кардинальное значение проективной геометрии по всей геометрии. "Милостивые государи! Между приобретениями, сделанными в области геометрии за последние пятьдесят лет, развитие проективной геометрии занимает свое место". Этими словами в старинном немецком городке Эрлангене в 1872 г. Клейн начал свою знаменитую лекцию, вошедшую в историю математики как Эрлангенская программа". В этой лекции, изменившей взгляд на геометрию в целом, Клейн дал новое определение древней науки: геометрия есть учение об инвариантах той или иной группы преобразований. Выбирая по-разному группу преобразований, можно получать разные геометрии. Заметим, что проективная геометрия лежит в основе теории аэрофотосъемки и находит сегодня важнейшее приложение при обработке снимков из космоса. Рассмотрим основные идеи проективной геометрии. Как отмечалось в конце предыдущей главы, Понселе возродил идею проективной плоскости Дезарга, т. е. плоскости, дополненной бесконечно удаленными точками и бесконечно удаленной прямой. На проективной плоскости стираются различия между параллельными и пересекающимися прямыми, свойство прямых пересекаться становится инвариантным относительно операции проектирования, а поведение точек и прямых определяется двумя аксиомами (см. с. 285). Поскольку метрические свойства геометрических фигур (расстояния и углы) при проектировании не сохраняются (см. с. 275), а проективная геометрия изучает свойства фигур, инвариантные относительно операции проектирования, то метрические свойства в проективной геометрии не рассматриваются. Именно поэтому проективную геометрию называют "геометрией положения" или "геометрией линейки без делений". Разумеется, проективная геометрия развилась не вдруг с появлением трактата Понселе. Известны три важнейшие предтечи проективной геометрии — три теоремы элементарной геометрии, которые не содержат в условиях метрических характеристик. Первая теорема известна с глубокой древности и носит имя александрийского геометра III века Паппа. Теорема Паппа. Пусть l и m — две прямые на плоскости; А, В, С — различные точки прямой l, а А', В', С' — различные точки прямой m. Тогда точки пересечения трех пар накрест лежащих прямых АВ' и А'В, ВС' и В'С, С А' и С'А принадлежат одной прямой. Проективный характер теоремы Паппа очевиден: в ней фигурируют только точки, прямые и их пересечения; поэтому теорема Паппа остается справедлива при любом проективном преобразовании. Через 1200 лет после Паппа шестнадцатилетний юноша Блез Паскаль (1623-1662) опубликовал свое лучшее математическое сочинение "Трактат о конических сечениях". В трактате Паскаль доказал теорему, которую он назвал Hexagramma mysticum (Волшебный шестиугольник) и которую он украсил почти 400 следствиями. Теорему Паскаля можно считать своего рода обобщением теоремы Паппа на случай конических сечений*, которые, как и прямые, обладают проективными свойствами. * (Коническими сечениями (линиями второго порядка) называют эллипс (и его частный вид — окружность), параболу и гиперболу — линии, которые могут быть получены как сечения прямого кругового конуса. В последнем легко убедиться, посветив обычным карманным фонариком (световой конус) на стену. Когда фонарик перпендикулярен стене, мы видим окружность, затем при наклоне фонарика — эллипс. Когда одна из образующих светового конуса станет параллельна стене, мы Увидим параболу и, наконец, при больших углах наклона — гиперболу. Математическое доказательство этих результатов принадлежит выдающемуся античному математику Апполонию из Перги.) Теорема Паскаля. Пусть А, В, С, А', В', С' — шесть точек, принадлежащих некоторому коническому сечению. Тогда точки пересечения трех пар накрест лежащих прямых АВ' и А'В, ВС' и В'С, СА' и С'А принадлежат одной прямой. Существует и другая формулировка теоремы Паскаля, в которой ее связь с теоремой Паппа не столь очевидна: три точки пересечения противоположных сторон шестиугольника, вписанного в коническое сечение, лежат на одной прямой (см. с. 294). Еще раз подчеркнем, что теорема Паскаля справедлива для любого конического сечения (окружности, эллипса, параболы и гиперболы). Более того, при надлежащем определении касательной в точке конического сечения теорема Паскаля будет выполняться в том случае, когда не все из шести точек различны.А. Грибоедов
 Теорема Паппа (а) и теорема Паскаля (б)
Наконец, третья теорема — одна из важнейших теорем проективной геометрии — носит имя Дезарга, который вместе с Понселе разделяет славу создания проективной геометрии.
Теорема Дезарга. Пусть ABC и А'В'С — два треугольника (необязательно лежащие в одной плоскости), такие, что прямые АА', ВВ' и СС', соединяющие соответственные вершины треугольников, сходятся в одной точке S. Тогда точки пересечения соответственных сторон этих треугольников АВ и А'В', ВС и В'С', СА и С'А' лежат на одной прямой. Плоский вариант теоремы Дезарга, как и теоремы Паппа и Паскаля, отнюдь не очевиден, тогда как ее пространственный вариант настолько прозрачен, что просто удивительно, как художники Возрождения, так много занимавшиеся теорией перспективы, не "заметили" его.
Теорема Паппа (а) и теорема Паскаля (б)
Наконец, третья теорема — одна из важнейших теорем проективной геометрии — носит имя Дезарга, который вместе с Понселе разделяет славу создания проективной геометрии.
Теорема Дезарга. Пусть ABC и А'В'С — два треугольника (необязательно лежащие в одной плоскости), такие, что прямые АА', ВВ' и СС', соединяющие соответственные вершины треугольников, сходятся в одной точке S. Тогда точки пересечения соответственных сторон этих треугольников АВ и А'В', ВС и В'С', СА и С'А' лежат на одной прямой. Плоский вариант теоремы Дезарга, как и теоремы Паппа и Паскаля, отнюдь не очевиден, тогда как ее пространственный вариант настолько прозрачен, что просто удивительно, как художники Возрождения, так много занимавшиеся теорией перспективы, не "заметили" его.
 Плоский (а) и пространственный (б) варианты теоремы Дезарга
В самом деле, пусть треугольник ABC лежит в горизонтальной плоскости Т, треугольник А'В'С' есть его изображение на картинной плоскости К и точка S — центр проектирования. Прямые, соединяющие соответственные вершины этих треугольников,- это "лучи зрения", а ΔА'В'С есть сечение "пирамиды зрения" с основанием ABC и вершиной в точке S. Соответственные стороны АВ и А'В' расположены на грани SAB "пирамиды зрения", т. е. лежат в одной плоскости и пересекаются в некоторой точке L. Но точка L одновременно принадлежит прямым АВ и А'В'. Значит, она одновременно принадлежит плоскости Т и плоскости К, т. е. лежит на линии пересечения этих плоскостей — прямой tt. Аналогично доказываем, что и точка пересечения сторон АС и А'С (точка М) и сторон ВС и В'С (точка N) лежат на той же прямой tt. Следовательно, все три точки L, М, N лежат на одной прямой. Пространственная теорема Дезарга доказана.
Для доказательства плоской теоремы Дезарга достаточно ΔА'В'С', лежащий в картинной плоскости К, спроектировать на плоскость Т из двух центров проекции S и S1 определяющих прямую S1 S'. В результате на плоскости Т мы получим два треугольника: ABC и А'В'С. Поскольку прямые S1A" и SA лежат в одной плоскости, то точки А" и А будут лежать на одной прямой S'A — линии пересечения этой плоскости с плоскостью Т (аналогично для точек В" и B, а также С" и С). Следовательно, прямые, соединяющие соответственные вершины треугольников ABC и А"В"С", пересекаются в одной точке S' т. е. удовлетворяют условию теоремы Дезарга. Для каждой из пар треугольников: ΔА'В'С' и ΔАВС, а также ΔА'В'С' и ΔА"В"С" -справедлива пространственная теорема Дезарга. Более того, так как в каждой паре этих треугольников имеется один й тот же ΔА'В'С', то всякий раз все три соответственные стороны этих треугольников будут пересекаться в одной точке. Так мы получим точки L, М и N, лежащее на прямой tt, т. е. придем к плоской теореме Дезарга.
Оба доказательства теоремы Дезарга настолько просты и изящны, что трудно было удержаться от соблазна привести их здесь. Но дело не только в этом. Мы доказали плоскую теорему Дезарга с помощью ее пространственного аналога, т. е. при помощи пространственных построений. Как показал в конце XIX века Д. Гильберт, без выхода из плоскости в пространство вообще невозможно доказать плоскую теорему Дезарга методами проективной геометрии (без привлечения метрических понятий). Следовательно, если задаться целью разрабатывать плоскую проективную геометрию лишь средствами плоскости, не используя пространство, то мы обязаны присоединить теорему Дезарга в качестве новой аксиомы этой плоской геометрии. Затем Гильберт показал, что, исключив "аксиому Дезарга", можно построить новую, так называемую недезар-гову, геометрию на плоскости. Так на протяжении веков раскрывалась чрезвычайно важная роль теоремы Дезарга в проективной геометрии.
Плоский (а) и пространственный (б) варианты теоремы Дезарга
В самом деле, пусть треугольник ABC лежит в горизонтальной плоскости Т, треугольник А'В'С' есть его изображение на картинной плоскости К и точка S — центр проектирования. Прямые, соединяющие соответственные вершины этих треугольников,- это "лучи зрения", а ΔА'В'С есть сечение "пирамиды зрения" с основанием ABC и вершиной в точке S. Соответственные стороны АВ и А'В' расположены на грани SAB "пирамиды зрения", т. е. лежат в одной плоскости и пересекаются в некоторой точке L. Но точка L одновременно принадлежит прямым АВ и А'В'. Значит, она одновременно принадлежит плоскости Т и плоскости К, т. е. лежит на линии пересечения этих плоскостей — прямой tt. Аналогично доказываем, что и точка пересечения сторон АС и А'С (точка М) и сторон ВС и В'С (точка N) лежат на той же прямой tt. Следовательно, все три точки L, М, N лежат на одной прямой. Пространственная теорема Дезарга доказана.
Для доказательства плоской теоремы Дезарга достаточно ΔА'В'С', лежащий в картинной плоскости К, спроектировать на плоскость Т из двух центров проекции S и S1 определяющих прямую S1 S'. В результате на плоскости Т мы получим два треугольника: ABC и А'В'С. Поскольку прямые S1A" и SA лежат в одной плоскости, то точки А" и А будут лежать на одной прямой S'A — линии пересечения этой плоскости с плоскостью Т (аналогично для точек В" и B, а также С" и С). Следовательно, прямые, соединяющие соответственные вершины треугольников ABC и А"В"С", пересекаются в одной точке S' т. е. удовлетворяют условию теоремы Дезарга. Для каждой из пар треугольников: ΔА'В'С' и ΔАВС, а также ΔА'В'С' и ΔА"В"С" -справедлива пространственная теорема Дезарга. Более того, так как в каждой паре этих треугольников имеется один й тот же ΔА'В'С', то всякий раз все три соответственные стороны этих треугольников будут пересекаться в одной точке. Так мы получим точки L, М и N, лежащее на прямой tt, т. е. придем к плоской теореме Дезарга.
Оба доказательства теоремы Дезарга настолько просты и изящны, что трудно было удержаться от соблазна привести их здесь. Но дело не только в этом. Мы доказали плоскую теорему Дезарга с помощью ее пространственного аналога, т. е. при помощи пространственных построений. Как показал в конце XIX века Д. Гильберт, без выхода из плоскости в пространство вообще невозможно доказать плоскую теорему Дезарга методами проективной геометрии (без привлечения метрических понятий). Следовательно, если задаться целью разрабатывать плоскую проективную геометрию лишь средствами плоскости, не используя пространство, то мы обязаны присоединить теорему Дезарга в качестве новой аксиомы этой плоской геометрии. Затем Гильберт показал, что, исключив "аксиому Дезарга", можно построить новую, так называемую недезар-гову, геометрию на плоскости. Так на протяжении веков раскрывалась чрезвычайно важная роль теоремы Дезарга в проективной геометрии.
 К доказательству плоской теоремы Дезарга
Заканчивая краткое знакомство с тремя великими предтечами проективной геометрии, нельзя не отметить и ту глубокую связь между теоремами Паскаля и Дезарга, которая также была раскрыта лишь спустя столетия. Если взять два треугольника, удовлетворяющих условию теоремы Дезарга (такие треугольники называются гомологическими, т. е. сходственными), то всего существует 9 возможных точек пересечения их сторон. Три точки пересечения соответственных сторон, как следует из теоремы Дезарга, лежат на одной прямой. А вот остальные шесть точек пересечения всегда лежат на некотором коническом сечении, т. е. удовлетворяют теореме Паскаля! Заинтересовавшийся читатель может сам построить массу интересных конфигураций с гомологическими треугольниками.
К доказательству плоской теоремы Дезарга
Заканчивая краткое знакомство с тремя великими предтечами проективной геометрии, нельзя не отметить и ту глубокую связь между теоремами Паскаля и Дезарга, которая также была раскрыта лишь спустя столетия. Если взять два треугольника, удовлетворяющих условию теоремы Дезарга (такие треугольники называются гомологическими, т. е. сходственными), то всего существует 9 возможных точек пересечения их сторон. Три точки пересечения соответственных сторон, как следует из теоремы Дезарга, лежат на одной прямой. А вот остальные шесть точек пересечения всегда лежат на некотором коническом сечении, т. е. удовлетворяют теореме Паскаля! Заинтересовавшийся читатель может сам построить массу интересных конфигураций с гомологическими треугольниками.
 Связь между теоремами Паскаля и Дезарга: из 9 возможных точек пересечения гомологических треугольников ABC и А'В'С' 3 точки пересечения сходственных сторон лежат на одной прямой (точки 1, 2, 3), а остальные 6 — на коническом сечении (гиперболе) — точки 4, 5, 6, 7, 8, 9
Наконец, теорема Дезарга является теоретическим фундаментом перспективных построений, о чем мы еще скажем в конце главы.
И снова вернемся к Понселе. Помимо того что Понселе возродил идею проективной плоскости Дезарга и придал "геометрии положения" самостоятельный статус, он обогатил новую науку и новыми идеями, среди которых, как уже отмечалось, были принципы непрерывности и двойственности.
Принцип непрерывности, позволяющий выводить свойства одной фигуры из свойств другой, Понселе сформулировал так: "Если одна фигура получается из другой непрерывным изменением и столь же обща, как и первая, тогда без дальнейших соображений можно отнести свойства, доказанные для первой фигуры, ко второй". Например, ясно, что противоположные стороны правильного шестиугольника, вписанного в окружность, пересекаются в бесконечно удаленных точках, т. е. лежат на одной бесконечно удаленной прямой. Но это есть доказательство простейшего случая теоремы Паскаля! Тогда согласно принципу непрерывности это утверждение должно быть справедливо и для любого шестиугольника, вписанного в коническое сечение, т. е. мы получаем доказательство общей теоремы Паскаля! Итак, сформулировав и доказав теорему проективной геометрии в простейшем частном случае, Понселе автоматически получал ее обобщение для любой проекции, в которой вид первоначальной конфигурации мог измениться до неузнаваемости.
Несмотря на неточную формулировку, в руках Понселе принцип непрерывности дал новые и верные результаты. Однако на пути применения принципа часто возникали подводные камни. Например, легко видеть, что эллипсы или параболы пересекаются на плоскости в четырех точках, тогда как окружности — только в двух. Между тем как конические сечения эти линии должны обладать одинаковыми свойствами. Вводя на плоскости систему координат и следуя принципу непрерывности, Понселе пришел к выводу, что все окружности помимо двух действительных точек пересечения имеют на плоскости еще две точки пересечения, которые являются не только бесконечно удаленными, но и мнимыми (точнее, комплексно-сопряженными). Так в геометрии появились комплексные числа.
Но если принцип непрерывности достаточно сложен и требует поистине математического полета фантазии, то принцип двойственности прост и прозрачен. Рассмотрим, как действует принцип двойственности в планиметрии.
Вспомним основные аксиомы проективной геометрии на плоскости, формулировка которых стала возможной с введением понятия бесконечно удаленных точек (см. с. 285). Принцип двойственности основан на том простом факте, что эти две аксиомы обнаруживают двойственность, т. е. переходят друг в друга, если поменять местами слова точки и прямые (соответственно из соображений литературности языка следует поменять глаголы лежат и проходят, а также предлоги на и через). Если же, говоря о точке, лежащей На прямой, или о прямой, проходящей через точку, ввести более общий термин прямая и точка инцидентны, то последние языковые различия устраняются и аксиомы проективной планиметрии примут наиболее универсальный вид:
А.1. Две различные точки на проективной плоскости определяют прямую, и притом только одну, которой они обе инцидентны.
А.2. Две различные прямые на проективной плоскости определяют точку, и притом только одну, которой они обе инцидентны.
Теперь эти две аксиомы отличаются друг от друга только выделенными словами, т. е. словами точки и прямые, а мы получаем возможность сформулировать сам принцип двойственности: все утверждения проективной планиметрии образуют пары, в которых одно из утверждений пары можно непосредственно получить из другого, взаимозаменив слова точка и прямая.
Понселе не только открыл принцип двойственности, но и применял его до пределов возможного. С легкой руки Понселе стало принято записывать теоремы проективной геометрии в два столбца: в одном столбце пишут доказанную теорему, а в другом — двойственную ей. Разумеется, доказательство двойственной теоремы становится излишним. Таким образом, с открытием Понселе стало возможным удвоить число теорем проективной геометрии, не затратив при этом никакого труда.
В качестве примера двойственных теорем приведем следующую пару. В левом столбце записана известная нам теорема Паскаля, которая сформулирована в удобном для "двойственного перевода" виде. Дополнив наш "словарь двойственных терминов" еще одной парой: точка пересечения двух прямых и прямая, проходящая через две точки,- мы легко получаем в правом столбце теорему, двойственную теореме Паскаля. (В обеих теоремах взаимозаменяемые термины выделены, а выражения, проясняющие смысл, взяты в скобки.)
Если А, B, С, D, Е, F — любые точки конического сечения, то три точки пересечения двух противоположных прямых (сторон вписанного шестиугольника) инцидентны одной прямой. Теорема Паскаля
Если А, В, С, D, Е, F — любые прямые (касательные) к коническому сечению, то три прямые, проходящие через две противоположные точки (вершины описанного шестиугольника), инцидентны одной точке. Теорема Брианшона
Каков же был восторг Понселе, когда в теореме, двойственной теореме Паскаля, он увидел теорему, доказанную в 1806 г. его однокашником, студентом Политехнической школы Шарлем Брианшоном (1785-1864)! Однако в отличие от Брианшона Понселе доказывал эту теорему "автоматически". Это открытие утвердило Понселе в могуществе принципа двойственности.
Связь между теоремами Паскаля и Дезарга: из 9 возможных точек пересечения гомологических треугольников ABC и А'В'С' 3 точки пересечения сходственных сторон лежат на одной прямой (точки 1, 2, 3), а остальные 6 — на коническом сечении (гиперболе) — точки 4, 5, 6, 7, 8, 9
Наконец, теорема Дезарга является теоретическим фундаментом перспективных построений, о чем мы еще скажем в конце главы.
И снова вернемся к Понселе. Помимо того что Понселе возродил идею проективной плоскости Дезарга и придал "геометрии положения" самостоятельный статус, он обогатил новую науку и новыми идеями, среди которых, как уже отмечалось, были принципы непрерывности и двойственности.
Принцип непрерывности, позволяющий выводить свойства одной фигуры из свойств другой, Понселе сформулировал так: "Если одна фигура получается из другой непрерывным изменением и столь же обща, как и первая, тогда без дальнейших соображений можно отнести свойства, доказанные для первой фигуры, ко второй". Например, ясно, что противоположные стороны правильного шестиугольника, вписанного в окружность, пересекаются в бесконечно удаленных точках, т. е. лежат на одной бесконечно удаленной прямой. Но это есть доказательство простейшего случая теоремы Паскаля! Тогда согласно принципу непрерывности это утверждение должно быть справедливо и для любого шестиугольника, вписанного в коническое сечение, т. е. мы получаем доказательство общей теоремы Паскаля! Итак, сформулировав и доказав теорему проективной геометрии в простейшем частном случае, Понселе автоматически получал ее обобщение для любой проекции, в которой вид первоначальной конфигурации мог измениться до неузнаваемости.
Несмотря на неточную формулировку, в руках Понселе принцип непрерывности дал новые и верные результаты. Однако на пути применения принципа часто возникали подводные камни. Например, легко видеть, что эллипсы или параболы пересекаются на плоскости в четырех точках, тогда как окружности — только в двух. Между тем как конические сечения эти линии должны обладать одинаковыми свойствами. Вводя на плоскости систему координат и следуя принципу непрерывности, Понселе пришел к выводу, что все окружности помимо двух действительных точек пересечения имеют на плоскости еще две точки пересечения, которые являются не только бесконечно удаленными, но и мнимыми (точнее, комплексно-сопряженными). Так в геометрии появились комплексные числа.
Но если принцип непрерывности достаточно сложен и требует поистине математического полета фантазии, то принцип двойственности прост и прозрачен. Рассмотрим, как действует принцип двойственности в планиметрии.
Вспомним основные аксиомы проективной геометрии на плоскости, формулировка которых стала возможной с введением понятия бесконечно удаленных точек (см. с. 285). Принцип двойственности основан на том простом факте, что эти две аксиомы обнаруживают двойственность, т. е. переходят друг в друга, если поменять местами слова точки и прямые (соответственно из соображений литературности языка следует поменять глаголы лежат и проходят, а также предлоги на и через). Если же, говоря о точке, лежащей На прямой, или о прямой, проходящей через точку, ввести более общий термин прямая и точка инцидентны, то последние языковые различия устраняются и аксиомы проективной планиметрии примут наиболее универсальный вид:
А.1. Две различные точки на проективной плоскости определяют прямую, и притом только одну, которой они обе инцидентны.
А.2. Две различные прямые на проективной плоскости определяют точку, и притом только одну, которой они обе инцидентны.
Теперь эти две аксиомы отличаются друг от друга только выделенными словами, т. е. словами точки и прямые, а мы получаем возможность сформулировать сам принцип двойственности: все утверждения проективной планиметрии образуют пары, в которых одно из утверждений пары можно непосредственно получить из другого, взаимозаменив слова точка и прямая.
Понселе не только открыл принцип двойственности, но и применял его до пределов возможного. С легкой руки Понселе стало принято записывать теоремы проективной геометрии в два столбца: в одном столбце пишут доказанную теорему, а в другом — двойственную ей. Разумеется, доказательство двойственной теоремы становится излишним. Таким образом, с открытием Понселе стало возможным удвоить число теорем проективной геометрии, не затратив при этом никакого труда.
В качестве примера двойственных теорем приведем следующую пару. В левом столбце записана известная нам теорема Паскаля, которая сформулирована в удобном для "двойственного перевода" виде. Дополнив наш "словарь двойственных терминов" еще одной парой: точка пересечения двух прямых и прямая, проходящая через две точки,- мы легко получаем в правом столбце теорему, двойственную теореме Паскаля. (В обеих теоремах взаимозаменяемые термины выделены, а выражения, проясняющие смысл, взяты в скобки.)
Если А, B, С, D, Е, F — любые точки конического сечения, то три точки пересечения двух противоположных прямых (сторон вписанного шестиугольника) инцидентны одной прямой. Теорема Паскаля
Если А, В, С, D, Е, F — любые прямые (касательные) к коническому сечению, то три прямые, проходящие через две противоположные точки (вершины описанного шестиугольника), инцидентны одной точке. Теорема Брианшона
Каков же был восторг Понселе, когда в теореме, двойственной теореме Паскаля, он увидел теорему, доказанную в 1806 г. его однокашником, студентом Политехнической школы Шарлем Брианшоном (1785-1864)! Однако в отличие от Брианшона Понселе доказывал эту теорему "автоматически". Это открытие утвердило Понселе в могуществе принципа двойственности.
 Принцип двойственности: теорема Паскаля (а) и теорема Брианшона (б)
И в заключение вновь перейдем от математики к искусству. Рождению проективной геометрии во многом способствовали геометрические исследования художников Возрождения. А появившись на свет, проективная геометрия стала теоретическим фундаментом искусства перспективы. Важную роль при построении перспективных изображений играет теорема Дезарга. Мы остановимся на двух приложениях этой теоремы к теории перспективы.
Теорема Дезарга и способ архитекторов. Способ-архитекторов, который мы применили в предыдущей главе для построения перспективы интерьера комнаты и перспективы параллелепипеда (см. с. 282), состоит, по существу, в построении двух точек: точки схода изображаемой линии и точки пересечения этой линии с основанием картины. Зная эти две точки, мы можем построить перспективное изображение данной линии. Метод построения точки схода на перспективе был нами разобран на с. 279, доказательство его справедливости очевидно из рисунка на с. 281. А вот найти точку пересечения образа данной линии с основанием картины позволяет нам теорема Дезарга.
Обратимся для определенности к рисунку на с. 282. Прежде всего заметим, что любую фигуру, состоящую из прямых линий, можно разбить на соответствующее число треугольников. Рассмотрим треугольник ABC на плоскости Т (рис. б) и его перспективное изображение треугольник abc на плоскости К (рис. а). По теореме Дезарга соответственные стороны этих треугольников пересекаются в одной точке на основании картины tt. Именно поэтому в наших построениях мы продолжили сторону ВС до пересечения с линией основания tt в точке М (рис. б), а затем перенесли эту точку ни линию tt в плоскости К. Так мы нашли неизвестную нам точку пересечения образа линии ВС с линией основания tt (точка m на рис. а). Аналогично найдена и точка п. Зная точки пересечения m, a, n и их точки схода Fl и F2, легко построить перспективу прямоугольника ABCD.
Теорема Дезарга и недоступные точки схода. Случается, что при построении перспективного изображения художник, а еще чаще архитектор сталкиваются с такой трудностью: точка схода некоторой линии оказывается за пределами картины (чертежа). Покажем, как теорема Дезарга может помочь в этом случае.
Пусть на плоскости картины К даны две прямые а и b, идущие в недоступную точку схода (в качестве одной из таких прямых чаще всего выступает линия горизонта). Требуется через некоторую точку С∈К провести прямую с в недоступную точку схода. Выберем на плоскости К произвольную точку L и проведем через эту точку три произвольных луча l1, l2, l3. Лучи l1, и l3 пересекут прямые а и b в точках А, В и А', В' соответственно. Через точку С проведем прямые МА и СВ, пересекающие луч l2 в точках М и N. Наконец, проведем прямые МА' и NB' до пересечения в точке С'. Как следует из теоремы Дезарга, прямая с, проходящая через точки С и С', пересекается с прямыми а и b в одной точке, т. е. прямая с и является искомой прямой, идущей в недоступную точку схода.
Принцип двойственности: теорема Паскаля (а) и теорема Брианшона (б)
И в заключение вновь перейдем от математики к искусству. Рождению проективной геометрии во многом способствовали геометрические исследования художников Возрождения. А появившись на свет, проективная геометрия стала теоретическим фундаментом искусства перспективы. Важную роль при построении перспективных изображений играет теорема Дезарга. Мы остановимся на двух приложениях этой теоремы к теории перспективы.
Теорема Дезарга и способ архитекторов. Способ-архитекторов, который мы применили в предыдущей главе для построения перспективы интерьера комнаты и перспективы параллелепипеда (см. с. 282), состоит, по существу, в построении двух точек: точки схода изображаемой линии и точки пересечения этой линии с основанием картины. Зная эти две точки, мы можем построить перспективное изображение данной линии. Метод построения точки схода на перспективе был нами разобран на с. 279, доказательство его справедливости очевидно из рисунка на с. 281. А вот найти точку пересечения образа данной линии с основанием картины позволяет нам теорема Дезарга.
Обратимся для определенности к рисунку на с. 282. Прежде всего заметим, что любую фигуру, состоящую из прямых линий, можно разбить на соответствующее число треугольников. Рассмотрим треугольник ABC на плоскости Т (рис. б) и его перспективное изображение треугольник abc на плоскости К (рис. а). По теореме Дезарга соответственные стороны этих треугольников пересекаются в одной точке на основании картины tt. Именно поэтому в наших построениях мы продолжили сторону ВС до пересечения с линией основания tt в точке М (рис. б), а затем перенесли эту точку ни линию tt в плоскости К. Так мы нашли неизвестную нам точку пересечения образа линии ВС с линией основания tt (точка m на рис. а). Аналогично найдена и точка п. Зная точки пересечения m, a, n и их точки схода Fl и F2, легко построить перспективу прямоугольника ABCD.
Теорема Дезарга и недоступные точки схода. Случается, что при построении перспективного изображения художник, а еще чаще архитектор сталкиваются с такой трудностью: точка схода некоторой линии оказывается за пределами картины (чертежа). Покажем, как теорема Дезарга может помочь в этом случае.
Пусть на плоскости картины К даны две прямые а и b, идущие в недоступную точку схода (в качестве одной из таких прямых чаще всего выступает линия горизонта). Требуется через некоторую точку С∈К провести прямую с в недоступную точку схода. Выберем на плоскости К произвольную точку L и проведем через эту точку три произвольных луча l1, l2, l3. Лучи l1, и l3 пересекут прямые а и b в точках А, В и А', В' соответственно. Через точку С проведем прямые МА и СВ, пересекающие луч l2 в точках М и N. Наконец, проведем прямые МА' и NB' до пересечения в точке С'. Как следует из теоремы Дезарга, прямая с, проходящая через точки С и С', пересекается с прямыми а и b в одной точке, т. е. прямая с и является искомой прямой, идущей в недоступную точку схода.
 Проведение прямой с в недоступную точку схода с помощью теоремы Дезарга
Мы познакомились с геометрическими методами отображения трехмерного пространства на плоскость картины. Методы эти составляют предмет изучения самостоятельной науки — начертательной геометрии, которая в свою очередь стимулировала развитие еще одной ветви математики — проективной геометрии. Но эти же геометрические методы живут полнокровной жизнью и в искусстве живописи. Они помогают художнику разрешать извечный парадокс искусства живописи: заставить зрителя в плоском холсте, покрытом красками, увидеть реальный трехмерный мир, окружающий человека. В разные эпохи эта "вечная" проблема живописи решалась по-разному, в том числе и разными геометрическими методами, в чем легко убедиться, прочитав следующую главу.
Проведение прямой с в недоступную точку схода с помощью теоремы Дезарга
Мы познакомились с геометрическими методами отображения трехмерного пространства на плоскость картины. Методы эти составляют предмет изучения самостоятельной науки — начертательной геометрии, которая в свою очередь стимулировала развитие еще одной ветви математики — проективной геометрии. Но эти же геометрические методы живут полнокровной жизнью и в искусстве живописи. Они помогают художнику разрешать извечный парадокс искусства живописи: заставить зрителя в плоском холсте, покрытом красками, увидеть реальный трехмерный мир, окружающий человека. В разные эпохи эта "вечная" проблема живописи решалась по-разному, в том числе и разными геометрическими методами, в чем легко убедиться, прочитав следующую главу.
22. Геометрия и живопись: страницы истории
И, поистине, живопись — это наука и законная дочь природы, ибо она порождена природой...Геометрия и живопись... Пути науки и искусства переплетались в них на протяжении столетий. Геометрия дарила живописи новые изобразительные возможности, обогащала язык живописи, а живопись эпохи Возрождения стимулировала исследования по геометрии, дала начало проективной геометрии. Сейчас нам предстоит взглянуть на геометрию с неожиданной, быть может, стороны. Мы увидим, что геометрия, будучи могучей ветвью древа математики, является в то же время и тем связующим стержнем, который проходит через всю историю живописи. В самом деле, существуют три принципиальных геометрических метода отображения трехмерного пространства на двумерную плоскость картины: метод ортогональных проекций, аксонометрия и перспектива (см. рис. на с. 277). Перспектива, как явствует из рисунка, может быть прямой или обратной. Все эти принципиальные возможности изображения пространства на плоскости были реализованы в искусстве живописи, причем в разных пластах художественной культуры каждый из этих методов находил свое наиболее полное и чистое выражение. Так, система ортогональных проекций составила геометрическую основу живописи Древнего Египта; аксонометрия (параллельная перспектива) характерна для живописи средневекового Китая и Японии; обратная перспектива — для фресок и икон Византии и Древней Руси; прямая перспектива — это геометрический язык ренессансной живописи, а также станковой и монументальной живописи европейского искусства XVII века и русского искусства XVIII- XIX веков. Итак, ортогональные проекции — аксонометрия — перспектива. Именно по такой схеме шло развитие геометрии живописи. Видимо, простота метода прежде всего определяла его положение в этой схеме. Метод ортогональных проекций как наиболее простой занял в ней первое место. Ортогональные проекции передавали без искажений контуры реальных предметов, а идея метода, как справедливо заметил Леонардо да Винчи (см. с. 274), была подсказана человеку самой природой: тень, отброшенная вечерним солнцем на стену, и была первой картиной, нарисованной этим методом. Однако ортогональные проекции никак не передавали глубину реального пространства, поэтому уже в искусстве Древнего Египта появились робкие ростки аксонометрии. Аксонометрия при надлежащем выборе точки зрения передавала без искажений фронтальную плоскость изображаемого предмета; она давала представление о глубине пространства, хотя и трудно было понять, сколь протяженна эта глубина. Строгий математический взгляд на аксонометрию как центральную проекцию с бесконечно удаленным центром сложился сравнительно недавно, в XVIII веке, в трудах немецкого математика и философа Иоганна Генриха Ламберта (1728- 1777). Однако как нестрогий метод изображения пространства на плоскости аксонометрия, именуемая тогда вольной перспективой, известна давно. Начиная с Птолемея (II в.) и вплоть до XVIII века (до появления начертательной геометрии) планы городов изображались в вольной перспективе, как бы с высоты птичьего полета. (Этот принцип и сегодня широко используется на туристских схемах.) Недостатки аксонометрии в передаче глубины пространства вместе с "вольностями" вольной перспективы были исправлены в ренессансной системе перспективы. Эта система имела единые правила, основанные на математических доказательствах, отчего за ней закрепилось название научной системы перспективы. Ренессансная перспектива — наиболее сложный геометрический метод в живописи. Построенный с учетом геометрических закономерностей зрения (геометрической оптики), он наиболее точно воспроизводил видимый человеком мир. Ренессансная перспектива, как и вся философия эпохи Возрождения, распахнула перед человеком "окно в Природу", беспредельно расширила горизонты человеческого мироощущения. Таким образом, каждый из трех геометрических методов был очередным этапом в развитии искусства живописи, новой ступенью в поисках более точной и совершенной системы передачи зрительных ощущений. Любопытно, что по такой же схеме идет развитие и детского рисунка, хотя многие так и не поднимаются выше ее первой ступени. Психологи много спорят, почему дети начинают рисовать именно с "ортогональных проекций", хотя, как нам кажется, главной причиной тому является простота и естественность метода, который с рождения демонстрирует ребенку само Солнце. Еще раз обратим внимание на то, что человека окружают два геометрических пространства, хотя и похожие, но различные. Одно — это объективное, или реальное, пространство. Другое пространство создается в нашем сознании совместной работой глаза и мозга. Это пространство мы "видим", воспринимаем в нашем сознании, поэтому его называют субъективным, или перцептивным* (вспомним пример с рельсами на с. 279). Таким образом, история развития живописи шла по линии приближения от изображения объективного пространства к пространству видимому, перцептивному. Вершиной на этом пути можно считать рождение системы так называемой перцептивной перспективы, которая интуитивно осознавалась художниками XIX — XX веков и проявлялась на их полотнах в виде всевозможных "отклонений" от ренессансной системы перспективы. Общая теория перспективы, включающая в себя как частные случаи и ренессансную, и перцептивную перспективы, была разработана в наши дни академиком Б. В. Раушенбахом (см. следующую главу). *(От лат. perceptio — восприятие.) Вместе с тем Раушенбахом было показано, что не существует идеальной системы перспективы в изображении перцептивного пространства, как не существует и идеальных (т. е. не дающих метрических искажений) методов отображения трехмерного пространства на двумерную плоскость. "Идеальное" изображение трехмерного пространства (как объективного, так и субъективного) в принципе невозможно, а значит, художник при всем своем желании способен дать на холсте лишь приближенную геометрическую картину внешнего мира. В зависимости от своих задач художник вправе избрать тот или иной геометрический метод, который позволит ему ярче раскрыть задуманный им образ. Поэтому вовсе не обязательно, как это любят делать искусствоведы, упрекать древнеегипетского художника в чрезмерной наивности, детскости его рисунка, японского — в недоработке глубины, древнерусского — в неправильности его перспективы, а ренессансного художника объявлять непререкаемой истиной в живописи, хотя и последнего нередко обвиняют в излишней фотографичности. В каждой геометрической системе живописи есть свои достоинства и свои недостатки: одна система лучше передает объективное пространство, а другая — субъективное. Следовательно, в каждой системе есть и свои выразительные возможности, и "невозможности", что станет более понятным из ближайшего рассмотрения этих систем. 22.1. "Ортогональная" живопись Древнего Египта. Идея незыблемости, вечности абсолютной власти фараона, почитавшегося сыном бога, пронизывала всю философию и весь жизненный уклад древнеегипетского общества. Эта идея не только откристаллизовалась в острых гранях пирамид — апофеозе вечности, но и нашла воплощение в древнеегипетской живописи. Согласно "философии вечности" образы древнеегипетской живописи также должны были вбирать в себя все непреходящее и наиболее устойчивое. Каждый предмет как бы вычленялся художником из окружающего мира, осмыслялась "идея" этого предмета, отбрасывалось все сиюминутное, нехарактерное, и в результате возникал живописный образ, который не зависел ни от места, ни от времени его создания и который сегодня удачно называют "образом-существительным". Образы-существительные слагались в картины-предложения и даже картины-повествования. Живопись Древнего Египта была близка к письменности, и образы-существительные часто перемежались с иероглифами, от которых они отличались лишь степенью детализации, количеством подробностей. Собственно говоря, в древнеегипетской живописи и произошло разделение древнего пиктографического письма[37] на иероглифическую письменность, которая все дальше отходила от изображения реальных объектов и все более приобретала знаковый характер, и живопись, в которой все зримее проступали художественные образы и все более стирались знаковые особенности. Какой же изобразительный прием, какая геометрия лучше всего подходили для создания образа-существительного, для воплощения идеи незыблемости? Таким геометрическим методом является, конечно, метод ортогональных проекций. В самом деле, если изобразить, например, крышку стола в аксонометрии или перспективе, то в зависимости от точки зрения мы будем иметь бесконечное разнообразие параллелограммов (в аксонометрии) или трапеций и даже неправильных четырехугольников (в перспективе). Такое разнообразие изображений, зависящее от точки зрения художника, такой "импрессионизм", без которого современный художник не мыслит своего существования, никак не могли устроить художника древнеегипетского. И он выбирает единственно правильный и единственно возможный в данном случае путь — метод ортогональных проекций. Только в ортогональной проекции форма предмета может быть зафиксирована единственным образом, только ортогональные проекции, как мы знаем, передают без искажений контуры реального предмета.Леонардо да Винчи
 Роспись гробницы Нахта, жреца Амона при фараоне Аменхотепе II. 1420 -1411 до н. э. Фивы. Стенопись древнеегипетских гробниц напоминала развернутый свиток папируса, где священные тексты 'Книги мертвых' перемежались с яркими иллюстрациями. Это была одновременно и научная книга, и художественный альбом. Особой живописностью отличались росписи некрополя фиванской знати, а среди них — гробница Нахта, подлинным украшением которой являются знаменитые музыкантши — высочайший образец изящества и пластики древнеегипетского искусства
Итак, ортогональные проекции позволяли древнеегипетскому художнику сообщать зрителю объективную информацию об окружающем мире. Что касается самой потребности в такой информации, то, во-первых, древнеегипетская живопись еще не совсем отошла от пиктографического письма: ее целью было сообщать о деяниях фараонов, военных походах, удачной охоте, о богах, загробной жизни и т. д.; во-вторых, изображения на стенах гробниц призваны были "служить" усопшему в потустороннем мире. Поэтому, естественно, эти изображения должны были носить объективный характер. Этими особенностями целей живописи Древнего Египта объясняется и выбор ее геометрического средства — метода ортогональных проекций.
Метод ортогональных проекций был в совершенстве разработан живописцами Древнего Египта. Поскольку художник не мог дать все три проекции предмета (все-таки это была живопись, а не чертеж!), он делал одну проекцию с наиболее характерной стороны, в наиболее выгодном ракурсе. Вот почему при изображении животных выбирался вид сбоку, профильное изображение как наиболее информативное. По той же причине человеческая фигура рисовалась в несколько странном ракурсе: голова и ноги давались в профиль (профильное изображение ног позволяло легко передать движение или покой), а грудь и плечи рисовались в фас, повернутыми к зрителю. В то же время убитые враги, лежащие на земле, показывались сверху, т. е. также с наиболее информативной точки зрения.
Роспись гробницы Нахта, жреца Амона при фараоне Аменхотепе II. 1420 -1411 до н. э. Фивы. Стенопись древнеегипетских гробниц напоминала развернутый свиток папируса, где священные тексты 'Книги мертвых' перемежались с яркими иллюстрациями. Это была одновременно и научная книга, и художественный альбом. Особой живописностью отличались росписи некрополя фиванской знати, а среди них — гробница Нахта, подлинным украшением которой являются знаменитые музыкантши — высочайший образец изящества и пластики древнеегипетского искусства
Итак, ортогональные проекции позволяли древнеегипетскому художнику сообщать зрителю объективную информацию об окружающем мире. Что касается самой потребности в такой информации, то, во-первых, древнеегипетская живопись еще не совсем отошла от пиктографического письма: ее целью было сообщать о деяниях фараонов, военных походах, удачной охоте, о богах, загробной жизни и т. д.; во-вторых, изображения на стенах гробниц призваны были "служить" усопшему в потустороннем мире. Поэтому, естественно, эти изображения должны были носить объективный характер. Этими особенностями целей живописи Древнего Египта объясняется и выбор ее геометрического средства — метода ортогональных проекций.
Метод ортогональных проекций был в совершенстве разработан живописцами Древнего Египта. Поскольку художник не мог дать все три проекции предмета (все-таки это была живопись, а не чертеж!), он делал одну проекцию с наиболее характерной стороны, в наиболее выгодном ракурсе. Вот почему при изображении животных выбирался вид сбоку, профильное изображение как наиболее информативное. По той же причине человеческая фигура рисовалась в несколько странном ракурсе: голова и ноги давались в профиль (профильное изображение ног позволяло легко передать движение или покой), а грудь и плечи рисовались в фас, повернутыми к зрителю. В то же время убитые враги, лежащие на земле, показывались сверху, т. е. также с наиболее информативной точки зрения.
 Бог Осирис у пруда с деревьями. Иллюстрация из 'Книги мертвых'. XV в. до н. э
Показ предмета с наиболее выразительной точки зрения не останавливал древнеегипетского художника перед явными с современной точки зрения казусами. Так, на иллюстрации из "Книги Мертвых" художник показывает бога Осириса в характерном профильном изображении с развернутыми к зрителю плечами. Если строго следовать методу ортогональных проекций, то пруд, у которого сидит Осирис, превратился бы в ничего не говорящий зрителю отрезок прямой. Поэтому художник показывает пруд сверху. Однако при такой проекции окружающие пруд деревья стали бы крайне невыразительными, попросту непонятными, и художник поворачивает деревья на прямой угол по каждой из сторон пруда. Таким образом в этом рисунке совмещены, по крайней мере, 6 точек зрения, 6 ортогональных проекций.
Вообще, древнеегипетский живописец творил не столько согласно зрению, сколько согласно умозрению. Умозрение позволяло художнику совмещать в одном рисунке разные точки зрения. Умозрение давало возможность изображать рыб и крокодилов, которых в действительности не видно в воде. Умозрение помогло выработать математическую систему правил в изображении фигуры человека — канон. С математическим содержанием древнеегипетского канона мы достаточно подробно познакомились в главе 19. Канон демонстрировал приобщенность живописца к знанию и власти, был символом посвященности в тайны жрецов, олицетворением подрядка. Поэтому канон древнеегипетским художником почитался как святыня.
Не следует думать, что ограниченная рамками канона и ортогональных проекций древнеегипетская живопись превратилась в безжизненный и бесстрастный чертеж. Напротив, чем жестче рамки канонов, тем большее мастерство требуется художнику, для того чтобы, не выходя за эти рамки, создать истинное произведение искусства. Именно по такому пути и шел древнеегипетский мастер. В качестве примера достаточно привести поразительное по пластике и изысканности рисунка изображение акробатки на кусочке черепка — остраконе.
Бог Осирис у пруда с деревьями. Иллюстрация из 'Книги мертвых'. XV в. до н. э
Показ предмета с наиболее выразительной точки зрения не останавливал древнеегипетского художника перед явными с современной точки зрения казусами. Так, на иллюстрации из "Книги Мертвых" художник показывает бога Осириса в характерном профильном изображении с развернутыми к зрителю плечами. Если строго следовать методу ортогональных проекций, то пруд, у которого сидит Осирис, превратился бы в ничего не говорящий зрителю отрезок прямой. Поэтому художник показывает пруд сверху. Однако при такой проекции окружающие пруд деревья стали бы крайне невыразительными, попросту непонятными, и художник поворачивает деревья на прямой угол по каждой из сторон пруда. Таким образом в этом рисунке совмещены, по крайней мере, 6 точек зрения, 6 ортогональных проекций.
Вообще, древнеегипетский живописец творил не столько согласно зрению, сколько согласно умозрению. Умозрение позволяло художнику совмещать в одном рисунке разные точки зрения. Умозрение давало возможность изображать рыб и крокодилов, которых в действительности не видно в воде. Умозрение помогло выработать математическую систему правил в изображении фигуры человека — канон. С математическим содержанием древнеегипетского канона мы достаточно подробно познакомились в главе 19. Канон демонстрировал приобщенность живописца к знанию и власти, был символом посвященности в тайны жрецов, олицетворением подрядка. Поэтому канон древнеегипетским художником почитался как святыня.
Не следует думать, что ограниченная рамками канона и ортогональных проекций древнеегипетская живопись превратилась в безжизненный и бесстрастный чертеж. Напротив, чем жестче рамки канонов, тем большее мастерство требуется художнику, для того чтобы, не выходя за эти рамки, создать истинное произведение искусства. Именно по такому пути и шел древнеегипетский мастер. В качестве примера достаточно привести поразительное по пластике и изысканности рисунка изображение акробатки на кусочке черепка — остраконе.
 Загрузка египетских кораблей. Рельеф из храма Хатшепсут. XV в. до н. э
Но вот чего не было в древнеегипетской живописи, так это глубины пространства. Созданные методом ортогональных проекций образы Древнего Египта были нарочито двумерными, плоскими, и это, казалось, нимало не смущало их авторов. Проблема изображения трехмерного пространства египтянами не ставилась. Их интересовали выделенные из среды и лишенные индивидуальных черт абстрактные образы-символы, а не то, как они взаимосвязаны между собой. Предмет как таковой подавлял в древнеегипетской живописи пространство, которое по сути и не интересовало художника.
Если же действие и развивалось в древнеегипетской картине, то оно развивалось не в глубину, а параллельно плоскости картины, по строкам. Пример строчной композиции мы находим в первом же приведенном нами рисунке — сцене охоты. Расположенные друг над другом строки следовало понимать как события, происходящие ближе или дальше от наблюдателя, т. е. смещенные по глубине картины. Это опять-таки умозрительный подход к изображаемому миру.
И все-таки, несмотря на хорошо разработанные условные приемы, проблема изображения глубины пространства неизбежно вырастала в древнеегипетской живописи. В ряде случаев художник заслонял одну фигуру другой, показывая тем самым взаимное расположение этих фигур в третьем измерении. Однако такой прием не всегда давал ожидаемые результаты. Например, на изображении фараона Эхнатона и сидящей рядом с ним супруги о существовании последней можно только догадываться по ее правой руке, которая, трепетно обнимая стан фараона, возникает будто бы из ниоткуда, и по ладони левой руки жены фараона, покоящейся в ладони властелина. Конечно, этот рисунок трудно назвать искусством. Это чистая математика, слепое следование методу ортогональных проекций.
Зато на другом рисунке передача глубины пространства древнеегипетскому мастеру явно удалась. Четкий профиль переднего лучника повторен со сдвигом чуть вправо и вверх. В результате возникает острое ощущение глубины пространства, стройная шеренга воинов. Но ведь с точки зрения геометрии живописи мы зДесь имеем не что иное, как фронтальную косоугольную аксонометрию!
Загрузка египетских кораблей. Рельеф из храма Хатшепсут. XV в. до н. э
Но вот чего не было в древнеегипетской живописи, так это глубины пространства. Созданные методом ортогональных проекций образы Древнего Египта были нарочито двумерными, плоскими, и это, казалось, нимало не смущало их авторов. Проблема изображения трехмерного пространства египтянами не ставилась. Их интересовали выделенные из среды и лишенные индивидуальных черт абстрактные образы-символы, а не то, как они взаимосвязаны между собой. Предмет как таковой подавлял в древнеегипетской живописи пространство, которое по сути и не интересовало художника.
Если же действие и развивалось в древнеегипетской картине, то оно развивалось не в глубину, а параллельно плоскости картины, по строкам. Пример строчной композиции мы находим в первом же приведенном нами рисунке — сцене охоты. Расположенные друг над другом строки следовало понимать как события, происходящие ближе или дальше от наблюдателя, т. е. смещенные по глубине картины. Это опять-таки умозрительный подход к изображаемому миру.
И все-таки, несмотря на хорошо разработанные условные приемы, проблема изображения глубины пространства неизбежно вырастала в древнеегипетской живописи. В ряде случаев художник заслонял одну фигуру другой, показывая тем самым взаимное расположение этих фигур в третьем измерении. Однако такой прием не всегда давал ожидаемые результаты. Например, на изображении фараона Эхнатона и сидящей рядом с ним супруги о существовании последней можно только догадываться по ее правой руке, которая, трепетно обнимая стан фараона, возникает будто бы из ниоткуда, и по ладони левой руки жены фараона, покоящейся в ладони властелина. Конечно, этот рисунок трудно назвать искусством. Это чистая математика, слепое следование методу ортогональных проекций.
Зато на другом рисунке передача глубины пространства древнеегипетскому мастеру явно удалась. Четкий профиль переднего лучника повторен со сдвигом чуть вправо и вверх. В результате возникает острое ощущение глубины пространства, стройная шеренга воинов. Но ведь с точки зрения геометрии живописи мы зДесь имеем не что иное, как фронтальную косоугольную аксонометрию!
 Остракон с изображением акробатки, делающей мостик. XII в. до н. э. Остраконы — своеобразные 'листки из альбома' древнеегипетских рисовальщиков — не несли на себе тяжести канонов и отличались свободой и непосредственностью. Акробатка, безусловно, жемчужина этого жанра
Остракон с изображением акробатки, делающей мостик. XII в. до н. э. Остраконы — своеобразные 'листки из альбома' древнеегипетских рисовальщиков — не несли на себе тяжести канонов и отличались свободой и непосредственностью. Акробатка, безусловно, жемчужина этого жанра
 К проблеме передачи глубины пространства в древнеегипетской живописи. Фараон Эхнатон с супругой (а) и лучники (б)
Таким образом, потребность в изображении пространственных отношений между предметами неизбежно приводит к новой геометрической системе в живописи — аксонометрии. Несмотря на то что отдельные ростки аксонометрии встречались уже в живописи Древнего Египта, свое подлинное развитие эта геометрическая система в живописи получила значительно позже.
Что касается живописи Древнего Египта в целом, то лучшая ее оценка, на наш взгляд, дана Б. Раушенбахом: "Среди искусств, взявших за основу изображение геометрии объективного пространства, древнеегипетское является наиболее цельным и законченным".
22.2. "Параллельная" живопись средневекового Китая и Японии. Попытки передать глубину пространства на плоскости картины, согласовать умозрение со зрением, которые мы обнаружили еще в живописи Древнего Египта, привели к образованию новой геометрической системы в живописи — аксонометрии, или параллельной перспективы. Явные признаки параллельной перспективы, точнее, суммы двух идущих навстречу друг другу параллельных перспектив, легко увидеть в живописи Древней Греции. Такая геометрическая система в живописи, именуемая искусствоведами "рыбья кость", имела ось схода и, безусловно, тяготела к линейной перспективе, хотя так и не переросла в нее. Та же "рыбья кость" имела место и взнаменитых помпейских росписях Древнего Рима, именуемых, впрочем, "запоздалым эхом древнегреческой живописи". Рим пал, не успев, а может, и не сумев развить живописную систему греков, и свое законченное развитие аксонометрия нашла много веков спустя на другом конце земли в живописи средневекового Китая и Японии.
В отличие от средневековой Европы искусство Китая не было сковано путами церковных догматов. Здесь мирно сосуществовали и три религиозно-философских учения: конфуцианство, даосизм и буддизм — и два направления искусства: религиозное и светское. Согласно этим учениям, путь познания истины проходил через отрешение от мирской суеты, растворение и духовное очищение в природе. Именно в природе китайские художники, многие из которых были монахами, искали и находили умиротворяющую гармонию. Природу и ее изображение на картине — пейзаж — китайский художник воспринимал как безбрежный океан, как непостижимый космос, в котором растворена созерцающая его личность художника-философа.
Поистине удивительно, как точно этой философии созерцания была найдена соответствующая геометрия живописи! Ведь аксонометрия, как мы знаем, есть центральная проекция с бесконечно удаленным центром проектирования. Таким образом, именно в этой геометрической системе точка зрения художника отодвигалась в бесконечность, художник растворялся в безграничных пространствах природы и бесстрастно взирал на ее мудрое спокойствие. В силу своей геометрии (параллельные линии остаются параллельными) аксонометрия не знает ни угла зрения, ни точек схода, ни линии горизонта. Горизонт как бы все время ускользает от наблюдателя, поднимаясь вверх и растворяясь там. Взгляд из бесконечности, кажется, может и бесконечно простираться за пределы картины. Картина не выглядит ограниченной рамой и будто в любой момент готова беспредельно разойтись, волшебным образом превратившись в изображенную на ней природу и поглотив своего бесконечно далекого наблюдателя.
Конечно, увидеть параллельную перспективу китайской живописи лучше всего не на примере горного пейзажа, где беспорядочно громоздятся бесформенные скалы, а в бытовых картинах, где упорядочение стоят оформленные творения рук человеческих, скажем, параллелепипеды домов. Аксонометрия здесь очевидна. Но очевидно также и то, что и сцены человеческой жизни видятся китайскому художнику очень издалека, "с высоты птичьего полета", откуда трудно различить заботы и тревоги отдельных людей, а видно лишь общее копошение человеческого муравейника.
Аксонометрия, как нам известно, имеет три координаты. Если оси координат выбрать так, чтобы по двум осям иметь фронтальную ортогональную проекцию (без искажения), то по третьей координате обязательно будут искажения. Это фронтальная косоугольная аксонометрия, в которой, как правило, и творили китайские мастера. Поскольку коэффициент искажения по третьей координате неизвестен (в лучшем случае он был известен только автору!), то судить о протяженности глубины по первым двум координатам (ширине и высоте) затруднительно, т. е. протяженность по глубине оказывается неопределенной. Эта неопределенность глубины в аксонометрии усиливается параллельностью "глубинных" линий, которые не сближаются по мере удаления от наблюдателя. Таким образом, в "параллельной" живописи возникают два противоположных начала: глубинное и плоское. Картина будто бы имеет глубинное начало, но это просто плоские срезы перемещаются по третьей координате (глубине) без всяких метрических сокращений.
К проблеме передачи глубины пространства в древнеегипетской живописи. Фараон Эхнатон с супругой (а) и лучники (б)
Таким образом, потребность в изображении пространственных отношений между предметами неизбежно приводит к новой геометрической системе в живописи — аксонометрии. Несмотря на то что отдельные ростки аксонометрии встречались уже в живописи Древнего Египта, свое подлинное развитие эта геометрическая система в живописи получила значительно позже.
Что касается живописи Древнего Египта в целом, то лучшая ее оценка, на наш взгляд, дана Б. Раушенбахом: "Среди искусств, взявших за основу изображение геометрии объективного пространства, древнеегипетское является наиболее цельным и законченным".
22.2. "Параллельная" живопись средневекового Китая и Японии. Попытки передать глубину пространства на плоскости картины, согласовать умозрение со зрением, которые мы обнаружили еще в живописи Древнего Египта, привели к образованию новой геометрической системы в живописи — аксонометрии, или параллельной перспективы. Явные признаки параллельной перспективы, точнее, суммы двух идущих навстречу друг другу параллельных перспектив, легко увидеть в живописи Древней Греции. Такая геометрическая система в живописи, именуемая искусствоведами "рыбья кость", имела ось схода и, безусловно, тяготела к линейной перспективе, хотя так и не переросла в нее. Та же "рыбья кость" имела место и взнаменитых помпейских росписях Древнего Рима, именуемых, впрочем, "запоздалым эхом древнегреческой живописи". Рим пал, не успев, а может, и не сумев развить живописную систему греков, и свое законченное развитие аксонометрия нашла много веков спустя на другом конце земли в живописи средневекового Китая и Японии.
В отличие от средневековой Европы искусство Китая не было сковано путами церковных догматов. Здесь мирно сосуществовали и три религиозно-философских учения: конфуцианство, даосизм и буддизм — и два направления искусства: религиозное и светское. Согласно этим учениям, путь познания истины проходил через отрешение от мирской суеты, растворение и духовное очищение в природе. Именно в природе китайские художники, многие из которых были монахами, искали и находили умиротворяющую гармонию. Природу и ее изображение на картине — пейзаж — китайский художник воспринимал как безбрежный океан, как непостижимый космос, в котором растворена созерцающая его личность художника-философа.
Поистине удивительно, как точно этой философии созерцания была найдена соответствующая геометрия живописи! Ведь аксонометрия, как мы знаем, есть центральная проекция с бесконечно удаленным центром проектирования. Таким образом, именно в этой геометрической системе точка зрения художника отодвигалась в бесконечность, художник растворялся в безграничных пространствах природы и бесстрастно взирал на ее мудрое спокойствие. В силу своей геометрии (параллельные линии остаются параллельными) аксонометрия не знает ни угла зрения, ни точек схода, ни линии горизонта. Горизонт как бы все время ускользает от наблюдателя, поднимаясь вверх и растворяясь там. Взгляд из бесконечности, кажется, может и бесконечно простираться за пределы картины. Картина не выглядит ограниченной рамой и будто в любой момент готова беспредельно разойтись, волшебным образом превратившись в изображенную на ней природу и поглотив своего бесконечно далекого наблюдателя.
Конечно, увидеть параллельную перспективу китайской живописи лучше всего не на примере горного пейзажа, где беспорядочно громоздятся бесформенные скалы, а в бытовых картинах, где упорядочение стоят оформленные творения рук человеческих, скажем, параллелепипеды домов. Аксонометрия здесь очевидна. Но очевидно также и то, что и сцены человеческой жизни видятся китайскому художнику очень издалека, "с высоты птичьего полета", откуда трудно различить заботы и тревоги отдельных людей, а видно лишь общее копошение человеческого муравейника.
Аксонометрия, как нам известно, имеет три координаты. Если оси координат выбрать так, чтобы по двум осям иметь фронтальную ортогональную проекцию (без искажения), то по третьей координате обязательно будут искажения. Это фронтальная косоугольная аксонометрия, в которой, как правило, и творили китайские мастера. Поскольку коэффициент искажения по третьей координате неизвестен (в лучшем случае он был известен только автору!), то судить о протяженности глубины по первым двум координатам (ширине и высоте) затруднительно, т. е. протяженность по глубине оказывается неопределенной. Эта неопределенность глубины в аксонометрии усиливается параллельностью "глубинных" линий, которые не сближаются по мере удаления от наблюдателя. Таким образом, в "параллельной" живописи возникают два противоположных начала: глубинное и плоское. Картина будто бы имеет глубинное начало, но это просто плоские срезы перемещаются по третьей координате (глубине) без всяких метрических сокращений.
 Ли Чжао-дао (?). Путники в горах. Фрагмент свитка на шелку. Конец VII — начало VIII в.
Ли Чжао-дао (?). Путники в горах. Фрагмент свитка на шелку. Конец VII — начало VIII в.

 Чжан Цзе-Дуань. Вверх по реке на праздник весны. Фрагмент свитка XII в.
Китайские живописцы умело пользовались противоречием глубинного и плоского начал. По сути дела аксонометрия явилась своеобразным компромиссом между философией "отдельного", плоского (живопись Древнего Египта) и "целого", глубинного (живопись Возрождения). Плоское начало в китайской живописи сдвинулось в пространство, однако оно еще не стало пространством. Но китайский художник и не ставил целью создать иллюзию пространства, он не рисовал с натуры, он только пристально вглядывался в нее и переосмысливал природу в свою философскую систему. Плоское, "похожее" начало шло от наблюдателя природы, а глубинное, "непохожее" начало, которое никогда не уменьшалось и никогда не достигало предела — линии горизонта, выражало философскую идею бесконечности мира и миросозерцания.
Вообще, диалектика двух противоборствующих начал была стержнем всей древнекитайской философии. Вспомним символы Ин-Ян, с которых началась эта книга. Живопись Китая, будучи частью его философии, не могла пройти мимо этих двух начал. Ян для китайского живописца — это светлые, чистые места на картине, это горы, омытые дождями или покрытые чистым снегом, гордо парящие в неприступной вышине. Ин — вместилище темного, тонированного, это темная вода, низина, куда стекаются все нечистоты. Вот почему многие пейзажи выполнены китайскими мастерами в черно-белой технике, в которой они достигли непревзойденного мастерства и проникновения.
Часто говорят о принципиальной асимметрии китайской и японской живописи. У этой асимметрии есть свои геометрические корни: отсутствие линии горизонта и центральной точки схода, а значит, и фиксированного центра композиции приводит к асимметричности всей композиции. Есть и философские предпосылки: человек китайскими философами мыслился частью природы, а не центром мироздания, человек растворялся в природе, а не располагал ее вокруг собственного "я", ставшего центром симметрии в ренессансных композициях.
Но вместе с тем есть в китайской живописи и своя удивительная симметрия. Это не симметрия "левого-правого", а симметрия глубины. Поскольку размеры по глубине в аксонометрии не сокращаются, то дальний план уравновешивает в ней план передний. Дальние горы, подернутые туманом, видны в аксонометрии так же "близко", как и предметы переднего плана. Поэтому у дальних предметов "хватает сил" уравновесить передние. Симметрия "дальнего-близкого" господствует в китайской живописи, придает ей мудрое спокойствие и умиротворение.
Заметим, что аксонометрия является не только условным геометрическим приемом живописи, отвечающим определенной философии. Как показал Б. Раушенбах, аксонометрия является совершенно законным вариантом перцептивной ("видимой") перспективы, применимым для изображения очень далеких или очень близких и не слишком протяженных предметов. Первый случай и реализуется в китайских пейзажах. Благодаря второму аксонометрия нашла широкое применение в начертательной геометрии для изображения небольших деталей, приборов и т. п. Одновременно для передачи архитектурного пространства (т. е. не слишком близких и весьма протяженных объектов) в той же начертательной геометрии пользуются ренессансной перспективой.
И в заключение скажем несколько слов о живописи средневековой Японии.
Чжан Цзе-Дуань. Вверх по реке на праздник весны. Фрагмент свитка XII в.
Китайские живописцы умело пользовались противоречием глубинного и плоского начал. По сути дела аксонометрия явилась своеобразным компромиссом между философией "отдельного", плоского (живопись Древнего Египта) и "целого", глубинного (живопись Возрождения). Плоское начало в китайской живописи сдвинулось в пространство, однако оно еще не стало пространством. Но китайский художник и не ставил целью создать иллюзию пространства, он не рисовал с натуры, он только пристально вглядывался в нее и переосмысливал природу в свою философскую систему. Плоское, "похожее" начало шло от наблюдателя природы, а глубинное, "непохожее" начало, которое никогда не уменьшалось и никогда не достигало предела — линии горизонта, выражало философскую идею бесконечности мира и миросозерцания.
Вообще, диалектика двух противоборствующих начал была стержнем всей древнекитайской философии. Вспомним символы Ин-Ян, с которых началась эта книга. Живопись Китая, будучи частью его философии, не могла пройти мимо этих двух начал. Ян для китайского живописца — это светлые, чистые места на картине, это горы, омытые дождями или покрытые чистым снегом, гордо парящие в неприступной вышине. Ин — вместилище темного, тонированного, это темная вода, низина, куда стекаются все нечистоты. Вот почему многие пейзажи выполнены китайскими мастерами в черно-белой технике, в которой они достигли непревзойденного мастерства и проникновения.
Часто говорят о принципиальной асимметрии китайской и японской живописи. У этой асимметрии есть свои геометрические корни: отсутствие линии горизонта и центральной точки схода, а значит, и фиксированного центра композиции приводит к асимметричности всей композиции. Есть и философские предпосылки: человек китайскими философами мыслился частью природы, а не центром мироздания, человек растворялся в природе, а не располагал ее вокруг собственного "я", ставшего центром симметрии в ренессансных композициях.
Но вместе с тем есть в китайской живописи и своя удивительная симметрия. Это не симметрия "левого-правого", а симметрия глубины. Поскольку размеры по глубине в аксонометрии не сокращаются, то дальний план уравновешивает в ней план передний. Дальние горы, подернутые туманом, видны в аксонометрии так же "близко", как и предметы переднего плана. Поэтому у дальних предметов "хватает сил" уравновесить передние. Симметрия "дальнего-близкого" господствует в китайской живописи, придает ей мудрое спокойствие и умиротворение.
Заметим, что аксонометрия является не только условным геометрическим приемом живописи, отвечающим определенной философии. Как показал Б. Раушенбах, аксонометрия является совершенно законным вариантом перцептивной ("видимой") перспективы, применимым для изображения очень далеких или очень близких и не слишком протяженных предметов. Первый случай и реализуется в китайских пейзажах. Благодаря второму аксонометрия нашла широкое применение в начертательной геометрии для изображения небольших деталей, приборов и т. п. Одновременно для передачи архитектурного пространства (т. е. не слишком близких и весьма протяженных объектов) в той же начертательной геометрии пользуются ренессансной перспективой.
И в заключение скажем несколько слов о живописи средневековой Японии.
 Чен-Тао. Горный пейзаж. XVI-XVII вв.
Духовная культура этой страны (философия, эстетика, религия) выросла на почве более древней китайской культуры. Также и японское искусство впитало в себя сложившиеся в Китае художественные системы и методы. Отгороженная от всего мира морями, лишь единственный раз, в XIII веке, подвергшаяся неудачной попытке завоевания, Япония вплоть до наших дней сохранила свою обособленную и потому своеобычную культуру. Обособленность и характерный для Востока неторопливый темп общественного развития привели к тому, что вплоть до XIX века в Японии сохранились феодальные отношения.
Чен-Тао. Горный пейзаж. XVI-XVII вв.
Духовная культура этой страны (философия, эстетика, религия) выросла на почве более древней китайской культуры. Также и японское искусство впитало в себя сложившиеся в Китае художественные системы и методы. Отгороженная от всего мира морями, лишь единственный раз, в XIII веке, подвергшаяся неудачной попытке завоевания, Япония вплоть до наших дней сохранила свою обособленную и потому своеобычную культуру. Обособленность и характерный для Востока неторопливый темп общественного развития привели к тому, что вплоть до XIX века в Японии сохранились феодальные отношения.
 Хокусай. Водопад Амида. Цветная ксилография. 1820-1832
На протяжении всей своей истории японская живопись, как и вся японская культура, не знала крутых переломов. Творчество Кацусика Хокусая (1760- 1849) считается естественным итогом всего долгого пути японского средневекового искусства. Жизнь Хокусая будто повторила историю средневекового искусства Японии: лишь после 50 лет обрел художник собственную манеру и стиль, а свои знаменитые серии "36 видов Фудзи", "Мосты", "Большие цветы", "Путешествие по водопадам" создал уже 70-летним старцем. Эти серии Хокусая — высший взлет творчества мастера, а само творчество Хокусая — вершина в развитии искусства старой Японии.
Излишне говорить, что геометрической основой японской живописи была та же параллельная перспектива. Даже Хокусая, творивший в XIX веке, через 400 лет после Леонардо да Винчи и Дюрера строго следует правилам параллельной перспективы! Так, на гравюре Хокусая "Водопад Амида", построенной по всем канонам "взгляда из бесконечности", помимо "ускользающего горизонта" мы видим и три параллелограмма ковров, показанных строго аксонометрически.
Творчество Хокусая явилось не только итогом развития искусства средневековой Японии, но и высочайшей вершиной геометрии параллельных в живописи.
22.3. Линейная перспектива Возрождения. Ветер Возрождения распахнул пыльные окна мастерских средневековых художников и впервые заставил их посмотреть на изумительный вид, открывающийся из окна.
Хокусай. Водопад Амида. Цветная ксилография. 1820-1832
На протяжении всей своей истории японская живопись, как и вся японская культура, не знала крутых переломов. Творчество Кацусика Хокусая (1760- 1849) считается естественным итогом всего долгого пути японского средневекового искусства. Жизнь Хокусая будто повторила историю средневекового искусства Японии: лишь после 50 лет обрел художник собственную манеру и стиль, а свои знаменитые серии "36 видов Фудзи", "Мосты", "Большие цветы", "Путешествие по водопадам" создал уже 70-летним старцем. Эти серии Хокусая — высший взлет творчества мастера, а само творчество Хокусая — вершина в развитии искусства старой Японии.
Излишне говорить, что геометрической основой японской живописи была та же параллельная перспектива. Даже Хокусая, творивший в XIX веке, через 400 лет после Леонардо да Винчи и Дюрера строго следует правилам параллельной перспективы! Так, на гравюре Хокусая "Водопад Амида", построенной по всем канонам "взгляда из бесконечности", помимо "ускользающего горизонта" мы видим и три параллелограмма ковров, показанных строго аксонометрически.
Творчество Хокусая явилось не только итогом развития искусства средневековой Японии, но и высочайшей вершиной геометрии параллельных в живописи.
22.3. Линейная перспектива Возрождения. Ветер Возрождения распахнул пыльные окна мастерских средневековых художников и впервые заставил их посмотреть на изумительный вид, открывающийся из окна.
(В. Брюсов)
 Леонардо да Винчи. Тайная вечеря. Фреска. 1495-1497
Леонардо да Винчи. Тайная вечеря. Фреска. 1495-1497
 Перспективный анализ 'Тайной вечери'
Двенадцать апостолов расположены вокруг своего учителя четырьмя группами: по две группы с каждой стороны от него и по три человека в каждой группе. Две ближние к Христу группы компактны и более динамичны: они словно вписаны в два треугольника, обрамляющих треугольник центральной фигуры. Две крайние группы показаны более спокойно и широко: они образуют статичные фигуры — четырехугольники. Наконец, две крайние фигуры, завершающие композицию, нарисованы в профиль и прямо: они как бы останавливают волны движения, идущие от центра к краям. Вся композиция строго симметрична и строго уравновешена относительно вертикальной оси, проходящей через ее главную точку.
Такова геометрия "Тайной вечери". Она очень проста и крайне строга, что наполняет фреску сдержанной внутренней динамикой. "Тайная вечеря" — это и наука, и искусство, которые для Леонардо были слиты в живописи воедино.
Наука и искусство, словно нити холста, переплетались в полотнах мастеров Возрождения. Живопись переходила в начертательную геометрию, а геометрия — в искусство. Пространство картины было не только симметрично, но и метрично. Всякий раз художник старался не просто показать глубину пространства кабины, но как бы вычислить эту глубину. Вот почему ренессансные художники так любили изображать квадраты плиток пола и кессоны (квадратные углубления) потолка, представляющие собой не то что иное, как систему координат на плоскости "ширина-глубина", анфилады комнат, ряды колонн или ковров (в "Тайной вечере"). Вот почему живописцы Возрождения так любили изображать архитектуру, которая органически перерастала в архитектонику изображения.
Все перечисленные приемы нетрудно найти в творчестве любого ренессансного мастера. Вот, к примеру, картина Рафаэля "Обручение Марии". Та же вертикальная симметрия композиции, те же квадраты плит пола, тот же архитектурный пейзаж, та же гармония частей и целого. Добавим к этому, что линия горизонта, проходящая через середину дверного проема ротонды, делит вертикаль картины точно в отношении золотого сечения. Таким образом, картина Рафаэля — не только результат вдохновенного порыва художника, но и плод его скрупулезных вычислений и геометрических построений.
Вернемся еще раз к "Меланхолии" Дюрера (см. с. 42) и посмотрим теперь на нее взором, умудренным знанием теории перспективы. Помимо высочайших художественных достоинств этот шедевр великого мастера Возрождения является и своеобразным учебником по перспективе, учебником геометрии живописи. В самом деле, на гравюре решена сложная геометрическая задача построения перспективы додекаэдра, решению которой много сил отдал Пьеро делла Франческа. Рядом показана перспектива круглого жернова, который изображается в виде эллипса. Перекладины лестницы параллельны линии горизонта, поскольку лестница прислонена к плоскости, параллельной плоскости картины. А вот и чистая математика "Меланхолии": в правом верхнем углу гравюры изображен магический квадрат — квадрат, составленный из первых чисел натурального ряда, сумма которых по любой строке, столбцу или диагонали одна и та же. Любопытно, что из 880 магических квадратов размером 4x4 выбран тот, у которого средние числа в последней строке изображают 1514 — год создания гравюры. Заметим, наконец, что шар на гравюре изображен в виде шара, хотя по правилам перспективы его следовало бы изобразить в виде эллипсоида. Здесь проявляют себя закономерности работы не только глаза, но и мозга при восприятии формы (законы "константности формы"), которые стали известны только в XX веке (см. с. 317), но которые и в начале XVI века угадывались гением Дюрера.
Итак, вместе с новой геометрией в живопись Возрождения пришло и новое художественное мышление. Ренессансная перспектива — это революция в искусстве! Это окно, распахнутое в окружающий человека мир. Как пишет Л. Мочалов в книге "Пространство мира и пространство картины", "перед европейскими художниками как бы открылось богатейшее "месторождение", новая золотоносная жила, которую они разрабатывали во множестве ее ответвлений почти на протяжении пятисот лет".
В живописи Высокого Возрождения XVI века нашел отражение пробуждающийся интерес к науке, который вскоре, в веке XVII, привел к рождению нового естествознания в трудах Галилея, Ньютона и Лейбница.
На протяжении почти 500 лет линейная перспектива считалась непререкаемым авторитетом в живописи. Такой "рекламе" линейная перспектива была обязана прежде всего математике. Именно благодаря тому что линейная перспектива основана на строгих единых геометрических правилах, она и казалась единственно возможной, единственно правильной и непогрешимой.
Перспективный анализ 'Тайной вечери'
Двенадцать апостолов расположены вокруг своего учителя четырьмя группами: по две группы с каждой стороны от него и по три человека в каждой группе. Две ближние к Христу группы компактны и более динамичны: они словно вписаны в два треугольника, обрамляющих треугольник центральной фигуры. Две крайние группы показаны более спокойно и широко: они образуют статичные фигуры — четырехугольники. Наконец, две крайние фигуры, завершающие композицию, нарисованы в профиль и прямо: они как бы останавливают волны движения, идущие от центра к краям. Вся композиция строго симметрична и строго уравновешена относительно вертикальной оси, проходящей через ее главную точку.
Такова геометрия "Тайной вечери". Она очень проста и крайне строга, что наполняет фреску сдержанной внутренней динамикой. "Тайная вечеря" — это и наука, и искусство, которые для Леонардо были слиты в живописи воедино.
Наука и искусство, словно нити холста, переплетались в полотнах мастеров Возрождения. Живопись переходила в начертательную геометрию, а геометрия — в искусство. Пространство картины было не только симметрично, но и метрично. Всякий раз художник старался не просто показать глубину пространства кабины, но как бы вычислить эту глубину. Вот почему ренессансные художники так любили изображать квадраты плиток пола и кессоны (квадратные углубления) потолка, представляющие собой не то что иное, как систему координат на плоскости "ширина-глубина", анфилады комнат, ряды колонн или ковров (в "Тайной вечере"). Вот почему живописцы Возрождения так любили изображать архитектуру, которая органически перерастала в архитектонику изображения.
Все перечисленные приемы нетрудно найти в творчестве любого ренессансного мастера. Вот, к примеру, картина Рафаэля "Обручение Марии". Та же вертикальная симметрия композиции, те же квадраты плит пола, тот же архитектурный пейзаж, та же гармония частей и целого. Добавим к этому, что линия горизонта, проходящая через середину дверного проема ротонды, делит вертикаль картины точно в отношении золотого сечения. Таким образом, картина Рафаэля — не только результат вдохновенного порыва художника, но и плод его скрупулезных вычислений и геометрических построений.
Вернемся еще раз к "Меланхолии" Дюрера (см. с. 42) и посмотрим теперь на нее взором, умудренным знанием теории перспективы. Помимо высочайших художественных достоинств этот шедевр великого мастера Возрождения является и своеобразным учебником по перспективе, учебником геометрии живописи. В самом деле, на гравюре решена сложная геометрическая задача построения перспективы додекаэдра, решению которой много сил отдал Пьеро делла Франческа. Рядом показана перспектива круглого жернова, который изображается в виде эллипса. Перекладины лестницы параллельны линии горизонта, поскольку лестница прислонена к плоскости, параллельной плоскости картины. А вот и чистая математика "Меланхолии": в правом верхнем углу гравюры изображен магический квадрат — квадрат, составленный из первых чисел натурального ряда, сумма которых по любой строке, столбцу или диагонали одна и та же. Любопытно, что из 880 магических квадратов размером 4x4 выбран тот, у которого средние числа в последней строке изображают 1514 — год создания гравюры. Заметим, наконец, что шар на гравюре изображен в виде шара, хотя по правилам перспективы его следовало бы изобразить в виде эллипсоида. Здесь проявляют себя закономерности работы не только глаза, но и мозга при восприятии формы (законы "константности формы"), которые стали известны только в XX веке (см. с. 317), но которые и в начале XVI века угадывались гением Дюрера.
Итак, вместе с новой геометрией в живопись Возрождения пришло и новое художественное мышление. Ренессансная перспектива — это революция в искусстве! Это окно, распахнутое в окружающий человека мир. Как пишет Л. Мочалов в книге "Пространство мира и пространство картины", "перед европейскими художниками как бы открылось богатейшее "месторождение", новая золотоносная жила, которую они разрабатывали во множестве ее ответвлений почти на протяжении пятисот лет".
В живописи Высокого Возрождения XVI века нашел отражение пробуждающийся интерес к науке, который вскоре, в веке XVII, привел к рождению нового естествознания в трудах Галилея, Ньютона и Лейбница.
На протяжении почти 500 лет линейная перспектива считалась непререкаемым авторитетом в живописи. Такой "рекламе" линейная перспектива была обязана прежде всего математике. Именно благодаря тому что линейная перспектива основана на строгих единых геометрических правилах, она и казалась единственно возможной, единственно правильной и непогрешимой.
 Рафаэль. Обручение Марии. 1504. Рафаэль обладал удивительным даром композиции. Мастерство, с которым он соединял элементы композиции в единое художественное целое, архитектоника его живописных произведений, острое чувство симметрии, пропорции, золотого сечения, ритма — все эти качества рафаэлевского гения не имеют себе равных
Рафаэль. Обручение Марии. 1504. Рафаэль обладал удивительным даром композиции. Мастерство, с которым он соединял элементы композиции в единое художественное целое, архитектоника его живописных произведений, острое чувство симметрии, пропорции, золотого сечения, ритма — все эти качества рафаэлевского гения не имеют себе равных
 Математический анализ 'Обручения Марии'
Но существовала и другая система перспективы, не столь громкая, не так хорошо научно разработанная и далеко не единогласно признанная. Однако право на жизнь этой системы перспективы отнюдь не должно перечеркиваться лишь фактом существования ренессансной системы перспективы. Об этой системе, которую до недавнего времени чаще всего называли "неправильной" или даже "извращенной", и пойдет речь далее.
22.4. Обратная перспектива живописи Древней Руси. У древнерусской живописи трагическая судьба. Дело в том, что олифа, которой для лучшей сохранности покрывали живопись, со временем темнела и по прошествии ста лет превращалась в черную непроницаемую пелену. Такие "черные доски" ждало два исхода: либо от них избавлялись — пускали плыть по реке, сжигали, выносили на чердаки и колокольни, либо их "подновляли" — звали новых иконописцев, и они по едва просвечивающим контурам, а более по собственному наитию и разумению заново писали. В любом случае старая живопись безвозвратно уходила.
Так было до конца прошлого века, когда кто-то как-то случайно под одним черным слоем обнаружил другой, потом третий и даже четвертый и пятый, пока вдруг из глубины веков не вспыхнули на иконе пронзительно-звонкие древние краски. Это было потрясающее открытие, вызволившее из небытия целую эпоху в культуре русского народа. Появились первые крупные коллекционеры: И. С. Остроухов, Н. П. Лихачев, А. В. Морозов, С. П. Рябушинский, В. М. Васнецов...
Математический анализ 'Обручения Марии'
Но существовала и другая система перспективы, не столь громкая, не так хорошо научно разработанная и далеко не единогласно признанная. Однако право на жизнь этой системы перспективы отнюдь не должно перечеркиваться лишь фактом существования ренессансной системы перспективы. Об этой системе, которую до недавнего времени чаще всего называли "неправильной" или даже "извращенной", и пойдет речь далее.
22.4. Обратная перспектива живописи Древней Руси. У древнерусской живописи трагическая судьба. Дело в том, что олифа, которой для лучшей сохранности покрывали живопись, со временем темнела и по прошествии ста лет превращалась в черную непроницаемую пелену. Такие "черные доски" ждало два исхода: либо от них избавлялись — пускали плыть по реке, сжигали, выносили на чердаки и колокольни, либо их "подновляли" — звали новых иконописцев, и они по едва просвечивающим контурам, а более по собственному наитию и разумению заново писали. В любом случае старая живопись безвозвратно уходила.
Так было до конца прошлого века, когда кто-то как-то случайно под одним черным слоем обнаружил другой, потом третий и даже четвертый и пятый, пока вдруг из глубины веков не вспыхнули на иконе пронзительно-звонкие древние краски. Это было потрясающее открытие, вызволившее из небытия целую эпоху в культуре русского народа. Появились первые крупные коллекционеры: И. С. Остроухов, Н. П. Лихачев, А. В. Морозов, С. П. Рябушинский, В. М. Васнецов...
 Андрей Рублев. Троица. Начало XV в. Икона из Троицкого собора Троице-Сергиева монастыря
Андрей Рублев. Троица. Начало XV в. Икона из Троицкого собора Троице-Сергиева монастыря
"Нас умиляет, поражает и почти обжигает в произведении Рублева вовсе не сюжет, не число "три" ... а то, что он воистину передал нам узренное им откровение. Среди мятущихся обстоятельств времени, среди раздоров, междоусобных распрей, всеобщего одичания и татарских набегов, среди этого глубокого безмирия, растлившего Русь, открылся духовному взору бесконечный, невозмутимый, нерушимый мир, "свышний мир" горнего мира... Вот этот-то неизъяснимый мир... эту ничему в мире не равную лазурь — более небесную, чем само земное небо, да, эту воистину пренебесную лазурь, несказанную мечту протосковавшего о ней Лермонтова, эту невыразимую грацию взаимных склонений, эту пре-мирную тишину безглагольности, эту бесконечную друг перед другом покорность — мы считаем творческим содержанием Троицы."Об этом счастливом для древнерусской живописи времени вспоминает советский живописец и искусствовед, действительный член Академии наук и Академии художеств И. Э. Грабарь (1871 — 1960): "По северу разъезжали офени (бродячие торговцы.- А. В.), выменивая у попов и церковных старост старые иконы на новые "благолепные". Древние иконы обыкновенно валялись на колокольнях и в рухлядных, выброшенные туда за ветхостью... Офени привозили иконы возами во Мстеру, где их поджидали перекупщики-иконники, а иногда и прямо в Москву, также к перекупщикам..." Но чудом открытая древнерусская живопись чуть было вновь не погибла в руках воинствующих иконоборцев. К счастью, этого не случилось. Собранная в лучших музеях древнерусская живопись радует сегодня чистотою своих красок и нравственных идеалов. Но вместе с радостью древнерусская живопись преподнесла и немало загадок, в том числе и загадок чисто геометрических. Воспитанные на ренессансной перспективе искусствоведы поспешили назвать ее "неправильной", "наивной", "примитивной". Это было продолжение трагедии живописи Древней Руси. Вот, к примеру, прославленная "Троица" Андрея Рублева — шедевр древнерусской живописи. Сотни статей написаны об этом совершенном творении великого мастера, о его величавом и мудром спокойствии, о его нежных красках, созвучных краскам русской природы: цвету поспевающей ржи и цветущего льна. Однако вопрос о геометрии пространства иконы либо обходят молчанием, либо глубокомысленно называют его "абстрактным пространством" или "пространством сердца" (о том, что прячется за этими фразами не говорится ни слова).П. Флоренский
 Дионисий. Митрополит Алексий в житии. Начало XVI в. Икона из Успенского собора Московского Кремля
А вопрос этот и в самом деле не простой! Приглядимся внимательнее. Подножие правого ангела показано в аксонометрии, в то время как подножие левого — в слабой обратной перспективе. Но даже если бы и левое подножие было дано в аксонометрии, то легко видеть, что показаны они с разных точек зрения: на правого ангела мы смотрим слева, а на левого — справа. Далее нетрудно обнаружить, что край правого табурета, не параллелен соответствующему краю правого подножия, а край левого табурета и края левого подножия не имеют общей точки схода. Следовательно, ни аксонометрия правой части иконы, ни обратная перспектива левой части строго не выдержаны. Наконец, легко представить, как ведут себя края стола, закрытые коленями ангелов. Следуя логике построения левой и правой частей иконы, им ничего не остается, как расходиться.
Но может быть, все эти геометрические несоответствия есть исключения из правил, причуды гения? Отнюдь. Даже беглого знакомства с древнерусской живописью достаточно, чтобы убедиться в обратном: это система, названная системой обратной перспективы. Обратимся еще только к двум примерам.
Рассмотрим икону Дионисия "Митрополит Алексий в житии". Обрамляющие фигуру митрополита картинки-клейма повествуют о жизни ("житии") Алексия. Нетрудно заметить, что гроб, изображенный на нижних клеймах, дан в сильной обратной перспективе. В среднем нижнем клейме в обратной перспективе показан стол. Строения в правом (или левом) нижнем клейме показаны в аксонометрии, но с двух точек зрения: правые — при виде слева, а левые — справа. Наконец, прямоугольный параллелепипед Евангелия, которое держит Алексий, также показан в сильной обратной перспективе: обрезы параллельных торцовых ребер Евангелия на иконе расходятся и его задняя обложка получается больше передней.
И в качестве последнего примера возьмем византийскую икону XII века "Григорий Чудотворец", на который мы также видим параллелепипед Евангелия в сильной обратной перспективе. Последний пример взят нами не случайно. Известно, что искусство Древней Руси уходит свои ми корнями в искусство Византии. Следовательно, истоки обратной перспективы лежат в византийской живописи, что очевидно из сравнения последних двух икон и времени их создания. Таким образом, как это ни парадоксально, обратная перспектива, будучи внешне полным антиподом перспективы прямой, была тем не менее непосредственной предшественницей системы прямой перспективы.
Но как объяснить появление в Византии столь странной системы? Ведь обратная перспектива явно выпадает из общего направления развития геометрии живописи (ортогональные проекции — параллельная перспектива — прямая перспектива), идущего от изображения реального пространства к изображению пространства видимого. Вопрос этот во многом остается открытым, хотя, разумеется, какие-то соображения по нему имеются.
Прежде всего заметим, что ни византийские, ни древнерусские живописцы никогда строго не выдерживали системы обратной перспективы. Применяя формулу "как мера и красота скажет" к обратной перспективе, древнерусский мастер явно отдавал предпочтение второму слагаемому. Иное дело — мастер Возрождения, который свято соблюдал правила "меры" линейной перспективы*. Такая геометрическая непоследовательность древнерусского мастера во многом способствовала несерьезному отношению к самой системе обратной перспективы. Как это часто бывает с непонятными явлениями, от нее спешили отмахнуться, спешили назвать ее "ошибочной" или "ложной". Конечно, понять противоречивую геометрию изображения трудно. Л. Мочалов, пытающийся понять обратную перспективу, пишет: "Если бы мы попробовали вступить в мир иконы, построенный по законам обратной перспективы, то ежеминутно рисковали бы поломать себе ноги..." Здесь автор не совсем точен: если бы мир обратной перспективы на иконе был последовательно выдержан, то, двигаясь по законам этого мира, мы смогли бы безбоязненно в нем перемещаться. Но в том-то и беда, что в геометрии обратной перспективы было допущено много ошибок, что и дало повод поспешно назвать всю систему обратной перспективы "ошибочной".
* (Конечно, исключения из правил были и здесь. Например, "Афинская школа". Ра фаэля (с. 55) написана с двух точек зрения: перспектива пола показана с верхней точки зрения, а своды и верхняя часть фрески — с нижней. Верхняя точка зрения для пола дала возможность показать на первом и втором планах всех действующих лиц, а нижняя — подчеркнуть величественность интерьера. Таким образом, здесь также перспективная "мера" была принесена в жертву "красоте". Заметим, что в картине Веронезе "Брак в Кане", одном из самых больших полотен в истории мировой живописи (666 X 990 см), специалисты насчитывают семь точек зрения и пять линий горизонта. )
Дионисий. Митрополит Алексий в житии. Начало XVI в. Икона из Успенского собора Московского Кремля
А вопрос этот и в самом деле не простой! Приглядимся внимательнее. Подножие правого ангела показано в аксонометрии, в то время как подножие левого — в слабой обратной перспективе. Но даже если бы и левое подножие было дано в аксонометрии, то легко видеть, что показаны они с разных точек зрения: на правого ангела мы смотрим слева, а на левого — справа. Далее нетрудно обнаружить, что край правого табурета, не параллелен соответствующему краю правого подножия, а край левого табурета и края левого подножия не имеют общей точки схода. Следовательно, ни аксонометрия правой части иконы, ни обратная перспектива левой части строго не выдержаны. Наконец, легко представить, как ведут себя края стола, закрытые коленями ангелов. Следуя логике построения левой и правой частей иконы, им ничего не остается, как расходиться.
Но может быть, все эти геометрические несоответствия есть исключения из правил, причуды гения? Отнюдь. Даже беглого знакомства с древнерусской живописью достаточно, чтобы убедиться в обратном: это система, названная системой обратной перспективы. Обратимся еще только к двум примерам.
Рассмотрим икону Дионисия "Митрополит Алексий в житии". Обрамляющие фигуру митрополита картинки-клейма повествуют о жизни ("житии") Алексия. Нетрудно заметить, что гроб, изображенный на нижних клеймах, дан в сильной обратной перспективе. В среднем нижнем клейме в обратной перспективе показан стол. Строения в правом (или левом) нижнем клейме показаны в аксонометрии, но с двух точек зрения: правые — при виде слева, а левые — справа. Наконец, прямоугольный параллелепипед Евангелия, которое держит Алексий, также показан в сильной обратной перспективе: обрезы параллельных торцовых ребер Евангелия на иконе расходятся и его задняя обложка получается больше передней.
И в качестве последнего примера возьмем византийскую икону XII века "Григорий Чудотворец", на который мы также видим параллелепипед Евангелия в сильной обратной перспективе. Последний пример взят нами не случайно. Известно, что искусство Древней Руси уходит свои ми корнями в искусство Византии. Следовательно, истоки обратной перспективы лежат в византийской живописи, что очевидно из сравнения последних двух икон и времени их создания. Таким образом, как это ни парадоксально, обратная перспектива, будучи внешне полным антиподом перспективы прямой, была тем не менее непосредственной предшественницей системы прямой перспективы.
Но как объяснить появление в Византии столь странной системы? Ведь обратная перспектива явно выпадает из общего направления развития геометрии живописи (ортогональные проекции — параллельная перспектива — прямая перспектива), идущего от изображения реального пространства к изображению пространства видимого. Вопрос этот во многом остается открытым, хотя, разумеется, какие-то соображения по нему имеются.
Прежде всего заметим, что ни византийские, ни древнерусские живописцы никогда строго не выдерживали системы обратной перспективы. Применяя формулу "как мера и красота скажет" к обратной перспективе, древнерусский мастер явно отдавал предпочтение второму слагаемому. Иное дело — мастер Возрождения, который свято соблюдал правила "меры" линейной перспективы*. Такая геометрическая непоследовательность древнерусского мастера во многом способствовала несерьезному отношению к самой системе обратной перспективы. Как это часто бывает с непонятными явлениями, от нее спешили отмахнуться, спешили назвать ее "ошибочной" или "ложной". Конечно, понять противоречивую геометрию изображения трудно. Л. Мочалов, пытающийся понять обратную перспективу, пишет: "Если бы мы попробовали вступить в мир иконы, построенный по законам обратной перспективы, то ежеминутно рисковали бы поломать себе ноги..." Здесь автор не совсем точен: если бы мир обратной перспективы на иконе был последовательно выдержан, то, двигаясь по законам этого мира, мы смогли бы безбоязненно в нем перемещаться. Но в том-то и беда, что в геометрии обратной перспективы было допущено много ошибок, что и дало повод поспешно назвать всю систему обратной перспективы "ошибочной".
* (Конечно, исключения из правил были и здесь. Например, "Афинская школа". Ра фаэля (с. 55) написана с двух точек зрения: перспектива пола показана с верхней точки зрения, а своды и верхняя часть фрески — с нижней. Верхняя точка зрения для пола дала возможность показать на первом и втором планах всех действующих лиц, а нижняя — подчеркнуть величественность интерьера. Таким образом, здесь также перспективная "мера" была принесена в жертву "красоте". Заметим, что в картине Веронезе "Брак в Кане", одном из самых больших полотен в истории мировой живописи (666 X 990 см), специалисты насчитывают семь точек зрения и пять линий горизонта. )
 М. Нестеров. Философы. 1917. Портрет П. А. Флоренского слева) и С. Н. Булгакова. Спокойствие летнего вечера подчеркивает в картине напряженную работу ума двух мыслителей. Явно укрупненный задний план картины, возможно, является данью Нестерова канонам обратной перспективы, столь горячо почитаемым Флоренским. В год создания портрета судьба обоих философов круто переменилась: первый был сослан в лагеря, второй — 'философским пароходом' выслан из России. Счастье, что сегодня своими многотомными сочинениями оба философа возвращаются на Родину
М. Нестеров. Философы. 1917. Портрет П. А. Флоренского слева) и С. Н. Булгакова. Спокойствие летнего вечера подчеркивает в картине напряженную работу ума двух мыслителей. Явно укрупненный задний план картины, возможно, является данью Нестерова канонам обратной перспективы, столь горячо почитаемым Флоренским. В год создания портрета судьба обоих философов круто переменилась: первый был сослан в лагеря, второй — 'философским пароходом' выслан из России. Счастье, что сегодня своими многотомными сочинениями оба философа возвращаются на Родину
 Григорий Чудотворец. Византийская икона. XII в.
А понять обратную перспективу, конечно, можно. Пожалуй, первой из таких попыток была замечательная работа математика, физика, искусствоведа, писателя и философа П. А. Флоренского (1882 — 1937?) "Обратная перспектива", написанная в 1919 г., но увидевшая свет лишь полвека спустя*. Главной задачей автора было сломать укоренившееся убеждение в том, что линейная перспектива является единственно возможной и непогрешимой. В полемическом задоре, сравнивая две системы перспективы — обратную и прямую, Флоренский, пожалуй, увлекается, называя первую систему "созерцательно-творческой", а вторую "хищнически-механической". Но Флоренский прав в том, что две системы перспективы — обратная и прямая — это "два отношения к жизни — внутреннее и внешнее... два типа культуры".
* (Имя Павла Александровича Флоренского и его энциклопедическое наследие лишь сегодня возвращаются к нам. Окончив физико-математический факультет Московского университета и Московскую духовную академию, Флоренский в своих работах значительное внимание уделял философии культуры, взаимосвязи материального и духовного, целостному мировосприятию. Усилиями Флоренского были сохранены сокровища Троице-Сергиевой лавры, ставшие основой ныне всемирно известного Загорского музея-заповедника. В 1933 г. Флоренский был репрессирован, сослан в Соловецкий лагерь, в 1937 г. вторично осужден, и дальнейшие сведения о его жизни неизвестны.)
И все-таки, как объяснить обратную перспективу? Чем вызвано расхождение параллельных линий в обратной перспективе? Есть два подхода к этому вопросу. В первом корни обратной перспективы ищутся в идейных задачах, которые она решала. Икона призвана была убедить верующего в реальности ирреального, она должна была "отстранить" молящегося от грешной земли. Поэтому, как считают сторонники философско-богословских взглядов на истоки обратной перспективы, изображение на иконе не должно было в точности походить на видимый человеком мир. Икона должна была походить и не походить на видимый мир. Именно так она и могла заставить верующего поверить в чудо, которое также есть одновременно реальное и сверхъестественное. Мир иконы не мог быть отображением мира реального; поэтому и появляются расходящиеся параллели обратной перспективы, которые дают некую "потустороннюю", "сверхъестественную" точку зрения на мир, некий отстраненный "взгляд изнутри". Заметим, что геометрически теория "взгляда изнутри" оправдана, в чем мы убедились на с. 283 (правда, при этом, кроме того что нужно за браться за плоскость картины, необходим еще и встать вверх ногами!). Но, несмотря: на верные частности, в целом, конечнс все эти объяснения слишком неясньные.
Другая точка зрения на истоки oбратной перспективы основана на чистом естествознании и прежде всего на закономерностях зрительного восприятия. Когда в 1966 г. Б. В. Раушенбах случае но попал в Музей древнерусского искусства имени Андрея Рублева, его порази необычный мир иконы. Но в то же время и покоробили слова экскурсовода, щедро раздававшей древнерусским живописцам ярлыки: "не умели", "не знали", "не смогли". И это мудрые, образованнейшие мастера, чьи произведения имена пережили столетия?! Раушенбах спешил назвать их "простодушными и наивными" (см. эпиграф к гл. 7). Он задумался...
20 лет спустя появилась на свет oбщая теория перспективы, в которой дре: нерусская обратная перспектива заняла свое достойное место.
Григорий Чудотворец. Византийская икона. XII в.
А понять обратную перспективу, конечно, можно. Пожалуй, первой из таких попыток была замечательная работа математика, физика, искусствоведа, писателя и философа П. А. Флоренского (1882 — 1937?) "Обратная перспектива", написанная в 1919 г., но увидевшая свет лишь полвека спустя*. Главной задачей автора было сломать укоренившееся убеждение в том, что линейная перспектива является единственно возможной и непогрешимой. В полемическом задоре, сравнивая две системы перспективы — обратную и прямую, Флоренский, пожалуй, увлекается, называя первую систему "созерцательно-творческой", а вторую "хищнически-механической". Но Флоренский прав в том, что две системы перспективы — обратная и прямая — это "два отношения к жизни — внутреннее и внешнее... два типа культуры".
* (Имя Павла Александровича Флоренского и его энциклопедическое наследие лишь сегодня возвращаются к нам. Окончив физико-математический факультет Московского университета и Московскую духовную академию, Флоренский в своих работах значительное внимание уделял философии культуры, взаимосвязи материального и духовного, целостному мировосприятию. Усилиями Флоренского были сохранены сокровища Троице-Сергиевой лавры, ставшие основой ныне всемирно известного Загорского музея-заповедника. В 1933 г. Флоренский был репрессирован, сослан в Соловецкий лагерь, в 1937 г. вторично осужден, и дальнейшие сведения о его жизни неизвестны.)
И все-таки, как объяснить обратную перспективу? Чем вызвано расхождение параллельных линий в обратной перспективе? Есть два подхода к этому вопросу. В первом корни обратной перспективы ищутся в идейных задачах, которые она решала. Икона призвана была убедить верующего в реальности ирреального, она должна была "отстранить" молящегося от грешной земли. Поэтому, как считают сторонники философско-богословских взглядов на истоки обратной перспективы, изображение на иконе не должно было в точности походить на видимый человеком мир. Икона должна была походить и не походить на видимый мир. Именно так она и могла заставить верующего поверить в чудо, которое также есть одновременно реальное и сверхъестественное. Мир иконы не мог быть отображением мира реального; поэтому и появляются расходящиеся параллели обратной перспективы, которые дают некую "потустороннюю", "сверхъестественную" точку зрения на мир, некий отстраненный "взгляд изнутри". Заметим, что геометрически теория "взгляда изнутри" оправдана, в чем мы убедились на с. 283 (правда, при этом, кроме того что нужно за браться за плоскость картины, необходим еще и встать вверх ногами!). Но, несмотря: на верные частности, в целом, конечнс все эти объяснения слишком неясньные.
Другая точка зрения на истоки oбратной перспективы основана на чистом естествознании и прежде всего на закономерностях зрительного восприятия. Когда в 1966 г. Б. В. Раушенбах случае но попал в Музей древнерусского искусства имени Андрея Рублева, его порази необычный мир иконы. Но в то же время и покоробили слова экскурсовода, щедро раздававшей древнерусским живописцам ярлыки: "не умели", "не знали", "не смогли". И это мудрые, образованнейшие мастера, чьи произведения имена пережили столетия?! Раушенбах спешил назвать их "простодушными и наивными" (см. эпиграф к гл. 7). Он задумался...
20 лет спустя появилась на свет oбщая теория перспективы, в которой дре: нерусская обратная перспектива заняла свое достойное место.
23. Академик Раушенбах: космонавтика — иконография — общая теория перспектив!
Дело не в том, чтобы научиться рисовать, а в том, что бы научиться мыслить.12 апреля 1961 года. Впервые в истории человечества космический корабль-спутник "Восток" с первым в мире космонавтом на борту Юрием Гагариным за 1 час 48 минут облетел земной шар и благополучно вернулся на Землю. Вслед за тем волны восхищения прокатились по Земле. Земной шар буквально содрогался от этих волн: "Первый полет человека в космос", "Утро космической эры", "Первый гражданин Вселенной",- сообщали газеты, радио, телевидение... В это же время видавший виды caм лет ИЛ-14 спешил с космодрома Байканур к месту приземления космонавтов! Никто не знал об этом рейсе ИЛ-14, никто не знал имен летевших пассажиров: академиков, профессоров сверхзасекреченных конструкторов. Bi среди них и ведущий специалист в области управления и ориентации космическ аппаратов, доктор технических наук, профессор, впоследствии действительный член Академии наук СССР и Международной академии астронавтики Борис Викторович Раушенбах. На борту "Востока" стояли три дублирующие друг друга системы ориентации, два комплекта органов управления и аппарат ручного управления. Все системы, созданные под руководством Б. В. Раушенбаха, сработали нормально, и их творец был счастлив. Как управлять ракетой в полете? Как делать ее полет устойчивым и целенаправленным? Эти вопросы стали актуальными в 30-е годы. Ракеты уже взлетали: и наши, и немецкие "Фау", но в воздухе они вытворяли безумные пируэты, ежесекундно грозя превратиться в чудовищный бумеранг. Не было ни теории правления, ни самих средств управления. После войны круг вопросов расширился: а как управлять спутником в космосе, в невесомости, где нет ни внешней среды, ни точки опоры? Как сориентировать космический аппарат в данном направлении? Ведь, летя по инерции, он кувыркался во всех мыслимых направлениях! Впереди снова открывалось белое поле нерешенных проблем. Вот этим проблемам Б. В. Раушенбах посвятил свою жизнь, пройдя путь от инженера до академика. С новыми полетами в космос появлялись и новые системы, новые проблемы. Если первые три спутника еще не имели системы ориентации кувыркались в полете, как слепые котята, то ровно через два года после запуска первого спутника, 4 октября 1959 г., межпланетной автоматической станки "Луна-3" была блестяще решена задача управления ориентацией станции. "Луна-3", как известно, облетела Луну, сфотографировала ее с обратной стороны передала изображение на Землю. Так человечество впервые увидело загадочную обратную сторону своего спутника, этом были "Венеры" и "Марсы", "Востоки" и "Восходы", "Молнии" и "Горизонты", "Союзы" и "Салюты". И с каждой новой станцией, новым кораблем вырастали все новые и новые проблемы. Работа над проблемой стыковки космических кораблей "Союз" пробудила интерес Б. В. Раушенбаха к... живописи. Откуда такие неожиданные параллели? Дело в том, что на корабле "Союз" нет переднего иллюминатора (на его месте расположен стыковочный узел). Поэтому для наблюдения во время стыковки за другим кораблем установлены специальные оптические приборы типа перископов и телекамер, которые, как известно,-дают изображение по законам геометрической оптики, т. е. в линейной перспективе. Но вот тут-то и возникает вопрос: а можно ли доверять этим изображениям? Насколько точно они передают ощущение пространства, видимого непосредственно глазом? Насколько перспектива оптическая, линейная, отличается от перспективы видимой, перцептивной? Ведь стыковка двух кораблей, происходящая на первой космической скорости, требует фантастической точности! Посещение музея Рублева стало последней каплей в чашу "перспективных" вопросов: у Раушенбаха появилось новое увлечение — геометрия живописи. Мы уже упоминали о существовании двух геометрических пространств: реальном и перцептивном (с. 297). Перцептивное пространство возникает в нашем сознании в результате совместной работы глаз и мозга. На первом этапе на сетчатке глаза возникает изображение реального пространства, которое подчиняется законам геометрической оптики, т. е. линейной перспективы. На втором — это изображение преобразуется в нашем сознании в результате деятельности мозга. Таким образом, линейная (ренессансная!) перспектива учитывает только работу глаза, но не учитывает работу мозга. Вот где корни излишней "фотографичности" ренессансных полотен! Какие же коррективы вносит мозг в сетчаточное (линейно-перспективное) изображение? Во-первых, заметим, что в линейно-перспективном изображении близкие предметы выходят чрезмерно большими, а далекие — слишком маленькими. Если бы такое изображение непосредственно передавалось в мозг, то, как отмечает Раушенбах, "человек мог бы испугаться близко сидящего котенка и остаться равнодушным к показавшемуся тигру". Поэтому сетчаточный образ в мозгу корректируется с учетом других признаков глубины пространства (таких, как заслонение близкими предметами далеких, "воздушная" перспектива, бинокулярные признаки). Корректировке подвергаются прежде всего сетчаточные образы малоудаленных предметов как наиболее необходимых в жизнедеятельности человека. В результате образы близких предметов становятся более похожими на их реальные прообразы, воспринимаемая величина близких предметов остается почти неизменной (константной), откуда и проистекает название этого корректирующего механизма работы мозга — механизм константности величины. Другим важнейшим механизмом работы мозга, преобразующим сетчаточный образ, является механизм константности формы. Суть этого механизма заключается в том, что на сравнительно малых расстояниях знакомые человеку формы кажутся ему почти такими, какими они являются реально, а не такими, каковыми они изображаются на сетчатке глаза. Поясним сказанное примером. Известно, что в линейной перспективе (т. е. на сетчатке глаза) круг или квадрат, если смотреть на них под углом, изображаются как эллипс или трапеция. Однако если человек заранее знает истинную форму рассматриваемых предметов, то они кажутся ему более близкими к их реальной форме: эллипс видится "более круглым", а трапеция — "более квадратной". В этом и состоит суть механизма константности формы. Вот почему, интуитивно осознавая действие механизма константности формы, даже такие последовательные перспективисты, как Дюрер или Рафаэль, никогда не изображали шар в виде эллипсоида, а всегда в виде шара (см. "Меланхолию" Дюрера на с. 42 или "Афинскую школу" Рафаэля на с. 55). Итак, перцептивное изображение, корректирующее линейный (сетчаточный) образ, существенно отличается от последнего. Это отличие сказывается прежде всего в увеличенных размерах удаленных предметов (например, цепи гор на горизонте), повышенной линии горизонта, сохранении метрических свойств ближних предметов. Последнее особенно важно для живописи: параллельные линии переднего плана в перцептивной перспективе выглядят параллельными. Более того, бинокулярность зрения может привести к тому, что параллельные линии переднего плана покажутся слегка расходящимися! Но ведь это же есть обратная перспектива! К сожалению, вопрос об истоках обратной перспективы не решается так просто. К нему мы еще вернемся. А пока резюмируем сказанное рисунками, заимствованными нами из книги Б. В. Раушенбаха "Пространственные построения в древнерусской живописи". На рисунке сравниваются линейная (а) и перцептивная (б — монокулярная, в — бинокулярная) перспективы. Предполагается, что основание картины совпадает с горизонтальной поверхностью земли и, следовательно (как и на рис., с. 281), ширина дороги в основании картины (жирная линия) является ее истинной шириной. Характерные особенности каждой перспективы очевидны из рисунка. Проводя математический анализ представленных перспективных изображений (для нас этот "анализ" сведется к сравнению всех трех рисунков), Раушенбах приходит к следующему выводу: 1) для среднего плана картинного пространства перцептивная перспектива практически совпадает с линейной: дальний план линейная перспектива преуменьшает; 2) для очень близкого и не слишком протяженного плана (т. е. оставаясь в области константности величины) или для очень далекого и не слишком большого объекта (т. е. для объекта с малыми угловыми размерами, для которого схождение параллельных пренебрежимо мало) перцептивная перспектива практически совпадает с аксонометрией; 3) при бинокулярном зрении возможен эффект "сверхконстантности" величины, когда для очень близкого и не слишком протяженного плана перцептивная перспектива, обычно совпадающая с аксонометрией, может принять вид обратной перспективы.Стендаль
 Изображение дороги и цепи гор на горизонте в линейной перспективе (а), перцептивной монокулярной (б) и бинокулярной (в) перспективе. Рисунок Б. В. Раушенбаха
Таким образом, все известные в живописи перспективные системы: параллельная, прямая и обратная — оказываются соответствующими частными случаями перспективы перцептивной.
Таковы современные психофизиологические представления о механизме зрения, с которых Раушенбах подошел к геометрическим загадкам древнерусской иконографии. Раушенбах исходил из естественного предположения о том, что древнерусский художник изображал мир таким, каким он его видел, т. е. в перцептивной перспективе. В самом деле, сам уровень развития средневековой науки и искусства говорит о том, что древнерусский художник не мог подобно художнику ренессансному пользоваться научно разработанной системой перспективы, а творил по наитию, т. е. как видел.
От того, как творил древнерусский мастер, перейдем к тому, что он творил. Слово "икона" в переводе с греческого означает образ, изображение. В центре внимания иконы было изображение Христа, Богоматери, святых и сцен из их жизни. Следовательно, в иконе господствовал "портрет", ближний план, и практически не было пейзажа, плана дальнего. Но согласно второму выводу перцептивная перспектива ближнего, не слишком протяженного плана практически совпадает с аксонометрией.
Так Раушенбах приходит к теоретическому выводу о том, что перспективной основой древнерусской живописи является аксонометрия. Перспективная основа — это еще не система перспективы, а только некоторое приближение к ней, приближение, допускающее разного рода отклонения. Этот вывод подтверждается анализом древнерусской живописи. Например, мы знаем, что подножие правого ангела в "Троице" Рублева дано в аксонометрии, а в изображении левого подножия допущено отклонение в сторону обратной перспективы. Более яркой иллюстрацией ксказанному является новгородская икона "Введение во храм", в которой аксонометрическая основа живописи очевидна. Но и здесь также хорошо видно, что древнерусский иконописец не был педантом от аксонометрии и легко допускал отклонения как в сторону прямой, так и в сторону обратной перспективы.
И все-таки отклонения в сторону обратной перспективы в древнерусской живописи преобладали. Чем же они были вызваны? На этот трудный вопрос нет однозначного ответа. Б. В. Раушенбах называет пять причин появления обратной перспективы:
1. Действие механизма константности формы. Мы знаем, что благодаря действию этого механизма форма знакомого предмета воспринимается человеком не как ее сетчаточный образ, а более близкой к реальным очертаниям этой формы. А как механизм константности формы "действует" на художника? Чтобы прояснить этот вопрос, Раушенбах рассматривает простой пример изображения параллелепипедов табурета и Евангелия, которые были излюбленными атрибутами древнерусской иконографии. На рисунке а показана аксонометрия этих предметов. Однако под действием механизма константности формы художник видит верхнюю крышку табурета (боковые грани книги) более плоско, ближе к их истинной форме, как показано штриховой линией на рисунке а. Но тогда сразу возникают трудности.
Изображение дороги и цепи гор на горизонте в линейной перспективе (а), перцептивной монокулярной (б) и бинокулярной (в) перспективе. Рисунок Б. В. Раушенбаха
Таким образом, все известные в живописи перспективные системы: параллельная, прямая и обратная — оказываются соответствующими частными случаями перспективы перцептивной.
Таковы современные психофизиологические представления о механизме зрения, с которых Раушенбах подошел к геометрическим загадкам древнерусской иконографии. Раушенбах исходил из естественного предположения о том, что древнерусский художник изображал мир таким, каким он его видел, т. е. в перцептивной перспективе. В самом деле, сам уровень развития средневековой науки и искусства говорит о том, что древнерусский художник не мог подобно художнику ренессансному пользоваться научно разработанной системой перспективы, а творил по наитию, т. е. как видел.
От того, как творил древнерусский мастер, перейдем к тому, что он творил. Слово "икона" в переводе с греческого означает образ, изображение. В центре внимания иконы было изображение Христа, Богоматери, святых и сцен из их жизни. Следовательно, в иконе господствовал "портрет", ближний план, и практически не было пейзажа, плана дальнего. Но согласно второму выводу перцептивная перспектива ближнего, не слишком протяженного плана практически совпадает с аксонометрией.
Так Раушенбах приходит к теоретическому выводу о том, что перспективной основой древнерусской живописи является аксонометрия. Перспективная основа — это еще не система перспективы, а только некоторое приближение к ней, приближение, допускающее разного рода отклонения. Этот вывод подтверждается анализом древнерусской живописи. Например, мы знаем, что подножие правого ангела в "Троице" Рублева дано в аксонометрии, а в изображении левого подножия допущено отклонение в сторону обратной перспективы. Более яркой иллюстрацией ксказанному является новгородская икона "Введение во храм", в которой аксонометрическая основа живописи очевидна. Но и здесь также хорошо видно, что древнерусский иконописец не был педантом от аксонометрии и легко допускал отклонения как в сторону прямой, так и в сторону обратной перспективы.
И все-таки отклонения в сторону обратной перспективы в древнерусской живописи преобладали. Чем же они были вызваны? На этот трудный вопрос нет однозначного ответа. Б. В. Раушенбах называет пять причин появления обратной перспективы:
1. Действие механизма константности формы. Мы знаем, что благодаря действию этого механизма форма знакомого предмета воспринимается человеком не как ее сетчаточный образ, а более близкой к реальным очертаниям этой формы. А как механизм константности формы "действует" на художника? Чтобы прояснить этот вопрос, Раушенбах рассматривает простой пример изображения параллелепипедов табурета и Евангелия, которые были излюбленными атрибутами древнерусской иконографии. На рисунке а показана аксонометрия этих предметов. Однако под действием механизма константности формы художник видит верхнюю крышку табурета (боковые грани книги) более плоско, ближе к их истинной форме, как показано штриховой линией на рисунке а. Но тогда сразу возникают трудности.
 Введение во храм. Новгородская икона. XV в.
В случае с табуретом можно показать его ножки, как и раньше, в аксонометрии (рис. б). Однако тогда возникает впечатление, будто ножки табурета повисли в воздухе. Отчего это происходит? Дело в том, что механизм константности формы действует лишь на материальные, видимые, предметы, форма которых заранее известна. А мыслимый квадрат, в углах которого ножки касаются пола, есть нечто абстрактное. Механизм константности формы не должен "поднимать" ножки табурета, они остаются на месте, и тогда возникает обратная перспектива табурета (рис. в). В такой обратной перспективе изображен табурет левого ангела в "Троице" Рублева. Еще лучше ее видно на миниатюре из Евангелия XVI века.
В случае с Евангелием механизм константности формы приводит к разрыву боковых сторон книги (рис. б). Однако даже самый смелый современный художник не позволяет себе допускать разрывы там, где хорошо известно, что изображаемая форма непрерывна. Не мог себе такой вольности позволить и древнерусский иконописец. Поэтому он "склеивает" боковые грани книги некоей средней линией, и в результате получается обратная перспектива Евангелия (рис. в). Такие изображения мы встречали на с. 313.
Введение во храм. Новгородская икона. XV в.
В случае с табуретом можно показать его ножки, как и раньше, в аксонометрии (рис. б). Однако тогда возникает впечатление, будто ножки табурета повисли в воздухе. Отчего это происходит? Дело в том, что механизм константности формы действует лишь на материальные, видимые, предметы, форма которых заранее известна. А мыслимый квадрат, в углах которого ножки касаются пола, есть нечто абстрактное. Механизм константности формы не должен "поднимать" ножки табурета, они остаются на месте, и тогда возникает обратная перспектива табурета (рис. в). В такой обратной перспективе изображен табурет левого ангела в "Троице" Рублева. Еще лучше ее видно на миниатюре из Евангелия XVI века.
В случае с Евангелием механизм константности формы приводит к разрыву боковых сторон книги (рис. б). Однако даже самый смелый современный художник не позволяет себе допускать разрывы там, где хорошо известно, что изображаемая форма непрерывна. Не мог себе такой вольности позволить и древнерусский иконописец. Поэтому он "склеивает" боковые грани книги некоей средней линией, и в результате получается обратная перспектива Евангелия (рис. в). Такие изображения мы встречали на с. 313.
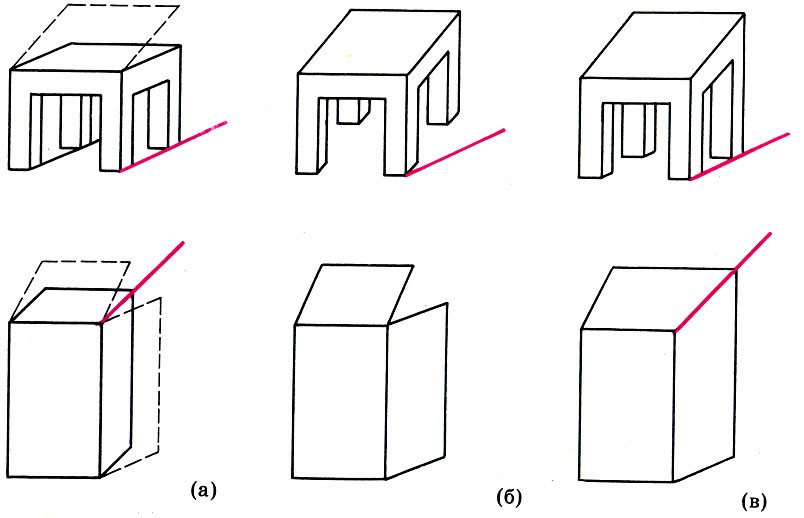 Схема возникновения обратной перспективы (по Б. В. Раушенбаху). Аксонометрическое изображение (а), действие механизма константности формы (б), обратная перспектива (в)
2. Учет бинокулярности зрения. Сегодня экспериментально установлено, что на небольших расстояниях бинокулярность зрения может привести к эффекту слабой обратной перспективы. Этот факт для нас, с детства воспитанных на линейной перспективе фотоаппарата, кино и телевидения, а также на прямой ренессансной перспективе, кажется парадоксальным. Даже в песенке поется о том, что "рельсы, как и водится, у горизонта сходятся", а тут вдруг расхождение параллельных! Но факты — вещь упрямая. Более того, существуют способы, позволяющие натренировать свой глаз на обратную перспективу. Такой "обратноперспективный" взгляд имеет, например, Б. В. Раушенбах.
Но тогда становится совершенно понятным и естественным, что древнерусский художник, еще не отягощенный канонами прямой ренессансной перспективы, рисовал ближний план таким, каким он его видел, т. е. в легкой обратной перспективе. В дальнейшем, правда, обратная перспектива часто принимала гипертрофированные формы. Но это можно понять, если учесть, что обратная перспектива стала своеобразным художественным каноном, а древнерусский иконописец никогда не писал с натуры.
Самые же удивительные открытия, касающиеся обратной перспективы, были сделаны в самое последнее время. В 1947 г. немецкий ученый, работавший в США, Р. Лунберг, опираясь на экспериментальные данные, построил математическую теорию, из которой следовало, что для участков горизонтальной плоскости, находящихся в непосредственной близости от наблюдателя, свойства перцептивного пространства могут быть описаны как свойства риманова пространства постоянной отрицательной кривизны, т. е. как свойства пространства Лобачевского. Тогда, согласно геометрии Лобачевского, всякий прямоугольник ABCD, у которого AD является ближней к наблюдателю стороной, а ВС — дальней, отобразится в перцептивном пространстве в так называемый четырехугольник Ламберта А'В'C'D' стороны которого удовлетворяют неравенству B'C'>A'D'. Следовательно, "дальняя" сторона четырехугольника Ламберта В'С' будет больше его "ближней" стороны A'D'. Но это же и есть обратная перспектива! Древнерусская икона и геометрия Лобачевского! Поистине нет предела удивительному на перекрестках науки и искусства!
3. Подвижность точки зрения. Как отмечалось в сноске на с. 313, даже мастера Возрождения, свято чтившие правила линейной перспективы, позволяли себе совмещать на одном полотне несколько точек зрения. Это была жертва геометрии в пользу искусства; она усиливала впечатление от картины, полнее раскрывала замыслы художника. Древнерусский иконописец, весьма вольно обращавшийся с геометрией живописи, тем более мог позволить себе не одну точку зрения.
Надо сказать, что подвижность точки зрения, в особенности при передаче ближнего пространства, имеет весьма веские причины. Дело в том, что поле четкого зрения человека невелико. Поэтому при осмотре пространства, особенно близкого, мы часто меняем направление осмотра, а иногда и саму точку зрения. В результате близкое пространство мы воспринимаем как совокупность нескольких перцептивных пространств, а значит, и нескольких локальных аксонометрий.
4. Увеличение информативности картины. Мы знаем, что коммуникативная функция играет важнейшую роль в искусстве. Мы видели также, что стремление к наибольшей информативности картины не останавливало древнеегипетского художника перед явными геометрическими казусами: совмещение двух видов в изображении человека (фигурка жреца на с. 266) или соединение нескольких проекций при передаче пространства (Осирис у пруда, с. 300). Все эти геометрические вольности преследовали единственную цель — увеличение информативности картины. Эти же причины часто приводили древнерусского иконописца к обратной перспективе.
Обратимся еще раз к иконе "Митрополит Алексий в житии". Желая показать на нижних клеймах иконы не только гроб, но и возложенное в него тело, Дионисий приподнимает дальнюю от зрителя стенку гроба, что приводит к сильной обратной перспективе. Также и на миниатюре Дионисия младшего. Стремясь подробнее показать содержание записи евангелиста, художник искусственно разворачивает его фолиант к зрителю, что опять-таки создает эффект обратной перспективы.
Схема возникновения обратной перспективы (по Б. В. Раушенбаху). Аксонометрическое изображение (а), действие механизма константности формы (б), обратная перспектива (в)
2. Учет бинокулярности зрения. Сегодня экспериментально установлено, что на небольших расстояниях бинокулярность зрения может привести к эффекту слабой обратной перспективы. Этот факт для нас, с детства воспитанных на линейной перспективе фотоаппарата, кино и телевидения, а также на прямой ренессансной перспективе, кажется парадоксальным. Даже в песенке поется о том, что "рельсы, как и водится, у горизонта сходятся", а тут вдруг расхождение параллельных! Но факты — вещь упрямая. Более того, существуют способы, позволяющие натренировать свой глаз на обратную перспективу. Такой "обратноперспективный" взгляд имеет, например, Б. В. Раушенбах.
Но тогда становится совершенно понятным и естественным, что древнерусский художник, еще не отягощенный канонами прямой ренессансной перспективы, рисовал ближний план таким, каким он его видел, т. е. в легкой обратной перспективе. В дальнейшем, правда, обратная перспектива часто принимала гипертрофированные формы. Но это можно понять, если учесть, что обратная перспектива стала своеобразным художественным каноном, а древнерусский иконописец никогда не писал с натуры.
Самые же удивительные открытия, касающиеся обратной перспективы, были сделаны в самое последнее время. В 1947 г. немецкий ученый, работавший в США, Р. Лунберг, опираясь на экспериментальные данные, построил математическую теорию, из которой следовало, что для участков горизонтальной плоскости, находящихся в непосредственной близости от наблюдателя, свойства перцептивного пространства могут быть описаны как свойства риманова пространства постоянной отрицательной кривизны, т. е. как свойства пространства Лобачевского. Тогда, согласно геометрии Лобачевского, всякий прямоугольник ABCD, у которого AD является ближней к наблюдателю стороной, а ВС — дальней, отобразится в перцептивном пространстве в так называемый четырехугольник Ламберта А'В'C'D' стороны которого удовлетворяют неравенству B'C'>A'D'. Следовательно, "дальняя" сторона четырехугольника Ламберта В'С' будет больше его "ближней" стороны A'D'. Но это же и есть обратная перспектива! Древнерусская икона и геометрия Лобачевского! Поистине нет предела удивительному на перекрестках науки и искусства!
3. Подвижность точки зрения. Как отмечалось в сноске на с. 313, даже мастера Возрождения, свято чтившие правила линейной перспективы, позволяли себе совмещать на одном полотне несколько точек зрения. Это была жертва геометрии в пользу искусства; она усиливала впечатление от картины, полнее раскрывала замыслы художника. Древнерусский иконописец, весьма вольно обращавшийся с геометрией живописи, тем более мог позволить себе не одну точку зрения.
Надо сказать, что подвижность точки зрения, в особенности при передаче ближнего пространства, имеет весьма веские причины. Дело в том, что поле четкого зрения человека невелико. Поэтому при осмотре пространства, особенно близкого, мы часто меняем направление осмотра, а иногда и саму точку зрения. В результате близкое пространство мы воспринимаем как совокупность нескольких перцептивных пространств, а значит, и нескольких локальных аксонометрий.
4. Увеличение информативности картины. Мы знаем, что коммуникативная функция играет важнейшую роль в искусстве. Мы видели также, что стремление к наибольшей информативности картины не останавливало древнеегипетского художника перед явными геометрическими казусами: совмещение двух видов в изображении человека (фигурка жреца на с. 266) или соединение нескольких проекций при передаче пространства (Осирис у пруда, с. 300). Все эти геометрические вольности преследовали единственную цель — увеличение информативности картины. Эти же причины часто приводили древнерусского иконописца к обратной перспективе.
Обратимся еще раз к иконе "Митрополит Алексий в житии". Желая показать на нижних клеймах иконы не только гроб, но и возложенное в него тело, Дионисий приподнимает дальнюю от зрителя стенку гроба, что приводит к сильной обратной перспективе. Также и на миниатюре Дионисия младшего. Стремясь подробнее показать содержание записи евангелиста, художник искусственно разворачивает его фолиант к зрителю, что опять-таки создает эффект обратной перспективы.
 Дионисий младший. Миниатюра из Евангелия. XVI в.
Дионисий младший. Миниатюра из Евангелия. XVI в.
 Новозаветная Троица. Икона XVI в.
Аналогичных примеров, когда поверхности книг с записями, поверхности столов с яствами и вообще горизонтальные поверхности с расположенными на них предметами "информационно" повернуты к зрителю в древнерусском искусстве немало. Все эти "информационные развороты" приводят к эффекту обратной перспективы.
5. Композиционные требования. Анализируя геометрические загадки древнерусской живописи, нельзя забывать, что средневековый иконописец был не только и не столько повествователем, стремящимся наиболее правдиво и наиболее информативно поведать о своем предмете, но прежде всего художником. Не только мера — геометрия, но и красота — искусство двигает рукою всякого истинного художника. В попытках наилучшим образом построить композицию картины, художник не по геометрическим или информативным, а по чисто художественным причинам мог обратиться к обратной перспективе, которая так или иначе становилась идейно-эстетической системой художественного языка древнерусской живописи.
Таковы основные причины возникновения обратной перспективы в древнерусской живописи, названные Б. В. Раушенбахом.
Именно так часто и воспринимал близкое пространство древнерусский художник: левую часть иконы он показывал с правой точки зрения, а правую — с левой. Так поступил Андрей Рублев в своей "Троице". Так поступали и многие другие безвестные иконописцы. В результате изображение становилось более "объемным": оно как бы разворачивалось перед зрителем, переводя его взгляд с одной точки зрения на другую.
Однако неизбежной была и плата за такую геометрическую вольность: там, где сходились две аксонометрии — левая и правая, возникала сильная обратная перспектива. Такую перспективу мы видим в изображении престола на иконе "Новозаветная Троица". Такая же сильная обратная перспектива угадывается и в рублевской "Троице". Однако Рублев мудро задрапировал этот геометрический дефект одеждами ангелов, и он явно не бросается в глаза.
Итак, "склейка" левой и правой аксонометрий являлась источником сильной обратной перспективы.
Необходимо отметить многообразие и разнородность источников обратной перспективы, среди которых есть и причины, никак не связанные с геометрией живописи. Тем не менее, действуя в совокупности, они привели к возникновению нового своеобразного стиля, в котором обратная перспектива стала геометрической основой.
Заметим, что обратная перспектива так и не стала единой геометрической системой древнерусской живописи, подобно линейной перспективе в живописи эпохи Возрождения. Но эта геометрическая непоследовательность придает древнерусской живописи удивительную открытость и очарование, мудрое отрешение от мелочной суетности, некую неопределенность и недосказанность, которые так свойственны истинным произведениям искусства.
Расставаясь с древнерусским искусством, вернемся еще раз к его шедевру, к тому, что "недосказал" Рублев и о чем веками продолжают "догадываться" его наследники. Предоставим слово Б. Раушенбаху: "Не изобразив боковых сторон престола, Рублев сознательно оставил поставленный вопрос без ответа. Представляется правдоподобным, что отмечавшаяся всеми исследователями творчества великого русского художника многогранность содержания "Троицы" требовала и "многогранной", т. е. не до конца определенной, геометрии изображения, чтобы эта геометрия "жила" и "изменялась", поворачиваясь то одной, то другой своей гранью, как и вложенные в "Троицу" идеи".
Но на древнерусском искусстве увлечение Раушенбаха живописью, точнее математикой живописи, не закончилось. Не только древние черные доски, но и яркие полотна мастеров XIX и XX веков таили в себе немало геометрических загадок. В какой перспективе творили Сезанн и Ван Гог, Поленов и Верещагин, Серов и Бенуа? Пока ясно было только одно: отнюдь не в ренессансной. Но тогда в какой? И снова вопросы, вопросы, вопросы.
Из этих вопросов и родилась общая теория перспективы. Новая теория учитывала не только законы геометрической оптики, по которым видит глаз, но и закономерности работы мозга при зрительном восприятии. Последние закономерности невозможно выразить на языке геометрии с помощью проектирования прямыми или искривленными лучами зрения, поэтому новая теория перспективы носит аналитический характер.
Переход к аналитическим методам математического описания вообще отражает процесс более глубокого проникновения математики в ту или иную область знания. В данном случае этот переход означает качественно новое математичекое описание механизма зрительного восприятия. В отличие от ренессансной системы в общей теории перспективы образа точки трехмерного пространства на картинной плоскости находится не путем геометрических построений, а путем вычислений.
Конечно, геометрические построена для художника более удобны и вряд ли найдется художник, который будет расчитывать пространство своей картин! Но теория и создавалась не для этог Новая теория позволила решить задач принципиально недоступную для рене сансной: количественно оценить отклонние полученного изображения от естесвенного зрительного восприятия и на основании этих количественных оценс дать качественное заключение о xapaктере допускаемых искажений (уточнит где преобладают ошибки: в передаче мен штаба изображения, либо в передаче глубины пространства, либо в подобии избражения). А уже на основании эти качественных оценок можно дать прость и удобные геометрические приемы пстроения перспективных изображений.
Мы не будем в самом конце книг утомлять читателя математическими выкладками общей теории перспективы которые к тому же отнюдь не элементарны и требуют знания дифференциального и интегрального исчисления. Остановимся на выводах и геометрически следствиях, которые вытекают из это теории.
Общая теория перспективы — это тория перцептивного изображения, в основе которой лежат обсуждавшиеся свойства перцептивного пространства. Системы перспективы, построенные на базе oбщей теории перспективы, будем назвать научными системами перспективы. Главный вывод, к которому приходит Б. В. Раушенбах, таков: не существует идеальной научной системы перспективы. Существует бесчисленное множество равноправных систем перспективы, каждая из которых содержит свои неизбежные ошибки изображения. Все системы отличаются друг от друга тем, на какие элементы изображения смещены эти ошибки, что и может в зависимости от художественных задач служить критерием выбора той или иной системы перспективы.
Этот вывод является частным случаем более общего математического факта: невозможно взаимнооднозначно и непрерывно отобразить трехмерное пространство на двумерную плоскость. Хотя на первый взгляд это кажется и странным, но взаимнооднозначное отображение пространства на плоскость возможно. Образно говоря, можно "истолочь" пространство на бесконечно малые точки и рассыпать эти точки бесконечно тонким слоем нa. плоскости. Однако при этом безвозвратно нарушается строение пространства, близкие элементы пространства не перейдут в близкие элементы плоскости, т. е. отображение не будет непрерывным. Разумеется, подобные отображения для изобразительных целей неприемлемы, ибo изобразительное искусство прежде всегo интересует именно форма. Рассмотренные нами способы проецирования пространства на плоскость (ортогональные проекции, аксонометрия, центральные проекции), равно как и научные системы перспективы, являются своеобразным компромиссом между взаимнооднозначностью и непрерывностью отображения пространства на плоскость. Аналогичное противоречие между "содержанием" (взаимнооднозначность) и "формой" (непрерывность) отображения приходится разрешать, например, в картографии при отображении сферы Земли на плоскость карты. Эта задача также не имеет "идеального" решения.
Проанализировав различные варианты научных систем перспективы, Раушенбах пришел к своеобразному "закону сохранения искажений в изобразительном искусстве". Суть этого закона, который наиболее ярко проявляется при изображении интерьера, т. е. не слишком протяженного пространства, заключается в том, что суммарная ошибка при передаче изображения для любой системы перспективы оказывается практически одной и той же. До обнаружения этого неожиданного факта казалось, что научная система перспективы должна носить абсолютный характер, так как она исходит из объективных законов природы (законов работы глаза и мозга). А оказалось, что научных систем перспективы сколь угодно много и все они с точки зрения математики (по суммарной ошибке искажений) равноценны. Поэтому проблема выбора подходящего варианта научной перспективы становится проблемой эстетической. Вот что по этому поводу пишет Раушенбах: "Эстетика "вторглась", казалось бы, в строго математическую область с неожиданной стороны... Именно эстетические соображения отбирают из бесчисленного множества предлагаемых математических вариантов тот, который является наиболее подходящим для решаемой художественной задачи".
"Закон сохранения искажений" еще раз убеждает нас в поразительной мудрости природы. Ведь если бы удалось найти систему перспективы, наиболее адекватную зрительному восприятию, то искусство живописи (по крайней мере, для художника-реалиста) должно было бы остановиться! Художнику не оставалось бы ничего, кроме как честно следовать этой наилучшей системе. И вот математика доказывает, что такой системы попросту нет, и последнее слово вновь остается за искусством!
Каковы же они, возможные научные системы перспективы? На рисунке показаны три варианта изображения условного пейзажа, взятые из книги Б. В. Paушенбаха "Системы перспективы в изобразительном искусстве. Общая теория перспективы". Горизонтальная поверхность Земли для большей наглядности разграфлена прямоугольной координатной сеткой. К цепи гор на горизонте ведет "дорога", проходящая по диагоналям прямоугольников. Вертикальные масштабы, построенные по правилам каждого варианта, показаны черными шестами, а прилегающие к ним белые шесты обозначают вертикальные размеры, соответствующие естественному зрительному восприятию. Все рисунки построены не "от руки", а рассчитаны согласно общей теории перспективы.
Вариант (а) соответствует системе перспективы, безошибочно передающей поверхность Земли (ширину и глубину пространства), а также дальний план (горы). Как видно из сравнения белых и черных шестов, неизбежные ошибки в этой системе смещены на вертикали, причем наибольшие ошибки допускаются при изображении вертикалей переднего плана, а по мере удаления к горизонту эти ошибки убывают. Здесь может воз никнуть естественный вопрос: а почему бы в этой системе, правильно передаю щей горизонтальные размеры, не пока зывать в соответствии с естественным восприятием и вертикальные линии? Тог да бы эта система стала "идеальной"? Однако такое насильственное вторжение в строение научной системы перспективы обернется тем, что при передаче полного пространства в изображении непрерыв них элементов появятся либо разрывы либо наложения одних элементов на другие. Подобные дефекты недопустимы, и поэтому в данном случае приходится жертвовать вертикалями.
Новозаветная Троица. Икона XVI в.
Аналогичных примеров, когда поверхности книг с записями, поверхности столов с яствами и вообще горизонтальные поверхности с расположенными на них предметами "информационно" повернуты к зрителю в древнерусском искусстве немало. Все эти "информационные развороты" приводят к эффекту обратной перспективы.
5. Композиционные требования. Анализируя геометрические загадки древнерусской живописи, нельзя забывать, что средневековый иконописец был не только и не столько повествователем, стремящимся наиболее правдиво и наиболее информативно поведать о своем предмете, но прежде всего художником. Не только мера — геометрия, но и красота — искусство двигает рукою всякого истинного художника. В попытках наилучшим образом построить композицию картины, художник не по геометрическим или информативным, а по чисто художественным причинам мог обратиться к обратной перспективе, которая так или иначе становилась идейно-эстетической системой художественного языка древнерусской живописи.
Таковы основные причины возникновения обратной перспективы в древнерусской живописи, названные Б. В. Раушенбахом.
Именно так часто и воспринимал близкое пространство древнерусский художник: левую часть иконы он показывал с правой точки зрения, а правую — с левой. Так поступил Андрей Рублев в своей "Троице". Так поступали и многие другие безвестные иконописцы. В результате изображение становилось более "объемным": оно как бы разворачивалось перед зрителем, переводя его взгляд с одной точки зрения на другую.
Однако неизбежной была и плата за такую геометрическую вольность: там, где сходились две аксонометрии — левая и правая, возникала сильная обратная перспектива. Такую перспективу мы видим в изображении престола на иконе "Новозаветная Троица". Такая же сильная обратная перспектива угадывается и в рублевской "Троице". Однако Рублев мудро задрапировал этот геометрический дефект одеждами ангелов, и он явно не бросается в глаза.
Итак, "склейка" левой и правой аксонометрий являлась источником сильной обратной перспективы.
Необходимо отметить многообразие и разнородность источников обратной перспективы, среди которых есть и причины, никак не связанные с геометрией живописи. Тем не менее, действуя в совокупности, они привели к возникновению нового своеобразного стиля, в котором обратная перспектива стала геометрической основой.
Заметим, что обратная перспектива так и не стала единой геометрической системой древнерусской живописи, подобно линейной перспективе в живописи эпохи Возрождения. Но эта геометрическая непоследовательность придает древнерусской живописи удивительную открытость и очарование, мудрое отрешение от мелочной суетности, некую неопределенность и недосказанность, которые так свойственны истинным произведениям искусства.
Расставаясь с древнерусским искусством, вернемся еще раз к его шедевру, к тому, что "недосказал" Рублев и о чем веками продолжают "догадываться" его наследники. Предоставим слово Б. Раушенбаху: "Не изобразив боковых сторон престола, Рублев сознательно оставил поставленный вопрос без ответа. Представляется правдоподобным, что отмечавшаяся всеми исследователями творчества великого русского художника многогранность содержания "Троицы" требовала и "многогранной", т. е. не до конца определенной, геометрии изображения, чтобы эта геометрия "жила" и "изменялась", поворачиваясь то одной, то другой своей гранью, как и вложенные в "Троицу" идеи".
Но на древнерусском искусстве увлечение Раушенбаха живописью, точнее математикой живописи, не закончилось. Не только древние черные доски, но и яркие полотна мастеров XIX и XX веков таили в себе немало геометрических загадок. В какой перспективе творили Сезанн и Ван Гог, Поленов и Верещагин, Серов и Бенуа? Пока ясно было только одно: отнюдь не в ренессансной. Но тогда в какой? И снова вопросы, вопросы, вопросы.
Из этих вопросов и родилась общая теория перспективы. Новая теория учитывала не только законы геометрической оптики, по которым видит глаз, но и закономерности работы мозга при зрительном восприятии. Последние закономерности невозможно выразить на языке геометрии с помощью проектирования прямыми или искривленными лучами зрения, поэтому новая теория перспективы носит аналитический характер.
Переход к аналитическим методам математического описания вообще отражает процесс более глубокого проникновения математики в ту или иную область знания. В данном случае этот переход означает качественно новое математичекое описание механизма зрительного восприятия. В отличие от ренессансной системы в общей теории перспективы образа точки трехмерного пространства на картинной плоскости находится не путем геометрических построений, а путем вычислений.
Конечно, геометрические построена для художника более удобны и вряд ли найдется художник, который будет расчитывать пространство своей картин! Но теория и создавалась не для этог Новая теория позволила решить задач принципиально недоступную для рене сансной: количественно оценить отклонние полученного изображения от естесвенного зрительного восприятия и на основании этих количественных оценс дать качественное заключение о xapaктере допускаемых искажений (уточнит где преобладают ошибки: в передаче мен штаба изображения, либо в передаче глубины пространства, либо в подобии избражения). А уже на основании эти качественных оценок можно дать прость и удобные геометрические приемы пстроения перспективных изображений.
Мы не будем в самом конце книг утомлять читателя математическими выкладками общей теории перспективы которые к тому же отнюдь не элементарны и требуют знания дифференциального и интегрального исчисления. Остановимся на выводах и геометрически следствиях, которые вытекают из это теории.
Общая теория перспективы — это тория перцептивного изображения, в основе которой лежат обсуждавшиеся свойства перцептивного пространства. Системы перспективы, построенные на базе oбщей теории перспективы, будем назвать научными системами перспективы. Главный вывод, к которому приходит Б. В. Раушенбах, таков: не существует идеальной научной системы перспективы. Существует бесчисленное множество равноправных систем перспективы, каждая из которых содержит свои неизбежные ошибки изображения. Все системы отличаются друг от друга тем, на какие элементы изображения смещены эти ошибки, что и может в зависимости от художественных задач служить критерием выбора той или иной системы перспективы.
Этот вывод является частным случаем более общего математического факта: невозможно взаимнооднозначно и непрерывно отобразить трехмерное пространство на двумерную плоскость. Хотя на первый взгляд это кажется и странным, но взаимнооднозначное отображение пространства на плоскость возможно. Образно говоря, можно "истолочь" пространство на бесконечно малые точки и рассыпать эти точки бесконечно тонким слоем нa. плоскости. Однако при этом безвозвратно нарушается строение пространства, близкие элементы пространства не перейдут в близкие элементы плоскости, т. е. отображение не будет непрерывным. Разумеется, подобные отображения для изобразительных целей неприемлемы, ибo изобразительное искусство прежде всегo интересует именно форма. Рассмотренные нами способы проецирования пространства на плоскость (ортогональные проекции, аксонометрия, центральные проекции), равно как и научные системы перспективы, являются своеобразным компромиссом между взаимнооднозначностью и непрерывностью отображения пространства на плоскость. Аналогичное противоречие между "содержанием" (взаимнооднозначность) и "формой" (непрерывность) отображения приходится разрешать, например, в картографии при отображении сферы Земли на плоскость карты. Эта задача также не имеет "идеального" решения.
Проанализировав различные варианты научных систем перспективы, Раушенбах пришел к своеобразному "закону сохранения искажений в изобразительном искусстве". Суть этого закона, который наиболее ярко проявляется при изображении интерьера, т. е. не слишком протяженного пространства, заключается в том, что суммарная ошибка при передаче изображения для любой системы перспективы оказывается практически одной и той же. До обнаружения этого неожиданного факта казалось, что научная система перспективы должна носить абсолютный характер, так как она исходит из объективных законов природы (законов работы глаза и мозга). А оказалось, что научных систем перспективы сколь угодно много и все они с точки зрения математики (по суммарной ошибке искажений) равноценны. Поэтому проблема выбора подходящего варианта научной перспективы становится проблемой эстетической. Вот что по этому поводу пишет Раушенбах: "Эстетика "вторглась", казалось бы, в строго математическую область с неожиданной стороны... Именно эстетические соображения отбирают из бесчисленного множества предлагаемых математических вариантов тот, который является наиболее подходящим для решаемой художественной задачи".
"Закон сохранения искажений" еще раз убеждает нас в поразительной мудрости природы. Ведь если бы удалось найти систему перспективы, наиболее адекватную зрительному восприятию, то искусство живописи (по крайней мере, для художника-реалиста) должно было бы остановиться! Художнику не оставалось бы ничего, кроме как честно следовать этой наилучшей системе. И вот математика доказывает, что такой системы попросту нет, и последнее слово вновь остается за искусством!
Каковы же они, возможные научные системы перспективы? На рисунке показаны три варианта изображения условного пейзажа, взятые из книги Б. В. Paушенбаха "Системы перспективы в изобразительном искусстве. Общая теория перспективы". Горизонтальная поверхность Земли для большей наглядности разграфлена прямоугольной координатной сеткой. К цепи гор на горизонте ведет "дорога", проходящая по диагоналям прямоугольников. Вертикальные масштабы, построенные по правилам каждого варианта, показаны черными шестами, а прилегающие к ним белые шесты обозначают вертикальные размеры, соответствующие естественному зрительному восприятию. Все рисунки построены не "от руки", а рассчитаны согласно общей теории перспективы.
Вариант (а) соответствует системе перспективы, безошибочно передающей поверхность Земли (ширину и глубину пространства), а также дальний план (горы). Как видно из сравнения белых и черных шестов, неизбежные ошибки в этой системе смещены на вертикали, причем наибольшие ошибки допускаются при изображении вертикалей переднего плана, а по мере удаления к горизонту эти ошибки убывают. Здесь может воз никнуть естественный вопрос: а почему бы в этой системе, правильно передаю щей горизонтальные размеры, не пока зывать в соответствии с естественным восприятием и вертикальные линии? Тог да бы эта система стала "идеальной"? Однако такое насильственное вторжение в строение научной системы перспективы обернется тем, что при передаче полного пространства в изображении непрерыв них элементов появятся либо разрывы либо наложения одних элементов на другие. Подобные дефекты недопустимы, и поэтому в данном случае приходится жертвовать вертикалями.
 Возможные варианты научной перспективы: (а) — правильная передача поверхности земли; (б) — правильная передача вертикальных размеров; (в) — ренессансная перспектива. Рисунки Б. В. Раушенбаха
Возможные варианты научной перспективы: (а) — правильная передача поверхности земли; (б) — правильная передача вертикальных размеров; (в) — ренессансная перспектива. Рисунки Б. В. Раушенбаха
 Сезанн. Каштановая аллея в Жа де Буффан. 1883-1887. Перспективный анализ Б. В. Раушенбаха
В варианте (б) ошибки в передаче вертикальных размеров исправлены. Более того, в этой системе правильно передается и ширина, а значит, сохраняется подобие фронтальных изображений. Однако какой "ценой" все это достигнуто, очевидно из самого рисунка: на нем крайне невыразительно, ослабленно передана глубина пространства, особенно глубина переднего плана.
Наконец, на рисунке (в) тот же условный пейзаж передан в ренессансной (линейной) системе перспективы. Сравнение этого рисунка с вариантами (а), (б) выявляет главный недостаток ренессансной системы: сильное преувеличение переднего плана и явное преуменьшение дальних объектов. Этот недостаток ренессансной (а значит, и фотографической) перспективы хорошо знаком альпинистам: запечатлев себя на фоне грандиозной горной панорамы, дома они обнаруживают на пленке жалкую гряду холмов на горизонте. Для среднего плана все ошибки ренессансной перспективы практически равны нулю.
Таким образом, анализ ошибок, неизбежно возникающих в той или иной системе перспективы, позволяет определить границы применимости известных систем перспективы и сделать выводы, которые были приведены на с. 317.
Анализ ошибок при изображении пейзажа (глубокого пространства) показывает, что в любой системе перспективы наибольшим искажениям подвержен именно передний план. Этот "закон наибольших искажений переднего плана" хорошо осознан художниками на практике. Поэтому при изображении пейзажа опытные мастера либо "отсекают" передний план границами картины, либо погружают его в тень.
Обратим внимание на то, что в варианте перспективы, правильно передающем глубину пространства (рис. а), образы прямых линий, уходящих к горизонту, становятся криволинейными (см. координатные линии, сходящиеся в точке А, и "дорогу"). Это свойство перспективы, правильно передающей глубину, было интуитивно "нащупано" некоторыми художниками XIX-XX вв., которые стали умело им пользоваться. А вот искусствоведы, подходившие к анализу живописи с позиций ренессансной системы перспективы либо приводившие в качестве аргументов фотографии (но это также линейная перспектива!), продолжали обвинять таких художников в своеволии и отступлении от "научных" канонов линейной перспективы.
Особенно "не повезло" здесь Полю Сезанну (1839-1906), чьи пейзажи в специальной монографии были тщательно сравнены с соответствующими фотографиями и где были указаны все его "ошибки". Возьмем, к примеру, акварель Сезанна "Каштановая аллея в Жа де Буффан". Эта акварель удобна для перспективного анализа тем, что ряды каштанов в натуре заведомо прямолинейны. Однако на акварели они явно искривлены, что и позволило сделать скоропалительный вывод о том, что Сезанн отступал от натуры. Однако, как показал Раушенбах, криволинейный треугольник ANP в соответствующем масштабе с удивительной точностью вписывается в криволинейную сетку координат на рисунке а (с. 325). Таким образом, именно горизонтальная поверхность Земли (а значит, и ряды каштанов) переданы Сезанном в полном соответствии со зрительным восприятием[39].
Не менее убедительным оказывается и сделанный Раушенбахом перспективный анализ этюда В. Д. Поленова (1844-1927) "Церковь св. Елены". Этот этюд был написан Поленовым в 1882 г. во время путешествия по Ближнему Востоку. В ренессансной системе перспективы (или на фотографии) образы параллельных линий равной высоты, проходящих по карнизам колонн и через середины (верхние точки) трех арок, должны быть прямолинейными. Как видно из иллюстрации, эти линии на этюде сильно искривлены. Пересекаясь на линии горизонта, они указывают на истинную главную точку картины, отмеченную кружком. Столь сильное искривление образов объективно прямых линий вызвано тем, что в изображаемом интерьере передний план вплотную приближен к зрителю. Однако такая геометрия этюда Поленова также не является "перспективной ошибкой", а, напротив, хорошо согласуется с вариантом (а), правильно передающим глубину пространства.
Эти два примера убеждают в том, что художники прежде всего предпочитают те варианты научной перспективы, которым свойственна правильная передача глубины пространства. Но это и понятно, ибо именно здесь решается извечный парадокс живописи: убедительно изобразить трехмерное пространство мира (а значит, прежде всего показать глубину пространства) на двумерной плоскости картины.
Еще раз отметим, что с позиций общей теории перспективы с помощью математического анализа ошибок изображения удалось строго указать границы применимости таких двух систем перспективы, как аксонометрия и слабая обратная перспектива. Эти две системы при определенных условиях (см. с. 318) являются совершенно естественными и равноправными вариантами научной системы перспективы. Аксонометрия и слабая обратная перспектива являются хорошими способами передачи формы и объема отдельного предмета, а не целостного пространства. При этом аксонометрия является счастливым исключением, абсолютно безошибочно передающим близкие и не слишком протяженные объекты. Так, в рамках общей теории перспективы обрели свое место аксонометрия и обратная перспектива, не имевшие прежде теоретического фундамента, но сыгравшие выдающуюся роль в истории искусства (см. гл. 22).
Сезанн. Каштановая аллея в Жа де Буффан. 1883-1887. Перспективный анализ Б. В. Раушенбаха
В варианте (б) ошибки в передаче вертикальных размеров исправлены. Более того, в этой системе правильно передается и ширина, а значит, сохраняется подобие фронтальных изображений. Однако какой "ценой" все это достигнуто, очевидно из самого рисунка: на нем крайне невыразительно, ослабленно передана глубина пространства, особенно глубина переднего плана.
Наконец, на рисунке (в) тот же условный пейзаж передан в ренессансной (линейной) системе перспективы. Сравнение этого рисунка с вариантами (а), (б) выявляет главный недостаток ренессансной системы: сильное преувеличение переднего плана и явное преуменьшение дальних объектов. Этот недостаток ренессансной (а значит, и фотографической) перспективы хорошо знаком альпинистам: запечатлев себя на фоне грандиозной горной панорамы, дома они обнаруживают на пленке жалкую гряду холмов на горизонте. Для среднего плана все ошибки ренессансной перспективы практически равны нулю.
Таким образом, анализ ошибок, неизбежно возникающих в той или иной системе перспективы, позволяет определить границы применимости известных систем перспективы и сделать выводы, которые были приведены на с. 317.
Анализ ошибок при изображении пейзажа (глубокого пространства) показывает, что в любой системе перспективы наибольшим искажениям подвержен именно передний план. Этот "закон наибольших искажений переднего плана" хорошо осознан художниками на практике. Поэтому при изображении пейзажа опытные мастера либо "отсекают" передний план границами картины, либо погружают его в тень.
Обратим внимание на то, что в варианте перспективы, правильно передающем глубину пространства (рис. а), образы прямых линий, уходящих к горизонту, становятся криволинейными (см. координатные линии, сходящиеся в точке А, и "дорогу"). Это свойство перспективы, правильно передающей глубину, было интуитивно "нащупано" некоторыми художниками XIX-XX вв., которые стали умело им пользоваться. А вот искусствоведы, подходившие к анализу живописи с позиций ренессансной системы перспективы либо приводившие в качестве аргументов фотографии (но это также линейная перспектива!), продолжали обвинять таких художников в своеволии и отступлении от "научных" канонов линейной перспективы.
Особенно "не повезло" здесь Полю Сезанну (1839-1906), чьи пейзажи в специальной монографии были тщательно сравнены с соответствующими фотографиями и где были указаны все его "ошибки". Возьмем, к примеру, акварель Сезанна "Каштановая аллея в Жа де Буффан". Эта акварель удобна для перспективного анализа тем, что ряды каштанов в натуре заведомо прямолинейны. Однако на акварели они явно искривлены, что и позволило сделать скоропалительный вывод о том, что Сезанн отступал от натуры. Однако, как показал Раушенбах, криволинейный треугольник ANP в соответствующем масштабе с удивительной точностью вписывается в криволинейную сетку координат на рисунке а (с. 325). Таким образом, именно горизонтальная поверхность Земли (а значит, и ряды каштанов) переданы Сезанном в полном соответствии со зрительным восприятием[39].
Не менее убедительным оказывается и сделанный Раушенбахом перспективный анализ этюда В. Д. Поленова (1844-1927) "Церковь св. Елены". Этот этюд был написан Поленовым в 1882 г. во время путешествия по Ближнему Востоку. В ренессансной системе перспективы (или на фотографии) образы параллельных линий равной высоты, проходящих по карнизам колонн и через середины (верхние точки) трех арок, должны быть прямолинейными. Как видно из иллюстрации, эти линии на этюде сильно искривлены. Пересекаясь на линии горизонта, они указывают на истинную главную точку картины, отмеченную кружком. Столь сильное искривление образов объективно прямых линий вызвано тем, что в изображаемом интерьере передний план вплотную приближен к зрителю. Однако такая геометрия этюда Поленова также не является "перспективной ошибкой", а, напротив, хорошо согласуется с вариантом (а), правильно передающим глубину пространства.
Эти два примера убеждают в том, что художники прежде всего предпочитают те варианты научной перспективы, которым свойственна правильная передача глубины пространства. Но это и понятно, ибо именно здесь решается извечный парадокс живописи: убедительно изобразить трехмерное пространство мира (а значит, прежде всего показать глубину пространства) на двумерной плоскости картины.
Еще раз отметим, что с позиций общей теории перспективы с помощью математического анализа ошибок изображения удалось строго указать границы применимости таких двух систем перспективы, как аксонометрия и слабая обратная перспектива. Эти две системы при определенных условиях (см. с. 318) являются совершенно естественными и равноправными вариантами научной системы перспективы. Аксонометрия и слабая обратная перспектива являются хорошими способами передачи формы и объема отдельного предмета, а не целостного пространства. При этом аксонометрия является счастливым исключением, абсолютно безошибочно передающим близкие и не слишком протяженные объекты. Так, в рамках общей теории перспективы обрели свое место аксонометрия и обратная перспектива, не имевшие прежде теоретического фундамента, но сыгравшие выдающуюся роль в истории искусства (см. гл. 22).
 В. Поленов. Церковь Св. Елены. 1882. Перспективный анализ Б. В. Раушенбаха
Книга Б. В. Раушенбаха "Системы перспективы в изобразительном искусстве. Общая теория перспективы" вышла в свет в 1986 г. До этой книги в течение почти 500 лет не появлялось фундаментальных трудов по перспективе! Проблема перспективы казалась решенной раз и навсегда еще в XV веке! И вот в конце XX века появляется труд, автор которого исходит из того, что не было известно науке XV века — математического анализа, дифференциальных уравнений, геометрии Лобачевского — и что так и осталось недоступным искусствоведам века XX. Только человек, соединяющий в одном лице глубокое знание математики с тонким чувством прекрасного, мог сделать это открытие!
Спираль науки сделала гигантский виток длиной в 500 лет и на качественно новом уровне решила, казалось бы, старую, как мир, задачу. Но вряд ли стоит думать, что все точки над i в теории перспективы расставлены окончательно. Пути науки, как и пути искусства, не имеют "точек схода", они простираются в бесконечность.
В. Поленов. Церковь Св. Елены. 1882. Перспективный анализ Б. В. Раушенбаха
Книга Б. В. Раушенбаха "Системы перспективы в изобразительном искусстве. Общая теория перспективы" вышла в свет в 1986 г. До этой книги в течение почти 500 лет не появлялось фундаментальных трудов по перспективе! Проблема перспективы казалась решенной раз и навсегда еще в XV веке! И вот в конце XX века появляется труд, автор которого исходит из того, что не было известно науке XV века — математического анализа, дифференциальных уравнений, геометрии Лобачевского — и что так и осталось недоступным искусствоведам века XX. Только человек, соединяющий в одном лице глубокое знание математики с тонким чувством прекрасного, мог сделать это открытие!
Спираль науки сделала гигантский виток длиной в 500 лет и на качественно новом уровне решила, казалось бы, старую, как мир, задачу. Но вряд ли стоит думать, что все точки над i в теории перспективы расставлены окончательно. Пути науки, как и пути искусства, не имеют "точек схода", они простираются в бесконечность.
Заключение
То, что я понял — превосходно. Думаю, таково же и то, чего я не понял.Сократ
Только кончая задуманное сочинение, мы уясняем себе, с чего нам следовало его начать.Книга закончена. Но именно поэтому хочется вернуться к ее началу, ибо, как сказал один мудрец задолго до Паскаля, "идет ветер к югу и переходит к северу, кружится, кружится на ходу своем, и возвращается ветер на круги свои". Поэтому, подойдя к заключению, хочется вернуться к началу книги, к мудрому древнему знаку Ин-Ян. Возможно, кому-то могло показаться, что автор предпринял попытку навести "математический" порядок в искусстве, а то и вовсе "математизировать" искусство, как это происходит сегодня со многими науками. Нет и еще раз нет! Автор полностью солидарен с замечательным русским поэтом Аполлоном Майковым, который писал:Б. Паскаль
Литература
К части I Архитектура математики.- М.: Знание, 1972. Вейль Г. Симметрия.- М.: Наука, 1968. Вернадский В. И. Философские мысли натуралиста.- М.: Наука, 1988. Вигнер Е. Этюды о симметрии.- М.: Мир, 1971. Гарднер М. Этот правый, левый мир.- М.: Мир, 1967. Глазычев В. Л. Гемма Коперника. Мир науки в изобразительном искусстве.- М.: Сов. художник, 1989. Гулыга А. В. Искусство в век науки.- М.: Наука, 1978. Гулыга А. В. Что такое эстетика? — М.: Просвещение, 1987. Данин Д. С. Перекресток.- М.: Сов. писатель, 1974. Каган М. С. Начала эстетики.- М.: Искусство, 1964. Клайн М. Математика: Утрата определенности.- М.: Мир, 1984. Курант Р., Роббинс Г. Что такое математика?: Элементарный очерк идей и методов.- М.: Просвещение, 1967. Мейлах Б. С. На рубеже науки и искусства: Спор о двух сферах познания и творчества.- Л.: Наука, 1971. Мигдал А. Б. Поиски истины.- М.: Мол. гвардия, 1983. Мигунов А. С. Искусство и процесс познания.- М.: Изд-во МГУ, 1986. Мороз. О. П. Прекрасна ли истина? — М.: Знание, 1989. Овсянников М. Ф. История эстетической мысли.- М.: Высшая школа, 1984. Платон. Пир // Соч.: В 3 т.- М.: Мысль, 1970.- Т. 2. Сноу Ч. П. Две культуры.- М.: Прогресс, 1973. Сонин А. С. Постижение совершенства.- М.: Знание, 1987. Столович Л. Н. Философия красоты.- М.: Политиздат, 1978. Тарасов Л. В. Этот удивительно симметричный мир.- М.: Просвещение, 1982. Толстой Л. Н. Что такое искусство? — М.: Худож. лит., 1964. Урманцев Ю. А. Симметрия природы и природа симметрии.- М.: Мысль, 1974. Фейнберг Е. Л. Кибернетика, логика, искусство.- М.: Радио и связь, 1981. Яковлев Е. Г. Проблема систематизации категорий в марксистско-ленинской эстетике.- М.: Искусство, 1983. К части II Ансерме Э. Беседы о музыке.- Л.: Музыка, 1985. Античная музыкальная эстетика.- М.: Музгиз, 1960. Анфилов Г. Б. Физика и музыка.- М.: Дет. лит., 1964. Дарваш Г. Книга о музыке.- М.: Музыка, 1983. Диоген Лаэртский. О жизни, учениях и изречениях знаменитых философов.- М.: Мысль, 1979. Зарипов Р. X. Кибернетика и музыка.- М.: Наука, 1971. Лосев А. Ф. История античной эстетики.- М., 1969- 1990.- Т. 1 — 8. Лосев А. Ф. Музыка как предмет логики // Из ранних произведений.- М.: Правда, 1990. Мазель Л. А. О природе и средствах музыки.- М.: Музыка, 1983. Марутаев В. М. Приблизительная симметрия в музыке // Проблемы музыкальной науки.- М.: Сов. композитор, 1979.- Вып. 4. Моль А., Фукс В., Касслер М. Искусство и ЭВМ.- М.: Мир, 1975. Музыкальная акустика.- М.: Музгиз, 1954. Платон. Тимей//Соч.: В 3 т. — М.: Мысль, 1971.- Т. 3.-Ч. 1. Розенов Э. К. Статьи о музыке: Избранное.- М.: Музыка, 1982. Тэйлор Ч. Физика музыкальных звуков.- М.: Легкая индустрия, 1976. Шилов Г. Е. Простая гамма.- М.: Наука, 1980. К части III Альберти Л. Б. Десять книг о зодчестве.- М.: ИАА, 1935. Бартенев И. А. Форма и конструкция в архитектуре.- Л.: Стройиздат, 1968. Борисовский Г. Б. Наука, техника, искусство.- М.: Наука, 1969. Витрувий М. П. Десять книг об архитектуре.- М.: ИАА, 1936. Воробьев Н. Н. Числа Фибоначчи.- М.: Наука, 1984. Гика М. Эстетика пропорций в природе и искусстве.- М.: ИАА, 1936. Гликин Я. Д. Методы архитектурной гармонии.- Л.: Стройиздат, 1979. Гримм Г. Д. Пропорциональность в архитектуре.- Л.; М.: ОНТИ, 1935. Иконников А. В. Художественный язык архитектуры.- М.: Искусство, 1985. Коуэн Г. Дж. Мастера строительного искусства.- М.: Стройиздат, 1982. Ле Корбюзье. Архитектура XX века.- М.: Прогресс, 1970. Смолина Н. И. Традиции симметрии в архитектуре.- М.: Стройиздат, 1990. Тиммердинг Г. Е. Золотое сечение.- Петроград, 1924. Цирес А. Искусство архитектуры.- М.: ИАА, 1946. Шевелев И. Ш. Принцип пропорции.- М.: Стройиздат, 1986. Шевелев И. Ш., Марутаев М. А., Шмелев И. П. Золотое сечение.- М.: Стройиздат, 1990. К части IV Вавилов С. И. Глаз и солнце: О свете, солнце и зрении.- М.: Наука, 1981. Дюрер А. Дневники. Письма. Трактаты.- М.,- Л.: Искусство, 1957.- Т. 2. Жегин Л. Ф. Язык живописного произведения.- М.: Искусство, 1970. Искусство и точные науки.- М.: Наука, 1979. Ковалев Ф. В. Золотое сечение в живописи.- Киев: Выща школа, 1989. Левитин К. Геометрическая рапсодия.- М.: Знание, 1984. Леонардо да Винчи. Книга о живописи.- М.: Изогиз, 1934. Мочалов Л. В. Пространство мира и пространство картины.- М.: Сов. художник, 1983. Петрович Д. Теоретики пропорций.- М.: Стройиздат, 1979. Пидоу Д. Геометрия и искусство.- М.: Мир, 1979. Раушенбах Б. В. Пространственные построения в древнерусской живописи.- М.: Наука, 1975. Раушенбах Б. В. Пространственные построения в живописи.- М.: Наука, 1980. Раушенбах Б. В. Системы перспективы в изобразительном искусстве: Общая теория перспективы.- М.: Наука, 1986. Рынин Н. А. Начертательная геометрия. Перспектива.- Петроград, 1918. Тадеев В. А. От живописи к проективной геометрии.- Киев: Выща школа, 1988. Федоров М. В. Рисунок и перспектива.- М.: Искусство, 1960. Фролов С. А., Покровская М. В. Начертательная геометрия: что это такое? — Минск, Вышэйшая школа, 1986.Примечания
1
В более распространенной русской транскрипции Инь-Ян теряется графическая симметрия (а значит, отчасти и философия) двух древнекитайских первоначал. (обратно)2
Слова "прекрасное" и "красота" мы употребляем в широком смысле как синонимы. (обратно)3
Дискурсия (лат. discursus) — рассуждение. (обратно)4
Кант безвыездно прожил всю свою долгую жизнь в родном Кенигсберге (ныне г. Калининград), учился в Кенигсбергском университете, затем стал его профессором, читал в нем только курсы философии, эстетики, истории, филологии, но и математики, физики, астрономии, космогонии и даже Фортификации. Всю свою жизнь этот "всеобъемлющий гений" посвятил науке, отказавшись от личной жизни и даже поездок в другие города. (обратно)5
За многие века система Птолемея была настолько хорошо разработана, что ею продолжали пользоваться и после Коперника. Ведь система Коперника, до тех пор пока она не подверглась математической обработке и ряду уточнений,имела только мировоззренческое значение. (обратно)6
3десь Вольтер (1694-1778) и Жан-Жак Руссо (1712-1778)для Блеика прежде всего не писатели, а философы и ученые-энциклопедисты, просветители. (обратно)7
Как стало известно впоследствии, "инженер Полетаев" оказался вымышленным персонажем. Его придумал поэт М. Светлов и для обострения полемики умышленно поставив на самые крайние позиции. Мистификация М. Светлова оказалась удачной. (обратно)8
Порфирий приводит любопытный эпизод. Проведуя вегетарианство, Пифагор тем не менее посоветовал самосскому атлету Евримену ежедневно питаться мясом, а не сыром и смоковами, как это делали остальные спортсмены. Евримен последовал Пифагоровой мудрости — набрался сил и, несмотря на свой малый рост, одержал победу в борьбе на Олимписких играх. (обратно)9
Известна легенда, рассказывающая, что однажды, увидев, как били собаку, Пифагор сказал: "Перестаньте ее бить, в этой собаке живет душа моего друга: я узнал его по голосу". (обратно)10
Некоторые отголоски пифагорейской числовой мистики мы встречаем и в наши дни: например, обычай дарить нечетное число цветов (четное число у пифагорейцев считалось несчастливым). (обратно)11
Вот это доказательство. Допустим противное, т. е пусть = m/n или m2 = 2n2, причем натуральные числа m и n не имеют oбщих делителей, кроме единицы, так как если бы они существовали, то на них дробь можно было бы сократить. Если m — нечетное число, мы получаем противоречие, так как 2n2 четно, а квадрат нечетного числа — число нечетное. Еcли m четно и равно 2k, то 4k2 = 2n2, или 2k2 = n2 так что n должно быть четным и, следовательно, числа m и n имеют общий делитель 2, что противоречит начальному предположению. Итак,
= m/n или m2 = 2n2, причем натуральные числа m и n не имеют oбщих делителей, кроме единицы, так как если бы они существовали, то на них дробь можно было бы сократить. Если m — нечетное число, мы получаем противоречие, так как 2n2 четно, а квадрат нечетного числа — число нечетное. Еcли m четно и равно 2k, то 4k2 = 2n2, или 2k2 = n2 так что n должно быть четным и, следовательно, числа m и n имеют общий делитель 2, что противоречит начальному предположению. Итак,  не является отношением двУх натуральных чисел
(обратно)
не является отношением двУх натуральных чисел
(обратно)
12
В теории музыки понятия интервала и интервального коэффициента строго не разграничены. Следуя традиции, мы часто для краткости будем называть интервальный коэффициент интервалом. (обратно)13
Характер звучания лада, конечно, не определяется столь грубо и однозначно. Вопрос этот очень деликатный, и о нем мы еще поговорим в конце главы. (обратно)14
Судьба Алексея Федоровича Лосева счастлива и трагична. Счастлива, потому что до последнего дня своей 95-летней жизни Лосев сохранил поразительную работоспособность и успел завершить главный труд — восьмитомную "Историю античной эстетики". Трагична, потому что другие восемь томов его сочинений, написанных на полвека ранее (1927 — 1930), были преданы анафеме, а сам автор, будучи незаконно репрессирован, продолжил свои философские изыскания на строительстве Беломорско-Балтийского канала, откуда он писал: "Я закован в цепи, когда в душе бурлят непочатые и неистощимые силы". Одна из этих работ Лосева — "Музыка как предмет логики" — могла бы служить путеводной звездой к этой книге. И все-таки судьба А. Ф. Лосева счастлива, ибо рукописи не горят. Сегодня огромное философское наследие А. Ф. Лосева обретает свое второе рождение. (обратно)15
Напомним, что остальные три планеты Солнечной системы — Уран, Нептун и Плутон — были открыты лишь в XVIII, XIX и XX веках соответственно. (обратно)16
Отсюда пошло выражение "Быть на седьмом небе", обозначающее высшую степень блаженства. (обратно)17
В самом деле, сумма плоских углов s при вершине выпуклого многогранника должна быть строго меньше 360°, а число граней при вершине m≥3. Тогда гранями правильного многогранника могут быть только три плоские фигуры: правильные треугольник, четырехугольник (квадрат) и пятиугольник, ибо уже для шестиугольников s = 120°*3 = 360°. Название правильному многограннику дается по общему числу граней М. Таким образом, из равносторонних треугольников можно составить три правильных многогранника при m = 3, 4, 5 (при m = 6 s = 60°*6 = 360°): 1. Тетраэдр (четырехгранник): m = 3, М = 4. 2. Октаэдр (восьмигранник): m = 4, М = 8. 3. Икосаэдр (двадцатигранник): m = 5, М = 20, а из квадратов и правильных пятиугольников — только по одному при m = 3 (при m = 4 s = 90°*4 = 360° — для квадратов и s = 108°*4 = 432° — для пятиугольников). 4. Гексаэдр (шестигранник), или куб: m = 3, М = 6. 5. Додекаэдр (двенадцатигранник): m = 3, М = 12. В любом выпуклом многограннике числа вершин L, граней М и ребер N связаны формулой Эйлера L + M — N = 2. (обратно)18
Пятая сущность - по-латыни квинтэсенция — у средневековых алхимиков ста означать тончайший элемент, составляющий якобы сущность вещей. Внастоящее время квинтэссенция — синоним самого главного, иболее существенного. (обратно)19
Любопытна история возникновения термина. Это название заимствовано американским физиком М. Гелл-Маном, высказавшим в 1964 г. гипотезу о существовании трех неизвестных частиц, из романа современного английского писателя Дж. Джойса "Поминки по Финегану". Хотя по-немецки "кварк" — это "творог", в романе слово означает нечто таинственное и непонятное. Герою романа снится сон, где чайки кричат: "Три кварка для мастера Марка". Так слово, изобретенное писателем Джойсом, стало едва ли не важнейшим термином современной ядерной физики. Вот они, узы науки и искусства! (обратно)20
Заинтересовавшийся читатель может легко воспроизвести эти расчеты. Например, для куба с ребром а имеем R = a√3/2, r = a/2, откуда R/r = √3 1,732. Современные усредненные pадиусы орбит Сатурна и Юпитера соответственно равны Rс = 1,427*109 км и Rю = 0,788*109 км, откуда Rс/Rю= 1,834. По Коgерyику, Rс/Rю= 1,758.
(обратно)
1,732. Современные усредненные pадиусы орбит Сатурна и Юпитера соответственно равны Rс = 1,427*109 км и Rю = 0,788*109 км, откуда Rс/Rю= 1,834. По Коgерyику, Rс/Rю= 1,758.
(обратно)
Последние комментарии
1 час 6 минут назад
5 часов 14 минут назад
5 часов 31 минут назад
5 часов 52 минут назад
8 часов 34 минут назад
15 часов 57 минут назад