Секреты числа пи [Почему неразрешима задача о квадратуре круга] (Мир математики. т.7.) [Хоакин Наварро] (fb2) читать онлайн

Хоакин Наварро «Мир математики» № 7 «Секрет числа π. Почему неразрешима задача о квадратуре круга»

…это загадочное число 3,14159…, которое пробирается в двери и окна и ускользает через дымоходы.

Огастес де Морган

Предисловие

Мир чисел бесконечен и неисчерпаем. Но чем дальше мы углубляемся в него, тем сложнее его понять. Если мы хотим познать его, нам не остается ничего другого, кроме как напрячь извилины. Так появилась и сформировалась теория чисел — сегодня это большая и прочная ветвь пышного дерева математики.

Теория чисел изучает дружественные числа, простые числа, избыточные числа, трансцендентные числа, рациональные числа, случайные числа, вычислимые числа, нормальные числа, вещественные числа, гиперреальные числа, трансфинитные числа, фигурные числа, комплексные числа, псевдопростые числа, неприкосновенные числа, апокалиптические числа и так далее. По правде говоря, за словами «и так далее» кроется немало других чисел.

Но чем вызвано увлечение числами? Почему многие люди с предубеждением относятся к числу 13? Число 666 упоминается в «Откровении Иоанна Богослова» и называется «числом зверя». Почему это число получило такое имя? Кому-нибудь интересно, что треугольник со сторонами 2166969314861378833054797972928630716401520276869946534608169199233884599269 и 2166969314861378833054797972928630716401520276869946534608169199233884599269 обязательно является прямоугольным? Знаете ли вы, что серьезные исследователи посвящают свое время изучению так называемых «самовлюбленных» чисел? Очевидно, что в мире, где существуют числа-палиндромы и дружественные числа, возможны любые, даже самые абсурдные вещи.

Существуют числа на любой вкус, каждое имеет свое определение, и в этом смысле число π не исключение: оно принадлежит к трансцендентным числам и, как считается, к множеству нормальных чисел и нескольким другим. Кроме того, это число — самое изучаемое и самое поразительное в истории. О нем написано столько книг, что сказать что-то новое практически невозможно. Поэтому автор ограничится лишь подробным и увлекательным рассказом о той мании, что окружает число π. Он попытался сделать повествование кратким и понятным любому заинтересованному читателю.

К сожалению, как говорил еще Евклид царю Птолемею I, «к геометрии нет царской дороги», и изучение чисел требует определенных умственных усилий. Оставим надежды на то, что книги о математике могут быть простыми. Книги о математике нельзя прочесть в один присест, но из-за этого столь велико удовольствие, получаемое от чтения. Однако книга о математике совершенно не обязана быть скучной.

Итак, сколько же усилий придется приложить? Почему ученые считают десятичные знаки числа π? Зачем нам нужно знать первый миллиард знаков π? Это число содержит бесконечно много цифр, и рассчитать их непросто. Возможно, простой метод расчета не существует или находится за гранью нашего понимания. Существует ли предел знаниям о числе π и его знаках? В чистой математике время от времени возникают вопросы о полезности подобных знаний. Возможно, лучшим ответом будет тот, что предложил выдающийся немецкий математик Карл Густав Якоби, который в 1830 году, защищая необходимость обучения математике, сказал: «Единственной целью науки является честь человеческого разума». Погрузимся же в чтение этой книги, вдохновленные этой мыслью. Мы не говорим о том, что нужно познать всё, познать многое или извлечь пользу из наших знаний. Речь идет о том, чтобы узнать некоторые интересные и занимательные факты о числах просто потому, что они красивы. Ради чести человеческого разума.

Глава 1 Все, что вы хотели узнать о числе π, но боялись спросить

Совместны у круга начало и конец.

Гераклит

Число π — самое известное, самое изученное, самое знаменитое и самое упоминаемое. Важность числа π невозможно преувеличить. Его десятичная запись начинается так:

3,14159265358979323846264338327950288419716939937510…

и этих пятидесяти магических цифр достаточно для любых практических вычислений. В математике или физике редко встретится задача, для которой необходимо использовать более десяти знаков π. Для простейших вычислений используются приближенные значения: 3,14 или 3,1416.

Айзек Азимов как-то написал: «Если бы Вселенная имела форму сферы диаметром 80 миллиардов световых лет, то с помощью 35 знаков числа π мы смогли бы вычислить длину ее небесного экватора с погрешностью меньше одной миллионной доли сантиметра».

Если мы запишем число π, рассчитанное на компьютере на данный момент, цифрами размером с эту книгу, то получившийся ряд цифр опишет 500 витков вокруг экватора Земли. Точно известно, что последовательность 0123456789 встречается в числе π начиная с 17387594880-го знака. Какой же наивной кажется убежденность известного голландского математика Лёйтзена Эгберта Яна Брауэра (1881–1966), который считал, что искать эту последовательность в числе π бессмысленно, поскольку необходимое для этого число знаков никогда не будет вычислено.

В XXI веке мы наконец нашли неоспоримую пользу от вычисления числа π с такой точностью: для тестирования суперкомпьютеров используются сложные вычисления, результат которых должен быть заранее известен, и для этого идеально подходит расчет знаков числа Я.

Повторное изобретение колеса

Число π не появилось из пустоты, как это можно было бы предположить. Оно возникло как результат несложных наблюдений. Соотношение между длиной окружности L и ее диаметром d постоянно:

L/d = π.

Или, что то же самое,

L = π∙d = π2r = 2πr,

где r — радиус окружности, d = 2r.

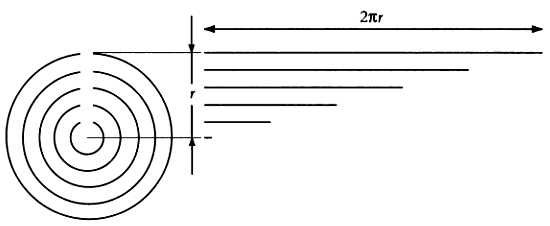
Отношение длины окружности к ее диаметру постоянно. Это соотношение интуитивно понятно и становится очевидно после несложных наблюдений. С увеличением диаметра (диаметр равен удвоенному радиусу r) пропорционально возрастает длина окружности.

Чем больше диаметр колеса, тем больше (и пропорционально больше) расстояние, пройденное точкой колеса при полном обороте. Иными словами,

длина окружности/диаметр окружности = константа ~ 3,14.

Знак ~ читается как «приближенно равно». На протяжении большей части истории числа π ученые старались сделать это приближение как можно более точным, находя всё новые знаки справа от 3,14.

Математики использовали все свое умение, чтобы рассчитать число π с наиболее возможной точностью, добавляя десятичные с героическими усилиями.

ВЫПРЯМЛЕНИЕ ОКРУЖНОСТИ

Выпрямление кривой означает измерение ее длины. В простейшей задаче о выпрямлении кривой речь идет об окружности.

При качении окружности длины р по прямой без скольжения окружность описывает один оборот, проходя расстояние, равное диаметру d, π раз. Этот процесс называется выпрямлением окружности. По результатам выпрямления окружности получим p/d = π.

* * *

Долгое время считалось, что когда-нибудь будет найдена последняя цифра числа π, но в 1882 году немецкий математик Фердинанд фон Линдеман (1852–1939) доказал, что это невозможно. Не существует и никогда не будет найдено способа получить «точное» значение π, пользуясь только циркулем и линейкой. Далее в этой книге мы попытаемся объяснить, почему это так.

Сначала число π имело другое название. Хотя к этому символу обращались многие математики, в частности Уильям Отред (1574–1660), Исаак Барроу (1630–1677) и Дэвид Грегори (1659–1708), «официально» его утвердил Уильям Джонс (1675–1749) в 1706 году в работе Synopsis Palmariorum Matheseos, где он использовал букву π, первую букву греческого слова «περιφε'ρεια» — «окружность». Впоследствии великий Леонард Эйлер (1707–1783), который сначала оперировал символами «с» и «р», остановился на греческой букве π, после чего это обозначение начало медленно, но верно распространяться в научном мире. Однако в XX веке в Египте число «пи» маркировали арабской буквой ta по нескольким причинам, в том числе из-за нежелания пользоваться европейскими обозначениями.

Сегодня символ π используется в математике в основном для обозначения числа π, но он также выполняет и другие задачи. Так, π(x) обычно отмечают функцию, показывающую «количество простых чисел, не превосходящих х». Если говорить о менее серьезных вещах, то этой буквой также обозначают гептамино — фигуру, состоящую из семи квадратов, соединенных сторонами, как показано на рисунке:

Многие авторитетные ученые, в том числе и Эйнштейн, считали число π фундаментальным в описании Вселенной. В том или ином виде число π всегда будет всплывать в описании любого явления природы, связанного с окружностями, кругами или вращением, подобно тому как пробка всплывает на поверхность воды. Как и другие константы, π всегда будет сопровождать нас.

С другой стороны, множество людей, которым в той или иной степени интересна нумерология, ищут число π буквально повсюду, как если бы существовала некая теория заговора, связанная с π. Так называемая постоянная тонкой структуры, обозначаемая как ОС, — излюбленная жертва поклонников числа π. Нобелевский лауреат Вернер Гейзенберг (1901–1976) много лет назад предположил, что

1/α = 2⁴∙3³/π

Но Гейзенберг был не единственным, кто искал связь между этими константами. В различных трудах фигурируют и другие подобные соотношения достаточно высокой точности, например:

ПЛАНЕТА МАЛЕНЬКОГО ПРИНЦА

Существует любопытный факт, который далеко не очевиден. Так как для окружности выполняется соотношение

длина/диаметр — константа,

то при увеличении знаменателя в некоторое число раз числитель увеличится в это же число раз. Проиллюстрируем это простым примером. В сказке французского писателя и авиатора Антуана де Сент-Экзюпери (1900–1944) «Маленький принц» главный герой обходит свою планету и чистит вулканы. Допустим, что он обходит всю планету по меридиану. Рост принца ровно 1 метр. Если он пройдет 1000 метров, какое расстояние пройдет его голова? Будем производить все расчеты в метрах. Так как Маленький принц проходит 1000 метров и

длина окружности = 2π∙r,

очевидно, что

пройденное расстояние = 1000 = 2π∙r.

Рост принца равен 1 метру. Приняв за С расстояние, пройденное его головой, получим

C = 2π∙(r + 1).

Вычтем первое равенство из второго. Имеем:

расстояние в метрах, пройденное головой — расстояние в метрах, пройденное ногами

С = 1000 — 2π∙(r + 1) — 2πr = 2π∙(r + 1 — r) = 2π ~ 6,28.

Разница составляет 6,28 м. Любопытно, что радиус планеты никак не влияет на это значение.

Фактически, если мы прибавим к радиусу исходной окружности 1 метр, ее длина увеличится на 6,28 м. Если бы радиус астероида составлял 1000 километров, то дополнительное расстояние, пройденное головой Маленького принца, осталось бы таким же: 6,28 м.

Обложка «Маленького принца» Антуана де Сент-Экзюпери.

Многовековая задача

Число π — не только соотношение между длиной окружности и ее диаметром. Удвоенное отношение между площадью круга и площадью вписанного в него квадрата также равно π. Как нам известно из школы, площадь круга радиуса г равняется

S = πr².

Так как площадь квадрата равна квадрату его стороны, по теореме Пифагора получим

S/Площадь вписанного квадрата = πг²/2r² = π/2

Но откуда мы знаем, что число π, используемое для расчета площади, — это то же самое π, с помощью которого рассчитывается длина окружности? Несомненно, это одно и то же число, однако доказать это не так просто. Строгое доказательство появилось только благодаря усилиям Архимеда.

Умы древних математиков волновала задача о построении квадрата, по площади равного данному кругу. Задача имела чисто практическое применение: площадь квадрата вычисляется элементарно, тогда как расчет площади круга был сложен и результатом являлось лишь приближенное значение. Во времена расцвета Древней Греции к этой задаче добавилось еще одно ограничение: искомый квадрат нужно было построить только с помощью циркуля и линейки. Этот метод считался «чистым», «божественным» и соответствовал духу греческой философии. В этом и заключается задача о квадратуре круга: необходимо построить искомый квадрат, используя только циркуль и линейку конечное число раз. Математики бились над задачей, решение которой всякий раз казалось столь близким и неизменно ускользало от них.

На протяжении веков все геометры пытались решить задачу о квадратуре круга, что равносильно построению отрезка длиной π с помощью циркуля и линейки, и всякий раз им удавалось найти лишь более точное приближенное значение и добавить еще один знак к десятичной записи π. Алгебраически задача о квадратуре круга площадью πr² равносильна нахождению квадрата со стороной l такого, что

πr² = l².

Иными словами, необходимо найти такое l, что

l = √(πr²) = r√π,

что тождественно нахождению √π с помощью циркуля и линейки. Если значение √π найдено, то найти π с помощью циркуля и линейки элементарно, построив прямоугольный треугольник с катетами 1 и √π, а затем продлив перпендикуляр к гипотенузе полученного треугольника до пересечения с продолжением единичного отрезка.

В силу подобия треугольников ABD и ADC выполняется соотношение АВ/AD = AD/АС, откуда AD² = АВ∙АС.

Подставляя известное значение АВ = 1 и найденное AD = √(1 + π), получаем: 1 + π = АС, то есть ВС = π.

Если бы значение π было определено, было бы возможным найти √π и решить задачу о квадратуре круга. Но за этой простой формулировкой кроется длинная история, герои которой безуспешно пытались достичь заветной цели, всякий раз все ближе подходя к ней. Очередной талантливый геометр находил следующий знак π и тем самым неявно продвигал всю математику в целом на шаг вперед.

РАДИАН И π

В математике для измерения углов не используются градусы, минуты и секунды. Также не применяются грады и метрические минуты и секунды. Появление математического анализа (производных, интегралов и пр.) привело к тому, что начала использоваться более естественная единица измерения, пусть на первый взгляд она и кажется сложнее. Радиан определяется как угловая величина дуги, длина которой равна ее радиусу.

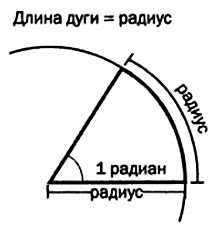
Так как длина всей окружности равна 2πr, то всю окружность можно представить в виде дуги в 2π радиан. Таким образом,

1 радиан — 360/2π градусов ~ 57°17′5''

Часто применяются следующие соотношения:

30° = π/6; 60° = π/3; 90° = π/2; 180° = π; 360° = 2π.

История числа π: гомеровская Греция

Из нескольких стихов Библии следует, что π = 3. В Библии это значение упоминается в описании постройки круглого алтаря, поэтому не следует расценивать это как попытку рассчитать его точное значение. Приведем цитату из 3-й книги Царств (7:23) для любопытного читателя: «И сделал литое [из меди] море — от края его до края его десять локтей — совсем круглое, вышиною в пять локтей, и снурок в тридцать локтей обнимал его кругом».

Проницательный читатель заметит, что значение числа π в этом тексте принято равным 3.

В египетском папирусе Ахмеса (древнеегипетское учебное руководство по математике, датированное примерно 1650 г. до н. э.) также неявно упоминается π. В задаче под номером 50 из 87 говорится: «Круглое поле имеет в диаметре 9 хет (1 хет ~ 50 м). Какова площадь поля?» На современном языке площадь этого круга выражается так:

π∙(9/2)² = π∙(81/4)

В самом папирусе Ахмеса предложено такое решение:

(64/81)∙d²

где d — диаметр. Так как d = 9, получим

π∙(81/4) = (64/81)∙d² = (64/81)∙9² = (64/81)∙81;

π = 256/81 ~ 3,160493827.

Согласно папирусу Ахмеса, квадрат со стороной 8 равен по площади кругу диаметра 9.

Однако это значение менее точно, чем полученное египтянами в Гизе еще в 2600 г. до н. э. Соотношение периметра и высоты пирамид Гизы равно 22/7, хотя считается, что оно подчинялось неким божественным законам, которым следовали архитекторы того времени. Многие исследователи считают это соотношение приближенным значением ТС, которое загадочным образом определили строители пирамид. Если мы допустим, что соотношение периметра и высоты пирамид не случайно, получим

π = 22/7 = 3,142…,

что соответствует π с хорошей точностью.

В Вавилонии в этом смысле прогресс шел медленнее: на глиняной табличке из древнего города Суса, датированной примерно 200 г. до н. э., приведено значение π, равное 25/8 = 3,125.

В ведических текстах Древней Индии, относящихся к IX веку до н. э., приводятся различные значения π, рассчитанные для разных практических задач. Наиболее точное значение основано на астрономических вычислениях и содержится в «Шата-патха-брахманы»: π = 339/108 = 3,1388…

История числа π: Архимед

Перенесемся в Древнюю Грецию — родину одного из величайших умов человечества, Архимеда из Сиракуз. Возможно, еще в V веке до н. э. вычислением числа π занимался Анаксагор, но письменных свидетельств этого не сохранилось. Мы не будем приводить здесь выкладки Архимеда о расчете приближенного значения π, так как они сложны и объемны. Оставим их историкам науки. Попробуем объяснить метод Архимеда простым и доступным образом, используя современное понятие предела. Представим себе многоугольник, вписанный в окружность, подобный тому, что изображен на рисунке.

Заметим, что он состоит из треугольников с основаниями Ь и высотой h. Общая площадь n треугольников, примерно равная площади круга, равна

S_n = п площадь треугольника.

Таким образом,

Перейдя к пределу и увеличивая число треугольников так, что n —> , получим

так как

и придем к следующему заключению:

Архимеду было неизвестно современное определение предела, и он использовал так называемый метод исчерпывания, созданный Евдоксом Книдским (400–347 до н. э.). Для этого Архимед использовал вписанные и описанные многоугольники, как показано на рисунке. Окружность заключалась между вписанным и описанным многоугольниками, соответственно, была ограничена и площадь окружности. С ростом числа углов многоугольников оценка площади окружности становилась все точнее.

Схема, на которой изображен так называемый переход к пределу, поможет понять, почему площадь круга равняется πr²:

Мы видим, как формируется криволинейный параллелограмм и его стороны постепенно распрямляются. Вспомним, что площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне. Высота постепенно приближается к значению радиуса r, а основание — к половине длины окружности. Площадь параллелограмма стремится к

r∙(l/2) = r∙(2πr/2) = rπr = πr²

Архимед вычислил верхнюю и нижнюю оценку значения π:

223/π = 3,140845… < π < 22/7 = 3,142857…

с отменной точностью.

АРХИМЕД ИЗ СИРАКУЗ (ОК. 287 — ОК. 212 ГГ. ДО Н.Э.)

Греческий инженер, физик, астроном и математик Архимед считается важнейшим ученым античности и одним из величайших умов человечества. В области математики фигурами сопоставимой величины можно назвать лишь Ньютона, Гаусса и фон Неймана. Его вклад в науку неоценим. Он создал червячную передачу, параболические зеркала, многочисленные системы блоков (полиспасты) и многие другие механизмы. Наверное, самым значимым стал открытый им закон гидростатики, известный нам как закон Архимеда. Образ Архимеда, который выскакивает из ванной и кричит «Эврика!» («Нашел!»), стал классическим образом первооткрывателя. Его открытия в математике бессчетны: помимо вычисления числа к он определил периметр, площадь, объем и центр тяжести для множества геометрических фигур и тел (в частности, для сферы, цилиндра, параболы, спирали и пр.), изучал диофантовы уравнения, построил счисление, позволяющее записывать и называть весьма большие числа, и так далее.

Он умер во время осады Сиракуз, при обороне которых использовались придуманные им механизмы. Согласно Плутарху, Архимед рассматривал чертеж на песке, когда к нему подошел римский солдат. Архимед настойчиво просил его подождать, сказав: «Не трогай мои чертежи», после чего разгневанный солдат зарубил Архимеда мечом. Плутарх пишет, что смерть Архимеда возмутила римского генерала, который считал ученого очень ценной добычей.

На могиле великого геометра изображен шар, вписанный в цилиндр. Соотношение между объемами цилиндра и вписанного шара открыл именно Архимед.

Одно из многочисленных изобретений, приписываемых Архимеду, — система бронзовых зеркал. С помощью этих зеркал защитники Сиракуз поджигали римские корабли, фокусируя на них солнечные лучи.

* * *

Метод, использованный Архимедом, стал фактически обязательным к применению в последующие несколько веков. Он доступен, прост и понятен. Математический гений Архимеда создал настоящее чудо. По существу, Архимед придумал алгоритм расчета π с любой точностью. Чтобы использовать этот алгоритм, нужен только калькулятор или компьютер и одна рекуррентная формула. Если n — число сторон вписанного или описанного многоугольника, а а_n и Ь_n — периметры таких многоугольников, то

a_2n = 2a_nb_n/(a_n + b_n),

b_2n = √(a_2nb_n).

В этом и заключается суть алгоритма Архимеда — рекуррентной формулы, с помощью которой рассчитывается приближенное значение π, точность которого повышается по мере роста п. Всегда выполняется соотношение а_n > π > Ь_n.

Используя алгоритм Архимеда начиная с правильного шестиугольника, в котором а₀ =4√3 и b₀ = 6, получим:

3,00000 < π < 3,46410

3,10583 < π < 3,21539

3,13263 < π < 3,15966

3,13935 < π < 3,14609

3,14103 < π < 3,14271.

Рассчитав значения этого неравенства для правильного 96-угольника, мы получим оценку числа π, вычисленную самим Архимедом.

История числа π: от Архимеда до наших дней

Примерно в 20 году до н. э. известный римский архитектор, военный инженер и писатель Марк Витрувий Поллион (ок. 85 — ок. 20 гг. до н. э.), более известный как Витрувий, создал монументальный труд «Десять книг об архитектуре», где используется соотношение, найденное в Месопотамии: π = 25/8. Сам Витрувий произвел оценку числа π с помощью колеса с нанесенными отметками. Тем не менее он известен потомкам не поэтому, а благодаря рисунку Леонардо да Винчи «Витрувианский человек» с каноническими пропорциями человека.

«Витрувианский человек» с каноническими пропорциями тела человека, определенными древнеримским архитектором Витрувием. Знаменитый рисунок Леонардо да Винчи (1452–1519).

Несмотря на столь широкую известность, Витрувий не добился более точного результата, чем Архимед. Это удалось египетскому астроному, астрологу и географу греческого происхождения Клавдию Птолемею (ок. 100 — ок. 170 гг.). Для расчетов он использовал 120-угольник, получив поразительно точный результат π = 3 + (17/120) = 3,141666… К сожалению, это не принесло ему заслуженной славы среди потомков. Он известен благодаря одному из своих трудов, «Альмагесту» в 13 книгах, название которого с древнегреческого переводится как «Великое построение». С этой книги началась традиция создания трудов, описывающих все известные на данный момент знания. Фактически «Альмагест» Птолемея не терял актуальности вплоть до появления работ Коперника.

Уделяя основное внимание западной культуре, мы часто забываем, что в эпоху Античности процветали и другие города помимо вавилонских, греческих, римских и египетских. Западная цивилизация наблюдала появление числа π, но что же происходило в это время на далеком Востоке?

Например, в Китае этому вопросу уделяли внимание Чань Цан (ок. 220 г. до н. э.), который принял значение π равным 3, и другие математики. Чжан Хэн (78-139 гг.н. э.), который занимался астрономией и математикой и изобрел прибор для регистрации землетрясений, в одной из своих книг рассчитал значение π = 736/232 = 3,1724… При вычислении объема шара, вписанного в куб, он использовал приближенное значение π = √10 = 3,162277…

Ван Фань (217–257 гг. н. э.) в 250 году рассчитал приближенное значение π = 142/45 = 3,155555…

Математик Лю Хуэй (ок. 220 — ок. 280 гг.) является автором комментариев к «Математике в девяти книгах». Именно по этим комментариям, изданным в 263 году, нам известно о существовании этого ученого и о его достижениях. Лю Хуэй приводит рекуррентную формулу для расчета периметра правильного многоугольника, имеющего 3∙2^k сторон при известном периметре многоугольника, число сторон которого равно 3∙2^k-1. Лю Хуэй рекомендовал использовать значение π = 3,14, хотя сам он вычислил значение π = 3,141592104…, для чего потребовалось использовать многоугольник с 3072 сторонами.

Несколько веков спустя Цзу Чунчжи (429–500 гг.), ученый и математик, который разработал новый календарь, с превосходной точностью оценил верхнюю и нижнюю границы числа π:

3,1415926 < π < 3,1415927.

Он также рекомендовал использовать значение 22/7 для простых вычислений и 355/113 — для более сложных.

Перенесемся в Древнюю Индию, где выдающийся мудрец Ариабхата (ок. 476–550 гг.) получил значение π, равное 3,1416, используя многоугольник с 384 сторонами.

Брахмагупта (598–665 гг.), вне всякого сомнения наиболее одаренный индийский математик, создал объемный труд «Брахма-спхута-сиддханта», где, к сожалению, приводится достаточно неточная оценка

π = √10 = 3,162277…

Марка, выпущенная в 1999 году Федеративными Штатами Микронезии, на которой изображен метод Лю Хуэя для расчета приближенного значения π.

Более точное значение было получено лишь в XII веке усилиями Бхаскары II (1114–1185) в его книге «Лилавати». Книга носит имя его дочери, которая, если судить по важности этого труда, должна была быть прекраснейшей девушкой — удивительно, но именно это и означает имя Лилавати. Бхаскара II приводит π = 3917/1250 = 3,1416.

Наша система счисления является позиционной с основанием 10. В ней используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, имеющие индо-арабское происхождение. Мы не уделяем этому особого внимания, но именно появление этой системы счисления способствовало развитию торговли: западная цивилизация получила математический инструмент, благодаря которому вычисления стали доступны для всех.

Индо-арабские цифры в том виде, в каком они впервые появились в западном мире (974–976 гг.) в Альбельденском (Вигиланском) кодексе, названном так по имени монаха — автора иллюстраций для этого собрания документов.

Подробная история индо-арабских цифр выходит за рамки нашего повествования. Отметим лишь, что свое название они получили по месту происхождения. Удивительно, но на Западе эти цифры и система счисления в целом появились лишь в X веке в «Книге Абака» Леонардо Пизанского (ок. 1170–1250), также известного как Фибоначчи. Индо-арабские цифры распространились в Европе с быстротой молнии, особенно среди торговцев и образованных людей. Расчеты в новой системе счисления перестали быть такими проблематичными благодаря простым правилам умножения и деления. Цивилизация сделала медленный, но важный шаг вперед.

На середине нашего повествования мы впервые встречаем имя Фибоначчи, который в 1220 году вычислил приближенное значение π = 3,141818 в одной из своих работ «Практика геометрии» (Practica geometriae), несколько вольно применив метод Архимеда.

Но не будем забегать вперед. Обратим внимание на фигуру Мухаммеда ибн Муса аль-Хорезми (ок. 780–850 гг.), также называемого аль-Хорезми. От видоизмененного имени аль-Хорезми берет начало термин «алгоритм». Аль-Хорезми является автором «Книги о восполнении и противопоставлении», от арабского названия которой происходит слово «алгебра». Его труды, переведенные на Западе, имели огромнейшее влияние. Аль-Хорезми также рекомендовал использовать значение 3,14 в простых расчетах и 3,1416 — в сложных, например, в астрономии.

Героический образ аль-Хорезми, запечатленный на советской марке 1983 года (аль-Хорезми жил на территории современного Узбекистана).

В 1424 году другой персидский ученый Джамшид ал-Каши (1380–1429) из Самарканда рассчитал значение 2π с точностью до 9 знаков, используя шестидесятиричную систему счисления (в ней числа записываются следующим образом: 1/60 = 0,1; 1/60² = 1/360 = 0,01 и т. д.). После перевода в десятичную систему счисления это соответствует точности в 16 знаков после запятой. Ал-Каши вычислил:

2π = 6 + 16/60 + 59/60² + 28/60³ + 1/60⁴ + 34/60⁵ + 51/60⁶ + 46/60⁷ + 14/60⁸ + 50/60⁹ + …,

используя многоугольники с числом сторон 3∙2²⁸. За четверть века до него, в 1400 году, индийский математик Мадхава из Сангамаграма (ок. 1350 — ок. 1425) вычислил π с точностью до 13 знаков. Кроме того, расчеты Мадхавы отличаются оригинальностью: в них впервые используется бесконечный ряд для оценки значения π. Формула Мадхавы позднее стала известна в западном мире как «ряд Лейбница», но Мадхава открыл ее намного раньше:

π/4 = 1–1/3 + 1/5 — 1/7 + 1/9 — …

Этот ряд сходится очень медленно. Чтобы получить более или менее приемлемый результат, необходимо сложить тысячи членов ряда. Мадхава использовал этот ряд в преобразованном виде:

π = √12∙[1 — (1/3∙3) + (1/5∙3²) — (1/7∙3³) +…]

что и помогло ему вычислить π.

Немецкий ученый Валентин Отто (ок. 1550–1603), ярый последователь Коперника, в 1573 году рекомендовал использовать π = 355/113 ~ 3,1415929… Однако это не идет ни в какое сравнение с результатами, полученными спустя некоторое время с помощью передовых способов вычисления, а не просто путем аккуратно проведенных расчетов. Французский математик Франсуа Виет вычислил девятый знак числа π обычным способом, используя метод Архимеда и многоугольник с 393216 (6∙2¹⁶) сторонами. Хотя ему и удалось вывести важную формулу, связанную с π, он не смог применить ее из-за сложных вычислений: его формула включает вычисление квадратного корня из квадратного корня числа. На современном языке математики формула Виета записывается следующим образом:

Вывод этой и других формул подробно объясняется в главе 4.

ФРАНСУА ВИЕТ (1540–1603)

Строго говоря, Виета нельзя назвать профессиональным математиком: он был адвокатом, а после восшествия на престол Генриха IV занял должность при дворе и даже служил королевским советником. Легендарную известность ему принесла криптография: он с легкостью расшифровывал послания испанского монарха Филиппа II, врага Генриха IV. Филипп II в конце концов заподозрил, что французский король заключил сделку с дьяволом, поскольку ему удавалось мгновенно угадывать все его дипломатические уловки, Виет достиг отличных результатов в геометрии и алгебре, продвинул вперед тригонометрию и решение уравнений. Возможно, важнейшим из его открытий является создание современного символического языка алгебры, который произвел революцию в математике и способствовал прогрессу в науке.

Его принципиальным соперником, а впоследствии другом был Адриан ван Роумен (1561–1615).

Виет предложил ему задачу о касающихся окружностях, известную как задача Аполлония.

В задаче Аполлония необходимо найти все окружности, касающиеся трех данных окружностей. По традиции, решение нужно было найти только с помощью циркуля и линейки.

* * *

Друг и соперник Виета, голландский геометр Адриан ван Роумен (1561–1615) бросил все силы на изучение метода Архимеда и, использовав многоугольники с огромным числом сторон, в 1593 году с точностью определил 16 десятичных знаков π.

Но огромный труд ван Роумена не сравнится с работой, которую проделал Аюдольф ван Цейлен (1540–1610). Этот немецкий математик был одержим идеей вычисления числа π. В 1596 году он нашел первые 20 знаков, позднее доведя число знаков до 35, которые стоит привести здесь:

π = 3,14159265358979323846264338327950288…

В общем случае эта задача имеет восемь различных решений.

Ван Цейлен получил такую известность, что во многих странах число π стало известно как лудольфово число. Свое любимое число ван Цейлен даже повелел высечь на своем надгробии в городе Лейден. К сожалению, во время Второй мировой войны его могила была разрушена. В главе 5 приведена иллюстрация, на которой изображена его могила с нанесенными на каменное надгробие знаками числа π, восстановленная в 2000 году. Упорные труды ван Цейлена заслуживают подобного памятника.

Виллеброрд Снелл (1580–1626), печатавшийся под латинизированным именем Снеллиус, прежде всего известен как первооткрыватель законов преломления света. Он также пробовал вычислить число π и рассчитал 35 его знаков, опубликованных в 1621 году в книге Cyclometricus. Он использовал ощутимо более точный способ по сравнению с методом Архимеда. Правильность расчетов Снелла позднее подтвердил великий Христиан Гюйгенс (1629–1695).

В 1630 году астроном Христоф Гринбергер (1561–1636), австрийский иезуит, установил новый рекорд, дойдя в расчетах до 39-го знака. Потомки достойно увековечили его память: его имя носит один из лунных кратеров. Нельзя представить лучшее вознаграждение для астронома и для того, чей сан священника не позволял принимать мирские подношения.

Большой скандал и открытие математического анализа

Готфрид Лейбниц и Исаак Ньютон обессмертили свои имена, создав анализ бесконечно малых величин — кошмар для многих студентов, видящих в этой дисциплине лишь нагромождение интегралов и производных. Лейбниц и Ньютон достигли математического рая: им удалось «приручить» бесконечность, более того, показать, как перейти от конечного к бесконечному и вернуться обратно, принеся с собой нужные результаты. Многие, подобно проницательному и мечтательному Архимеду, ступали на этот путь. Лейбниц и Ньютон смело прошли по нему и показали входы и выходы лабиринта, в котором скрывалось неизведанное.

Степенные ряды и интегралы — результат применения приемов анализа в математике. Расчет числа π перестал заключаться в механическом измерении многоугольников и стал математической задачей, требующей работы «маленьких серых клеточек», как говорил знаменитый сыщик Эркюль Пуаро.

Далее мы не будем упоминать об ученых Востока, занимавшихся вычислением π, за исключением случаев, когда им удавалось рассчитать π с крайне большой точностью или использовать оригинальные передовые методы.

ГОТФРИД ВИЛЬГЕЛЬМ ЛЕЙБНИЦ (1646–1716)

Коротко изложить самые важные достижения столь разностороннего ученого, как Лейбниц, далеко не просто. Достаточно упомянуть, что полное собрание его сочинений насчитывает 25 томов и 200000 страниц. Этот исключительный ученый родился в Лейпциге. Он занимался адвокатурой, дипломатией, математической логикой, религией, историографией, а также востоковедением, двоичной арифметикой, этикой, физикой, биологией, инженерным делом. Возможно, важнейшим его вкладом в науку является интегральное исчисление и анализ бесконечно малых.

Лейбниц был вундеркиндом, много читал и схватывал все на лету, жил, не стесняясь в средствах, зарабатывая юриспруденцией и дипломатией. Он участвовал в создании первого в истории научного журнала Acta Eruditorum, в котором публиковались многие, если не все его исследования и открытия.

Ему был присущ дар метко обозначать вещи. Так, именно ему мы обязаны введением знака интеграла  и дифференциала (dх), а также многих выражений, например «жизненная сила». Часть его жизни прошла в спорах с приверженцами Ньютона (за которыми стоял сам великий Ньютон) о том, кто же является подлинным автором исчисления. Сегодня считается, что и Ньютон, и Лейбниц совершили свои открытия независимо друг от друга, а совпадение по времени является случайным. Как математик Лейбниц также внес очень важный вклад в математическую логику, теорию автоматов, двоичную систему счисления и топологию, которую сам ученый называл analysis situs.

В 1673 году Лейбниц изобрел счетную машину, способную производить четыре основных арифметических действия. Годом позже он построил первый работающий образец.

* * *

Ньютон и Лейбниц на протяжении долгого времени вели спор о том, кому же принадлежит авторство исчисления, и можно сказать, что этот спор в итоге вылился в скандал. Не будем вдаваться в суть спора и сосредоточимся на его итогах.

Около 1666 года, в разгар Великого Лондонского пожара сэр Исаак Ньютон, казалось, прохлаждался без работы, поскольку год спустя он говорил, что занялся вычислением числа π «оттого, что тогда мне было решительно нечем заняться». Оставим в стороне мотивы, которыми он руководствовался, и рассмотрим суть его расчетов. Ньютон использовал биномиальную формулу и открыл ряд

с помощью которого точно вычислил 16 знаков π. Как и во многих других случаях, Ньютон не придал этому большого значения и не упомянул об этом ни в одной из своих книг. Этот результат был опубликован после его смерти.

Следовать по пути гения всегда интересно. Проследуем путем, который прошел Ньютон.

Площадь выделенного на рисунке сектора равна π/24, так как он равен одной шестой части окружности. Если вычесть площадь треугольника, равную √(3/32), то получим площадь части сектора, обозначенной 5. Уравнение окружности, показанной на рисунке, выглядит так:

у² + х² = х,

СЭР ИСААК НЬЮТОН (1642–1727)

Ньютон больше известен как физик и математик, хотя он занимался алхимией, богословием, политикой, астрономией и, естественно, многими другими дисциплинами. В любом случае он является одним из важнейших ученых в истории человечества.

Его основной труд Philosophiae naturalis principia mathematica («Математические начала натуральной философии») был издан в 1687 году главным образом благодаря влиянию родных, что говорит о том, насколько замкнутым и необщительным был Ньютон. В этой книге описываются его важнейшие открытия: закон всемирного тяготения (по легенде, Ньютон открыл этот закон после того, как ему на голову упало яблоко) и исчисление бесконечно малых. Среди его достижений в физике в первую очередь стоит отметить создание теории цветов и дифракции, первого зеркального телескопа и корпускулярной теории света. Он также сформулировал законы сохранения импульса и энергии. В его работах по астрономии удивительно точно описано движение планет и природа их орбит. В чистой математике помимо дифференциального и интегрального исчисления он также изучал множество степенных рядов, формулу бинома, теорию ошибок и численный метод нахождения нулей функции.

Ньютон дважды избирался в парламент, где почти всегда хранил молчание. Единственным легендарным исключением стал случай, когда он попросил закрыть окно, потому что ему мешал сквозняк. Став в 1699 году управляющим Монетного двора и проведя много реформ, Ньютон лично отправил на виселицу нескольких фальшивомонетчиков. Он всегда считал, что его открытия в алхимии и богословии (Ньютон был наполовину монофизитом и сохранял в тайне принадлежность к этой еретической доктрине) переживут его. Ньютона практически обожествляли еще при жизни, а после смерти и похорон в Вестминстерском аббатстве на все восхваления, казалось, был наложен строгий запрет. Это объяснимо, если мы вспомним историю расправы над фальшивомонетчиками.

Исаак Ньютон на картине Уильяма Блейка (1757–1827). Величие ученого и его влияние на научный мир вдохновили Александра Поупа (1688–1744) написать такие строки:

Природы строй, ее закон

В извечной тьме таился.

И бог сказал: «Явись, Ньютон!»

И всюду свет разлился.

(Перевод А. П. Павлова)

* * *

что можно представить в виде у² = х(1 — х) или у = √(x(1 — x)) = х^1/2(1 — х)^1/2 Применив методы интегрального исчисления, изобретенного самим Ньютоном, получим:

Теперь осталось лишь правильно выполнить интегрирование и не ошибиться в расчетах… либо нужно быть Ньютоном.

Его соотечественник Абрахам Шарп (1651–1742) использовал следующее равенство, полученное астрономом Эдмундом Галлеем (1656–1742):

π/6 = arctg(√3/3)

которое сегодня изучается в элементарной тригонометрии, а также важное соотношение, полученное еще одним британским ученым Джеймсом Грегори (1638–1675):

arctg x = x — (x³/3) + (x⁵/5) — …

и получил ряд, который на современном языке математики записывается так:

что в 1699 году позволило ему правильно вычислить 71 знак π. На самом деле Шарп рассчитал 72 знака, но ошибся в последнем. Это простительно, если учесть, что для этого пришлось сложить около 300 членов указанного ряда.

Заметим также, что в 1667 году Джеймс Грегори попытался доказать, что задача о квадратуре круга не имеет решения, но потерпел неудачу.

Несколько лет спустя, в 1706 году, Джон Мэчин (ок. 1686–1751), преподаватель астрономии, позднее ставший секретарем Лондонского королевского общества, вывелформулу, носящую теперь его имя:

π/4 = 4∙arctg (1/5) — arctg (1/239)

* * *

ДЖЕЙМС ГРЕГОРИ (1638–1675)

Не следует пугать Джеймса Грегори с его племянником Дэвидом Грегори (1659–1708), который также был математиком, дружил с Ньютоном и был одним из тех, кто ввел в употребление символ π, Джеймс Грегори известен в астрономии как изобретатель телескопа-рефлектора, а также благодаря разложению в бесконечные ряды тригонометрических функций (sin x, cos x, tg x) и обратных тригонометрических функций (arcsin х, arccos x и arctg x). Ряд, который был открыт также и Мадхавой из Сангамаграма и носит имя Мадхавы-Лейбница или Грегори-Лейбница, может быть записан в следующем виде:

Этот ряд сходится на интервале от — π/4 до π/4. Грегори одним из первых понял, что задача о квадратуре круга нерешаема.

Чтобы получить эту формулу, он выполнил следующие действия:

tg α = 1/5,

tg 2α = 2∙tg α/(1 — tg² α) = 5/12,

tg 4α = 2∙tg 2α/(1 — tg² 2α) = 120/119,

tg (4α — π/4) = (tg 4α — 1)/(1 + tg 4α) = 1/239.

Отсюда следует искомое равенство, так как

4α — π/4 = arctg tg (4α — π/4) = arctg 1/239.

Ha основе этой формулы вкупе с известными выражениями, например

arctg (x) = x — (x³/3) + (x⁵/5) — …

выводятся быстро сходящиеся ряды, с помощью которых Мэчин рассчитал π до сотого знака. Вне всякого сомнения, большой заслугой Мэчина является полученная им формула, записываемая в тригонометрическом виде, которую можно быстро преобразовать в ряд. Далее, когда мы будем рассказывать о Захариусе Дазе, то упомянем еще один любопытный факт, имеющий отношение к Мэчину.

Формулы, подобные той, что вывел Мэчин (так называемые формулы Мэчина), очень распространены, их изучением занимались многие исследователи независимо друг от друга. Мэчин стал первым среди них.

В девятом томе первого издания Французской энциклопедии, созданной силами Дени Дидро, упоминается Том Фанте де Ланьи (1660–1734), преподаватель гидрографии и математики, чей некролог редактировал сам Фонтенель. В 1719 году де Ланьи вычислил (сущая безделица!) 112 знаков π, использовав тот же степенной ряд, что и Шарп.

ЗАДАЧА, ПЕРЕД КОТОРОЙ НЕЛЬЗЯ УСТОЯТЬ

Математик Том Фанте де Ланьи (1660–1734), родившийся во французском городе Лионе; занял свое, пусть скромное, место в истории благодаря тому, что первым верно вычислил 112 знаков числа π — абсолютный мировой рекорд в то время. С ним также связан занимательный эпизод, произошедший незадолго до его смерти. Рассказывают, что его коллега Мопертюи пришел навестить его на смертном одре и обнаружил тело без признаков жизни. Чтобы удостовериться в этом, Мопертюи еле слышно прошептал: «Сколько будет 12 в квадрате?», предполагая, что ни один математик не устоит перед подобной задачей. Де Ланьи вскочил, громко воскликнул: *144!* — и умер.

* * *

На самом деле де Ланьи вычислил 127 знаков, но лишь 112 из них были верными, что подтвердил Георг Вега (1754–1802). Этот немецкий математик к концу жизни был удостоен высокого титула барона в Австрийской империи, что не спасло его от судьбы простолюдина: он был убит неким вором из-за денег и часов. В 1794 году Вега использовал одну из формул Мэчина, которую вывел Эйлер, чтобы вычислить 137 знаков π, на этот раз без ошибок. Он использовал следующую формулу:

π/4 = 5∙arctg (1/7) + 2∙arctg (3/79).

Банкнота в 50 словенских толаров, на которой изображен Гэорг Вега, а также геометрические построения и фазы Луны. На обороте слева от изображения Солнечной системы можно увидеть фасад Словенской академии наук в Любляне.

Между 1760 и 1800 годами параллельно были получены заслуживающие упоминания результаты. Так, Иоганн Генрих Ламберт (1728–1777), создатель неевклидовой геометрии, в 1761 или 1767 году (точная дата неизвестна) доказал иррациональность числа π. Адриен Мари Лежандр (1752–1833) несколькими годами позже показал, что π² также иррационально. Возможно, наиболее значимым является достижение великого Леонарда Эйлера (1707–1783), который искал многочисленные ряды для вычисления π и предположил, что число π является трансцендентным. Гипотеза Эйлера тем примечательнее, что само существование трансцендентных чисел доказал Жозеф Лиувилль (1809–1882) лишь много лет спустя, в 1840 году! Лиувилль также нашел первое трансцендентное число.

ИОГАНН ГЕНРИХ ЛАМБЕРТ (1728–1777)

Этот немецкий математик, астроном и врач изобрел гигрометр и фотометр. Он также первым доказал иррациональность числа тс, но этим его вклад в математику не ограничивается. Он изучал гиперболические функции и связал их с неевклидовой геометрией. Также он внес заметный вклад в картографию, и его имя носит одна из географических проекций. Ламберт был самоучкой, но когда речь заходила о признании его собственных заслуг, скромность покидала его. Фридрих II, сделав математика членом Прусской академии наук, спросил Ламберта, в каких же науках он преуспел. «Во всех», — последовал ответ, близкий к истине. Король с иронией заметил: «Значит, вы разбираетесь и в математике?» — «И в ней тоже», — честно ответил Ламберт. Несколько раздосадованный, Фридрих II продолжил: «И кто же был вашим учителем?» — «Я сам, Ваше Величество!» — и снова Ламберт не погрешил против истины. Король иронично сказал: «Ну и ну! Я стою перед вторым Паскалем!» — «По меньшей мере», — был ответ. Его доказательство иррациональности числа тс достаточно изобретательно и доступно для понимания. С помощью цепных дробей Ламберт показал (это наиболее сложная часть его доказательства), что если х — ненулевое рациональное число, то tg х иррационально. Так как tg π/4 = 1, а единица является рациональным числом, следовательно, π/4 и π являются иррациональными.

* * *

Говоря о вычислении π, мы специально не упоминаем об Эйлере, так как он никогда не добивался рекордной точности вычислений. Вероятно, это случилось лишь потому, что он не уделял этому достаточно внимания: как-то раз, используя формулы Мэчина, он вычислил 20 знаков π всего за час!

В 1841 году Уильям Резерфорд (1798–1871) использовал формулу Мэчина

π/4 = 4∙arctg (1/5) — arctg (1/79) + arctg (1/99).

и получил 208 знаков π, из которых 152 были верными. В 1853 году он вернулся к этой задаче и с помощью формулы Мэчина установил новый рекорд — 440 знаков.

ЧТО ТАКОЕ ТРАНСЦЕНДЕНТНОЕ ЧИСЛО?

Число называется алгебраическим, если оно является корнем многочлена

a_nxⁿ + a_n-1x^n-1 +… + a₁x + a₀

все коэффициенты которого а_n, а_n-1…., a₁, а₀ являются рациональными числами. В высшей математике доказывается, что любое число, которое можно получить, используя лишь циркуль и линейку конечное число раз, обязательно является алгебраическим. Неалгебраическое число называется трансцендентным. Таким образом» очевидно, что трансцендентное число нельзя получить построением с помощью циркуля и линейки.

* * *

Иоганн Мартин Захариус Дазе (1824–1861) занимает особое место в истории математики. Его друг Шульц фон Штрасницкий (1803–1852) показал ему следующую формулу Мэчина:

π/4 = arctg (1/2) + arctg (1/5) + arctg (1/8).

и в 1844 году Дазе вычислил с ее помощью 200 знаков π. Невероятно, но на это ему потребовалось лишь два месяца, и все расчеты он производил в уме. Он был настоящим человеком-компьютером и обладал невероятной способностью к вычислениям. Сам Гаусс, известнейший математик своего времени, советовал властям использовать Дазе для расчетов. Была учреждена премия, вручаемая тому, кто получит список делителей чисел N таких, что 7 000 000 < N < 10 000 000. Дазе начал работать над этой задачей, но смерть помешала ему найти решение. Дазе страдал синдромом саванта: он был поразительно одарен в математике, имел невероятную память, но в остальном был весьма и весьма средних способностей. Например, он мог перемножить два восьмизначных числа меньше чем за минуту. Для перемножения 100-значных чисел ему требовалось около девяти часов. Он обладал почти фотографической памятью, что позволяло ему с удивительной точностью пересчитывать любые предметы, будь то овцы, буквы или костяшки домино. Писатель и ученый Артур Кларк в письме к палеонтологу Стивену Джею Гулду задавался вопросом, какую пользу для эволюции биологического вида может иметь способность вычислить в уме 200 знаков числа π. Ответ на этот вопрос нам неизвестен.

В 1847 году датский астроном и математик-самоучка Томас Клаусен (1801–1885), используя две формулы Мэчина:

(1/4)∙π = 2∙arctg (1/3) + arctg (1/7),

(1/4)∙π = 4∙arctg (1/5) — arctg (1/239).

точно вычислил 248 знаков Я. Он также ошибся в вычислениях, но допустил ошибку в самом конце расчетов, всего вычислив 250 знаков.

В 1853 году его немецкий коллега Якоб Гейнрих Вильхельм Леманн (1800–1863) рассчитал 261 знак Я, что принесло ему известность в математике. Его именем также назван кратер на Луне. В следующем году немецкий профессор Рихтер вычислил 330, затем 400 и, наконец, 500 знаков.

Английский математик-любитель Уильям Шэнкс (1812–1882) посвятил свою жизнь вычислениям. Наряду с расчетами других констант в 1875 году он получил 707 знаков π, что увековечено на знаменитом фризе Дворца открытий в Париже. Но это стоило музею немалых затрат: фриз был построен в 1937 году, а в 1946 году Дэниел Фергюсон в статье в журнале Nature показал, что верными являются лишь первые 527 знаков. Огастеса де Моргана (1806–1871) крайне удивил тот факт, что цифра 7 встречается в записи числа π заметно чаще остальных.

Подобно многим ученым, занимавшимся объемными расчетами, Шэнкс допускал ошибки. Он не располагал правильным ответом, с которым можно было бы свериться, поэтому считал свои вычисления верными. Не стоит забывать, что в те времена не было ни компьютеров, ни калькуляторов, все расчеты выполнялись на листах бумаги, испещренных бесчисленными цифрами. Теперь во Дворце открытий можно посмотреть на исправленное значение π. Такова дань уважения объяснимой человеческой ошибке. В наши дни было обнаружено, где именно ошибся Шэнкс, который вычислял π поэтапно.

Не стоит умалчивать о достижении Фергюсона — последнего, о котором мы расскажем, прежде чем перейдем к повествованию о компьютерной эре. В 1947 году он опубликовал 808 знаков π. Для расчетов ему понадобился целый год, арифмометр, много терпения и следующая формула:

π/4 = 3∙arctg (1/4) + arctg (1/20) + arctg (1/1985)

В 1882 году немецкий математик фон Линдеман изрядно охладил пыл тех, кто занимался расчетами числа π, доказав, что оно не является алгебраическим, поэтому не может быть найдено построением с помощью циркуля и линейки. Линдеман доказал трансцендентность числа π. Следует отметить, что в его объемном доказательстве ни разу не использовались геометрические методы. Таким образом, число π покинуло мир геометрии, и это произошло точно в тот день, когда была доказана его трансцендентность.

Оригинальное доказательство Линдемана основано на тех же примерах, которые за несколько лет до того использовал Шарль Эрмит (1822–1901) для доказательства трансцендентности числа е — еще одной известной константы. Линдеман пришел к выводу, что линейная комбинация степеней е с коэффициентами A_k и показателями степени B_k (вещественными или комплексными)

А₁е^в1 + А₂е^в2 + … + А_nе^вn

не может быть равной нулю (за исключением случая, когда все коэффициенты нулевые). Так как знаменитая формула Эйлера может быть записана в следующем виде:

e^πi + 1 = e^πi + e⁰ = 0,

она удовлетворяет условиям Линдемана (А₁ = A₂ = 1, B₁ = πi, В₂ = 0), поэтому πi не может являться алгебраическим числом, равно как и само π. Число π не является алгебраическим, следовательно, оно трансцендентно. Так как оно трансцендентно, его нельзя получить построением с помощью циркуля и линейки. Конечно, за этим последовали новые, менее сложные доказательства, но и приведенных выкладок было достаточно, чтобы снять завесу тайны с числа π. До Линдемана было известно, что трансцендентность числа π означает, что задача о квадратуре круга нерешаема. Доказательство Линдемана положило конец поискам решения этой легендарной задачи. Было окончательно установлено: задача о квадратуре круга не имеет решения.

Глава 2 Бесконечная незначительность и трансцендентность числа π

Лицо π было скрыто маской. Все понимали, что сорвать ее, оставшись при этом в живых, не сможет никто. Сквозь прорези маски пронзительно, безжалостно, холодно и загадочно смотрели глаза.

Бертран Рассел

Мы подробно, знак за знаком, проследили путь числа π в поисках трансцендентности. Линдеман завершил поиски и расставил все по местам. Теперь мы знаем, что π трансцендентно, его нельзя построить с помощью циркуля и линейки, поэтому задача о квадратуре круга не имеет решения.

Чтобы лучше понять значимость и важность π в мире математики, совершим небольшую экскурсию в неспокойный мир бесконечности. Это отдельная вселенная, очень обширная и запутанная, полная вопросов, лежащих между философией и реальным миром. Этот мир настолько необычен, что некоторыми его аспектами занимается высшая математика, в которой действия с бесконечностью предельно упрощаются. Мы рассмотрим эту область лишь поверхностно, особенно не углубляясь. Тем не менее обзор бесконечности в математике нетривиален, требует определенных усилий, а иногда просто скучен и повергает в уныние.

Предупредив читателя, мы начинаем нашу экскурсию в мир бесконечности с почти что абсурдного вопроса: «Что такое число?» Чтобы ответить на него, начнем с рассмотрения самого представления о числах.

Числа и множества

В основе практически всех основных понятий лежат множества — простые совокупности объектов, которые мы будем перечислять в фигурных скобках, разделяя запятыми. Например,

А = {а, Ь, с, d}

обозначает множество А, образованное символами а, Ь, с и d. Вместо букв могут использоваться животные, люди, музыкальные инструменты и так далее. Это не принципиально. Будем использовать наиболее простое определение, которое эксперты называют «наивным»: будем считать множество совокупностью объектов, называемых «элементами множества».

Множества могут соответствовать друг другу — так обычно говорят о множествах, между которыми установлено взаимно однозначное соответствие. Например, множества

{а, Ь, с} и {Наполеон, , автор этой книги}

соответствуют друг другу, так как между их элементами можно установить взаимно однозначное соответствие и при этом не останется лишних элементов. Напротив, множества

{а, Ь} и {Наполеон, , автор этой книги}

не могут соответствовать друг другу, поскольку в правом множестве всегда будет оставаться один элемент, которому не будет соответствовать никакой элемент левого множества. Из этого следует, что определение числа имеет отношение к множествам. Современное рекурсивное определение числа может выглядеть так:

1 = {0}

2 = {0, 1}

3 = {0, 1, 2}

4 = {0, 1, 2, 3}

5 = {0, 1, 2, 3, 4}

…

n = {0, 1, 2, 3, 4…. n — 1}

Говорят, что множество А имеет n элементов, если А соответствует n, иными словами, если между А и n имеется взаимно однозначное соответствие. Так, множество игроков футбольной команды на поле содержит 11 элементов, множество апостолов содержит 12 элементов. Согласно вышеприведенному перечню, множество 11 выглядит так:

11 = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Нет никаких сомнений в том, что между этим множеством и любым множеством футболистов на поле можно установить взаимно однозначное соответствие.

Как же мы определим ноль? Когда говорят, что множество содержит 0 элементов? В «наивной» теории множеств множество является совокупностью объектов. Поэтому логично, что среди таких совокупностей встречаются пустые, которые не содержат ничего — как пустые коробки.

Не стоит путать пустое множество и ничто — метафизический объект, больше подходящий для философских споров. Пустое множество — это как раз то, внутри чего находится ничто. Это множество, которое не содержит элементов, но это не «ничто».

Для обозначения подобного множества (оно единственно, так как все пустые множества равны), французский математик Андре Вейль (1906–1998) предложил использовать датскую букву . Вайль был прекрасно знаком с алфавитами скандинавских языков, поскольку во время Второй мировой войны находился в заключении в Финляндии.

Будем обозначать символом пустое множество, которое не содержит элементов. Его можно определить многими способами, от забавных до вовсе абсурдных, например

 = {летающие коровы}.

Обозначим ноль так:

0 =

и будем говорить, что множество содержит 0 элементов, если между ним и множеством  можно установить взаимно однозначное соответствие.

Для обозначения числа элементов множества А используется следующее выражение: |А|. Также число элементов множества называется его кардинальным числом. Таким образом,

число элементов А = кардинальное число А = |А|.

В целом различают конечные и бесконечные множества, и понятие «число элементов» используется для конечных множеств. Так, конечное множество может иметь 6241 или 123456789012 элементов.

Конечные множества имеют одну особенность: их кардинальное число больше, чем кардинальное число любой из частей множества. Например, если А содержит 7 элементов, любая часть А имеет меньше 7 элементов. Если

А = {гномы из сказки про Белоснежку},

то |A| = 7. Любое подмножество или подгруппа гномов В будет удовлетворять условию |B| < |A| и будет содержать меньше 7 гномов. Эта особенность, которая может показаться тривиальной, на самом деле отличает конечные и бесконечные множества: часть бесконечного множества и само множество целиком могут иметь одинаковые кардинальные числа. Как бы удивительно это ни было, существуют объекты, часть которых содержит столько же элементов, что и целое.

ГОСТИНИЦА С БЕСКОНЕЧНЫМ ЧИСЛОМ НОМЕРОВ

В качестве примера многие математики приводят парадокс гостиницы с бесконечным числом номеров, придуманный немецким математиком Давидом Гильбертом. Он формулируется так. Есть гостиница, владельца которой не пугает толпа народа. Все номера гостиницы пронумерованы от 1 и далее в порядке возрастания. В сезон отпусков гостиница оказалась полностью заполнена, к радости ее владельца. Однако внезапно китайский туроператор прислал срочное сообщение: на следующий день должно приехать множество китайских путешественников. Для всех них нужно найти номера, но никого из уже заселившихся постояльцев выселять нельзя. Владелец отеля прекрасно знает математику и без труда нашел решение. Он попросил всех постояльцев переехать в комнату, номер которой в два раза больше, чем номер прежней комнаты, как показано на рисунке.

В гостинице снова появилось бесконечное число комнат, и всем новоприбывшим путешественникам хватило мест. Счастливый владелец гостиницы с бесконечным числом номеров продолжает работу благодаря своим знаниям о бесконечности.

* * *

Рассмотрим простейший пример бесконечности, образуемой всеми целыми положительными числами, так называемыми натуральными:

 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}.

Множество натуральных чисел обозначается латинской буквой .

Мы с удивлением обнаружим, что часть N, множество четных чисел, соответствует самому :

Поэтому

|{четные числа}| = ||.

Часть чего-либо бесконечного также может быть бесконечной и иметь то же кардинальное число.

Натуральные, рациональные и алгебраические числа

Люди много веков жили, повернувшись спиной к бесконечности. С подобным безразличием покончил немецкий математик высшего класса и непревзойденного ума, хоть и несколько эксцентричный. Его звали Георг Кантор.

Кардинальными числами конечных множеств являются натуральные числа. Кардинальные числа бесконечных множеств намного больше. Специалисты называют их трансфинитными, что дословно означает «находящиеся за пределами конечного». Наименьшее из трансфинитных чисел — это ||, которое Кантор обозначил как . Оно соответствует кардинальному числу множества натуральных чисел, иначе говоря,

|{1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11,}| = || = .

Происхождение этого необычного знака таково:  (читается «алеф») — первая буква еврейского алфавита. Ноль, указанный как индекс, означает, что речь идет о наименьшем из всех алеф (алеф-нуле). Существует много кардинальных чисел, каждое имеет свой индекс:

Число  отражает множества, которые соответствуют . Например, это могут быть четные числа, нечетные числа, числа, кратные 3, кратные 5, и многие другие. Множества, соответствующие , называются счетными, поскольку их элементы можно пронумеровать или подсчитать, как показано ниже:

* * *

ГЕОРГ КАНТОР (1845–1918)

Этот немецкий математик русского происхождения считается одним из величайших умов человечества. Он известен как создатель современной теории множеств и трансфинитных чисел. Его передовые идеи навлекли на себя нападки многих могущественных недоброжелателей, что заметно препятствовало академической карьере Кантора. Депрессии, которым был подвержен Кантор (он умер в психиатрической больнице), вероятно, были вызваны невозможностью проверить некоторые из его гипотез. Сегодня нам известно, что ответов на некоторые вопросы, которыми задавался Кентор, не существует, но определенные методы, которые он использовал в доказательствах, могут по праву называться гениальными.

* * *

Но здесь нас подстерегает множество сюрпризов: бесконечное множество

 = {…, -11, -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ….}

математики называют множеством целых чисел, и  является частью . Очевидно, что всякое натуральное число является целым. Но что можно сказать о кардинальных числах этих множеств? Чему равно кардинальное число ? Если мы посмотрим на рисунок ниже, демонстрирующий процесс пересчета целых чисел,

то увидим, что || = || = , поэтому множество  также является счетным.

Сделаем еще один шаг вперед: рассмотрим множество дробей, или так называемых дробных чисел. Дробь определяется числителем и знаменателем и записывается в виде а/Ь. Если а кратно Ь, то а/Ь обозначают целым числом с, которое равно делению а на Ь без остатка:

а/Ь = с.

Фактически одним и тем же числом могут обозначаться разные дроби:

756/378 = 524/262 = 6/3 = 2.

Однако очевидно, что существуют и другие дроби, которые нельзя выразить целым числом, например 1/2 или 5/3. Существует больше дробных чисел, чем целых, так как всякое целое число можно представить в виде дроби. Имеем

Символ  означает «строгое включение подмножества». Это своеобразная разновидность знака < для множеств.

Множество дробных чисел обозначается буквой . Можно убедиться, что  является частью . Или же, если так будет удобнее читателю,

Можно было бы ожидать, что кардинальное число  больше, чем кардинальное число , но вы уже видели, что здравый смысл не всегда применим к бесконечности.

Кантор «пронумеровал» дроби с помощью извилистой линии, изобразив нечто похожее на этот рисунок:

Нет никаких сомнений, что на рисунке помещаются все дроби, так как в каждом ряду содержатся все возможные числители, а в каждом столбце — все возможные знаменатели. Если мы хотим найти число а/Ь, то это очень просто сделать, перейдя к строке а и столбцу Ь. Также не вызывает сомнений, что каждой дроби (иными словами, каждому рациональному числу) соответствует последовательность стрелок, идущая к нему. Поэтому достаточно пронумеровать стрелки (1, 2, 3, 4, 5…), чтобы прийти к результату:

Сделаем еще один шаг. Говорят, что число является алгебраическим, когда оно является корнем многочлена

а_nхⁿ + а_n-1х^n-1 +… + а₁х + а₀,

все коэффициенты которого (а_n, а_n-1…, а₁, а₀) являются рациональными числами.

Существует великое множество алгебраических чисел. По сути, любое рациональное число является алгебраическим. Если мы рассмотрим произвольное рациональное число а/Ь, уравнение

х — а/Ь = 0

имеет решение х = а/Ь, а его коэффициенты являются рациональными числами: a₁ = 1 и а₀ = — а/Ь.

Существует множество других алгебраических чисел: так, число √2 является иррациональным и является корнем уравнения х² — 2 = 0, то есть удовлетворяет всем необходимым условиям. Алгебраическим также является такое известное число, как золотое число Ф — оно является корнем уравнения х² — х — 1 = 0.

В 1874 году Кантор был еще молод и не страдал от психических расстройств. В одной из своих работ он доказал, что множество алгебраических чисел (будем обозначать его ), включающее все рациональные числа, является счетным множеством. Следовательно,

При этом каждое из этих множеств строго больше последующего:

Появление вещественных чисел

Мир чисел огромен. Пока что мы видели лишь его часть, которая является счетной.

Возможно, лучший способ рассказать о числах — это рассмотреть подробно их десятичную запись. Исследуем подробно множество всех десятичных чисел. Вообще говоря, десятичное число вида

34658,124796

является лишь формой записи следующего выражения

3∙10⁴ + 4∙10³ + 6∙10² + 5∙10¹ + 8∙10⁰ + 1∙10^-1 + 2∙10^-2 + 4∙10^-3 + 7∙10^-4 + 9∙10^-5 + 6∙10^-6

Цифры слева от запятой соответствуют положительным степеням 10, справа от запятой — отрицательным степеням. Вспомним, что

a∙10^-n = a/10ⁿ

Десятичная система счисления — это позиционная система счисления по основанию 10. Это лишь способ записи чисел, но сколь удобный способ! Это поистине великое достижение человечества.

СИМОН СТЕВИН (1548–1620)

Этот голландский ученый родился в бельгийском городе Брюгге. Он был военным инженером, занимался музыкой, физикой, математикой и бухгалтерией. Он вошел в историю как изобретатель двойной бухгалтерской записи, которая в значительной мере способствовала прогрессу в экономике и торговле. Но его вклад в математику еще важнее: в своем труде De Thiende («Десятая») он представил десятичную форму записи чисел. Эта система была слишком сложна, поэтому широкое распространение получили более поздние версии, например вариант, предложенный Джоном Непером,

Страница книги De Thiende, на которой приведен пример десятичной записи Стевина, не слишком удобной для повседневного использования. Единицы обозначаются кружком, обведенным вокруг 0, десятки — другим кружком вокруг 1, сотни — кружком вокруг 2 и так далее.

* * *

Десятичная дробь может быть конечной или бесконечной. Ниже приведен пример для обоих случаев:

1,234567890101112131415161718192021223242526…

127,789564.

Первое число — бесконечная десятичная дробь. Вторая дробь также содержит бесконечное количество знаков после запятой, но в ином виде:

127,789564 = 127,789564000000000000000000…

Фактически мы можем записать число 127,789564 более «сложным» способом:

= 127,789563999999999999999999…

Тем не менее в этих случаях речь идет о конечной десятичной дроби. Простейшие десятичные числа — это натуральные числа (): они являются положительными и не имеют знаков после запятой. За ними следуют целые числа (), которые могут быть отрицательными, но также не имеют знаков после запятой. Рациональные числа () включают в себя эти множества и имеют любопытную десятичную запись: цифры рационального числа имеют период, то есть некая группа цифр с определенного момента начинает повторяться. Вспомним, что рациональные числа являются дробями, или дробными числами, которые записываются в виде а/Ь, где а — целое, a Ь — натуральное число. Чтобы перейти от этой формы к десятичной записи, нужно разделить а на Ь, и каков же будет результат? Остаток не может превышать Ь, и после деления, выполненного Ь раз, числа начнут повторяться снова и снова. Это прекрасно видно на примере простейших дробей, в частности

11/7 = 1,571428571428571428…,

где период, или множество повторяющихся цифр, всегда равен 571428. Иногда период имеет гигантские размеры, но это не означает, что десятичное число будет иметь бесконечное количество знаков — они будут повторяться бесконечное число раз.

В этот момент неизбежно возникает вопрос: если периодические дроби соответствуют рациональным числам, то как быть с непериодическими десятичными дробями? Все очень просто: они являются не рациональными, а иррациональными.

ДИАГОНАЛЬНОЕ ДОКАЗАТЕЛЬСТВО

Рассуждения Кантора, которые лежат в основе доказательства счетности множества десятичных дробей (то есть ), останутся в истории как доказательство его гениальности. Они оригинальны, но в то же время понятны. Это доказательство приобрело такую известность, что получило собственное название: диагональный метод, метод диагонализации, или диагональное доказательство. Посмотрим, почему это доказательство называется «диагональным».

Мы выполним действия, которые в математике именуются «сведением к абсурду», когда некая гипотеза предполагается истинной, а затем показывается, что из нее вытекает абсурдное заключение. Это означает, что исходная гипотеза ложна. Предположим (ниже мы докажем ложность этого утверждения), что множество десятичных дробей (т. е. вещественных чисел) является счетным. Будем говорить о счетности не всего множества , а лишь десятичных дробей, лежащих на интервале (0; 1), то есть удовлетворяющих условию 0 < х < 1, - лишь малой части . Предположим, что десятичные дроби пронумерованы и перечислены друг под другом, не обязательно по порядку, так, как показано ниже:

В этом списке должны фигурировать все десятичные дроби, заключенные в промежутке между 0 и 1, так, чтобы нельзя было записать никакую десятичную дробь л, которая бы не содержалась в этом списке. Кантор, основываясь на этом утверждении, создал новую десятичную дробь D

D = 0, d₁ d₂ d₃ d₄ d₅… d_n…,

которой не было в списке. Для каждого n он определил d_n, отличное от того, которое находится в строке n и столбце n.

d отличается от десятичной дроби, которая соответствует числу 1? Да, поскольку d отличается от этой дроби в первом знаке после запятой.

d отличается от десятичной дроби, которая соответствует следующему числу в списке? Да, поскольку d отличается от второй дроби во втором знаке после запятой.

d отличается от десятичной дроби, которая соответствует третьему числу в списке? Да, поскольку d отличается от третьей дроби во третьем знаке после запятой.

Это же верно и для четвертой, пятой и n-й дробей:

d_n не равно r_n

D отличается от всех десятичных дробей в списке, следовательно, оно не содержится в этом списке. Но разве мы не говорили, что в этом списке содержатся все десятичные дроби? Имеется противоречие с исходным утверждением, которое гласит, что все десятичные дроби пронумерованы и перечислены в списке. В действительности это не так. Это доказывает, что множество всех десятичных дробей не является счетным.

|| > ||

* * *

Существует множество иррациональных чисел, начиная с √2 и всевозможных комбинаций корней, например , и заканчивая универсальными константами, например π. Будет логичным спросить: «Сколько всего иррациональных чисел?»

Обозначим множество всех десятичных дробей , иными словами, объединение рациональных и иррациональных чисел:

Мы знаем, что первое из этих множеств  = {рациональные числа} счетно. Кантор доказал, что множество  не является счетным. Следовательно, множество в правой части равенства также не может быть счетным. В противном случае  было бы образовано двумя счетными множествами, следовательно, оно также должно было быть счетным.

Наконец-то мы нашли нечто неисчислимое — множество , элементы которого нельзя сосчитать. Следовательно, это бесконечное множество, бесспорно, больше всех бесконечных множеств, о которых мы говорили до этого.

Множество  известно как множество вещественных чисел.

В простейшей теории множеств, которую сегодня изучают в школах, вышеизложенное обычно изображают с помощью диаграмм:

Множества ,  и , содержащиеся в , являются счетными, в то время как  таковым не является. Можно сказать, пусть и немного неточно, что почти все числа являются иррациональными, за исключением рациональных, образующих меньшую бесконечность, которая является счетной. Число π является иррациональным, что доказал Иоганн Генрих Ламберт (1728–1777) в 1760-е годы. Следовательно, оно принадлежит к несчетному большинству, куда также входят почти все десятичные дроби. С этой точки зрения π не является каким-то необычным. Кроме того, что оно иррационально, оно также является вещественным, как почти все остальные числа.

Алгебраические и трансцендентные числа

Ранее мы говорили об алгебраических числах. Вспомним, что

1) алгебраическими числами называются числа, которые являются корнями уравнения

а_nхⁿ + а_n-1х^n-1 +… + а₁х + а₀ = 0,

где а_n, а_n-1…., а₁, a₀ — рациональные числа;

2) алгебраические числа образуют счетное бесконечное множество.

Почему мы снова вспомнили о них? Причина в том, что во всех геометрических построениях используются лишь циркуль и линейка, причем конечное число раз.

Таковы своеобразные «правила игры», и таким достаточно простым способом строятся ничем не примечательные отрезки.

Тот факт, что древние греки использовали для построений только циркуль и линейку, привел к появлению особых отрезков (и, как следствие, чисел), которые, в отличие от остальных, можно построить (иногда их называют построимыми числами). Возьмем в качестве примера обычное число √2. Это число можно построить с помощью циркуля и линейки, как показано на рисунке:

Это первое иррациональное число, с которым встретились древние греки. Именно это число дало название иррациональным числам. Это число также является алгебраическим и его можно построить. Как мы уже говорили, √2 является корнем уравнения второй степени х² — 2 = 0.

Все числа, которые можно построить, являются алгебраическими. Рассмотрим, почему это так. Если говорить о построениях с помощью циркуля и линейки, то максимум, что мы можем построить, — это числа вида

x₁ = a₀ + b₀√x₀,

где a₀, b₀ и x₀ — рациональные. Опустим доказательство этого утверждения: оно несложное, но очень громоздкое. Число является алгебраическим, так как является решением квадратного уравнения с рациональными коэффициентами, а именно

х² — 2а₀х + а₀² — Ь₀²х₀ = 0.

Это уравнение с рациональными коэффициентами: числа 1, -2a₀ и -Ь²х₀ принадлежат . Все числа, подобные x₀, образуют так называемое поле, обозначаемое К₀ и удовлетворяющее условию

Иными словами,  является подмножеством K₀.  и K₀ образованы построимыми числами, но содержат только алгебраические числа. K₀ больше, чем , и включает его. Все числа K₀ являются алгебраическими, некоторые из них рациональные (те, что принадлежат ), другие — нет (те, что принадлежат K₀ и не принадлежат ).

Выберем для построения

x₂ = a₁ + b₁√x₁,

где a₁, b₁ и x₁ принадлежат K₀, и тем самым образуем еще большее поле:

также образованное алгебраическими числами, которые можно построить. Очевидно, что можно сформировать любое количество полей К_n:

В целом геометрические фигуры, в которых содержатся эти числа, описываются уравнениями второй степени (квадратными уравнениями). Они могут существенно различаться, но результатом построений все равно будут алгебраические числа.

Благодаря так называемой аналитической геометрии, изобретенной Рене Декартом в XVII веке, любое геометрическое построение можно описать уравнением второй степени. Сложное построение может описываться цепочкой уравнений второй степени, вложенных друг в друга.

Но сколь бы велика ни была эта цепочка, результатом всегда будет число, которое можно построить. Это число будет являться решением уравнения второй степени с коэффициентами, которые также можно построить, и, следовательно, будет являться алгебраическим. Используя геометрические построения, мы никогда не сможем выйти за пределы множества алгебраических чисел. Любое число, которое можно построить, является алгебраическим.

Мы не будем приводить подробное доказательство этого утверждения, поскольку для этого потребуется использовать методы из теории Галуа, относящиеся к высшей математике. Вышесказанное можно представить в виде следующей диаграммы:

В царстве чисел все числа вплоть до алгебраических принадлежат к счетной бесконечности. Но мы уже знаем, что множество  не является счетным и намного больше этих множеств.  без алгебраических чисел, то есть «почти все» множество , также имеет трансфинитное, несчетное число элементов.

Математики называют неалгебраические числа (вспомним, что это все вещественные числа за исключением алгебраических, то есть множество  за вычетом ) трансцендентными числами, поскольку Эйлер писал, что эти числа «превосходят мощь алгебраических методов» (название «трансцендентные» происходит от латинского transcendere — «превосходить»). Следующее определение не содержит никаких философских подсмыслов, но является точным и однозначным: трансцендентным называется число, которое не может быть корнем многочлена с рациональными коэффициентами. Все трансцендентные числа являются иррациональными, множество трансцендентных чисел не является счетным. Его кардинальное число больше, чем .

Какое отношение все это имеет к числу π? π является не только иррациональным, но и трансцендентным, что доказал Линдеман в 1882 году. Так как π является трансцендентным, оно не является алгебраическим и его нельзяпостроить с помощью циркуля и линейки за конечное число действий. Таким образом, поиски классического решения задачи о квадратуре круга оказались завершены. Однако и в наши дни некоторые известные математики все еще получают «решения» задачи о квадратуре круга. Но тем, кто якобы решил нерешаемую задачу, уже готовы ответы.

Так, один известный математик передавал полученные решения задачи о квадратуре круга наиболее одаренным ученикам. Когда ошибка была найдена (иначе и быть не могло), автору возвращался заполненный формуляр: «Любезный друг! Благодарим за предоставленное решение задачи о квадратуре круга. Возвращаем ваше доказательство и указываем на первую обнаруженную нами ошибку. Она находится на странице… в строке… Искренне ваш, и проч.». Столь остроумным способом этот математик отвечал упрямцам, не желавшим признать очевидное.

Итак, число π принадлежит к трансцендентным числам, составляющим большую часть царства чисел. На первый взгляд, в нем нет ничего необычного — это всего лишь заурядное трансцендентное число. Оно столь обыденно и незначительно, что никто до сих пор не нашел среди его знаков никакой закономерности.

ТРАНСЦЕНДЕНТНЫЕ СВЯЗИ π

Число е является основанием натурального логарифма. Его значение равно 2,71828… После числа π это самая известная и наиболее часто встречающаяся математическая постоянная. Несомненно,

π + е = 5,859874482…,

но неизвестно, является ли это число трансцендентным. Удивительно, но известно, что одно из чисел π + е или π∙е является трансцендентным, но неизвестно, какое именно. Также неизвестно, является ли трансцендентным π^π.

Напротив, е^x является трансцендентным, что было доказано благодаря теореме Александра Гельфонда (1906–1968) и Теодора Шнайдера (1911–1988). Однако это нельзя доказать для π^e. В действительности неизвестно, является ли это число рациональным или иррациональным. Трансцендентными также являются е^n√n (при n не равно 0), π + In 2 и π + In 2 + √ln3. Неизвестно, являются ли иррациональными π + е или π/е. J них известно, что если они являются алгебраическими, то многочлены, корнями которых они являются, имеют восьмую степень или выше и коэффициенты порядка 10⁹. Этого недостаточно для строгого математического доказательства, но на бытовом уровне выглядит убедительно.

Квадратура круга

После анализа природы числа π и подтверждения его трансцендентности очевидно, что любые попытки решения задачи о квадратуре круга бесполезны. Несмотря на это, до Линдемана многие добросовестно прилагали все усилия в поисках решения с разумной степенью точности. Большинство охотников за числом π в действительности охотились за мимолетной квадратурой круга. Подобную одержимость в шутку называли болезнью morbus cyclometricus. Некто описывал искателей квадратуры круга как зрелых и благородных мужей, которым неведомо слово «невозможно», но которые обладают недостаточными знаниями математики и убеждены, что эта задача крайне важна и решившему ее полагается большая награда; как лишенных логики отшельников и вдобавок крайне плодовитых писателей. Эта мрачная картина тем не менее очень близка к реальности.

АРИСТОФАН И КВАДРАТУРА КРУГА

Греческий драматург Аристофан (ок. 446 — ок. 386 гг. до н. э.) в одной из своих комедий, которые изобиловали сатирой, упоминал о квадратуре круга скорее в шутливом тоне. В комедии «Птицы», впервые поставленной в 414 году до н. э., жители Афин, уставшие от городской суеты, решают построить город в воздухе и переехать жить туда. Архитекторы и градостроители предлагают свои услуги главному герою Писфетеру.

[Метон): Я к вам пришел.

[Писфетер]: Еще несчастье новое. Зачем пришел ты? И каков твой замысел? С какими ты сюда явился целями?

[Метон]: Я землемер. Хочу отмерить каждому полоску воздуха.

[Писфетер]: О боги правые! Ты что за человек?

[Метон]: Зовусь Метоном я. Знаком всем грекам и колонцам в частности.

[Писфетер]: А это что?

[Метон]: Орудья измерения. Напоминает очень воздух формою кастрюлю для тушенья. Здесь линейку я изогнутую приложу и циркулем отмерю расстоянье, понимаешь?

[Писфетер]: Нет.

[Метон]: Затем прямую, тоже по линеечке, я проведу, чтоб круг квадратом сделался. Здесь, в центре, будет рынок. К рынку улицы пойдут прямые. Так лучи расходятся, сверкая, от звезды. Звезда округлая, лучи прямые.

[Писфетер]: Ты Фалес поистине!

* * *

Римский философ Боэций (ок. 480–524), в латинизированной форме Anicius Boethius, впоследствии казненный королем Теодорихом Великим по обвинению в измене, в своей книге Liber Circuli подтвердил, что задача о квадратуре круга имеет решение, но доказательство слишком объемно, чтобы привести его полностью.

Это выражение стало еще популярнее, когда его использовал Ферма в отношении своей знаменитой теоремы. Вкупе с тем неоспоримым фактом, что задача о квадратуре круга не имеет решения, предполагаемое доказательство Боэция более чем сомнительно.

Намного позднее Боэция жил знаменитый немецкий кардинал Николай Кузанский (1401–1464). Благодаря своему уму он заслужил лестные отзывы Кеплера и Кантора, так как высказывал передовые идеи о бесконечности. Он был выдающимся полиглотом, юристом, философом, астрономом, но больше нумерологом, чем математиком. Он пытался решить задачу о квадратуре круга и, по его собственным словам, преуспел в этом. Но его современник Иоганн Мюллер (1436–1476), взявший себе латинизированный псевдоним Региомонтан, был лучшим математиком, чем кардинал, и вдобавок большим почитателем Архимеда. В своем труде De cuadratura circuli он опроверг доказательство кардинала и показал, что задача о квадратуре круга не имеет решений. Тем не менее следует отметить, что Николай Кузанский вычислил приближенное значение π (сам он считал это значение окончательным и точным) с очень хорошей точностью: 3,1423… Стоит заметить, что Региомонтан использовал значение π = 3,14243.

Кардинал Николай Кузанский утверждал, что решил задачу о квадратуре круга.

В 1525 году великий художник Альбрехт Дюрер (1471–1528) также попытался решить эту задачу, но отметил, что выполненное им построение является лишь приближенным.

Страница книги Дюрера «Правила измерения линий, плоскостей и целых тел при помощи циркуля и угольника», где приведено приближенное построение квадратуры круга.

Немного позднее, в 1585 году, Адриан Антониш (ок. 1543–1620), отец Адриана Метиуса (15π–1635), рассчитал, что значение π лежит между 377/120 и 333/106. Его сын пробовал решить задачу о квадратуре круга; он вычислил нечто подобное среднему числителей и знаменателей и получил

Это очень точное значение, но его одного явно недостаточно для решения задачи.

Возможно, самая известная история, связанная с квадратурой круга, произошла со знаменитым философом и главой школы эмпиризма Томасом Гоббсом (1588–1679) и со знаменитым английским математиком Джоном Валлисом (1616–1703). Гоббс, вне сомнения, очень умный человек, но не получивший математическое образование, в 1655 году в труде «О теле» заявил, что решил задачу о квадратуре круга наряду с другими задачами, в частности о выпрямлении различных кривых. Понятно, что он ошибался, и Валлис в кратком труде Elenchus geometriae hobbianae описал различные ошибки и в язвительном тоне, но правдиво, отозвался о геометрических способностях Гоббса. Следует заметить, что Валлис исповедовал пресвитерианское учение, что было еще более ненавистно Гоббсу, который был противником всякой религии. Математическая подготовка Гоббса была недостаточной, ведь он познакомился с учением Евклида лишь в 40 лет, но, в конце концов, другие философы были столь же посредственными математиками, и в этом не было ничего особенного. Упомянем лишь один пример: уже в XIX веке Маркс утверждал, что диалектический материализм выводится логическими рассуждениями из уравнения второй степени. Гоббсу повредило то, что он не хотел признать своих ошибок, перевел спор на личности и возвращался к дискуссии снова и снова. В частности, его перу принадлежит книга «Замечания об абсурдной геометрии, деревенском языке, церковной политике в Шотландии и невежестве Джона Валлиса». Спор изобиловал придирками, к сожалению небеспочвенными. Так, Валлис обвинил Гоббса в плагиате работ его современников: «…Если в его изложении попадется нечто правдивое, то оно принадлежит не ему, а взято у кого-либо еще».

Томас Гоббс (слева) и Джон Валлис вели длинный спор, в котором оскорбления и клевета были в порядке вещей. Причиной ссоры была задача о квадратуре круга.

ДЖОН ВАЛЛИС (1616–1703)

Знаменитый знак бесконечности  был введен именно этим блестящим английским математиком. Будучи членом Лондонского королевского общества, Валлис занимался расшифровкой сообщений и в первую очередь модной темой той эпохи — вычислением бесконечно малых, в которое он внес новые интересные концепции. Наиболее примечательное его творение принадлежит к теории рядов. Это красивая и полезная формула:

Валлис великолепно производил вычисления в уме. Возможно, причиной этому было то, что он страдал от бессонницы. Также он занимался грамматикой и, что еще более незаурядно, вложил немало сил в обучение глухонемых.

* * *

Бельгийскому иезуиту Грегуару де Сен-Венсану (1584–1667) мы обязаны, помимо прочего, созданием полярных координат, открытием новой системы, близкой к понятию интеграла, и точным расчетом площади под гиперболой. Он также утверждал, что решил задачу о квадратуре круга. Его современники восприняли это с изрядным скептицизмом, и в конце концов Гюйгенс нашел неизбежную ошибку в его рассуждениях. Он упомянут в этой книге за выдающиеся труды и в связи с тем, что ему принадлежит множество корректных и интересных математических доказательств.

Классический пример квадратуры круга представил производитель мыла Якоб Марцелис (1636 — ок. 1714), который утверждал, что

Огастес де Морган в своем сборнике математических ужасов A budget of paradoxes («Запас парадоксов») не слишком благосклонно заметил: «Как и следовало ожидать, в мыловарении он добился больших успехов, чем в вычислении знаков π».

Со временем нелепостей становилось все больше: в 1728 году некий Малтулон заявил, что разгадал тайну вечного движения и квадратуры круга одновременно. Кроме этого, он предложил вознаграждение тому, кто смог бы опровергнуть хотя бы один шаг доказательства, что свидетельствовало о недюжинной уверенности в себе. Итог оказался предсказуем: было показано, что его доказательство ошибочно, и Малтулону не оставалось другого выбора, кроме как выплатить обещанное. Неудивительно, что в 1753 году Французская академия наук постановила не рассматривать присылаемые решения задачи о квадратуре круга. Возможно, академиков испугало все большее число присылаемых решений и связанные с этим неизбежные издержки. Быть может, они решили таким способом избавиться от определенных личностей, подобных некоему Восенвиллю, который потребовал от Академии премию, полагавшуюся первому, кто решит эту задачу.

Даже после выхода доказательства Линдемана поток энтузиастов не иссякал, однако благодаря этому доказательству стала точно известна заведомая ошибочность всех подобных решений. Особо следует выделить тех, кто, подобно Сриниваса Рамануджану (1887–1920), знал, что задача не имеет решения, и находил приближенные построения с удивительной точностью. Так, с помощью одного из построений Рамануджана можно получить значение

Построение квадратуры круга (приближенное) за авторством Рамануджана. Погрешность составила лишь 0,0000000010072!

Глава 3 Число π и теория вероятностей

В основе теории вероятностей — только здравый смысл, сведенный до исчисления.

Пьер Симон маркиз де Лаплас

Может показаться, что теория вероятностей никак не связана с π. Тем не менее это далеко от истины. Скажем для начала, что 0,6079271018… = 6/π² — это вероятность того, что два произвольно выбранных числа окажутся взаимно простыми. Это доказал Р. Шартр в 1904 году. Кроме этого, π²/6 = ζ (2), что устанавливает любопытную связь между π и загадочной функцией Римана ζ. Это также идет в копилку взаимосвязи между π и теорией вероятностей, хотя в теории вероятностей π — явный незваный гость. Наконец, это указывает на определенную корреляцию между π и простыми числами.

Огастес де Морган как-то объяснял страховому агенту математическую задачу о расчете вероятности того, что все члены определенной группы людей будут живы по прошествии некоторого времени. Из теории вероятностей следовало, что в итоговом значении будет фигурировать π. Страховой агент, убежденный, что де Морган ошибся, указал ему на это. Как может случиться, что число π применимо к продаже страховок? Откуда оно взялось? Тем не менее де Морган был прав: связь между ожидаемой продолжительностью жизни, страховыми полисами и числом π действительно существует, и называется она «нормальное распределение».

В этой главе мы покажем подобные таинственные соотношения. История начинается с вторжения благородного французского графа де Бюффона в мир математики. Бюффон решил изучить поведение иглы, которая падает на плоскость, не прокалывая ее, с математической точки зрения.

Иголка в стоге сена…

На листе бумаги нарисовано несколько параллельных прямых, расстояние между которыми одинаково. На лист произвольным образом бросают иголку. Когда игла пересечет одну из линий?

В простейшем случае длина иглы l равна расстоянию d между линиями. Обозначим за у расстояние между центром иглы (ее предполагаемым центром тяжести) и одной из линий сетки. Примем d = l = 1 для упрощения вычислений. Обозначим за х угол, образованный иглой и горизонтальной осью. Будем измерять этот угол в радианах, так как нам понадобятся минимально необходимые инструменты математического анализа, в частности некоторые интегралы.

Из элементарной геометрии очевидно, что если верно неравенство

y =< (1/2)∙sin x,

то игла пересечет линию. Это будет отправной точкой наших расчетов. На следующем рисунке изображен график функции y = (1/2)∙sin x:

ЖОРЖ ЛУИ ЛЕКЛЕРК ГРАФ ДЕ БЮФФОН (1707–1788)

Этот французский ученый оставил свой след в различных науках. Он был биологом, писателем, занимался космологией и математикой. Его главным трудом является монументальная «Естественная история» в 36 томах с 8 приложениями. В области космологии наиболее значительным вкладом Бюффона стала гипотеза о возрасте Земли, вычисленном по результатам исследований охлаждения железа. Гипотеза вызвала серьезный протест со стороны церкви. Он перевел на французский труды Ньютона и внес вклад в теорию вероятностей, опубликовав работу «Опыт моральной арифметики», в которой, помимо прочего, содержалась знаменитая задача о падении иглы на лист с нанесенными параллельными линиями.

Граф де Вюффон занимался многими науками, но известен прете всего как натуралист.

* * *

Чтобы оценить площадь закрашенной области, множество точек которой является решением неравенства y =< (1/2)∙sin x, необходимо вычислить интеграл

Площадь прямоугольника равна π/2, и вероятность того, что игла упадет на линию, равна отношению двух площадей:

1/(π/2) = 2/π ~ 0,6366197…

Именно здесь и появляется число π.

Задачу можно также решить для случая, когда l не равно d. При l < d вероятность равна 2l/πd, при l > d вероятность равна

В этом случае необходимо вычислить двойной интеграл. Предпринимались попытки вычислить значение π на основании данных рассуждений, но результаты оказались неудовлетворительными. Фактически малейшая неровность иглы приводит к появлению заметных ошибок, поэтому использовать этот метод не рекомендуется. Предпочтительнее бросать виртуальные иглы на разлинованные листы в киберпространстве. Для этого разработаны специальные программы.

…и иголка на листе бумаги

Более сложный вариант предыдущей задачи называется задачей Бюффона-Лапласа. Ее решение приводит Лаплас в своей «Аналитической теории вероятностей». В этом варианте задачи игла падает не на равноудаленные друг от друга параллельные прямые, а на сетку из клеток с перпендикулярными сторонами. Каждая клетка имеет стороны а и b (а не равно Ь). Предполагается, что иголка короче, чем обе стороны.

Чтобы найти ответ, необходимо вычислить несколько более сложный интеграл, чем в предыдущей задаче. Вероятность того, что игла пересечет одну из сторон клетки, равна

(2l(a + b) — l²)/πab.

При а = b вероятность того, что игла не пересечет ни одну из линий, равна

1 — (l(4a — l)/πa²)

Вероятность пересечения одной линии равна

2l(2a — l)/πa²

и вероятность пересечения двух линий равна

l²/πa²

Можно обобщить эту задачу, преобразовав квадратные клетки, скажем, в треугольники. Но эту задачу мы оставляем специалистам.

ПЬЕР СИМОН МАРКИЗ ДЕ ЛАПЛАС (1749–1827)

Французский астроном и математик, друг и протеже Наполеона, автор «Небесной механики» в пяти томах и других фундаментальных работ в области физики и универсальных знаний. Лаплас, который уже в юном возрасте продемонстрировал блестящие способности, с удивительной легкостью усваивал математический анализ и физику. Он внес вклад в развитие множества новых концепций в теории вероятностей (производящая функция последовательности, условная вероятность, задача Бюффона), в чистой математике (теория потенциала, преобразование Лапласа, гармонический анализ) и астрономии (форма Земли, образование Солнечной системы из туманности, теория возмущений). Его можно считать практически универсальным гением. Его научные достижения были столь удивительны для современников, что после смерти Лапласа его мозг извлекли для изучения, но ничего особенного в нем обнаружено не было. Наполеон сделал его министром, что не помешало Лапласу принять благородный титул после реставрации Бурбонов. Как гласит знаменитый исторический анекдот, Наполеон ознакомился с сочинением Лапласа об астрономии и удивился полному отсутствию слова «Бог» в его труде. «Это потому, что я в этой гипотезе не нуждался», — ответил ученый.

Нормальная кривая

Во многих задачах, связанных с теорией вероятностей и статистикой, например, в распределении роста, коэффициента интеллекта, инструментальных ошибок телескопа, интенсивности лазерного луча (и это лишь некоторые примеры), фигурирует так называемая кривая Гаусса, или нормальная кривая. Она соответствует распределению вероятностей с кривой плотности, в которой определяющую роль играет π.

Стандартное представление кривой можно получить, взяв среднее значение, равное нулю, и дисперсию δ² = 1. В этом случае кривая будет иметь знакомую нам форму колокола, который слегка вытянут вдоль вертикальной оси.

Эта кривая описывается уравнением

Вероятность рассчитывается с помощью интеграла

Как можно убедиться, в этой формуле всегда присутствует π.

Закону нормального распределения подчиняется, например, распределение возраста смерти. Можно сказать, перефразируя Джона Донна, что всякий раз, когда кто-то умирает, по числу π звонит колокол — колокола Гаусса.

ИОГАНН КАРЛ ФРИДРИХ ГАУСС (1777–1855)

Никакая характеристика не может точно выразить весь масштаб личности математика, астронома и физика Гаусса. Достаточно сказать, что современники называли его «принцем математиков» (лат. Princeps mathematicorum). Гаусс был родом из очень простой семьи. Уже в раннем детстве он продемонстрировал незаурядные способности. По легенде, он показал свой удивительный талант, когда учитель предложил найти сумму всех чисел от 1 до 100. Всего через несколько минут Гаусс нашел верный ответ: 5 050. Как мог ребенок так быстро дать верный ответ, когда любому другому на это потребовалось бы намного больше времени? Он заметил, что числа от 1 до 100 образуют 50 пар чисел, сумма каждой из которых равна 101:

1 + 100 = 2 + 99 = 3 + 98 = … = 48 + 53 = 49 + 52 = 50 + 51.

Следовательно, 50∙101 = 5 050.

Гаусс очень рано добился заметных результатов. Его интересовало буквально все, он создал бесчисленное множество трудов в самых различных областях: нашел критерий возможности построения правильных многоугольников, сформулировал теорему о распределении простых чисел, доказал основную теорему алгебры, рассчитал орбиту карликовой планеты Цереры, предсказал важнейшие моменты неевклидовой геометрии, не считая многочисленных достижений в математическом анализе, алгебре, теории чисел, теории вероятностей и других разделах математики. В прикладной математике и физике выделяются его работы по геодезии, электричеству и магнетизму. Он изобрел гелиотроп, гелиограф и электрический телеграф.

Гелиотроп — один из приборов, изобретенных Гауссом, который в значительной степени помог ему в геодезических исследованиях. Этот прибор с движущимся зеркалом отражает солнечный свет в определенном направлении, что делает возможной настройку топографических инструментов.

π и другие вероятности

Расскажем о некоторых любопытных фактах, связанных с π и понятных неподготовленному читателю. Если треугольник имеет произвольно выбранные стороны а, b < 1 и с = 1, то вероятность того, что а, b и с образуют тупоугольный треугольник, равна (π — 2)/4.

Среднее число вариантов записи натурального числа в виде суммы двух квадратов (с учетом их порядка) равно π/4.

Говорят, что комплексное число является гауссовым целым числом, если его можно представить в виде х + yi, где х и у — целые. При сложении, вычитании и умножении гауссовых целых чисел результат всегда будет также гауссовым целым числом. Они образуют так называемое поле, на котором можно определить признак делимости, наибольший общий делитель, наименьшее общее кратное и простые числа. Вероятность того, что два гауссовых целых числа являются взаимно простыми, равна 6К/π², где К — так называемая постоянная Каталана. Для обычных целых чисел эта вероятность равна 6/π².

Глава 4 Формулы с числом π

Государь, чей оракул находится в Дельфах, не говорит и не скрывает, но знаками указывает.

Гераклит

Лорд Кельвин как-то написал на доске формулу

и, обращаясь к слушателям, сказал: «Математик — это тот, для кого эта формула столь же очевидна, как 2 + 2 = 4».

Мы не будем заходить так далеко, как лорд Кельвин, но все же приведем несколько формул, в которых используется π. Присутствие формулы в тексте гарантирует, что не слишком заинтересованный читатель непременно отвлечется, поэтому мы постарались использовать как можно меньше формул и объединить их в одной главе.

Некоторые из них обязательно знать всем, кто интересуется этой темой, поэтому их нельзя было не включить в эту главу. Более сложные формулы будет непросто понять, но с ними следует ознакомиться, чтобы осознать, каких усилий стоило открыть их.

Физика и число π

Выражения, в которых используется π, полезно знать. Те, что касаются физики, порой столь же интересны, сколь трудны для понимания.

Формула ниже — это закон Кулона, описывающий силу взаимодействия между двумя зарядами q₁ и q₂, расположенными на расстоянии r, где ε₀ — электрическая постоянная:

F = |q₁q₂|/4πε₀r²

Это третий закон Кеплера, где Р — период обращения планеты вокруг Солнца, m₁ и m₂ — масса Солнца и планеты, а — большая полуось орбиты, G — гравитационная постоянная:

p² = [4π²/G(m₁ +m₂)]∙a³

Принцип неопределенности Гейзенберга для частицы со средним значением координаты х и средним импульсом р, где h — нередуцированная постоянная Планка:

ΔxΔy >= h/4π

Космологическая константа, где G — гравитационная постоянная, с — скорость света, р — плотность материи и излучения:

 = (8πG/3c²)∙p.

Можно предположить, что следующие формулы будут интересны только специалистам, поэтому мы не будем продолжать. Стоит отметить, что эти и другие физические формулы не используются для расчетов Я, но их полезно знать каждому образованному человеку.

Элементарная геометрия и число π

Простейшие формулы прежде всего относятся к так называемым коническим сечениям — кривым, получаемым в результате рассечения конуса плоскостью. В следующих формулах r обозначает радиус.

Длина окружности:

L = 2πг.

Площадь круга:

S = πr².

Площадь эллипса с полуосями а и Ь:

S = πаЬ.

Площадь правильного многоугольника с n сторонами и длиной стороны а:

S = (1/4)∙na²ctg (π/n)

Площадь поверхности сферы:

S = 4πr²

Общая площадь поверхности цилиндра с высотой h:

S = 2πr∙(r + h).

Общая площадь поверхности конуса с образующей g:

S = πr∙(r + g).

Объем сферы:

V = (4/3)∙πr³.

Объем эллипсоида с полуосями а, Ь и с:

V = (4/3)∙πabc

Объем цилиндра с высотой h:

V = πr²h.

Объем конуса с высотой h:

V = πr²h/3.

Также, разумеется, существуют и другие формулы, в которых используется π и очень сложные интегралы.

Простые формулы

Под простой формулой будем понимать любую формулу, найденную до наступления компьютерной эры. С наступлением эпохи компьютеров математики сосредоточили внимание на вычислении знаков π с наибольшей эффективностью. Красота расчетов уступила место эффективности вычислений. Простое перечисление формул будет достаточно громоздким, но у нас не остается другого выхода:

В последней формуле использован круговой интеграл. Предполагается, что обход дуги окружности осуществляется против часовой стрелки.

Важное место среди математических формул с числом π занимают ряды:

Подобные ряды могут иметь и такой вид:

Существуют также ряды, связывающие π и загадочную дзета-функцию Римана ζ (s):

В последнем случае В_2n — числа Бернулли, изучаемые в высшей математике. Для справки приведем первые несколько чисел Бернулли:

Возможно, перечисление рядов — не совсем то, чего ожидал читатель. Рассмотрим подробнее простой пример: первый ряд из нашего списка, именуемый формулой Лейбница. Рассмотрим ряд

1/(1 + x²) = 1 — x² + x⁴ — x⁶ + x⁸ — …,

сходящийся при |х| < 1. Можно проинтегрировать его почленно и использовать интегральное исчисление для расчетов:

Приняв х = 1, увидим, что доказательство близится к завершению. Чтобы подтвердить правильность полученного результата для х = 1, учитывая, что этот результат верен для |х| < 1, нужно выполнить еще несколько действий. Запишем исходный ряд, но остановимся на (n — 1) — м члене, записав остаток так, как если бы речь шла об n-м члене:

Проинтегрировав почленно от 0 до 1 и приняв х = 1, имеем

При переходе к пределу при n —> оо последний член стремится к нулю. Следовательно,

actg 1 = π/4 = 1–1/3 + 1/5 — 1/7 + 1/9 — …

К сожалению, этот ряд не слишком удобен для расчетов π, так как он сходится слишком медленно. Чтобы получить десять знаков π, нужно найти сумму 10⁵⁰ членов ряда — число поистине астрономическое. Из очевидных соображений мы не будем повторять эти действия для всех ранее приведенных рядов. Это было бы слишком трудоемко, но мы не получили бы никаких новых результатов. Следующий ряд иногда называют рядом Грегори-Лейбница. В действительности его нужно было бы именовать рядом Мадхавы из Сангамаграма, так как именно этот индийский математик первым открыл формулу. Этот ряд записывается так:

где F_n — это числа Фибоначчи, элементы числовой последовательности, в которой каждое число является суммой двух предыдущих:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144….

Также π фигурирует в так называемых бесконечных произведениях. Следующую формулу вывел Джон Валлис (1616–1703):

Ее можно свести к интегралу

путем трудоемких математических преобразований. Лорд Броункер (1620–1684) преобразовал эту формулу в цепную дробь.

Авторство следующего бесконечного произведения принадлежит Эйлеру:

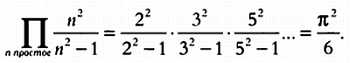
Оно имеет особенность: в нем используются только простые числа, как и в другом бесконечном произведении, еще более необычном:

Здесь используются простые числа p_k вкупе с тригонометрическими функциями. Воображение Эйлера поистине не знало пределов.

ЛЕОНАРДО ПИЗАНСКИЙ (ОК. 1170 — ОК. 1250)

Этот итальянский математик известен под многими именами. После смерти его стали называть Фибоначчи (сын Боначчи), и именно под этим именем он известен потомкам. Его отец был торговцем, постоянно путешествовал и брал Фибоначчи с собой. В путешествиях Фибоначчи познакомился со многими культурами и хорошо изучил индийскую систему счисления и арабскую математику. Он был уважаемым человеком своего времени, другом императора Священной Римской империи Фридриха II. Фибоначчи получал жалование от города Пизы, где ему платили за занятия наукой, точнее, за то, что он размышлял на полезные темы, связанные с торговлей. Его современники не проявляли особого интереса к абстрактным вопросам: некоторые результаты, полученные Фибоначчи, привлекли к Себе внимание лишь спустя 300 лет после его смерти. Самое известное его произведение — «Книга абака» 1202 года, в которой встречается знаменитая последовательность, носящая его имя:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89….,

в которой каждый элемент равен сумме двух предыдущих. Фибоначчи применил этот ряд в решении известной задачи о кроликах. В «Книге абака» содержатся другие похожие задачи, но известность в Европе книга приобрела благодаря изложению практических задач современным и понятным языком. Иными словами, читатели не возражали против рассуждений о π, но на самом деле их больше интересовали советы по использованию позиционной системы счисления с цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9 и 0. Вопросы, связанные с бухгалтерией, мерами, весами, монетами, распределением прибыли, требовали ответов и разъяснений. Фибоначчи написал и другие книги по чистой математике, в которых освещались важные задачи геометрии, теории чисел и уравнения, но в свое время они не вызвали того резонанса, которого заслуживали.

* * *

Классический результат, приведенный ниже, принадлежит французскому математику Франсуа Виету (1540–1603):

Это произведение, само по себе красивое с точки зрения математики, можно преобразовать в еще более прекрасное выражение, что сделал Хоаким Мунхаммар в 2000 году:

Число пар кроликов F_n в поколении n при отсутствии смертей и при условии, что первая пара кроликов в первом поколении не размножается, подчиняется правилу F_n = F_n-1 + F_n-2ⁿ

F_n называются числами Фибоначчи.

* * *

Вывод формулы Виета на современном языке выглядит следующим образом. Будем использовать треугольник, который применял еще Архимед. Обозначим основание треугольника за Ь, угол, образованный высотой h и стороной треугольника, за ОС.

Имеем

S_n = n ∙ площадь треугольника.

Используя элементарную тригонометрию (в развитие которой сам Виет внес заметный вклад), получим:

S_n = (1/2)∙nr²∙sin 2α = nr²∙sin α∙cos α.

Следуя по пути Архимеда и используя многоугольник с удвоенным числом сторон, имеем

S_2n = (1/2)∙2∙nr²∙sin 2α = nr²∙sin α.

Тогда

S_n/S_2n = cos α

Это ключевой момент рассуждений, поскольку далее с помощью простых алгебраических преобразований выводится следующее выражение:

Заметим, что при переходе к пределу при k —» oo

После еще одного элементарного преобразования имеем

что сводится к исходной формуле. Как оценить начальное значение α? Если, подобно Виету, взять в качестве исходного многоугольника квадрат, где

n = 4, cos α = √(1/2),

и использовать тригонометрическую формулу половинного угла, согласно которой

cos (χ/2) = √[(1/2) + (1/2)∙cos χ]

получим, пусть и другим способом, искомое выражение:

Не будем забывать, что Виету нельзя было отказать в изобретательности. Отдельное место занимают две формулы, которые считаются королевами математической красоты. Они известны как формула Эйлера:

e^π' + 1 = 0

и формула Стирлинга:

n! ~ √(2πn)∙(n/e)''.

ДЗЕТА-ФУНКЦИЯ РИМАНА

Эта легендарная функция, которую обозначают греческой буквой дзета (ζ), возможно, в будущем поможет нам узнать ранее немыслимое о простых числах и откроет их тайны. Благодаря исследованиям Эйлера эту функцию можно выразить в виде ряда, равно как и в виде бесконечного произведения:

Эта функция определяется на области, образованной комплексными числами, для которых вещественная часть больше 1. Она допускает аналитическое продолжение на всю комплексную плоскость без единицы, что показал Георг Фридрих Бернхард Риман (1826–1866). Гипотеза Римана гласит, что «нетривиальные нули» ζ имеют действительную часть, равную ¹/₂. Все это выглядит достаточно сложно (и является таковым на самом деле). Столь же непросто обнаружить связь между π и функцией ζ. Эту связь можно заметить, проанализировав значения ζ(s) и выявив, что к соответствует всем целым четным s. Илан Варди и Филипп Флажоле обнаружили следующий любопытный ряд:

Если говорить о цепных дробях, то с их помощью π выражается весьма непросто (первым с помощью бесконечной дроби значение π вычислил Ламберт):

Существуют и другие дроби, не столь известные, но намного более симметричные:

Последняя из формул — это формула лорда Броункера в несколько измененном виде. Цепные дроби отличаются одним положительным свойством: стоит нам остановиться в вычислениях на каком-либо этапе, полученная дробь будет наилучшим из возможных приближенных значений искомого числа. Если при вычислении π с помощью цепной дроби мы остановимся на определенном этапе и «раскрутим» этот клубок в обратную сторону, получим наилучшее из возможных приближенных рациональных значений. Так, если мы остановимся на дроби [3; 7, 15], то получим

ЧТО ТАКОЕ ЦЕПНАЯ ДРОБЬ

Обучить читателя построению цепных дробей, возможно, непросто, но это поможет лучше понять материал, изложенный в книге.

Возьмем число N, которое не является целым. Если мы вычтем из этого числа его целую часть, которую будем называть [N], получим N — [N], то есть дробную часть числа N. Очевидно, что значение этого выражения лежит в интервале от 0 до 1.

Число, обратное N — [N], равно — 1/(N — [N]). Оно больше 1. Для простоты будем называть его N₁.

N — [N] = 1/N₁ или N = [N] + 1/N₁.

Отделив целую часть N₁ и повторив вышеуказанные действия, получим вторую дробь;

И так далее:

Эти действия можно повторять бесконечно. Результатом будет

Если это разложение прекратится, это будет означать, что N — рациональное число (целое или дробное), иными словами, что оно выражается в виде конечной или периодической десятичной дроби. В случае с числом к, которое является иррациональным, разложение в цепную дробь бесконечно. Последовательность, которая обычно записывается так:

[[N]; [N₁], [N₂], [N₃]…]

однозначно определяет N и цепную дробь, в которую раскладывается это число.

* * *

Дробь 333/106 является наилучшим рациональным приближенным значением: чтобы получить любое более точное значение, будет необходимо увеличивать знаменатель. Приближенное значение π = 333/106 в свое время получил Ривар, причем погрешность этого значения крайне мала.

Из так называемой формулы Мэчина

π/4 = 4∙arctg (1/5) — arctg (1/239)

были выведены другие формулы, которые применялись для вычисления знаков π. Позднее мы приведем две подобные формулы, которые использовал японский специалист Канада при расчетах 1241100 000 000 знаков π.

ДЖОН МЭЧИН (ОК. 1680–1751)

Этот английский математик в течение 29 лет занимал пост секретаря Лондонского королевского общества, но остался в истории благодаря единственной формуле, носящей его имя. Эту формулу в сочетании с рядом Тейлора удобно использовать для расчетов числа к, так как полученный ред сходится достаточно быстро. Сегодня известно множество формул подобного вида, например

π/4 = 183∙arctg (1/239) + 32∙arctg (1/1023) — 68∙arctg (1/5832) + 12∙arctg (1/113021) — 100∙arctg (1/6826318) — 12∙arctg (1/33366019650) + 12∙arctg (1/43599522992503626068)

которую вывел Хван Чен Ли в 2003 году.

Сложные формулы

Индийский математик Рамануджан примерно в 1910 году получил первую из этих формул (и еще 16 подобных ей):

Эта формула отличается удивительным свойством: с вычислением каждого последующего члена она дает 8 новых десятичных знаков π. Однако для доказательства этой формулы пришлось подождать три четверти столетия, так как Рамануджан не потрудился привести доказательство. Билл Госпер, один из первых хакеров в истории, использовал эту формулу для расчета 17 миллионов знаков π. Вариант

позволил находить не 8, а 14 знаков на каждом шаге вычислений. Помимо этого, вычисления стало возможным разделить между несколькими компьютерами.

Приведенная формула была получена братьями Чудновскими в 1987 году. Мы приводим ее, чтобы подчеркнуть, насколько быстро развивается все, связанное с информатикой: в XXI веке эту формулу используют для расчетов на персональных компьютерах, а не суперкомпьютерах.

Эти формулы могут показаться сложными, что не помешало им появиться в фильме «Классный мюзикл» (High School Musical): в одной из сцен они написаны на доске, причем одна формула содержит ошибку, которую исправляют прямо по ходу действия. В чувстве юмора сценаристам не откажешь.

В 1946 году с появлением ENIAC (сокр. от Electronic Numerical Integrator and Computer — электронный числовой интегратор и вычислитель) в вычислениях начали использоваться компьютеры, и все, в том числе расчет знаков π, изменилось навсегда. ENIAC был первым электронным компьютером, предназначенным исключительно для вычислений. Его ближайшим предком была ЭВМ «Колосс», использованная Аланом Тьюрингом (1912–1954) в Блетчли-парке в военных целях, а именно для расшифровки секретных сообщений немцев. ENIAC разработали Джон Пресперт Экерт (1919–1995) и Джон Уильям Мокли (1907–1980). Этот компьютер обладал колоссальными размерами и потреблял неимоверное количество электроэнергии: в нем насчитывалось почти 100000 резисторов, реле, диодов, вакуумных ламп, конденсаторов и т. д. Его вес превышал 27 тонн, а длина составляла свыше 30 метров. ENIAC выделял столько тепла, что помещение прогревалось почти до 50 °C. Этот гигант совершал 5000 операций сложения в секунду — в тысячу раз больше, чем его предшественники (ив несколько тысяч раз меньше, чем современные персональные компьютеры). Кроме этого, он мог хранить в памяти 200 цифр. ENIAC программировался с помощью множества штекеров, подобностаринным телефонным станциям. Он был столь огромен потому, что в то время не существовало ни транзисторов, ни микросхем. В нем также не использовалась современная архитектура фон Неймана, в соответствии с которой данные и программы хранятся в одной и той же памяти.

СРИНИВАСА РАМАНУДЖАН (1887–1920)

Этот индийский математик — один из удивительнейших талантов, известных человечеству. Он был родом из очень бедной семьи. После прочтения краткого конспекта лекций по математике, где не приводились доказательства, юноша почувствовал тягу к знаниям. Он написал нескольким известным европейским математикам и отправил им результаты своего труда (120 теорем), но получил единственный ответ — от англичанина Готфрида Харолда Харди (1877–1947). Харди вместе со своим другом Джоном Литлвудом (1885–1977) за одну ночь прочитал присланную ему рукопись и не поверил своим глазам. Как объяснял сам Харди, формулы Рамануджана «должны быть истинными, поскольку если бы они не были истинными, то ни у кого не хватило бы воображения, чтобы изобрести их». Некоторые из них были похожи на те, что получили Харди и Литлвуд, прочие были в равной степени странны и оригинальны. Позднее, сначала за счет самого Харди, а затем за счет Кембриджского университета Рамануджан переехал в Великобританию, где и работал до самой смерти, наступившей в раннем возрасте от туберкулеза. Ввиду оригинальности его работ его вклад в математику беспорядочен и слабо поддается оценке, поскольку Рамануджан часто не приводил подробный вывод своих формул.

Он был очень религиозным человеком и вегетарианцем. Его в точности описывает наиболее известный анекдот о нем. Как-то Рамануджан попал в больницу и Харди отправился навестить его. Харди заметил, что приехал в такси с номером 1729. Он назвал это число скучным и непримечательным. «Вовсе нет, — последовал ответ. — Это наименьшее натуральное число, представимое в виде суммы кубов двумя различными способами!». Действительно, 1729 = 9³ + 10³ = 1³ + 12³, и 1729 является наименьшим возможным числом, которое обладает подобным свойством. Этот случай не был бы чем-то из ряда вон выходящим, если бы Харди не потребовалось несколько недель на доказательство этого утверждения. На тщательное же изучение этой темы у него ушло почти 35 лет. Сегодня математики продолжают изучать подобные числа, так называемые номера такси.

* * *

Вычисление первых 2037 знаков π на компьютере ENIAC заняло 70 часов. В таблице ниже указано рассчитанное количество знаков π и год, чтобы дать представление о том, какие изменения вызвало появление компьютеров:

1947 ∙ Д. Фергюсон и Джон Ренч с использованием механического калькулятора ∙ 808

1949 ∙ Джон Ренч-младший и Леви Смит с помощью ENIAC ∙ 2037

1958 ∙ Франсуа Женюи ∙ 10 000

1961 ∙ Дэниел Шенке и Джон Ренч ∙ 100 265

1973 ∙ Жан Гийу и Мартин Буйе ∙ 1001 250

1983 ∙ Ясумаса Канада и Ясунори Уширо ∙ 10 013 395

1987 ∙ Ясумаса Канада, Йошияки Тамура и Йошинобу Кубо ∙ 134 214 700

1989 ∙ Григорий и Давид Чудновские ∙ 1011196 691

2002 ∙ Ясумаса Канада с группой из девяти специалистов ∙ 1241100 000 000

2009 ∙ ДайсукеТакахаши и группа программистов ∙ 2576 980 370 000

2011 ∙ Сигеру Хондо ∙ 10 000 000 000 050

В 1973 году старинная формула Эйлера вкупе с формулой Мэчина позволила Гийу и Буйе вычислить миллион знаков π:

Любопытно, что для вычисления второго слагаемого достаточно вычислить первое и перенести запятую на несколько позиций. Вне зависимости от их абсолютной величины два первых слагаемых будут отличаться только количеством нулей.

В 1976 году Юджин Саламин и Ричард Брент предложили алгоритм, основанный на давней гипотезе Гаусса и Лежандра о последовательном вычислении средних арифметических и средних геометрических. Суть алгоритма непросто описать вкратце. Алгебраический алгоритм — это метод расчета некой величины, в данном случае Я. Саламин и Брент использовали следующие исходные равенства:

a₀ = 1; b₀ = 1/√2; t₀ = 1/4; p₀ = 1,

затем рекуррентным способом вычислили

a_n+1 = (a_n + b_n)/2;

b_n+1 = √(a_nb_n);

t_n+1 = t_n — p_n(a_n - a_n + 1)²;

p_n+1 = 2p_n.

В пределе справедливо следующее соотношение:

π ~ (a_n + b_n)²/4t_n.

Этот алгоритм, который было бы невозможно использовать без помощи компьютера, обладает квадратичной скоростью сходимости, то есть на каждом шаге число знаков, полученное на предыдущем, удваивается. С использованием этого алгоритма было получено 206158430000 знаков π.

Но и это еще не все: в 1980-е годы Петер и Джонатан Борвейны создали алгоритм со скоростью сходимости четвертой степени, с помощью которого было рассчитано 1241100 000 000 знаков. Мы не станем приводить его здесь, так как он будет понятен лишь узким специалистам.

ВЕЛИКОЛЕПНАЯ ЧЕТВЕРКА

Любой специалист, интересующийся вычислением я, знаком с выдающейся канадской семьей Борвейнов. Отец, Давид Борвейн (род. в 1924 году), литовец по происхождению, — известнейший математик своей страны. Он изучал многие разделы математики, особое внимание уделяя теории рядов. Его старший сын Джонатан (род. в 1951 году), автор множества книг, известных в компьютерном мире, отличается особым отношением к числу я. Он увлекается преподаванием математики и разрабатывает специальные обучающие программы. Питер (род. в 1953 году) — один из создателей формул ВВР для расчета числа я, названных так в честь их создателей — Бэйли, Борвейна и Плуффа. Он также достиг выдающихся результатов в информатике. Мать Джонатана и Питера, супруга Давида Борвейна, тоже известна в научных кругах, но не математических, а анатомических.

* * *

В конце 2002 года группа японских специалистов, возглавляемая Ясумасой Канадой, достигла результата, который теперь уже не так удивляет научный мир. Тем не менее последняя страница в этой истории еще не написана. Прогресс в этой области, кажется, не прекращается: в 2011 году был получен 10 000 000 000 050 знак числа π.

Сколь далек этот результат от предсказания Дэниела Шенкса (не путать с Уильямом Шенксом), который в 1983 году заявил, что вычисление миллиарда знаков π станет неприступной задачей! Сохраним для истории две формулы Мэчина, которые использовал Канада:

π/4 = 12∙arctg (1/49) + 32∙arctg (1/57) — 5∙arctg (1/239) + 12∙arctg (1/110443)'

π/4 = 44∙arctg (1/57) + 7∙arctg (1/239) — 12∙arctg (682) + 24∙arctg (1/12943).

Первая формула была открыта в 1982 году, а вторая была найдена Фредериком Карлом Штермером еще в 1896 году (опубликована в журнале Французского математического общества). Кто бы мог подумать, что эта формула будет использована для подобной задачи спустя столько лет! В математике никогда нельзя загадывать наперед: то, что сегодня кажется несущественным, завтра может стать основополагающим.

Возможно, помимо рекордных вычислений читателя заинтересуют не совсем традиционные вычислительные методы. Применение формулы

позволяет вычислить любой n-й знак π без необходимости рассчитывать все предыдущие. Увы, но результатом является только двоичное или шестнадцатеричное число. Формулы, подобные этой, создали Дэвид Бэйли, Питер Борвейн и Симон Плуфф. Они известны как формулы ВВР (по первым буквам фамилий их создателей). Считается, что эти формулы указывают на наступление новой эпохи в вычислениях.

Формула Фабриса Беллара (род. в 1972 году)

является производной от формул ВВР, и с ее помощью вычисления выполняются на 43 % быстрее.

При расчетах в двоичной системе находятся значения битов (0 или 1). Уже вычислен квадриллион знаков числа π. Используя эту формулу, мы можем определить, находится ли на определенной позиции 0 (возможны лишь два варианта: 0 или 1), не зная при этом предшествующих знаков. Совершенству нет предела, хотя реальная полезность подобной формулы представляется сомнительной.

В заключение упомянем, что уже найдены формулы, с помощью которых можно найти произвольный знак π в любой системе счисления.

ЦИФРА, ПОЛУЧЕННАЯ БЕЗ ФОРМУЛ

Колумнист журнала Scientific American Мартин Гарднер (1914–2010), известный писатель, полемист и математик, в 1966 году предсказал, что миллионным знаком π является 5. Это предположение основывалось на англоязычной версии Библии, в частности на 3-й книге, 14-й главе, стихе 16 (3-14-16), где используется магическое число 7 и седьмое слово содержит пять букв. Поэтому миллионный знак π после запятой (в те годы его значение еще не было вычислено) — должен быть равен 5. Никто не воспринимал это предположение всерьез, но в 1974 году были проведены необходимые расчеты, и, как и следовало ожидать, этот знак оказался равен 5. Мартин Гарднер не использовал ни одной формулы.

В стороне от формул

В завершение этой главы приведем еще несколько любопытных примеров. Например, формула

iⁱ = e^-π/2

объединяет комплексные и вещественные числа.

Следующее равенство связывает π с простыми числами:

где

ф(k) — количество целых чисел, меньших k и взаимно простых с ним.

Следующая формула касается квазицелых чисел. Эти числа очевидно являются иррациональными, но при расчетах на обычном калькуляторе выглядят как целые. Эти числа начинают отличаться от «реальных» целых чисел спустя множество знаков после запятой, и нужен очень точный калькулятор, чтобы увидеть этот десятичный знак после запятой, которому предшествует множество нулей. Выражение справа является квазицелым числом 427:

При расчетах на обычном калькуляторе значение этого выражения равно 427. Более точные расчеты показывают, что это число отличается от целого числа 427 только с 52-го знака после запятой. Именно с этого знака в десятичной записи этой дроби перестают фигурировать только нули. Выражение в скобках действительно заслуживает название квазицелого.

Нельзя отрицать, что π встречается во множестве областей. Например, рассмотрим гипотезу Кеплера об упаковке, чрезвычайно далекую от числа π. Какова максимальная плотность упаковки дисков на плоскости? Она равна

π/(2√3)

Глава 5 Пи-мания

Число π особенное. Мы уже говорили, что оно самое известное, самое изученное, самое знаменитое и самое упоминаемое. Энтузиазм, страсть и настоящую одержимость этим числом называют «пи-манией». Она одновременно академична и экстравагантна, интересна и занимательна. Читатель может удивиться, что мы уделяем столько внимания этому вопросу, слабо связанному с математикой. Такова реальность: π — это намного больше, чем просто число.

Вокруг числа π

Число π не обошли вниманием даже маркетологи. Изображение π можно встретить на футболках (даже для домашних животных!), пуговицах, запонках, чашках, чайниках, часах, ковриках для компьютерной мыши, фартуках, плюшевых мишках, подушках, шкатулках, кафельной плитке, кепках, плакатах, автомобильных аксессуарах и многом, многом другом.

Эти футболка и кружка с изображением числа π — одни из многих товаров с изображением греческой буквы π.

Плакат для математиков и фанатов числа π.

Круги, которые якобы рисуют инопланетяне на полях, стали очень известными еще в 70—80-х годах прошлого века. Было обнаружено, что круги на фотографии слева вычерчены на основе знаков π. Фигуру на фотографии справа сложно истолковать как-то иначе.

Mazda 3 с изображенным на ней числом π.

День числа π – 14 марта. Этот праздник придумал американец Ларри Шоу, который заметил, что дата 14 марта в американском формате записывается как 3/14, что соответствует приближенному значению числа π. Это может показаться абсурдным, но праздник получил широкую известность и мгновенно распространился в университетских кругах.

Фирменное блюдо этого праздника — круглая пицца, так как она хранит в себе секреты числа π. Торжества поражают своим размахом, и участники не скупятся на выдумки.

Плакат с приглашением на празднование Дня числа к 14 марта.

День числа π совпадает с днем рождения Альберта Эйнштейна, что в немалой степени способствует популярности праздника. Число π можно встретить на бутылках вина, кругах сыра и даже на упаковках парфюмерии.

Праздничный "Пи-торт" в день числа π можно подать в такой тарелке.

Знак π приобрел популярность достаточно давно: еще в 1915 году 22-я эскадрилья королевских ВВС использовала его в качестве эмблемы. При первоначальном размещении акций Google номер последней акции был равен 14159265 (вспомним, что π = 3,14159265…). Благодаря математическому образованию владельцев Google число π проникло и на Уолл-Стрит.

В 1982 году, когда о консолях еще не было известно, а в мире видеоигр безраздельно властвовали ZX Spectrum и Dragon 32, компания Automata UK выпустила игру «Пи-мания», главного героя которой звали, естественно, Пи-мэн. Эта игра уже устарела, и в ближайшее время какая-нибудь компания наверняка создаст ее ремейк.

Возможно, самым удивительным проявлением пи-мании можно назвать компьютерный поисковик, позволяющий найти желаемую последовательность цифр среди, например, первых восьми миллионов знаков π. Если вам интересно, начиная с какой позиции в записи π встречается день, месяц и год вашего рождения, посетите интернет-сайт The Pi Searcher. Введите желаемое число, и если заданная последовательность встречается среди первых нескольких миллионов знаков (в первой версии сайта было доступно восемь миллионов, позднее — 200 миллионов, и это число продолжает расти), поисковый механизм выдаст ответ с номером позиции. Если нужные цифры не встречаются среди знаков π, вы увидите оповещение об этом.

Конечно, вероятность найти среди знаков π дату своего рождения в сокращенном виде (то есть 181 146 для даты 18.11.46) составляет почти 100 %. Если вы ищете всего четыре цифры (например, дату 1.3.56, то есть 1 марта 1956 года), то поисковый механизм гарантированно даст ответ, поскольку к 60872-му знаку π встречаются все возможные комбинации из четырех цифр. Если же вы укажете более полную форму записи (например, представив дату 18.11.46 как 18 111 946), вероятность снизится до 63 %. Чем длиннее последовательность, тем меньше вероятность, что ее удастся найти.

Можно попробовать найти среди знаков π номер телефона, номер автомобиля или любое другое число.

Кроме того, с помощью этого поискового механизма можно найти любопытные циклы. Например, начнем цикл с числа 40, которое впервые обнаруживается на 70-й позиции, затем найдем, на какой позиции находится число 70 и так далее. Кажется, что этот цикл бесконечен. Но на самом деле он имеет завершение. Дэн Сикорски обнаружил следующую последовательность: 40, 70, 96,180, 3664, 24 π7,15 492, 84 198, 65 489, 3725,16 974, 41 702, 3788, 5757,1958,14 609, 62 892, 44 745, 9385,169, 40. Как видим, после множества этапов этот цикл возвращается к началу. Вероятность появления подобных циклов еще не изучена.

Стихотворения и фразы для запоминания

Почти все авторы, которые хотят привести стихотворение о числе π, обращаются к одному и тому же источнику. Вислава Шимборская, польская поэтесса, удостоенная в 1996 году Нобелевской премии по литературе, написала удивительное стихотворение, известное во многих переводах. Вот один из вариантов:

(Перевод Т. Бонч-Осмоловской)

Существуют «оды числу пи» и многие подобные произведения, но стоит отметить, что стихотворение Шимборской великолепно.

Многие фанаты π рассматривают поэзию как инструмент. Так, появилось множество стихотворений, которые помогают запомнить первые знаки π. Обычно цифры зашифрованы количеством букв в словах. Например, в слове «знаю» 4 буквы, оно соответствует цифре 4. «Прекрасно» соответствует цифре 9, так как в нем 9 букв. Фраза «это я знаю и помню прекрасно» — не просто ответ самоуверенного ученика. В ней зашифрована последовательность цифр 314 159.

С помощью этой техники можно запоминать любые случайные последовательности чисел, в том числе и знаки числа π. Хотите знать первые знаки π наизусть? Найдите стихотворения или фразы, которые легко запомнить. Кажется, что это сложно, но на самом деле запомнить слова проще, чем цифры. Главное — знать, что каждое слово соответствует числу букв в нем, нужно просто внимательно считать буквы.

Так поэзия превращается в инструмент для запоминания, и самыми лучшими стихотворениями становятся не самые красивые, а самые длинные, потому что они помогают запомнить больше цифр. Приведем несколько примеров.

Это четверостишие соответствует 18 цифрам:

3,14159265358979323.

Вот другое стихотворение, первую строку которого мы уже приводили:

Существуют стихотворения, позволяющие запомнить почти 80 знаков. В 1986 году на английском языке было написано стихотворение для запоминания более 400 знаков.

Есть и короткие фразы, построенные по тому же принципу. Их очень легко запомнить, например:

«Вот и знаю я число, именуемое пи. — Молодец!»

Последняя цифра (7) — приближенное значение, соответствующее правилам округления. В действительности на этом месте должна находиться цифра 6.

Подобные фразы были написаны и на других языках. Например, сэр Джеймс Хопвуд Джинс (1877–1946) придумал ставшую очень популярной фразу для запоминания первых 14 цифр π:

How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!

(«Как бы я хотел выпить чего-нибудь, спиртного разумеется, после трудных лекций по квантовой механике!»)

Эту фразу можно продолжить, не нарушая мнемонических правил:

How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics and if the lectures were boring or tiring, then any odd thinking was on quartic equations again.

(«Как бы я хотел выпить чего-нибудь, спиртного, разумеется, после трудных лекций по квантовой механике, и если лекции скучны или утомительны, то после них я не могу думать ни о чем, кроме уравнений четвертой степени».)

На 32-м слове фраза заканчивается, хотя ничто не мешает продолжать ее и дальше. Многие мнемонические стихотворения и фразы заканчиваются именно на 32-м слове, потому что 32-м знаком π после запятой является ноль, и выразить это словами не так-то просто. На французском языке есть следующее стихотворение:

В этом стихотворении зашифровано 126 знаков π. Заметьте, что французское слово mysterieux состоит из 10 букв, но читается как 09, чтобы таким способом представить 0. Похожим способом ноль обозначается и в других подобных примерах.

Если читателя интересуют произведения на других языках, он с легкостью найдет их в Интернете. Последний совет: главное при запоминании подобных стихов — не сбиваться со счета. Одного из пионеров применения ядерной физики к вопросам эволюции звезд, физика Георгия Гамова, известного также под именем Джордж Гамов, как-то упрекнули в журнале Scientific American, что он ошибочно привел значение π = 3,14158 вместо 3,14159. Оказалось, что Гамов, американский физик русского происхождения и полиглот, неверно запомнил французскую фразу Que j’aime a faire apprendre для запоминания π, забыв одну букву «р» в слове apprendre.

Особое место среди стихов занимают японские трехстишия хайку. Сейчас они написаны на многих языках и на многие темы, не стало исключением и число π. Хотя существуют хайку о числе π, высшим мастерством считается умение написать пику — математический вариант хайку. Классические хайку — трехстишия со структурой слогов 5-7-5 (первая строка состоит из 5 слогов, вторая — из 7, третья — снова из 5). Пику также является трехстишием, но в нем есть дополнительное условие: число букв в словах должно совпадать с соответствующим знаком π.

Предлагаем читателю пример пику на английском языке:

Некоторые авторы используют уже известные стихотворения и специальную систему кодов. Среди них особо выделяется Майк Кейт, фанат числа π, который создал единственную в своем роде версию стихотворения «Ворон» Эдгара Аллана По. Она носит название Near a raven («Около ворона»). Но и это еще не все: тот же Майк Кейт написал рассказ Cadaeic cadenza, в который включил свое же стихотворение, а также фрагменты произведений Льюиса Кэррола, Омара Хайяма, Уильяма Шекспира и других авторов. В Cadaeic cadenza зашифрованы 3834 знака π, что кажется феноменальным, если не сказать невозможным. В самом названии также зашифрованы знаки π (обратите внимание на порядковые номера букв в английском алфавите):

С a d а е i с

3, 1 4 1 5 9 3

Интерес также вызывает способность некоторых людей запоминать бесчисленное множество знаков π, используя для этого подобные стихотворения или другие приемы. Неудивительно, что многие любители таких упражнений, настоящие спортсмены, обладающие безграничной памятью, попали на страницы Книги рекордов Гиннесса.

Рекорды по запоминанию π быстро сменяют друг друга, каждый участник стремится во что бы то ни стало побить прошлое достижение. Иногда также учитывается не только количество верно названных знаков, но и скорость, с которой рекордсмен может их воспроизвести. Но не будем углубляться в тонкости. Если говорить об абсолютном рекорде по числу запомненных знаков, то он принадлежит украинцу Андрею Слюсарчуку, который запомнил 30 миллионов цифр. Это достижение выглядит столь невероятным, что даже в Книге рекордов Гиннеса оно не было отмечено как мировой рекорд.

Официально утвержденный рекорд был установлен в 2006 г. и принадлежит японцу Акире Харагучи, который запомнил сто тысяч знаков. Не следует полагать, что эти рекорды устанавливают лишь фанатики числа π: в списке рекордсменов фигурируют и всемирно известные ученые, например американец Александр Айкен или канадец Саймон Плуфф.

Пи-музыка

В музыке число π встречается не столь широко, несмотря на традиционную близость музыки и математики. Вспомним, что в повсеместно применяемом равномерно темперированном строе каждая октава делится на математически равные интервалы с соотношением частот ¹²√2. Диатоническая гамма, сформулированная еще в древности, представляется в виде так называемых квинт с соотношением частот 3:2. Мы приводим эти технические моменты в качестве введения к последующим объяснениям.

Натуральный строй

Современный музыкальный строй берет начало еще во времена Пифагора. В его основе лежат ноты так называемой диатонической системы (до, ре, ми, фа, соль, ля, си). В пифагорейском строе ноты соответствовали частоте вибрации струны. Грубо говоря, разным частотам соответствовали разные ноты. Различие между вибрациями (нотами) измерялось в интервалах. Интервалы получаются не вычитанием одной частоты из другой, как можно было бы думать, а их делением. Результат деления двух частот выражался в виде простой дроби. Например, квинта — интервал шириной в пять ступеней — означает результат деления частоты данной ноты на частоту ноты, отстоящей от нее на пять ступеней, и равен 3/2. Интервал октавы охватывает восемь ступеней диатонического ряда, например от «ре» до следующего «ре». Соотношение частот между звуками равно 2/1 = 2.

Рассмотрим пример. Если нажать на центральную клавишу пианино, мы услышим ноту «ля» частотой в 440 герц (колебаний в секунду). Если нажать на следующую «ля», расположенную на семь белых клавиш правее, новый звук будет иметь частоту в 880 герц. Разница между этими нотами (то есть интервал между ними) в музыке выражается дробью 880/440 = 2.

Этот интервал и является так называемой октавой. Две ноты, разделенные между собой интервалом в одну октаву (в нашем примере это нота «ля»), звучат одинаково, но явно различаются по высоте. Пифагор, во времена которого пианино еще не существовало, обнаружил этот факт, играя на одной струне: если зажать струну точно посередине, то полученная нота будет той же, что и для всей струны.

Этот строй идеально подходил для струнных инструментов, но с его помощью нельзя было качественно измерить небольшие различия между нотами, например диезы и бемоли. Это привело к появлению так называемого равномерно темперированного строя: в него наряду с обычными нотами включены диезы и бемоли. Это делается с помощью равных интервалов. Соотношение частот между соседними интервалами равно ¹²√2. Полученный таким образом строй получил название темперированного.

Значение ¹²√2 получается следующим образом. Нам нужно разделить на 12 равных частей интервал длиной 2 (2 — это отношение частот в начале и конце интервала) так, чтобы отношение частот между соседними частями интервала было неизменным. Полученные частоты образуют геометрическую прогрессию со знаменателем ¹²√2.

Ноты равномерно темперированного строя, слева направо: до, до-диез, ре, ре-диез, ми, фа, фа-диез, соль, соль-диез, ля, си-диез, си, до. Ноты диатонического строя: до, ре, ми, фа, соль, ля, си, до.

Последовательность из 12 интервалов, по одному на каждую ноту, выглядит так:

¹²√2, (¹²√2)², (¹²√2)³, (¹²√2)⁴, (¹²√2)⁵, (¹²√2)⁶, (¹²√2)⁷, (¹²√2)⁸, (¹²√2)⁹, (¹²√2)¹⁰, (¹²√2)¹¹, (¹²√2)¹² = 2 

В XVIII веке появилась новая система интервалов, в которой значение квинты было равно 600 + 300/π. Новый музыкальный строй относительно недавно был предложен Чарльзом Люси (род. в 1946) и носит его имя. Необходимо пояснить, что это отдельная, уже запатентованная система.

Другое музыкальное проявление числа π — возможность «услышать» его знаки: в Интернете можно найти программы, которые позволяют «сыграть число π». Для этого всем десяти цифрам присваиваются определенные ноты. Для каждой следующей цифры программа воспроизводит соответствующую ей ноту. Поскольку знаки π являются (или кажутся) случайными, то полученная композиция также будет случайной. Вероятнее всего, слушателю станет скучно слушать бесконечные цифры, но нельзя отрицать, что очень, очень длинная случайная композиция может звучать даже приятно. В диатоническом строе существует 7¹⁰ различных способов образовать мелодию из семи нот (в этом строе нет ни диезов, ни бемолей). В комбинаторике говорят, что существует 7¹⁰ сочетаний с повторениями. Из этого числа нужно вычесть последовательности из одной повторяющейся ноты, поскольку результат окажется особенно скучным. В зависимости от выбора ноты для каждой цифры существует семь вариантов генерации непрерывного шума.

Кино, литература и число π

Число π использовалось в кино тысячи раз, но, как правило, с его помощью лишь создают ореол таинственности в простых ситуациях, как, например, в фильме «Разорванный занавес» (Torn Curtain) Альфреда Хичкока, где π используется как кодовое слово в организации перебежчиков. Математическая природа π раскрывается редко, либо же это делается излишне эффектно и поверхностно, как в фильме «Пи» американского режиссера Даррена Аронофски, вышедшем на экраны в 1998 году. В основе фильма лежат приключения гениального математика Макса Коэна, который постепенно сходит с ума, одержимый числами. В этом фильме обыграно оккультное значение чисел, но математическая строгость неизменно уступает место драматическим эффектам.

Число π могло сыграть главную роль в научно-фантастическом фильме «Контакт» (1997) режиссера Роберта Земекиса с Джоди Фостер в роли астронома Элеонор Эрроу эй. К сожалению, все упоминания о π были исключены из финального варианта сценария. В оригинальном романе «Контакт» (1985) известного космолога Карла Сагана, на основе которого и снят фильм, число π настолько важно, что этот эпизод романа спровоцировал дискуссию в научном мире. Но не будем забегать вперед.

Плакат фильма «Пи» (вверху). В 1997 году Роберт Земекис экранизировал роман Карла Сагана «Контакт», в котором инопланетяне утверждают, что в знаках к спрятано таинственное сообщение.

«Контакт» — это фильм о возможности общения с внеземными цивилизациями и о проблемах, в том числе религиозных, которые могут возникнуть вследствие такого контакта. В фильме рассказывается история доктора Эрроуэй, которая с помощью радиотелескопа улавливает сигнал из космоса, строит генератор «кротовых нор» для путешествия по Вселенной и встречается с инопланетянами. Инопланетяне сообщают Элеонор, что среди знаков π, возможно, скрыто некое послание. Расшифровать это таинственное сообщение не под силу даже им, потому что шифр знает лишь Бог, создатель Вселенной.

Инопланетяне предполагают, что сообщение зашифровано с помощью знаков π: начиная с определенной позиции, знаки π перестают изменяться случайно и образуют последовательность из нулей и единиц. Если расположить эти цифры в форме квадрата, единицы и нули образуют идеальную окружность, вписанную в этот квадрат. Этот шифр — часть π, часть самой природы. Значит ли это, что он помещен туда Богом? В последней главе мы вернемся к этому фильму и обсудим возможность существования подобного квадрата и круга, образованного знаками π.

В романе британского автора Дугласа Адамса «Автостопом по галактике», классике современной юмористической литературы, огромный компьютер сообщает людям ответ на главный вопрос жизни и Вселенной. Удивительно, но ответ на этот вопрос — «42». Некоторые фанаты числа π восприняли ответ компьютера слишком серьезно и начали поиски. Они отвергли число 42 как слишком простое и начали искать среди знаков π последовательности вида 424 242 с помощью поискового механизма The Pi Searcher. Эта последовательность встречается в записи π, начиная с 242 423-й позиции. Нет никаких сомнений, что энтузиасты продолжат свои поиски.

Число π и законы

Немного странно упоминать здесь о столь далекой от π области знаний, как право и законодательство, но это число встречается и здесь. В 1836 году в послереволюционной Франции жил некий ученый Лакомм, который не только считал π равным 3,25, но, что удивительно, был награжден многими авторитетными учреждениями за свои открытия, связанные с этим числом. Напомним, что на тот момент было точно вычислено уже более сотни знаков π.

Наиболее известный законодательный курьез, связанный с π, произошел в Индиане, США. В 1897 году некий Эдвард Гудвин, весьма искушенный в геометрии, опубликовал в серьезном журнале American Mathematical Monthly короткую статью и убедил законодательные органы штата обсудить текст нового закона (билль № 246), который затем должен был поступить на рассмотрение в палату представителей. Казалось бы, в этом нет ничего необычного. Но в случае принятия этого закона значение числа π считалось бы равным

π = 16∙√2/7 = 3,232

что подтверждали сложные и объемные расчеты. Закон также требовал включить это значение π в официальные учебники, а в случаях использования «истинного» значения π (иными словами, прежнего, общеизвестного значения) необходимо было уплатить Гудвину авторские отчисления. Гудвин и законодательные органы не приняли во внимание, что за 30 лет до этих событий Линдеман доказал трансцендентность числа π и невозможность решения задачи о квадратуре круга. Они также проигнорировали все прочие расчеты и известные на тот момент более 100 точных знаков π. Высокопоставленных лиц Индианы это ничуть не интересовало.

Проект закона был одобрен несколькими комиссиями нижней палаты парламента и был передан в сенат с положительной рекомендацией. К счастью, пусть и по воле случая, этот закон так и не был принят. Кто-то показал текст закона специалисту, который случайно проходил мимо, — профессору математики Кларенсу Авиафару Уолдо (1852-1926), чтобы тот написал предисловие к тексту закона. Тот вежливо отказался, сказав, что его несколько утомили искатели квадратуры круга.

Внимательно прочитав текст закона, он пришел в ужас и незамедлительно рассказал сенаторам об истинном положении вещей. В итоге благодаря усилиям Кларенса Уолдо члены сената поняли всю абсурдность закона, и знаменитый билль № 246 не был утвержден.

Профессор математики Кларенс Авиафар Уолдо.

Он помешал тому, чтобы впервые в истории полная бессмыслица с точки зрения науки была возведена в ранг закона.

Число  π искусство

Число π увековечено на фризе Дворца открытий в Париже, что как нельзя лучше соответствует духу этого места. На фризе высечено более 600 знаков, рассчитанных Уильямом Шэнксом в 1873 году. На самом деле этот английский математик вычислил 707 знаков, но Дэниел Фергюсон в 1944 году обнаружил в его расчетах ошибку, начиная с 528 знака. По этому случаю Николас Роуз написал такие стихи:

Фриз Дворца открытий, на котором изображены первые 600 знаков π.

Настоящее произведение искусства, основанное на π и его знаках, находится в Торонто. Канадская художница Арлин Стамп создала гигантскую мозаику, которая находится в вестибюле станции метро Даунсвью. Мозаику образуют прямо угольники разной ширины, которые накладываются друг на друга. Если не знать заранее, то сложно заметить, что ширина наложения прямоугольников друг на друга не случайна. Каждый прямоугольник накладывается на следующий по определенному правилу: ширина прямоугольника принята за 1, а видимая часть каждого следующего прямоугольника пропорциональна соответствующему знаку π. Мозаика начинается с 1 — первого знака после запятой в записи 3,1415926535… — и продолжается в точном соответствии с последующими знаками.

Так как эти цифры случайны (или кажутся случайными), непосвященный зритель не может догадаться, что расположение частей мозаики подчиняется какому-то правилу. Однако, как в свое время обнаружил математик Иварс Петерсон, кажущаяся случайность распределения цифр подчиняется определенному закону.

Цветные прямоугольники имеют одинаковые размеры, но расположены так, что их видимая часть пропорциональна соответствующему знаку π. Каждый следующий прямоугольник частично накладывается на предыдущий.

На входе в Техническую школу Генри Эббота в Данбери, штат Коннектикут, США, установлена скульптура в форме π высотой почти 20 метров авторства Барбары Грайгатис. Скульптура освещается ночью и напоминает будущим инженерам о том, что им еще не раз предстоит встретиться с этой константой во время учебы.

Скульптура Барбары Грайгатис в Коннектикуте, изображающая π.

В американском городе Сиэтле скульптура в виде π установлена на парадной лестнице у входа в Музей искусств. Вход в Берлинский технический университет украшен мозаикой в виде π.

Существует чисто математическое произведение искусства — формула

е^πi + 1 = 0,

которая связывает пять самых значимых констант (е, π, i, 1 и 0). Считается, что это самая красивая формула во всей науке. Ее открыл Леонард Эйлер, он же доказал ее корректность.

Людольф ван Цейлен (1540–1610) считал иначе. Используя многоугольники с 2⁶² сторон, этот немецкий геометр вычислил приближенное значение π с точностью до 20-го, а затем — до 35-го знака. Он работал столь усердно, а его энтузиазм был столь велик, что он завещал высечь найденное им значение π на своем надгробии в память потомкам. Это не шедевр искусства, но ван Цейлен высоко оценил бы его.

ЛЕОНАРД ЭЙЛЕР (1707–1783)

Швейцарский математик Леонард Эйлер был одним из самых выдающихся математиков в истории. Он был невероятно одарен, обладал феноменальной памятью и превосходно считал в уме. Благодаря зтомудаже слепота, настигшая его в 1766 году, не помешала ему заниматься наукой еще 17 лет, до самой смерти. Он умер в России, куда его пригласила Екатерина II. Императрицу привлекла его известность, да и рекомендации другого швейцарского математика, Даниила Бернулли, были не лишними. Эйлер с перерывами жил в России с 1737 года. При подготовке полного собрания только научных его трудов оказалось, что оно насчитывает свыше 80 томов; Эйлер окончательно ввел в употребление греческую букву я для обозначения числа пи и разработал многие другие обозначения, например f(x) для обозначения функций от х, i для мнимой единицы и Σ для обозначения суммы. Его вклад в науку огромен: он занимался исчислением бесконечно малых, функциями, теорией чисел, топологией, теорией графов, физикой и астрономией. Его именем назван астероид. Эйлер открыл множество рядов, в которых фигурирует π.

Марка СССР, выпущенная в 1957 году к 250-летию со дня рождения Эйлера.

Могила Людольфа ван Цейлена в Лейдене. На надгробии высечены 35 знаков π, которые он рассчитал.

Математик и автор научно-популярных книг Клиффорд Пиковер считал формулу Стирлинга (1692–1770)

очень красивой и полагал, что ею можно любоваться как произведением искусства. Не знаем, разделит ли читатель подобную точку зрения, но формула действительно примечательна: она объединяет экспоненту от n, число n, возведенное в степень n, его же факториал (n! = n∙(n — 1)∙(n — 2)∙… ∙2∙1) и корень из этого числа.

Глава 6 Второй взгляд на бесконечность

Компьютеры бесполезны. Они могут только давать ответы.

Пабло Пикассо

Обратим взгляд на бесконечные знаки π. Эта бесконечность находится от нас нарасстоянии вытянутой руки. Чтобы понять ее, возможно, не требуется столь широкого воображения, каким обладал Георг Кантор.

Нобелевский лауреат по физике Ричард Фейнман (1918–1988) увидел среди бесконечных знаков π любопытную последовательность девяток:

Эта последовательность начинается с 762-й цифры и называется точкой Фейнмана. Учитывая, что в десятичной дроби со случайными знаками вероятность появления семи девяток подряд крайне мала (всего 0,08 %), открытие Фейнмана тем более важно. Но имеет ли это какое-нибудь значение? Неизвестно, сколько еще подобных тайн хранит в себе π.

Другая примечательная последовательность — 0123456789 — начинается с 17387594880-й цифры. Ее обнаружил уже не Фейнман, а компьютерная программа.

Взглянем на магический квадрат, то есть квадрат, в котором сумма чисел в строках, столбцах и диагоналях одинакова. В нашем случае эта сумма равна 65.

Этот магический квадрат составил американец Т. Лобек.

Теперь посмотрим на знаки числа π. Для каждого числа в квадрате (обозначим его за n) возьмем n-й знак π. Например, для первого числа в квадрате, 17, возьмем 17-й знак π, который равен 2. Запишем его в магическом квадрате вместо числа 17 и так далее. Таким образом мы получим новый квадрат. Запишем на полях суммы чисел в его строках и столбцах:

Живительно, но каждая сумма в столбце встречается среди сумм чисел в строках. Это похоже на фокус, но в мире математики никакая магия не действует. Как же это возможно? Это тоже неизвестно. Нам почти ничего не известно ни о π, ни о бесконечности…

Обезьяны, печатные машинки и библиотеки

Совершим прогулку по неизведанному пути, возможно, несколько далекому от числа π. Мы изучим вершины человеческой мысли и приблизимся к границам неизвестного, но на этом пути мы попадем в мир мифов и легенд.

В англосаксонской традиции Дарвин и дарвинизм занимают особое место. Публикация «Происхождения видов» оскорбила многих «благочестивых граждан», которых задела мысль о том, что эволюция человека и животных шла одним путем. Фраза «человек произошел от обезьяны» — весьма грубое изложение дарвиновских идей, но именно так вкратце формулируется суть эволюционизма. Следовательно, любое упоминание обезьян немедленно воскрешает в памяти научные споры. С другой стороны, клавиатура печатной машинки в викторианскую эпоху считалась чем-то современным и высокотехнологичным. Обезьяны и печатные машинки — настоящая взрывоопасная смесь. История о печатных машинках и обезьянах, ставшая сейчас классической, в свое время выглядела одновременно и новаторской, и провокационной.

Представим, что нескольким обезьянам вручили по печатной машинке. Такой эксперимент был проведен с настоящими макаками, и оказалось, что они печатают бесчисленные страницы, полные букв «s», которая по какой-то причине кажется им наиболее привлекательной. Предположим, что в нашем мысленном эксперименте обезьяны ведут себя ответственно и печатают более или менее случайные последовательности символов на листах, и этот процесс длится очень и очень долго.

Так называемая теорема о бесконечных обезьянах гласит, что абстрактная обезьяна, ударяя случайным образом по клавишам печатной машинки в течение неограниченно долгого времени, рано или поздно напечатает любой наперед заданный текст. Иными словами, за неограниченно долгое время группа обезьян воспроизведет, например, «Дон Кихота» с точностью до буквы.

С точки зрения теории вероятностей, «рано или поздно» в формулировке теоремы означает «в пределе» или «с вероятностью, стремящейся к единице». Подобная формулировка не содержит никакой неоднозначности и является математически точной. Однако это не противоречит следующему факту: по прошествии невообразимо большого промежутка времени обезьяны могут не напечатать ничего осмысленного. Теорема утверждает лишь то, что вероятность стремится к единице (событие произойдет со стопроцентной вероятностью), если промежуток времени стремится к бесконечности.

Множество обезьян напечатает любой заданный конечный текст, располагая неограниченно долгим временем.

В более литературном варианте эту теорему изложил великий аргентинский писатель Хорхе Луис Борхес, который уделял пристальное внимание бесконечности и создал множество образов Вселенной. В рассказе «Вавилонская библиотека» из книги «Вымыслы» (1944) Борхес описывает воображаемую библиотеку, в которой хранятся все возможные книги. Размер книги ограничен N страницами или знаками, при этом N достаточно велико, чтобы одна книга вместила даже самую большую энциклопедию. По Борхесу, в этой библиотеке содержатся все возможные перестановки печатных знаков (символов, знаков пунктуации и пробелов, разделяющих слова), напечатанные в виде книг.

Проведя некоторые вычисления, получим, что воображаемая библиотека Борхеса состоит минимум из 25^1132000 ~ 1,956∙10^1834097 книг.

Мы не будем приводить здесь подробное доказательство теоремы о бесконечных обезьянах, поскольку оно слишком объемно и требует объяснения многих понятий из теории вероятностей, но в общих чертах можно предположить, что теорема верна.

Допустим, что на клавиатуре 60 клавиш. Простая последовательность символов, например to be or not to be (знаменитое «быть или не быть» Гамлета), требует 18 нажатий. Вероятность того, что эта фраза не будет напечатана после n попыток, равна

(1 - (1/60¹⁸))ⁿ,

и при n —> оо это выражение стремится к нулю. Чтобы упростить расчеты, предположим, что вместо одной обезьяны за печатными машинками сидят k обезьян. Казалось бы, этот предел не изменится, но интуитивно понятно, что он будет достигнут быстрее.

Несколько более сложные рассуждения приводят к ожидаемому выводу: с точки зрения математики нет никаких сомнений в том, что за неограниченное время обезьяны напечатают всего «Гамлета». Любая книга, по сути, лишь конечная последовательность повторяющихся знаков. Бесконечное число обезьян напечатает любую книгу за бесконечное время.

Но с бытовой точки зрения кажется невероятным, что эта задача будет выполнена за конечное время. Какую ценность нам несет знание о том, что обезьяны могут напечатать «Дон Кихота», если для этого им потребуется время, превышающее возраст Вселенной? Чтобы написать хотя бы что-то осмысленное, хотя бы простую фразу, не говоря уже о «Дон Кихоте», обезьянам потребуется невероятно длинный промежуток времени.

Более того, любой физик — эксперт по вопросам термодинамики — скажет, что эта задача возможна математически, но невозможна с точки зрения физики. Вселенная содержит конечное число частиц, и время в ней также конечно. Даже если Вселенная содержит гугол частиц (это число придумал девятилетний племянник математика Эдварда Казнера, оно равняется 10¹⁰⁰), а Большой взрыв произошел 10 миллиардов лет назад, и даже если число обезьян будет равно числу частиц во всей Вселенной, вероятность того, что обезьяны за это время напечатают «Гамлета», будет ничтожно мала.

Аргентинский писатель Хорхе Луис Борхес описал огромную библиотеку, в каждой книге которой ровно 410 страниц.

Рассказ Борхеса «Всемирная библиотека» намного поэтичнее, и с ним не сравнится никакое описание автора этой книги. Процитируем фрагмент этого произведения, в котором изображена эта удивительная библиотека:

«В ее слепых томах заключено все. Буквально все: скрупулезная история будущего, “Египтяне” Эсхила, точное число раз, когда воды Ганга отражали полет сокола, хранимое в тайне подлинное имя Рима, энциклопедия, которую мог бы создать Новалис, мои сны и полусны утром четырнадцатого августа 1924 года, разгадка теоремы Пьера Ферма, ненаписанные главы “Эдвина Друда”, те же главы в переводе на язык племени гарамантов, парадоксы о природе Времени, придуманные и не опубликованные Беркли, железные книги Уризена, отроческие эпифании Стивена Дедала, к смыслу которых подступятся лет через тысячу, гностическое Евангелие Василида, песни сирен, точнейший каталог Библиотеки, справочник неточностей этого каталога. Буквально все, но на одну осмысленную строку или достоверное свидетельство здесь будут приходиться миллионы безумных какофоний, груды словесного мусора и неразберихи. Буквально все, но пройдут поколения людей, прежде чем головокружительные полки — полки, затмившие свет и приютившие хаос, — подарят им хоть одну связную страницу».

(Хорхе Луис Борхес, «Всемирная библиотека»)

Бесконечные знаки числа π

Все, о чем мы только что рассказали, достаточно интересно и при этом не так далеко от числа π и его бесконечных знаков, как может показаться. Если вместо обычных пишущих машинок в нашем мысленном эксперименте дать обезьянам цифровые клавиатуры, то мы получим более или менее произвольные последовательности цифр. Один очень длинный ряд цифр. А что такое π, как не длинный ряд цифр?

В библиотеке, описанной Борхесом, могут храниться книги, где вместо литературных шедевров (большая часть из которых представляет собой лишь бессмысленную последовательность знаков) будут напечатаны последовательности цифр, имеющие начало и конец.

Но существует принципиальная разница между нашим мысленным экспериментом с печатными машинками, библиотекой Борхеса и последовательностью цифр числа π. Различие в том, что в первом случае речь идет о книгах или текстах конечной длины, а число знаков π бесконечно.

Ни одна обезьяна в нашем эксперименте не сможет напечатать π и ни одна библиотека, сколь велика бы она ни была, не сможет вместить число π и все его знаки. Мы мельком взглянули на бесконечность, но бесконечность, заключенная в числе π, смотрит на нас — невозмутимая, недоступная.

Недоказуемая нормальность числа π

Является ли π нормальным числом? Парадоксально, но этим вопросом, на который пока нет ответа, задаются многие математики. Говорят, что иррациональное число является нормальным в десятичной системе счисления, если в его десятичной записи цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 встречаются с одинаковой частотой. Это же справедливо для последовательностей из двух цифр от 00 до 99, из трех цифр от ООО до 999 и так далее.

Если число является нормальным во всех системах счисления, говорят, что оно является абсолютно нормальным.

Когда японский специалист Канада вычислил триллион знаков π, он подсчитал, сколько раз встретилась каждая цифра:

Десятичная цифра ∙ Частота среди первого триллиона знаков π

0 ∙ 99 999 485 134

1 ∙ 99 999 945 664

2 ∙ 100 000 480 057

3 ∙ 99 999 787 805

4 ∙ 100 000 357 857

5 ∙ 99 999 671 008

6 ∙ 99 999 807 503

7 ∙ 99 999 818 723

8 ∙ 100 000 791469

9 ∙ 99 999 854 780

Итого

1000 000 000 000

Распределение цифр, продемонстрированное Канадой, показывает, что π не является нормальным, хотя анализ первого триллиона знаков может показаться недостаточным.

Одно дело — предполагать, другое — доказать. Нормальность числа π, несмотря на все предположения, доказать пока не удалось.

Фактически не доказана нормальность ни одного из этих чисел: π, е, √2, log2, ни даже числа, описывающего золотое сечение (Ф).

Ниже мы приведем примеры чисел, о которых достоверно известно, что они являются нормальными, но эти числа были специально созданы человеческим гением. В 1917 году польский математик Вацлав Серпинский (1882–1969) нашел первое нормальное число.

Так называемая константа Хайтина

Ω = 0,00787499699…

является вероятностью того, что случайно выбранная программа на машине Тьюринга остановится. Ее определение достаточно сложно. Чтобы понять его, необходимо знать, как работают сумматоры, как обрабатываются биты программы, каков принцип действия машины Тьюринга и многое другое. Ω является нормальным числом, пусть даже его определение заставляет предполагать обратное.

Нормальные числа встречаются не так уж редко: их количество бесконечно. Число элементов множества нормальных чисел соизмеримо с количеством вещественных чисел. Почти все числа являются нормальными, но их очень сложно обнаружить математически. Предполагается, что любое алгебраическое иррациональное число является нормальным.

Недостаточная случайность числа π

Знаки π кажутся случайными, но это только кажущаяся случайность. Специалисты по числу π братья Чудновские провели все возможные проверки случайности знаков π, и все они были пройдены успешно. Случайным числам пытались дать точное определение различными способами и на протяжении длительного времени. В итоге наиболее корректным было признано определение Андрея Колмогорова, который сделал упор не на случайности, а на сложности. По Колмогорову, число тем сложнее, чем длиннее программа, необходимая для описания этого числа. Очевидно, что если кратчайший алгоритм или процесс описания числа столь же велик, как и само число, то это число должно быть очень сложным (или случайным). Если для расчета N нужно дать инструкции, по размерам сопоставимые с самим N, то речь идет об очень сложном, случайном числе.

АНДРЕЙ КОЛМОГОРОВ (1903–1987)

Андрей Колмогоров родился в Тамбове. Его мать умерла при родах, отца отправили в ссылку за участие в революционном движении, и мальчика воспитывали сестры матери. Уже в 1930-е годы он стал известен в мировых математических кругах благодаря публикации «Основных понятий теории вероятностей», где заложил фундамент этого раздела математики. Его известность возросла еще больше, когда вместе с одним из учеников, Владимиром Арнольдом (1937–2010), он решил тринадцатую проблему Гильберта (в 1900 году Давид Гильберт, лучший математик мира того времени, опубликовал список из 23 крупнейших задач математики, не решенных на тот момент). Среди разделов математики, которым Колмогоров уделял наибольшее внимание, отметим теорию случайных процессов и цепи Маркова. Его важнейшим вкладом в науку стала теория сложности, или теория вероятностей, — по сути, две стороны одной медали. В последние годы жизни, став непререкаемым авторитетом российской математики, он занимался этими теориями и прикладной математикой.

* * *

Это не выполняется для числа π, так как существуют конечные и относительно простые алгоритмы по расчету его знаков, причем отдельных знаков, находящихся на определенных позициях. Получается, что число π не может быть абсолютно случайным. Например, существует программа из 158 символов, позволяющая рассчитать 2400 знаков π. Проще говоря, можно сказать, что π является случайным, но не абсолютно случайным.

Последовательность знаков π кажется нам подчиненной воле случая. До сих пор не найден образец или эталон, который позволил бы определить, какая цифра находится на данной конкретной позиции. Да, для этого существуют алгоритмы, использующие формулу ВВР и аналогичные, но не существует никакого эталона или образца. Предполагается, что π является «не абсолютно случайным», но доказательство этому до сих пор не найдено.

Если бы любая последовательность знаков π была случайной, π являлось бы нормальным числом. Но обратное в общем случае неверно: число может быть нормальным и очевидно не являться случайным. Так называемое число Чамперноуна, о котором мы поговорим несколько позже, является нормальным, но не случайным, так как способ его построения объясняется несколькими словами.

Недоступная универсальность числа π

Ограничимся десятичной системой счисления для простоты рассуждений. Будем называть число универсальным, если его можно представить в виде десятичной дроби, в записи которой содержатся все возможные последовательности цифр. Если мы каким-либо способом преобразуем цифры в буквы, то в записи числа π будет содержаться «Гамлет», «Дон Кихот», эта книга или любая из книг всемирной библиотеки Борхеса, диссертации и их опровержения, научные труды и их копии, отличающиеся от оригинала на единственную букву, бессмысленные наборы букв и длинные последовательности повторяющихся символов. Все это будет содержаться в записи числа π и будет вечно ожидать своего читателя.

Вернемся ненадолго к Карлу Сагану и его роману «Контакт». В этом романе инопланетяне поручают доктору Эрроуэй найти некое сообщение предположительно божественного происхождения, которое с момента появления Вселенной зашифровано в самой природе, точнее в знаках π (причем записанных по основанию И, но не будем углубляться в детали). Начиная с определенного знака, спустя много миллионов цифр после запятой, цифры складываются в четкую последовательность из нулей и единиц. Если расположить их определенным образом, то получится изображение квадрата со вписанной в него окружностью. Является ли существование подобного квадрата доказательством существования Творца?

Если сложить первые 20 цифр π, получим 100. Если сложить первые 144 цифры, получим апокалиптическое число зверя 666 из «Откровения Иоанна Богослова». Но мы не вправе считать подобные совпадения проявлением чего-то высшего, поскольку они зависят от выбранной системы счисления, которая целиком и полностью придумана человеком.

Так, Дэвид Чамперноун (1912–2000) придумал нормальное число по основанию 10. Он обнаружил это число в 21 год, еще не закончив обучение. Это пример трансцендентного числа, которое одновременно является нормальным и универсальным. Оно определяется очень просто: достаточно записать по порядку все натуральные числа:

С₁₀ = 0,123456789101112131415161π81920212223…

Нет никаких сомнений, что это число является универсальным, так как в десятичной записи числа Чамперноуна встречается любая последовательность из N цифр. Оно обозначается С₁₀, где 10 означает десятичную систему счисления. Кроме этого, существует бесконечное множество вариантов С₁₀, обладающих теми же свойствами.

Оставим дальнейшее рассмотрение этого вопроса читателю в качестве упражнения. Следует добавить, что так называемое число Коупленда — Эрдёша, формируемое аналогичным способом, но только из простых чисел, также является нормальным (по основанию 10):

0,235711131719232931…

С определенной точки зрения особенность числа π, о которой пишет Саган, не является чем-то уникальным. Числа, содержащие в себе круг, образованный нулями и единицами, встречаются не так уж редко. Фактически существует бесконечное множество таких чисел, но они не связывают между собой длину и диаметр окружности.

Является ли π универсальным числом? Неизвестно. Известно лишь, что все универсальные числа являются нормальными, но это нисколько не помогает найти ответ на этот вопрос.

Что можно и что нельзя доказать

Чешский математик и логик Курт Гёдель (1906–1978) доказал утверждение, которое смущает умы и ставит пределы человеческому знанию. Представим логическую систему с теоремами и аксиомами, которая также описывает элементарные арифметические операции. Например, это может быть обычная математика. Можно ли представить, что она содержит противоречие? «Что за ерунда!» — скажет большинство. Возможно ли, что она является неполной? Может ли она содержать формулы, которые нельзя ни доказать, ни опровергнуть методами этой логической системы? Большинство также скажет, что это невозможно. Как может быть неполной область знаний, содержащая правила элементарной арифметики? Любая теорема верна либо неверна. Возможно, чтобы окончательно узнать это для некоторых теорем, потребуется много времени, но однажды они будут доказаны либо опровергнуты. Наглядный пример этому — теорема Ферма: прошло несколько веков, прежде чем было получено ее доказательство.

Гёдель доказал, что любая формальная система является неполной или противоречивой и не может являться полной и непротиворечивой одновременно. Если она является полной и любое утверждение в ней можно доказать или опровергнуть, то какое-то из ее положений противоречиво. Если же система не содержит противоречий, то, по Гёделю, она является неполной. Всегда будет существовать утверждение, которое нельзя будет доказать или опровергнуть.

КОНТИНУУМ-ГИПОТЕЗА

Георг Кантор провел большую часть жизни в попытках доказать гипотезу, которую можно сформулировать так: пусть А — счетное множество, кардинальное число которого равно Х₀. Определим как кардинальное число Ф(А), где Ф(А) является множеством подмножеств А:

|Ф(А)| = Х₁

Обозначим количество вещественных чисел, или кардинальное число множества вещественных чисел, за с и назовем его континуумом. Кантор пришел к следующему неравенству:

Х₀ < c < Х₁.

Он был точно уверен, что между Х₀ и Х₁ не может находиться никакого кардинального числа, так как с = Х₁. Это так называемая континуум-гипотеза.

В 1963 году американский математик Пол Коэн (1934–2007) доказал, что эта гипотеза является недоказуемой, поэтому ее можно считать истинной или ложной. При этом в общей математике ничего не изменится.

* * *

Гёдель поставил нас в очень интересное положение. Бертран Рассел в шутку говорил, что чистая математика — это такой предмет, где мы не знаем, о чем мы говорим, и не знаем, истинно ли то, что мы говорим. Рёдель окончательно испортил дело. Мы также не знаем, сможем ли мы когда-либо что-либо доказать. Теорема Гёделя не выдумка, так как уже найдены некоторые недоказуемые утверждения, среди которых — континуум-гипотеза.

Очевидно, что недоказуемые утверждения не следует искать среди общеупотребительных. Если недоказуемость какого-либо утверждения как-то повлияет на другие области стандартной математики (яркий пример — теорема Ферма), то маловероятно, что мы имеем дело с гёделевским утверждением.

Вспомним последние вопросы, которые перед нами поставило число π. Есть ли на них ответ? На данный момент нет. Будет ли он получен в будущем? Возможно.

Мы не заявляем, что многие утверждения о π являются недоказуемыми. Многие полагают, что эти утверждения будут недоказуемы, если их доказательство или опровержение не повлияет на «стандартную» математику.

Допустим, что некоторые утверждения о числе π связаны с бесконечностью — весьма тонкой областью, расположенной на переднем рубеже математики. Именно в этой области выводы Гёделя уже получили подтверждение.

КУРТ ГЁДЕЛЬ (1906–1978)

Этот американский математик чешского происхождения специализировался на логике. В Европе он участвовал в семинарах Венского кружка. Эмигрировал в США из-за растущей угрозы нацизма. Известность ему принесла публикация «О формально неразрешимых предложениях Principia mathematica и родственных систем». Его работы настолько сложны для неспециалистов, что научно-популярная книга Эрнеста Нагеля «Доказательство Гёделя» более известна, чем оригинальный труд Гёделя. В этом труде представлены теоремы о неполноте, которые гласят, что формальная система, в которой можно определить основные арифметические понятия, не может быть одновременно полной и непротиворечивой. Он также доказал, что внутри такой системы есть аксиомы, недоказуемые в рамках этой системы. Оба вывода до сих пор не перестают вызывать смущение и ограничивают математику в той же мере, в какой принцип неопределенности Гейзенберга ограничивает физику.

Этот и другие результаты сделали Гёделя почти легендарной фигурой среди ученых всего мира. Книга Дугласа Роберта Хофштадтера «Гёдель, Эшер, Бах: эта бесконечная гирлянда» стала бестселлером.

На протяжении всей жизни Гёдель страдал от депрессии и паранойи, что в конечном итоге привело к его смерти. Эта история больше напоминает приключенческий роман: Гёдель соглашался есть только то, что сперва пробовала его жена, поэтому когда она заболела и ее положили в больницу, он отказался принимать пищу и в итоге умер от истощения.

Курт Гёдель и Альберт Эйнштейн в Институте перспективных исследований в Принстоне, Нью-Джерси.

Глава 7 Первые 10 000 знаков числа π

Пока не вычисленные знаки π дремлют в таинственном абстрактном мире, наслаждаясь зыбкой реальностью. Пока они не вычислены, они не полностью реальны, но даже и тогда их реальность будет лишь относительна.

Уильям Джеймс

π = 3, : число знаков

1415926535 8979323846 2643383279 5028841971 6939937510: 50

5820974944 5923078164 0628620899 8628034825 3421170679: 100

8214808651 3282306647 0938446095 5058223172 5359408128: 150

4811174502 8410270193 8521105559 6446229489 5493038196: 200

4428810975 6659334461 2847564823 3786783165 2712019091: 250

4564856692 3460348610 4543266482 1339360726 0249141273: 300

7245870066 0631558817 4881520920 962829254 09171536436: 350

7892590360 0113305305 4882046652 1384146951 9415116094: 400

3305727036 5759591953 0921861173 8193261179 3105118548: 450

0744623799 6274956735 1885752724 8912279381 8301194912: 500

9833673362 4406566430 8602139494 6395224737 1907021798: 550

6094370277 0539217176 2931767523 8467481846 7669405132: 600

0005681271 4526356082 7785771342 7577896091 7363717872: 650

1468440901 2249534301 4654958537 1050792279 6892589235: 700

4201995611 2129021960 8640344181 5981362977 4771309960: 750

5187072113 4999999837 2978049951 0597317328 1609631859: 800

5024459455 3469083026 4252230825 3344685035 2619311881: 850

7101000313 7838752886 5875332083 8142061717 7669147303: 900

5982534904 2875546873 1159562863 8823537875 9375195778: 950

1857780532 1712268066 1300192787 6611195909 2164201989: 1000

3809525720 1065485863 2788659361 5338182796 8230301952: 1050

0353018529 6899577362 2599413891 2497217752 8347913151: 1100

5574857242 4541506959 5082953311 6861727855 8890750983: 1150

8175463746 4939319255 0604009277 0167113900 9848824012: 1200

8583616035 6370766010 4710181942 9555961989 4676783744: 1250

9448255379 7747268471 0404753464 6208046684 2590694912: 1300

9331367702 8989152104 7521620569 6602405803 8150193511: 1350

2533824300 3558764024 7496473263 9141992726 0426992279: 1400

6782354781 6360093417 2164121992 4586315030 2861829745: 1450

5570674983 8505494588 5869269956 9092721079 7509302955: 1500

3211653449 8720275596 0236480665 4991198818 3479775356: 1550

6369807426 5425278625 5181841757 4672890977 7727938000: 1600

8164706001 6145249192 1732172147 7235014144 1973568548: 1650

1613611573 5255213347 5741849468 4385233239 0739414333: 1700

4547762416 8625189835 6948556209 9219222184 2725502542: 1750

5688767179 0494601653 4668049886 2723279178 6085784383: 1800

8279679766 8145410095 3883786360 9506800642 2512520511: 1850

7392984896 0841284886 2694560424 1965285022 2106611863: 1900

0674427862 2039194945 0471237137 8696095636 4371917287: 1950

4677646575 7396241389 0865832645 9958133904 7802759009: 2000

9465764078 9512694683 9835259570 9825822620 5224894077: 2050

2671947826 8482601476 9909026401 3639443745 5305068203: 2100

4962524517 4939965143 1429809190 6592509372 2169646151: 2150

5709858387 4105978859 5977297549 8930161753 9284681382: 2200

6868386894 2774155991 8559252459 5395943104 9972524680: 2250

8459872736 4469584865 3836736222 6260991246 0805124388: 2300

4390451244 1365497627 8079771569 1435997700 1296160894: 2350

4169486855 5848406353 4220722258 2848864815 8456028506: 2400

0168427394 5226746767 8895252138 5225499546 6672782398: 2450

6456596116 3548862305 7745649803 5593634568 1743241125: 2500

1507606947 9451096596 0940252288 7971089314 5669136867: 2550

2287489405 6010150330 8617928680 9208747609 1782493858: 2600

9009714909 6759852613 6554978189 3129784821 6829989487: 2650

2265880485 7564014270 4775551323 7964145152 3746234364: 2700

5428584447 9526586782 1051141354 7357395231 1342716610: 2750

2135969536 2314429524 8493718711 0145765403 5902799344: 2800

0374200731 0578539062 1983874478 0847848968 3321445713: 2850

8687519435 0643021845 3191048481 0053706146 8067491927: 2900

8191197939 9520614196 6342875444 0643745123 7181921799: 2950

9839101591 9561814675 1426912397 4894090718 6494231961: 3000

5679452080 9514655022 5231603881 9301420937 6213785595: 3050

6638937787 0830390697 9207734672 2182562599 6615014215: 3100

0306803844 7734549202 6054146659 2520149744 2850732518: 3150

6660021324 3408819071 0486331734 6496514539 0579626856: 3200

1005508106 6587969981 6357473638 4052571459 1028970641: 3250

4011097120 6280439039 7595156771 5770042033 7869936007: 3300

2305587631 7635942187 3125147120 5329281918 2618612586: 3350

7321579198 4148488291 6447060957 5270695722 0917567116: 3400

7229109816 9091528017 3506712748 5832228718 3520935396: 3450

5725121083 5791513698 8209144421 0067510334 6711031412: 3500

6711136990 8658516398 3150197016 5151168517 1437657618: 3550

3515565088 4909989859 9823873455 2833163550 7647918535: 3600

8932261854 8963213293 3089857064 2046752590 7091548141: 3650

6549859461 6371802709 8199430992 4488957571 2828905923: 3700

2332609729 9712084433 5732654893 8239119325 9746366730: 3750

5836041428 1388303203 8249037589 8524374417 0291327656: 3800

1809377344 4030707469 2112019130 2033038019 7621101100: 3850

4492932151 6084244485 9637669838 9522868478 3123552658: 3900

2131449576 8572624334 4189303968 6426243410 7732269780: 3950

2807318915 4411010446 8232527162 0105265227 2111660396: 4000

6655730925 4711055785 3763466820 6531098965 2691862056: 4050

4769312570 5863566201 8558100729 3606598764 8611791045: 4100

3348850346 1136576867 5324944166 8039626579 7877185560: 4150

8455296541 2665408530 6143444318 5867697514 5661406800: 4200

7002378776 5913440171 2749470420 5622305389 9456131407: 4250

1127000407 8547332699 3908145466 4645880797 2708266830: 4300

6343285878 5698305235 8089330657 5740679545 7163775254: 4350

2021149557 6158140025 0126228594 1302164715 5097925923: 4400

0990796547 3761255176 5675135751 7829666454 7791745011: 4450

2996148903 0463994713 2962107340 4375189573 5961458901: 4500

9389713111 7904297828 5647503203 1986915140 2870808599: 4550

0480109412 1472213179 4764777262 2414254854 5403321571: 4600

8530614228 8137585043 0633217518 2979866223 7172159160: 4650

7716692547 4873898665 4949450114 6540628433 6639379003: 4700

9769265672 1463853067 3609657120 9180763832 7166416274: 4750

8888007869 2560290228 4721040317 2118608204 1900042296: 4800

6171196377 9213375751 1495950156 6049631862 9472654736: 4850

4252308177 0367515906 7350235072 8354056704 0386743513: 4900

6222247715 8915049530 9844489333 0963408780 7693259939: 4950

7805419341 4473774418 4263129860 8099888687 4132604721: 5000

5695162396 5864573021 6315981931 9516735381 2974167729: 5050

4786724229 2465436680 0980676928 2382806899 6400482435: 5100

4037014163 1496589794 0924323789 6907069779 4223625082: 5150

2168895738 3798623001 5937764716 5122893578 6015881617: 5200

5578297352 3344604281 5126272037 3431465319 7777416031: 5250

9906655418 7639792933 4419521541 3418994854 4473456738: 5300

3162499341 9131814809 2777710386 3877343177 2075456545: 5350

3220777092 1201905166 0962804909 2636019759 8828161332: 5400

3166636528 6193266863 3606273567 6303544776 2803504507: 5450

7723554710 5859548702 7908143562 4014517180 6246436267: 5500

9456127531 8134078330 3362542327 8394497538 2437205835: 5550

3114771199 2606381334 6776879695 9703098339 1307710987: 5600

0408591337 4641442822 7726346594 7047458784 7787201927: 5650

7152807317 6790770715 7213444730 6057007334 9243693113: 5700

8350493163 1284042512 1925651798 0694113528 0131470130: 5750

4781643788 5185290928 5452011658 3934196562 1349143415: 5800

9562586586 5570552690 4965209858 0338507224 2648293972: 5850

8584783163 0577775606 8887644624 8246857926 0395352773: 5900

4803048029 0058760758 2510474709 1643961362 6760449256: 5950

2742042083 2085661190 6254543372 1315359584 5068772460: 6000

2901618766 7952406163 4252257719 5429162991 9306455377: 6050

9914037340 4328752628 8896399587 9475729174 6426357455: 6100

2540790914 5135711136 9410911939 3251910760 2082520261: 6150

8798531887 7058429725 9167781314 9699009019 2116971737: 6200

2784768472 6860849003 3770242429 1651300500 5168323364: 6250

3503895170 2989392233 4517220138 1280696501 1784408745: 6300

1960121228 5993716231 3017114448 4640903890 6449544400: 6350

6198690754 8516026327 5052983491 8740786680 8818338510: 6400

2283345085 0486082503 9302133219 7155184306 3545500766: 6450

8282949304 1377655279 3975175461 3953984683 3936383047: 6500

4611996653 8581538420 5685338621 8672523340 2830871123: 6550

2827892125 0771262946 3229563989 8989358211 6745627010: 6600

2183564622 0134967151 8819097303 8119800497 3407239610: 6650

3685406643 1939509790 1906996395 5245300545 0580685501: 6700

9567302292 1913933918 5680344903 9820595510 0226353536: 6750

1920419947 4553859381 0234395544 9597783779 0237421617: 6800

2711172364 3435439478 2218185286 2408514006 6604433258: 6850

8856986705 4315470696 5747458550 3323233421 0730154594: 6900

0516553790 6866273337 9958511562 5784322988 2737231989: 6950

8757141595 7811196358 3300594087 3068121602 8764962867: 7000

4460477464 9159950549 7374256269 0104903778 1986835938: 7050

1465741268 0492564879 8556145372 3478673303 9046883834: 7100

3634655379 4986419270 5638729317 4872332083 7601123029: 7150

9113679386 2708943879 9362016295 1541337142 4892830722: 7200

0126901475 4668476535 7616477379 4675200490 7571555278: 7250

1965362132 3926406160 1363581559 0742202020 3187277605: 7300

2772190055 6148425551 8792530343 5139844253 2234157623: 7350

3610642506 3904975008 6562710953 5919465897 5141310348: 7400

2276930624 7435363256 9160781547 8181152843 6679570611: 7450

0861533150 4452127473 9245449454 2368288606 1340841486: 7500

3776700961 2071512491 4043027253 8607648236 3414334623: 7550

5189757664 5216413767 9690314950 1910857598 4423919862: 7600

9164219399 4907236234 6468441173 9403265918 4044378051: 7650

3338945257 4239950829 6591228508 5558215725 0310712570: 7700

1266830240 2929525220 1187267675 6220415420 5161841634: 7750

8475651699 9811614101 0029960783 8690929160 3028840026: 7800

9104140792 8862150784 2451670908 7000699282 1206604183: 7850

7180653556 7252532567 5328612910 4248776182 5829765157: 7900

9598470356 2226293486 0034158722 9805349896 5022629174: 7950

8788202734 2092222453 3985626476 6914905562 8425039127: 8000

5771028402 7998066365 8254889264 8802545661 0172967026: 8050

6407655904 2909945681 5065265305 3718294127 0336931378: 8100

5178609040 7086671149 6558343434 7693385781 7113864558: 8150

7367812301 4587687126 6034891390 9562009939 3610310291: 8200

6161528813 8437909904 2317473363 9480457593 1493140529: 8250

7634757481 1935670911 0137751721 0080315590 2485309066: 8300

9203767192 2033229094 3346768514 2214477379 3937517034: 8350

4366199104 0337511173 5471918550 4644902636 5512816228: 8400

8244625759 1633303910 7225383742 1821408835 0865739177: 8450

1509682887 4782656995 9957449066 1758344137 5223970968: 8500

3408005355 9849175417 3818839994 4697486762 6551658276: 8550

5848358845 3142775687 9002909517 0283529716 3445621296: 8600

4043523117 6006651012 4120065975 5851276178 5838292041: 8650

9748442360 8007193045 7618932349 2292796501 9875187212: 8700

7267507981 2554709589 0455635792 1221033346 6974992356: 8750

3025494780 2490114195 2123828153 0911407907 3860251522: 8800

7429958180 7247162591 6685451333 1239480494 7079119153: 8850

2673430282 4418604142 6363954800 0448002670 4962482017: 8900

9289647669 7583183271 3142517029 6923488962 7668440323: 8950

2609275249 6035799646 9256504936 8183609003 2380929345: 9000

9588970695 3653494060 3402166544 3755890045 6328822505: 9050

4525564056 4482465151 8754711962 1844396582 5337543885: 9100

6909411303 1509526179 3780029741 2076651479 3942590298: 9150

9695946995 5657612186 5619673378 6236256125 2163208628: 9200

6922210327 4889218654 3648022967 8070576561 5144632046: 9250

9279068212 0738837781 4233562823 6089632080 6822246801: 9300

2248261177 1858963814 0918390367 3672220888 3215137556: 9350

0037279839 4004152970 0287830766 7094447456 0134556417: 9400

2543709069 7939612257 1429894671 5435784687 8861444581: 9450

2314593571 9849225284 7160504922 1242470141 2147805734: 9500

5510500801 9086996033 0276347870 8108175450 1193071412: 9550

2339086639 3833952942 5786905076 4310063835 1983438934: 9600

1596131854 3475464955 6978103829 3097164651 4384070070: 9650

7360411237 3599843452 2516105070 2705623526 6012764848: 9700

3084076118 3013052793 2054274628 6540360367 4532865105: 9750

7065874882 2569815793 6789766974 2205750596 8344086973: 9800

5020141020 6723585020 0724522563 2651341055 9240190274: 9850

2162484391 4035998953 5394590944 0704691209 1409387001: 9900

2645600162 3742880210 9276457931 0657922955 2498872758: 9950

4610126483 6999892256 9596881592 0560010165 5256375678: 10000

Библиография

BECKMANN, P., A History of Pi, Nueva York, St. Martin’s Griffin, 1976. Existe una edition alemana de 2004.

BLATNER, D., The Joy of Pi, Nueva York, Walker and Company, 1999.

DELAHAYE, J.-P., Le Fascinant Nombre Pi, Paris, Belin-Pour la Science, 2001.

PISA Men£ndez, P., La cuadratura del circulo: geodesia у metrologia en el mundo antiguo, Oviedo, Cincopiedras, 2007.

POSAMENTER, A. у LEHMAN, I., La proportion transcendental. La historia de Pi, el niimero mas misterioso del mundo, Barcelona, Ariel, 2006.

TORIJA HERRERA, R., Arquimedes: alrededor del circulo, Madrid, Nivola, 1999.

* * *

_{Научно-популярное издание}

_{Выходит в свет отдельными томами с 2014 года}

_{Мир математики}

_{Том 7}

_{Хоакин Наварро}

_{Секреты числа π. Почему неразрешима задача о квадратуре круга}

_РОССИЯ

_{Издатель, учредитель, редакция:}

_{ООО «Де Агостини», Россия Юридический адрес: Россия, 105066, г. Москва, ул. Александра Лукьянова, д. 3, стр. 1}

_{Письма читателей по данному адресу не принимаются.}

_{Генеральный директор: Николаос Скилакис}

_{Главный редактор: Анастасия Жаркова}

_{Старший редактор: Дарья Клинг}

_{Финансовый директор: Наталия Василенко}

_{Коммерческий директор: Александр Якутов}

_{Менеджер по маркетингу: Михаил Ткачук}

_{Менеджер по продукту: Яна Чухиль}

_{Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт www.deagostini.ru, по остальным вопросам обращайтесь по телефону бесплатной горячей линии в России:}

_{8-800-200-02-01 Телефон горячей линии для читателей Москвы:}

_{в 8-495-660-02-02}

_{Адрес для писем читателей:}

_{Россия, 170100, г. Тверь, Почтамт, а/я 245,}

_{«Де Агостини», «Мир математики»}

_{Пожалуйста, указывайте в письмах свои контактные данные для обратной связи (телефон или e-mail).}

_{Распространение:}

_{ООО «Бурда Дистрибьюшен Сервисиз»}

_{УКРАИНА}

_{Издатель и учредитель:}

_{ООО «Де Агостини Паблишинг» Украина Юридический адрес: 01032, Украина, г. Киев, ул. Саксаганского, 119}

_{Генеральный директор: Екатерина Клименко}

_{Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт www.deagostini.ua, по остальным вопросам обращайтесь по телефону бесплатной горячей линии в Украине:}

_{0-800-500-8-40}

_{Адрес для писем читателей:}

_{Украина, 01033, г. Киев, а/я «Де Агостiнi»,}

_{«Мир математики»}

_{Украiна, 01033, м. Киiв, а/с «Де Агоспт»}

_{БЕЛАРУСЬ}

_{Импортер и дистрибьютор в РБ:}

_{ООО «Росчерк», 220037, г. Минск, ул. Авангардная, 48а, литер 8/к, тел./факс: +375 17 331 94 27 Телефон «горячей линии» в РБ:}

_{+ 375 17 279-87-87 (пн-пт, 9.00–21.00)}

_{Адрес для писем читателей:}

_{Республика Беларусь, 220040, г. Минск, а/я 224, ООО «Росчерк», «Де Агостини»,}

_{«Мир математики»}

_{КАЗАХСТАН}

_{Распространение:}

_{ТОО «КГП «Бурда-Алатау Пресс»}

_{Издатель оставляет за собой право увеличить рекомендуемую розничную цену книг. Издатель оставляет за собой право изменять последовательность заявленных тем томов издания и их содержание.}

_{Отпечатано в соответствии с предоставленными материалами в типографии:}

_{Grafica Vfcneta S.p.A Via Malcanton 2 35010 Trebaseleghe (PD) Italy Подписано в печать: 07.09.2013 Дата поступления в продажу на территории России: 04.03.2014}

_{Формат 70х100/16. Гарнитура «Academy». Печать офсетная. Бумага офсетная. Печ. л. 4,5. Усл. печ. л. 5,832.}

_{Тираж: 200 000 экз.}

_{© Joaquin Navarro, 2010 (текст)}

_{© RBA Collecionables S.А., 2011 © ООО «Де Агостини», 2014}

_{ISBN 978-5-9774-0682-6 ISBN 978-5-9774-0629-1 (т. 7)}

_{Данный знак информационной продукции размещен в соответствии с требованиями Федерального закона от 29 декабря 2010 г. № 436-Ф3 «О защите детей от информации, причиняющей вред их здоровью и развитию».}

_{Издание для взрослых, не подлежит обязательному подтверждению соответствия единым требованиям, установленным Техническим регламентом Таможенного союза «О безопасности продукции, предназначенной для детей и подростков» ТР ТС 007/2011 от 23 сентября 2011 г. № 797.} 

Оглавление

Предисловие

Глава 1 Все, что вы хотели узнать о числе π, но боялись спросить

Глава 2 Бесконечная незначительность и трансцендентность числа π

Глава 3 Число π и теория вероятностей

Глава 4 Формулы с числом π

Глава 5 Пи-мания

Глава 6 Второй взгляд на бесконечность

Глава 7 Первые 10 000 знаков числа π

Библиография